At the end of last year, a new strain of coronavirus emerged in China, which was called SARS-CoV-2. The virus quickly spread throughout the world, reaching pandemic proportions, and is now considered a worldwide public health emergency. In line with this, several studies aimed to postulate and elucidate possible risk factors involved not only in the genesis of coronavirus disease 2019 (COVID-19) but also in the susceptibility and severity of the condition. Among the most reported elements in patients with a more critical clinical scenario and adverse outcomes is metabolic syndrome (MS), a condition consisting of chronic diseases such as obesity, type 2 diabetes mellitus, dyslipidemia, and systemic arterial hypertension. In this light, this work aims to build a descriptive review of the relationship between the factors inherent to MS and COVID-19, in order to better clarify the mechanisms belonging to this association. Resistance to the action of insulin caused by centripetal obesity is permeated by an environment abundant in pro-inflammatory cytokines, which favors the immune imbalance, leading to the modulation of dysfunctional and inefficient responses. Besides, it is important to mention the overlapping of inflammatory secretory patterns of MS with the cytokine storm of COVID-19, leading to a worse prognosis. SARS-CoV-2 and arterial hypertension share pathways through a common enzyme: ACE2, widely expressed in the respiratory epithelium and belonging to the pressure regulation cascade. However, dyslipidemia promotes higher morbidity and mortality through increased cardiovascular risk due to thrombotic events. In short, MS represents a critical element to be considered through association with COVID-19, since it interferes in greater severity and mortality through several factors.
1.
Introduction
In 2000, Laskin established the nonlinear Schrödinger (NLS) model [18] with fractional Laplacian operator by extending the Feynmann path integral to the Lévy path [17]. The derived equation is more accurate than the traditional NLS equation in describing the variation law of quantum states of nonlocal physical systems with time [16]. In recent, scholars have done a lot of research on the fractional NLS equation in theoretical analysis and numerical algorithms, and achieved fruitful results [11,13,34].
In this paper, we aim to present and analyze high-order schemes with conservation properties for the fractional CNLS equation with periodic boundary conditions that can be written in the form [28]
where i is the imaginary unit root, Ω⊂Rd(d=1,2), ϑ, ζ and ε are real constants, φ(x,t) and ϕ(x,t) are complex valued functions, 1<s≤2, and Ls2 denotes the fractional Laplacian operator and can be expressed by the Fourier transform, namely
where ˆφ(ξ)=∫Ωφ(x)e−iξxdx represents the Fourier transform for φ(x). The fractional CNLS equation will reduce to the classical CNLS equation when s=2. Therefore, similar to the classical system, the fractional CNLS equation with periodic boundary conditions possesses the following physical invariants that do not change with time [30]
where M is the fractional mass, and we refer to H as the fractional Hamiltonian energy.
By setting φ=˜p+i˜q, ϕ=ˆp+iˆq, the original system (1.1), (1.2) can be rewritten as the following real system
According to the variational derivative formula [33], the original fractional CNLS system (1.6)–(1.9) can be expressed by an infinite-dimensional Hamiltonian system
where δH(y)δy is the vector of variational derivatives for y, y=(˜q,ˆq,˜p,ˆp)T, I2 is the second order unit matrix, and
In recent years, some numerical algorithms [15,23,24,37] have been given for solving the fractional NLS equation as explicit analytical solutions of fractional differential equations can not be obtained [10]. However, these traditional algorithms can not inherit the conservative laws of the equation and can not be implemented in long-time numerical calculations. Inspired by the idea of the structure-preserving algorithm of the classical Hamiltonian system, scholars have developed many conservative schemes for the fractional CNLS system. For example, Wang and Xiao [29,30,31] first derived invariants of system (1.1) and (1.2) and constructed finite difference schemes to conserve these invariants; the existence and uniqueness of solutions and convergence of schemes are discussed in these works. In [22,26], Li et al. developed an efficient conservative difference and finite element scheme for solving the strongly fractional CNLS equation. There are many corresponding structure algorithms for fractional NLS-type equations, and the readers can refer to the literature [6,32,35].
Unfortunately, these numerical schemes mentioned above only have second-order accuracy temporally or require small time step sizes to obtain satisfactory numerical solutions for NLS-type equations. Therefore, it is necessary to construct and analyze high-accuracy conservative numerical schemes for the equation. Over the past decade, some numerical methods have been proposed to construct high-accuracy conservative methods for Hamiltonian systems [1,21]. These methods can also be applied to develop high order conservative schemes for fractional NLS-type equations. But, these schemes can both preserve not the mass and energy. Fortunately, some energy quadratic methods exist, including the invariant energy quadratization (IEQ) [9,36] and the scalar auxiliary variable (SAV) approaches [3,25,27], originally developed for gradient flow models. These methods have been applied to construct high-accuracy modified energy-preserving schemes for conservative equations [7,8,14,19,20] by combining with the symplectic Runge-Kutta method [12]. The quadratic auxiliary variable (QAV) approach is newly proposed to construct high-accuracy schemes for the KdV equation [2], the derived schemes can conserve the original energy of the system. This method provides us with a way to construct some numerical schemes that can preserve the original energy of conservative systems. But, the QAV method is not applicable for some equations with complex energy functionals.
As is shown in Eq (1.5), the Hamiltonian energy functional is very complicated and has high degree polynomials, and cannot be handled by introducing a single auxiliary variable. Therefore, the original QAV approach can not be used to construct numerical schemes to inherit the Hamiltonian energy for the equation. Influenced by the idea of the QAV method, we developed a new method which we called the multiple quadratic auxiliary variables (MQAV) approach by introducing more quadratic auxiliary variables and construct conservative schemes for system (1.1), (1.2) based on the symplectic Runge-Kutta method. The constructed schemes can preserve the mass and Hamiltonian energy of the system and have high-accuracy in the temporal direction. In addition, the MQAV approach also can be applied to other conservative systems with complex energy functionals and high degree polynomials.
The following is the outline of this paper. Section 2 gives an equivalent system for the fractional CNLS equation by introducing two quadratic auxiliary variables. Section 3 applies the symplectic Runge-Kutta method to the equivalent system in the time direction can derive a conservative semi-discrete scheme, and discusses the scheme's conservation properties. Section 4 uses the Fourier pseudo-spectral method to approximate the semi-discrete system to obtain a fully-discrete conservative scheme and gives the proposed schemes' stability. In Section 5, numerical results are displayed to illustrate the theoretical results. The final section contains some conclusions.
2.
Multiple quadratic auxiliary variable system
We first derive an equivalent system for the fractional CNLS system based on the idea of the MQAV method.
By setting u=|φ|2, v=|ϕ|2, the original Hamiltonian energy can be rewritten as
Considering the following initial conditions
and taking the variational derivative for the new energy Eq (2.1), the original fractional CNLS system (1.1), (1.2) can be rewritten as the following equivalent MQAV system
here (∗,∙):=∫Ω∗ˉ∙dx, ˉ∙ is the conjugate of ∙, Re(∗) represents taking the real part of ∗.
Theorem 2.1. The newly proposed MQAV system can inherit some invariants, namely
where
and M(t), E(t) are given in Eqs (1.4) and (2.1), respectively.
Proof. First, system (2.4), (2.5) can be rewritten as
and adding the above two formulas we can derive
Then, we compute the inner products of equation (2.2), (2.3) with φ and ϕ, and take the imaginary part of the derivation, leading to
Further, by computing the inner products of system (2.2)–(2.5) with φt,ϕt,u,v, respectively, we derive
Remark 2.1. It is worth noting that the equivalent MQAV system not only preserves the modified energy and mass but also conserves a new invariant I(t), which implies the modified energy E(t) is equivalent to the original Hamiltonian energy H(t) in the continuous case. For the constructed new system, the auxiliary variables relation can be regarded as weak properties, while the original energy reduces to a weak invariant [12].
3.
Conservative semi-discrete MQAV-RK scheme
We all know that the construction of the high-accuracy conservative schemes for the fractional CNLS equation is challenging. Fortunately, the MQAV system (2.2)–(2.5) can preserve the quadratic conserved quantities. This allows us to use the symplectic RK method that can conserve the system's quadratic invariants to construct a high-order accuracy conservative scheme for the fractional CNLS equation. First, we outline some notations of the symplectic RK method.
3.1. Symplectic RK methods
We consider the following ordinary differential equation
We define τ=TN as the time step, and set tn=nτ, n=0,1,⋯,N. An s-stage RK method for system (3.1) in [tn,tn+1] is given by
where aij,bi, ci=s∑i=1aij (i,j=1,2,⋯,s) are real coefficients. If these coefficients have the following relationship
the proposed RK method is called as the symplectic RK method [12].
3.2. Semi-discrete high-order conservative scheme
To develop a high-order conservative scheme for the MQAV system that preserves some quadratic invariants in the time direction, a natural idea is to use the symplectic RK method to approximate system (2.2)–(2.5). The resulting semi-discrete RK scheme is given as follows
Then (φn+1,ϕn+1,un+1,vn+1)T can be updated by
where zn represents the numerical approximation to z(⋅,t) and tn for any function z. For the semi-discrete scheme, we can derive the following theorem for the structure-preserving properties.
Theorem 3.1. The system (3.5), (3.6) can inherit the following invariants, i.e.,
where Mn is the mass function and is defined by
and
En is the energy function, which has the form
Proof. According to system (3.6) and the definition of Mn, we have
Plugging kiφ=−i(ϑLs2φin−ζ(uin+εvin)φin), kiϕ=−i(ϑLs2ϕin−ζ(vin+εuin)ϕin) into above system, we derive
where symplectic condition (3.4) and s∑i,j=1aijbikikj = s∑i,j=1ajibjkikj were used. Noticing that
and
This together with Eq (3.12) can derive
Then, we further obtain
where the symplectic condition (3.4) and s∑i,j=1aijbikikj = s∑i,j=1ajibjkikj were used. Furthermore, similar discussions, we obtain
Therefore, we derive
Based on the definition of En, we can deduce
The proof is completed.
Then, under the consistent initial condition u0=|φ0|, v0=|ϕ0|, we have the following original energy conservation theorem for the semi-discrete MQAV-RK system.
Theorem 3.2. The MQAV-RK system (3.5), (3.6) can also inherit the original semi-discrete Hamiltonian energy of the fractional CNLS system, namely
where Hn is the original semi-discrete energy function and given by
Proof. Based on Theorem 3.1 and the two introduced quadratic auxiliary variable u=|φ|2, v=|ϕ|2, one can obtain un=|φn|2, vn=|ϕn|2 for 0≤n≤N, which leads to
and we can immediately obtain Hn=H0.
4.
Fully-discrete conservative scheme
4.1. Fourier pseudo-spectral method
The proposed conservative scheme has fourth-order accuracy in time, and the Fourier pseudo-spectral method is chosen to approximate the semi-discrete system in space so that the accuracy of time direction is not affected. We consider system (1.1), (1.2) in a periodic region Ω=[−L,L], and define xj=−L+jh=−L+j2LN,0≤j≤N−1, N is a positive even integer, and h:=2LN. Furthermore, we denote
be a vector space of grid functions with vj=v(xj). Then defining the interpolation space SpN:=span{gj(x)} with
where μ=πL, al={1,|l|<N/2,2,|l|=N/2,. Then, we set IN:L2(Ω)→SpN as the interpolation operator
with
where ˆv−N/2=ˆvN/2. Applying the Laplacian operator Ls2 to INv(x) leads to
where v∈Vh, and
and the discrete Fourier transform and its inverse are given by
It is can be computed by using the FFT technique in long time simulations.
4.2. Conservative Fourier pseudo-spectral scheme
This subsection aims to give a high-order fully-discrete scheme for the Eqs (1.1), (1.2), and the scheme is derived by using the Fourier pseudo-spectral method to approximate equation (3.5), (3.6) in space, namely
Then (φn+1,ϕn+1,un+1,vn+1)T can be updated by
For a fully-discrete scheme, we can derive the following theorem for the structure-preserving properties.
Theorem 4.1. System (4.4), (4.5) can conserve some conservation laws, i.e.,
where Mn is the mass function and defined by
and
and En is the energy function, which has the form
where ⟨⋆,∙⟩=hN−1∑j=0⋆jˉ∙j.
Proof. The proof process is the same as the Theorem 3.1.
In addition, we can also prove the developed schemes can inherit the original Hamiltonian energy.
Theorem 4.2. System (4.4), (4.5) can conserve the original Hamiltonian energy of the fractional CNLS system, namely
where
Remark 4.1. Actually, the QAV method is similar to the IEQ and SAV methods, both of which are energy quadratic methods. Therefore, they can also be used to develop high-order conservative schemes for conservative equations. However, the derived schemes based on the IEQ and SAV methods can only inherit the modified energy [5,8]. Theorem 4.1 and Theorem 4.2 indicate that the constructed high-order MQAV-RK scheme can inherit both the modified energy and the Hamiltonian energy.
According to the mass conservation law of Theorem 4.1, we can conclude that the proposed schemes are stable.
5.
Numerical experiments
We give some examples to confirm the conservation properties and the high-accuracy of the developed schemes. The exact solution of the system is not given, and thus we compute the numerical errors by using the formula
The accuracy of the constructed schemes can be computed by
where τj, errorj,(j=1,2) are the time step and the maximum-norm errors with τj, respectively. Furthermore, to test the conservation properties, we define the relative errors of some invariants as
where Mn, Hn and En denote the invariant at t=nτ. Without losing generality, the paper will consider the following 2s-4th order symplectic RK method [12]
To compare the advantages of the constructed scheme with some conservative schemes, we define
● MQAV-RK4: The constructed fourth-order conservative MQAV-RK scheme in this paper;
● SAV-RK4: The proposed fourth-order conservative RK scheme based on the SAV method [8].
● CN2: The proposed second-order Crank-Nicolson conservative scheme for the Eqs (1.1) and (1.2) [30].
Example 5.1. First, consider a decoupled fractional NLS equation in Ω=(−π,π) with the form
with the exact solution
In the simulation, we take η=2, γ=1, θ=2 to exhibit the theoretical results.
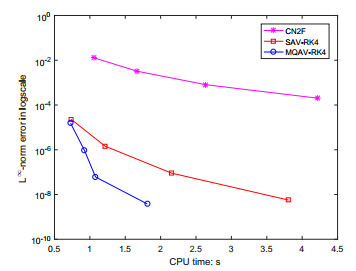
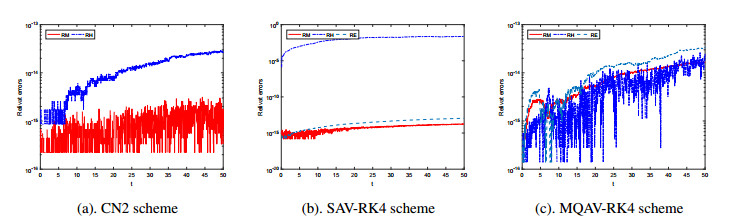
First, we set s=1.6 and T=1 to test the convergence of the given three numerical schemes. The maximum-norm errors and convergence rates are shown in Table 2. The listed data in the table indicate that the MQAV-RK4 and SAV-RK4 both have fourth-order convergence rates in time, and the CN2 scheme only gets second-order accuracy. Furthermore, we investigate the maximum-norm errors of the numerical solution versus the CPU time using the three selected schemes. The results are summarized in Figure 1. For a given global error, we observe that (ⅰ) the cost of the CN2 scheme is the most expensive because of the low-order accuracy in time; (ⅱ) the cost of SAV-RK4 is much cheaper than the CN2 scheme; (ⅲ) the cost of our proposed MQAV-RK4 scheme is the cheapest. We test the conservative properties of four conservative schemes at T=100 by using the denoted formulas in (5.3). Figure 2 reveals relative errors of conservation laws. As is shown above, the SAV-RK4 scheme can only conserve the modified energy and mass of the equation. But, our proposed methods can both inherit the original energy and mass.
Example 5.2. This example considers the fractional CNLS equation with initial conditions [30]
In this example, x∈(−20,20), and we choose δ0=5,ω0=3,ϑ=1,ζ=2, ε=1.
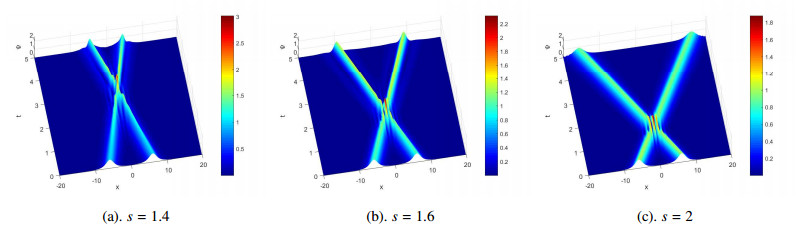
First, Eqs (5.1) and (5.2) are used to compute the L∞−normal and corresponding convergence rate of time for some conservative schemes at T=1. The obtained numerical results are given in Table 3. From Table 3, we can find the MQAV-RK4 scheme has fourth-order convergence. By using the denoted formulas in (5.3), we test the conservative properties of four conservative schemes at T=50. Figure 3 reveals relative errors of conservation laws. As is shown above, the proposed method can both inherit the mass and original energy exactly. Finally, we define Ψ=|φn|+|ϕn| and study the relationship between the evolution of numerical solution and the fractional s. As is shown in Figure 4, the s affects the evolution of solitons, and the shape of the solitons change quickly as s changes.
Example 5.3. In this example, we choose the initial condition
where (x,y)∈[−8,8]2, and, some parameters are given as follows
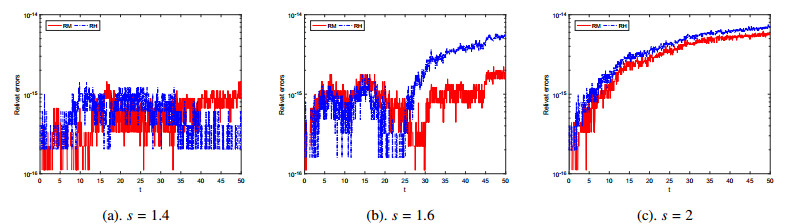
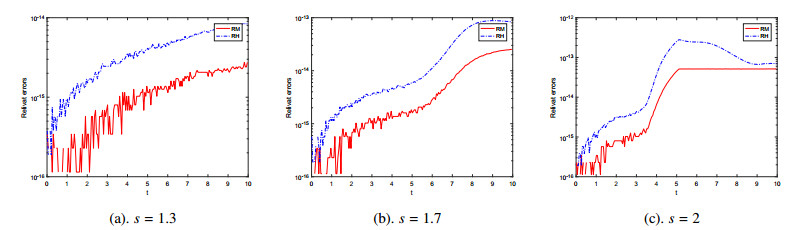
In Table 4, we give the accuracy of the proposed scheme at s=1.3,1.7,2. As is shown in the table, the scheme has fourth-order accuracy in the time direction for different s. In addition, the numerical errors also increase with the increase of s. Figure 5 implies that the scheme can inherit the original energy and mass of the system for different s.
6.
Conclusions
In this paper, we first propose the Hamiltonian structure of the fractional CNLS equation, and then develop the MQAV approach for the fractional CNLS equation with a complex energy function that can not be handled by using the original QAV approach. Then, a class of MQAV-RK schemes is proposed by combining with the symplectic Runge-Kutta method. The constructed schemes have high-accuracy and inherit the mass and Hamiltonian energy. Numerical results also demonstrate that the schemes have good numerical stability. In addition, the approaches presented in this work can be used to solve other conservative differential equations.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The research is supported by the Science Foundation of Henan (No. 212300410323).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: