The rapid increase in the number of cases of corona virus (COVID-19) in 2020 and the lack of effective drug treatment, required the need for social restrictions measures, causing an important impact on the population's physical activity pattern. The decrease in the level of the population's physical activity is not only restricted to the practice of systematic physical exercise, but also the reduction of caloric expenditure with locomotor physical activities, work and leisure. Sedentary lifestyle is associated with an increased risk of the respiratory system infections and with more severe complications as well. On the other hand, systematic physical exercise has a positive effect on the immune system and in reducing the risk of diseases. However, high loads of physical exercise, with an increased amount or intensity, can compromise the immune system's response and increase the risk of respiratory infections. Thus, the aim of the study was to summarize the recommendations for physical exercise during the COVID-19 pandemic, and its relationship between exercise overload and health benefits.
At the end of 2019, a new virus, the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) (COVID-19), causing severe acute respiratory syndrome, expanded globally [1], and significantly changed the patterns of population's physical activity. Due to the recommendations of social isolation and restrictions on daily behaviors, activities with greater energy expenditure has been significantly reduced, changing the population's physical exercise patterns, increasing sedentary lifestyle [2]. Considering the effects of quarantine in reducing the level of physical activity, the World Health Organization published recommendations so that the population can remain physically active [3].
During quarantine levels of physical activity (PA) and exercises suffer a radical change, affecting the person's lifestyle and behaviors. In addition, prolonged quarantine has a negative psychological impact, including symptoms of post-traumatic stress, confusion and anger, related to fear of infection, frustration, boredom, inadequate supplies and information, financial loss and stigma [4]. There is evidence that just a few weeks of physical inactivity is enough to increase risk of cardiovascular disease, reduce muscle mass and produce significant changes in metabolism and in the immune system [5], especially in the elderly population [6].
Additionally to PA level reduction, changes in eating habits and associated negative psychological factors, quarantine increases risk of cardiovascular disease in the entire population and it is related to increased oxidative stress [7]. However, these lifestyle changes can be even more serious in people with cancer and cardiovascular disease (CVD). Patients with cancer and COVID-19, the most serious cardiovascular complications are related to antineoplastic therapy. Patients with CVD, the possible relationship between COVID-19 and the development of acute myocarditis, heart failure and arrhythmias, increases complications risk especially in the elderly with diabetes and hypertension [8]. Thus, the clinical management of these patients must pay special attention to monitoring cardiovascular problems associated with COVID-19 and other traditional cardiovascular problems, both during and after this quarantine period [9].
However, precautions in the physical exercise prescription should not be considered only for patients with severe COVID-19, CVD and risk factors, as there are no studies that indicate that asymptomatic or symptomatic people who have not been hospitalized may have some cardiovascular impairment due to exposure to COVID-19 [10]. Thus, complementary exams for the diagnosis of cardiovascular abnormalities should be considered for physical exercise prescription, including the young population and athletes, who are submitted to high amounts and exercises intensities [11], especially when quarantine period is over and they return to their physical exercise routines.
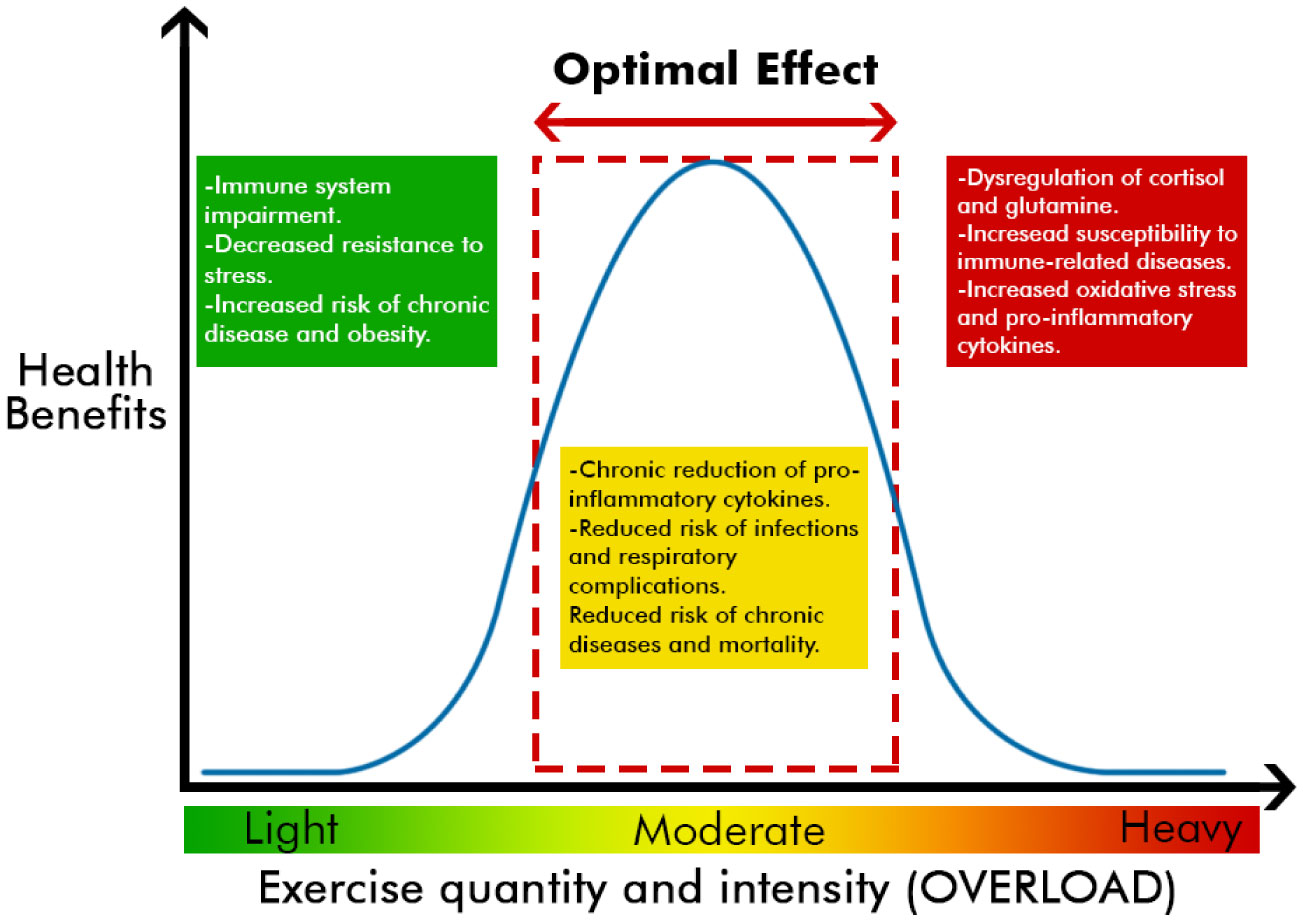
On the other hand, PA and exercise have shown a positive effect in multiple pathological conditions and have demonstrated epidemiological evidence of their preventive/therapeutic benefits, mainly in the elderly population [12]. The immune system is highly responsive to moderate-intensity physical activity and is associated with a lower incidence, duration and severity of respiratory tract infections, as well as in reducing symptoms of depression and anxiety [13]. However, cardiovascular abnormalities due to COVID-19 can compromise the ability to perform physical exercise, requiring greater attention on its prescription [2].
Aerobic exercise is related to improved cardiorespiratory fitness, which can be perceived by a greater oxygen consumption (VO2max) in ergonometric test. The VO2max, has been shown to be an important indicator for risk stratification of surgical complications, interventions and hospital admissions [14]. Although the performance of the oxygen consumption test may not be possible due to the pandemic, it is believed that people with greater cardiorespiratory capacity associated with physical exercise have lower complication risk and a mortality rate by COVID-19. In addition to aerobic capacity, a greater strength performance has also been associated to lower risk of mortality [15].
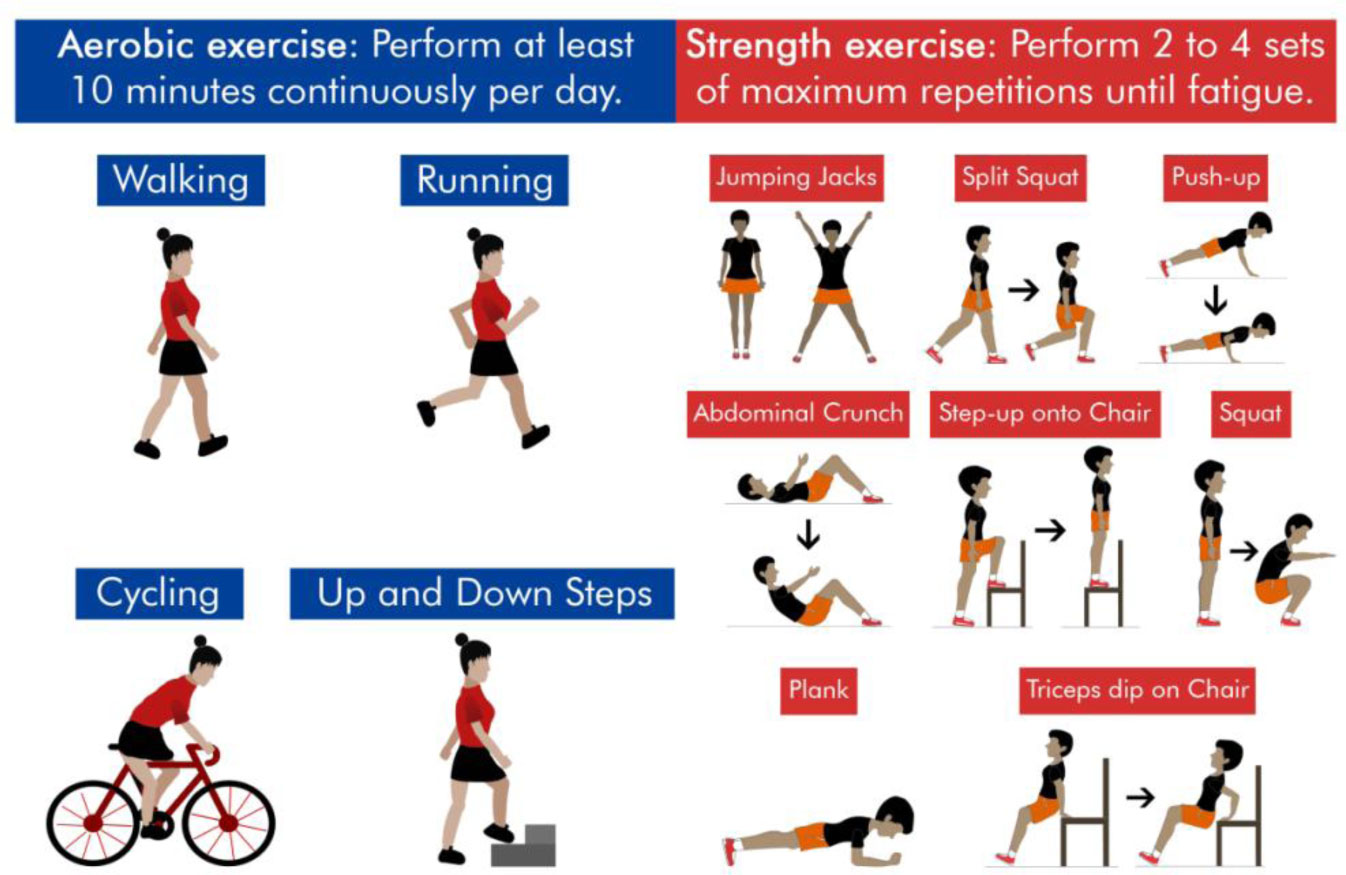
For health promotion, the recommendation is at least 150 minutes per week of aerobic exercise [16], however 10 minutes per day is enough to promote health benefits [17]. Considering the imposed condition of social isolation, aerobic exercises can be performed through walking, cycling or running outdoors, however if the person may not feel comfortable leaving their home, it is possible to perform aerobic exercise stepping up and down continuously for at least 10 minutes daily (Figure 1).
Strength, flexibility and balance exercises are also recommended and should be performed at least twice a week [18]. Although strength and flexibility exercises need attention in the movements' biomechanics, these exercises can be practiced at home and are easily found on the internet, using body weight and objects available at home such as product packages, towels, broomsticks and furniture (Figure 1). It is worth mentioning that for physical exercises at home, both remotely supervised interventions and exercises performed without supervision, they proved to be viable, safe and effective for people with cardiovascular diseases [5].
Because of load limitation imposed by the resources available at home, to perform the strength exercises, it is recommended to perform 2 to 4 series of maximum repetitions. However, when feeling pain symptoms during strength exercise, the load must be reduced or the exercise should be avoided. The minimum number of strength exercise recommended are three exercises per day considering the trunk, upper and lower body.
Considering that drug treatment for SARS-CoV-2 (COVID-19) has not yet been established, body strengthening systems by non-medication means has great relevance [1]. Improving both cardiorespiratory fitness and muscle strength together, may be the most effective strategy to reduce all-cause mortality risk, than separately [19]. Consequently, based on indirect evidence, it appears that moderate physical activity can be recommended as a non-pharmacological, inexpensive and viable way to prevent severe cases of COVID-19 and reduce population's risk of cardiovascular disease. On the other hand, the prescription for more intense exercises should be considered with caution [20] (Figure 2).
There is evidence that high-intensity exercise for a long-term can lead to higher levels of inflammatory mediators, and consequently, may increase the risk of injury and chronic inflammation [21], and immune system suppression, which can cause an increase in susceptibility to respiratory diseases due to the production of oxidants [22].
However, performing the exercise at home may not be an easy task requiring the supervision of a specialist in physical exercise. Nyenhuis et al. (2020) [23] present apps suggestions for physical exercise programs at home, for people who have access to residential equipment and resources and also for those who don't.
Current levels of physical inactivity are due to insufficient frequency in physical activity during free time and to increase sedentary behavior during occupational and domestic activities [24]. It is worth mentioning that sedentary lifestyle and physical inactivity are highly prevalent, and it is estimated that one third of the population does not perform any type of physical exercise [25].
However, this new condition imposed by the pandemic can lead us to two different scenarios of the population's physical activity pattern. The first is related to the activities levels reduction of those who were previously involved in physical exercise programs due to restrictions on access to the practice sites. And the second refer to the population that used to have a sedentary behavior and due to the social isolation aroused interest in this new possibility of exercising at home.
In both scenarios, it is clear that the amount of energy expenditure with non-systematized physical activities related to work, mobility and leisure activities is compromised by the pandemic. Thus, the systematic and planned physical activity used to promote and improve the physical fitness components, represents prevention and health promotion strategy of great relevance. However, habits changes in home routine should also be considered in this situation of social isolation, as they can contribute to the maintenance of the physical activities pattern.









 DownLoad:
DownLoad: