Efficient numerical schemes for variable-order mobile-immobile advection-dispersion equation

1.   Introduction

Fractional differential equations (FDEs) have become an essential mathematical framework for modeling a wide range of complex phenomena, including long-range memory effects, anomalous mechanical dynamics, and advanced control processes. By generalizing classical calculus, fractional calculus enables a more accurate and flexible representation of physical systems that are inadequately captured by traditional integer-order models. This mathematical approach has been successfully applied in various disciplines, including quantitative finance, engineering, biology, chemistry, and hydrology ^[1,2]. Among recent developments, variable-order (VO) fractional calculus has garnered significant attention due to its capacity to describe systems with time- or space-dependent memory characteristics and evolving dynamical behavior ^[3].

In recent years, a wide variety of numerical methods have been developed to solve fractional partial differential equations (FPDEs), which are often analytically intractable due to the nonlocal nature of fractional operators. Among these, finite element methods have been widely applied and rigorously analyzed for various types of time- and space-fractional models ^[4,5,6,7,8]. Finite volume methods have been adopted to handle anomalous transport and advection-diffusion processes with fractional dynamics ^[9,10,11]. Finite difference methods, known for their simplicity and effectiveness, have also been extensively investigated, with significant progress in high-order, compact, and implicit schemes ^{[12,13,14,15,16]}. Spectral and spectral-Galerkin methods offer highly accurate solutions and have demonstrated spectral convergence for a variety of FPDEs ^[17,18,19]. Meshless methods such as radial basis function and local interpolation approaches have emerged as powerful alternatives for multidimensional and complex-geometry problems ^{[20,21,22,23]}. Approximate analytical methods provide efficient solutions by combining analytical and numerical approaches, often using perturbation or homotopy techniques to simplify complex fractional equations ^[24,25,26]. To improve flexibility and accuracy, discontinuous Galerkin methods have been developed for both constant- and variable-order fractional equations ^{[27,28,29,30]}.

The discontinuous Galerkin (DG) method combines the advantages of finite element and finite volume methods. By employing a discontinuous solution space, the DG method provides high accuracy and flexibility in solving a wide range of partial differential equations, including those with complex geometries or discontinuous solutions. This method is particularly effective for approximations of arbitrary order, making it a preferred choice for a variety of computational problems. A key strength of the DG method lies in its ability to handle adaptive meshing and high-order polynomial approximations. Furthermore, the method is supported by rigorous theoretical analysis, including error estimates and stability results.

The time-variable-order (VO) fractional mobile-immobile advection-dispersion equation effectively captures solute transport processes in porous and fractured media, providing a robust framework for studying complex migration phenomena ^[31,32,33]. A comprehensive overview of the physical background and formulation of this model is provided in ^[34,35]. Sadri et al. ^[36] employed a spectral collocation method utilizing sixth-kind Chebyshev polynomials to solve the VO time-fractional mobile-immobile advection equations, demonstrating the efficiency and accuracy of the method. Ma et al. ^[37] introduced the Jacobi spectral collocation method for the variable-order advection-dispersion equation, validating its higher-order convergence through numerical analysis. Liu et al. ^[38] analyzed a second-order finite difference scheme for fractal mobile-immobile transport equations. Golbabai et al. ^[39] applied meshless methods with radial basis functions to approximate solutions for the time-fractional mobile-immobile advection-dispersion model within bounded regions. Zhang et al. ^[40] proposed an implicit Euler method to solve the mobile-immobile advection-dispersion model, rigorously demonstrating its unconditional stability. Jiang et al. ^[41] developed a numerical method based on reproducing kernel theory combined with the collocation method to address the mobile-immobile advection-dispersion model. Saffarian and Mohebbi ^[42] developed a robust numerical scheme for the two-dimensional time-variable-order fractional mobile-immobile advection-dispersion model, proving the unconditional stability of the fully discrete scheme.

In this paper, we propose and analyze a DG method based on generalized alternating numerical fluxes to solve the following variable-order mobile-immobile advection-dispersion equaiton

where $0 < \rho(t) < 1$, $c_1 > 0$, $c_2 > 0$, and $d_1, d_2 > 0$. In this paper, $g$ and $\omega_0$ are assumed to be smooth functions, and the solution is considered to be either periodic or compactly supported.

The variable-order (VO) fractional derivative operator ^[43] is defined in the Caputo sense

where $0 < \rho(t) < 1$.

The mobile-immobile advection-dispersion equation is a fundamental tool for describing solute transport, yet its standard formulation assumes constant-order derivatives, which may not accurately reflect the varying memory effects and heterogeneous diffusion characteristics observed in real-world systems. To address these limitations, we employ a variable-order (VO) fractional derivative, allowing the diffusion process to dynamically adapt to spatial and temporal variations in the medium. The main contributions of this paper are as follows:

(1) A high-order DG scheme with generalized alternating numerical fluxes is presented to efficiently solve the VO fractional mobile-immobile advection-dispersion equation.

(2) The stability and convergence of the proposed scheme are analyzed, ensuring its reliability for practical applications.

(3) Extensive numerical experiments are conducted to validate the theoretical findings and demonstrate the accuracy of the method for the variable-order equation.

In Section 2, the symbols, projections, and theorems required for the proof are introduced. Section 3 presents the construction of the numerical scheme for Eq (1.1) using the LDG method, and it is demonstrated that the scheme is unconditionally stable and convergent with an accuracy of $O(\Delta t + h^{k+1})$. In Section 4, numerical experiments are conducted to validate the effectiveness and reliability of the proposed scheme. Finally, the conclusions are summarized in Section 5.

2.   Notations

The interval $\Omega = [a, b]$ is partitioned into subintervals, denoted by $J$, where $a = x_{\frac{1}{2}} < x_{\frac{3}{2}} < \cdots < x_{N+\frac{1}{2}} = b$. For $j = 1, \dots, N$, each subinterval is defined as $I_j = [x_{j-\frac{1}{2}}, x_{j+\frac{1}{2}}]$, with the element size given by $\Delta x_j = x_{j+\frac{1}{2}} - x_{j-\frac{1}{2}}$. The maximum element size is denoted by $h = \max\limits_{1 \leq j \leq N} \Delta x_j$.

The time interval $[0, T]$ is discretized uniformly into $M$ time steps, such that $\Delta t = \frac{T}{M}$. The discrete time points are given as $t_n = n \Delta t$ for $n = 0, 1, \dots, M$.

At each boundary point $x_{j + \frac{1}{2}}$, the left and right limits of the function $\omega$ are defined as $\omega_{j+\frac{1}{2}}^-$ and $\omega_{j+\frac{1}{2}}^+$, respectively. Specifically, $\omega_{j+\frac{1}{2}}^-$ corresponds to the value in the left cell $I_j$, while $\omega_{j+\frac{1}{2}}^+$ corresponds to the value in the right cell $I_{j+1}$.

The discontinuous Galerkin space $V^k$ is defined as:

where $P^k(I_j)$ denotes the space of polynomials of degree $k$ defined on each subinterval $I_j$.

In the paper, $C$ is used to represent a positive constant, which may take different values in different cases. The inner product on $L^2(D)$ is denoted by $(\cdot, \cdot)_D$, and the associated norm is represented by $\Vert \cdot \Vert_D$. For $D = \Omega$, the subscript is omitted for simplicity.

3.   The scheme

First, we introduce some lemmas that will be used to design the scheme.

Lemma 3.1. ^[1] For $0 < \rho(t) < 1$ and $t > 0$, the left-sided Caputo fractional derivative is defined as

is equivalent to the Riemann-Liouville fractional derivative, expressed as

provided that the condition $h(x, 0) = 0$ is satisfied.

Lemma 3.2. ^[1] (Grünwald formula)

The function space $\Psi^{m+a}(R)$ is defined as

Let $\omega \in \Psi^{1+a}(R)$. It follows that

where $r$ is an integer, and $\theta_j^{\rho(t)}$ is given by

The coefficients $\theta_j^{\rho(t)}$ satisfy the following properties for $0 < \rho(t) < 1$:

Moreover, these coefficients can be evaluated recursively as

Lemma 3.3. There is a constant $\sigma > 0$ such that the following condition holds:

Let $M$ be a positive integer, and define $t_n = \frac{n}{M}T$. The values of $\omega_t$ and $P_{t}^{\rho(t_n)}u$ at $t_n$ are approximated as follows:

where $\gamma_1^n(x)$ represents the truncation error in the approximation of $\omega_t$. Additionally, by applying Lemmas 3.1 and 3.2, it is obtained that

where $\gamma_2^n(x)$ denotes the truncation error associated with the approximation of $P_{t}^{\rho(t_n)}\omega$. The total truncation error in the temporal direction is given by $\gamma^n(x) = \gamma_1^n(x) + \gamma_2^n(x)$, and it satisfies the bound $\Vert \gamma^n(x)\Vert \leq C\Delta t$.

The problem (1.1) can be reformulated into the following system:

Let $\omega_h^n, \; p_h^n \in V^k$ denote the approximations of $\omega(\cdot, t_n)$ and $p(\cdot, t_n)$, respectively, and define $g^n(x) = g(x, t_n)$. The fully discrete scheme is then formulated as follows: find $\omega_h^n, \; p_h^n \in V^k$ such that, for all $v, \mu \in V^k$,

The hat functions in the boundary terms, which arise from the integration by parts in Eq (3.4), are referred to as numerical fluxes. The choice of an appropriate numerical flux plays a critical role in the theoretical analysis of the LDG scheme. From a practical perspective, generalized alternating numerical fluxes offer greater flexibility and broader applicability compared to traditional numerical fluxes ^[44]. The generalized alternating numerical fluxes are defined as follows:

where $\delta \in [0, \frac{1}{2}) \cup (\frac{1}{2}, 1]$. For $\delta = \frac{1}{2}$, the properties related to the uniqueness and approximation of the generalized Gauss-Radau projection become more intricate.

For convenience, we denote

To simplify the analysis, we focus on the case where $g = 0$ in the theoretic analysis.

3.1.   Stability analysis

Theorem 3.1. Suppose that $\omega(x, t) \in C([0, T], H^s(\Omega))$ with $s \geq k+1$. Then, the fully discrete LDG scheme (3.4), with the flux (3.5), is unconditionally stable. Furthermore, $\omega_h^n$ satisfies

Proof. Taking $v = \omega_h^{n}$ and $\mu = d_2p_h^n$ in Eq (3.4) and using the flux choice in Eq (3.5), we derive the following equation:

Next, consider the cell $\mathcal{I}_{j} = [x_{j-\frac{1}{2}}, x_{j+\frac{1}{2}}]$. The term $\Phi_{\mathcal{I}_j}(\omega_h^n, p_h^n; d_2p_h^n, \omega_h^n)$ is computed as:

By summing over $j = 1, \ldots, N$ in Eq (3.9), we observe that all boundary terms cancel out. Therefore, we have:

By Lemma 3.2, we have

Combining Eq (3.10) and the Cauchy-Schwarz inequality, Eq (3.8) becomes

where the last inequality uses Eq (3.11).

Dividing both sides by $\Vert \omega_h^{n}\Vert$, we obtain

To prove the theorem, we use mathematical induction.

For $n = 1$, Eq (3.13) simplifies to

Assume that

Using Eq (3.13), we need to prove that $\Vert \omega_h^{n}\Vert \leq \Vert \omega_h^0\Vert$. Substituting the inductive hypothesis into Eq (3.13), we have

Dividing through by $\frac{c_1}{\Delta t} + \frac{c_2}{(\Delta t)^{\rho(t_n)}}\theta_0^{\rho(t_n)}$, we obtain

By mathematical induction, the inequality holds for all $n$. Hence, the theorem is proved. □

3.2.   Error estimate

First, we introduce the generalized Gauss–Radau projection, which will be used in proving convergence.

For any periodic function $\varpi$ defined on the interval $[a, b]$, the generalized Gauss-Radau projection ^[44], denoted by $\mathcal{Q}_\delta \varpi$, is uniquely determined. Let $\varpi^e = \mathcal{Q}_\delta \varpi - \varpi$ be the corresponding projection error. When $\delta \neq \frac{1}{2}$, the following conditions are satisfied for $j = 1, 2, \ldots, N$:

Based on these conditions, the following result can be established ^[44,45].

Lemma 3.4. Let $\delta \neq \frac{1}{2}$. If $\varpi \in H^{s+1}[a, b]$, the inequality below holds:

where $C > 0$ is a constant independent of $h$ and $\varpi$.

Theorem 3.2. Let $\omega(x, t)\in C([0, T], H^s(\Omega))$, with $s\geq k+1$, denote the exact solution of the problem (1.1), and let $\omega_h^n$ represent the numerical solution obtained using the LDG scheme (3.4). The following error estimate holds

where $C$ is a constant that depends on $u$ and $T$.

Proof.

The terms $\eta_\omega^n$ and $\eta_p^n$ are estimated using inequality (3.4).

Starting from the flux expression (3.5), with the test functions $v = \xi_\omega^n$ and $\mu = d_2 \xi_p^n$, we obtain the following equation:

Using properties (3.17), it follows that

Next, applying Eqs (3.10) and (3.11), and the Cauchy-Schwarz inequality, the following inequality is obtained

Using the estimate

we obtain

and thus, we have the following inequality:

There exists a constant $\chi > 0$ such that

using Lemma 3.3 and noticing the fact that

Let $k = \frac{c_1}{\Delta t} + \frac{c_2}{(\Delta t)^{\rho(t_n)}} \theta_0^{\rho(t_n)}$, and then we use the fact (3.23) twice, first let

then let $a = \Vert \eta_p^n \Vert, b = \Vert \xi_p^n \Vert, \varepsilon = \frac{1}{2}$. Since

so

then the inequality (3.22) becomes

By the fact that

multiplying Eq (3.24) by $2k$, and let

we can obtain the following inequality:

When $n = 1$, Eq (3.25) becomes

Note that $\Vert \xi_\omega^0 \Vert = 0$, and from Eq (3.4), we obtain

We assume that the inequality holds for all $m = 1, 2, \dots, n-1$, that is

It is noted that

From Eqs (3.25) and (3.28), the following inequality is obtained:

Thus, we conclude that

Finally, by applying the triangle inequality and the interpolation property, the proof of Theorem 3.2 is completed.

4.   Numerical experiment

Example 4.1. Consider the problem (1.1) with parameters $c_1 = 1$, $c_2 = 2$, $d_1 = 1$, $d_2 = 2$, and the initial condition $u(x, 0) = 0$. The function $g(x, t)$ is defined as

The exact solution for this problem is given by $\omega(x, t) = t^2\sin(2\pi x)$.

The spatial convergence properties of the scheme (3.4) are evaluated using this example. The temporal step size is fixed at $\Delta t = 1/1000$, while the spatial mesh sizes are varied as $h = 1/5$, $1/10$, $1/15$, and $1/20$, respectively. The resulting numerical errors and convergence rates in both the $L^2$-norm and $L^\infty$-norm, corresponding to various fractional orders, are presented in Tables 1 and 2. It is evident that the proposed scheme achieves the optimal convergence rates when using piecewise $P^k$ polynomial.

By fixing a sufficiently small spatial mesh size $h = \frac{1}{500}$ and choosing various temporal step sizes $\Delta t = \frac{1}{5}, \frac{1}{10}, \frac{1}{20}, \frac{1}{40}$, we observe from Table 3 that the numerical results exhibit a first-order convergence in time, which is consistent with our theoretical results.

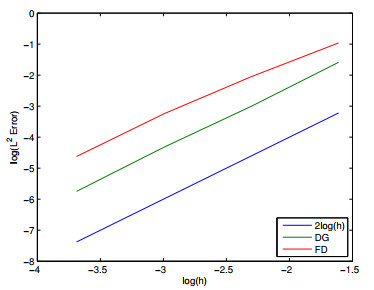
To further validate the accuracy of the proposed high-order DG method, we perform a comparison with a finite difference (FD) method for solving the variable-order fractional advection-dispersion Eq (1.1) with the same parameters and the initial condition. We first divide the spatial domain $[a, b]$ into $N$ equal subintervals with mesh size $h_1 = \frac{b-a}{N}$, and denote $x_j = a + jh_1$, for $j = 0, 1, \dots, N$. We approximate the spatial derivatives of $\omega(x, t_n)$ at the grid points $x_j$ using finite differences as follows:

Substitute Eqs (4.1), (3.1) and (3.2) into the original equation, we obtain the fully discrete scheme

where

● $\omega_j^n \approx \omega(x_j, t_n)$,

● $g_j^n = g(x_j, t_n)$ is the known source term,

● $\theta_k^{\rho(t_n)}$ are weights from the fractional convolution quadrature,

● $\gamma_j^n$ is the total truncation error at $(x_j, t_n)$, satisfying $\|\gamma_j^n\| \leq C (\Delta t+h_1^2)$.

The variable fractional order is chosen as $\rho(t) = \frac{8-t}{15}$.

In the comparison, we fix the time step as $\Delta t = 1/1000$ and vary the spatial mesh size $h_1 = 1/10, 1/20, 1/30, 1/40$. The numerical errors and observed convergence rates in the $L^2$-norm for both the DG method (using piecewise $P^1$ polynomials) and the FD method (4.2) are shown in Figure 1. It is observed that both methods exhibit second-order convergence in space now. However, the DG method demonstrates higher accuracy than the finite difference scheme. Moreover, the DG method is capable of achieving $(k+1)$-th order spatial convergence when using piecewise $P^k$ polynomials. For example, third-order convergence is attained with piecewise $P^2$ polynomials, as evidenced by the results in Tables 1 and 2.

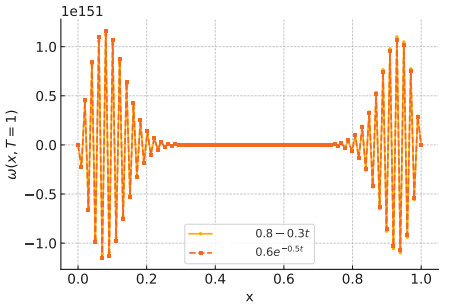
Example 4.2. To illustrate the impact of different variable-order fractional derivatives, we consider the initial condition:

We solve the variable-order mobile-immobile advection-dispersion equation (1.1) using two different choices for the fractional order function:

● Case 1: A linear function, $\rho(t) = 0.8 - 0.3t$.

● Case 2: An exponential function, $\rho(t) = 0.6 e^{-0.5t}$.

The final time is set to $T = 1$, and the computed solutions are plotted in Figure 2. We can observe

● The solution with linear order $\rho(t) = 0.8 - 0.3t$ leads to a gradual decrease in diffusion, resulting in a smoother and more spread-out profile.

● The solution with exponential order $\rho(t) = 0.6 e^{-0.5t}$ exhibits initially strong diffusion that slows down over time, leading to a more localized concentration of the solution.

● This comparison highlights how different variable-order fractional derivatives influence the dispersion behavior, with lower orders leading to slower diffusion and more localized effects.

These results demonstrate the flexibility of variable-order fractional models in capturing complex transport phenomena, making them more suitable for describing real-world diffusion processes compared to classical integer-order models.

5.   Conclusions

In this study, a high-order numerical method is introduced for solving the time-variable-order fractional mobile-immobile advection-dispersion model. The proposed scheme combines the finite difference method with the local discontinuous Galerkin (LDG) method. Through the careful selection of projections and numerical fluxes, it is demonstrated that the scheme is unconditionally stable and achieves a convergence rate of $O(\Delta t + h^{k+1})$ in the $L^2$ norm.

It is worth noting that while this work focuses on the time-fractional model, the method could also be extended to handle fractional derivatives with respect to the spatial variable, as explored in ^[46]. The numerical scheme and stability analysis would require modifications to accommodate the nonlocal nature of spatial fractional derivatives, which will be considered in our future work.

Author contributions

L. Zou wrote the main manuscript text. Y. Zhang analyzed the stability and convergence of the scheme. All authors reviewed the manuscript.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare there is no conflict of interest.