Analysis and optimization control of lung cancer treatment based on surgical resection and immune cell therapy

1.   Introduction

Lung cancer is the most common malignancy in the world and one of the cancers with the highest incidence, with about 230,000 new cases and 140,000 deaths in 2020 ^[1,2]. By 2022, there was about 20 million new cancer cases and 9.7 million deaths worldwide, including about 2.5 million new cases of lung cancer. It accounts for 12.4% of new cancer cases and about 1.8 million deaths worldwide, accounting for 18.7% of all cancer deaths. Due to various factors, such as smoking, environmental pollutants, and genetic susceptibility ^[3,4,5], the number of lung cancer patients is still increasing. Therefore, the study of lung cancer treatment has become an important direction of current cancer research. The most important reason for tumor progression is cancer cells' constant proliferation and metastasis potential ^[6]. Due to the limited level of medical technology in the early diagnosis and treatment of lung cancer and the relatively backward diagnosis and treatment technology, such as insufficient biomarkers for early detection, disease tracking methods, and physical examination ^[7], many patients with lung cancer are not diagnosed until the advanced stage. When cancer develops to the advanced stage, the 5-year relative survival rate of patients is 6% ^[8], which significantly reduces the survival rate of patients.

Lung cancer is usually divided into small cell lung cancer (SCLC) and non-small cell lung cancer (NSCLC) ^[9,10]. In the past decade, advancements in NSCLC treatment have primarily been driven by a deeper understanding of the molecular biology of lung cancer ^[11]. This improved understanding has led to the development of innovative and effective treatments that have contributed to the overall survival rates ^[12]. Treatment options for lung cancer encompass surgical intervention, chemotherapeutic regimens, radiotherapy, and targeted drug therapies ^[13,14]. Dwight Owen et al. proposed a review of immunotherapy for surgically resectable non-small cell lung cancer (NSCLC) ^[15], detailing that patients with NSCLC who were treated with immunotherapy using PD-1 and PD-L1 monoclonal antibodies in addition to their surgical excision regimen, compared to standard chemotherapy. This can lead to better outcomes for specific patients. They also mentioned the use of several other immunotherapy drugs, including combination immunotherapy, chemical immunotherapy, and chimeric antigen receptor (CAR) T-cell therapy. The efficacy of immunotherapy across various patient groups, its minimal risk of side effects, and its capacity to generate long-lasting therapeutic responses represent significant shifts in cancer treatment approaches ^[16]. In addition to these methods, there are numerous other strategies for regulating drug dosage, such as maximum tolerated dose (MTD) and adaptive treatment (ADT), among others. Adaptive treatment is grounded in Darwinian evolutionary dynamics. It diverges from the traditional maximum tolerated dose concept by adjusting medication based on the tumor growth rate through interactions between susceptible and resistant cells. The objective is not to destroy the tumor but to control it by varying dosage and treatment intervals to prolong therapy response time and patient survival. Adaptive therapy is increasingly gaining popularity as a therapeutic approach for treating tumors ^[17].

The tumor microenvironment is characterized by complex fluid interactions that make the development of cancer therapies challenging ^[18,19]. Under constant favorable conditions, normal cells follow the four basic "rules" of cell cycle regulation and produce new cells through DNA replication and division ^[20]. In the literature ^[21], Bashar et al. proposed an "executable model" that can be well translated into various quantitative concrete models and can be used as the basis for developing quantitative models to explain the interactions between various components and proteins that control the cell during mitosis. The establishment of microscopic mathematical models is of great significance to understanding the interactions of various substances in the cell microenvironment. In ^[22], the authors studied an integer-order kinetic mathematical model of tumor-macrophage interaction to study the interaction between tumor cells, M1 macrophages, and M2 macrophages by considering the pro-tumor and anti-tumor effects of macrophages. Geng et al. ^[23] developed a mathematical model to predict Kaplan-Meier survival curves of chemotherapy combined with radiotherapy in patients with non-small cell lung cancer for use in clinical trial design. In the study of Ophir et al.^[24], they proposed a mathematical model for the treatment of ER-positive breast cancer, introduced two control parameters (drug dose and treatment interval), and described the relationship among variables, including tumor cells, immune cells, and drug circulation in the body, through ordinary differential equations. According to the size of the tumor, the dosage and time interval can be changed to achieve personalized treatment and improve the therapeutic effect.

Although integer-order differential equations can well reflect the physical basis and interaction between components, they cannot reflect the "memory" between cells or fractional-order models. Therefore, in the study of Novák et al. ^[25], the differential equation of protein-mRNA concentration dynamics was proposed to simulate the oscillation process. One of the conditions for maintaining this oscillation process is that there is enough "memory" in the negative feedback loop to enable the system to "remember" the recent history. In recent years, fractional calculus has been increasingly used to model cancer growth. Studies have shown that fractional derivatives can more accurately reflect cancer progression than integer derivatives ^[26,27]. Pang et al. investigated an innovative fractional-order mathematical model that illuminated the population dynamics between tumor cells, macrophages, activated macrophages, and host cells ^[28]. Finding that fractional derivatives better reflect experimental data than integer derivatives, the authors proposed and applied a fractional model of the lung tumor hypothesis, using mathematical modeling and a forced oscillation technique (FOT) device to select the optimal clinical decision process for lung cancer management ^[29]. Ahmed et al. ^[30] described how to augment the immune system with antibody cells and use the fractal fraction operator (FFO) to transform the model into a fractional-order model that mathematically describes the interactions between tumor cells, CD8+ T cells, dendritic cells, IL2, and anti-PD-L1 inhibitors. In ^[31], Amilo et al. established a dynamic model between lung cancer cells and immune cells and added the method of surgery combined with monoclonal antibody immunotherapy in the study to explore the impact on lung cancer. They used a mathematical model of fractional-order dynamics to understand the dynamics of the disease, showing that higher fractional-order leads to faster convergence, and treatment strategies are obtained through feedback control. See the included references for more lung cancer models ^[32,33,34].

Based on existing research on lung cancer and the establishment of a fractional-order lung cancer model, this paper builds upon the model presented in ^[31]; we modified the immunotherapy with the input of monoclonal antibodies to the immunotherapy with the input of in vitro immuno-enhanced T lymphocytes, which reduces the immune rejection of patients, and also combined with surgical resection, the treatment results are apparent. According to the adaptive control input and the relevant parameters of different patients, they can also get different treatment results and plans to achieve personalized treatment for patients. Compared with the reference ^[31], this paper gives the specific results after the addition of treatment under relevant initial conditions and the specific input of relevant doses. The rest of this paper is organized as follows: In Section 2, we give some definitions of fractional derivatives and some important theorems of fractional derivatives. In Section 3, we describe the dynamic interaction between normal cells, tumor cells, and immune cells; the existence and uniqueness of the solution; and the stability of the equilibrium point. In Section 4, parameter sensitivity analysis is carried out to explore which parameters have a more significant impact on the model. In Section 5, the formalization of the optimal control problem is given, and the necessary and sufficient conditions of optimal control are found. In Section 6, numerical simulation is used to explain the results in detail. In Section 7, the research results are discussed with those of the predecessors, and in Section 8, the direction of future work is summarized.

2.   Fundamentals and definitions

Definition 1 ^[35,36]. The Riemann–Liouville fractional derivative of order $\alpha > 0$ for a function $f:\left (0, \infty \right) \longrightarrow \mathcal{R}$ is formulated as

Definition 2 ^[31,35,36]. The Caputo fractional derivative of order $\alpha > 0$ for the function provided in Definition 1 is defined as follows:

For simplicity, we denote the Caputo fractional integral operator $\mathbb{D}^{\alpha }f(t)$ as $_{0}^{C}\mathbb{D} _{t}^{\alpha }f(t).$

Definition 3 ^[31,36]. Gamma function.

The gamma function $\Gamma (x)$ is specified for $Re(x) > 0$ through the following integral:

Definition 4 ^[31]. Laplace transform.

When $z \ge 0$, the Laplace transform of the function $f(z)$ is denoted as $\mathfrak{L}f(z)(x)$ by the formula:

In this context, $x$ represents a complex number that guarantees the convergence of the integral.

Theorem 1 ^[37,38]. Pontryagin's minimum principle.

Consider the following optimal control problems:

where $X(t)\in \mathbb{R}^{n}$ is the state variable, $u(t)\in \mathbb{U}\subseteq \mathbb{R}^{m}$ is the control variable, $\mathbb{U}$ is the closed set ($\left | u(t) \right |\le \mathbb{U}$), and $f$ is a continuously differentiable vector function. Construct the target functional:

where $\Phi (X(T), T)$ is the final state and $\int_{0}^{T}L(t, X(t), u(t))dt$ is the transition cost.

Introducing Hamiltonian functions and costate variables:

Suppose $X^{*}$ is the optimal state, and $u^{*}$ is the optimal input. For optimal control $u^{*}$, the following conditions are satisfied on $t\in [0, T]$ :

Equation of state:

Costate equation:

Transversal condition:

3.   Model analysis

3.1.   Model frame

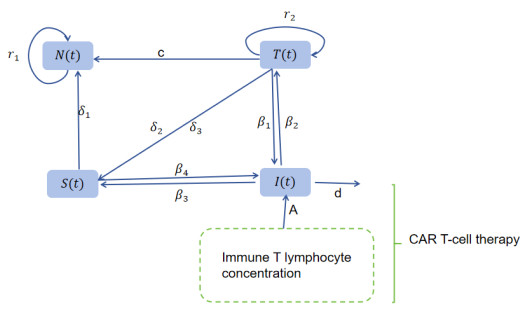
The following illustration shows the interactions among immune cells, tumor cells, healthy cells, and disseminated tumor cells within the scope of lung cancer:

In the scenario of lung cancer, the dynamics between immune cells, tumor cells, healthy cells, and migrating tumor cells can be represented by the subsequent set of fractional-order differential equations:

The variables $N$, $T$, and $I$ denote the number of normal, tumor, and immune cells within lung tissue at time $t$, respectively. The variable $S$ indicates the quantity of tumor cells that have metastasized to different body areas.

System (3.1) can be used to model how lung cancer develops and spreads. To investigate the impact of immunotherapy and surgical intervention on lung cancer development and metastasis, we modified the model as follows:

Here, $C$ represents the number of tumor cells in lung tissue to be cleared at time $t$, and $u(t)$ represents the control input function of immunotherapy at time $t$. $\theta (t-\tau)$ represents a step function with a delay $\tau$. For other parameters, see Table 1.

3.2.   The existence and uniqueness of the solution

For the initial conditions $N(0) = N_{0}, \; T(0) = T_{0}, \; I(0) = I_{0}, \; S(0) = S_{0}$, and $C(0) = C_{0}$, we express system (3.2) as follows:

where

The definitions required for existence and uniqueness are given as follows:

Definition 5 ^[35,39]. Let $\mathfrak{D}^{*}\left [ 0, a \right ]$ be the space of continuous column vectors $X$. The elements of $X$ consist of $N$, $T$, $I$, $S$, and $C$, all belonging to $\mathfrak{D}^{*}\left [ 0, a \right ]$, which comprises continuous functions over the interval $[ 0, a]$. The norm of $X$ within $\mathfrak{D}^{*}\left [ 0, a \right ]$ is given by the following definition:

If $t > \varpi \ge 0$, one can write $\mathfrak{D}_{\varpi }^{*}[0, \Lambda ]$ and $\mathfrak{D}_{\varpi }[0, \Lambda ].$

Definition 6 ^[35,39]. $X\in \mathfrak{D}^{*}[0, \Lambda ]$ is considered a solution to system (3.2) if

(ⅰ) $(X, t)\in D$, $t \in [0, \Lambda]$ where $D = [0, \Lambda]\times Q$,

where $p$, $q$, $g$, $h$, and $z$ are constants.

(ⅱ) $X$ satisfies Eq (3.2).

Theorem 2. The initial value problem (3.2) possesses a unique solution $X \in \mathfrak{D}^{*}[ 0, \Lambda]$.

Proof. The differential equations in system (3.2) are reformulated according to the principles of fractional calculus in Definitions 1 and 2 as follows:

Operating with $I^{\alpha}$, we have

Let $\mathcal{F}:\mathfrak{D}^{*}[ 0, \Lambda ]\longrightarrow \mathfrak{D}^{*}[ 0, \Lambda ]$ be given by

Then,

That gives us that $\left \| \mathcal{F}Y -\mathcal{F}X \right \|\le \frac{W_{1}+pW_{2}+qW_{3}+gW_{4}+hW_{5}+zW_{6}}{\mathcal{N}^{\alpha }} \left \| Y-X \right \|$. We make $\mathcal{N}$ sufficiently large such that $\mathcal{N}^{\alpha }\ge W_{1}+pW_{2}+qW_{3}+gW_{4}+hW_{5}+zW_{6}.$ Hence, we have $\left \| \mathcal{F}Y -\mathcal{F}X \right \|\le \left \| Y-X \right \|.$ Thus the operator $\mathcal{F}$ defined by Eq (3.7) has a unique fixed point, and hence Eq (3.3) has a unique solution $X\in \mathfrak{D}^{*}[ 0, \Lambda ]$.

From Eq (3.7), we have

From this, we infer that ${X}' \in \mathfrak{D}^{*}[ 0, \Lambda ]$. Subsequently, from Eq (3.4), we obtain

Hence, Eq (3.7) constitutes the sole solution to the initial value problem posed in Eq (3.3).

3.3.   The equilibrium points

First, we make the right end of the system (3.2) equal to 0, so that $D^{\alpha }N = D^{\alpha }T = D^{\alpha }I = D^{\alpha }S = D^{\alpha }C = 0$, and therefore

In this part, $u(t) = 0$ because immunotherapy was not added under the initial conditions. We then consider the Eq (3.17) when $T = 0$:

So we calculate that when $N = 0$, $I = \frac{\mu I_{0} }{d}$; and when $N = k_{1}$, $I = \frac{\mu I_{0} }{d}$.

For $T\neq 0$, Eq (3.17) involves five independent variables and several parameters. We use MATLAB tools to solve the equations analytically and simplify the results to get the equilibrium points $E_{3}$ and $E_{4}$, and the conditions for their existence are given through the characteristics of the equilibrium point.

To sum up, we can get the following two balance points:

(ⅰ) Tumor-Free State of Equilibrium:

$\quad\quad E_{1} = \left (0, 0, \frac{I_{0}\mu}{d}, 0, 0 \right),$ $\quad\quad E_{2} = \left (k_{1}, 0, \frac{I_{0}\mu}{d}, 0, 0 \right).$

(ⅱ) Tumor-Endemic State of Equilibrium:

$\quad\quad E_{3} = \left (0, T^{*}, I^{*}, 0, 0 \right)$, its existence condition is $1 > r_{2}\ge \frac{4k_{2}r_{2}\beta _{1}\beta _{2}I_{0}\mu}{(d+k_{2}\beta _{2})^{2}},$

where

$\quad\quad E_{4} = \left (N^{**}, T^{**}, I^{**}, 0, 0 \right)$, its existence condition is $1 > r_{2}\ge \frac{4k_{2}r_{2}\beta _{1}\beta _{2}I_{0}\mu}{(d+k_{2}\beta _{2})^{2}}$ and $k_{2}\ge \frac{(1+r_{2})d}{(1-r_{2}) \beta _{2}},$

where

3.4.   Local stability of equilibrium points

Theorem 3 ^[35,47]. Consider the following fractional-order system:

Let $z \in \mathcal{R} ^n$ and $\alpha \in (0, 1)$. The equilibrium points of system (3.18) are the vectors $z$ where the function $f(z) = 0$. An equilibrium point is considered locally asymptotically stable if all the eigenvalues $\lambda_i$ ($i = 1, 2, \ldots, n$) of the Jacobian matrix $J = \frac{\partial f}{\partial z}$, computed at the equilibrium point, satisfy the following criterion:

Conversely, if $\left | arg(\lambda_{i})\right | < \frac{\alpha \pi }{2}$, the equilibrium point is unstable.

Now, we use Theorem 3 to analyze the stability of the equilibrium point. The Jacobian matrix of system (3.2) is:

Therefore, the Jacobian matrix at $E_{1} = (0, 0, \frac{\mu I_{0}}{d}, 0, 0)$ is

Its characteristic equation is $P(\lambda) = (\lambda -r_{1})(\lambda -r_{2})(\lambda +d)(\lambda +\beta _{4}\frac{\mu I_{0}}{d})(\lambda+\varphi _{2})$, and its characteristic root can be solved as $\lambda_{1} = r_{1}$, $\lambda_{2} = r_{2}$, $\lambda_{3} = -d$, $\lambda_{4} = -\beta _{4}\frac{\mu I_{0}}{d}$, $\lambda_{5} = -\varphi _{2}$. So for $\lambda_{1} = r_{1} > 0$, $\lambda_{2} = r_{2} > 0$, then $\left | arg(\lambda _{1})\right | = \left | arg(\lambda _{2})\right | = 0 < \frac{\alpha \pi }{2}$; and for $\lambda_{3} = -d$, $\lambda_{4} = -\beta _{4}\frac{\mu I_{0}}{d}$, $\lambda_{5} = -\varphi _{2}$, since $d$, $\beta _{4}$, $\mu$, $I_{0}$, and $\varphi _{2}$ are all greater than 0, in the complex plane the real axis is negative, and then $\left | arg(\lambda _{3})\right | = \left | arg(\lambda _{4})\right | = \left | arg(\lambda _{5})\right | = \pi > \frac{\alpha \pi }{2}$.

Similarly, the eigenroot at the equilibrium point $E_{2} = (k_{1}, 0, \frac{\mu I_{0}}{d}, 0, 0)$ is $\lambda_{1} = -r_{1}$, $\lambda_{2} = r_{2}-\beta _{1}\frac{\mu I_{0} }{d}$, $\lambda_{3} = -d$, $\lambda_{4} = -\beta _{4}\frac{\mu I_{0}}{d}$, $\lambda_{5} = -\varphi _{2}$, so $\left | arg(\lambda _{1})\right | = \left | arg(\lambda _{3})\right | = \left | arg(\lambda _{4})\right | = \left | arg(\lambda _{5})\right | = \pi > \frac{\alpha \pi }{2}$; for $\lambda_{2} = r_{2}-\beta _{1}\frac{\mu I_{0} }{d}$, when $r_{2} > \beta _{1}\frac{\mu I_{0} }{d}$, $\left | arg(\lambda _{2})\right | = 0 < \frac{\alpha \pi }{2}$; and when $r_{2} < \beta _{1}\frac{\mu I_{0} }{d}$, $\left | arg(\lambda _{2})\right | = \pi > \frac{\alpha \pi }{2}$.

Theorem 4 ^[31,35]. Consider the following characteristic equation.

1. For $n = 1$, the criteria for Eq (3.19) is $0 < b_{2}$.

2. For $n = 2$, the criteria for Eq (3.19) are the Routh–Hurwitz conditions

$b_{1}, b_{2}, b_{3} > 0$ or $b_{1}b_{3} > 0, b_{2} < 0, \; 4b_{1}b_{3} > b_{2}^{2}, \left | \tan^{-1} (4b_{1}b_{3}-b_{2}^{2}) \right | > \frac{\alpha \pi }{2}.$

3. For $n = 3$, the criteria for Eq (3.19) are the Routh-Hurwitz conditions

$b_{1} > 0, \; \frac{b_{2}b_{1}-b_{3}}{b_{1}} > 0, \; \frac{b_{3}b_{1}-b_{2}}{b_{1}} > 0.$

Therefore, satisfying these conditions implies that all eigenvalues possess negative real parts, signifying the system's stability. Let us now address the issue of the local stability of the equilibrium point $E_{3} = (0, T^{*}, I^{*}, 0, 0)$. The Jacobian matrix of system (3.2) evaluated at the equilibrium point $E_{3}$ is as follows:

where

So we obtained the feature matrix at $E_{3}$ as follows:

The characteristic equation is $P(\lambda) = (\lambda^{3} +b_{1}\lambda^{2}+b_{2}\lambda)(\lambda^{2} +b_{3}\lambda+b_{4}),$ where

Theorem 5 ^[35]. The equilibrium point $E_{3}$ is deemed to be locally asymptotically stable provided that at least one of the subsequent conditions is satisfied:

1. The Routh-Hurwitz conditions $b_{1}, b_{2}, b_{3}, b_{4} > 0.$

2. $b_{1}, b_{2} > 0$ and $0 > b_{3}, 4b_{4} > b_{3}^{2}, \left | \tan^{-1} (4b_{4}-b_{3}^{2}) \right | > \frac{\alpha \pi }{2}.$

Likewise, the Jacobian matrix of system (3.2), when computed at the equilibrium point $E_{4}$, is expressed as follows:

where

so we obtained the feature matrix at $E_{4}$ as follows:

The characteristic equation is $P(\lambda) = (\lambda^{3} +l_{1}\lambda^{2}+l_{2}\lambda)(\lambda^{2} +l_{3}\lambda+l_{4})$, where,

When $E_{3}$ and $E_{4}$ satisfy Theorem 5, they are locally stable.

From the above, we can derive a summary table of equilibrium conditions for the equilibrium point to reach a stable state (Table 2):

4.   Sensitivity analysis

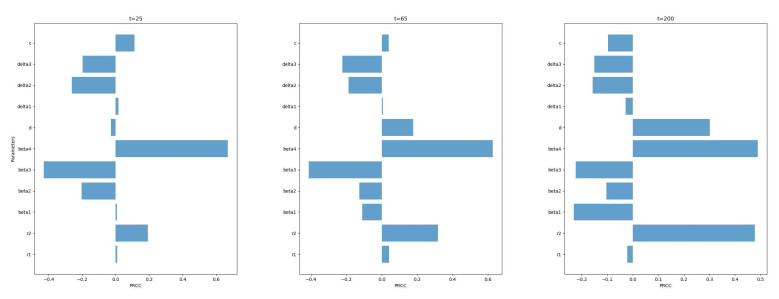
To evaluate the sensitivity of the parameters in the model, we used the partial rank correlation coefficient (PRCC) method to perform a sensitivity analysis of parameters in the system (3.2) to test whether the model is robust to parameter changes. We used Latin hypercube sampling (LHS) ^[40,41] to generate 1000 samples for 11 estimated parameters in the model to calculate the PRCC and P-values for tumor size on days 25, 65, and 200, with values ranging from [0.001, 1.0] for each parameter.

In the sensitivity analysis, we observed the correlation between model parameters at different simulation time points and tumor cell size, as shown in Figure 2. The interaction of immune cells with metastatic tumor cells ($\beta_{4}$) was significantly positively correlated with tumor size at all three times. The growth rate of tumor cells ($r_{2}$) and the natural mortality rate of immune cells ($d$) were significantly positively correlated with tumor size at day 200. The interaction of metastatic tumor cells with immune cells ($\beta_{3}$) was significantly negatively correlated with tumor size on days 25 and 65. The rate of metastasis of tumor cells from lung tissue to other sites ($\delta _{2}$), the rate of metastasis of tumor cells from lung tissue to other sites ($\delta _{3}$), and the interaction of tumor cells with immune cells ($\beta_{2}$) were negatively correlated with tumor size at all three times. Perturbations of other parameters had no substantial effect on the results. Therefore, in our subsequent analysis, we mainly consider the influence of parameters $\beta_{2}$, $\beta_{3}$, $\beta_{4}$, $\delta _{2}$, $\delta _{3}$, $r_{2}$, and $d$ on the model dynamics.

5.   Optimal control

In this paper, we created a modified normal-tumor-immune cell model that accounts for prior interactions between cell groups. We examine the model's local stability at each equilibrium point. Additionally, the optimal control approach for drug administration reduces tumor cell development. Because the best control technique maintained a high proportion of normal and immune cells, we observed that it helped eradicate tumor cells with fewer harmful side effects. The ideal control approach also reduces the time required to process the policy. The numerical outcomes substantiate the validity of our theoretical analysis.

In combination therapy, we design each treatment to begin with surgical removal of the metastasized tumor cells so that most of the tumor cells are removed from the body and do not spread further and worsen the disease. After surgical resection, the immune capacity of the patient will decline. The tumor cells in the body will continue to grow and metastasize, so the patient will be injected with enhanced autoimmune cells in vitro for immunotherapy, so that there are enough immune cells in the patient's body to kill the tumor cells. The self-enhanced immune cells will not produce an immune rejection reaction in the body. This dramatically enhances the cells' survival rate and makes the immunotherapy's effect obvious. This is a testament to the combination of immunotherapy and surgical treatment to obtain a more effective treatment while protecting patients from opportunistic infections and fighting the tumor itself. Immunotherapy also activates and stimulates the growth of immune cells, primarily T cells and NK cells, which can directly destroy tumor cells. Therefore, the main goal of combined immunosurgical therapy is to eradicate tumor cells with minimal side effects while maintaining a sufficient amount of healthy tissue.

Based on the above considerations, the optimal control problem consists in determining control functions $(L^{\infty }([0, T_{f}], R))$ that maximize the objective functional:

with $m_{1}, \; m_{2}, \; m_{3}$, and $M$ being non-negative constants. It should be highlighted that $m_{1}, m_{2}, m_{3}$, and $M$ serve as weight coefficients in the objective function, employed to adjust the relative importance of the various terms. The squared optimal combination of control variables will be adequate to reduce tumor density and mitigate adverse side effects within a defined temporal window. We define the following control set:

where the control functions $u(t)$ satify the following control constraint:

In this paper, based on Table 3 and the results of numerical analysis, we take $u_{max} = 20$.

5.1.   The existence of optimal control solutions

The central objective of the control problem is to identify the optimal control $u$. We can ensure the optimal solution by following the approaches described in ^[13,39,42].

Theorem 6^[13,39,42]. For the optimal control problem (4.1), if the system satisfies the conditions (i–v), then there is an optimal solution $(X^{*}, u^{*})\in U^{*(1, \infty)}([0, T_{f}], R^{5})\times L^{\infty }([0, T_{f}], R)$, and the solution is

where $X^{*} = [N^{*}, T^{*}, I^{*}, S^{*}, C^{*}]$.

ⅰ. The set of allowable controls $U^{*}$ and the related states with initial conditions are not empty.

ⅱ. The set of permissible controls, $U^{*}$, is both closed and convex.

ⅲ. A linear combination of the state and control variables bounds the right-hand side of the state equations.

ⅳ. The integrand of the cost functional, given by $L(T, S, C, u) = m_{1}T(t)+m_{2}S(t)-m_{3}C(t)+\frac{1}{2}Mu^{2}(t)$, exhibits convexity and possesses a minimum bound.

ⅴ. Positive constants $h_{1}, h_{2} > 0$ and $\xi > 0$ exist that fulfill the integrand $L(T, S, C, u)$ of the cost functional, ensuring that $L(T, S, C, u) \geq h_{1} + h_{2} |u|^{\xi}.$

Proof of Theorem 6. To confirm the conditions, it is necessary to initially establish the existence of a system solution (3.2). First, as shown in Section 3, we have proved the existence and uniqueness of knowledge, thereby proving that the system satisfies condition ⅰ.

Second, it is clear from the definition of the control set $U^{*}$ that $U^{*}$ is a non-empty, convex, closed set, and therefore the system satisfies condition ⅱ.

Again, verify condition ⅲ. Since system (3.2) is bilinear, it is rewritten as

Given that $X(t) = [N, T, I, S, C]$ and $v$ are functions with column-vector values, and because the solutions of system (3.2) are bounded, we can infer that

Therefore, the system satisfies condition ⅲ. The value of $s$ in this context is contingent upon the system's coordination efficiency and

Finally, verify conditions ⅳ and ⅴ. To prove the convexity sum and minimum bound of the integrand $L(T, S, C, u)$ in the cost function, we therefore need to prove

where

$u$ and $v$ represent two control vectors, and $\eta$ is an element within the interval (0, 1). Now,

and

so

Hence, $L(X, u, t)$ is convex.

Finally, for condition v, $L(X, u, t)\ge m_{1}T+m_{2}S+\frac{1}{2}Mu^{2} \ge h_{1}+h_{2}\left | u \right | ^{\xi }$, where $h_{1}$ is the lower bound of $m_{1}T+m_{2}S$, $h_{2} = \frac{M}{2}$, and $\xi > 1$. The proof is complete. As a result, we can assert that there is an optimal control, $u^{*}$, that minimizes the value of $L(u)$.

In summary, the system satisfies all the conditions of Theorem 6, so there is an optimal solution.

5.2.   Necessary optimality conditions

Subsequently, we utilize the Pontryagin maximum principle alongside the Hamiltonian function. We introduce four adjoint variables $\lambda _{i}$ ($i = 1, 2, 3, 4, 5$), leading to the following formulation of the Hamiltonian function:

By substituting Eq (3.2) with Eq (4.12), we find

The Pontryagin minimum principle can be obtained as follows:

Equation of state:

Costate equation:

Transversal condition:

Governing equation:

The necessary conditions for the governing equation are

and we solve

Next, we advance to numerically address the proposed model with the related optimal control issue.

6.   Numerical format of the tumor immune model in the sense of the Caputo derivative

To study the dynamics of the proposed fractional-order model (3.2), L1 discretization and the Adams-Bashforth-Moulton (ABM) method ^[35] are used for numerical processing. From Theorem 2, remember the model (3.2) as $D^{\alpha } f(t, X)$, where $X = \left [ N, T, I, S, C \right ]$. Set the time step to $\Delta t$ and time node to $t_{n} = n\Delta t, n = 0, 1, 2, ...$. First, L1 discretization is used to process $D^{\alpha } f(t, X)$ to obtain:

where

For the discretized fractional-order equation, the second-order ABM method is used to construct a prediction correction formula for an iterative solution, where the prediction process expression is as follows:

Since $X_{n+1}$ is unknown, the predicted value $X_{n+1}^{p}$ is brought into $f(t_{n+1}, X)$ to correct the value of $X_{n+1}$, so the corrected formula is

By the same token, $T_{n+1}^{p}$, $I_{n+1}^{p}$, $S_{n+1}^{p}$, and $C_{n+1}^{p}$ can be obtained as follows:

Based on the above numerical analysis steps, we perform numerical results and visualization in Python 3.12.

7.   Numerical results

We will provide numerical results in this part to confirm whether the treatment outcome was good or bad. In the numerical simulation that follows, we consider a 200-day treatment period. This study resolves fractional differential equations using the Adams-Bashforth-Moulton and L1 discretization methods. This work assesses the impact of altering the treatment outcome by adjusting various time intervals for the optimal control problem within the treatment framework. The adaptive treatment time is determined using the classical genetic algorithm. In Figures 3–12, the values of each parameter are $r_{1} = 0.04$, $r_{2} = 0.1$, $k_{1} = 100$, $k_{2} = 100$, $c = 0.008$, $\beta_{1} = 0.008$, $\beta_{2} = 0.001$, $\beta_{3} = 0.001$, $\beta _{4} = 0.02$, $\mu = 0.03$, $N_{0} = 15$, $T_{0} = 18$, $I_{0} = 10$, $S_{0} = 10$, $\delta_{1} = 0.01$, $\delta_{2} = 0.003$, $\delta _{3} = 0.07$, $d = 0.035$, $A = 0.05$, $\tau = 0.5$, $\phi_{1} = 0.05$, $\phi_{2} = 1$.

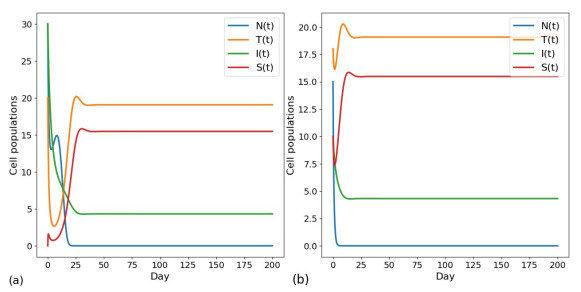
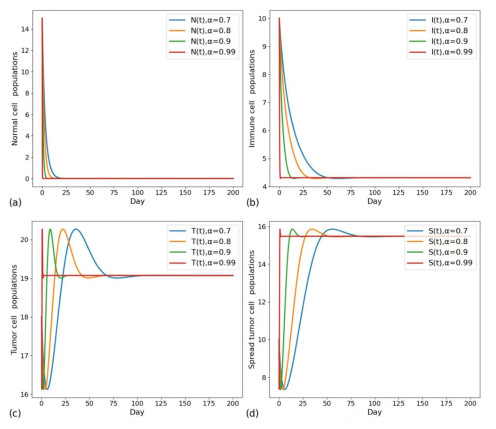
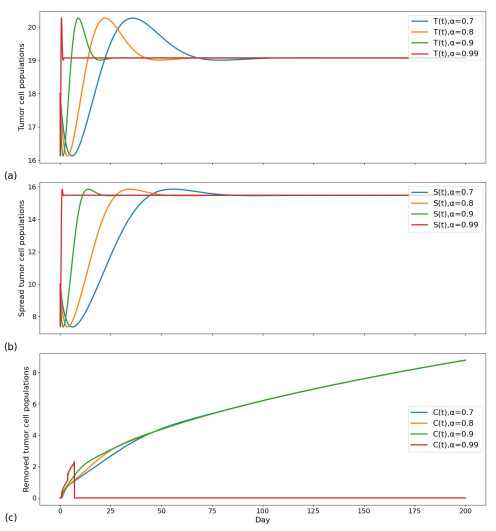
The order $\alpha$ of a fractional-order system represents the rate of activation or proliferation of cells in response to external stimuli since this rate is not instantaneous (as indicated by the order derivative) or completely static (as indicated by the zero-order derivative), but a rate of change in between, and $\alpha$ also represents the intensity or speed of this memory effect of the system, that is, how quickly and efficiently cells "recall" and respond to previous "actions". Figure 3 shows the changes of the two groups with different initial values at $\alpha = 0.9$. The value simulated in Figure 3(a) is that the number of tumor cells in the body of patients is relatively small, but metastasis has not occurred, and normal cells and immune cells will continue to kill tumor cells in large numbers so that the time for tumor cells to reach the maximum value is relatively long, and the survival time of patients is relatively long. The simulated patient in Figure 3(b) has a relatively small number of various cells in the body, and the tumor cells have metastasized. The patient's condition has deteriorated, and treatment is urgently needed to prolong survival.

As can be seen from Figure 3, when there are relatively few cells in the patient's body and tumor cells have metastasized, if no therapeutic measures are added at this time, we can see that without any treatment, tumor cells will gradually increase and quickly reach the maximum number and eventually maintain this number, while normal cells and immune cells will rapidly decrease. This makes the patient's condition worse. As can be seen from Figure 4, the initial value are $N_{0} = 15$, $T_{0} = 18$, $I_{0} = 10$, and $S_{0} = 10$, respectively, under $\alpha = [0.7, 0.8, 0.9, 0.99]$. We can see that with the increase of order, the intensity and speed of this memory effect become stronger and faster, and the time for the number of the same cells to reach stability becomes shorter. However, there is almost no memory effect in time, which is not in line with the real situation.

Figures 3 and 4 show us that without treatment, tumor cells will continue to multiply and destroy the immune system and normal cells in the patient's body, worsening their health. With an increasing number of tumor cells in their body, the patient's condition will worsen, and their rapid decline may cause them to pass very quickly. Consequently, we initiated treatment for lung cancer patients utilizing a regimen that combines surgery with adoptive immune cell therapy. It is assumed that since the number of tumor cells reaches a certain level, and since each tumor cell has the same reproductive capacity, the same number of tumor cells will be produced every day, so the number of tumor cells that are surgically removed at different surgical moments will also increase. The result should look like Figure 5.

Under surgical treatment, most cancer cells can be removed, but surgical treatment cannot remove all cancer cells, and it is useless for some tumor cells that have metastasized. Therefore, to clear tumor cells in the patient's body as much as possible and cure the patient, we add immunotherapy and adjuvant surgical treatment for the patient based on the surgical treatment. It is better to kill tumor cells and prolong the life of patients as much as possible. In immunotherapy, we observe the changes of tumor cells in the patient's body after surgery in real time according to the adaptive treatment and inject the corresponding number of immune cells into the patient according to the number of tumor cells at different time intervals, which reduces the number of treatments for the patient and maximizes the therapeutic effect.

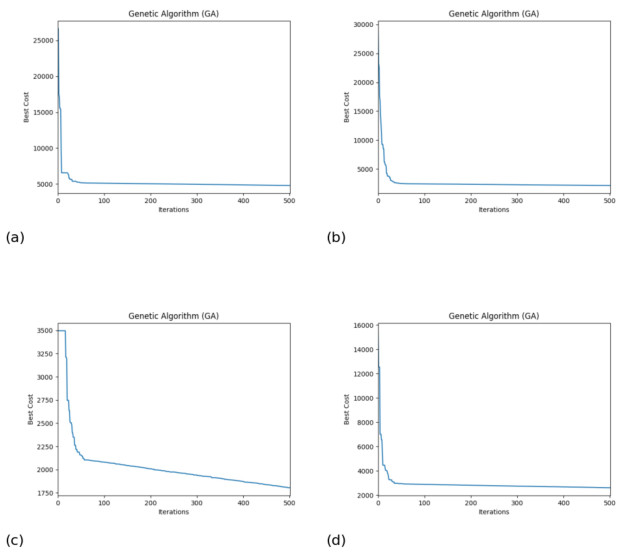
The target cost values for time intervals of 1, 3, 5, and 10 days are shown in Figure 6(a)–(d), respectively. From the figures, we can clearly see the change in the target value. Although the decline rate of 1, 3, and 10 days is fast, the result is not as good as that of 5 days.

Table 3 shows the values of the control inputs at different time intervals and the values of the optimal cost target after 500 iterations. As can be seen from the table, when immune cell input is performed every day, the average input value is the largest, and when immune cell input is performed at an interval of 5 days, the average input value is the smallest. The control target value is also the smallest, indicating that one immunotherapy at an interval of 5 days has the best effect. For different time intervals, the input of control $u$ is different, and the optimal cost is also different, but they can bring the tumor reduction under control and extend the life span of patients.

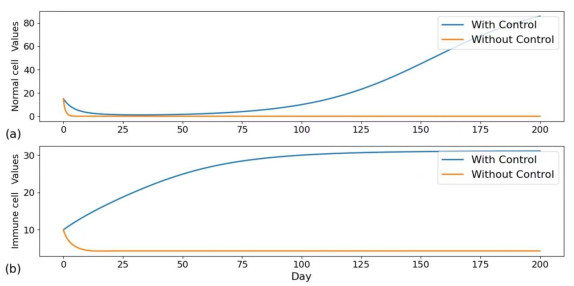
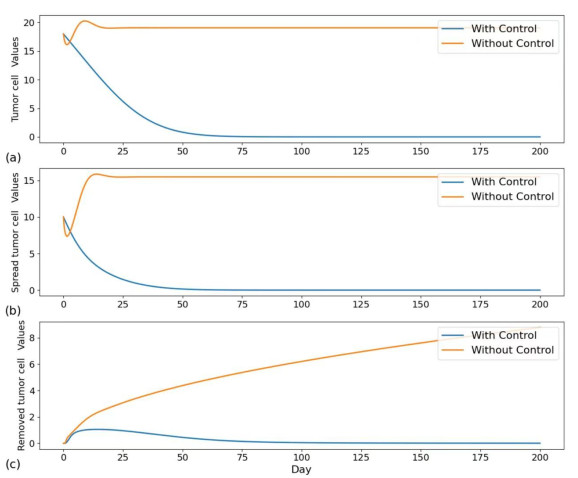
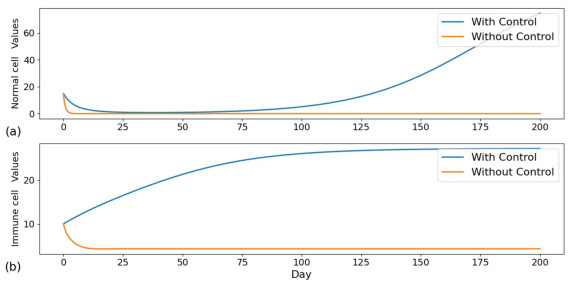
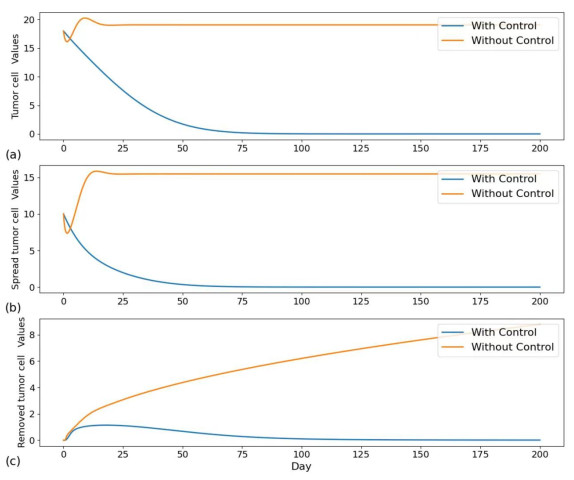
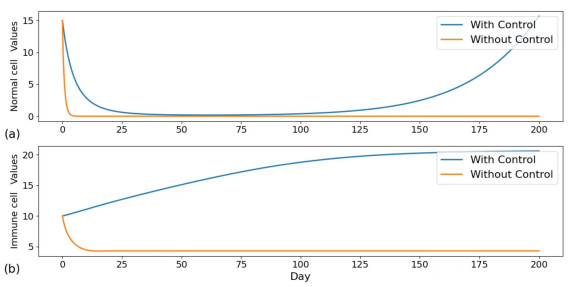
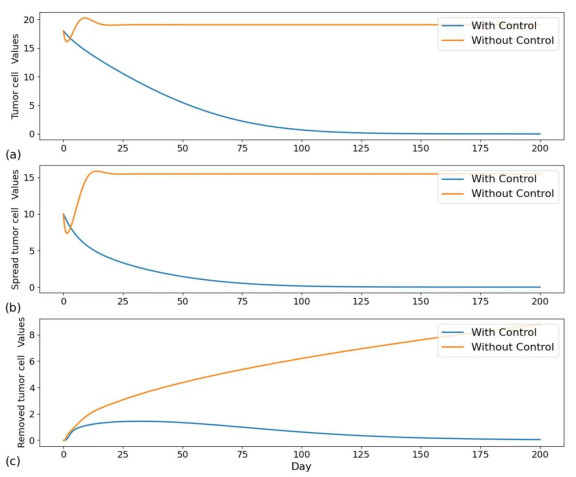
Compare Figures 7–12 to compare the changes in the number of each cell during immunotherapy at different time intervals between no treatment and combination therapy. According to Figures 7 and 8, normal cells $(N)$ began to ascend on the 50th day, with a time interval of one day, whereas immune cells $(I)$ continued to rise until they reached a stable time at approximately the 125th day. On the 65th day, the tumor cells $(T)$ eventually reach zero; on the 50th day, the spread tumor cells $(S)$ reach zero; and on the 75th day, the resected tumor cells $(C)$ reach zero; at that point, no more tumor cells need to be removed.

According to Figures 9 and 10, normal cells $(N)$ started to rise on the 60th day; immune cells $(I)$ increased to attain stability at approximately the 150th day; tumor cells $(T)$ fell to 0 at about the 90th day; and spreading tumor cells $(S)$ decreased to 0 at about the 65th day. All of these time intervals are five days. Once the excised tumor cells $(C)$ reach 0, which happens on the 95th day, there is no need to remove any additional tumor cells because they have not spread behind.

As can be seen from Figures 11 and 12, the time interval of 10 days for normal cells ($N$) began to rise on day 85, and the time for immune cells ($I$) to increase to reach stability was on day 175 or so, the time for tumor cells ($T$) to decrease to 0 was on day 125 or so, and the time for spreading tumor cells ($S$) to decrease to 0 was on day 115 or so, followed by no tumor cell spreading. The time when the removed tumor cells ($C$) become zero was on day 150, after which no tumor cells need to be removed.

In combination with Figures 7–12 and Table 3, it can be seen that immune cell input every 5 days can eliminate tumor cells earlier while minimizing the target value.

8.   Discussion

This study looks at the best way to control a group of dynamic fractional-order differential equations that show how the immune system, the tumor, and the normal cell interact during adoptive and surgical immune cell therapy. Findings from Amilo et al. reveal the dynamic interaction among immune cells $(I)$, tumor cells $(N)$, and spreading tumor cells $(P)$. The primary regeneration number, basic regeneration coefficient, and normalized sensitivity coefficient analyses were used to determine the essential parameters in this paper, including the tumor cell growth rate. In the study by Amilo et al. ^[31], the PD-L1 monoclonal antibody administration was adjusted with a PID controller, setting precise target levels for tumor cell populations. Treatment objectives and anticipated results were customized according to the tumor's stage and severity. These may require modification in response to patient reactions and the evolution of the tumor over time. The artificial intelligence algorithm used in this investigation was genetic ^{[43,44,45,46]}. To achieve patient-specific treatment, the best control input can be determined based on the pertinent parameters that have been defined, and various treatment outcomes and plans can be determined based on the relevant parameters of various patients.

Our research aims to combine surgical treatment and immunotherapy to shorten the time it takes for tumor cells to be destroyed and extend the life of patients. The numerical simulation results depicted in Figure 5 indicate that without treatment, when the value reaches 0.9, the patient's tumor cells will annihilate all normal cells and most immune cells in roughly 25 days. By that point, the patient's condition has significantly deteriorated, and the patient's life will soon come to an end. Figures 7–12 show that it was under control by the 65th day at the earliest and by the 125th day at the latest, following the combination of immunotherapy and surgical treatment, demonstrating the continued efficacy of our treatment. When setting the control input, we look at the different adaptive control input values at different time intervals and the control target value at different times. We do this by using the classical genetic algorithm to calculate the control input value, self-adapt, and change the time interval as needed. As demonstrated in Section 6, the control target value is ideal when the period is set at T lymphocyte input every 5 days, and this is the optimal control in our investigation.

In our study, the patient's immune cells are grown in vitro to strengthen immunity, increase lethality, and prevent immunological rejection and adverse effects on their cells. This significantly boosts the effectiveness of use and raises the patient's survival rate. Immunotherapy technology is a promising new form of cancer treatment. By combining immunotherapy with other treatment modalities (such as chemotherapy, targeted therapy, surgical resection, etc.), a comprehensive approach to cancer treatment will significantly increase the cancer's cure rate. This study combined adoptive cell immunotherapy and surgical resection to examine lung cancer treatment. The amount of surgical resection determined the rate at which tumor cells increased. The target for adjusting immune cell input was the body's total immune cell count, which was maintained to suppress and eliminate tumor cells and aid in patient recovery.

9.   Conclusions

This study provides a new perspective on treatment strategies for lung cancer through an adaptive output control approach, and oncologists and clinicians need to improve drug treatment planning. For example, the clinician can set an appropriate treatment interval in advance, use the adaptive control input to more accurately understand the input amount at each moment according to the current condition of the patient, and automatically generate the optimal drug input or immune cell input number for treatment at the next moment to achieve the best treatment effect each time. In this way, it avoids the consequence that the patient's immunity is decreased or there are too many side effects due to excessive drug use. It also avoids the therapeutic effect of insufficient drug use or the input of immune cells being too small. Specifically, our model can help clinicians adjust treatment regimens based on real-time patient responses, thereby increasing the level of personalization of treatment, and this control approach can directly affect the speed of recovery and quality of life of patients, optimizing the treatment process by reducing unnecessary side effects and reducing treatment costs.

However, this paper has some limitations. For example, the simplified assumptions about the biological process of a lung tumor in our model are based on ideal conditions, which are different from the actual situation, and the acquisition and estimation of parameters are also inconsistent with the actual situation due to the lack of data. Therefore, the application range of the model in clinical trials is limited due to these problems. Therefore, future studies can consider a wider group of patients, obtain more real patient data, train and optimize the model according to the data, further improve the model structure to more accurately describe the development process of lung cancer, and adopt more advanced parameter estimation methods to make the results of adaptive output control more accurate.

Author contributions

Wen Fang: Methodology, Formal Analysis, Software, and Writing - Original Draft. Xuewen Tan: Validation and Writing - Review & Editing. Yanbin Feng: Conceptualization, Visualization and Writing - Review & Editing.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

We are grateful to the two anonymous reviewers for their valuable comments and suggestions, which significantly enhanced the presentation of this work. This work was supported by the National Natural Science Foundation of China (No. 12361104, 12261104), the Youth Talent Program of Xingdian Talent Support Plan (XDYC-QNRC 2022-0514), the Yunnan Provincial Basic Research Program Project (No. 202301AT070016, No. 202401AT070036), the Yunnan Province International Joint Laboratory for Intelligent Integration and Application of Ethnic Multilingualism (202403AP140014).

Conflict of interest

The authors declare there is no conflict of interest.