A numerical method based on barycentric interpolation collocation for nonlinear convection-diffusion optimal control problems

1.   Introduction

Optimal control problems governed by convection-diffusion equations arise in many real-world problems such as wastewater treatment problems ^[1] and air pollution problems ^[2]. Especially it is also an important step toward optimal control problems of the fluid. Such problems have profound application prospects, which simulate some chemical or biological process between different species. It is difficult or impossible to obtain their analytical solutions, and the only way to solve them is to seek approximate solutions by using numerical methods. Thus, the extraction of their numerical algorithms is of great practical significance for scholars. In this paper, we will propose the barycentric interpolation collocation methods for optimal control problems governed by the nonlinear convection-diffusion equation, which can be written as

where $\Delta$ is the Laplace operator, $\nabla$ is the gradient operator and $v$ and $u$ are the state variable and control variable, respectively. $\hat{v}$ is the desired variable, and $\phi(v)$ represents the nonlinear term. $w$ is the so-called regularization parameter. $J\left(v, u \right)$ stands for the cost function. $\Omega$ is a bounded domain with the boundary $\partial \Omega$.

In recent years, a large number of numerical methods have been presented for optimal control problems.

Weng et al. ^[3] presented a stabilized finite element method for optimal control problems governed by a convection dominated diffusion equation. Sandilya and Kumar ^[4] proposed a discontinuous interpolated finite volume approximation of semilinear elliptic optimal control problems. Y$\rm \ddot{u}$cel et al. ^[5] applied a discontinuous Galerkin method for optimal control problems governed by a system of convection-diffusion PDEs with nonlinear reaction terms. Lu et al. ^[6] presented a priori error estimates of interpolation coefficients mixed finite element methods for semilinear Dirichlet boundary optimal control problems. Lin et al. ^[7] developed Galerkin spectral methods for optimal control problem governed by elliptic equations. Porwal and Shakya ^[8] presented a finite element method for an elliptic optimal control problem with integral state constraints. In ^[9], a bilinear pseudo-spectral method based on Chebyshev polynomials was used for convection-diffusion optimal control problems, and the coupled Sylvester system was solved by some direct and iterative methods. Wang et al. ^[10] investigated a spectral Galerkin approximation of an optimal control problems governed by a fractional advection-diffusion-reaction equation with an integral fractional Laplacian. Casanova et al. ^[11] adopted radial basis function techniques for optimal constrained optimization problems governed by linear convection-diffusion PDEs.

Recently, many researchers have developed a variety of meshless methods ^[12,13,14] for convection-diffusion problems. In particular, the barycentric interpolation collocation is a novel meshless method, which is different from the traditional element-based numerical method. It can effectively avoid the cumulative error caused by the difference scheme. Additionally, it can handle irregular domains. This method has attracted the attention of scholars due to its high precision, fast speed, good stability and convenient program execution. It was extended to solve various PDEs including linear optimal control problems ^[15,16], Sine-Gordon equations ^[17], high-dimensional Fredholm integral equations ^[18], telegraph equations ^[19], viscoelastic wave equations ^[20], the Allen-Cahn equation ^[21], nonlinear parabolic partial differential equations ^[22], etc. Lately, Yi and Yao ^[23] presented error analysis of a barycentric Lagrange interpolation (BLI) collocation scheme.

To the best of our knowledge, there are few studies about using the barycentric interpolation collocation method for the nonlinear optimal control problem described by Eq (1.1). Based on the above work, we proposed two numerical schemes for the nonlinear optimal control in two-dimensions by using BLI collocation or barycentric rational interpolation (BRI) collocation. Moreover, consistency analysis of discrete schemes is presented.

The rest of this paper is organized as follows: First, we obtain the continuous optimality system using Lagrangian multipliers in Section 2. Then, barycentric interpolation collocation methods are briefly introduced in Section 3. Two barycentric interpolation collocation schemes are proposed in Section 4, and we also provide the consistency analysis of discrete schemes. In Section 5, numerical simulations are presented to verify the accuracy and efficiency of the proposed collocation methods. Finally, conclusions are drawn in Section 6.

2.   Optimality conditions

In this section, we consider the optimize-then-discretize approach based on the Lagrangian multiplier method for solving Eq (1.1). First, we define the Lagrangian multiplier $p$ on $\Omega$ as follows

Then, the state equations are obtained by differentiating the derivative of $\mathcal{L}$ with respect to $p$

Similarly, the adjoint equations are gained by calculating the $\rm Fr\acute{e}chet$ derivative of $\mathcal{L}$ with respect to $v$

Finally, by differentiating with respect to $u$, the optimality equation is written as follows

Combining Eqs (2.2)–(2.4), Eq (1.1) can be transformed into a continuous optimality system

3.   Barycentric interpolation collocation method

In this section, we mainly introduce BLI and BRI collocation.

3.1.   Barycentric Lagrange interpolation collocation method

This part presents a novel meshless method named BLI to solve nonlinear optimal control problems. Suppose that $m\text{+}1$ distinct nodes ${{x}_{k}}$($k = 0, 1, \cdots, m$) are given together with a set of functional values ${{h}_{k}}$ at the discrete nodes ${{x}_{k}}$ correspondingly. Let $q\left(x \right)$ denote the approximate interpolation polynomial of $h(x)$, satisfying $q\left({{x}_{k}} \right) = {{h}_{k}}$ ($k = 0, 1, \cdots, m$).

As $q\left(x \right)$ is unique, we can rewrite it in the Lagrange interpolation polynomial form

where $L_{k}(x)$ is the Lagrange basis function, and $L_{k}(x) = \dfrac{{\prod\limits_{i\ne k}^{m}{(x-{{x}_{i}})}}}{{\prod\limits_{i\ne k}^{m}{({{x}_{k}}-{{x}_{i}})}}}, \text{ }i = 0, 1, \cdots, m$.

Define $\tilde{L}\left(x \right) = \left(x-{{x}_{0}} \right)\left(x-{{x}_{1}} \right)\cdots \left(x-{{x}_{m}} \right)$; thus, the basis function ${{L}_{k}}\left(x \right)$ can be expressed as

where ${\omega_{k}} = \dfrac{1}{\prod\limits_{k\ne i}{\left({{x}_{k}}-{{x}_{i}} \right)}}$ is the barycentric weight.

Supposing that $q(x) = 1$ in Eq (3.1) and inserting Eq (3.2) into Eq (3.1), the results are shown as

By dividing Eq (3.3b) by Eq (3.3a) and canceling the common polynomial $\tilde{L}(x)$, the BLI formula for $v(x)$ can be expressed as

As a matter of fact, the BLI formula has excellent numerical stability when Chebyshev points are selected, so the nodes selected in this article and the corresponding barycentric weights are

3.2.   Barycentric rational interpolation collocation method

In this subsection, we consider the derivation process of the BRI collocation method. Suppose that $(x_{0}, h_{0}), (x_{1}, h_{1}), \cdots(x_{m}, h_{m})$ are given $m+1$ interpolation nodes of the interval $[a, b]$, and that the function $h(x)$ satisfies $h(x_{k}) = h_{k}, k = 0, 1, 2\cdots m$. Additionally, $d (0\leq d \leq m)$ is a chosen integer; We define the following BRI formula:

where ${{r }_{k}}\left(x \right) = \dfrac{\dfrac{{{w }_{k}}}{x-{{x}_{k}}}}{{\sum\limits_{k = 0}^{m}{\dfrac{{{w }_{k}}}{x-{{x}_{k}}}}}}$ is the basic function and the interpolation weight ${{w }_{k}} = \sum\limits_{i\in {{J}_{k}}}{{{\left(-1 \right)}^{i}}\prod\limits_{l = i, l\ne k}^{i+d}{\dfrac{1}{{{x}_{k}}-{{x}_{l}}}}}$, ${{J}_{k}} = \left\{ i\in J|k-d\le i\le k \right\}$, $J = \left\{ 0, 1, \cdots, m-d \right\}$. More details about the BRI formula are available ^[24,25].

Similarly, the BRI formula for the binary function $h(x, y)$ with $r_{M, N}(x, y)$ can be obtained. Let us partition the domain $\Omega = [a, b]\times [c, d]$ into $\Omega_{h} = {(x_{k}, y_{j}), k = 0, 1, \cdots M, j = 0, 1, 2, \cdots N}$. Then $d_{1}\; and \; d_{2}$ are two integers, where $0\leq d_{1}\leq M$, $0\leq d_{2} \leq N$, $h(x_{k}, y_{j}) = h_{kj}$. Thus, $r_{M, N}(x, y)$ can be expressed as

where $r_{k}(x)$ and $r_{j}(y)$ are basis functions, which can be expressed as

3.3.   Differential matrix

In order to solve the optimal control problem, derivatives expressions of the barycentric interpolation formula should be derived. Obviously, the $\mu$-order derivative of $q(x)$ at the different nodes $x_{i}$ ($i = 0, 1, \cdots, M$) can be obtained as follows:

where $D_{ik}^{(\mu)}$ denotes the element of the differential matrix $D^{(\mu)}$, the recursive formula of which ^[26,27] is as follows according to the principles of mathematical induction

4.   Discrete system and consistency analysis

4.1.   Discrete scheme based on barycentric interpolation collocation method

In this part, we will establish numerical schemes for Eq (1.1) by discretizing $x$ and $y$ directions with barycentric interpolation formulae. We consider the domain $\Omega = [0, 1]\times[0, 1]$, and that the $x$ direction is discretized by $M+1$ nodes with $N+1$ nodes along the $y$ direction. Supposing that $\beta = (\beta_{1}, \beta_{2})$, the optimality conditions of Eq (1.1) are as follows

According to the barycentric interpolation formula, $v(x, y)$ and $p(x, y)$ can be written as follows

where $C_{k}(x)$ and $D_{j}(y)$ represent basis functions of the barycentric interpolation method along the $x$ and $y$ directions. And ${{v}_{kj}} = v({{x}_{k}}, {{y}_{j}})\; and\; {{p}_{kj}} = p({{x}_{k}}, {{y}_{j}}).$

Consider the $\lambda+\mu$ order partial derivative of $v\left(x, y \right)$ with respect to the spatial variables $x$ and $y$; we have

Thus, the approximate values of the partial derivatives of $v(x, y)$ at the node $\left({{x}_{q}}, {{y}_{s}} \right)$ can be written as

Similarly, we consider the $\lambda+\mu$ order partial derivative of $p(x, y)$ with respect to the variables $x$ and $y$, and its approximate value at the node $\left({{x}_{q}}, {{y}_{s}} \right)$ is

Selecting a suitable $\lambda$ and $\mu$ and then substituting Eqs (4.4)–(4.6) into Eqs (4.1) and (4.2), is implied that

with the following boundary conditions

This system can be derived by applying the matrix form

where $\otimes$ stands for the Kronecker product of the matrix, $C^{(i)}, D^{(i)} (i = 1, 2)$ are differentiating matrices of order $i$ and ${\bf V}, {\bf P}, {\bf F}, and\; \hat{{\bf V}}$ are column vectors, which can be respectively expressed as follows

4.2.   Consistency analysis

In this section, we present consistency estimates of proposed schemes based on the approximation properties of the BLI or BRI. For the unknown function $v(x, y)$, the corresponding barycentric Lagrange interpolation is $v_{h}(x, y)$, so the error $\zeta(x, y)$ can be defined as

The approximation properties of BLI have been presented ^[23] as follows

Lemma 1. If $\zeta\left(x, y\right)\in {{C}^{\left(n+1 \right)}}\left(\Omega \right)$, $\Omega = [a, b]\times[c, d]$ is a smooth and bounded domain, it holds that

where e is the natural logarithm, $c_{x}, c_{y}, \dot{c_{x}}, \dot{c_{y}}, \ddot{c_{x}}\; and\; \ddot{c_{y}}$ are positive constants, $L_{x} = \dfrac{b-a}{2}$ and $L_{y} = \dfrac{d-c}{2}$.

Suppose that $v(x_{q}, y_{s})$ and $p(x_{q}, y_{s})$ are the corresponding BLIs of $v(x, y)$ and $p(x, y)$, and we define the differential operators $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ as follows

and

Next, the consistency analysis of the BLI scheme is presented.

Theorem 1. If $v(x, y)$, $p(x, y)$ and $u(x, y)$ $\in {{C}^{(n+1) }}\left(\Omega \right)$, $\Omega = [a, b]\times[c, d]$ and the nonlinear term $\phi(v) \in W^{2, \infty}(\Omega)$ satisfies the Lipschitz condition, it holds that

where $C, \hat{C}\; and\; \tilde{C}$ are positive constants and $W^{2, \infty}(\Omega) = \{v\in L^{\infty}(\Omega) \mid \partial^{\alpha}v \in L^{\infty}(\Omega), |\alpha|\leq 2\}$ is the Sobolev space.

Proof. The definitions of the operators $\mathcal{G}_{1}$ and $\mathcal{G}_{2}$ lead to the following result

The discrete equation corresponding to Eq (4.18) is as follows

To simplify the analysis process, we first consider the terms related to the state variable $v(x, y)$. Combining Eq (4.18) with Eq (4.19), we obtain

where $\zeta_{1}, \zeta_{2}, \zeta_{3}, \zeta_{4}, \zeta_{5}\; and\; \zeta_{6}$ represent

Similarly, we have

where $R_{1}, R_{2}, R_{3}, R_{4}, R_{5}\; and\; R_{6}$ represent

Applying Lemma 1, it holds that

Since $\phi(v)$ satisfies the Lipschitz condition, assuming a positive constant $K$, we obtain

As for the $\zeta_{6}$, we have

Taking $C = max\{C_{1}, C_{2}, C_{3}, C_{4}, C_{5}, C_{6}\},$ and substituting Eqs (4.24)–(4.29) into Eq (4.20), we complete the proof of Eq (4.15).

Similarly, the approximation errors of $R_{1}, R_{2}, R_{3}\; and\; R_{4}$ can be straightforwardly proved. Now we consider the derivation process of $R_{5}\; and\; R_{6}$. Applying the Lemma 1, we derive

As $\phi(v(x, y)) \in W^{2, \infty}(\Omega)$, we have

Finally, substituting the error results of $R_{1}, R_{2}, R_{3}, R_{4}, R_{5}\; and\; R_{6}$ into Eq (4.22), the proof of Eq (4.16) can be completed.

As for the variable $u(x, y)$, it can be proved that

This completes the proof of Eq (4.17).

In the following part, we present the error analysis of Eq (1.1), as solved by the BRI scheme. The compatibility errors of two-dimensional nonlinear optimal control problems solved by the BRI method are as follows based on Theorem 1 in ^[19]

Theorem 2. If $v(x, y)$, $p(x, y)$ and $u(x, y)$ $\in {{C}^{d_{1}+4}[a, b]}\times{{C}^{d_{1}+4}[c, d]}$, $v(x_{q}, y_{s})$ and $p(x_{q}, y_{s})$ are corresponding numerical solutions solved by BRI. The nonlinear term $\phi(v) \in W^{2, \infty}(\Omega)$ satisfies the Lipschitz condition, so we have

where $C$ is the positive constant independent of the grid size $h_x$ and $h_y$; $h_{x} and h_{y}$ are step sizes of the discretized grids in the $x$ and $y$ directions, respectively.

4.3.   Fully discrete scheme based on Newton's iteration

The nonlinear term $\phi(V^{k+1})$ is expanded by using Taylor's formula at $V^{k}$, and $\phi'(V^{k+1})P^{k+1}$ is treated with

Thus, we derive the numerical scheme of Eq (1.1) based on Eq (4.9) as follows

Rewrite Eq (4.37) in matrix form

where $\textbf{A} = diag(-\alpha)\cdot(C^{(2)}\otimes I_{N}+I_{M}\otimes D^{(2)}$, $\textbf{B} = diag(\beta_{1})\cdot(C^{(1)}\otimes I_{N})+diag(\beta_{2})\cdot(I_{M}\otimes D^{(1)})\}$ and $\textbf{C} = diag(\gamma+\phi'(\textbf{V}^{k}))$.

5.   Numerical experiments

We will present two numerical examples to illustrate the accuracy and stability of our proposed methods in this section.

5.1.   Problem 1

Consider $\Omega = [0, 1]\times[0, 1]$; the exact solutions of the state and adjoint functions are as follows

with

Take the simulation parameters as follows: $\alpha = 0.3$, $\beta = [1, 1]$, $\gamma = 1$, $w = 0.5$, $d_{1} = [\dfrac{3M}{4}]$, $d_{2} = [\dfrac{3N}{4}]$, and vary the numbers of mesh nodes $M, N$, $\phi(v(x, y)) = (v(x, y))^{3}.$ The $L^\infty$ norm errors of different variables $v, p, u$ solved by a BLI, BRI or five-point finite difference (FD) scheme are shown in Tables 1–3. The computational results in Tables 1, 2 show that. Obviously, both $\rm BLI$ and $\rm BRI$ schemes for Eq (1.1) produce the higher-order accurate solutions when selecting fewer nodes. Furthermore, it is observed that the accuracy of the BLI method is slightly higher than that of the BRI method when taking the same mesh nodes. In Table 3, the obtained results illustrate that the convergence rates of FD scheme are almost second order, and thus are in line with the theoretical analysis. It can be seen that the barycentric interpolation collocation method achieves a high accuracy on the order of $10^{-7}$ with $8\times 8$ mesh nodes, while the five-point FD approach can only achieve an accuracy on the order of $10^{-4}$ using $64\times 64$ mesh nodes. This shows that the barycentric interpolation collocation method possesses higher accuracy than the FD approach.

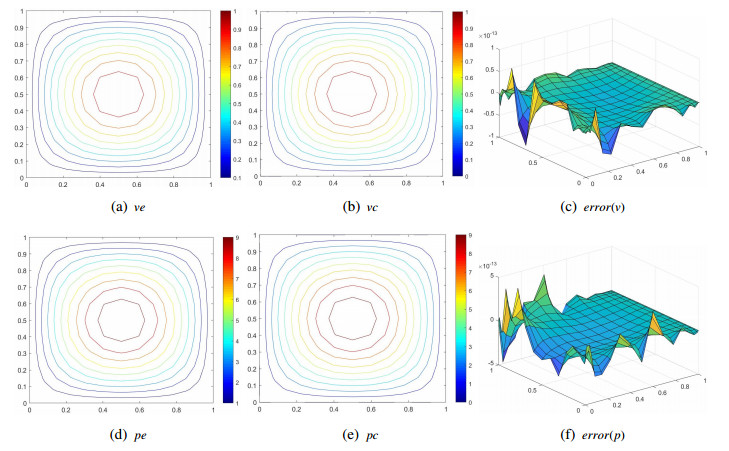
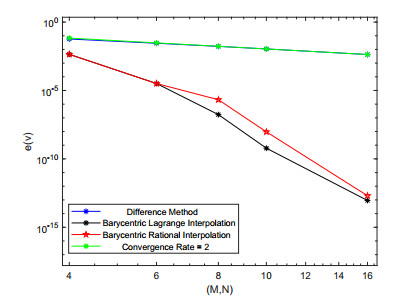
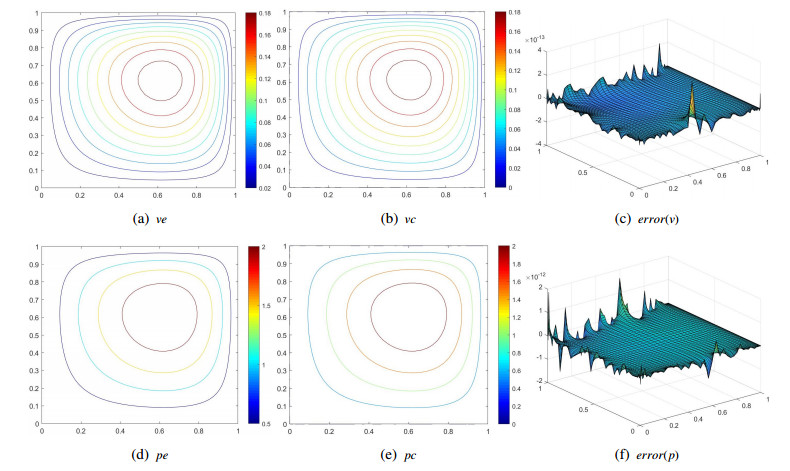
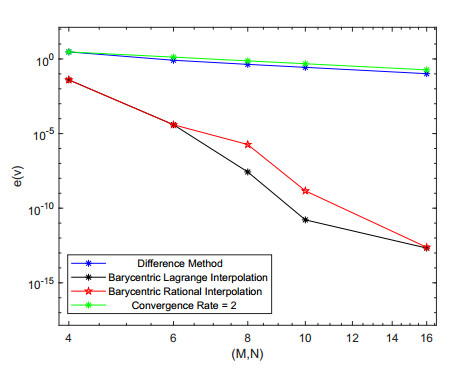
Select the nodes $M = N = 16$ to obtain the exact solution images, numerical solution images and error images of $v$, $p$, as shown in Figures 1 and 2. We can conclude that numerical solution images solved by the BLI and BRI schemes are all consistent with analytical solution images, indicating that collocation schemes are stable. Figure 3 shows that BLI and BRI schemes have exponential convergence effect when choosing different nodes. In addition, the five-point FD scheme has a second-order convergence rate.

5.2.   Problem 2

In this simulation, we consider the following exact solutions

with

We consider Eq (1.1) on the computational domain $\Omega = [0, 1]\times [0, 1]$ with homogeneous Dirichlet boundary condition and set the parameters $\alpha = 0.1, \beta = [1, 1], \gamma = 1, w = 0.3$ respectively, $d_{1} = [\dfrac{3M}{4}]$, $d_{2} = [\dfrac{3N}{4}]$. The simulation has confirmed the high accuracy and efficiency of the proposed schemes through the calculated errors in Tables 4, 5. Furthermore, the convergence rate of the FD method is almost second order in Table 6.

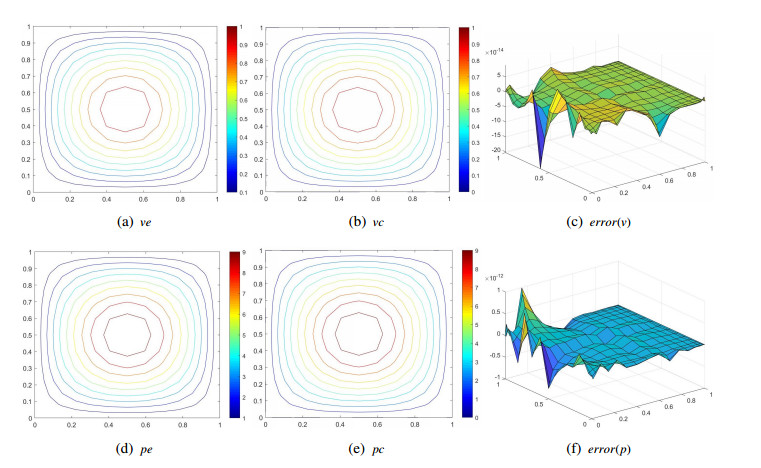
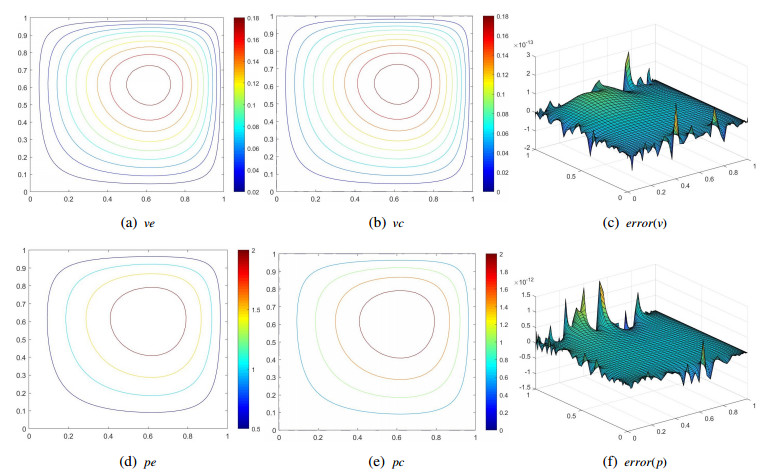
Figures 4, 5 show the exact solutions, numerical solutions and error estimates for the state and adjoint functions when selecting Chebyshev nodes $M = N = 48$. From these images, it is obvious that two barycentric interpolation collocation schemes are effective and stable with higher accuracy compared with the FD method.

Figure 6 illustrates the convergence rates of different schemes and shows that both the BLI and BRI schemes can achieve exponential convergence.

6.   Conclusion

In this paper, we proposed two barycentric interpolation collocation schemes for optimal control problems governed by the nonlinear convection-diffusion equation. The consistency analyses of the two collocation schemes have been derived. The numerical examples show that the efficiency of our proposed schemes which can achieve the higher-oder accurate solutions with fewer nodes compared with the FD method. Our future work will focus on other kinds of PDE-constrained optimal control problems such as parabolic equations, fluid equations and so on.

Acknowledgments

This work is was supported in part by the NSF of China (No. 11701197) and the Natural Science Foundation of Fujian Province (No. 2022J01308).

Conflict of interest

The authors declare that there is no conflict of interest.