A Hilliges-Weidlich-type scheme for a one-dimensional scalar conservation law with nonlocal flux

1.   Introduction

1.1.   Scope

Nonlocal conservation laws model various phenomena, such as the dynamics of crowds ^[8,9,10], vehicular traffic ^[7,18], supply chains ^[3], granular materials ^[1], and sedimentation phenomena ^[5]. These nonlocal equations are given by expressions of the type

where $\boldsymbol{\rho} = \boldsymbol{\rho}(\boldsymbol{x}, t)\in\mathbb{R}^{N}$, $N\geq1$ is the vector of the conserved quantities and the variable $W = W(\boldsymbol{x}, t, \boldsymbol{\rho})$ depends on an integral evaluation of $\boldsymbol{\rho}$. The aim of this work is to propose an approach for a rigorous treatment of boundary conditions in the case of a spatially one-dimensional nonlocal problems, through development of new numerical schemes that are more accurate and less diffusive. The strategies that we employ are inspired by the results obtained in ^[5,6,17]. Particularly, we propose to study a simplification of the problem studied in ^[5], we adopt the treatment of the boundary conditions proposed in ^[17] and we present a numerical scheme based on local one studied in ^[6,19]. Our proposed scheme takes advantage of the form in which the flow is written, namely density $\rho$ times a local decreasing factor $g(\rho)$ times a nonlocal convolution term $V(x, t) = (\omega \ast v(\rho))$, where $v$ is a given velocity function and $\omega$ is a convolution kernel such that the governing conservation law becomes

In the case of a standard (local) conservation law, captured by setting $V = \mathrm{const.}$, the above-mentioned approach results in a monotone scheme ^[6], so it is possible to invoke standard arguments to prove its convergence to an entropy solution. This idea is extended herein to the nonlocal equation (1.1), although we emphasize that the resulting scheme is not monotone.

1.2.   Related work.

There are many works about existence and uniqueness results for nonlocal equations, see e.g., ^[2,14,15,17] for the scalar case in one space dimension. In these papers a first-order Lax-Friedrichs (LxF)-type numerical scheme is used to approximate the problem and to prove the existence of solutions and the nonlocal term is considered as a convolution between a kernel function and the unknown (mean downstream density approach). LxF-type schemes are the most common approach used to solve nonlocal conservation laws because they are easy to implement and due to their monotonicity, they make it possible to numerically analyze nonlocal flux problems. Their well-known main disadvantage is, however, their large amount of numerical diffusion that smears out sharp features of the exact solution. To reduce this phenomenon, Friedrich et al. ^[16] proposed a Godunov-type numerical scheme where the nonlocal term is considered as a convolution between a kernel function and the velocity of unknown (mean downstream velocity approach). We adopt this idea about the convolution to propose and develop our model and computations. A well-known early analysis of initial-boundary value problems (IBVP) for conservation laws is due to Bardos et al. ^[4], where existence, uniqueness and continuous dependence of the solution on initial data in the case of zero boundary data are proved. These results were extended to more general but smooth boundary data by Colombo and Rossi ^[11]. Rossi ^[21] studied an IBVP for a general scalar balance law in one space dimension. Under rather general assumptions on the flux and source functions, the author proves the well-posedness of the problem and stability of its solutions with respect to variations in the flux and the source terms. For both results, the initial and boundary data are required to be bounded functions with bounded total variation. In ^[14] a global well-posedness result for a class of weak entropy solutions of bounded variations of scalar conservation laws with nonlocal flux on bounded domains is established under suitable regularity assumptions on the flux function. The nonlocal operator is the standard convolution product. The existence of solutions is obtained by proving the convergence of an adapted LxF algorithm. Lipschitz continuous dependence from initial and boundary data is derived applying Kružkov's doubling of variables technique. In ^[17] Goatin and Rossi study the same problem as De Filippis and Goatin ^[14], but with a different approach, namely following the treatment of the boundary conditions proposed by Colombo and Rossi in ^[12] where a particular multi-dimensional system of conservation laws in bounded domains with zero boundary conditions was considered. More specifically, the nonlocal operator in the flux function is not a mere convolution product, but it is assumed to be 'aware' of boundaries and by introducing an adapted LxF algorithm, various estimates on the approximate solutions that allow to prove the existence of solutions to the original IBVP are introduced. Uniqueness was derived from the Lipschitz continuous dependence on initial and boundary data, which is proved exploiting results available for the local problem.

1.3.   Outline of the paper.

This work is organized as follows: In Section 2 we present the class of nonlocal conservation laws considered and the assumptions needed the problem studied as well as the main result of this paper, whose proof is postponed to end of Section 3. Lipschitz continuous dependence of solutions to the problem on initial and boundary data is proved in Section 3. Afterwards, in Section 4 we introduce the numerical scheme and derive some of its important properties such as the maximum principle and $BV$ and $L^1$ Lipschitz continuity in time estimates. These imply convergence of the scheme proposed, which in turn covers existence part of the well-posedness of the governing model. Throughout the paper we address the new scheme as a "HW scheme" according to the proponents of the original idea (Hilliges and Weidlich ^[19]), and in Section 5 we provide a second-order version of a HW-type numerical scheme. Finally, in Section 6 we present some numerical examples, analyzing the $L^1$-error of the approximate solutions of studied problem computed with different schemes. Appendix A collects some estimates necessary throughout the paper.

2.   Initial-boundary value problem

We consider a particular initial-boundary value problem which is a version of a nonlocal model of sedimentation proposed in ^[5]. Our model has the following structure:

where

with $W(x): = \int_{a}^{b}\omega(y-x)\, \mathrm{d} y$ for a suitable convolution kernel $\omega$.

Remark 2.1. The particular combination of local and nonlocal evaluations of $\rho$ present in Eqs (2.2) and (2.3) can be motivated by following the discussion of [5, Sect. 1.2] for a model of sedimentation. Namely, if we assume that the nonlocal model describes the volume fraction of solids $\rho \in [0, 1]$ within a solid-fluid two-phase flow system, then the solid and fluid conservation equations in differential form are $\partial_t \rho + \partial_x (\rho v_{\mathrm{s}}) = 0$ and $\partial_t (1-\rho) + \partial_x ((1-\rho) v_{\mathrm{f}}) = 0$, where $v_{\mathrm{s}}$ and $v_{\mathrm{f}}$ are the solid and fluid phase velocities and $x$ is the vertical spatial coordinate. One then defines the volume average velocity of the mixture $q: = \rho v_{\mathrm{s}} +(1-\rho) v_{\mathrm{f}}$ and the solid-fluid relative velocity $v_{\mathrm{r}} = v_{\mathrm{s}} - v_{\mathrm{f}}$. Now for the particular case of batch settling in a closed column, we have $q = 0$ for all $x$ and $t$, and then $\rho v_{\mathrm{s}} = \rho(1-\rho)v_{\mathrm{r}}$, so that the unique PDE to be solved is

where $v_{\mathrm{r}}$ is specified by some constitutive function. This scenario corresponds to Eqs (2.1)–(2.3) if we choose $g(\rho) = 1-\rho$ and assume that $v_{\mathrm{r}}$ is given through the nonlocal convolution

where $\rho \mapsto v(\rho)$ is a given, in general nonlinear function. In other words, the local and nonlocal evaluations of $\rho$ in Eq (2.1) arise from the combination of properly defined volume fractions in mixture theory with the constitutive assumption in Eq (2.5). The standard local evaluation $v_{\mathrm{r}}(x, t) = v(\rho(x, t))$ corresponds to the well-known kinematic sedimentation model, while utilizing $v(\omega \ast \rho)(x, t)$ instead of $(\omega \ast v(\rho))(x, t)$ is the model alternative explored in ^[5].

Assumptions 2.1. The initial-boundary value problem (2.1) is studied under the following assumptions:

(i) The initial function satisfies $\rho_0 \in BV(I; \mathbb{R}^{+})$, where $I: = ]a, b[\subseteq \mathbb{R}^+$.

(ii) The function $g$ satisfies $g\in C^{2}([0, 1];\mathbb{R}^{+}_0)$, $g'(\rho)\leq 0$ for $\rho\in [0, 1]$, and $g(1) = 0$.

(iii) The function $v$ satisfies $v\in C^{2}([0, 1];\mathbb{R}^+)$, $v'(\rho)\leq 0$ for $\rho\in[0, 1]$, and $0 = v(1)\leq v(\rho)\leq v(0) = 1$.

(iv) The convolution kernel $\omega$ satisfies $\omega\in(C^{2}\cap W^{2, 1} \cap W^{2, \infty})(\mathbb{R}; \mathbb{R})$ such that $\int_{\mathbb{R}}\omega(y) \, \mathrm{d} y = 1$, and there exists $K_{\omega} > 0$ such that for all $x\in I$, $W(x) = \int_{a}^{b}\omega(y-x)\, \mathrm{d} y\geq K_{\omega}$.

In what follows, we denote $\| \cdot \|_{L^{\infty}([0, 1])}: = \| \cdot \|_{\infty}$. The weak entropy solution of problem (2.1) is defined, as in ^[14,17], in the following sense:

Definition 2.1. A function $\rho\in(L^1\cap L^{\infty}\cap BV)(]a, b[\times\mathbb{R}^{+}; \mathbb{R})$ is an entropy weak solution if for all $\varphi\in C_{\mathrm{c}}^{1}(\mathbb{R}^2;\mathbb{R}^{+})$ and $k\in\mathbb{R}$,

Definition 2.2. A function $\rho\in L^{\infty}(]a, b[\times\mathbb{R}^{+}; [0, 1])$ is an entropy weak solution to problem (2.1) if, for all $\varphi\in C_{\mathrm{c}}^{1}(\mathbb{R}^{2}, \mathbb{R}^{+})$ and $k\in\mathbb{R}$,

where

Here we have used the notation $s^{+}: = \max\{s, 0\}$, $s^{-}: = \max\{-s, 0\}$, and

Definition 2.1 will be useful in the existence proof, while Definition 2.2 will be used in the uniqueness proof. We need to remark that in the frame of functions in $L^{\infty}$, Definition 2.2 implies Definition 2.1, for more details see ^[20]. In the rest of the paper, we denote $\mathcal{I}(r, s): = [\min\{r, s\}, \max\{r, s\}]$ for any $r, s\in\mathbb{R}$.

Our main result concerning the new model is given by the following theorem, which states the well-posedness of the problem.

Theorem 2.1 (Well-posedness). Let $\rho_0\in BV(I; \mathbb{R}^{+})$, $\rho_{a}, \rho_{b}\in BV(\mathbb{R}^{+}; [0, 1])$ and Assumptions 2.1 be in effect. Then, for all $T > 0$, the Cauchy problem (2.1) admits a unique entropy weak solution $\rho\in(L^1\cap L^{\infty}\cap BV)(I\times [0, T];\mathbb{R}^{+})$ in the sense of the Definitions 1 and 2. Moreover, the following estimates hold: for any $t\in[0, T]$,

and for $\tau > 0$,

where $L$ is defined by Eq (2.6) and

The proof consists of two parts: existence and uniqueness of entropy solutions. While uniqueness follows from the Lipschitz continuous dependence of weak entropy solutions on initial and boundary data, existence is based on a construction of a converging sequence of approximate solutions defined by a numerical scheme.

3.   Uniqueness of entropy solutions

One part of the proof of Theorem 2.1 is to show uniqueness of weak entropy solutions for the model (2.1). Therefore, we prove the Lipschitz continuous dependence of weak entropy solutions with respect to initial and boundary data. Here, we follow ^[17]. We define $V(x, t)$ by Eq (2.3) and analogously $U(x, t)$ by replacing $\rho$ in Eq (2.3) by another function $\sigma$. Furthermore, we let $r(x, t, u) : = ug(u)V(x, t)$ and $h(x, t, u) : = ug(u)U(x, t)$. Observe that by the definition of $V$ and $U$,

furthermore, we have the following estimates derived in Appendix A:

In order to obtain the desired estimate, we first consider the local initial-boundary value problem

By Assumptions 2.1, $r \in C^{2}(I\times[0, T] \times \mathbb{R}; \mathbb{R})$ and $\partial_{u} r \in L^{\infty}(I\times[0, T]\times\mathbb{R}; \mathbb{R})$ and by estimation Eq (3.1), $\partial_{xu}^{2} r (x, t, u) < \infty$. Thus, we may apply Theorem 2.4 of ^[21] to deduce that problem (3.1) admits a unique solution in $(L^{\infty}\cap BV)(I\times]0, T[;\mathbb{R})$ which satisfies, for all $t\in[0, T[$, $0\leq\phi(x, t) \leq1$ for all $x\; \in I$ and

where

Assume that $\rho$ is a solution to the IBVP

and that $\sigma$ is a solution to the analogous IBVP

Therefore, for $t > 0$ we compute

where the first term on the right-hand side of Eq (3.7) evaluates the distance between solutions to IBVPs with the same flux function, but different initial and boundary data. Then, we can apply Proposition 3.7 of ^[21] to get

Now, the second term on the right-hand side of Eq (3.7) evaluates the distance between solutions to IBVPs with different flux functions, but same initial and boundary data. Therefore, we apply Theorem 2.6 of ^[21] to obtain

where

Next, we estimate all terms appearing in Eq (3.8). First of all, by Theorem 2.1,

with

Thus, by Eqs (3.6) and (3.9), we get

To handle the first term on the right-hand side of Eq (3.8), we use the estimate

which implies

Next, in view of $\partial_{u}(r-h)(x, t, u) = \partial_{u}(ug(u))(V-U)$ we get

The third integral on the right-hand side of Eq (3.8) is estimated by considering that

hence

the fourth integral is treated similarly. Finally, combining Eq (3.10) to Eq (3.13) we get

where we define

Inserting $A (t)$ and Eq (3.14) into Eq (3.7) yields

so by an application of Gronwall's lemma we arrive at the estimate

Consequently, we have proved the following lemma.

Lemma 3.1 (Lipschitz continuous dependence on initial and boundary data). If Assumptions Eq (2.1) are in effect and $\rho$ and $\sigma$ are two entropy solutions to Eq (2.1) with initial data $\rho_{0}, \ \sigma_{0}\in BV{(I; \mathbb{R}^{+})}$ and $\rho_{a}, \rho_{b}, \sigma_{a}, \sigma_{b}\in BV{(]0, T[;[0, 1])}$, then the estimate

holds for any $T > 0$, where $B(T)$ is defined in Eq (3.15).

4.   Existence of solutions

The proof of existence of solutions consists of several steps that are developed in this section. We construct a sequence of approximate solutions to Eq (2.1) and derive the compactness estimates necessary to prove its convergence by Helly's theorem. We then show that the limit function is a weak entropy solution to the IBVP (2.1).

4.1.   Numerical scheme

Fix $T > 0$, we take a space step $\Delta x = (b-a)/M$ with $M\in\mathbb{N}$ and a time step $\Delta t$ that is subject to a CFL condition specified later, and we set $\lambda = \Delta t/\Delta x$. We denote the center of the cells by $x_j: = a+(j-1/2)\Delta x$ for $j = 1, \dots, M$, and $x_{j+1/2} = a+j\Delta x, \; j = 0, \dots, M$ are the cells interfaces. Moreover, we set $N_{T} = \lfloor T\Delta t \rfloor$ and, for $n = 0, \dots, N_{T}$ let $t^{n} = n\Delta t$ be the time mesh. The initial datum and the boundary data are approximated as

furthermore, we set $\rho_{0}^{n}: = \rho_{a}$ and $\rho_{M+1}^{n}: = \rho_{b}$. For $n = 0, \dots, N_{T}-1$, we set $\omega^{k}: = \omega((k-1/2)\Delta x)$ for $k\in\mathbb{Z}$ and define

We define a piecewise constant approximate solution $\rho_{\Delta}(x, t)$ to Eq (2.1) as

where $n = 0, \dots, N_{T}-1$, $j = 1, \dots, M$, through the numerical scheme

where a nonlocal version of the monotone numerical flux proposed in ^[19] and also used in ^[6] is employed, namely

Next, we study the properties of the numerical scheme (4.2) and (4.3). Particularly, we are going to prove that the sequence of approximate solutions $\rho_{\Delta}(x, t)$ satisfies the assumptions of Helly's compactness theorem.

4.2.   Uniform bounds of numerical solutions

Lemma 4.1 (Maximum principle). If Assumptions 2.1 and the CFL condition

hold, then if $\rho_0(x)\in [0, 1]$ for $x\in I$, the approximate solution satisfies

Proof. We assume that $0\leq\rho^{n}_{j}\leq1$ for $j = 1, \dots, M$. From Eq (4.2) we have

In view of $\smash{G'(\rho) = 1+\lambda g'(\rho)V^{n}_{j-1/2}}$, under the CFL condition (4.4), $G$ is a non-decreasing function of $\rho$. Thus

which implies that $\rho^{n+1}_{j}\leq1$. Returning to Eq (4.2), we obtain that

Consequently, if Eq (4.4) is in effect, then $\rho^{n+1}_{j}\geq0$.

Lemma 4.2 ($L^1$ bound). Let Assumptions 2.1 and the CFL condition (4.4) hold. If $\rho_0\in L^{\infty}(I; [0, 1])$ and $\rho_{a}, \rho_{b}\in L^{\infty}(\mathbb{R}^{+}; [0, 1])$, then, for all $t > 0$, $\rho_{\Delta}$ satisfies

where $L$ is defined in Eq (2.6).

Proof. Lemma 4.1 (for $n = 0, \dots, N$) and the assumption $g(1) = 0$ imply

where $\smash{\zeta_j^n\in \mathcal{I}(\rho_b^n, 1)}$. Now, using item (ii) of Assumptions 2.1 and the nonnegativity of $\rho_a^n$ and $\rho_b^n$ we have

An iterative argument yields the desired estimate (4.5).

Lemma 4.3 ($BV$ estimate in space). Let Assumptions 2.1 hold, $\rho_0\in BV(I; \mathbb{R}^{+})$, $\rho_{a}, \rho_{b}\in BV(\mathbb{R}^{+}, [0, 1])$ and let $\rho_{\Delta}$ be given by Eq (4.2). If the CFL condition (4.4) holds, then for all $n = 1, \dots, N_{T}$ the discrete space $BV$ estimate

is satisfied, where we define the time-dependent bound

and $\mathcal{K}_{1}$ and $\mathcal{K}_{2}$ are defined as

Proof. Subtracting two versions of Eq (4.2) from each other, we obtain

where

A straightforward computation reveals that $\smash{\mathcal{A}_{j}^{n}}$ can be written in the form

where $\smash{\xi_{j+3/2}^{n}\in\mathcal{I}(\rho^n_{j+1}, \rho^n_{j+2})}$. By the CFL condition (4.4), the first term in the right-hand side of Eq (4.9) is positive, thus summing over $j\in\{1, \dots, M-1\}$ yields

On the other hand,

Taking absolute values and summing over $j\in\{1, \dots, M-1\}$ we have

By using the following estimations (which are proved in Appendix A)

we obtain

We now deal with the boundary terms, first for the left boundary term. By the definition of the scheme (4.2),

Taking absolute values, invoking Eq (4.4) and using Eq (4.11) we obtain

An analogous discussion of the other boundary term yields

Finally, collecting the estimates Eqs (4.10), (4.12), (4.13) and (4.14) we arrive at

with $\mathcal{L}$, $\mathcal{W}$, $\mathcal{K}_{1}$ and $\mathcal{K}_{2}$ defined as in Eqs (2.10), (2.11), and (4.8). The previous estimate implies Eqs (4.6) and (4.7) by standard arguments.

Lemma 4.4 ($BV$ estimate in space and time). Let $\rho_{0}\in BV(I; \mathbb{R}^{+})$ and $\rho_{a}, \ \rho_{b}\in BV(\mathbb{R}^{+}; [0, 1])$. If Assumptions 2.1 and the CFL condition (4.4) hold, then for all $n = 0, \dots, N_{T}$, the estimate

holds, where

Proof. By Lemma 4.3 we have

By the definition of numerical scheme (4.2), for $m\in\{0, \dots, n-1\}$ and $j\in\{1, \dots, M\}$ we get

Multiplying the last inequality by $\Delta x$ and summing for $j$ from $1$ to $M$ we get

Lemmas 4.2 and 4.3 now imply that

where we define

In particular,

which, summed over $m = 0, \dots, n-1$, yields

Summing Eqs (4.16) and (4.18) we get the desired estimate Eq (4.15).

4.3.   Convergence analysis

Lemmas 4.1 and 4.4 allow us to apply Helly's compactness theorem that ensures the existence of a subsequence of $\rho_{\Delta}$, still denoted by $\rho_{\Delta}$, that converges in $L^1$ to a function $\rho\in L^{\infty}(I\times[0, T])$, for all $T > 0$. Now we need to prove that this limit function is indeed an entropy weak solution to Eq (2.1) in the sense of Definition 2.2. First we will show that the approximate solutions obtained by the scheme (4.2) satisfies a discrete entropy inequality. To this end, for $j = 1, \dots, M$, $n = 0, \dots, N_{T}-1$, and $k\in\mathbb{R}$, we define

where $w\wedge z: = \min \{ w, z \}$, $w\vee z: = \max \{w, z\}$, and $\smash{F_{j+1/2}^{n}(u, w)}$ is defined as in Eq (4.3). Observe that due to the definition of the scheme,

and we also recall the equivalence $(s-k)^{+} = s\vee k-k$ and $(s-k)^{-} = k-s\wedge k$.

Lemma 4.5 (Discrete entropy inequalities). If Assumptions 2.1 and the CFL condition (4.4) are in effect, then the approximate solution $\rho_{\Delta}$ in Eq (4.1) satisfies the discrete entropy inequalities

for $j = 1, \ldots, M, \ n = 0, \ldots, N_{T}-1$ and $k\in\mathbb{R}$.

Proof. By the CFL condition (4.4), the map $\smash{(u, w, z)\mapsto H_{j}^{n}(u, w, z)}$ satisfies

Notice that

The monotonicity properties Eq (4.21) imply that

moreover, we also have

hence

which proves Eq (4.19), while Eq (4.20) is proven in an entirely analogous way.

Remark 4.1. Lemma 4.5 and its proof mimic standard arguments known for monotone schemes of local conservation laws ^[13], although the scheme is not monotone in the proper sense since the argument Eq (4.21) suppresses the presence of $\smash{\rho_{j-1}^n}$, $\smash{\rho_{j}^n}$ and $\smash{\rho_{j+1}^n}$ within $\smash{V_{j-1/2}^n}$ and $\smash{V_{j+1/2}^n}$.

Lemma 4.6. Let $\rho_{0}\in BV(]a, b[;\mathbb{R}^{+})$, $\rho_{a}, \rho_{b}\in BV(\mathbb{R}^{+}; \mathbb{R}^{+})$, and Assumptions 2.1 and the CFL condition (4.4) be in effect. Then the piecewise constant approximate solutions $\rho_{\Delta}$ in Eq (4.1) resulting from the HW scheme (4.2) converge, as $\Delta x\to 0$, towards an entropy weak solution of initial boundary value problem (2.1).

Proof. Adding and subtracting $\smash{\lambda G_{j+1/2}^{n, k}(\rho_{j}^{n}, \rho_{j}^{n})}$ we may rewrite Eq (4.19) as

Let $\varphi\in C_{\mathrm{c}}^{1}([0, T]\times I; \mathbb{R}^{+})$ for some $T > 0$. Multiplying the inequality above by $\Delta x\varphi(x_{j}, t^{n})$ and summing over $j = 1, \dots, M$ and $n\in\mathbb{N}$ yields

where we define the terms

Summing by parts, we obtain

and by the dominated convergence theorem,

Again by the dominated convergence theorem,

Concerning $T_{2}$ and $T_{3}$, we get

where we define

Now we define

Since

it follows that

Let us rewrite $S$ in Eq (4.22) as follows:

where we define

Adding and subtracting $\smash{G_{j+1/2}^{n, k}(\rho_{j}^{n}, \rho_{j}^{n})}$, we may rewrite $S_{20}$ as

We evaluate now the distance between $T_{20}$ and $S_{20}$:

since

in light of the uniform $BV$ estimate Eq (4.6) we deduce that

Furthermore, we obtain

which we can write as $S_{30}-T_{30} = R_{1}+R_{2}+R_{3}$ with

Observe that

meaning that the numerical flux is increasing with respect to the first variable and the decreasing with respect to the second one. Consequently,

hence

Taking into account that

we get

thanks to the maximum principle estimate. Hence, $S_{30}-T_{30}\leq\mathcal{O}(\Delta x),$ so that we finally get

This concludes the proof.

Proof of Theorem 2.1. The existence of solutions to problem (2.1) follows from the results of Section 4. The uniqueness is ensured by the Lipschitz continuous dependence of solutions to Eq (2.1) on initial and boundary data, see Section 3. The estimates on the solution to Eq (2.1) are obtained from the corresponding discrete estimates passing to the limit. In particular, the $L^1$ bound follows from Eq (3), the maximum principle from Eq (2), the total variation bound from Eq (4) and the Lipschitz continuity in time from Eq (4.17), since $\Delta x = \Delta t / \lambda$ and taking $\lambda = 1 / L$.

5.   A second-order scheme

The scheme given by Eqs (4.2), (4.3) is only first-order accurate. We propose here a second-order accuracy scheme, constructed using MUSCL-type variable extrapolation and Runge-Kutta temporal differencing. To implement it, we approximate $\rho(x, t^{n})$ by a piecewise linear functions in each cell, i.e. $\hat{\rho}_{j}(x, t^{n}) = \rho_{j}^{n}+\sigma_{j}^{n}(x-x_{j}),$ where the slopes $\sigma_{j}^{n}$ are calculated via the generalized minmod limiter, i.e.

where $\vartheta\in[1, 2]$ and

This extrapolation enables one to define left and right values at the cell interfaces respectively by

and

where $\hat{W}_{j+1/2} = \int_{a}^{b}\omega(y-x_{j+1/2})\mathrm{d} y$ is computed in exact form, and $y_e$ are the Gauss-Lobatto-Quadrature points. The MUSCL version of the numerical flux reads

To achieve formal second-order accuracy also in time, we use second-order Runge-Kutta (RK) time stepping. More precisely, if we write our scheme with first-order Euler time differences and second-order spatial differences formally as

then the RK version takes the two-step form

6.   Numerical examples

In this section we solve Eq (2.1) by using the numerical scheme (4.2) on the $x$-interval $I = [0, 1]$ with suitable boundary conditions and $t\in[0, T]$, with $T$ specified later. In the numerical examples we consider the equation (2.1) with $g(\rho) = 1-\rho$ and $v(\rho) = (1-\rho)^{4}$, where we recall that $f(\rho) = \rho g(\rho)$ and $V(x, t) = (\omega \ast v(\rho))(x, t)$, where the kernel function $\omega(x)$ is specified later in each case. For numerical experiments the interval $I$ is subdivided into $M$ subintervals of length $\Delta x = 1/M$, and the time step is computed taking account the CFL condition (4.4), and for each numerical experiment, we specify the inital and boundary conditions.

6.1.   Example 1

In this example we compare numerical approximations obtained by scheme (4.2) with those generated by an adapted LxF-type scheme proposed by Goatin and Rossi in ^[17], starting from the initial and boundary conditions

Here we employ the symmetric kernel function

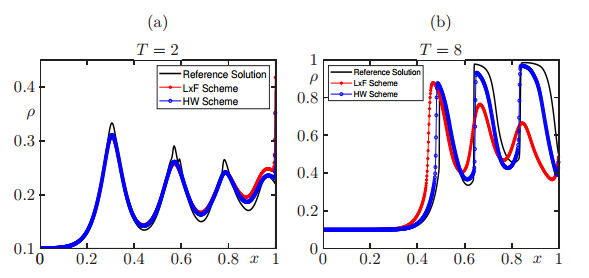
with $\eta = 0.05$. In Figure 1 we display the numerical approximations for $M = 800$ at simulated times $T = 2$ and $T = 8$ and compare them with the reference solution which is computed with the LxF scheme with $M_{\mathrm{ref}} = 12800$. We observe better accuracy for the proposed scheme. This property also becomes apparent in Table 1 where we show the corresponding approximate $L^1$ errors for discretizations $M = 100\times 2^l$, $l = 0, 1, \dots, 4$ and respective experimental orders of convergence (E.O.C.). We observe that the approximate $L^1$ errors decrease as the grid is refined and E.O.C. assumes values close to one, in agreement with the formal first order of acccuracy of the scheme.

6.2.   Example 2

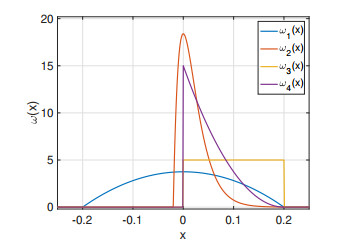
We now compare the dynamics in the solution of model (2.1) by using various kernel functions. We consider the symmetric kernel $\omega_{1}$ Eq (6.1) as in Example 1 along with a non-symmetric kernel

and the anisotropic discontinuous kernels

where in all cases we choose $\eta = 0.2$. In Figure 2 we display the different kernel functions. The initial and boundary conditions are given by

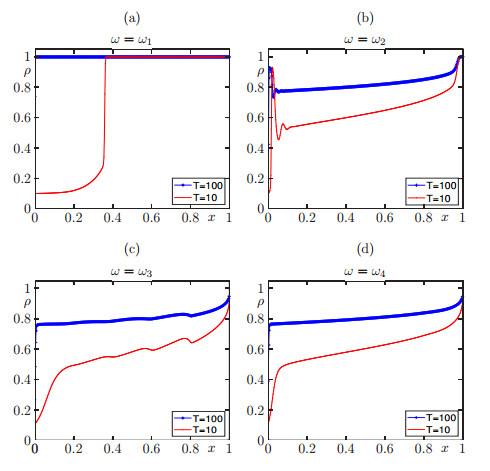
In Figure 3 we display numerical approximations with $\Delta x = 1/400$ at times $T = 10$ and $T = 100$. We can evidence that the dynamics of the solution is different for each kernel functions; by using $\omega_1$ we observe that numerical solution goes faster to a stationary state solution than for other kernel functions, in which this stationary state is not observed for enough large simulation time. Regarding the kernel $\omega_{2}$ we can see the formation of some oscillations. Now, for the kernel $\omega_{3}$ we can see the formation of some layers on the numerical solution and that the period of these layers are proportional to $\eta$. Finally, for $\omega_{4}$ we can observe a numerical solution more smooth than in the previous solutions.

6.3.   Example 3

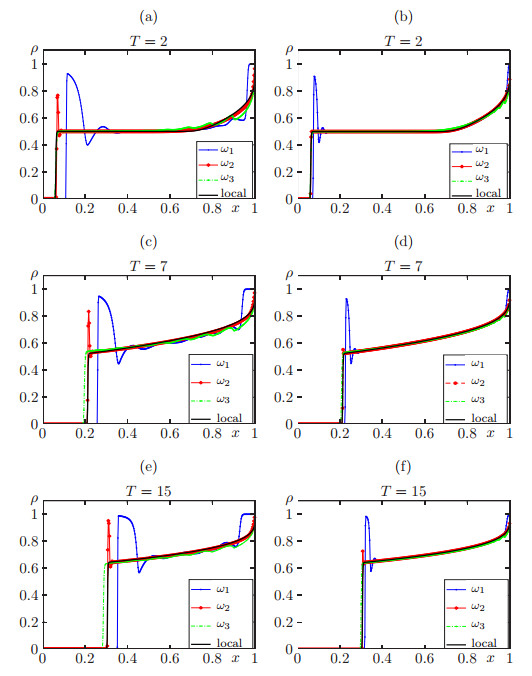
The aim of the present example is to investigate the behavior of numerical solutions considering the kernel functions $\omega_{1}$, $\omega_{2}$, and $\omega_{3}$ as well as for two different values of the parameter $\eta$, namely $\eta = 0.1$ and $\eta = 0.025$. The initial and boundary conditions are

which leaves zero flow conditions at boundary, i.e., $f_{1/2} = f_{M+1/2} = 0$. Numerical approximations are computed at simulated times $T = 2$, $T = 7$ and $T = 15$ with discretization $M = 400$. In Figure 4, first we observe that numerical solutions for the nonlocal problem (2.1) get closer to the solution of the local problem as $\eta$ takes a smaller value, but $\omega_{1}$ and $\omega_{2}$ make it slower due to the presence of the oscillations that the numerical solutions present when we use these functions.

6.4.   Example 4: Error test for second order scheme

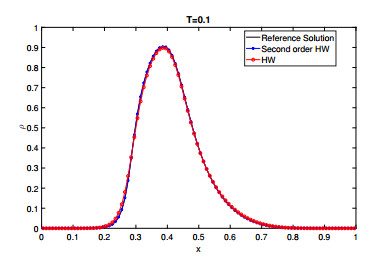
We consider the problem (2.1), with a smooth initial datum

with boundary conditions $\rho_a = \rho_b = 0$, and with the symmetric kernel function $\omega_1$ with $\eta = 0.2$. In Figure 5 we display the numerical approximations obtained with the second order scheme (5.1), (5.2), computed with $M = 100$ at $T = 0.1$. The reference solution is computed with $M = 6400$. As expected, the numerical solutions obtained with second order version of the HW scheme capture the reference solution better than the first order one. In Table 2 we compute the $L^{1}-$error and E.O.C. We recover the correct order of accuracy for the second order HW scheme. Instead, we obtain just first order accuracy for HW scheme (4.2). We also can observe for scheme (4.2) that the $L^{1}-$error for each level of refinement is bigger than the error of the second order version scheme.

7.   Conclusions

In this paper we extend to its nonlocal version a numerical scheme presented in ^[6,19] where we take advantages of the form in which the flow is written, $\rho v(\rho)V(x, t)$, where $v(\rho)$ is a positive and non-increasing function, and $V(x, t)$ is a positive function containing the nonlocal terms. We have proved maximum principle, $L^1$-bound, and $BV$ estimations, also, a discrete entropy inequality in order to prove the well-posedness of an 1-D and nonlocal IBVP. In future work, we aim to investigate how to extend this numerical scheme in applications such as crowd dynamics models where the function $V(x, t)$ is a vector field containing the preference directions and nonlocal corrections terms.

Acknowledgments

RB, HDC and LMV are supported by project MATH-Amsud 22-MATH-05 "NOTION - NOn-local conservaTION laws for engineering, biological and epidemiological applications: theoretical and numerical" (2022–2023). RB, HDC and LMV are supported by ANID (Chile) through Anillo project ANID/PIA/ACT210030; Centro de Modelamiento Matemático (BASAL projects ACE210010 and FB210005). RB, HDC and LMV are supported by the Inria Associated team "NOLOCO - efficient numerical schemes for non-local transport phenomena" (2018-2022). RB is supported by CRHIAM, project ANID/Fondap/ 15130015 and Fondecyt project 1210610. HDC is supported by the National Agency for Research and Development, ANID-Chile through Scholarship Program, Doctorado Becas Chile 2021, 21210826.

Conflict of interest

The authors declare there is no conflict of interest.

Appendix A.   Technical estimates

In this appendix we show the computations for some estimates used in the proofs of above sections. First, we prove estimates Eq (4.11) in the proof of Lemma 4.3. We denote $y_{k}: = (k-1/2)\Delta x$, for $k\in\mathbb{Z}$ and then we compute

with $\mathcal{L} = 2 K_{\omega}^{-1} \|v\|_{\infty}\|\omega'\|_{L^{1}(\mathbb{R})}$. Now following closely ^[17], we compute

where we set $\mathcal{W}: = 2 K_{\omega}^{-1}\|v\|_{\infty}\|\omega''\|_{L^{1}(\mathbb{R})} + 4K_{\omega}^{-2} \|\omega'\|_{L^{1}(I)}^{2}\|v\|_{\infty}$ and $\xi_{k-j+1/2}\in]y_{k-j-1}, y_{k-j}[$. This concludes the proof of estimates Eq (4.11) in the proof of Lemma 4.3. Next, we establish estimates Eq (3.1) to Eq (3.4) in Section 3.1. To this end we calculate

with $\mathcal{M}$ as in Eq (3.4).