On the local theory of prescribed Jacobian equations revisited

Neil S. Trudinger; Neil S. Trudinger

doi:10.3934/mine.2021048

Mathematics in Engineering

2021, Volume 3, Issue 6: 1-17. doi: 10.3934/mine.2021048

Previous Article Next Article

Research article Special Issues

On the local theory of prescribed Jacobian equations revisited

Neil S. Trudinger ^,

Mathematical Sciences Institute, Australian National University, Canberra, ACT 0200, Australia

Received: 17 December 2020 Accepted: 14 January 2021 Published: 01 February 2021

In this paper we revisit our previous study of the local theory of prescribed Jacobian equations associated with generating functions, which are extensions of cost functions in the theory of optimal transportation. In particular, as foreshadowed in the earlier work, we provide details pertaining to the relaxation of a monotonicity condition in the underlying convexity theory and the consequent classical regularity. Taking advantage of recent work of Kitagawa and Guillen, we also extend our classical regularity theory to the weak form A3w of the critical matrix convexity conditions.

Keywords:

Citation: Neil S. Trudinger. On the local theory of prescribed Jacobian equations revisited[J]. Mathematics in Engineering, 2021, 3(6): 1-17. doi: 10.3934/mine.2021048

Related Papers:

[1]	M. Mossa Al-Sawalha, Safyan Mukhtar, Azzh Saad Alshehry, Mohammad Alqudah, Musaad S. Aldhabani . Chaotic perturbations of solitons in complex conformable Maccari system. AIMS Mathematics, 2025, 10(3): 6664-6693. doi: 10.3934/math.2025305
[2]	M. B. Almatrafi, Mahmoud A. E. Abdelrahman . The novel stochastic structure of solitary waves to the stochastic Maccari's system via Wiener process. AIMS Mathematics, 2025, 10(1): 1183-1200. doi: 10.3934/math.2025056
[3]	Naseem Abbas, Amjad Hussain, Mohsen Bakouri, Thoraya N. Alharthi, Ilyas Khan . A study of dynamical features and novel soliton structures of complex-coupled Maccari's system. AIMS Mathematics, 2025, 10(2): 3025-3040. doi: 10.3934/math.2025141
[4]	Mohammad Alqudah, Manoj Singh . Applications of soliton solutions of the two-dimensional nonlinear complex coupled Maccari equations. AIMS Mathematics, 2024, 9(11): 31636-31657. doi: 10.3934/math.20241521
[5]	Mahmoud A. E. Abdelrahman, S. Z. Hassan, R. A. Alomair, D. M. Alsaleh . Fundamental solutions for the conformable time fractional Phi-4 and space-time fractional simplified MCH equations. AIMS Mathematics, 2021, 6(6): 6555-6568. doi: 10.3934/math.2021386
[6]	Hammad Alotaibi . Solitary waves of the generalized Zakharov equations via integration algorithms. AIMS Mathematics, 2024, 9(5): 12650-12677. doi: 10.3934/math.2024619
[7]	E. S. Aly, Mahmoud A. E. Abdelrahman, S. Bourazza, Abdullah Ali H. Ahmadini, Ahmed Hussein Msmali, Nadia A. Askar . New solutions for perturbed chiral nonlinear Schrödinger equation. AIMS Mathematics, 2022, 7(7): 12289-12302. doi: 10.3934/math.2022682
[8]	Jamshad Ahmad, Zulaikha Mustafa, Mehjabeen Anwar, Marouan Kouki, Nehad Ali Shah . Exploring solitonic wave dynamics in the context of nonlinear conformable Kairat-X equation via unified method. AIMS Mathematics, 2025, 10(5): 10898-10916. doi: 10.3934/math.2025495
[9]	Azzh Saad Alshehry, Safyan Mukhtar, Ali M. Mahnashi . Optical fractals and Hump soliton structures in integrable Kuralay-Ⅱ system. AIMS Mathematics, 2024, 9(10): 28058-28078. doi: 10.3934/math.20241361
[10]	Yousef F. Alharbi, E. K. El-Shewy, Mahmoud A. E. Abdelrahman . New and effective solitary applications in Schrödinger equation via Brownian motion process with physical coefficients of fiber optics. AIMS Mathematics, 2023, 8(2): 4126-4140. doi: 10.3934/math.2023205

Abstract

1. Introduction

Nonlinear evolution equations (NLEEs) are utilized in order to display many complex phenomena arising in various fields of applied sciences, such as superfluid, chemical engineering, thermal engineering, plasma physics, optical fibers and so on ^{[1,2,3,4,5,6,7,8]}. There are many scientists in various fields of natural sciences are interested in investigation of the nonlinear phenomena. Various vital analytical methods have been proposed and developed to extract the solutions of different kinds of NLEEs, see ^{[9,10,11,12,13,14,15,16,17,18]}. Moreover, there are recent development in studying the dynamics of soliton solutions and analytical closed-form solutions ^{[19,20,21,22,23,24,25,26,27,28,29,30]}.

The Maccari (MS) system, derived by Maccari in 1996 with a reduction technique based on spatio-temporal rescaling, from the Kadomtsev-Petviashvili equation ^[31]. This system is a kind of NLEEs that are often introduced to prescribe the motion of the isolated waves, localized in a small part of space, in various fields such as plasma physics, quantum mechanics, Bose-Einstein condensates, optical fiber communications and so on ^{[32,33,34,35,36,37,38,39]}. Recently, some investigations presented new novel concepts in wave motions and pulses in the study of nonlinear unforeseen critical behaviors such as the electrostatic noise in auroura, the acoustics wave in fluid and telltales wiggle electric fields ^{[40,41,42,43]}.

In this article, we consider the coupled MS ^[32,35,44], given as follows:

$\begin{equation} \begin{array}{l} iQ_t+Q_{xx}+RQ = 0, \\ R_{t}+R_{y}+(\mid Q \mid^2)_{x} = 0, \end{array} \end{equation}$

(1.1)

where $Q = Q(x, y, t)$ denotes the complex scalar field and $R = R(x, y, t)$ denotes the real scalar field. The independent variables are $x, y$ and $t$ denotes the temporal variable.

Also, we can consider the coupled nonlinear MS ^[45], given as follows:

$\begin{equation} \begin{array}{l} iQ_t+Q_{xx}+RQ = 0, \\ i\, S_{t}+S_{xx}+RS = 0, \\ R_{t}+R_{y}+(\mid Q+S \mid^2)_{x} = 0, \end{array} \end{equation}$

(1.2)

where $Q = Q(x, y, t)$ and $S = S(x, y, t)$ denote the complex scalar fields and $R = R(x, y, t)$ denotes the real scalar field.

Moreover, we consider the coupled nonlinear MS ^[34], described as follows:

$\begin{equation} \begin{array}{l} i\, Q_t+Q_{xx}+RQ = 0, \\ i\, S_{t}+S_{xx}+RS = 0, \\ i\, N_{t}+N_{xx}+RN = 0, \\ R_{t}+R_{y}+(\mid Q+S+N \mid^2)_{x} = 0, \end{array} \end{equation}$

(1.3)

where $Q = Q(x, y, t)$ , $S = S(x, y, t)$ , $N = N(x, y, t)$ denote the complex scalar fields and $R = R(x, y, t)$ denotes the real scalar field.

Our study is motivated to grasp some new solutions for the three coupled models of MS by using the unified solver method. This solver introduces some families of solutions in explicit way with free physical parameters. These solutions admit pivotal applications in plasma environments, superfluid, plasma physics, nonlinear optic^[46,47]. The proposed solver will be utilized as a box solver for solving many other nonlinear models arising in applied science and new physics. In contrast to other methods, this solver preserves several advantages, such as, it avoids complex and tedious calculations and presents pivotal solutions in an explicit way. Moreover, this solver is simple, robust, well ordered and efficacious. The proposed solver will be significant for mathematicians, engineers and physicists. To the best of our knowledge, no previous work has been done using the proposed solver for solving the MS systems.

The present article is organized as follows. Section 2 describes the unified solver technique. Section 3 presents the solutions for three coupled of the Maccari's systems. Section 4 gives the physical interpretation of the presented results. Moreover, some graphs of some acquired solutions are depicted. Conclusions and future directions for research are all reported in Section 5.

2. Unified solver method

We give the unified solver for the widely used NLEEs arising in the nonlinear science. For a given NLEE with some physical field $\Psi(x, y, t)$

$\begin{equation} F(\Psi , \Psi _{t}, \Psi _{x}, \Psi _{tt}, \Psi _{xx}, ....) = 0, \end{equation}$

(2.1)

we construct its explicit solutions in the form:

$\begin{equation} \Psi (x, y, t) = \Psi (\xi ), \ \xi = k_1 x+k_2 y+k_3t, \end{equation}$

(2.2)

where $k_1$ , $k_2$ and $k_3$ are constants. Consequently the nonlinear evolution Eq (2.1) transformed to the following ordinary differential equation (ODE):

$\begin{equation} G(\Psi , \Psi ^{\prime }, \Psi ^{\prime \prime }, \Psi ^{\prime \prime \prime}, ...) = 0. \end{equation}$

(2.3)

Based on He's semi-inverse method ^[48,49,50], if possible, integrate (2.3) term by term one or more times. The variational model for the differential Eq (2.3) can be obtained by the semi-inverse method ^[51] which reads:

$\begin{equation} J(\Psi) = \underset{0}{\overset{\infty}{\int}}L\, d\xi, \end{equation}$

(2.4)

where $L$ is the Lagrangian function, of the problem described by the Eq (2.3), depending on $\Psi$ and its derivatives given in the form:

$\begin{equation} L = \frac{1}{2}\Psi^{^{\prime}2}-V, \end{equation}$

(2.5)

where $V$ is the potential function. By a Ritz method, we can find different forms of solitary wave solutions, such as $\Psi(x, y, t) = \alpha$ $\mbox{sech}(\beta \xi)$ , $\Psi(x, y, t) = \alpha$ $\mbox{csch}(\beta \xi)$ , $\Psi(x, y, t) = \alpha$ $\mbox{tanh}(\beta \xi)$ , $\Psi(x, y, t) = \alpha$ $\mbox{cotch}(\beta \xi)$ and $\Psi(x, y, t) = \alpha$ $\mbox{sech}^2(\beta \xi)$ where $\alpha$ and $\beta$ are constants determined later.

We look for a solitary wave solution in the form

$\begin{equation} \Psi(x, y, t) = \alpha, \mbox{sech}(\beta \xi), \Psi(x, y, t) = \alpha, \mbox{sech}^2(\beta \xi), \Psi(x, y, t) = \alpha, \tanh(\beta \xi). \end{equation}$

(2.6)

In this section we give the unified solver for the widely used NLEEs arising in the nonlinear science. Suppose a system of equations can be reduced to the form:

$\begin{equation} L_{1}\Psi^{\prime\prime}+L_{2}\Psi^{3}+L_{3}\Psi = 0, \end{equation}$

(2.7)

where $L_{i}, i = 1, 2, 3$ are constants. Multiplying (2.7) by $\Psi^{^{\prime}}$ and integrating with respect to $\Psi$ we get the equation:

$\begin{equation} \frac{1}{2}\Psi^{^{\prime}2}+\frac{L_2}{4L_1} \Psi^{4}+\frac{L_3}{2L_1} \Psi^{2}+L_{0} = 0 \end{equation}$

(2.8)

and $L_{0}$ is a constant of integration. Thus the Eq (2.7) can be written in the form:

$\begin{equation} \Psi^{\prime\prime} = -\frac{\partial V}{\partial\Psi}, \; V = -(\gamma_{2}\Psi ^{4}+\gamma_{1}\psi^{2}+\gamma _{0}), \end{equation}$

(2.9)

where

$\begin{equation} \gamma_2 = -\frac{L_2}{4L_1}, \gamma_1 = -\frac{L_3}{2L_1}, \gamma_{0} = - L_0 \end{equation}$

(2.10)

and $V$ is the potential function (Sagadev potential).

We apply He's semi-inverse technique^[48,49,50] for solving Eq (2.7), which construct the following variational formulation from Eq (2.8)

$\begin{equation} J = \int_{0}^{\infty}\left[\frac{1}{2}\Psi^{\prime2}+\gamma_{2}\Psi^{4}+\gamma_{1}\Psi^{2}+\gamma_{0}\right] d\xi. \end{equation}$

(2.11)

By Ritz-like method, we look for a solitary wave solution in the form given by Eq (2.6). Substituting from Eq (2.6) into Eq (2.11) and making $J$ stationary with respect to $\alpha$ and $\beta$ we obtain:

$\begin{equation} \frac{\partial J}{\partial \alpha} = 0;\; \frac{\partial J}{\partial \beta} = 0. \end{equation}$

(2.12)

Solving simultaneously the system of equations given by (2.12) we obtain $\alpha$ and $\beta$ . Consequently the solitary wave solution given by Eq (2.6) is well determined.

2.1. The first family

The first family of solutions takes the form:

$\begin{equation} \Psi(\xi) = \alpha\, \mbox{sech}^{{}}\theta, \; \theta = \beta\xi. \end{equation}$

(2.13)

Substituting from Eq (2.13) in Eq (2.11), we get

$\begin{align*} J & = \frac{1}{\beta}\int_{0}^{\infty}[\frac{1}{2}\alpha^{2}\beta^{2}, \mbox{sech}^{2}, \theta\; \mbox{tanh}^{2}\theta+ \gamma_2, \alpha^{4} \mbox{sech}^{4}\theta+\gamma_1 , \alpha^{2}\mbox{sech}^{2}\theta+\gamma_{0}]d\theta. \end{align*}$

Since $\gamma_{0}$ is a constant of integration we can let $\gamma_{0} = 0$ and consequently:

$\begin{align} J = \frac{\alpha}{12 \beta}\left[ 2\alpha \beta^{2}+8\gamma_{2}\alpha^{3}+12 \gamma_{1}\alpha\right]. \end{align}$

(2.14)

Making $J$ stationary with respect to $\alpha$ and $\beta$ leads to

$\begin{equation} \frac{\partial J}{\partial \alpha} = \frac{1}{12\beta}\left[ 32\gamma_{2}\alpha^{3}+24\gamma_{1}\alpha+4\alpha\beta^2\right] = 0, \end{equation}$

(2.15)

$\begin{equation} \frac{\partial J}{\partial \beta} = -\frac{\alpha}{12\beta^{2}}\left[ 8\gamma_{2}\alpha^{3}+12\gamma_{1}\alpha-2\alpha\beta^{2}\right] = 0. \end{equation}$

(2.16)

Solving these equations and using (2.13), the solutions of Eq (2.9) take the form:

$\begin{equation} \Psi(\xi) = \pm\sqrt{\frac{-\gamma_1}{\gamma_2}}, \mbox{sech}\left(\pm\sqrt{2\gamma_{1}}\xi\right). \end{equation}$

(2.17)

Consequently by using (2.10) the first family of solutions takes the form:

$\begin{equation} \Psi(\xi) = \pm \sqrt{\frac{-2L_3}{L_2}}, \mbox{sech}\left( \pm \sqrt{-\frac{L_3}{L_1}}\xi\right). \end{equation}$

(2.18)

2.2. The second family

The second family of solutions takes the form:

$\begin{equation} \psi(\xi) = \alpha\, \mbox{sech}^{2}\theta\; ;\theta = \beta\xi. \end{equation}$

(2.19)

The substitution from Eq (2.19) in Eq (2.11) leads to

$\begin{align*} J & = \frac{\alpha}{\beta}\int_{0}^{\infty}[2\alpha \beta^{2}\mbox{sech}^{4}\theta\; \mbox{tanh}^{2}\theta+\gamma_{2}\alpha^{3} \mbox{sech}^{8}\theta+ \gamma_{1} \alpha\, \mbox{sech}^{4}\theta+\frac{\gamma_{0}}{\alpha}] d\theta. \end{align*}$

Assuming that $\gamma_{0} = 0$ we find that

$\begin{equation} J = \frac{2\alpha^{2}}{105\beta}\left[ 14\alpha \beta^{2}+24\gamma_{2}\alpha^{3}+35 \gamma_{1}\alpha\right]. \end{equation}$

(2.20)

Making $J$ stationary with respect to $\alpha$ and $\beta$ leads to

$\begin{align} 14\alpha \beta^{2}+48\gamma_{2}\alpha^{3}+35\gamma_{1}\alpha & = 0, \end{align}$

(2.21)

$\begin{align} 14\alpha \beta^{2}-24\gamma_{2} \alpha^{3}-35\gamma_{1}\alpha & = 0. \end{align}$

(2.22)

Solving these equations and using (2.19), the second family of solutions of Eqs (2.9) and (2.7) take the form:

$\begin{equation} \Psi(\xi) = \pm \sqrt{\frac{-35\gamma_{1}}{36\gamma_{2}}}\, \mbox{sech}^{2}\left( \pm \sqrt{\frac{5}{6}\gamma_{1}} \, \xi\right) \end{equation}$

(2.23)

and

$\begin{equation} \Psi(\xi) = \pm\sqrt{\frac{-35\, L_{3}}{18\, L_{2}}} \mbox{sech}^{2}\left( \pm \sqrt{-\frac{5\, L_{3}}{12\, L_{1}}} \, \xi\right), \end{equation}$

(2.24)

respectively.

2.3. The third family

The third family of solutions takes the form:

$\begin{equation} \psi (\xi ) = \alpha, \tanh (\beta\xi ). \end{equation}$

(2.25)

Substituting from Eq (2.25) into Eq (2.11), we have

$\begin{align*} J & = \frac{1}{\beta}\int_{0}^{\infty}[\frac{1}{2}\alpha^{2}\, \beta^{2}\, \mbox{sech}^{4}\theta +\gamma_{2}\alpha^{4}\tanh^{4}\theta+ \gamma_{1}\, \alpha^{2}\tanh^{2}\theta+ \gamma_{0}]d\theta \\ & = \frac{1}{\beta}\int_{0}^{\infty}[\alpha^{2}( \gamma_{2}\alpha^{2}+\frac{1}{2} \beta^{2})\, \mbox{sech}^{4}\theta-\alpha^{2}(2 \gamma_{2} \alpha^{2}+\gamma_{1})\, \mbox{sech}^{2}\theta ]d\theta \\& +\frac{1}{\beta}(\gamma_{2}\alpha^{4}+ \gamma_{1}\alpha^{2}+\gamma_{0})\int_{0}^{\infty }d\theta \notag. \end{align*}$

Under the condition

$\begin{equation} \gamma_{0} = -\alpha^{2}(\gamma_{2} \alpha^{2}+\gamma_{1}), \end{equation}$

(2.26)

we find that

$\begin{align} J & = \frac{-\alpha^{2}}{3\beta}\left[ 4\gamma_{2}\alpha^{2}+3\gamma _{1}-\beta^{2}\right]. \end{align}$

(2.27)

The values of $\alpha$ and $\beta$ which makes $J$ stationary with respect to $\alpha$ and $\beta$ are obtained by solving the two conditions

$\begin{align} \frac{\partial J}{\partial \alpha} & = \frac{-\alpha}{3\beta}\left[ 16\gamma_{2}\alpha^{2}+6\gamma_{1}-2\beta^{2}\right] = 0, \end{align}$

(2.28)

$\begin{align} \frac{\partial J}{\partial \beta} & = \frac{\alpha^{2}}{3\beta^{2}}\left[ 4\gamma_{2}\alpha^{2}+3\gamma_{1}+\beta^{2}\right] = 0. \end{align}$

(2.29)

Solving these equations and using (2.25), the solutions of Eq (2.9) take the form:

$\begin{equation} \Psi(\xi) = \pm\sqrt{\frac{-\gamma_{1}}{2\, \gamma_{2}}} \tanh\left( \pm \sqrt{-\gamma_{1}}\xi\right). \end{equation}$

(2.30)

Consequently the third family of solutions of (2.7) take the form:

$\begin{equation} \Psi(\xi) = \pm\sqrt{\frac{-L_{3}}{L_{2}}} \tanh\left( \pm \sqrt{\frac{L_3}{2L_1}}\xi\right). \end{equation}$

(2.31)

3. Applications

In this section we introduce the solutions for the coupled nonlinear Maccari's systems.

3.1. Solutions of system (1.1)

Utilizing the wave transformation:

$\begin{equation} \begin{split} Q(x, y, t) = &e^{i(kx+\alpha\, y+\lambda\, t)}u(\zeta), \; \; \; R(x, y, t) = R(\zeta), \zeta = x + \beta y -2k t, \end{split} \end{equation}$

(3.1)

$k, \alpha, \lambda$ and $\beta$ are constants. Then the system of Eq (1.1) is converted to the following system

$\begin{equation} \begin{array}{l} u''+u R-(\lambda+k^2)u = 0, \\ (u^2)'-(2k-\beta)R' = 0. \end{array} \end{equation}$

(3.2)

Integrating second equation of Eq (3.2) and taking integration constant as zero, gives

$\begin{equation} R = \left(\frac{1}{2k-\beta}\right)u^2. \end{equation}$

(3.3)

Substituting Eq (3.3) into first equation of system (3.2), yields

$\begin{equation} L_{1} u''+L_{2}u^3+L_{3}u = 0, \end{equation}$

(3.4)

where

$\begin{equation} L_{1} = 1, L_{2} = \frac{1}{2k-\beta}, L_{3} = -(\lambda+k^2). \end{equation}$

(3.5)

Applying the unified solver method described in Section 2, three families of solutions of Eq (1.1) are given as follows:

3.1.1. The first family of solutions

$\begin{equation} u_{1, 2}(\zeta) = \pm \sqrt{2 (2k-\beta)(\lambda+k^2)}\, \mbox{sech}\left( \pm \sqrt{\lambda+k^2}\, \zeta\right). \end{equation}$

(3.6)

Thus,

$\begin{equation} Q_{1, 2}(x, y, t) = \pm e^{i(kx+\alpha\, y+\lambda\, t)}\sqrt{2 (2k-\beta)(\lambda+k^2)}\, \mbox{sech}\left( \pm \sqrt{\lambda+k^2}\, \zeta\right). \end{equation}$

(3.7)

$\begin{equation} R_{1, 2}(x, y, t) = 2(\lambda+k^2)\, \mbox{sech}^{2}\left( \pm \sqrt{\lambda+k^2}\, \zeta\right), \; \; \; \lambda+k^2 > 0. \end{equation}$

(3.8)

3.1.2. The second family of solutions

$\begin{equation} u_{3, 4}(\zeta) = \pm \sqrt{\frac{35(\lambda+k^2)(2k-\beta)}{18}}\, \mbox{sech}^{2}\left( \pm \sqrt{\frac{5(\lambda+k^2)}{12}} \, \zeta\right). \end{equation}$

(3.9)

Thus,

$\begin{equation} Q_{3, 4}(x, y, t) = \pm e^{i(kx+\alpha\, y+\lambda\, t)} \sqrt{\frac{35(\lambda+k^2)(2k-\beta)}{18}}\, \mbox{sech}^{2}\left( \pm \sqrt{\frac{5(\lambda+k^2)}{12}} \, \zeta\right). \end{equation}$

(3.10)

$\begin{equation} R_{3, 4}(x, y, t) = \frac{35(\lambda+k^2)}{18}\, \mbox{sech}^{4}\left( \pm\sqrt{ \frac{5(\lambda+k^2)}{12}} \, \zeta\right) , \; \; \; \lambda+k^2 > 0. \end{equation}$

(3.11)

3.1.3. The third family of solutions

$\begin{equation} u_{5, 6}(\zeta) = \pm\sqrt{(\lambda+k^2)(2k-\beta)} \tanh\left( \pm \sqrt{-\frac{(\lambda+k^2)}{2}}\zeta\right). \end{equation}$

(3.12)

Thus,

$\begin{equation} Q_{5, 6}(x, y, t) = \pm\, e^{i(k+\alpha\, y+\lambda\, t)}\sqrt{(\lambda+k^2)(2k-\beta)} \tanh\left( \pm \sqrt{-\frac{\lambda+k^2}{2}}\zeta\right). \end{equation}$

(3.13)

$\begin{equation} R_{5, 6}(x, y, t) = (\lambda+k^2) \tanh^{2}\left( \pm \sqrt{-\frac{\lambda+k^2}{2}}\zeta\right), \; \; \lambda+k^2 < 0. \end{equation}$

(3.14)

3.2. Solutions of system (1.2)

Consider the wave transformation:

$\begin{equation} \begin{split} Q(x, y, t)& = e^{i(kx+\alpha\, y+\lambda\, t)}u(\zeta), \\ S(x, y, t)& = e^{i(kx+\alpha\, y+\lambda\, t)}v(\zeta), \\ R(x, y, t)& = R(\xi), \zeta = x + \beta y -2k t, \end{split} \end{equation}$

(3.15)

where $k, \alpha, \lambda$ and $\beta$ are constants. By applying this transformation to the system (1.2) we get

$\begin{equation} \begin{array}{l} u''-(\lambda+k^2) u + u R = 0, \\ v''-(\lambda+k^2) v + v R = 0, \\ ((u+v)^2)'-(2k-\beta)R' = 0. \end{array} \end{equation}$

(3.16)

Integrating third equation of the system of Eq (3.16) and taking integration constant as zero, gives

$\begin{equation} R = \left(\frac{1}{2k-\beta}\right)(u+v)^2. \end{equation}$

(3.17)

Substituting Eq (3.17) into first two equations of (3.16), yields

$\begin{equation} \begin{array}{l} u''+ \frac{1}{2k-\beta}u(u+v)^2-(\lambda+k^2)u = 0, \\ v''+ \frac{1}{2k-\beta}v(u+v)^2-(\lambda+k^2)v = 0. \end{array} \end{equation}$

(3.18)

In order to solve the last system of equations, we use a simple relation between $u$ and $v$ , as follows:

$\begin{equation} v = r\, u, \end{equation}$

(3.19)

where $r$ is an arbitrary constant. Substituting (3.19) into the system (3.18), gives

$\begin{equation} \Gamma_{1} u''+\Gamma_{2}u^3+\Gamma_{3}u = 0, \end{equation}$

(3.20)

where $\Gamma_{1} = 1, \Gamma_{2} = \frac{(1+r)^2}{2k-\beta}, \Gamma_{3} = -(\lambda+k^2)$ .

In view of the unified solver illustrated in Section 2 solutions of Eq (1.2) can be given in the following formulas:

3.2.1. The first family of solutions

$\begin{equation} u_{1, 2}(\zeta) = \pm \sqrt{\frac{2(\lambda+k^2)(2k-\beta)}{(1+r)^2}}\, \mbox{sech}\left( \pm \sqrt{\lambda+k^2}\zeta\right). \end{equation}$

(3.21)

Thus,

$\begin{equation} v_{1, 2}(\zeta) = \pm r \sqrt{\frac{2(\lambda+k^2)(2k-\beta)}{(1+r)^2}}\, \mbox{sech}\left( \pm \sqrt{\lambda+k^2}\zeta\right). \end{equation}$

(3.22)

$\begin{equation} Q_{1, 2}(x, y, t) = \pm e^{i(kx+\alpha\, y+\lambda\, t)}\sqrt{\frac{2(\lambda+k^2)(2k-\beta)}{(1+r)^2}}\, \mbox{sech}\left( \pm \sqrt{\lambda+k^2}\zeta\right). \end{equation}$

(3.23)

$\begin{equation} S_{1, 2}(x, y, t) = \pm r e^{i(kx+\alpha\, y+\lambda\, t)}\sqrt{\frac{2(\lambda+k^2)(\beta-2k)}{(1+r)^2}}\, \mbox{sech}\left( \pm \sqrt{\lambda+k^2}\zeta\right). \end{equation}$

(3.24)

$\begin{equation} R_{1, 2}(x, y, t) = 2(\lambda+k^2)\mbox{sech}^2\left( \pm \sqrt{\lambda+k^2}\xi\right), \lambda+k^2 > 0. \end{equation}$

(3.25)

3.2.2. The second family of solutions

$\begin{equation} u_{3, 4}(\zeta) = \pm \sqrt{\frac{35(\lambda+k^2)(2k-\beta)}{18(1+r)^2}}\, \mbox{sech}^2\left( \pm \sqrt{\frac{5}{12}(\lambda+k^2)}\zeta\right). \end{equation}$

(3.26)

Thus,

$\begin{equation} v_{3, 4}(\zeta) = \pm r \sqrt{\frac{35(\lambda+k^2)(2k-\beta)}{18(1+r)^2}}\, \mbox{sech}^2\left( \pm \sqrt{\frac{5}{12}(\lambda+k^2)}\zeta\right). \end{equation}$

(3.27)

$\begin{equation} Q_{3, 4}(x, y, t) = \pm e^{i(kx+\alpha\, y+\lambda\, t)}\sqrt{\frac{35(\lambda+k^2)(2k-\beta)}{18(1+r)^2}}\, \mbox{sech}^2\left( \pm \sqrt{\frac{5}{12}(\lambda+k^2)}\zeta\right). \end{equation}$

(3.28)

$\begin{equation} S_{3, 4}(x, y, t) = \pm r e^{i(kx+\alpha\, y+\lambda\, t)}\sqrt{\frac{35(\lambda+k^2)(2k-\beta)}{18(1+r)^2}}\, \mbox{sech}^2\left( \pm \sqrt{\frac{5}{12}(\lambda+k^2)}\zeta\right). \end{equation}$

(3.29)

$\begin{equation} R_{3, 4}(x, y, t) = \frac{35}{18}(\lambda+k^2)\mbox{sech}^4\left( \pm \sqrt{\frac{5}{12}(\lambda+k^2)}\xi\right), \; \; \lambda+k^2 > 0. \end{equation}$

(3.30)

3.2.3. The third family of solutions

$\begin{equation} u_{5, 6}(\zeta) = \pm \sqrt{\frac{(\lambda+k^2)(2k-\beta)}{(1+r)^2}}\, \tanh\left( \pm \sqrt{-\frac{\lambda+k^2}{2}}\zeta\right). \end{equation}$

(3.31)

Thus,

$\begin{equation} v_{5, 6}(\zeta) = \pm r\sqrt{\frac{(\lambda+k^2)(2k-\beta)}{(1+r)^2}}\, \tanh\left( \pm \sqrt{-\frac{\lambda+k^2}{2}}\zeta\right). \end{equation}$

(3.32)

$\begin{equation} Q_{5, 6}(x, y, t) = \pm e^{i(kx+\alpha\, y+\lambda\, t)} \sqrt{\frac{(\lambda+k^2)(2k-\beta)}{(1+r)^2}}\, \tanh\left( \pm \sqrt{-\frac{\lambda+k^2}{2}}\zeta\right). \end{equation}$

(3.33)

$\begin{equation} S_{5, 6}(x, y, t) = \pm re^{i(kx+\alpha\, y+\lambda\, t)} \sqrt{\frac{(\lambda+k^2)(2k-\beta)}{(1+r)^2}}\, \tanh\left( \pm \sqrt{-\frac{\lambda+k^2}{2}}\zeta\right). \end{equation}$

(3.34)

$\begin{equation} R_{5, 6}(x, y, t) = (\lambda+k^2)\tanh^2\left( \pm \sqrt{-\frac{\lambda+k^2}{2}}\zeta\right), \; \; \lambda+k^2 < 0. \end{equation}$

(3.35)

3.3. Solutions of system (1.3)

In order to solve the system of Eq (1.3), we first consider the following wave transformation:

$\begin{equation} \begin{split} Q(x, y, t)& = e^{i(kx+\alpha\, y+\lambda\, t)}u(\zeta), \\ S(x, y, t)& = e^{i(kx+\alpha\, y+\lambda\, t)}v(\zeta), \\ N(x, y, t)& = e^{i(kx+\alpha\, y+\lambda\, t)}w(\zeta), \\ R(x, y, t)& = R(\zeta), \; \zeta = x + \beta y -2k t, \end{split} \end{equation}$

(3.36)

where $k, \alpha, \lambda$ and $\beta$ are constants. Substituting this transformation to system (1.3) gives

$\begin{equation} \begin{array}{l} u''-(\lambda+k^2) u + u R = 0, \\ v''-(\lambda+k^2) v + v R = 0, \\ w''-(\lambda+k^2) w + w R = 0, \\ ((u+v+w)^2)' -(2k-\beta)R' = 0. \end{array} \end{equation}$

(3.37)

As illustrated before, we integrate the third equation of (3.37) with assuming the integration constant to be zero and this gives

$\begin{equation} R = \left(\frac{1}{2k-\beta}\right)(u+v+w)^2. \end{equation}$

(3.38)

Substituting Eq (3.38) into first three equation of (3.37), implies

$\begin{equation} \begin{array}{l} u''+ \frac{1}{2k-\beta}u(u+v+w)^2-(\lambda+k^2)u = 0, \\ v''+ \frac{1}{2k-\beta}v(u+v)^2-(\lambda+k^2)v = 0, \\ w''+ \frac{1}{2k-\beta}w(u+v+w)^2-(\lambda+k^2)w = 0. \end{array} \end{equation}$

(3.39)

To solve these equations, we use a simple relations between $v, w$ and $u$ , as follows

$\begin{equation} v = r_{1}\, u, \; \; \; w = r_{2}\, u, \end{equation}$

(3.40)

where $r_{1}, r_{2}$ are arbitrary constants. Substituting (3.40) into the Eq (3.39), gives

$\begin{equation} \Gamma_{1} u''+\Gamma_{2}u^3+\Gamma_{3}u = 0, \end{equation}$

(3.41)

where $\Gamma_{1} = 1, \Gamma_{2} = \frac{(1+r_{1}+r_{2})^2}{2k-\beta}, \Gamma_{3} = -(\lambda+k^2)$ .

Similarly, solutions of system (1.3) can be obtained using the unified solver, presented in Section 2, and are described in the following:

3.3.1. The first family of solutions

$\begin{equation} u_{1, 2}(\zeta) = \pm \sqrt{\frac{2(\lambda+k^2)(2k-\beta)}{(1+r_1+r_2)^2}}\, \mbox{sech}\left( \pm \sqrt{\lambda+k^2}\zeta\right). \end{equation}$

(3.42)

Thus,

$\begin{equation} v_{1, 2}(\zeta) = \pm r_1 \sqrt{\frac{2(\lambda+k^2)(2k-\beta)}{(1+r_1+r_2)^2}}\, \mbox{sech}\left( \pm \sqrt{\lambda+k^2}\zeta\right). \end{equation}$

(3.43)

$\begin{equation} w_{1, 2}(\zeta) = \pm r_2 \sqrt{\frac{2(\lambda+k^2)(2k-\beta)}{(1+r_1+r_2)^2}}\, \mbox{sech}\left( \pm \sqrt{\lambda+k^2}\zeta\right). \end{equation}$

(3.44)

$\begin{equation} Q_{1, 2}(x, y, t) = \pm e^{i(kx+\alpha\, y+\lambda\, t)}\sqrt{\frac{2(\lambda+k^2)(2k-\beta)}{(1+r_1+r_2)^2}}\, \mbox{sech}\left( \pm \sqrt{\lambda+k^2}\zeta\right). \end{equation}$

(3.45)

$\begin{equation} S_{1, 2}(x, y, t) = \pm r_1 e^{i(kx+\alpha\, y+\lambda\, t)}\sqrt{\frac{2(\lambda+k^2)(2k-\beta)}{(1+r_1+r_2)^2}}\, \mbox{sech}\left( \pm \sqrt{\lambda+k^2}\zeta\right). \end{equation}$

(3.46)

$\begin{equation} N_{1, 2}(x, y, t) = \pm r_2 e^{i(kx+\alpha\, y+\lambda\, t)}\sqrt{\frac{2(\lambda+k^2)(2k-\beta)}{(1+r_1+r_2)^2}}\, \mbox{sech}\left( \pm \sqrt{\lambda+k^2}\zeta\right). \end{equation}$

(3.47)

$\begin{equation} R_{1, 2}(x, y, t) = 2(\lambda+k^2)\, \mbox{sech}^2\left( \pm \sqrt{\lambda+k^2}\zeta\right), \; \; \lambda+k^2 > 0. \end{equation}$

(3.48)

3.3.2. The second family of solutions

$\begin{equation} u_{3, 4}(\zeta) = \pm \sqrt{\frac{35(\lambda+k^2)(2k-\beta)}{18(1+r_1+r_2)^2}}\, \mbox{sech}^2\left( \pm \sqrt{\frac{5}{12}(\lambda+k^2)}\zeta\right). \end{equation}$

(3.49)

Thus,

$\begin{equation} v_{3, 4}(\zeta) = \pm r_1 \sqrt{\frac{35(\lambda+k^2)(2k-\beta)}{18(1+r_1+r_2)^2}}\, \mbox{sech}^2\left( \pm \sqrt{\frac{5}{12}(\lambda+k^2)}\zeta\right). \end{equation}$

(3.50)

$\begin{equation} w_{3, 4}(\zeta) = \pm r_2 \sqrt{\frac{35(\lambda+k^2)(2k-\beta)}{18(1+r_1+r_2)^2}}\, \mbox{sech}^2\left( \pm \sqrt{\frac{5}{12}(\lambda+k^2)}\zeta\right). \end{equation}$

(3.51)

$\begin{equation} Q_{3, 4}(x, y, t) = \pm e^{i(kx+\alpha\, y+\lambda\, t)}\sqrt{\frac{35(\lambda+k^2)(2k-\beta)}{18(1+r_1+r_2)^2}}\, \mbox{sech}^2\left( \pm \sqrt{\frac{5}{12}(\lambda+k^2)}\zeta\right). \end{equation}$

(3.52)

$\begin{equation} S_{3, 4}(x, y, t) = \pm r_1 e^{i(kx+\alpha\, y+\lambda\, t)}\sqrt{\frac{35(\lambda+k^2)(2k-\beta)}{18(1+r_1+r_2)^2}}\, \mbox{sech}^2\left( \pm \sqrt{\frac{5}{12}(\lambda+k^2)}\zeta\right). \end{equation}$

(3.53)

$\begin{equation} N_{3, 4}(x, y, t) = \pm r_2 e^{i(kx+\alpha\, y+\lambda\, t)}\sqrt{\frac{35(\lambda+k^2)(2k-\beta)}{18(1+r_1+r_2)^2}}\, \mbox{sech}^2\left( \pm \sqrt{\frac{5}{12}(\lambda+k^2)}\zeta\right). \end{equation}$

(3.54)

$\begin{equation} R_{3, 4}(x, y, t) = \frac{35}{18}(\lambda+k^2)\mbox{sech}^4\left(\pm \sqrt{\frac{5}{12}(\lambda+k^2)}\zeta\right), \; \; \lambda+k^2 > 0. \end{equation}$

(3.55)

3.3.3. The third family of solutions

$\begin{equation} u_{5, 6}(\zeta) = \pm \sqrt{\frac{(\lambda+k^2)(2k-\beta)}{(1+r_1+r_2)^2}}\, \tanh\left( \pm \sqrt{-\frac{\lambda+k^2}{2}}\zeta\right). \end{equation}$

(3.56)

Thus,

$\begin{equation} v_{5, 6}(\zeta) = \pm r_1 \sqrt{\frac{(\lambda+k^2)(2k-\beta)}{(1+r_1+r_2)^2}}\, \tanh\left( \pm \sqrt{-\frac{\lambda+k^2}{2}}\zeta\right). \end{equation}$

(3.57)

$\begin{equation} w_{5, 6}(\zeta) = \pm r_2 \sqrt{\frac{(\lambda+k^2)(2k-\beta)}{(1+r_1+r_2)^2}}\, \tanh\left( \pm \sqrt{ -\frac{\lambda+k^2}{2}}\zeta\right). \end{equation}$

(3.58)

$\begin{equation} Q_{5, 6}(x, y, t) = \pm\, e^{i(kx+\alpha\, y+\lambda\, t)}\sqrt{\frac{(\lambda+k^2)(2k-\beta)}{(1+r_1+r_2)^2}}\, \tanh\left( \pm \sqrt{-\frac{\lambda+k^2}{2}}\zeta\right). \end{equation}$

(3.59)

$\begin{equation} S_{5, 6}(x, y, t) = \pm r_1 e^{i(kx+\alpha\, y+\lambda\, t)}\sqrt{\frac{(\lambda+k^2)(2k-\beta)}{(1+r_1+r_2)^2}}\, \tanh\left( \pm \sqrt{-\frac{\lambda+k^2}{2}}\zeta\right). \end{equation}$

(3.60)

$\begin{equation} N_{5, 6}(x, y, t) = \pm r_2 e^{i(kx+\alpha\, y+\lambda\, t)}\sqrt{\frac{(\lambda+k^2)(2k-\beta)}{(1+r_1+r_2)^2}}\, \tanh\left( \pm \sqrt{-\frac{\lambda+k^2}{2}}\zeta\right). \end{equation}$

(3.61)

$\begin{equation} R_{5, 6}(x, y, t) = (\lambda+k^2) \tanh^{2}\left( \pm \sqrt{-\frac{\lambda+k^2}{2}}\zeta\right), \; \; \lambda+k^2 < 0. \end{equation}$

(3.62)

4. Results and discussions

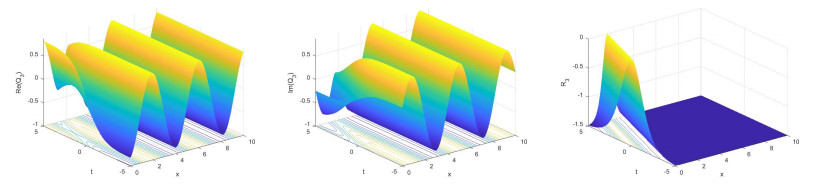
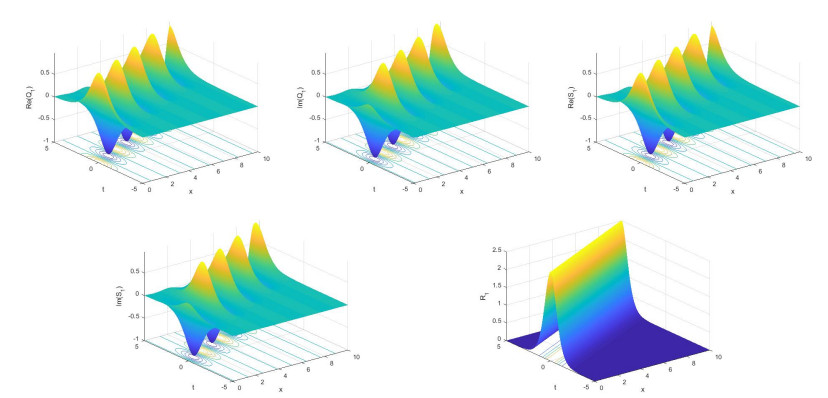
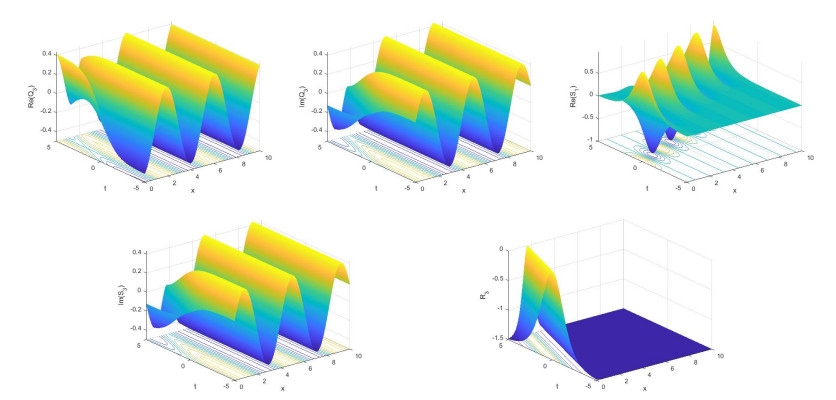
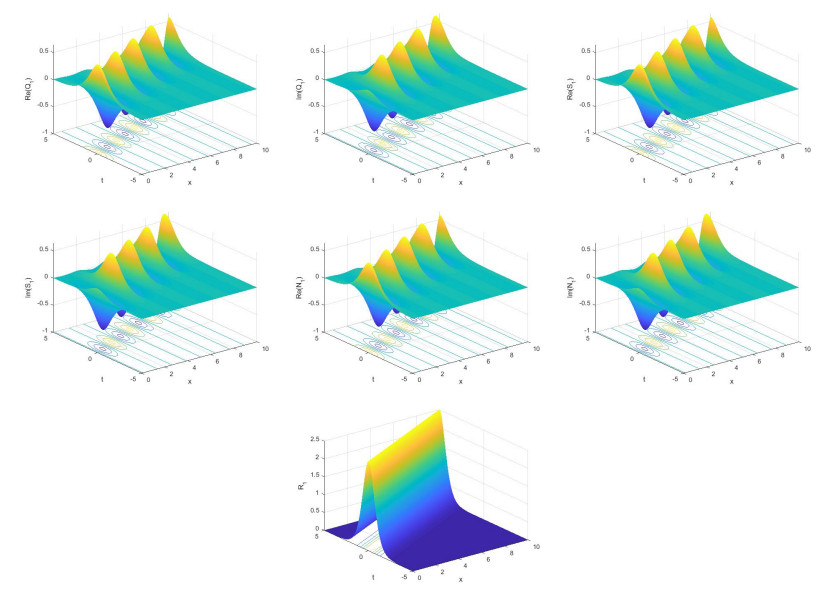
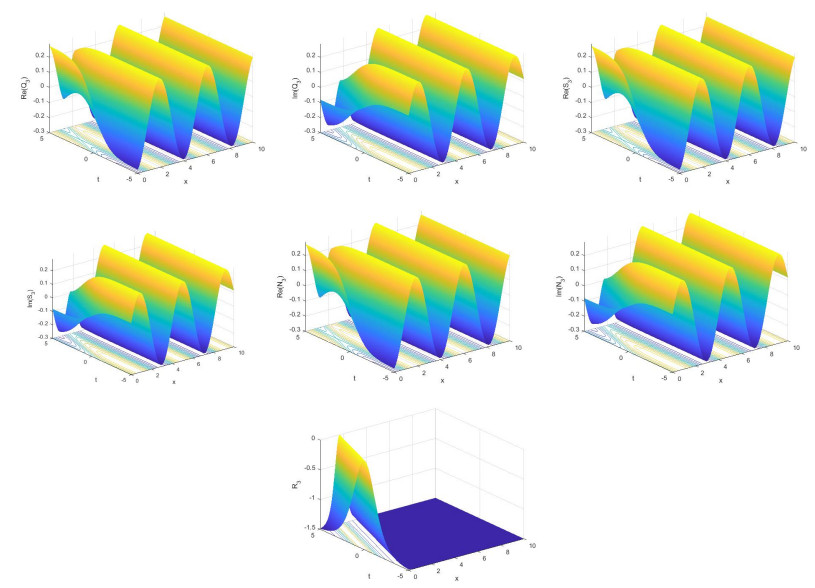
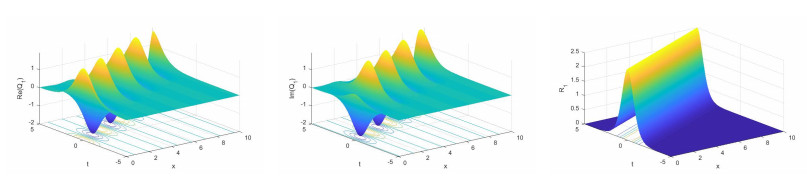
Some new solutions for three coupled nonlinear Maccari's systems were achieved in explicit form. These systems are the complex nonlinear models that characteristic the dynamics of isolated waves, confined in a small part of space, in some fields such as plasma physics, superfluid and optical fiber communications ^[35,45]. The acquired solutions are hyperbolic function solutions. These solutions explain some interesting physical phenomena in applied science and new physics. E.g., the hyperbolic secant arises in the profile of a laminar jet whereas the hyperbolic tangent emerges in the study of magnetic moment and special relativity. Indeed, the presented solutions included bright and dark and soliton solutions of the nonlinear Maccari's systems.

According to the presented results in Section 3 we found that

1) The last model generalize the first two models.

2) There is no change in the form of the real field $R(x, y, t)$ in the three models.

Remark 1. 1) The proposed solver in this study can be implemented for the wide classes of nonlinear stochastic partial differential equations (NSPDEs).

2) The proposed solver can be easily extended for solving nonlinear stochastic fractional partial differential equations (NSFPDEs) ^[52,53,54].

3) The proposed solver averts monotonous and complex computations and introduces vital solutions in an explicit form.

For certain values of the parameters in each three cases, Figures 1–6 display the nonlinear dynamical behaviour of the bright and dark soliton solutions.

Figure 1. 3D profile of bright soliton solution for Eq (1.1).

DownLoad: Full-Size Img PowerPoint

Figure 2. 3D profile of dark soliton solution for Eq (1.1).

DownLoad: Full-Size Img PowerPoint

Figure 3. 3D profile of bright soliton solution for Eq (1.2).

DownLoad: Full-Size Img PowerPoint

Figure 4. 3D profile of dark soliton solution for Eq (1.2).

DownLoad: Full-Size Img PowerPoint

Figure 5. 3D profile of bright soliton solution for Eq (1.3).

DownLoad: Full-Size Img PowerPoint

Figure 6. 3D profile of dark soliton solution for Eq (1.3).

DownLoad: Full-Size Img PowerPoint

5. Conclusions

In this article, three coupled nonlinear Maccari's systems were solved using the unified solver technique. Some vital soliton solutions are presented. These solutions have vital physical aspects in many fields such as nonlinear optics plasma physics, hydrodynamic. In the view of such information, it has been seen that the unified solver method has been influential for the analytical solutions of nonlinear Maccari's systems and it is highly effective and reliable in terms of finding new solutions. Moreover, our analysis shows that the proposed solver is simple, powerful and efficient. Some graphs are presented to prescribe the dynamical behaviour of selected solutions. Finally, the used solver can be applied for so many other models emerging in natural science.

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

[1]	D. Gilbarg, N. S. Trudinger, Elliptic partial differential equations of second order, Springer, 1983.
[2]	N. Guillen, J. Kitagawa, Pointwise inequalities in geometric optics and other generated Jacobian equations, Commun. Pure Appl. Math., 70 (2017), 1146–1220. doi: 10.1002/cpa.21691
[3]	C. E. Gutiérrez, F. Tournier, Regularity for the near field parallel refractor and reflector problems, Calc. Var., 45 (2015), 917–949.
[4]	S. Jeong, Local Hölder regularity of solutions to generated Jacobian equations, arXiv: 2004.12004.
[5]	F. Jiang, N. S. Trudinger, On Pogorelev estimates in optimal transportation and geometric optics, Bull. Math. Sci., 4 (2014), 407–431. doi: 10.1007/s13373-014-0055-5
[6]	F. Jiang, N. S. Trudinger, On the second boundary value problem for Monge Ampère type equations and geometric optics, Arch. Ration. Mech. Anal., 229 (2018), 547–567. doi: 10.1007/s00205-018-1222-8
[7]	A. Karakhanyan, X. J. Wang, On the reflector shape design, J. Differ. Geom., 84 (2010), 561–610.
[8]	Y. H. Kim, R. J. McCann, Continuity, curvature and the general covariance of optimal transportation, J. Eur. Math. Soc., 12 (2010), 1009–1040.
[9]	J. K. Liu, N. S. Trudinger, On Pogorelov estimates for Monge-Ampère type equations, Discrete Contin. Dyn. A, 28 (2010), 1121–1135. doi: 10.3934/dcds.2010.28.1121
[10]	J. K. Liu, N. S. Trudinger, X. J. Wang, Interior $C^{2, \alpha}$ regularity for potential functions in optimal transportation, Commun. Part. Diff. Eq., 35 (2010), 165–184.
[11]	G. Loeper, On the regularity of solutions of optimal transportation problems, Acta Math., 202 (2009), 241–283. doi: 10.1007/s11511-009-0037-8
[12]	G. Loeper, N. S. Trudinger, Weak formulation of the MTW condition and convexity properties of potentials, arXiv: 2007.02665.
[13]	G. Loeper, N. S. Trudinger, On the convexity theory of generating functions, 2020, preprint.
[14]	X. N. Ma, N. S. Trudinger, X. J. Wang, Regularity of potential functions of the optimal transportation problem, Arch. Ration. Mech. Anal., 177 (2005), 151–183. doi: 10.1007/s00205-005-0362-9
[15]	C. Rankin, Distinct solutions to GPJE cannot intersect, Bull. Aust. Math. Soc., 102 (2020), 462–470. doi: 10.1017/S0004972720000052
[16]	N. S. Trudinger, Recent developments in elliptic partial differential equations of Monge-Ampère type, In: Proceedings of the International Congress of Mathematicians, 2006,291–302.
[17]	N. S. Trudinger, On generated prescribed Jacobian equations, Oberwolfach Reports, 38 (2011), 32–36.
[18]	N. S. Trudinger, The local theory of prescribed Jacobian equations, Discrete Contin. Dyn. A, 34 (2014), 1663–1681. doi: 10.3934/dcds.2014.34.1663
[19]	N. S. Trudinger, X. J. Wang, On convexity notions in optimal transportation, 2008, preprint.
[20]	N. S. Trudinger, X. J. Wang, On the second boundary value problem for Monge-Ampère type equations and optimal transportation, Ann. Scuola Norm. Sup. Pisa Cl. Sci., Ⅷ (2009), 143–174.
[21]	N. S. Trudinger, X. J. Wang, On strict convexity and continuous differentiability of potential functions in optimal transportation, Arch. Ration. Mech. Anal., 192 (2009), 403–418. doi: 10.1007/s00205-008-0147-z
[22]	C. Villani, Optimal transportation: old and new, Springer, 2008.

This article has been cited by:

1.	R.A. Alomair, S.Z. Hassan, Mahmoud A.E. Abdelrahman, Ali H. Amin, E.K. El-Shewy, New solitary optical solutions for the NLSE with δ-potential through Brownian process, 2022, 40, 22113797, 105814, 10.1016/j.rinp.2022.105814
2.	Hanan A. Alkhidhr, Mahmoud A. E. Abdelrahman, Mohammad Mirzazadeh, Simulating New CKO as a Model of Seismic Sea Waves via Unified Solver, 2023, 2023, 1687-9139, 1, 10.1155/2023/2514899
3.	H. G. Abdelwahed, A. F. Alsarhana, E. K. El-Shewy, Mahmoud A. E. Abdelrahman, Higher-Order Dispersive and Nonlinearity Modulations on the Propagating Optical Solitary Breather and Super Huge Waves, 2023, 7, 2504-3110, 127, 10.3390/fractalfract7020127
4.	Mahmoud A.E. Abdelrahman, Hanan A. Alkhidhr, Ali H. Amin, E.K. El-Shewy, A new structure of solutions to the system of ISALWs via stochastic sense, 2022, 37, 22113797, 105473, 10.1016/j.rinp.2022.105473
5.	Mahmoud A.E. Abdelrahman, S.Z. Hassan, Munerah Almulhem, A new structure of optical solitons to the (n+1)-NLSE, 2022, 37, 22113797, 105535, 10.1016/j.rinp.2022.105535
6.	Hanan A. Alkhidhr, The new stochastic solutions for three models of non-linear Schrödinger’s equations in optical fiber communications via Itô sense, 2023, 11, 2296-424X, 10.3389/fphy.2023.1144704
7.	H. G. Abdelwahed, A. F. Alsarhana, E. K. El-Shewy, Mahmoud A. E. Abdelrahman, The Stochastic Structural Modulations in Collapsing Maccari’s Model Solitons, 2023, 7, 2504-3110, 290, 10.3390/fractalfract7040290
8.	H. G. Abdelwahed, A. F. Alsarhana, E. K. El-Shewy, Mahmoud A. E. Abdelrahman, Dynamical energy effects in subsonic collapsing electrostatic Langmuir soliton, 2023, 35, 1070-6631, 037129, 10.1063/5.0141228
9.	Emad K. El-Shewy, Noura F. Abdo, Mahmoud A. E. Abdelrahman, Modulations of Stochastic Modeling in the Structural and Energy Aspects of the Kundu–Mukherjee–Naskar System, 2023, 11, 2227-7390, 4881, 10.3390/math11244881
10.	Yousef F. Alharbi, Ahmed M. T. Abd El-Bar, Mahmoud A. E. Abdelrahman, Ahmed M. Gemeay, Arne Johannssen, A new statistical distribution via the Phi-4 equation with its wide-ranging applications, 2024, 19, 1932-6203, e0312458, 10.1371/journal.pone.0312458
11.	Munerah Almulhem, Samia Hassan, Alanwood Al-buainain, Mohammed Sohaly, Mahmoud Abdelrahman, Characteristics of Solitary Stochastic Structures for Heisenberg Ferromagnetic Spin Chain Equation, 2023, 15, 2073-8994, 927, 10.3390/sym15040927
12.	Maged A. Azzam, H. G. Abdelwahed, Emad K. El-Shewy, Mahmoud A. E. Abdelrahman, Langmuir Forcing and Collapsing Subsonic Density Cavitons via Random Modulations, 2023, 15, 2073-8994, 1558, 10.3390/sym15081558
13.	M. Mossa Al-Sawalha, Saima Noor, Mohammad Alqudah, Musaad S. Aldhabani, Rasool Shah, Formation of Optical Fractals by Chaotic Solitons in Coupled Nonlinear Helmholtz Equations, 2024, 8, 2504-3110, 594, 10.3390/fractalfract8100594
14.	Amira F. Daghistani, Ahmed M. T. Abd El-Bar, Ahmed M. Gemeay, Mahmoud A. E. Abdelrahman, Samia Z. Hassan, A Hyperbolic Secant-Squared Distribution via the Nonlinear Evolution Equation and Its Application, 2023, 11, 2227-7390, 4270, 10.3390/math11204270
15.	H. G. Abdelwahed, A. F. Alsarhana, E. K. El-Shewy, Mahmoud A. E. Abdelrahman, Characteristics of New Stochastic Solitonic Solutions for the Chiral Type of Nonlinear Schrödinger Equation, 2023, 7, 2504-3110, 461, 10.3390/fractalfract7060461
16.	Hadil Alhazmi, Sanaa A. Bajri, E. K. El-Shewy, Mahmoud A. E. Abdelrahman, Effect of random noise behavior on the properties of forcing nonlinear Maccari’s model structures, 2024, 14, 2158-3226, 10.1063/5.0228465
17.	Shan Zhao, Zhao Li, The analysis of traveling wave solutions and dynamical behavior for the stochastic coupled Maccari's system via Brownian motion, 2024, 15, 20904479, 103037, 10.1016/j.asej.2024.103037
18.	Jamil Abbas Haider, Abdullah M.S. Alhuthali, Mohamed Abdelghany Elkotb, Exploring novel applications of stochastic differential equations: Unraveling dynamics in plasma physics with the Tanh-Coth method, 2024, 60, 22113797, 107684, 10.1016/j.rinp.2024.107684
19.	Hesham G. Abdelwahed, Reem Alotaibi, Emad K. El-Shewy, Mahmoud A. E. Abdelrahman, Rajesh Sharma, An insight into the stochastic solitonic features of the Maccari model using the solver technique, 2024, 19, 1932-6203, e0312741, 10.1371/journal.pone.0312741
20.	S. Z. Hassan, D. M. Alsaleh, Munerah Almulhem, R. A. Alomair, A. F. Daghestani, Mahmoud A. E. Abdelrahman, Innovative solutions to the 2D nonlinear Schrödinger model in mathematical physics, 2025, 15, 2158-3226, 10.1063/5.0249246
21.	M. B. Almatrafi, Mahmoud A. E. Abdelrahman, The novel stochastic structure of solitary waves to the stochastic Maccari's system via Wiener process, 2025, 10, 2473-6988, 1183, 10.3934/math.2025056
22.	Mahmoud A. E. Abdelrahman, M. A. Sohaly, Yousef F. Alharbi, Optical random soliton solutions to conformable fractional NLSE via statistical distributions, 2025, 34, 0218-8635, 10.1142/S0218863523500911
23.	Zhimin Yan, Jinbo Li, Shoaib Barak, Salma Haque, Nabil Mlaiki, Delving into quasi-periodic type optical solitons in fully nonlinear complex structured perturbed Gerdjikov–Ivanov equation, 2025, 15, 2045-2322, 10.1038/s41598-025-91978-x
24.	Jin-Jin Mao, ∂̄-dressing method for the coupled third-order flow equation of the Kaup-Newell system, 2025, 10075704, 108841, 10.1016/j.cnsns.2025.108841

Reader Comments

Your name:*

Email:*
© 2021 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

Mathematics in Engineering

1.3 2.9

Metrics

Article views(2874) PDF downloads(684) Cited by(6)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Mathematics in Engineering

On the local theory of prescribed Jacobian equations revisited

Related Papers:

Abstract

1. Introduction

2. Unified solver method

2.1. The first family

2.2. The second family

2.3. The third family

3. Applications

3.1. Solutions of system (1.1)

3.1.1. The first family of solutions

3.1.2. The second family of solutions

3.1.3. The third family of solutions

3.2. Solutions of system (1.2)

3.2.1. The first family of solutions

3.2.2. The second family of solutions

3.2.3. The third family of solutions

3.3. Solutions of system (1.3)

3.3.1. The first family of solutions

3.3.2. The second family of solutions

3.3.3. The third family of solutions

4. Results and discussions

5. Conclusions

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. Unified solver method

2.1. The first family

2.2. The second family

2.3. The third family

3. Applications

3.1. Solutions of system (1.1)

3.1.1. The first family of solutions

3.1.2. The second family of solutions

3.1.3. The third family of solutions

3.2. Solutions of system (1.2)

3.2.1. The first family of solutions

3.2.2. The second family of solutions

3.2.3. The third family of solutions

3.3. Solutions of system (1.3)

3.3.1. The first family of solutions

3.3.2. The second family of solutions

3.3.3. The third family of solutions

4. Results and discussions

5. Conclusions

Conflict of interest

References