A study of dynamical features and novel soliton structures of complex-coupled Maccari's system

Naseem Abbas; Amjad Hussain; Mohsen Bakouri; Thoraya N. Alharthi; Ilyas Khan; Naseem Abbas; Amjad Hussain; Mohsen Bakouri; Thoraya N. Alharthi; Ilyas Khan

doi:10.3934/math.2025141

AIMS Mathematics

2025, Volume 10, Issue 2: 3025-3040. doi: 10.3934/math.2025141

Previous Article Next Article

Research article

A study of dynamical features and novel soliton structures of complex-coupled Maccari's system

1.
Department of Mathematics, Quaid-i-Azam University 45320, Islamabad 44000, Pakistan
2.
Department of Medical Equipment Technology, College of Applied Medical Science, Majmaah University, Majmaah 11952, Saudi Arabia
3.
Department of Physics, College of Arts, Fezzan University, Traghen 71340, Libya
4.
Department of Mathematics, College of Science, University of Bisha, P.O. Box 551, Bisha 61922, Saudi Arabia
5.
Department of Mathematics, College of Science Al-Zulfi, Majmaah University, Al-Majmaah 11952, Saudi Arabia
6.
Hourani Center for Applied Scientific Research, Al-Ahliyya Amman University, Amman, Jordan

Received: 27 December 2024 Revised: 22 January 2025 Accepted: 10 February 2025 Published: 18 February 2025
MSC : 35C08

This investigation focuses on solitary wave solutions and dynamic analysis of the complex coupled Maccari system. We employ the new extended hyperbolic function method to establish bright-wave and dark-wave profiles of the model. The resulting solutions include hyperbolic, trigonometric, and exponential-type functions. Furthermore, we explore the model's dynamical characteristics via multiple perspectives, including phase portrait analysis, quasi-periodic and chaotic patterns, sensitivity analysis and Lyapunov exponent. The analysis validates the robustness of the new extended hyperbolic function method on one hand and extends the understanding of complex wave structures in Maccari's system on the other hand.

Keywords:

Citation: Naseem Abbas, Amjad Hussain, Mohsen Bakouri, Thoraya N. Alharthi, Ilyas Khan. A study of dynamical features and novel soliton structures of complex-coupled Maccari's system[J]. AIMS Mathematics, 2025, 10(2): 3025-3040. doi: 10.3934/math.2025141

Related Papers:

[1]	István P. Sugár . Density of electric field energy around two surface-charged spheres surrounded by electrolyte II. The smaller sphere is inside the larger one. AIMS Biophysics, 2022, 9(1): 61-71. doi: 10.3934/biophy.2022006
[2]	István P. Sugár . Electric energies of a charged sphere surrounded by electrolyte. AIMS Biophysics, 2021, 8(2): 157-164. doi: 10.3934/biophy.2021012
[3]	István P. Sugár . A generalization of the Shell Theorem. Electric potential of charged spheres and charged vesicles surrounded by electrolyte. AIMS Biophysics, 2020, 7(2): 76-89. doi: 10.3934/biophy.2020007
[4]	István P. Sugár . A generalization of the Shell Theorem. Electric potential of charged spheres and charged vesicles surrounded by electrolyte. AIMS Biophysics, 2023, 10(1): 23-24. doi: 10.3934/biophy.2023003
[5]	Ganesh Prasad Tiwari, Santosh Adhikari, Hari Prasad Lamichhane, Dinesh Kumar Chaudhary . Natural bond orbital analysis of dication magnesium complexes [Mg(H₂O)₆]²⁺ and [[Mg(H₂O)₆](H₂O)_n]²⁺; n=1-4. AIMS Biophysics, 2023, 10(1): 121-131. doi: 10.3934/biophy.2023009
[6]	Hanieh Hadady, Doug Redelman, Sage R. Hiibel, Emil J. Geiger . Continuous-flow sorting of microalgae cells based on lipid content by high frequency dielectrophoresis. AIMS Biophysics, 2016, 3(3): 398-414. doi: 10.3934/biophy.2016.3.398
[7]	Klemen Bohinc, Leo Lue . On the electrostatics of DNA in chromatin. AIMS Biophysics, 2016, 3(1): 75-87. doi: 10.3934/biophy.2016.1.75
[8]	Piotr H. Pawłowski, Piotr Zielenkiewicz . The role of electric charge in SARS-CoV-2 and other viral infections. AIMS Biophysics, 2024, 11(2): 166-188. doi: 10.3934/biophy.2024011
[9]	Massimo Fioranelli, Maria Grazia Roccia, Aroonkumar Beesham, Dana Flavin, M. Ghaeni, Faissal AZIZ . A model for considering effects of extremely low frequency electromagnetic fields on quail embryonic cells. AIMS Biophysics, 2022, 9(3): 198-207. doi: 10.3934/biophy.2022017
[10]	David E. Shoup . Diffusion-controlled reaction rates for clusters of binding sites on a cell. AIMS Biophysics, 2016, 3(4): 522-528. doi: 10.3934/biophy.2016.4.522

Abstract

1. Introduction

Let $\mathcal{A}$ denote the class of functions of the normalized form

$\begin{align} f(z) = z+\sum\limits^{\infty}_{k = 2}a_{k}z^{k}, \end{align}$

(1.1)

which are analytic in the unit open disk

$\mathbb{D} = \{z\in\mathbb{C}:|z| < 1\}$

and all coefficients are complex numbers. Let $\Phi$ denote the set of analytic function with positive real part on $\mathbb{D}$ with

$\phi(0) = 1,\ \ \phi^{\prime}(0) > 0$

and $\phi(z)$ maps $\mathbb{D}$ onto a region starlike with respect to 1 and symmetric with respect to the $x$ -axis. And, the function $\phi(z)$ has a series expansion of the form

$\phi(z) = 1+\sum\limits^{\infty}_{k = 1}A_{k}z^{k},$

where all coefficients $A_k(k\geq 1)$ are real number and $A_1 > 0$ . Also let $\mathcal{U}$ denote the class of Schwartz functions, which is analytic in $\mathbb{D}$ satisfying

$u(0) = 0 \ \; \; \text{and}\; \; \; |u(z)| < 1.$

In 1970, Robertson ^[1] introduced the concept of quasi-subordination. For two analytic functions $f_1(z)$ and $f_2(z)$ , the function $f_1(z)$ is quasi-subordinate to $f_2(z)$ in $\mathbb{D}$ , denoted by

$f_1(z)\prec _{q}f_2(z), z\in\mathbb{D},$

if there exists a Schwarz function $u(z)\in\mathcal{U}$ and an analytic function $h(z)$ with

$|h(z)|\leq 1$

such that

$f_1(z) = h(z)f_2(u(z)).$

Observe that when

$h(z) = 1,$

then

$f_1(z) = f_2(u(z))$

and it is said that $f_1(z)$ is subordinate to $f_2(z)$ and written

$f_1(z)\prec f_2(z)$

in $\mathbb{D}$ . Also notice that if

$u(z) = z,$

then

$f_1(z) = h(z)f_2(z)$

and it is said that $f_1(z)$ is majorized by $f_2(z)$ and written

$f_1(z)\ll f_2(z)$

in $\mathbb{D}$ . Hence it is obvious that quasi-subordination is a generalization of subordination as well as majorization. For works related to early study of the quasi-subordination concept, see ^[2,3,4].

In order to further explore the concept of quasi-subordination, some researchers have extended the construction of function classes and obtained some geometric properties of function classes. In 2012, Mohd and Darus generalized Ma-Minda starlike and convex classes in ^[5] and defined the generalized starlike class $\mathcal{S}^*_q(\phi)$ and the generalized convex class $\mathcal{C}_q(\phi)$ by using quasi-subordination, as below

$\begin{align*} \mathcal{S}^*_q(\phi)& = \left\{f(z)\in \mathcal{A}:\frac{zf^{\prime}(z)}{f(z)}-1\prec_q\phi(z)-1,\phi(z)\in\Phi,z\in\mathbb{D}\right\},\\ \mathcal{C}_q(\phi)& = \left\{f(z)\in \mathcal{A}:\frac{zf^{\prime\prime}(z)}{f^{\prime}(z)}\prec_q\phi(z)-1,\phi(z)\in\Phi,z\in\mathbb{D}\right\}. \end{align*}$

And, they defined the following function class (also see ^[6])

$\mathcal{M}_q(\alpha;\phi) = \left\{f(z)\in \mathcal{A}:(1-\alpha)\frac{zf^{\prime}(z)}{f(z)}+\alpha\left(1+\frac{zf^{\prime\prime}(z)}{f^{\prime}(z)}\right)-1\prec_q\phi(z)-1,\phi(z)\in\Phi,\alpha\geq0,z\in\mathbb{D}\right\}.$

In 2015, El-Ashwah et al. ^[7] introduced the generalized starlike class $\mathcal{S}^*_q(\mu; \phi)$ of complex order and the generalized convex class $\mathcal{C}_q(\mu; \phi)$ of complex order as follows,

$\begin{align*} \mathcal{S}^*_q(\mu;\phi)& = \left\{f(z)\in \mathcal{A}:1+\frac{1}{\mu}\left(\frac{zf^{\prime}(z)}{f(z)}-1\right)\prec_q\phi(z),\phi(z)\in\Phi,\mu\in\mathbb{C}\backslash \{0\} , z\in\mathbb{D}\right\},\\ \mathcal{C}_q(\mu;\phi)& = \left\{f(z)\in \mathcal{A}:1+\frac{1}{\mu}\frac{zf^{\prime\prime}(z)}{f^{\prime}(z)}\prec_q\phi(z),\phi(z)\in\Phi,\mu\in\mathbb{C}\backslash \{0\},z\in\mathbb{D}\right\}. \end{align*}$

In 2020, Ramachandran et al. ^[8] defined the class $\mathcal{M}^*_q(\alpha, \beta, \lambda; \psi)$ by using quasi-subordination. The function $f(z)\in \mathcal{A}$ is in the class $\mathcal{M}^*_q(\alpha, \beta, \lambda; \phi)$ if

$\left(\frac{zf^\prime (z)}{f(z)}\right)^{\alpha}\left[(1-\lambda)\frac{zf^\prime (z)}{f(z)}+\lambda\left(1+\frac{zf^{\prime \prime} (z)}{f(z)}\right)\right]^{\beta}-1\prec_q\phi(z)-1,$

where $\phi(z)\in\Phi$ and $0\leq\alpha, \beta, \lambda\leq1$ . Many authors have studied various function subclasses defined by quasi-subordination. For example, Vays et al. ^[9], Altinkaya et al. ^[10], Goyal et al. ^[11] and Choi et al. ^[12] studied bi-univalent functions using quasi-subordination. Shah et al. ^[13] and Aoen et al. ^[14] introduced meromorphic functions using quasi-subordination. Karthikeyan et al. ^[15] studied Bazilević function using quasi-subordination. Shah et al. ^[16] studied non-Bazilević function using quasi-subordination. And, there are some function subclasses of linear and nonlinear operators (such as, hohlov operator ^[17], difference operator ^[18] and derivative operator ^[19]) using quasi-subordination.

Recently, some researchers have begun to generalize close-to-convex function classes by using quasi-subordination relationship. In 2019, Gurmeet Singh et al. ^[20] introduced the subclass of bi-close-to-convex function defined by quasi-subordination. In 2023, Aoen et al. ^[21] introduced the class of generalized close-to-convex function with complex order written as $\mathcal{K}_q(\gamma; \phi, \psi)$ . This class were defined as below

$\mathcal{K}_q(\gamma;\phi,\psi) = \left\{f(z)\in \mathcal{A}:\frac{1}{\gamma}\left(\frac{zf^{\prime}(z)}{g(z)}-1\right)\prec_q\psi(z)-1, g(z)\in\mathcal{S}^*_q(\phi),\phi(z),\psi(z)\in\Phi,\gamma\in\mathbb{C}\backslash\{0\},z\in\mathbb{D}\right\}.$

In order to denote a new function class, we need to introduce the following function subclasses.

Definition 1.1. Let

$\alpha\in[0,1],\ \ \mu\in\mathbb{C}\backslash\{0\}.$

Also let $\phi(z)\in\Phi$ . A function $f(z)\in\mathcal{A}$ given by $(1.1)$ is said to be in the class $\mathcal{M}_{q}(\alpha, \mu; \phi)$ if the following condition is satisfied

$\frac{1}{\mu}\left[(1-\alpha)\frac{zf^{\prime}(z)}{f(z)}+\alpha\frac{(zf^{\prime}(z))^{\prime}}{f^{\prime}(z)}-1\right] \prec_q\phi(z)-1,\ \ \ z\in\mathbb{D}.$

Example 1.2. Let

$\alpha\in[0,1],\ \ \mu\in\mathbb{C}\backslash\{0\},\ \ \phi(z)\in\Phi.$

The function

$f(z):\mathbb{D}\rightarrow \mathbb{C}$

defined by the following

$\frac{1}{\mu}\left[(1-\alpha)\frac{zf^{\prime}(z)}{f(z)}+\alpha\frac{(zf^{\prime}(z))^{\prime}}{f^{\prime}(z)}-1\right] = z[\phi(z)-1]$

belongs to the class $\mathcal{M}_{q}(\alpha, \mu; \phi)$ .

Remark 1.3. There are some suitable choices of $\alpha, \mu$ which would provide some classical subclasses of analytic functions.

(1) By taking $\mu = 1$ in Definition 1.1, we have

$\mathcal{M}_{q}(\alpha,1;\phi)\equiv\mathcal{M}_{q}(\alpha;\phi)$

which is introduced by Mohd et al. ^[5].

(2) By taking $\alpha = 0$ in Definition 1.1, we have

$\mathcal{M}_{q}(0,\mu;\phi)\equiv\mathcal{S}^*_{q}(\mu;\phi)$

which is introduced by El-Ashwah et al.^[7]. Specially, for $\mu = 1$ we have

$\mathcal{M}_{q}(0,1;\phi)\equiv\mathcal{S}^*_{q}(\phi)$

which is introduced and studied by Mohd et al. ^[5].

(3) By taking $\alpha = 1$ in Definition 1.1, we have

$\mathcal{M}_{q}(1,\mu;\phi)\equiv\mathcal{C}_{q}(\mu;\phi)$

which is introduced by El-Ashwah et al. ^[7]. Specially, for $\mu = 1$ we have

$\mathcal{M}_{q}(1,1;\phi)\equiv\mathcal{C}_{q}(\phi)$

which is introduced and studied by Mohd et al. ^[5].

Now we define a generalization class of close-to-convex function by using quasi-subordination relationship.

Definition 1.4. Let

$\alpha\in[0,1],\beta\in[0,1],\ \ \mu\in\mathbb{C}\backslash\{0\},\gamma\in\mathbb{C}\backslash\{0\}.$

Also let

$\psi(z)\in\Phi,\ \ g(z)\in \mathcal{M}_{q}(\alpha,\mu;\phi).$

A function $f(z)\in\mathcal{A}$ given by $(1.1)$ is said to be in the class $\mathcal{C}_{q}(\alpha, \beta, \mu, \gamma; \phi, \psi)$ if the following condition is satisfied

$\frac{1}{\gamma}\left[(1-\beta)\frac{zf^{\prime}(z)}{g(z)}+\beta\frac{(zf^{\prime}(z))^{\prime}}{g^{\prime}(z)}-1\right] \prec_q\psi(z)-1,\ \ \ z\in\mathbb{D}.$

Example 1.5. Let

$\alpha\in[0,1],\ \ \beta\in[0,1],\ \ \mu\in\mathbb{C}\backslash\{0\},\ \ \gamma\in\mathbb{C}\backslash\{0\},\ \ \phi(z)\in\Phi,\ \ g(z)\in \mathcal{M}_{q}(\alpha,\mu;\phi).$

The function

$f(z):\mathbb{D}\rightarrow \mathbb{C}$

defined by the following

$\frac{1}{\gamma}\left[(1-\beta)\frac{zf^{\prime}(z)}{g(z)}+\beta\frac{(zf^{\prime}(z))^{\prime}}{g^{\prime}(z)}-1\right] = z[\psi(z)-1]$

belongs to the class $\mathcal{C}_{q}(\alpha, \beta, \mu, \gamma; \phi, \psi)$ .

Remark 1.6. There are some suitable choices of $\alpha, \beta, \mu, \gamma$ which would provide the following subclasses of the class $\mathcal{C}_{q}(\alpha, \beta, \mu, \gamma; \phi, \psi)$ .

(1) By taking $\beta = 0$ in Definition 1.4, the class $\mathcal{C}_{q}(\alpha, \beta, \mu, \gamma; \phi, \psi)$ reduces to the new subclass $\mathcal{K}_{q}(\alpha, \mu, \gamma; \phi, \psi)$ which is the class of generalized close-to-convex function satisfied by

$\frac{1}{\gamma}\left(\frac{zf^\prime(z)}{g(z)}-1\right)\prec_q\psi(z)-1,\ \ \ g(z)\in\mathcal{M}_{q}(\alpha,\mu;\phi),\phi(z),\psi(z)\in\Phi,z\in\mathbb{D}.$

Specially, for $\alpha = 1, \mu = 1$ in the class $\mathcal{K}_{q}(\alpha, \mu, \gamma; \phi, \psi)$ , we have

$\mathcal{H}_{q}(\gamma;\phi,\psi) = \left\{f(z)\in \mathcal{A}:\frac{1}{\gamma}\left(\frac{zf^\prime(z)}{g(z)}-1\right)\prec_q\psi(z)-1,g(z)\in\mathcal{C}_{q}(\phi),\phi(z),\psi(z)\in\Phi,z\in\mathbb{D}\right\};$

for $\alpha = 0, \mu = 1$ in the class $\mathcal{K}_{q}(\alpha, \mu, \gamma; \phi, \psi)$ , we have

$\mathcal{K}_{q}(0,1,\gamma;\phi,\psi)\equiv \mathcal{K}_{q}(\gamma;\phi,\psi)$

which is introduced and studied by Aoen et al. ^[21]. Also, for $\gamma = 1$ in the class $\mathcal{K}_{q}(\gamma; \phi, \psi)$ , we have the class $\mathcal{K}_{q}(\phi, \psi)$ which is introduced and studied by Aoen et al. ^[21].

(2) By taking $\beta = 1$ in Definition 1.4, the class $\mathcal{C}_{q}(\alpha, \beta, \mu, \gamma; \phi, \psi)$ reduces to the new subclass $\mathcal{C}^*_{q}(\alpha, \mu, \gamma; \phi, \psi)$ which is the class of generalized quasi-convex function satisfied by

$\frac{1}{\gamma}\left(\frac{(zf^{\prime}(z))^\prime}{g^\prime(z)}-1\right)\prec_q\phi(z)-1,\ \ \ g(z)\in\mathcal{M}_{q}(\alpha,\mu;\phi),\phi(z),\psi(z)\in\Phi,z\in\mathbb{D}.$

Specially, for $\alpha = 1, \mu = 1$ in the class $\mathcal{C}^*_{q}(\alpha, \mu, \gamma; \phi, \psi)$ , we have

$\mathcal{C}^*_{q}(\gamma;\phi,\psi) = \left\{f(z)\in\mathcal{A}: \frac{1}{\gamma}\left(\frac{(zf^{\prime}(z))^\prime}{g^\prime(z)}-1\right)\prec_q\phi(z)-1,g(z)\in\mathcal{C}_{q}(\phi),\phi(z),\psi(z)\in\Phi,z\in\mathbb{D}\right\};$

for $\alpha = 0, \mu = 1$ in the class $K_{q}(\alpha, \mu, \gamma; \phi, \psi)$ , we have

$\mathcal{L}_{q}(\gamma;\phi,\psi) = \left\{f(z)\in\mathcal{A}: \frac{1}{\gamma}\left(\frac{(zf^{\prime}(z))^\prime}{g^\prime(z)}-1\right)\prec_q\phi(z)-1,g(z)\in\mathcal{S}^*_{q}(\phi),\phi(z),\psi(z)\in\Phi,z\in\mathbb{D}\right\}.$

Studying the theory of analytic functions has been an area of concern for many researchers. The study of coefficients estimate is a more special and important field in complex analysis. For example, the bound for the second coefficient $a_2$ of normalized univalent functions readily yields the growth and distortion bounds for univalent functions. The coefficient functional $|a_3-\mu a_2^2|$ (that is, Fekete-Szegö problem) also naturally arises in the investigation of univalency of analytic functions. There are now many results of this type in the literature, each of them dealing with coefficient estimate for various classes of functions. In particular, some authors start to study the coefficient estimates for various classes using quasi-subordination. For example, Arikan et al. ^[22] and Marut et al. ^[23] studied the Fekete-Szegö problem for some function subclasses using quasi-subordination. Aoen et al. ^[24] and Ahman et al. ^[25] obtained the results on coefficient estimates for various subclasses using quasi-subordination. The purpose of this paper is to study some properties of the class $\mathcal{C}_{q}(\alpha, \beta, \mu, \gamma; \phi, \psi)$ and some of its subclasses, such as the integral expression, the first two coefficient estimate problems and Fekete-Szegö problem. Our results are new in this direction and they give birth to many corollaries.

In order to derive our main results, we have to recall here the following lemmas.

Lemma 1.7. Let $f(z)\in \mathcal{C}_{q}(\phi)$ , then

$\begin{align} f(z) = \displaystyle {\int}_0^z\exp\left(\displaystyle {\int}_0^t\frac{h(\xi)[\phi(u(\xi))-1]}{\xi}d\xi\right)dt, \end{align}$

(1.2)

where

$|h(z)|\leq1,\ \ u(z)\in\mathcal{U},\ \ \phi(z)\in\Phi.$

Proof. Since

$f(z)\in\mathcal{C}_{q}(\phi),$

then there exist two analytic functions $h(z), u(z)$ with

$|h(z)|\leq1,\ \ |u(z)| < 1,\ \ u(0) = 0$

such that

$\begin{align} \frac{zf^{\prime\prime}(z)}{f^{\prime}(z)} = h(z)[\phi(u(z))-1]. \end{align}$

(1.3)

By substitution, the Eq (1.3) can be reduced to a first-order differential equation. According to the method of solving the first-order differential equations, we can obtain the general solution of the equation. That is,

$\begin{align} f^{\prime}(z) = \exp\left(\displaystyle {\int}_0^z\frac{h(t)[\phi(u(t))-1]}{t}dt\right). \end{align}$

(1.4)

Integrating both sides of Eq (1.4), we get (1.2). Thus, the proof of Lemma 1.7 is complete.□

Lemma 1.8. ^[21] Let $f(z)\in\mathcal{S}_q^*(\phi)$ , then

$f(z) = z\exp\left(\displaystyle {\int}_0^z\frac{h(\xi)[\phi(u(\xi))-1]}{\xi}d\xi\right),$

where

$|h(z)|\leq1,\ \ u(z)\in\mathcal{U},\ \ \phi(z)\in\Phi.$

Lemma 1.9. ^[26] Let

$\varphi(z) = c_0+\sum\limits^{\infty}_{k = 1}c_kz^k$

be an analytic function in $\mathbb{D}$ with $|\varphi(z)|\leq1$ , then

$|c_0|\leq1,\ \ \ |c_1|\leq1-|c_0|^2.$

Lemma 1.10. ^[27] Let

$t(z) = \sum\limits^{\infty}_{k = 1}t_kz^k$

be an analytic function in $\mathbb{D}$ with $|t(z)| < 1$ , then

$|t_1|\leq1,|t_2-\mu t^2_1|\leq\max\{1,|\mu|\},$

where $\mu\in\mathbb{C}.$ The result is sharp for the functions

$t(z) = z\; \; \; \text{or} \; \; t(z) = z^2.$

2. Integral expressions

In this section, we discuss the integral expressions for the class $\mathcal{C}_{q}(\alpha, \beta, \mu, \gamma; \phi, \psi)$ and some of its subclasses by using methods for solving differential equations.

Theorem 2.1. Let

$\alpha\in[0,1],\ \ \beta\in[0,1],\ \ \mu\in\mathbb{C}\backslash\{0\},\ \ \gamma\in\mathbb{C}\backslash\{0\},$

the function $f(z)\in\mathcal{C}_{q}(\alpha, \beta, \mu, \gamma; \phi, \psi)$ be given by (1.1). Then,

(ⅰ) If $\beta\neq0$ , then

$\begin{align} f(z) = \frac{1}{\beta}\displaystyle {\int}_0^z\frac{[g(t)]^{1-\frac{1}{\beta}}}{t}\left(\displaystyle {\int}_0^t[g(\xi)]^{\frac{1}{\beta}-1}g^{\prime}(\xi) [1+\gamma h(\xi)\left(\psi(u(\xi))-1\right)]d\xi\right)dt. \end{align}$

(2.1)

(ⅱ) If $\beta = 0$ , then

$f(z) = \displaystyle {\int}_0^z\frac{g(t)}{t}[1+\gamma h(t)\left(\psi(u(t))-1\right)]dt,$

where

$|h(z)|\leq1,\ \ u(z)\in\mathcal{U},\ \ \psi(z)\in\Phi,\ \ g(z)\in \mathcal{M}_{q}(\alpha,\mu;\phi).$

Proof. Since $f(z)\in\mathcal{C}_{q}(\alpha, \beta, \mu, \gamma; \phi, \psi)$ , then there exist two analytic functions $h(z), u(z)$ with

$|h(z)|\leq1,\ \ |u(z)| < 1,\ \ u(0) = 0$

such that

$\frac{1}{\gamma}\left[(1-\beta)\frac{zf^{\prime}(z)}{g(z)}+\beta\frac{(zf^{\prime}(z))^{\prime}}{g^{\prime}(z)}-1\right] = h(z)[\psi(u(z))-1].$

Then, we have

$\left(zf^\prime(z)\right)^{\prime} = \frac{(\beta-1)g^\prime(z)}{\beta g(z)}zf^\prime(z)+ \frac{\left[1+\gamma h(z)(\psi(u(z))-1)\right]g^{\prime}(z)}{\beta}.$

Let

$zf^\prime(z) = F(z),$

then we have

$F^\prime(z) = \frac{(\beta-1)g^\prime(z)}{\beta g(z)}F(z)+\frac{\left[1+\gamma h(z)(\psi(u(z))-1)\right]g^{\prime}(z)}{\beta}.$

Then, the above equation is a first-order nonhomogeneous linear differential equation. According to the method of solving first-order linear differential equations, we can obtain the general solution of the equation. That is,

$\begin{align} f^{\prime}(z) = \frac{1}{\beta}\frac{\left[g(z)\right]^{1-\frac{1}{\beta}}}{z}\displaystyle {\int}_0^z\left[g(t)\right]^{\frac{1}{\beta}-1}g^{\prime}(t) \left[1+\gamma h(t)\left(\psi(u(t))-1\right)\right]dt. \end{align}$

(2.2)

Integrating both sides of Eq (2.2), we get (2.1). Thus, the proof of Theorem 2.1 is complete. □

By taking $\beta = 1$ in Theorem 2.1, we obtain the following result.

Corollary 2.2. Let the function $f(z)\in \mathcal{C}^*_{q}(\alpha, \mu, \gamma; \phi, \psi)$ be given by (1.1). Then

$f(z) = \displaystyle {\int}_0^z\frac{1}{t}\left(\displaystyle {\int}_0^tg^{\prime}(\xi)[1+\gamma h(\xi)\left(\psi(u(\xi))-1\right)]d\xi\right)dt,$

where

$|h(z)|\leq1,\ \ u(z)\in\mathcal{U},\ \ \psi(z)\in\Phi,\ \ g(z)\in \mathcal{M}_{q}(\alpha,\mu;\phi).$

According to Lemmas 1.7 and 1.8 and Corollary 2.2, we can obtain the following two results.

Corollary 2.3. Let the function $f(z)\in \mathcal{C}^*_{q}(\gamma; \phi, \psi)$ be given by (1.1). Then

$f(z) = \displaystyle {\int}_0^z\frac{1}{t}\left(\displaystyle {\int}_0^t[1+\gamma h(\xi)\left(\psi(u(\xi))-1\right)] \exp\left(\displaystyle {\int}_0^\xi\frac{h_1(\zeta)[\phi(u_1(\zeta))-1]}{\zeta}d\zeta\right)d\xi\right)dt,$

where

$|h(z)|\leq1,\ \ |h_1(z)|\leq1,u(z),\ \ u_1(z)\in\mathcal{U},\ \ \phi(z),\psi(z)\in\Phi.$

Corollary 2.4. Let the function $f(z)\in \mathcal{L}_{q}(\gamma; \phi, \psi)$ be given by (1.1). Then

$\begin{equation*} \begin{aligned} f(z) = \displaystyle {\int}_0^z\frac{1}{t}\left(\displaystyle {\int}_0^t[1+\gamma h(\xi)\left(\psi(u(\xi))-1\right)][1+h_1(\xi)(\phi(u_1(\xi))-1)] \exp\left(\displaystyle {\int}_0^\xi\frac{h_1(\zeta)[\phi(u_1(\zeta))-1]}{\zeta}d\zeta\right)d\xi\right)dt,\end{aligned} \end{equation*}$

where

$|h(z)|\leq1,|h_1(z)|\leq1,\ \ u(z),u_1(z)\in\mathcal{U},\ \ \phi(z),\psi(z)\in\Phi.$

3. Coefficient estimates problem

In this section, we obtain the first two coefficient estimate and Fekete-Szegö problem for the class $\mathcal{C}_{q}(\alpha, \beta, \mu, \gamma; \phi, \psi)$ and some subclasses of this class by using algebraic operations, fundamental inequalities of analytic functions.

In addition to special statements, suppose the Taylor series expression for the following functions, as follows

$\begin{align*} f(z)& = z+\sum\limits_{k = 2}^{\infty}a_kz^k,\ \ \ \ g(z) = z+\sum\limits_{k = 2}^{\infty}b_kz^k,\\ \phi(z)& = 1+\sum\limits_{k = 1}^{\infty}A_kz^k(A_1\in\mathbb{R},A_1 > 0),\ \ \ \ \psi(z) = 1+\sum\limits_{k = 1}^{\infty}B_kz^k(B_1\in \mathbb{R},B_1 > 0),\\ \varphi(z)& = c_0+\sum\limits_{k = 1}^{\infty}c_kz^k,\ \ \ \ h(z) = h_0+\sum\limits_{k = 1}^{\infty}h_kz^k,\\ u(z)& = \sum\limits_{k = 1}^{\infty}u_kz^k,\ \ \ \ v(z) = \sum\limits_{k = 1}^{\infty}v_kz^k. \end{align*}$

In order to derive our main results, we have to discuss the first two coefficient estimates and Fekete-Szegö problem for the class $\mathcal{M}_{q}(\alpha, \mu; \phi)$ .

Theorem 3.1. Let $\alpha\in[0, 1], \mu\in\mathbb{C}\backslash\{0\},$ the function $f(z)\in\mathcal{M}_{q}(\alpha, \mu; \phi)$ be given by (1.1). Then

$\begin{align} |a_2|&\leq \frac{|\mu|A_1}{1+\alpha}, \end{align}$

(3.1)

$\begin{align} |a_3|&\leq\frac{|\mu|A_1}{2(1+2\alpha)}\max\left\{1,\left|\frac{\mu(1+3\alpha)}{(1+\alpha)^2}A_1+\frac{A_2}{A_1}\right|\right\}, \end{align}$

(3.2)

and for any $\eta\in\mathbb{C}$ ,

$\begin{align} |a_3-\eta a_2^2|\leq \frac{|\mu|A_1}{2(1+2\alpha)}\max\left\{1,\left|MA_1-\frac{A_2}{A_1}\right|\right\} , \end{align}$

(3.3)

where

$M = \frac{\mu[2\eta(1+2\alpha)-(1+3\alpha)]}{(1+\alpha)^2}.$

Proof. If $f(z)\in\mathcal{M}_{q}(\alpha, \mu; \phi)$ , according to Definition 1.1, there exist analytic functions $\varphi(z)$ and $u(z)$ , with

$|\varphi(z)|\leq 1,\ \ u(0) = 0\; \; \text{and}\; \; |u(z)| < 1$

such that

$\begin{align} \frac{1}{\mu}\left[(1-\alpha)\frac{zf^{\prime}(z)}{f(z)}+\alpha\frac{(zf^{\prime}(z))^{\prime}}{f^{\prime}(z)}-1\right] = \varphi(z)[\phi(u(z))-1]. \end{align}$

(3.4)

By substituting the Taylor series expression for the function $f(z)$ to the left of the above expression, we have

$\frac{zf'(z)}{f(z)} = 1+a_2z+(2a_3-a_2^2)z^2+\cdots,$

$\frac{(zf'(z))'}{f'(z)} = 1+2a_2z+2(3a_3-2a_2^2)z^2+\cdots.$

Thus we get the following expression

$\begin{align} \frac{1}{\mu}\left[(1-\alpha)\frac{zf^{\prime}(z)}{f(z)}+\alpha\frac{(zf^{\prime}(z))^{\prime}}{f^{\prime}(z)}-1\right] = \frac{1}{\mu}\left\{(1+\alpha)a_2z+[2(1+2\alpha)a_3-(1+3\alpha)a_2^2]z^{2}+\cdots\right\}. \end{align}$

(3.5)

And by substituting the power series expression of the functions $\varphi(z), \phi(z), u(z)$ to the right of (3.4), we can get the following expression

$\begin{align} \varphi(z)[\phi(u(z))-1]& = (c_0+c_1z+c_2z^2+\cdots)\left[A_1(u_1z+u_2z_2^2+\cdots)+A_2(u_1z+u_2z_2^2+\cdots)^2+\cdots\right]\\ & = A_{1}c_{0}u_{1}z+[A_{1}c_{1}u_{1}+c_{0}\left(A_{1}u_{2}+A_{2}u_1^2\right)]z^{2}+\cdots. \end{align}$

(3.6)

By substituting (3.5) and (3.6) into (3.4) and comparing the coefficients of the same power terms on both sides, we can get

$\begin{align} a_{2} = \frac{\mu A_{1}c_{0}u_{1}}{1+\alpha}, \end{align}$

(3.7)

$a_{3} = \frac{\mu A_1}{2(1+2\alpha)} \left[c_1u_1+c_0\left(u_2+\frac{A_2}{A_1}u_1^2\right)+\frac{(1+3\alpha)\mu}{(1+\alpha)^2}A_1c_0^2u_1^2\right].$

Further,

$\begin{align} a_{3}-\eta a_{2}^2 = \frac{\mu A_1}{2(1+2\alpha)} \left[c_1u_1+c_0\left(u_2+\frac{A_2}{A_1}u_1^2\right)-\frac{2\eta(1+2\alpha)-(1+3\alpha)}{(1+\alpha)^2}\mu A_1c_0^2u_1^2\right]. \end{align}$

(3.8)

Applying Lemmas 1.9 and 1.10 to $(3.7)$ , we obtain

$|a_{2}|\leq\frac{|\mu|A_1}{1+\alpha}.$

Since $\varphi(z)$ is analytic and bounded in $\mathbb{D}$ , using ^[28], for some

$y,|y| < 1:|c_0|\leq1,c_1 = (1-c_0^2)y.$

Replacing the value of $c_1$ as defined above, we get

$\begin{align} a_{3}-\eta a_{2}^2 = \frac{\mu A_1}{2(1+2\alpha)}\left[yu_1+c_0\left(u_2+\frac{A_2}{A_1}u_1^2\right)-\left(\frac{2\eta(1+2\alpha)-(1+3\alpha)}{(1+\alpha)^2}\mu A_1u_1^2+yu_1\right)c_0^2\right]. \end{align}$

(3.9)

If $c_0 = 0$ , then applying Lemmas 1.9 and 1.10 to $(3.9)$ , we obtain

$|a_{3}-\eta a_{2}^2|\leq\frac{|\mu| A_1}{2(1+2\alpha)}.$

If $c_0\neq0$ , let

$\begin{align} G(c_0) = yu_1+c_0\left(u_2+\frac{A_2}{A_1}u_1^2\right)-\left(\frac{2\eta(1+2\alpha)-(1+3\alpha)}{(1+\alpha)^2}\mu A_1u_1^2+yu_1\right)c_0^2, \end{align}$

(3.10)

which is a polynomial in $c_0$ and have analytic in $|c_0|\leq1$ .

According to Maximum modulus principle, we get

$\max|G(c_0)| = \max\limits_{0\leq\theta\leq2\pi}|G(e^{i\theta})| = |G(1)|.$

Thus

$\begin{align} |a_{3}-\eta a_{2}^2|\leq\frac{|\mu| A_1}{2(1+2\alpha)}\left|u_2-\left(\frac{2\eta(1+2\alpha)-(1+3\alpha)}{(1+\alpha)^2}\mu A_1-\frac{A_2}{A_1}\right)u_1^2\right|. \end{align}$

(3.11)

Applying Lemma 1.10 to (3.11), we can conclude (3.3). For $\eta = 0$ in (3.3), we have (3.2).

Let

$\frac{1}{\mu}\left[(1-\alpha)\frac{zf^{\prime}(z)}{f(z)}+\alpha\frac{(zf^{\prime}(z))^{\prime}}{f^{\prime}(z)}-1\right] = \phi(z)-1$

$\frac{1}{\mu}\left[(1-\alpha)\frac{zf^{\prime}(z)}{f(z)}+\alpha\frac{(zf^{\prime}(z))^{\prime}}{f^{\prime}(z)}-1\right] = z[\phi(z^2)-1].$

then the results of (3.1)–(3.3) are sharp. Thus, the proof of Theorem 3.1 is complete. □

Remark 3.2. (1) For $\mu = 1$ in Theorem 3.1, we can obtain the result which is Theorem 2.10 in ^[5].

(2) For $\mu = 1, \alpha = 0$ and $\mu = 1, \alpha = 1$ in Theorem 3.1, we can obtain the results which are Theorems 2.1 and 2.4 in ^[5], respectively.

(3) For $\alpha = 0$ and $\alpha = 1$ in Theorem 3.1, we improve the results which are Theorems 2.1 and 2.7 in ^[7], respectively.

Theorem 3.3. Let

$\alpha\in[0,1],\ \ \beta\in(0,1],\ \ \mu\in\mathbb{C}\backslash\{0\},\ \ \gamma\in\mathbb{C}\backslash\{0\},$

the function $f(z)\in\mathcal{C}_{q}(\alpha, \beta, \mu, \gamma; \phi, \psi)$ be given by (1.1). Then

$\begin{align} |a_2|\leq& \frac{|\mu|A_1}{2(1+\alpha)}+\frac{|\gamma|B_1}{2(1+\beta)}, \end{align}$

(3.12)

$\begin{align} |a_3|\leq&\ \frac{|\mu|A_1}{6(1+2\alpha)}\max\left\{1,\left|\frac{\mu(1+3\alpha)}{(1+\alpha)^2}A_1+\frac{A_2}{A_1}\right|\right\}+ \frac{|\gamma|B_1}{3(1+2\beta)}\max\left\{1,\frac{|B_2|}{B_1}\right\}\\&+ \frac{|\mu\gamma|(1+3\beta)}{3(1+\alpha)(1+\beta)(1+2\beta)}A_1B_1, \end{align}$

(3.13)

and for any $\tau\in\mathbb{C}$

$\begin{align} |a_3-\tau a_2^2|\leq& \frac{|\mu|A_1}{6(1+2\alpha)}\max\left\{1,\left|PA_1-\frac{A_2}{A_1}\right|\right\}+ \frac{|\gamma|B_1}{3(1+2\beta)}\max\left\{1,\left|QB_1-\frac{B_2}{B_1}\right|\right\}\\&+ \frac{|\mu\gamma[2(1+3\beta)-3\tau(1+2\beta)]|}{6(1+\alpha)(1+\beta)(1+2\beta)}A_1B_1, \end{align}$

(3.14)

where

$P = \frac{\mu[3\tau(1+2\alpha)-2(1+3\alpha)]}{2(1+\alpha)^2},\ \ \ Q = \frac{3\tau\gamma(1+2\beta)}{4(1+\beta)^2}.$

Proof. If $f(z)\in\mathcal{C}_{q}(\alpha, \beta, \mu, \gamma; \phi, \psi)$ , then there exist analytic functions $h(z)$ and $v(z)$ , with

$|\varphi(z)|\leq 1,\ \ v(0) = 0\; \; \text{and}\; \; |v(z)| < 1$

such that

$\begin{align} \frac{1}{\gamma}\left[(1-\beta)\frac{zf^{\prime}(z)}{g(z)}+\beta\frac{(zf^{\prime}(z))^{\prime}}{g^{\prime}(z)}-1\right] = h(z)[\psi(v(z))-1]. \end{align}$

(3.15)

By substituting the Taylor series expression for the functions $f(z), g(z)$ to the left of the above expression, we have

$\begin{align*} \frac{zf'(z)}{g(z)}& = 1+(2a_2-b_2)z+(3a_3-b_3+b_2^2-2a_2b_2)z^2+\cdots,\\ \frac{(zf'(z))'}{g'(z)}& = 1+2(2a_2-b_2)z+2(9a_3-3b_3+4b_2^2-8a_2b_2)z^2+\cdots. \end{align*}$

Thus we get the following expression

$\begin{align} &\frac{1}{\gamma}\left[(1-\beta)\frac{zf^{\prime}(z)}{g(z)}+\beta\frac{(zf^{\prime}(z))^{\prime}}{g^{\prime}(z)}-1\right] \\ & = \frac{1}{\gamma}\left\{(1+\beta)(2a_2-b_2)z+\left[(1+2\beta)(3a_3-b_3)+(1+3\beta)(b_2^2-2a_2b_2)\right]z^{2}+\cdots\right\}. \end{align}$

(3.16)

Similar to the proof of Theorem 3.1, by substituting the power series expression of the functions $h(z), \psi(z), v(z)$ to the right of (3.15), we can get the following expression

$\begin{align} h(z)[\psi(v(z))-1] = B_{1}h_{0}v_{1}z+[B_{1}h_{1}v_{1}+h_{0}(B_{1}v_{2}+B_{2}v_1^2)]z^{2}+\cdots. \end{align}$

(3.17)

By substituting (3.16) and (3.17) into (3.15) and comparing the coefficients of the same power terms on both sides, we can get

$\begin{align} a_{2} = \frac{1}{2}\left(\frac{\gamma B_1h_0v_1}{1+\beta}+b_2\right) \end{align}$

(3.18)

and

$a_{3} = \frac{1}{3(1+2\beta)}\left\{(1+2\beta)b_3-(1+3\beta)(b_2^2-2a_2b_2)+\gamma[B_1h_1v_1+h_0(B_1v_2+B_2v_1^2)]\right\}.$

Further,

$\begin{align} a_{3}-\tau a_{2}^2 = &\frac{1}{3}\left(b_3-\frac{3}{4}\tau b_2^2\right)+ \frac{\gamma[2(1+3\beta)-3\tau(1+2\beta)]}{6(1+\beta)(1+2\beta)}B_1h_0v_1b_2\\&+\frac{\gamma B_1}{3(1+2\beta)}\left[h_1v_1+h_0\left(v_2+\frac{B_2}{B_1}v_1^2\right)-\frac{3\tau\gamma(1+2\beta)}{4(1+\beta)^2}B_1h_0^2v_1^2\right]. \end{align}$

(3.19)

Applying Lemmas 1.9 and 1.10 to (3.18) and (3.19), we obtain

$\begin{align} |a_{2}|\leq\frac{1}{2}\left(\frac{|\gamma|B_1}{1+\beta}+|b_2|\right) \end{align}$

(3.20)

and

$\begin{align} |a_{3}-\tau a_{2}^2|\leq& \frac{1}{3}\left|b_3-\frac{3}{4}\tau b_2^2\right|+ \frac{|\gamma[2(1+3\beta)-3\tau(1+2\beta)]|}{6(1+\beta)(1+2\beta)}B_1|b_2|\\&+\frac{|\gamma|B_1}{3(1+2\beta)} \left|h_1v_1+h_0\left(v_2+\frac{B_2}{B_1}v_1^2\right)-\frac{3\tau\gamma(1+2\beta)}{4(1+\beta)^2}B_1h_0^2v_1^2\right|. \end{align}$

(3.21)

According to Theorem 3.1, it follows that

$\begin{align} |b_2|\leq \frac{|\mu|A_1}{1+\alpha} \end{align}$

(3.22)

and, for any complex number $\tau$ , we have

$\begin{align} |b_3-\frac{3}{4}\tau b_2^2|\leq\frac{|\mu|A_1}{2(1+2\alpha)}\max\left\{1,\left|PA_1-\frac{A_2}{A_1}\right|\right\}, \end{align}$

(3.23)

where

$P = \frac{\mu[3\tau(1+2\alpha)-2(1+3\alpha)]}{2(1+\alpha)^2}.$

Similar to the proof of Theorem 3.1, we can also get the following inequality

$\begin{align} \left|h_1v_1+h_0\left(v_2+\frac{B_2}{B_1}v_1^2\right)-\frac{3\tau\gamma(1+2\beta)}{4(1+\beta)^2}B_1h_0^2v_1^2\right|\leq \max\left\{1,\left|QB_1-\frac{B_2}{B_1}\right|\right\}, \end{align}$

(3.24)

where

$Q = \frac{3\tau\gamma(1+2\beta)}{4(1+\beta)^2}.$

By substituting (3.22) into (3.20), we get (3.12). And by substituting (3.22)–(3.24) into (3.21), we can conclude (3.14). For $\tau = 0$ in (3.14), we have (3.13).

The results of (3.12) and (3.13) are sharp for $\beta\neq0$ if

$f(z) = \frac{1}{\beta}\displaystyle {\int}_0^z\frac{[g(t)]^{1-\frac{1}{\beta}}}{t}\left(\displaystyle {\int}_0^t[g(\xi)]^{\frac{1}{\beta}-1}g^{\prime}(\xi) [1+\gamma\left(\psi(\xi)-1\right)]d\xi\right)dt$

and the results of (3.14) and (3.15) are sharp for $\beta = 0$ if

$f(z) = \displaystyle {\int}_0^z\frac{g(t)}{t}[1+\gamma\left(\psi(t)-1\right)]dt$

$f(z) = \displaystyle {\int}_0^z\frac{g(t)}{t}[1+\gamma\left(\psi(t^2)-1\right)]dt.$

Thus, the proof of Theorem 3.3 is complete. □

By taking special values of parameters $\alpha, \beta, \mu$ in Theorem 3.3, we can obtain coefficient estimates for functions belonging to some subclasses of the class $\mathcal{C}_{q}(\alpha, \beta, \mu, \gamma; \phi, \psi)$ .

Corollary 3.4. Let the function $f(z)\in\mathcal{K}_{q}(\alpha, \mu, \gamma; \phi, \psi)$ . Then

$\begin{align*} |a_2|&\leq \frac{|\mu|A_1}{2(1+\alpha)}+\frac{|\gamma|B_1}{2},\\ |a_3|&\leq\ \frac{|\mu|A_1}{6(1+2\alpha)}\max\left\{1,\left|\frac{\mu(1+3\alpha)}{(1+\alpha)^2}A_1+\frac{A_2}{A_1}\right|\right\}+ \frac{|\gamma|B_1}{3}\max\left\{1,\frac{|B_2|}{B_1}\right\}+ \frac{|\mu\gamma|}{3(1+\alpha)}A_1B_1, \end{align*}$

and for any $\tau\in\mathbb{C}$ ,

$\begin{align*} |a_3-\tau a_2^2|\leq& \frac{|\mu|A_1}{6(1+2\alpha)}\max\left\{1,\left|\frac{\mu[3\tau(1+2\alpha)-2(1+3\alpha)]}{2(1+\alpha)^2}A_1-\frac{A_2}{A_1}\right|\right\}\\&+ \frac{|\gamma|B_1}{3}\max\left\{1,\left|\frac{3\tau\gamma}{4}B_1-\frac{B_2}{B_1}\right|\right\}+ \frac{|\mu\gamma(2-3\tau)|}{6(1+\alpha)}A_1B_1. \end{align*}$

Remark 3.5. For $\alpha = \beta = 0, \mu = 1$ in Theorem 3.3 or $\alpha = 0, \mu = 1$ in Corollary 3.4, we obtain the result which is Corollary 3 in ^[21].

Corollary 3.6. Let the function $f(z)\in\mathcal{H}_{q}(\gamma; \phi, \psi)$ . Then

$\begin{align*} |a_2|&\leq \frac{A_1+2|\gamma|B_1}{4},\\ |a_3|&\leq\ \frac{A_1}{18}\max\left\{1,\left|A_1+\frac{A_2}{A_1}\right|\right\}+ \frac{|\gamma|B_1}{3}\max\left\{1,\frac{|B_2|}{B_1}\right\}+ \frac{|\gamma|}{6}A_1B_1, \end{align*}$

and for any $\tau\in\mathbb{C}$

$|a_3-\tau a_2^2|\leq \frac{A_1}{18}\max\left\{1,\left|\frac{9\tau-8}{8}A_1-\frac{A_2}{A_1}\right|\right\}+ \frac{|\gamma|B_1}{3}\max\left\{1,\left|\frac{3\tau\gamma}{4}B_1-\frac{B_2}{B_1}\right|\right\}+ \frac{|\gamma(2-3\tau)|}{12}A_1B_1.$

Especially, let

$\gamma = 1,\ \ \ \phi(z) = \psi(z) = \frac{1+z}{1-z},$

we can obtain the following result.

Remark 3.7. Let the function

$f(z)\in\mathcal{H}_{q}(1;\frac{1+z}{1-z},\frac{1+z}{1-z}).$

Then

$|a_2|\leq \frac{3}{2},\quad |a_3|\leq\ \frac{5}{3},$

and for any $\tau\in\mathbb{C}$

$|a_3-\tau a_2^2|\leq \frac{1}{9}\max\left\{1,\left|\frac{9\tau-12}{4}\right|\right\}+ \frac{2}{3}\max\left\{1,\left|\frac{3\tau}{2}-1\right|\right\}+ \frac{|2-3\tau|}{3}.$

The sharpness of the estimates is demonstrated by the functions

$f_1(z) = \frac{2z}{1-z}+\log(1-z)$

$f_2(z) = \frac{z}{1-z}+\frac{1}{2}\log(1-z^2),$

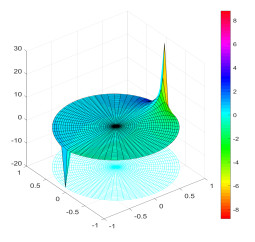
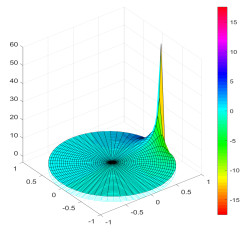
and the graph of the functions $f_1(z)$ and $f_1(z)$ are shown as follows,

In and , the three-dimensional coordinate system, coupled with color, is used to represent complex functions. Specifically, the $x$ -axis corresponds to the real part of the variable $z$ , the $y$ -axis to the imaginary part of $z$ , the $z$ -axis indicates the real part of the function, and the color signifies the imaginary part of the function.

Figure 1. The image of

$f_1(z)$ .

DownLoad: Full-Size Img PowerPoint

Figure 2. The image of

$f_2(z)$ .

DownLoad: Full-Size Img PowerPoint

Corollary 3.8. Let the function $f(z)\in\mathcal{C}^*_{q}(\alpha, \mu, \gamma; \phi, \psi)$ . Then

$\begin{align*} |a_2|&\leq \frac{|\mu|A_1}{2(1+\alpha)}+\frac{|\gamma|B_1}{4},\\ |a_3|&\leq\ \frac{|\mu|A_1}{6(1+2\alpha)}\max\left\{1,\left|\frac{\mu(1+3\alpha)}{(1+\alpha)^2}A_1+\frac{A_2}{A_1}\right|\right\}+ \frac{|\gamma|B_1}{9}\max\left\{1,\frac{|B_2|}{B_1}\right\}+ \frac{2|\mu\gamma|}{9(1+\alpha)}A_1B_1, \end{align*}$

and for any $\tau\in\mathbb{C}$ ,

$\begin{align*} |a_3-\tau a_2^2|\leq& \frac{|\mu|A_1}{6(1+2\alpha)}\max\left\{1,\left|\frac{\mu[3\tau(1+2\alpha)-2(1+3\alpha)]}{2(1+\alpha)^2}A_1-\frac{A_2}{A_1}\right|\right\}\\&+ \frac{|\gamma|B_1}{9}\max\left\{1,\left|\frac{9\tau\gamma}{16}B_1-\frac{B_2}{B_1}\right|\right\}+ \frac{|\mu\gamma(8-9\tau)|}{36(1+\alpha)}A_1B_1. \end{align*}$

Corollary 3.9. Let the function $f(z)\in\mathcal{C}^*_{q}(\gamma; \phi, \psi)$ . Then

$\begin{align*} |a_2|\leq& \frac{A_1+|\gamma|B_1}{4},\\ |a_3|&\leq\ \frac{A_1}{18}\max\left\{1,\left|A_1+\frac{A_2}{A_1}\right|\right\}+ \frac{|\gamma|B_1}{9}\max\left\{1,\frac{|B_2|}{B_1}\right\}+ \frac{|\gamma|}{9}A_1B_1, \end{align*}$

and for any $\tau\in\mathbb{C}$ ,

$|a_3-\tau a_2^2|\leq \frac{A_1}{18}\max\left\{1,\left|\frac{9\tau-8}{8}A_1-\frac{A_2}{A_1}\right|\right\}+ \frac{|\gamma|B_1}{9}\max\left\{1,\left|\frac{9\tau\gamma}{16}B_1-\frac{B_2}{B_1}\right|\right\}+ \frac{|\gamma(8-9\tau)|}{72}A_1B_1.$

Corollary 3.10. Let the function $f(z)\in\mathcal{L}_{q}(\gamma; \phi, \psi)$ . Then

$\begin{align*} |a_2|&\leq \frac{2A_1+|\gamma|B_1}{4},\\ |a_3|&\leq\ \frac{A_1}{6}\max\left\{1,\left|A_1+\frac{A_2}{A_1}\right|\right\}+ \frac{|\gamma|B_1}{9}\max\left\{1,\frac{|B_2|}{B_1}\right\}+ \frac{2|\gamma|}{9}A_1B_1, \end{align*}$

and for any $\tau\in\mathbb{C}$ ,

$|a_3-\tau a_2^2|\leq \frac{A_1}{6}\max\left\{1,\left|\frac{3\tau-2}{2}A_1-\frac{A_2}{A_1}\right|\right\}+ \frac{|\gamma|B_1}{9}\max\left\{1,\left|\frac{9\tau\gamma}{16}B_1-\frac{B_2}{B_1}\right|\right\}+ \frac{|\gamma(8-9\tau)|}{36}A_1B_1.$

4. Conclusions

In this paper, we introduce the new function class $\mathcal{C}_{q}(\alpha, \beta, \mu, \gamma; \phi, \psi)$ , which is a expanded close-to-convex functions defined by quasi-subordination. We mainly study the integral expression, the first two coefficient estimates and Fekete-Szegö problem for this class and some of its subclasses. In the future, we can consider to study other forms of coefficient estimation, such as Milin coefficient eatimate, Zal-cman functional estimate, high order Hankel Determinant estimate for these classes using the concepts dealt with in the paper.

Author contributions

Aoen: conceptualization, methodology, software, investigation, writing—original draft preparation, writing—review and editing, project administration, funding acquisition, visualization; Shuhai Li: conceptualization, methodology, formal analysis, resources; Tula: validation, data curation; Shuwen Li and Hang Gao: supervision. All authors have read and agreed to the published version of the manuscript.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The present investigation was supported by the Natural Science Foundation of Inner Mongolia Autonomous Region of China under Grant (No. 2025MS01034, 2024MS01014, 2020MS01010), the National Natural Science Foundation of China (Grant No.11561001) and the Program for Young Talents of Science and Technology in Universities of Inner Mongolia Autonomous Region under Grant (No. NJYT-18-A14).

Conflicts of interest

The authors declare no conflicts of interest.

References

[1]	S. Zhang, Exp-function method for solving Maccari's system, Phys. Lett. A, 371 (2007), 65–71. https://doi.org/10.1016/j.physleta.2007.05.091 doi: 10.1016/j.physleta.2007.05.091
[2]	S. Y. Arafat, K. Fatema, M. E. Islam, M. A. Akbar, Promulgation on various genres soliton of Maccari system in nonlinear optics, Opt. Quant. Electron., 54 (2022), 206. https://doi.org/10.1007/s11082-022-03576-0 doi: 10.1007/s11082-022-03576-0
[3]	A. Maccari, The Kadomtsev-Petviashvili equation as a source of integrable model equations, J. Math. Phys., 37 (1996), 6207–6212. https://doi.org/10.1063/1.531773 doi: 10.1063/1.531773
[4]	N. Cheemaa, S. Chen, A. R. Seadawy, Propagation of isolated waves of coupled nonlinear (2+1)-dimensional Maccari system in plasma physics, Results Phys., 17 (2020), 102987. https://doi.org/10.1016/j.rinp.2020.102987 doi: 10.1016/j.rinp.2020.102987
[5]	R. Ali, D. Kumar, A. Akgul, A. Altalbe, On the periodic soliton solutions for fractional Schrodinger equations, Fractals, 32 (2024), 2440033. https://doi.org/10.1142/S0218348X24400334 doi: 10.1142/S0218348X24400334
[6]	M. G. Hafez, M. N. Alam, M. A. Akbar, Traveling wave solutions for some important coupled nonlinear physical models via the coupled Higgs equation and the Maccari system, J. King Saud Uni. Sci., 27 (2015), 105–112. https://doi.org/10.1016/j.jksus.2014.09.001 doi: 10.1016/j.jksus.2014.09.001
[7]	M. G. Hafez, B. Zheng, M. A. Akbar, Exact travelling wave solutions of the coupled nonlinear evolution equation via the Maccari system using novel $(G^{'}/G)$ -expansion method, Egypt. J. Basic Appl. Sci., 2 (2015), 206–220. https://doi.org/10.1016/j.ejbas.2015.04.002 doi: 10.1016/j.ejbas.2015.04.002
[8]	M. Inc, A. I. Aliyu, A. Yusuf, D. Baleanu, E. Nuray, Complexiton and solitary wave solutions of the coupled nonlinear Maccari's system using two integration schemes, Modern Phys. Lett. B, 32 (2018), 1850014. https://doi.org/10.1142/S0217984918500148 doi: 10.1142/S0217984918500148
[9]	H. Kumar, F. Chand, Exact traveling wave solutions of some nonlinear evolution equations, J. Theor. Appl. Phys., 8 (2014), 114. https://doi.org/10.1007/s40094-014-0114-z doi: 10.1007/s40094-014-0114-z
[10]	H. Bulut, G. Yel, H. M. Baskonus, Novel structure to the coupled nonlinear Maccari's system by using modified trial equation method, Adv. Math. Models Appl., 2 (2017), 14–19.
[11]	T. Xu, Y. Chen, Z. Qiao, Multi-dark soliton solutions for the (2+1)-dimensional multi-component Maccari system, Modern Phys. Lett. B, 33, (2019), 1950390. https://doi.org/10.1142/S0217984919503901 doi: 10.1142/S0217984919503901
[12]	A. Neirameh, New analytical solutions for the coupled nonlinear Maccari's system, Alex. Eng. J., 55 (2016), 2839–2847. https://doi.org/10.1016/j.aej.2016.07.007 doi: 10.1016/j.aej.2016.07.007
[13]	N. Cheemaa, M. Younis, New and more exact traveling wave solutions to integrable (2+1)-dimensional Maccari system, Nonlinear Dyn., 83 (2016), 1395–1401. https://doi.org/10.1007/s11071-015-2411-8 doi: 10.1007/s11071-015-2411-8
[14]	A. Saha, S. Banerjee, Dynamical systems and nonlinear waves in plasmas, New York: CRC Press, 2021. https://doi.org/10.1201/9781003042549
[15]	N. K. Pal, P. Chatterjee, A. Saha, Solitons, multi-solitons and multi-periodic solutions of the generalized Lax equation by Darboux transformation and its quasiperiodic motions, Int. J. Modern Phys. B, 38 (2023), 2440001. https://doi.org/10.1142/S0217979224400010 doi: 10.1142/S0217979224400010
[16]	A. Jhangeer, W. A. Faridi, M. Alshehri, Soliton wave profiles and dynamical analysis of fractional Ivancevic option pricing model, Sci. Rep., 14 (2024), 23804. https://doi.org/10.1038/s41598-024-74770-1 doi: 10.1038/s41598-024-74770-1
[17]	N. Abbas, A. Hussain, Novel soliton structures and dynamical behaviour of coupled Higgs field equations, Eur. Phys. J. Plus, 139 (2024), 327. https://doi.org/10.1140/epjp/s13360-024-05124-z doi: 10.1140/epjp/s13360-024-05124-z
[18]	A. Hussain, N. Abbas, S. Niazai, I. Khan, Dynamical behavior of Lakshamanan-Porsezian-Daniel model with spatiotemporal dispersion effects, Alex. Eng. J., 96, (2024), 332–343. https://doi.org/10.1016/j.aej.2024.03.024 doi: 10.1016/j.aej.2024.03.024
[19]	A. Hussain, N. Abbas, Periodic, quasi-periodic, chaotic waves and solitonic structures of coupled Benjamin-Bona-Mahony-KdV system, Phys. Scr., 99 (2024), 125231. https://doi.org/10.1088/1402-4896/ad896b doi: 10.1088/1402-4896/ad896b
[20]	V. I. Arnold, Ordinary differential equations, Berlin: Springer Science & Business Media, 1992.
[21]	R. Ali, E. Tag-eldin, A comparative analysis of generalized and extended $(G^\prime/G)$ -Expansion methods for traveling wave solutions of fractional Maccari's system with complex structure, Alex. Eng. J., 79, (2023) 508–530. https://doi.org/10.1016/j.aej.2023.08.007 doi: 10.1016/j.aej.2023.08.007
[22]	Z. M. Emad, S. S. M. A. Shehata, M. N. Alam, A. Lanre, Exact propagation of the isolated waves model described by the three coupled nonlinear Maccari's system with complex structure, Int. J. Modern Phys. B, 35 (2021), 2150193. https://doi.org/10.1142/S0217979221501939 doi: 10.1142/S0217979221501939
[23]	H. U. Rehman, M. A. Imran, N. Ullah, A. Akgul, Exact solutions of (2+1)‐dimensional Schrodinger's hyperbolic equation using different techniques, Numer. Meth. PDE, 39 (2023), 4575–4594. https://doi.org/10.1002/num.22644 doi: 10.1002/num.22644
[24]	D. Jordan, P. Smith, Nonlinear ordinary differential equations: an introduction for scientists and engineers, Cambridge: OUP Oxford, 2007.

Reader Comments

Your name:*

Email:*
© 2025 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)