1.
Introduction
Many theoretical and applied problems in different fields of study, such as physical sciences, biomedical engineering, chemistry, biological and chemical sciences, computer sciences, finance, statistics, economics and applied mathematical sciences contain symmetry, which may result a nonlinear polynomial equation
with m distinct roots ℘1,...,℘m. There are numerous numerical iterative methods for computing the roots of polynomial equations. These methods can be classified into two types: numerical iterative methods that approximate a single root at a time and iterative numerical methods that approximate all of the roots of a nonlinear polynomial equation simultaneously.
The Newton-Raphson method given as
is one the most commonly used numerical methods to approximate a single root of Eq (1.1) at a time, thanks to its local quadratic convergence. Iterative methods, such as Eq (1.2), have a significant drawback in that they require derivative evaluation at each iteration, which incurs a significant computational cost, and diverge if ϑ′(ϰ(i))=0 or the initial guess is far from the root. See, for example, the work of Akram et al.[1], Cordero et al.[2], Agarwal et al. [3], Chicharro et al. [4], Behl et al.[5], Chun et al. [6], Zafar et al.[7] and many others). Simultaneous methods having global convergence property, are stable and applicable for parallel execution as well. Convergence analysis, computational efficiency and parallel implementation of simultaneous iterative techniques have been studied by McNamee [8], Nedzhibov [9], Proinov et al. [10], Mir et al. [11], Cholakov [12], Proinov and Vasileva [13], Proinov and Petkova [14], Sanchez et al.[15], Ivanov [16], Kanno et al.[17] as well as the references cited therein.
Weierstrass method (WDM)[18], which approximates all the roots of Eq (1.1) simultaneously, given by
is one of the most famous iterative techniques used in comparison to Newton Raphson. The term ϑ(ϰ(i)t)mΠr≠tr=1(ϰ(i)t−ϰ(i)r) is called Weierstrass correction. The Weierstrass method, which simultaneously approximates all roots of Eq (1.1), has local quadratic convergence. Weierstrass introduced the method in 1891, and it was rediscovered by Kerner [19], Durand [20], Dochev [21], and Presic [22]. Dochev demonstrated the first local quadratic convergence of the Weierstrass iterative technique in 1962.
Later on, in 2015, Proinov [23] presented the general convergence theorem for the iterative process and discussed the use of the Weierstrass root approximating technique. In 2016, Nedzibove [24] developed a modified version of Eq (1.3), and Marcheva et al.[25] presented the local convergence theorem of the modified Weierstrass method in 2020. Song et al.[26] created and verified three new derivative-free simultaneous iterative Weierstrass computational methods for calculating all polynomial problem roots.
The goal of this paper is to develop and analyze the derivative-free family of Weierstrass-type methods with accelerated convergence in order to find the roots of the above problem, which should have better convergence behavior than the Weierstrass method. We analyze the convergence behavior of the proposed method by computing CPU-time, log of residual errors, computational errors, and drawing dynamical planes while solving numerical test problems. Several graphs are plotted to demonstrate that the newly constructed method outperforms existing methods in the literature in efficiency and accuracy.
2.
Derivation and theoretical convergence analysis of the simultaneous root finding method
First, we present the third order family of the single root finding method (MS), and then we generalize this scheme to simultaneously find all the roots of Eq (1.1):
where y(i)=ϰ(i)−ϑ(ϰ(i))ϑ′(ϰ(i)) and α∈ℜ.
The convergence theorem that follows validates our assumption.
Theorem 1. Let ¯−T be an open interval and ℘∈¯−T indicate the precise root of a function that is sufficiently differentiable for ϑ:¯−T⊆ℜ⟶ ℜ in an open interval ¯−T. The following error equation is satisfied if the convergence order of the family of iterative numerical procedures is three and ϰ(0) is close to ℘:
where ℑm=ϑm(℘)m!ϑ′(℘),m≥2.
Proof. Let ℘ be a single exact-root of ϑ and ϰ(i)=℘+ς(i), where e(i) is the error at ith iterative step. The following is the result of expanding ϑ(ϰ(i)) around ϰ=℘, using Taylor's series with ϑ(℘)=0:
and
Dividing (2.3) by (2.4), we have:
and
Using ϑ′(y(i)) and ϑ′(u(i)) in the 2nd-step of (2.1), we have:
Thus,
and it becomes
Hence the theorem is proved. □
Now, we convert iterative method (2.1) to simultaneous method by using Weierstrass correction [8] given by
as follows:
where y(i)t=ϰ(i)t−ϑ(ϰ(i)t)mΠr≠tr=1(ϰ(i)t−ˆϰ(i)r),(t,r=1,2,3,...,n) and ˆϰ(i)r is a modified two step Steffensen-type [27] fourth-order convergent method, i.e., ˆϰ(i)r=y(i)r−ϑ(y(i)r)ϑ[ϰ(i)r,y(i)r]+ϑ[y(i)r,t(i)r]−ϑ[ϰ(i)r,t(i)r]+α(y(i)r−ϰ(i)r)(y(i)r−t(i)r), y(i)r=ϰ(i)r−ϑ(ϰ(i)r)ϑ[ϰ(i)r,t(i)r],t(i)r=ϰ(i)r+ϑ(ϰ(i)r), α∈ℜ. In this case, ϑ[.,.] is the divided difference of order one and two, respectively.
Remark 1. The family of derivative-free methods (2.8) determines all distinct roots of (1.1) simultaneously and is abbreviated as MM.
2.1. Convergence analysis
This section discusses MM convergence analysis.
Theorem 2. Let ℘1,℘2,...,℘m be m simple roots of (1.1). If ϰ(0)1, ϰ(0)2,...,ϰ(0)m are, respectively, the initial estimates of the roots and close to exact roots, then MM has fifth-order convergence.
Proof. Let ϵt=ϰt−℘t, ϵ′t=yt−℘t and ϵ′′t=zt−℘t be the residual errors in ϰt,yt and zt estimations, respectively. To simplify things, we leave out iteration index i. From the 1st-step of (2.8), we have:
where Δ(ϰt)=ϑ(ϰt)mΠj≠tj=1(ϰi−ˆuj) and
with
and ˆϰj−℘j=O (ϵ4) (see [27]). Now, for a small enough ϵ: if ℘t is a simple root, then |ϰi−ϰj| is bounded away from zero, resulting in the following expression:
Then it implies that:
From (2.9), we have
Now by taking the 2nd-step of Eq (2.8), we have:
where
Assume ϵt=ϵj are same order, say O(ϵt), then it follows that
Using Eq (2.14) in Eq (2.12), we have:
Hence, the theorem is proved. □
3.
Basins of attraction
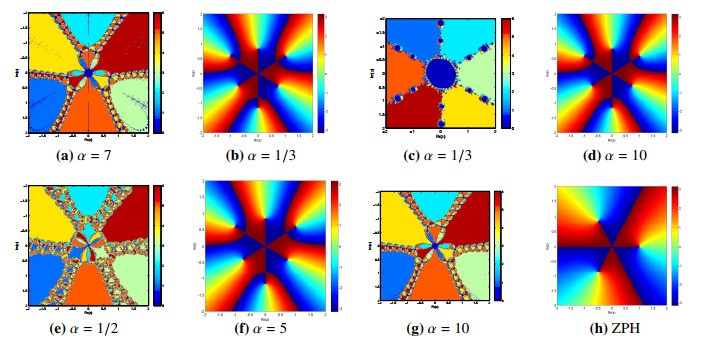
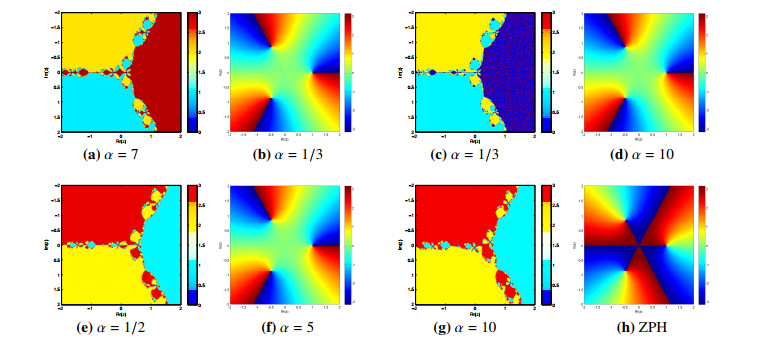
We employ the real and imaginary portions of the initial approximations across a grid of 250×250 of square [−2.5×2.5]2∈C in the complex plane to construct the basins of attraction of the iterative procedures used by MS, MM and the Zhang et al.[28] method (ZPH). Due to the global convergence behavior of the simultaneous technique, the maximum number of iterations was set at 15 and the stopping criterion was |ϑ(ϰ(i)t)|<10−5. We employ various colors to show the root at which the iterative technique converges, and black in all other cases. Basin colors sharpness signifies fewer iterations. We consider the following two non-linear functions for the generation of basins: ϑ1(ϰ)=ϰ3−1 with exact roots -1, -0.5+0.866i, -0.5-0.866i, and ϑ2(ϰ)=ϰ6−1i∗ϰ3+1 with exact roots -1.0167+0.587i, -1.1740i, 1.0167+0.587i, -0.7377-0.4259i, 0.8518i, 0.7377-0.4259i. Figures 1(a, c, e, g) and 2(a, c, e, g), present the basins of attraction of numerical iterative scheme MS for various parameter values of α and Figures 1(b, d, f, h) and 2(b, d, f, h) show basins of attraction of simultaneous methods MM (for various parameter values of α) and ZPH respectively for non-linear equation ϑ1(ϰ)−ϑ2(ϰ). Table 1 and color brightness in Figure 1(b, d, f) shows the ascendancy in efficiency of MM as compared to MS and ZPH.
Table 1 clearly demonstrates that the simultaneous method MM surpasses MS and ZPH in terms of actual time and number of cycles required for convergence to the exact root of the equation ϑ1(ϰ) and ϑ2(ϰ) for any initial guessed value used to generate basins of attraction.
4.
Percentage computational efficiency
Here, we compare the computation % efficiency of Zhang et al.'s [28] convergence order five technique (abbreviated as ZPH), i.e.,
with our newly proposed method based on the efficiency index E defined in [29]
where D is the cost of numerical computer calculation
and τ is the convergence order of iterative numerical schemes. Thus, (4.2) becomes:
By using (4.4) and the information in Table 2, the percentage efficiency ratio of simultaneous numerical iterative methods can be determined employing the following formula forρ((MM),(ZPH)) given by:
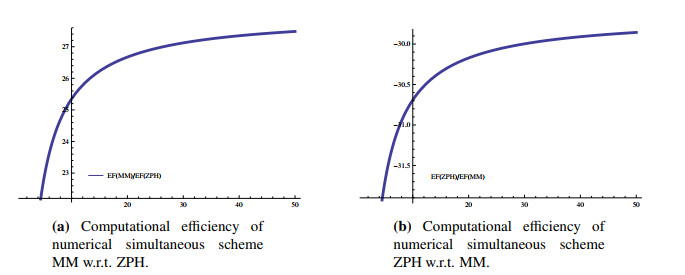
where O(m)=B. The dominance efficiency of MM over ZPH is demonstrated clearly in Figure 3(a, b).
5.
Numerical results
The ZPH and MM family of techniques were utilized to demonstrate the use and effectiveness of several nonlinear problems from biological engineering [12] and applied sciences [29,30,31,32,33,34,35,36] are considered in this section. All calculations utilize CAS-Maple 18 64-digit floating point arithmetic, and the process of iteration is terminated when
where ¯ς(i)t represents the absolute error. For simultaneous calculations of all roots of Eq (1.1), we set
as the fixed stopping criteria. In Tables 3–12, the quantity denoted CPU represents the time required to compute the root using the iterative schemes ZPH and MM, respectively. We use α=13 and β=12 in all numerical calculations. In Tables 4, 6, 8, 10, 12 for random initial vectors ((0)ϑ1-(0)ϑ3) taken from Appendix Table 13, MM and ZPH are represented by MMϑ1−MM3ϑ3 and ZPHϑ1−ZPHϑ3, respectively.
Example 1. An engineering application.
A non-linear expression described in [30]
depicts the minute modification of nitrogen hydrogen (NH) supply at 250 atm and 227 K. The exact roots of Eq (5.1) are ℘1=3.9485+0.3161i,℘2=3.9485−0.31610i,℘3=−0.38410,℘4=0.2778. The initial guessed values for calculating ϑ3(ϰ) are taken as equal to (0)ϰ1=3.50+0.30i, (0)ϰ2=3.50−0.30i, (0)ϰ3=−0.30+0.010i,(0)ϰ4=1.80+0.010i.
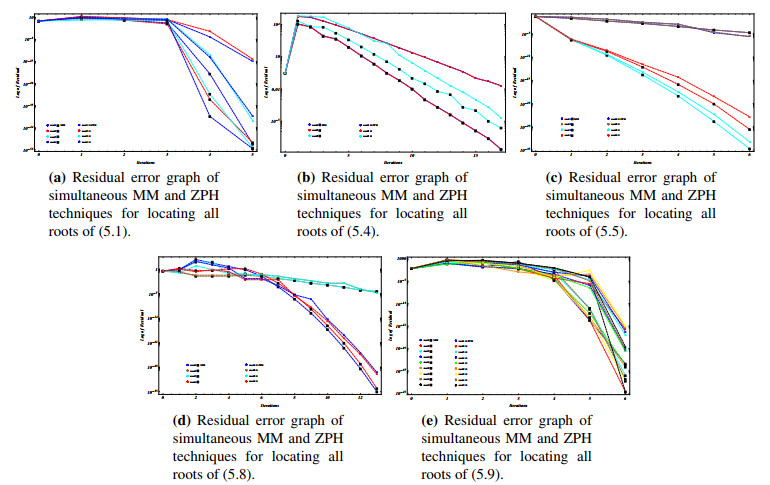
On the basis of efficiency achieved after five iterations, Table 3 unequivocally shows that the MM technique outperforms the ZPH method. Table 1 displays the global convergence behavior of the proposed numerical schemes on various randomly generated initial guesses (see Appendix Table 13).
In Table 4, ZPHϑ1−ZPHϑ3 and MMϑ1−MMϑ3 the numerical scheme ZPH and MM outputs for random initial vectors generated by the MATLAB computing tool. Numerical results of Table 4 clearly indicate numerical schemes are far better than ZPH for solving (5.1) and more complex engineering problems. The number of iterations and CPU time significantly increase when compared to the numerical results obtained in Table 3. Table 4 shows that for any initial vector choice, the method MM converges to exact roots with greater efficiency than ZPH.
Example 2. Predator-prey model (PPM).
Consider PPM in which predication rate [7] is denoted by
where ϰ is the amount of aphids as victims [31] and female microbes as a predator. Malthusian Model holds G(ϰ)=rϰ, as the growth rate of aphids. For solution of the PPM we take ¯P(ϰ)=¯G(ϰ). This implies
Taking ¯k=30 (the way pests are devoured), ¯a=20 (amount of bugs) and i=2−13 (hourly amount) in (5.3), we get:
The exact roots of Eq (5.4) are ℘1=25.198,℘2=25.198,℘3=12.84. The initial guessed estimates for ϑ4(ϰ) are selected as:
After seventeen iterations, Table 5 clearly shows that the MM methodology outperforms the ZPH method in terms of efficiency. Table 6 displays the global convergence behavior of the proposed numerical schemes on various randomly generated initial guesses (see Appendix Table 13).
Table 6 shows the numerical schemes ZPHϑ1−ZPHϑ3 and MMϑ1−MMϑ3 outputs for random initial vectors generated by the MATLAB computing tool. The numerical results of the table clearly show that the proposed numerical schemes are superior to ZPH for solving (5.4) and more difficult engineering problems. The number of iterations and CPU time significantly increase when compared to the numerical results obtained in Table 5. Table 6 shows that for any initial vector choice, the method MM converges to exact roots with greater efficiency than ZPH on iteration 37.
Example 3. Beam positioning problem.
In this example, we look at a beam positioning problem [32], which yields a nonlinear function
The exact roots of Eq (5.5) are
The initial estimates for ϑ3(ϰ) are
On the basis of efficiency achieved after six iterations, Table 7 unequivocally shows that the MM technique outperforms the ZPH method. Table 8 displays the global convergence behavior of the proposed numerical schemes on various randomly generated initial guesses (see Appendix Table 13).
Table 8 shows the numerical schemes ZPHϑ1−ZPHϑ3 and MMϑ1−MMϑ3 outputs for random initial vectors generated by the MATLAB computing tool. The numerical results of the Table 8 clearly show that the proposed numerical schemes are superior to ZPH for solving (5.5) and more difficult engineering problems. The number of iterations and CPU time significantly increase when compared to the numerical results obtained in Table 7. Table 8 shows that for any initial vector choice, the method MM converges to exact roots with greater efficiency than ZPH on iteration 11.
Example 4. [33] Nuclear boiler.
Consider a nuclear boiler, with the substances ˘A˘A and ˇRˇR, breastfed to the apparatus at rates of ˆQ and q-ˆQ, respectively. The following are the results of the multifaceted reaction system produced in the container:
Douglas et al. [34] tested this issue in order to create straightforward feedback control systems as:
or
where ˆHℑ denotes the proportional controller's gain. This control system is stable for all values of ˆHℑ that yield transfer function roots with negative real parts. Taking ˆHℑ=0 in (5.7), we have:
ϑ6(ϰ) has the four negative real roots listed below:
We take the root as ℘=−4.45 and
are chosen as initial estimates for finding all roots of (5.8) simultaneously.
On the basis of efficiency achieved after seventh iterations, Table 9 unequivocally shows that the MM technique outperforms the ZPH method.
Table 10 displays the global convergence behavior of the proposed numerical schemes on various randomly generated initial guesses (see appendix Table 13).
Table 10 shows the numerical schemes ZPHϑ1−ZPHϑ3 and MMϑ1−MMϑ3 outputs for random initial vectors generated by the MATLAB computing tool. The numerical results of Table 10 clearly show that the proposed numerical schemes are superior to ZPH for solving (5.8) and more difficult engineering problems. The number of iterations and CPU time significantly increase when compared to the numerical results obtained in Table 9. Table 10 shows that for any initial vector choice, the method MM converges to exact roots with greater efficiency than ZPH on iteration 10.
Example 5. [27,35,36] Polynomial of higher degree.
Consider
with exact roots:
The initial approximations of (5.9) have been taken as:
On the basis of efficiency achieved after sixth iterations, Table 11 unequivocally shows that the MM technique outperforms the ZPH method. Table 12 displays the global convergence behavior of the proposed numerical schemes on various randomly generated initial guesses (see Appendix Table 13).
Table 12 shows the numerical schemes ZPHϑ1−ZPHϑ3 and MMϑ1−MMϑ3 outputs for random initial vectors generated by the MATLAB computing tool. The numerical results of the Table 12 clearly show that the proposed numerical schemes are superior to ZPH for solving (5.9) and more difficult engineering problems. The number of iterations and CPU time significantly increase when compared to the numerical results obtained in Table 11. Table 12 shows that for any initial vector choice, the method MM converges to exact roots with greater efficiency than ZPH on iteration 35.
6.
Conclusions and observation
● In comparison to the well-known Weierstrass-type method ZPH, our newly developed methods is more efficient and stable.
● The results of the numerical test problems from Tables 3-12, computational efficiency from Figure 3, residual error graphs from Figure 4(a-e), and dynamical planes from Figures 1(a-h) and 2(a-h) show that the proposed family of iterative techniques MM outperforms ZPH in terms of efficiency and convergence behavior.
● Furthermore, the elapsed time of iterative technique MM from Table 1 is faster than ZPH.
● This paper proposes a family of Weierstrass-type derivative-free simultaneous techniques of order five. Tables 1–12 and Figures 1–4 show that our MM techniques outperform the Weierstrass-type method ZPH in terms of efficiency, CPU time, basins of attraction, and residual errors. Color brightness inspection in the basins reveals that MM requires fewer iteration steps than the simultaneous method ZPH. The results of the numerical test examples in terms of CPU-time and residual errors demonstrate the effectiveness and rapid convergence of our proposed derivative-free family of iterative algorithms, MM, in comparison to ZPH.
In summary, the comprehensive empirical results establish that these novel MM techniques outperform ZPH in terms of efficiency, CPU time, basins of attraction, and residual errors. Examination of the color brightness in the basins reveals MM requires fewer iteration steps than ZPH. Overall, the test examples clearly demonstrate the effectiveness, rapid convergence, and computational advantages of the proposed MM algorithms over ZPH.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The work is supported by Provincia autonoma di Bolzano/Alto Adigeâ euro Ripartizione Innovazione, Ricerca, Universitá e Musei (contract nr. 19/34). Bruno Carpentieri is a member of the Gruppo Nazionale per it Calcolo Scientifico (GNCS) of the Istituto Nazionale di Alta Matematia (INdAM) and this work was partially supported by INdAM-GNCS under Progetti di Ricerca 2022.
Conflict of interest
All authors declare no conflicts of interest in this paper.
Appendix









 DownLoad:
DownLoad: