Mathematical assessment of the impact of different microclimate conditions on malaria transmission dynamics

1.   Introduction

Malaria is an infectious vector-borne disease caused by female Anopheles mosquitoes infected with the Plasmodium parasite. It remains a major cause of mortality and morbidity in many tropical and subtropical regions of the world ^[38]. Even with resolute disease control efforts advocated by several health authorities, government and non-governmental organizations, the World Health Organization (WHO) estimated that there were 216 million cases of malaria in 2016 in 91 countries globally, where as there were 211 million cases in 2015 ^[39]. Also, there were roughly 445 thousand malaria deaths in 2016 ^[39]. Nigeria accounted for 27% of this global incidence and 24% of this global malaria deaths ^[39].

The dynamics and distribution of malaria have been shown to be strongly influenced by environmental factors such as temperature, rainfall, relative humidity and their daily fluctuations ^[5,30]. These factors have been shown to have significant impact on a range of mosquito life history traits such as the life cycle of mosquitoes as well as the development of sporogonic stages of the parasite within the body of the mosquito and hence, malaria transmission ^[38,21]. Since mosquitoes are highly sensitive to environmental conditions, which can trigger their dynamics and as well affect disease spread ^[7], there has been predictions that climate change will altar the transmission dynamics of malaria and also put at risk previously unexposed populations ^[5,7]. Thus, the understanding of the relationship between the malaria vector and its environment is necessary for effective control of mosquito population and disease prevention ^[7].

Particularly, the study by Paaijmans et al. ^[24] showed that fluctuations in temperature can substantially alter the length of parasite incubation in mosquitoes and that temperature fluctuation can reduce the impact of increases in mean temperature. In other words, fluctuations in temperature can make possible malaria transmission at lower mean temperatures than currently predicted and can potentially prevent transmission at higher mean temperatures than currently predicted ^[25]. The study in ^[25] thus highlighted the need to incorporate the effects of daily temperature variation into predictive models. Also, Blanford et al. ^[6] compared the effect of three measures of temperature; mean monthly temperature, mean daily temperature, and hourly temperatures on estimates of the extrinsic incubation period (EIP). They showed that under low temperature, using mean monthly temperature underestimates the EIP and overestimates it under high temperature. Recently, Shapiro et al. ^[32] used the Asian mosquito, Anopheles stephensi and the malaria parasite, Plasmodium falciparum to show how temperature affects a range of mosquito and parasite traits relevant to transmission.

In addition to daily temperature fluctuations, studies have shown the use of outdoor air temperature in malaria risk models will fail to capture the important features of the actual microclimate experienced by mosquitoes ^[28]. In particular, water temperature influences development rates of immature mosquitoes whereas outdoor and indoor air temperature (as studies have reported the tendency of mosquito species to be endophilic or exophilic or both) determines adult longevity as well as the rate of parasite development within the adult mosquito ^[27]. Therefore, the need for incorporating the variations of indoor and outdoor temperatures in the dynamics of malaria transmission is important as endophilic mosquitoes, and parasites within them, will be exposed more to indoor temperatures than the outdoor air temperature ^[27]. Hence, estimating malaria transmission intensity requires both indoor as well as outdoor temperatures. This is so because indoor temperatures differ from outdoor temperature ^[2,27] and parasite development rate (extrinsic incubation period (EIP)) in endophilic mosquitoes will be faster than predicted from ambient conditions. Also, this difference tend to become larger at higher altitudes as indoor and outdoor temperatures become more divergent with increase in altitude ^[27].

Many studies have explored the impact of climatic variables on the transmission dynamics of malaria. A study by Mondzozo et al. ^[11], showed that a marginal change in temperature and precipitation could lead to a significant change in malaria incidence in African countries. The study in ^[11] made use of a semi-parametric econometric model that investigated the relationship between malaria cases and climatic factors. Mordecai et al. ^[18], using a model which includes empirically derived nonlinear thermal responses, showed that the optimal malaria transmission occurs at 25℃ and decreases for temperature greater than 28℃. Agusto et al. ^[3] showed that for cities across different regions in Sub-Saharan Africa, the malaria burden increases with increasing temperature in the range (16℃–28℃). The work by Christiansen-Jucht et al. ^[8] showed that including age dependence in the vector component of the mosquito-borne disease model may be important to predict (more reliably) disease transmission dynamics. Ngarakana-Gwasira et al. ^[19] showed that as a result of climate change, malaria burden is likely to increase in the tropics, the highland regions and East Africa. Okuneye and Gumel ^[23] developed and analyzed a temperature and rainfall dependent mechanistic malaria model and incorporated features such as host age structure, dynamics of immature mosquitoes (with the egg, larva and pupa stages fused into one class) and reduced susceptibility to malaria infection due to prior malaria infection. Beck-Johnson et al. ^[5] explored the effects of temperature fluctuations on mosquito population dynamics in a stage-structured, delay-differential equation (DDE) model using diurnal, annual, and a combined annual and diurnal sinusoidal temperature fluctuations.

The purpose of this current study is to design, and analyze, a non-autonomous model for assessing the impact of the actual microclimates experienced by mosquitoes on the transmission dynamics of malaria and its control. Specifically, the model will be used to study the impact of the differences in indoor vs outdoor environments on the efficacy of control strategies. To the best of our knowledge, there is no study that has used mathematical models to quantify the differential effects of indoor and outdoor temperatures (explicitly) on the dynamics of malaria in a population. The model is formulated in Section 2. The autonomous version of the model is analyzed in Section 3, while the non-autonomous model will be analyzed in Section 4. Numerical simulations are considered in Section 5. The main conclusions from this study are summarized in Section 6.

2.   Materials and method

2.1.   Model formulation

The total human population at time t, denoted by $N_h(t)$, is split into sub-populations of susceptible humans $(S_h(t))$, exposed humans $(E_h(t))$, infectious humans $(I_h(t))$ and recovered humans $(R_h(t))$. Thus, $N_h(t) = S_h(t)+E_h(t)+I_h(t)+R_h(t)$.

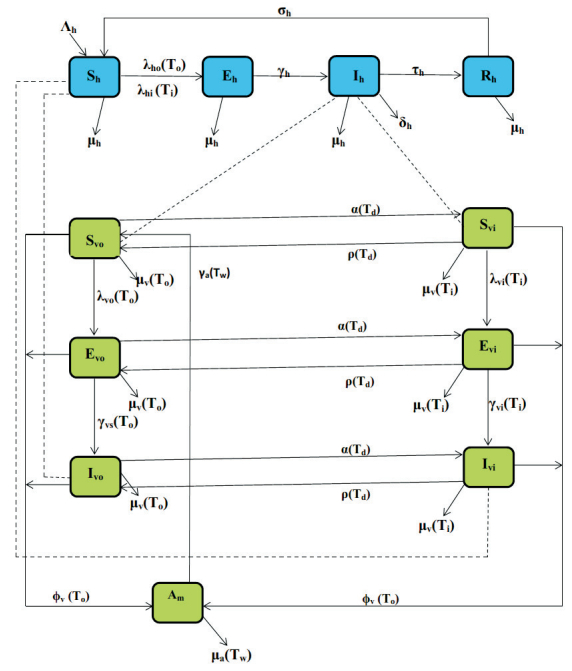
The total vector population, denoted by $N_v(t)$, is divided into sub-populations of aquatic and adult mosquitoes. The aquatic mosquito sub-population is denoted by $A_m(t)$. While the adult mosquito population $N_m(t)$, include outdoor susceptible mosquitoes ($(S_{vo}(t))$), indoor susceptible mosquitoes ($(S_{vi}(t))$), outdoor exposed mosquitoes ($(E_{vo}(t))$), indoor exposed mosquitoes ($(E_{vi}(t))$), outdoor infectious mosquitoes ($(I_{vo}(t))$) and indoor infectious mosquitoes ($(I_{vi}(t))$), so that $N_m(t) = S_{vo}(t)+S_{vi}(t)+E_{vo}(t)+E_{vi}(t)+I_{vo}(t)+I_{vi}(t)$. Thus, $N_v(t) = A_m(t)+N_m(t)$.

The non-autonomous model for malaria transmission dynamics in a population is given by the following system of deterministic non-linear differential equations (Table 1 describes the associated state variables and parameters in the model (2.1) while Figure 1 gives the flow diagram of model (2.1).$b$ and $\epsilon$ accounts for the efficacy of the bed-nets and door and window nets respectively.):

where the forces of infection for humans (outdoor and indoor) and vectors (outdoor and indoor) are given, respectively, by

2.1.1.   Temperature-dependent parameters

The temperature-dependent parameters for mosquito egg deposition rate, the per-capita death rate of the immature mosquitoes, maturation rate of immature mosquitoes, mosquito biting rate, natural mortality rate for adult vectors and progression rate of exposed vectors of the model (2.1), (defined using the functions in ^[3,23] where $T_w$, $T_o$, $T_i$ denote water, outdoor and indoor temperature, respectively, at time t), are given below:

We used a temperature-dependent carrying capacity ($k_v(T_o)$) modeled following ^[40] which assumed that the carrying capacity increases for temperature values in the range $(15^oC to 26.6^oC)$ and begins to decrease for temperature values above $26.6^oC$ due to evaporation and low rainfall. To model mosquito movement rates, it was shown in ^[21] that mosquitoes shift location from indoors to outdoors relative to differences in indoor and outdoor temperature conditions. Therefore, the carrying capacity ($k_v(T_o)$), the outdoor to indoor ($\alpha(T_d)$) and indoor to outdoor ($\rho(T_d)$) movements of mosquitoes are given as follows

Studies have shown that indoor temperatures are warmer than outdoors but show less variation ^[27] (and other references therein). Water temperature has also been shown to be $4-6^oC$ higher than the mean air temperature through out most part of the day ^[26]. Therefore, the following sinusoidal functions given below are used to explore in detail the dynamic consequences of variable temperatures (where $T_w$, $T_o$ and $T_i$ denote water, outdoor and indoor temperature, respectively, at time t).

The model (2.1) is an extension of numerous published malaria transmission models that investigated the impact of climatic variables such as temperature on the population dynamics of malaria. (e.g., ^[3,19,23,29]) inter alia:

(ⅰ) Including the role of indoor and outdoor temperature variations on the dynamics of malaria. None of the works in ^[3,19,23,29] or any other (to the best of our knowledge) considered the impact of such variations.

(ⅱ) Including control measures such as door and window nets as well as bed-net usage. The models in ^[3,19,23,29] did not include all such control measures put together.

(ⅲ) Including outdoor and indoor movement of mature mosquitoes.

2.1.2.   Basic properties

The basic properties of the non-autonomous model (2.1) will now be explored. Consider the rate of change of the total human population $N_h'(t)$ and vector population $N_v'(t)$

where $\mu_V(t) = min\{\mu_a(t), \mu_v(t), \mu_v(t)(1+b)\}$ and $N_m(t) = S_{vo}(t)+S_{vi}(t)+E_{vo}(t)+E_{vi}(t)+I_{vo}(t)+I_{vi}(t)$ is the total population of adult mosquitoes.

In a periodic environment, it is often assumed that the mosquito population stabilizes at a periodic steady state ^[16]. It is then assumed that there exists a positive number $n_o$ ^[16] such that

Lemma 2.1. Consider the model (2.1) with non-negative initial conditions satisfying $N_h(t) > 0$ for all $t > 0$. Then, the model has a unique non-negative solution in $C([0], \mathbb{R}^{11}_+)$ and all solutions are ultimately and uniformly-bounded.

Proof. Following ^[10], the non-autonomous model (2.1) can be written in the form

with $Y = (S_h, E_h, I_h, R_h, A_m, S_{vo}, S_{vi}, E_{vo}, E_{vi}, I_{vo}, I_{vi})$, $G = (\Lambda_h, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)^T$ and $\mathcal{E}(Y)$ is a $11\times11$ matrix given as

where

Now, using the fact that $G\geq0$ and that the matrix $\mathcal{E}(Y)$ is quasi-positive, it follows that the model (2.9) is positively-invariant in $C([0], \mathbb{R}^{11}_+)$. Furthermore, by the comparison theorem ^[14], the solutions of (2.6) and (2.7) exist for all $t\geq0$. Moreover, from (2.6), we see that

The unique $\tau$-periodic solution of (2.7) in $C([0], \mathbb{R}_+)\backslash\{0\}$ $N_v^*(t)$ is given by

so that

Hence all solutions of the model (2.1) are ultimately bounded. Moreover, it follows from (2.6) and (2.8) that $N'_h(t) < 0$ and $N'_v(t) < 0$ whenever $N_h(t) > \frac{\Lambda_h}{\mu_h}$ and $N_v(t) > n_o$, respectively. Thus all solutions of the model (2.1) are uniformly bounded.

2.2.   Analysis of the autonomous model

It is important to analyze the dynamics of the autonomous version of the non-autonomous model (2.1). Consider the case of the non-autonomous model (2.1) where all the temperature-dependent parameters are constants, then the reduced model is denoted as the autonomous model. We define the threshold quantity

to be the production rate of mosquitoes offsprings. It is a product of the egg deposition rate $\phi_v$, probability that an egg becomes an adult $\frac{\gamma_a}{g_4}$ and the duration spent in the adult stage $\frac{\mu_v(1+b)+(1-\epsilon)(\alpha+\rho)}{\mu_v(\mu_v(1+b)+(1-\epsilon)(\alpha+\rho))}.$

The autonomous model has two disease-free equilibria. We shall call them the trivial disease free equilibrium (TDFE) and the realistic disease free equilibrium (RDFE), explained thus:

(ⅰ) If $\mathcal{R}_v\leq1$, the autonomous model has a TDFE (where there are no mosquitoes). This is given as

(ⅱ) If $\mathcal{R}_v > 1$, the autonomous model has a RDFE (where we have mosquitoes present) given as

where

2.2.1.   Asymptotic stability of disease-free equilibria

Global asymptotic stability of the trivial disease free equilibrium (TDFE)

Theorem 2.1. The TDFE of the autonomous version of the model (2.1), denoted by $\mathcal{T}_o$, is globally asymptotically stable (GAS) in $C([0], \mathbb{R}^{11}_+)$ whenever $\mathcal{R}_v\leq1$.

Proof. Following the approach in ^[10,23], let $\mathcal{R}_v\leq1$, so that only the TDFE $(\mathcal{T}_o)$ exist. Also, let $Y = X-TDFE$. So that, $\frac{\mathrm{d}Y}{\mathrm{d}t} = \mathcal{B}(Y)Y$, where $S_h = Y_1, \quad E_h = Y_2, \quad I_h = Y_3, \quad R_h = Y_4, \quad A_m = Y_5, \quad S_{vo} = Y_6, \quad S_{vi} = Y_7, \quad E_{vo} = Y_{8}, \quad E_{vi} = Y_{8}, \quad I_{vo} = Y_{10}, \quad I_{vi} = Y_{11} \quad \text{and}\quad \mathcal{B}(Y)\quad \text{is given as}$

with

Consider the Lyapunov function

It then follows that

It is easy to see that for $0\leq b\leq 1$, $\frac{\mu_v(1+b)+\rho(1-\epsilon)+\alpha(1-\epsilon)}{\mu_v(1+b)+\rho(1-\epsilon)+\alpha(1-\epsilon)(1+b)}\leq1$.

Hence, $\mathcal{\dot{V}}\leq0$. Furthermore, it follow from LaSalle's Invariance Principle (Theorem 6.4 of ^[15]) that the maximal invariant set contained in $\{\mathcal{V}|\dot{\mathcal{V}}(Y)\}$ is the $TDFE_Y$. Thus, the transformed equilibrium $TDFE_Y$ is GAS in $C([0], \mathbb{R}^{11}_+)$ if $\mathcal{R}_v\leq1$. Hence, $\mathcal{T}_o$ is also GAS in $C([0], \mathbb{R}^{11}_+)$ whenever $\mathcal{R}_v\leq1$.

Local asymptotic stability of the realistic disease free equilibrium (RDFE)

Let $\mathcal{R}_v > 1$ so that the RDFE $(\mathcal{E}_o)$ exist. The local stability of $\mathcal{E}_o$ in $C([0], \mathbb{R}^{11}_+)\setminus{\mathcal{T}_o}$ can be established using the next generation operator method on the autonomous version of the model (2.1) ^[9,36]. Using closely related notations in ^[36], the matrices $F$ and $V$, for the new infection terms and the remaining transfer terms are, respectively, given by

Hence it follows from ^[36] that the reproduction number of the autonomous version of the model (2.1) is given by

and $\mathcal{R}_v$ is defined as

It should be noted from (2.12) that $\mathcal{R}_T$ is positive if and only if $\mathcal{R}_v > 1$ (so that $\mathcal{E}_o$ exist). The result below follows from Theorem 2 of ^[36].

Theorem 2.2. The RDFE, $\mathcal{E}_o$, of the autonomous version of the model (2.1) is locally asymptotically stable (LAS) in $C([0], \mathbb{R}^{11}_+)\setminus{\mathcal{T}_o}$ if $\mathcal{R}_T < 1$, and unstable if $\mathcal{R}_T > 1$.

The threshold quantity $\mathcal{R}_{T}$ is the effective or control reproduction number for the autonomous version of the model (2.1). It represents the average number of secondary malaria infections generated by a typical infected individual in a completely susceptible population where there are control measures are present ^[36]. By Theorem 2.2, biologically speaking, malaria can be eliminated from the population when $\mathcal{R}_{T} < 1$ if the initial sizes of the population of the model are in the region of attraction $\mathcal{E}_o$.

2.2.2.   Global Asymptotic Stability of the RDFE: special case

We now prove the global asymptotic stability of the RDFE of the autonomous version of the model (2.1) for the special case when $\delta_h = 0$, since it has been repeatedly shown in literature that the presence of disease-induced mortality in humans can cause a backward bifurcation in vector-borne diseases ^[12,13,22]. We claim the following result.

Theorem 2.3. The RDFE of the special case of the autonomous version of the model (2.1) with $\delta_h = 0$ is globally asymptotically stable in $C([0], \mathbb{R}^{11}_+)\setminus{\mathcal{T}_o}$ if $\mathcal{R}_T^m\leq1$ (with $\mathcal{R}_T^m$ given as)

Proof. Consider the following Lyapunov function:

with a Lyapunov derivative given by,

Substituting the expressions of the derivatives of $\dot{E}_h \quad \dot{I}_h \quad \dot{E}_{vo}\quad \dot{E}_{vi}\quad \dot{I}_{vo}\quad \text{and} \quad \dot{I}_{vi}$, from the autonomous version of the model (2.1) with $\delta_h = 0$, into (2.14) (and after some algebraic calculations) leads to

Since all the parameters and variables of the mass action model of the autonomous version of the model (2.1) are non-negative, it follows that $\mathcal{\dot{L}}\leq 0$ for $\mathcal{R}_T^m\leq1$. Furthermore, $\mathcal{\dot{L}} = 0$ if and only if $E_h = I_h = E_{vo} = E_{vi} = I_{vo} = I_{vi} = 0$. Hence, $\mathcal{L}$ is a Lyapunov function. Thus, it follows, by LaSalle's Invariance Principle ^[15], that every solution to the equations in the autonomous version of the model (2.1) with initial conditions in $C([0], \mathbb{R}^{11}_+)\setminus{\mathcal{T}_o}$ converges to the RDFE $\mathcal{E}_{o}$ as $t\rightarrow\infty$. That is,

$(E_h (t), I_h (t), E_{vo} (t), E_{vi} (t), I_{vo} (t), I_{vi} (t))\rightarrow(0, 0, 0, 0, 0, 0)$ as $t\rightarrow\infty$. Substituting $E_h = I_h = E_{vo} = E_{vi} = I_{vo} = I_{vi} = 0$ into the first, fifth, sixth, seventh eighth and ninth equations of the autonomous version of the model (2.1) gives the following as $t\rightarrow\infty$

Thus the RDFE of the special case of the autonomous version of the model (2.1) with $\delta_h = 0$ is globally asymptotically stable in $C([0], \mathbb{R}^{11}_+)\setminus{\mathcal{T}_o}$ if $\mathcal{R}_T^m\leq1$.

2.3.   Analysis of the non-autonomous model

Just like the autonomous version, the non-autonomous version has two disease free equilibria, namely, the trivial disease free equilibrium and the realistic disease free equilibrium. We will however analyze only the realistic disease free equilibrium as the former is ecologically unrealistic. We define the threshold quantity $\mathcal{R}_v(t)$ (the production rate of mosquitoes offsprings), given as

The realistic disease free equilibrium (RDFE) is obtained by setting $E_h = I_h = R_h = E_{vo} = E_{vi} = I_{vo} = I_{vi} = 0$ in the model (2.1),

with ($A_m^a, S_{vo}^a, S_{vi}^a$) being the unique periodic solution (for $\mathcal{R}_v(t) > 1 \quad for\quad all\quad t\geq0$), satisfying:

2.3.1.   Local asymptotic stability of RDFE ($\mathcal{E}_{0N}$)

The basic reproduction ratio associated with the non-autonomous model (2.1) will now be computed using the the approach in ^[37]. The next generation matrix $F_N(t)$ (of the new infection terms) and the M-Matrix $V_N(t)$ (of the remaining transfer terms), associated with non-autonomous model (2.1), are given respectively by

Following ^[23,37], let $\Phi_M$ be the monodromy matrix of the linear $\tau$-periodic system

Also, let $\rho(\Phi_M(\tau))$ be the spectral radius of $\Phi_M(\tau)$ and $Y(s, t), \quad t = s$, be the evolution operator of the linear $\tau$-periodic system $\frac{dy}{dt} = -V_N(t)y$. So that for each $s\in\mathbb{R}$, the associated $6\times6$ matrix $Y(t, s)$ satisfies ^[37]

Furthermore, let $\phi(s)\quad (\tau-periodic\quad in \quad s)$ be the initial distribution of infectious individuals. Thus, $F_N(s)\phi(s)$ is the rate at which new infections are produced by infected individuals who were introduced into the population at time $s$ ^[37]. Since $t = s$, it follows that $Y(t, s)F_N(s)\phi(s)$ represents the distribution of those infected individuals who were newly infected at time $s$, and remain infected at time $t$. Hence, the cumulative distribution of new infections at time $t$, produced by all infected individuals $(\phi(s))$ introduced at a prior time $s = t$, is given by

Let $\mathbb{C}_\tau$ be the ordered Banach space of all $\tau-periodic$ functions from $\mathbb{R}$ to $\mathbb{R}^6$, equipped with a maximum norm $\parallel.\parallel$ and positive cone

Define a linear-operator$L:\mathbb{C}_\tau\rightarrow\mathbb{C}_\tau$ ^[37]

The basic reproduction number $\mathcal{R}_T(t)$ is then given as the spectral radius of $L$, denoted by $\rho(L)$. The proof that the model (2.1) satisfies the conditions A1-A7 in ^[37,4] is given in Appendix A. The result below follows from Theorem 2.2 in ^[37].

Theorem 2.4. The RDFE of the non-autonomous model (2.1) is locally asymptotically stable if $\mathcal{R}_T(t) < 1$ (given that $\mathcal{R}_v(t) > 1$) and unstable if $\mathcal{R}_T(t) > 1$.

2.3.2.   Global asymptotic stability of RDFE ($\mathcal{E}_{0N}$)

The global stability of the realistic disease free equilibrium of the non-autonomous model (2.1) will now be explored for the special case where $\delta_h = 0$. We claim the following result, with the proof in Appendix B.

Theorem 2.5. Consider the special case of the non-autonomous model (2.1) with $\delta_h = 0$ so that $N_h^*(t)\rightarrow\frac{\Lambda_h}{\mu_h}$ as $t\rightarrow\infty$. The RDFE of the resulting model is GAS in $C([0], \mathbb{R}^{11}_+)\setminus{\mathcal{T}_o}$ if $\mathcal{R}_T^m(t) = \mathcal{R}_T(t)|_{\delta_h = 0} < 1$

The proof of Theorem 2.5, based on using comparison theorem ^[34], is given in Appendix B. The epidemiological implication of Theorem 2.5 is that malaria can be effectively controlled(if not eliminated) if the reproduction threshold $\mathcal{R}_T^m(t)$ can be brought to as well as maintained at a value less than unity.

2.3.3.   Uniform persistence of the disease

We now explore the possibility of the existence of a positive periodic equilibrium for the model (2.1) using the uniform persistence theory. Let $\mathcal{E}_N(t)$ be any arbitrary positive periodic equilibrium of the model (2.1). Following ^[16,17,23], it is convenient to define the following sets:

We claim the following result, with the proof in Appendix C.

Theorem 2.6. Consider the non-autonomous model (2.1). Suppose that $\mathcal{R}_T(t) > 1$ and $\mathcal{R}_v(t) > 1$ for all $t\geq0$. Then the model has at least one positive periodic equilibrium, and there exists a $q > 0$ such that any equilibrium $\Phi_t(\phi)$ of the model with initial value $\phi\in X_0$ satisfies

The proof of Theorem 2.6, based on using the approach in ^[16,23], is given in Appendix C. The epidemiological implication of Theorem 2.6 is that malaria will persist in the population whenever $\mathcal{R}_T(t) > 1$ and $\mathcal{R}_v(t) > 1$, for all $t\geq0$.

3.   Results: Numerical simulations of the model (2.1)

The model (2.1) is simulated numerically to investigate the impact of the variation in indoor and outdoor conditions on the transmission of malaria using parameter values given in Table 2.

3.1.   Numerical simulation of the reproduction number

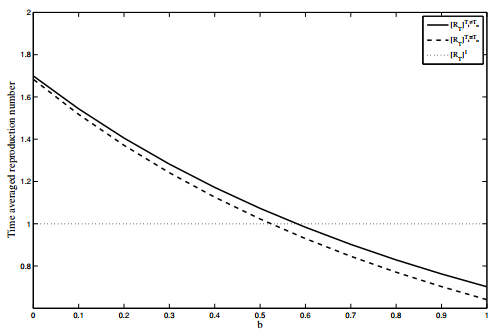
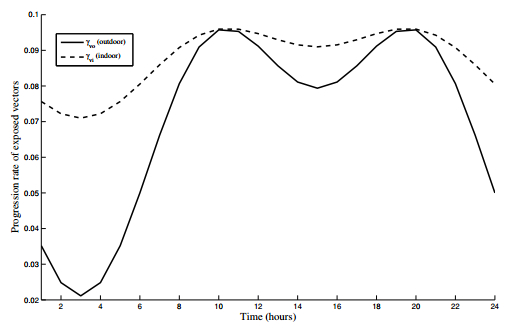
The time-averaged basic reproduction number ($[\mathcal{R}_T(t)]$) of the model (2.1) is simulated for two different scenarios namely $T_i\neq T_o$ and $T_i = T_o$. In Figure 3, it is seen that the reproduction threshold is under-estimated when $T_i = T_o$ (i.e when the variation between indoor and outdoor conditions are not incorporated). This is may be due to the higher progression rate experienced by indoor vectors (see Figure 4) as studies have shown that the extrinsic incubation period (EIP) is highly temperature dependent and affects the basic reproduction number in an exponential manner (as it influences the number of infected mosquitoes that become infections) ^[6,24] (and other references therein).

3.2.   Numerical Investigation of the impact of indoor and outdoor temperature variation

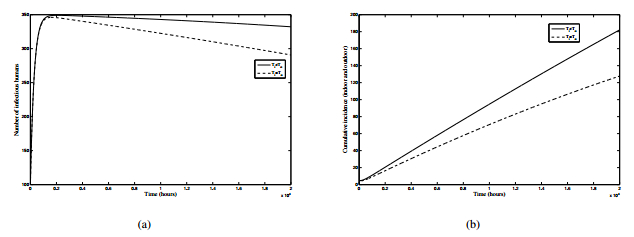
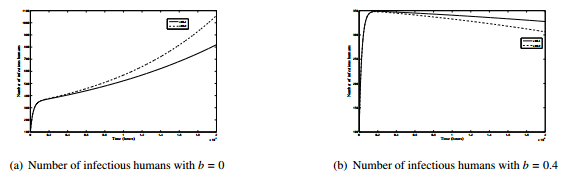
We now investigate the effect of variability in outdoor and indoor microclimates on the transmission dynamics of malaria. Figure 5 shows the impact of the difference between indoor and outdoor temperature on the number of infectious humans as well as the cumulative incidence. Results from Figure 5(a) show that the model under-estimates the number of infectious humans when indoor temperature is assumed to be equal to outdoor temperature. In the same vein, this finding is supported by results from Figure 5(b) when the cumulative incidence (outdoor and indoor) is used instead of the number of infectious humans.

3.3.   Numerical Investigation of the impact of indoor and outdoor temperature variation on efficacy of controls

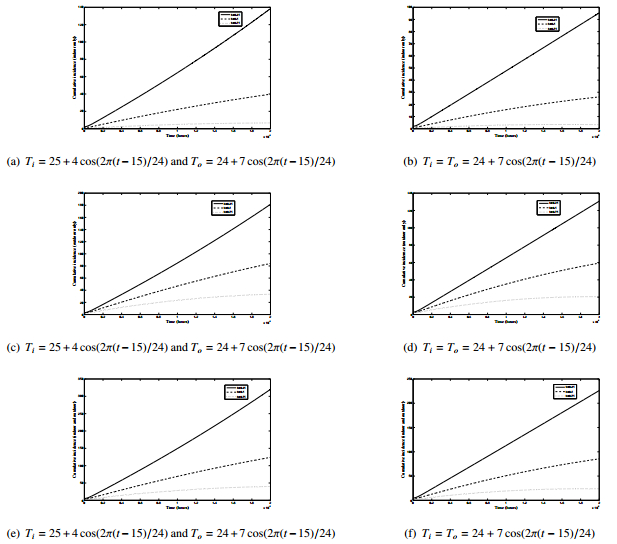
Investigating the effect of the differences in indoor and outdoor temperature on the efficacy $(b)$ of bed-net, it is seen from Figure 8 that the cumulative incidence are higher when $T_i\neq T_o$ (Figures 6(a), 6(c) and 6(e)) for the different values of $b$ than when indoor temperature is assumed to be equal to outdoor temperature i.e $T_i = T_o$ (Figures 6(b), 6(d) and 6(f)). These results therefore indicate that differences in the micro habitats where mosquitoes rest can impact on the transmission dynamics of malaria as well as efficacy of control measures.

Again, Figure 7 clearly shows that the differences in indoor and outdoor environment impacts on the efficacy $(\epsilon)$ of the door and window nets. It is seen that the cumulative incidences that occur both outside and inside a human dwelling for various values of $\epsilon$ when $T_i = 25+4\cos(2\pi(t-15)/24)$ and $T_o = 24+7\cos(2\pi(t-15)/24)$ (Figures 7(a), 7(c) and 7(e)) are higher than in the case when $T_i = T_o = 24+7\cos(2\pi(t-15)/24)$ (Figures 7(b), 7(d) and 7(f)).

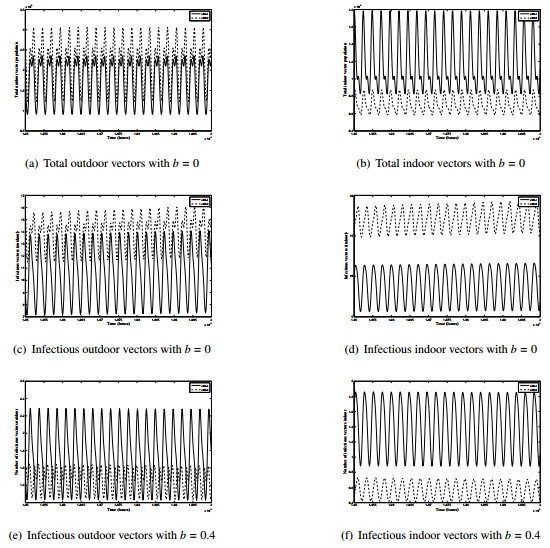
Additionally, we can see from Figures 6(c) and 6(d) that the use of indoor bed-nets significantly affects the outdoor dynamics. This is a pointer to how much malaria transmission intensity can be affected by indoor conditions.

Furthermore, we can observe from Figures 7(a) and 7(e) that increasing $\epsilon$ leads to a decrease in the indoor cumulative incidence as well as the cumulative incidence comprising both outdoor and indoor incidences. However, there is an increase in the outdoor cumulative incidence when $\epsilon$ is increased (Figure 7(c)). This leaves us with a very interesting finding of how much the indoor environment affects the transmission intensity. So, although an increase in $\epsilon$ (a situation that does not just prevent indoor entry of mosquitoes and allow for increase in outdoor transmission intensity but also prevents the exit of indoor mosquitoes) led to an increase in the outdoor cumulative incidence, there is however a far more significant reduction in the indoor incidence that results in a decrease in total cumulative incidence (indoor and outdoor). This reduction in the total cumulative incidence may be due to the efficacy of the indoor bed nets which repel or kill indoor mosquitoes and so reduces the population of infectious vectors. It might also be as a result of the outdoor conditions which makes for a longer extrinsic incubation period (see Figure 4) and further reduces the number of infectious vectors.

Considering the cases above, we set $b = 0$ and investigate how $\epsilon$ effects the dynamics of the vector population. From Figures 8(a) and 8(b) we observe that when $\epsilon = 0.9$ results in a larger vector population oudoor. However, we observe that though we have more vectors outdoor, the number of infectious vectors indoor is grater than the number of infectious vectors outdoor (Figures 8(c) and 8(d)). The faster progression rate experienced by vectors indoor (due to the different indoor microclimate) may account for this rise in the number of infectious vectors in the absence of an indoor control while the slower progression rate of the outdoor vectors account for the lower number of infectious vectors outdoor though we had more mosquitoes outdoor. Both cases are shown to be true as seen from Figures 8(e) and 8(f). Therefore, the use of the bed-net reduces though more significantly the number of infectious vectors indoors, it also reduces the number of infectious mosquitoes outdoor (Figures 8(e) and 8(f)) and thereby decreases the total population of infectious vectors. Generally, we see that if there is no indoor control, the transmission intensity would significantly increase.

3.4.   Numerical Investigation of the interaction between the controls

Numerical results from Figure 9 show the interaction between the controls. If there is an indoor control, putting more mosquitoes outdoor will result in a decrease in the number of infectious humans this is so because the a higher percentage of infectious vectors which are indoor will have contact with the bed-nets as seen in Figure 9(b). On the other hand, if there is no indoor control, having $\epsilon = 0.1$ will result in less disease prevalence. In summary, we can say that the impact of the indoor environment on the transmission intensity is felt most in the absence of any form of indoor control.

4.   Discussion

A new mathematical model for the transmission dynamics of malaria in a community is designed (and rigorously analyzed) and used to assess the impact of indoor and outdoor temperature variations in a population where control measures are in place (like indoor bed-nets and door and window nets). Some of the theoretical findings are given below.

$(1)$ The autonomous version of the model (2.1) has a trivial disease free equilibrium (TDFE)(when there are no mosquitoes in the population) as well as a realistic disease free equilibrium (RDFE)(when mosquitoes are present). The trivial disease free equilibrium is globally asymptotically stable whenever the threshold $\mathcal{R}_v$ is less than unity while the realistic disease free equilibrium is locally asymptotically stable whenever the associated reproduction number is less than unity. Also, the RDFE is globally asymptotically stable in the absence of disease induced mortality for humans whenever the associated reproduction number is less than unity.

$(2)$ The model (2.1) has a globally asymptotically stable realistic disease free equilibrium in the absence of disease induced mortality for humans whenever the associated reproduction number is less than unity ($\mathcal{R}_T(t) < 1$). The model (2.1) has at least a periodic solution whenever the associated reproduction number is greater than unity ($\mathcal{R}_T(t) > 1$). In this case, the disease persist.

Results from the numerical simulations of the model (2.1) are given below.

$(1)$ When the variation of the indoor and outdoor temperatures are taken into consideration, i.e. $T_o = 24+6\cos(2\pi(t-15)/24)$ and $T_i = 23+3\cos(2\pi(t-15)/24)$, the bed-net efficacy needed to bring the time averaged basic reproduction number $[\mathcal{R}_T(t)]$ below unity is greater than when $T_i = T_o = 24+6\cos(2\pi(t-15)/24)$. Also, having a 100% bed-net efficacy $(b)$ results in 58.69% reduction in the time averaged basic reproduction number $[\mathcal{R}_T(t)]$ when the variation of the indoor and outdoor temperatures are taken into consideration. However, if indoor and outdoor temperatures are assumed to be the same, having a 100% bed-net efficacy results in 61.93% reduction. This shows that the differences in indoor and outdoor conditions impacts on the efficacy of the bed-nets and hence on malaria transmission.

It is interesting to state that Paaijmans and Thomas ^[27], reported that small differences in indoor and outdoor temperatures can have significant impact on the length of the (EIP) and consequently on the basic reproduction number as the EIP is one of the most influential parameters that determines disease reproduction threshold. Clearly our results support this finding reported in ^[27] as seen from Figures 3 and 4. Therefore, Thomas et al. ^[35] concluded that since the actual microclimates experienced by mosquitoes in different microhabitants play a significant role in most mosquito and parasite life history traits, appropriate characterization of the local microclimate conditions is important in understanding transmission intensity.

$(2)$ When indoor temperature is assumed to be the same as outdoor temperature, the model underestimates the number of infectious humans as well the cumulative incidence of the disease. This again strongly agrees with the results in ^[27] which reported that better knowledge of endophilic and exophilic behaviours of mosquitoes (resting behaviour) and the associated microclimate is needed to fully understand malaria transmission intensity. This study (^[27]) stated that differences in microclimate of places where mosquitoes rest translate to increases in transmission risk. Furthermore, it was reported in ^[28] that models that use outdoor air temperatures only will underestimate the speed of processes such as parasite development, blood meal digestion and egg-production of endophilic mosquitoes.

$(3)$ In the absence of an indoor control measure having $\epsilon = 0.1$ (a conditions that allows for higher movement rate of mosquitoes in and out of a human dwelling) may be more helpful. However, when we an indoor control measure restricting vector movement (i.e. having $\epsilon = 0.9$) may be of a better advantage. This may be as a result of the different temperature conditions experienced by the vectors in the different micro niches as they move in and out of a human dwelling since temperature has been shown to altar the length of the extrinsic incubation period (EIP). This study may be pointing to the fact that both the mosquito resting behaviour and how long it rest there may determine the transmission intensity. This may be due to the fact that having $\epsilon = 0.9$ does not just prevent indoor entry but also prevents exit of indoor vectors so vectors are confined to a particular microclimate for a longer period. When $\epsilon = 0.1$ the movement rate ($\alpha$ and $\rho$) are higher and so vectors are exposed to variable microclimate from time to time as they move in and out of a human dwelling. Therefore, if mosquitoes spend a greater parts of their adult life resting indoors (in a population without any form of indoor control measures), this may lead to a considerable increase in transmission risk as ^[27] reported that that mosquitoes that rest indoor could transmit malaria between 0.3 and 22.5 days earlier than outdoor-resting counterparts.

5.   Conclusion

This study has shown the significance of including the variation between outdoor and indoor temperatures on the dynamics of malaria in a given population as the difference between indoor and outdoor temperatures is expected to alter temperature-related estimates of transmission intensity. This agrees with the findings in ^[28] where indoor and outdoor temperature data from a study carried out in Tanzania were used to assess the effects of these different microclimate on the extrinsic incubation period of the parasite as well as the gonotrophic cycle length of mosquitoes. This study has confirmed that warmer indoor temperatures result in faster parasite development as well as leads to an increase in the transmission intensity. Also, both where the mosquitoes rest and how long they rest there may determine the the population of the infectious vectors and thus the transmission intensity.

In this work, the variations in indoor temperature due to house design and construction materials and relative humidity were not considered. However, since indoor temperature has been shown to vary considerably depending on house design, construction materials, housing density, adjacent vegetation cover and altitude as noted in ^[27,35], it would be interesting to study the impact of this on malaria dynamics. Moreover, it would be interesting to study the combined impact of microclimate variables like temperature and relative humidity on the transmission dynamics of malaria.

Acknowledgments

We would like to thank the anonymous reviewers for their constructive comments.

Conflict of interest

There are no conflict of interests.

Appendix A:.   Verification of assumptions $A1-A7$ in ^[37]

Verification of the Assumptions A1-A7 in ^[37,4]. Following ^[31] and using the notation in ^[37], the model (2.1) can be written as:

where,

and

The functions $\mathcal{F}$, $\mathcal{V}^-$ and $\mathcal{V}^+$ satisfy the following conditions in ^[37].

(A1) For each $1\leq i\leq11$, $\mathcal{F}_i(t, x)$, $\mathcal{V}_i^+(t, x)$ and $\mathcal{V}_i^-(t, x)$ are non-negative, continuous on $\mathbb{R}\times\mathbb{R}^{11}_+$ and continuously differentiable with respect to $x$.

(A2) There is a real number $\omega > 0$ such that for each $1\leq i\leq = 11$, the functions $\mathcal{F}_i(t, x)$, $\mathcal{V}^+_i(t, x)$ and $\mathcal{V}_i^-(t, x)$ are $\tau$-periodic in $t$.

(A3) If $x_i = 0$, then $\mathcal{V}_i^- = 0$ for $i = 2, 3, 4, 8, 9, 10, 11$

(A4) $\mathcal{F}_i = 0$ for $i = 1, 5, 6, 7.$

(A5) Define $X_s = {x\geq0:x_i = 0\quad for\quad i = 2, 3, 4, 8, 9, 10, 11}$. It is clear that if $x\in X_s$, then $\mathcal{F}_i = \mathcal{V}_i^+ = 0$ for $i = 2, 3, 4, 8, 9, 10, 11$. The model (2.1) has RDFE given by $\mathcal{E}_{0N} = (S_h^*, 0, 0, 0, A_m^*, S_{vo}^*, S_{vi}^*, 0, 0, 0, 0)$. Define a $5\times5$ matrix

It follows from ^[31], and the definitions of the matrices $\mathcal{F}$ and $\mathcal{V}$, that

(A6) Since $M(t)$ is a diagonalize matrix with negative eigenvalues, then $\rho(\Phi_M(\tau)) < 1$.

(A7) Similarly, $-\mathcal{V}(t)$ is a diagonalize matrix with negative eigenvalues. Hence, $\rho(\Phi_{-v}(\tau)) < 1$.

Therefore, the model (2.1) satisfies the conditions $A1-A7$ in ^[37].

Appendix B:.   Proof of Theorem 2.5

Consider the model (2.1) where $\delta_h = 0$ with $\mathcal{R}_v(t) > 1$ for all $t\geq0$. Let $\mathcal{R}_T^m(t) < 1$. The proof is based on the comparison theorem ^[34]. Using the fact that $S_h(t)\leq\frac{\Lambda_h}{\mu_h}$, $A_m(t)\leq k_v(t)(1-\frac{1}{\mathcal{R}_v(t)})$, $S_{vo}(t)\leq \frac{k_v(t)\gamma_a(t)k_6}{k_5 k_6-\alpha\rho(1-\epsilon)^2)}(1-\frac{1}{\mathcal{R}_v(t)})$ and $S_{vi}(t)\leq \frac{k_v(t)\gamma_a(t)\alpha(t)(1-\epsilon)}{k_5 k_6-\alpha\rho(1-\epsilon)^2)}(1-\frac{1}{\mathcal{R}_v(t)})$, for all $t\geq0$ in $C([0], \mathbb{R}^{11}_+)\setminus{\mathcal{T}_o}$. We can then re-write the non-autonomous model (2.1) as

The equations with equalities used in place of inequalities can be written in terms of the next generation matrices $\mathcal{F}(t)$ and $\mathcal{V}(t)$ following ^[37]

There exist a positive $\tau$-periodic function $w(t) = (E_h(t), I_h(t), E_{vo}(t), E_{vi}(t), I_{vo}(t), I_{vi}(t))$, (following lemma 2.1 in ^[41]) such that $W(t) = \exp^{\theta t}w(t)$ with $\theta = \frac{1}{\tau}\ln\rho[\phi_{\mathcal{F}-\mathcal{V}}(\tau)]$ is a solution of the linearized system (5.1). Furthermore, the assumption that $\mathcal{R}_T^m(t) < 1$ implies that $\rho[\phi_{\mathcal{F}-\mathcal{V}}(\tau)] < 1$. Hence, $\theta$ is a negative constant. Thus, $W(t)\rightarrow0$ as $t\rightarrow\infty$.

The unique realistic disease free solution of the linear system (9.1) given by $W(t) = 0$, is GAS. For any non-negative initial condition $(E_h(0), I_h(0), E_{vo}(0), E_{vi}(0), I_{vo}(0), I_{vi}(0))$ of the system (9.1) there exists a sufficiently large $M^* > 0$ such that

$((E_h, I_h, E_{vo}, E_{vi}, I_{vo}, I_{vi})(0))^T\leq M^*((E_h, I_h, E_{vo}, E_{vi}, I_{vo}, I_{vi})(0))$

Thus, it follows by comparison theorem that $(E_h(t), I_h(t), E_{vo}(t), E_{vi}(t), I_{vo}(t), I_{vi}(t))\leq M^*W(t)$ for all $t > 0$ where $M^*W(t)$ is also a solution of the model (5.1). Hence,

$((E_h(t), I_h(t), E_{vo}(t), E_{vi}(t), I_{vo}(t), I_{vi}(t)))\rightarrow(0, 0, 0, 0, 0, 0)$ as $t\rightarrow\infty$.

It also follows that $S_h(t)\rightarrow\frac{\Lambda_h}{\mu_h}$ as $t\rightarrow\infty$ and $(A_m(t), S_{vo}(t), S_{vi}(t))$ satisfy for ($\mathcal{R}_v(t) > 1$ for all $t$)

Thus for $\mathcal{R}_T^m(t) < 1$, $(S_h, E_h, I_h, R_h, A_m, S_{vo}, S_{vi}, E_{vo}, E_{vi}, I_{vo}, I_{vi})\rightarrow \mathcal{E}_{0N}$ as $t\rightarrow\infty$

Appendix C:.   Proof of Theorem 2.6

Consider the non-autonomous model (2.1) with $\mathcal{R}_v(t) > 1$ and $\mathcal{R}_T(t) > 1$ for all $t\geq0$. Both conditions are needed to ensure that mosquitoes are present in the population and that the realistic disease free solution is unstable. The proof of Theorem 2.6 is based on using the technique of in ^[16]. Define the sets

Let $u(t, \phi)$ be the unique solution of the model (2.1) (through the initial condition $u(0, \phi) = \phi$). Define $\Phi(t)\varphi = u(t, \varphi)$, the flow generated by the model (2.1) with respect to $\varphi$.

Let $P:X\rightarrow X$ be the poincar$\acute{e}$ map associated with the model (2.1). That is $P(\phi) = u(\tau, \phi)$ for all $\phi\in X$. Then using the approach in the proof of lemma 2.1 in ^[16], it can be shown that $X_0$ is a positively invariant and compact set with respect to the model (2.1). Since the model's solutions are uniformly bounded, it follows that $P$ is point-dissipative. ^[16,23]. Furthermore, it follows from theorem 1.1.2 in ^[42] that in $X$, $P$ admits a global attractor.

Next, we show that $P$ is uniformly persistent with respect to ($X_0$, $\partial X_0$). It is convenient to define where $P^n(\phi), n\geq0$, are the periodic points of the poincar$\acute{e}$ map ^[16]:

It follows from (5.2) that

In the case where $0$ is a solution, of the equation (2.10) for the total mosquito population $N_v^*(t)$. We claim the following

Lemma 5.1. $K_\partial = D_1\cup D_2$.

Proof. We can define the set $K_\partial$ and $D_1\cup D_2$ as given below

By the definition of $\partial X_0$, $\{(\frac{\Lambda_h}{\mu_h}, 0, 0, 0, A_m^*, S_{vo}^*, S_{vi}^*, 0, 0, 0, 0):\frac{\Lambda_h}{\mu_h} > 0, S_{vs} > 0, S_{vr} > 0\}\subset K_\partial$. Therefore, $D_1\cup D_2\subset K_\partial$.

Let $(S_h(0), E_h(0), I_h(0), R_h(0), A_m(0), S_{vo}(0), S_{vi}(0), E_{vo}(0), E_{vi}(0), I_{vo}(0), I_{vi}(0))\in \partial X_0\backslash D_1\cup D_2$.

If $E_h(0) = 0$, $I_h(0) = 0$, $R_h(0) = 0$, $E_{vo}(0) = 0$, $E_{vi}(0) = 0$, $I_{vo}(0) > 0$ and $I_{vi}(0) > 0$, then $S_h(0) > 0$, $S_{vo}(0) > 0$, $S_{vi}(0) > 0$, $I_{vo}(0) > 0$ and $I_{vi}(0) > 0$.

It follows from the second equation in (2.1) that

Similarly, the above result holds for other cases such as $E_h(0) > 0$, $I_h(0) = 0$, $R_h(0) = 0$, $E_{vo}(0) > 0$, $E_{vi}(0) > 0$, $I_{vo}(0) = 0$ and $I_{vi}(0) = 0$, then $S_h(0) > 0$, $A_m(0)$, $S_{vo}(0) > 0$, $S_{vi}(0) > 0$, $E_h(0) > 0$, $E_{vo}(0) > 0$ and $E_{vi}(0) > 0$.

Therefore, $(S_h(0), E_h(0), I_h(0), R_h(0), A_m(0), S_{vo}(0), S_{vi}(0), E_{vo}(0), E_{vi}(0), I_{vo}(0), I_{vi}(0))\not \in \partial X_0$ for all $0 < t\ll1$.

Hence, $K_\partial\subset D_1\cup D_2$. Thus, it then follows that $K_\partial = D_1\cup D_2$.

From 5.3, it can be verified that $P^n(\phi)$, $n\geq0$ contains two disease free states namely $\mathcal{T}_{0}$ and $\mathcal{E}_{0N}$. The sets $\mathcal{T}_{0}$ and $\mathcal{E}_{0N}$ disjoint, compact, and isolated invariant sets for the poincar$\acute{e}$ map $P$ in $K_\partial$ and $\bigcup_{\phi\in K_\partial}\omega(\phi) = \{\mathcal{T}_{0}, \mathcal{E}_{0N}\}$ ^[16]. No subset of {$\mathcal{T}_{0}$, $\mathcal{E}_{0N}$} forms a cycle of in $K_\partial$ and hence in $\partial X_0$ ^[16]. In addition, it follows from the proof of Theorem 3.2 in ^[16] that since $N_v^*(t)$ is a positive periodic solution with respect to $X_0$ then, there exist a $\delta > 0$ and an $\epsilon > 0$ such that $\lim_{t\rightarrow\infty}\sup|\Phi(n\tau)\phi-\mathcal{T}_{0}|\geq\delta$ and $\lim_{t\rightarrow\infty}\sup|\Phi(n\tau)\phi-\mathcal{E}_{0N}|\geq\epsilon$ for all $\phi\in X_0$.

Define the sets $A_1: = \mathcal{T}_{0}$ and $A_2: = \mathcal{E}_{0N}$. In view of the claims above, it follows that $A_1$ and $A_2$ are isolated invariant sets for $P$ in $X$, and $W^s(A_i)\cap X_0 = \varnothing$, for all $i = 1, 2$ where $W^s(A_i)$ is the stable set of $A_i$ for $P$ ^[16]. In the case where $0$ is not a solution of the equation (2.10), we can show that $K_\partial = D_2$ in a similar manner. It then follows that ${A_2}$ is the only compact invariant set for $P$ in $K_\partial$ ^[16].

Hence, every solution in $K_\partial$ converges to either $A_1$ or $A_2$ and ${A_1}$ or ${A_2}$ are acyclic in $K_\partial$ ^[42]. It then follows from Theorem 1.3.1 in ^[42] that $P$ is uniformly persistent with respect to $X_0$. Thus, from Theorem 3.1.1 in ^[42] the periodic semiflow $\Phi(t):X\rightarrow X$ is also uniformly-persistent to $X$ ^[16] where $\Phi(t)\varphi = u(t, \varphi)$. It then follows from Theorem 4.5 in ^[17] that the non-autonomous model (2.1) has a positive periodic solution denoted by $\mathcal{E}^*_N(t) = \Phi(t)\phi$ with $\phi\in X_0$.

It again follows from Theorem 4.5 in ^[17] that $P:X_0\rightarrow X_0$ has a compact global attractor, denoted by $\mathcal{A}_0$. Hence, $\mathcal{A}_0$ is invariant for $P$ (that is $\mathcal{A}_0 = P(\mathcal{A}_0) = \Phi(\tau)\mathcal{A}_0$). Also, using the notation in ^[43], let $\mathcal{A}^*_0: = \bigcup_{t\in [0, \tau]}\Phi(t)\mathcal{A}_0$. Then, $\psi_i(0) > 0$ for all $\psi\in \mathcal{A}^*_0, \quad i\in[1, 11]$ ^[16]. Since $\Phi(t)\phi\in X_0$, for all $t\geq0$ and $\phi\in X_0$ (as $X_0$ is invariant), it follows that $\Phi(t)X_0\subset X_0$. Thus, $\mathcal{A}^*_0\subset X_0$ and $\limsup_{t\rightarrow\infty}d(\Phi(t)\phi, \mathcal{A}^*_0) = 0$ for all $\phi\in X_0$ ^[16,43]. Also, it follows from the continuity of $\Phi(t)\phi$ for all $(t, \phi)\in [0, \infty)\times X_0$ and the compactness of $[0, \tau]\times\mathcal{A}_0$ ^[43], that $\mathcal{A}^*_0$ is compact in $X_0$ ^[16,43]. Thus, $\inf_{\phi\in\mathcal{A}^*_0}d(\phi, \partial X_0) > 0$ ^[16,43]. Consequently, there exist $q > 0$ such that

In particular, $\liminf_{t\rightarrow\infty}\min(\Phi(t)\phi^*)\geq q$, and hence, $u_i(t, \phi) > 0$, $1\leq i\leq11$ for all $t\geq0$.