A delayed vector-bias model for malaria transmission with
incubation period in mosquitoes is studied. The delay $\tau$
corresponds to the time necessary for a latently infected vector
to become an infectious vector. We prove that the global stability
is completely determined by the threshold parameter, $R_0(\tau)$.
If $R_0(\tau)\leq1$, the disease-free equilibrium is globally
asymptotically stable. If $R_0(\tau)>1$ a unique
endemic equilibrium exists and is globally asymptotically stable.
We apply our results to Ross-MacDonald malaria models with an
incubation period (extrinsic or intrinsic).
1.
Introduction
Business Process Management (BPM) is the discipline to design, analyse, execute and monitor business processes, with the aim of improving their performance in three dimensions: time, cost, and quality [1]. Process mining is a set of techniques primarily utilized in the discovery, conformance checking, and enhancement of business processes based on event logs in business information systems (BIS), with the purpose of supporting the BPM activities. Various BIS automations store detailed information about the identity and sequence of actual activities performed during the execution of the business processes they support [1,2]. This information is called event logs, which is the starting point of process mining [3].
Each event record symbolizes one activity and each activity is a part of a process. Event logs store detailed information on events concerning the source; i.e., the person or organization that started and performed the activity, the starting and finishing time of the activity, and the data element; e.g., age, gender, size, and comments. All such information in the event logs can be used to discover processes from different perspectives. In process mining, there are many perspectives such as control-flow, resource, data, function, conformance, and time [4]. Also, there are various discovery algorithms that provide mining results separately for these perspectives. The perspectives, however, are not isolated and are all related to each other. Since the perspectives require different kinds of data to mine as specific to them, the formats of the produced outputs vary, e.g., Petri-net [5], Heuristic net, Fuzzy model, BPMN [6], Petri-net with data, and XML. In order to obtain a holistic process model, firstly, the control-flow perspective is discovered by using algorithms such as Inductive Miner [7]. A skeleton model is created by using these algorithms and other perspectives such as data, resources, and performance, are added to this skeleton model. The results of the mined perspectives are represented in Petri-net which has token-based semantics or in BPMN. Both notations allow one to integrate the outputs of the multiple perspectives mined into a single process model. However, as different from Petri-net, BPMN is able to hold the output of the resource perspective easily due to its elements to represent different roles; and this makes it an attractive notation for process mining experts.
Based on the motivation stated above, in this article, we introduce a framework for applying multi-perspective process mining and creating a BPMN process model as an output that is kept in blockchain. More specifically, the main contributions of this research are: (1) Proposing a plugin to ProM [8] for multi-perspective process mining; (2) Combining distinct outputs of control-flow, data, and resource perspectives in a single, multi-perspective process model in BPMN; (3) Enriching the representation of Data Petri-net produced by the data perspective with percentage of transition (relative frequency), average time and instance count information; (4) Using a BPMN Data Model, which has been developed recently [9,10], in order to keep the multi-perspective process model in the blockchain in a secure and immutable way; (5) Validating the correctness of the multi-perspective process mining proposed by the framework over a case study in medical domain, where most processes are complex, variable, dynamic, and multi-disciplinary in nature [11].
The remaining of this article is organized as follows: Section 2 overviews the background on process mining and Section 3 summarizes the related studies. Section 4 explains briefly the BPMN Data Model. Section 5 describes the proposed framework in detail. Section 6 presents the validation of the framework over a case study. Finally, Section 7 concludes the article by providing overall results and suggestions for future work.
2.
Background
2.1. Process mining and process perspectives
Process Mining is a process management technique that bridges the data-oriented techniques and traditional process modelling techniques. In the last decade, it has been increasingly used for business process management [1,12]. Process mining is applied for three main aims [13]; i) process discovery, ii) conformance checking of process implementations according to the discovered or modelled process, and iii) process enhancement by detecting the differences in process implementations.
Process discovery is the most important activity of the process mining since it provides a base for further analyses involving the application of the remaining two types of process mining, conformance checking and enhancement. In process discovery, event logs are used as input and a process model is automatically set up without prior information [13]. When an actual process is created from event logs, many organizations can face challenges due to the differences in theory and implementation.
In conformance checking, the process model and its flow discovered from the event logs are analysed and it is checked whether the process has been carried out as identified in the model [13]. Conformance checking measures the differences between the actual process and the process model specifications. The main aim of this technique is to identify the areas that need improvement using the information gained from the actual process [14].
Process enhancement is the improvement of the process model based on event data. This can be undertaken by adding further perspectives to the process model using event data, an activity also known as extension. Another type of enhancement is repair, in which the quality of the process model is improved using event data and a new repaired model is defined [15].
In the multi perspective-process mining (MPM) technique, there are many perspectives; e.g., control-flow, resource, data, time, and function [13]. The control-flow perspective focuses on the sequences of activities and the discovery of the process model, and aims to find the best definitions for all possible paths. The data perspective enables the analysis of the data that has an impact on the occurrence of the activities in the process model. The case perspective focuses on the definition of cases and the factors which influence the real data. The resource/organizational perspective concerns the actors (human, system, and role) and the relations between these actors to classify the process model based on roles and organization. The time perspective is concerned with the occurrence time and frequencies of events and helps identify bottlenecks, measure service levels, track the use of resources, and predict the remaining time for ongoing events. The performance perspective allows the performance problems in the process model to be exposed, and measures can be taken in advance for future problems with performance measurement based on time information as in the time perspective.
Further details are provided in the following paragraphs with regard to the perspectives used in this study.
Control-flow perspective: Its name is also known as process perspective. The hidden workflow in the event log is expressed through notations such as Petri-net [5], BPMN [6], Heuristic net [2] by using process mining discovery algorithms. Alpha Miners [16], Inductive Miner [17], and Heuristics Miner [2] can be given as examples to the algorithms used in this perspective.
Data perspective: It plays a role in showing the conditions (data guards) in transitions on the discovered control-flow output through notations such as Data Petri-net or BPMN. In discovering this perspective, Data Aware Discovery algorithm [16] can be used.
Resource/organizational perspective: If there are roles performing activities in the event log, one can use this perspective in the discovery phase. Role-activity matching can be accomplished through the Organizational Miner algorithm [8], which can be exported as XML output. Social Network Analysis plugin [18] can also be used for this perspective, but the resulting output cannot be exported except for pdf and image display.
Time perspective: If there is timestamp data in the event log, this perspective becomes available. This way, bottlenecks can be discovered and resource usage can be measured. In turn, possible future problems in the use of resources are determined in advance and precautions are taken. While discovering this perspective, Dotted Chart [19] algorithm can be used.
Performance perspective: It is the perspective that is effective in discovering the performance problems in the business process. With this perspective, it can be determined how well the performance of the business process is and measures can be taken in advance for future problems with performance measurement. While discovering this perspective, Multi-perspective Process Explorer [20] can be used.
To bring all process mining perspectives together, the flow is started with the control-flow perspective which finds all possible paths of activities from the event log in the discovery step [21]. Then the generated process model is checked for whether the reality conforms to the model in the conformance checking step. Finally, additional perspectives are applied to the process model in the enhancement step [12].
Various software products have process mining capabilities [13], e.g., ProM (TU/e) [8], Disco (Fluxicon) [22], PALIA-ER [23], CELONIS [24], pMineR [25] and bupaR [26]. ProM is the most comprehensive process mining tool, which provides a standard environment incorporating a generic open-source framework for implementing process mining techniques. PALIA-ER is specific to emergency processes, Disco and Celonis are commercial tools, pMineR and bupaR combine data science techniques and process mining techniques. Although ProM's user interface is difficult to understand for beginners in comparison to other tools, it is the most preferred tool by researchers and practitioners due to its large number of plugins [27,28] and targeting both academic and industry communities. Also, it supports several multi-perspective process mining plugins [20,29].
2.2. Petri-net vs BPMN
Petri-net [5] offers a graphical notation for step-by-step processes that require selection, iteration, and concurrent operation, similar to industry standards such as Unified Modelling Language (UML) [30], BPMN [6], and Event-driven process chain (EPC) [31]. But beyond these standards, it can model the operation of processes related to the mathematical theory developed for process analysis with mathematical precision. BPMN is typically designed to provide a standard notation that can be easily understood by all business stakeholders. Therefore, BPMN helps prevent communication gaps that may arise between the stakeholders in a project that adopts a common language to explain business processes. A well-modelled business process in BPMN can be understood by people who do not know BPMN at all, because BPMN 2.0 [32] is a high-level notation. In other words, a process model in BPMN can be thought of as "high level" representation of the process, which can be used to display a low level, mathematically formalized process description in Petri-net [5]. A comparison of representations in Petri-net and BPMN is shown in Table 1.
Petri-net output may be sufficient for control-flow representation of a process. It is also possible to convert it to BPMN if a higher-level representation is desired. In this way, a more understandable demonstration is provided. For the data perspective, the Data Petri-net output is obtained. Since this output is placed on the skeleton model that has already been discovered with control-flow perspective; the more comprehensible the control flow representation is, the more comprehensible the data perspective becomes. For the resource perspective, pools are created by establishing an activity and originators relation through BPMN lanes. It is typically not preferred to represent the resource perspective in Petri-net. As a result, BPMN becomes an attractive notation for process mining experts. BPMN can be used for MPM process discovery solutions since it enables to include the outputs of control-flow, data, resource, performance, and time perspectives in a single process model. An integrated multi-perspective solution can be obtained by converting these outputs to a single BPMN model by running different perspective algorithms/methods.
2.3. Process discovery algorithms and outputs
A process model created by process discovery step of process mining should describe the observed behaviour and not explain more of that observed behaviour. In addition, this model should contain unobserved but possible behaviour without unnecessary complexity. There are four dimensions that show the quality of the process model created by process discovery: fitness, simplicity, precision, and generalization [33]. There are also trade-offs among these dimensions, and this is enough to make process discovery a challenging task. When process discovery algorithms are grouped according to the quality dimensions [33] as shown in Table 2, it is seen that the models produced by the algorithms used in process discovery can be represented in different notations such as Petri-net, EPC, BPMN, and Heuristic Net.
The process model that is created by process discovery algorithms can be addressed to one of four situations [38]: (1) the model can only contain frequent behaviours, which is the most ideal process model, (2) it may include some of the frequent and infrequent behaviours, which is the non-fitting model, (3) it includes only frequent and infrequent behaviours, which is the over-fitting model and cannot cover new situations, or (4) it contains all behaviours, including the uncommon behaviour, which would be an under-fitting model. The ideal representation of the discovered process model with correct representational bias is as important as the comprehensibility of the process model. Representational bias defines the search space by having the ability to rep- resent concurrency, loops, silent actions, duplicate actions, OR-splits/joins, non-free-choice behaviour and hierarchy. It helps capture the quality and ideal representation for discovered model of the process while exploring the process in the event log. Each process discovery method should have its own most effective representational bias. Because each notation has its own capabilities, and thanks to the correct algorithm and notation matching, the most ideal process models can be obtained in a way that ideally covers the event logs. In other words, representation of the process with different notations and representational bias are not the same thing. When the relevant process model is not represented with its ideal notation, this may lead to some losses.
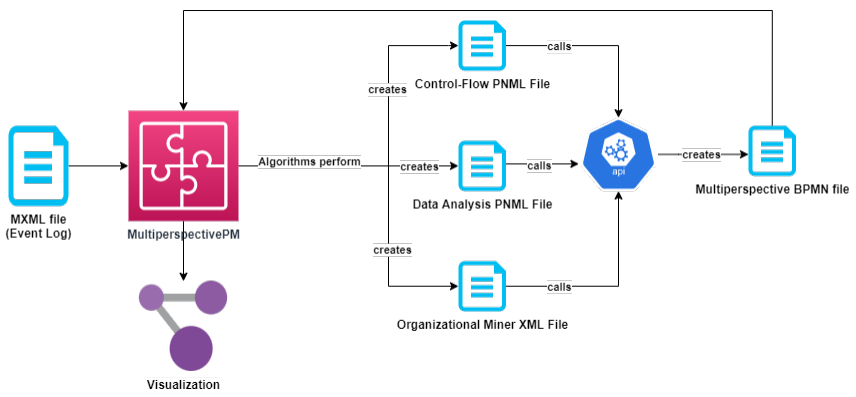
As shown in Figure 1, the event log with mxml file extension is given as input to the introduced plugin MPCM. Then, algorithms are run for the discovery of the process from the perspectives of control-flow, data, and resource. Algorithm outputs are pnml file for control-flow perspective, data pnml file for data data perspective, and xml file for resource perspective. These outputs are given as input to the BPMN Data Model API and a hybrid BPMN Data Model is obtained. In addition, the data model is enriched with performance data. However, this structure is not shown as hybrid in BPMN.
3.
Related work
In this section, the literature is examined by focusing on the perspectives of process discovery algorithms, and then the existing multi-perspective process mining studies are examined in terms of the perspectives they address.
Since the process model created as a result of process discovery is based on the control-flow perspective, there are a lot of studies on mining control-flow perspective in the literature. Dakic et al. [28] report that 94% of the process mining studies are based on the control-flow perspective. The examination of the most widely used control-flow algorithms can be started with the alpha algorithm proposed by Aalst et al. [15]. Mohamed [18] mentions that this algorithm fills the gap between the event log and the process model but it has a flaw in producing a reliable model since it ignores frequencies, and therefore, does not guarantee completeness and soundness of the model. In the same article, the Heuristic Miner algorithm proposed by Weijters et al. [2], which can deal with noise, is mentioned as an improvement of the alpha algorithm. It is also mentioned that Heuristic Miner algorithm can filter noisy or infrequent behaviours because it takes frequencies into account, but it remains short too in guaranteeing sound process models. Another control-flow perspective study by Aalst et al. [39] presents a new approach based on genetic algorithms. With this approach, noise and deficiency are dealt with the genetic process mining approach using causal-matrix. Weber et al. [40] states that existing algorithms currently used in the control-flow perspective in general does not discover the probabilistic nature of the process. In this study, a framework is proposed and applied on the Alpha algorithm, and it is shown how much data is required to achieve a certain accuracy by using the structures in the model. In another study, Ghawi [41] mentions that the models formed as a result of the Inductive Miner algorithm developed by Leemans et al. [17] correspond to sound, block-structured workflow (WF) net systems, and they always fit.
As the control-flow perspective studies have been emerging, Rozinat et al. [42] have conducted a study on the data perspective by using machine learning techniques, data dependencies, and decision-point analysis. Following that, Decision Miner algorithm has been implemented in ProM. The article by Leoni et al. [16] is based on the fact that the algorithms used for the control-flow perspective have discovered the decision points, but not because they have discovered the rules required for the data-flow. With the latest developments in conformance-checking, it is mentioned in the study that data-flow could also be discovered and added to the process model with an adaptation process.
While examining other perspectives in process discovery, it is seen that the perspectives such as organizational, time and performance are also included in the studies. Mans et al. [43] mention that process mining techniques can be used to determine patient care-flow, and the health process has been examined from different perspectives such as control, organizational and performance. Bozkaya et al. [44] propose a method on process discovery, where the process has been examined from various perspectives such as control-flow, performance (Dotted Chart Analysis), and organizational (Organizational Miner and Social Network Analysis). Aalst [45] explains that it is possible to apply the control-flow perspective by converting the logs obtained when web services are communicating with each other into event logs, and that different perspectives can be added to the model by replaying event logs. This study gives information about the process mining manifesto and provides information about the situations that may be encountered while doing service mining. Gupta [46] has studied about the comparison and operation of process mining algorithms in order to guide the companies in choosing the most suitable algorithm for their needs. Mohamed [18] mentions in his study that the process model can be expanded by using Social Network analysis to show the organizational perspective.
When the related studies are examined, it can be seen which perspective is used in which study. With this information, a road map has been drawn about which algorithm could be used for which perspective. Therefore, the review summarized in the table has helped in selecting algorithms that explore different perspectives that can be used for MPM. It is also seen from the related literature that the methods used for process discovery are based on the control-flow perspective. In other words, the process model is first discovered using the control-flow perspective, then other perspectives are added on this process model. In our study, the algorithms used in developing the MPM framework have been selected from the studies in Table 3 by considering their advantages and drawbacks. As an example, since the Alpha algorithm does not address frequencies, it would be more advantageous to use the Heuristic Miner algorithm, which is an improved version of the Alpha algorithm and addresses the frequencies. As a result, different perspective algorithms have been integrated to provide a single, multi-perspective process mining solution, with some additional features such as data guards with average time, percentage of transition, and instance count information. More specifically; percentage, average time, and instance count properties have been added to the branches in the process model formed by the Data Aware Explorer algorithm in the data perspective. If the user wishes, s/he will be able to use this feature and display these properties on Petri-net or BPMN diagrams; that is, this part is left optional.
After examining the studies that mine different perspectives on the process model, multi-perspective process mining studies have also been examined. The studies in the literature on MPM are marked according to their included perspectives in Table 3.
Folino et al. [47] propose a new approach that can be used while exploring the process model. In this approach, they mention the control-flow perspective as structural, and other data such as activity executors, parameter values, and time-stamps, as non-structural. It is also mentioned in the study that the process would be explored by characterizing it from structural and non-structural viewpoints. With this approach, the process could be discovered in a multi-perspective way. Mannhardt et al. [20] define the Multi-perspective Process Explorer (MPE) tool in which they have integrated already existing process mining techniques such as data-aware discovery, conformance checking, and performance analysis. Schönig et al. [49] propose a framework to discover Multi-Perspective Declare Models, where a process is analysed from different perspectives such as control-flow, data, time, and organizational. Sturm et al. [52] offer a distributed mining framework called Multi-perspective DECLARE, which includes an efficient big data technology for MP-DECLARE models. Mannhardt [4] proposes a multi-perspective process mining method considering problems in multiple interacting process perspectives of control-flow, data, resources, time, and function. He makes two contributions regarding multi-perspective process discovery: Data-aware heuristic process discovery and the Guided Process Discovery. Jablonski et al. [50] develop multi-perspective process trace clustering approach with tool support, which enables reducing the complexity of mined process models in terms of improving the homogeneity of trace subsets. Kalenkova et al. [29] integrate various process mining algorithms for the discovery of multi-perspective hierarchical BPMN models, and bridge the gap between the PM techniques and BPMN tools. Sikal et al. [51] propose a variability discovery approach for resource perspective in configurable processes, and use the dependencies between the activity and the resource variability. Pini et al. [48] present a multi-perspective visualization framework to compare processes. In this article, the authors propose a design approach that allows to address the multiple perspectives like control-flow, time, performance, and resource.
Considering the integrated multi-perspective process mining solutions, in our study, the alternatives for mining the control-flow perspective are presented in the MPM framework and this way, the opportunity to experiment and work with the algorithm most suitable for the dataset is provided. In addition, perspective selection is enabled prior to representing the process model in BPMN. As also different from the studies in this table, additional features have been added to represent the data perspective and the performance perspective (including information of percentage, average time, instance count) together and separately in Petri-net or BPMN.
It is seen that there is no solution that includes the perspectives of control-flow, data with performance information, and resource, which is applied directly on the event logs to create a process model in BPMN. Therefore, the proposed framework contributes to the body of knowledge and practice by addressing these features. In addition, the BPMN model is kept in blockchain in our solution via BPMN Data Model [9], which can be considered a timely and motivating contribution for the following similar proposals and also for future MPM applications.
4.
BPMN data model in blockchain for multi-perspective process mining
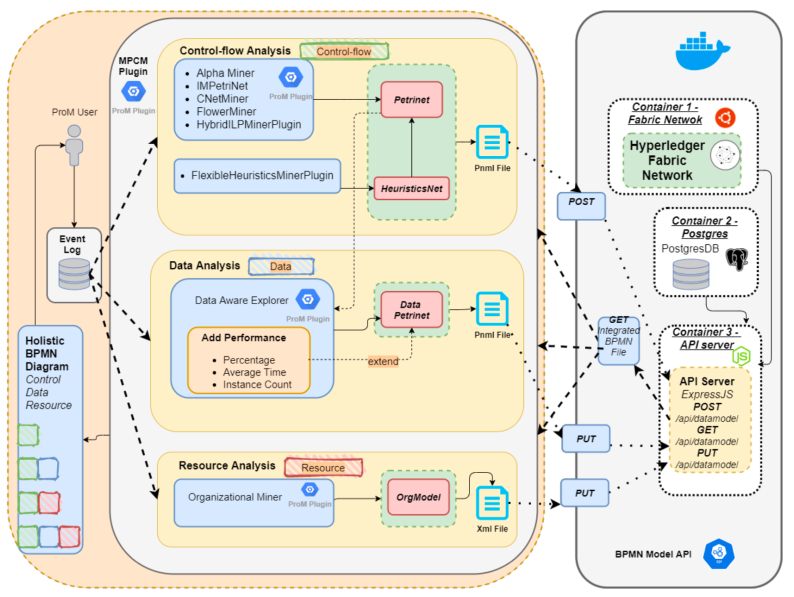
The Data Model has been proposed to keep the outputs from the low-level process models, which are produced via multi-perspective process mining techniques, together in a new model that is extended from BPMN [9]. Since each technique used in an additional perspective produces a different low-level model, an operation to modify the results of analysis methods to proper forms and to transfer them to the Data Model is required. Accordingly, three basic perspectives (i.e., control-flow, data, and resource) are applied one by one, and the Data Model is enriched during this process by creating the necessary elements that correspond to what the perspectives describe. What those elements are and how they are determined are explained below in detail as specific to each perspective.
The construction process of the Data Model includes the activities of log creation, log preparation, control-flow analysis, decision analysis, and role analysis. In control-flow analysis, a process model is discovered based on pre-processed event logs and is produced in a Petri-net file as an outcome. This is the first type of process mining analysis where control-flow is used as backbone, and the other elements will be attached to the control-flow backbone. This Petri-net file is used as an input in addition to the event logs, in order to discover process model from data or resource perspectives. While creating the process skeleton, the Inductive Miner algorithm is used as control-flow algorithm. In data perspective, Decision Miner algorithm [42], which extracts the knowledge about decision rules, is applied for decision analysis. In resource perspective, Organizational Miner Algorithm, which derives the organizational concepts of the process, is used for role analysis. After these steps, the Data Model gets the last and most meaningful form which is capable to describe what the actual process looks like, i.e., representing which characteristics or attributes belong to case influence decisions in the process, who executes or performs activities, and what the organizational roles are.
After control-flow analysis, startEvent, endEvent, task, exclusiveGateway, parallelGateway, and sequenceFlow elements are filled in the Data Model. After data analysis, the dataObject, dataObjectRef, ioSpesification, dataInput, dataInputAssociation, dataOutput, dataOutputAssociation elements are transferred to the Data Model. Aside from these elements, the task and sequenceFlow elements are updated in this analysis. After resource analysis, the laneSet, lane, collaboration, and participant elements are filled in the Data Model. Further information on the Data Model and data transformations can be obtained from [9].
5.
Framework for multi-perspective process mining
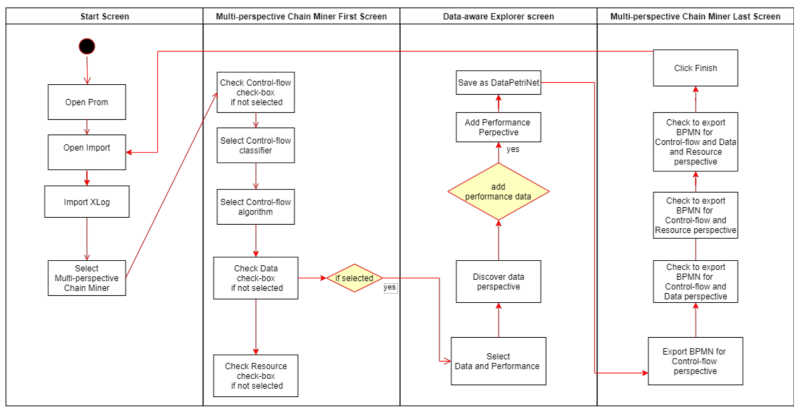
This section introduces the framework presented in this paper. It provides an overview about supported process mining perspectives and algorithms, then shows the details of plugin functionalities to explain its usage. This integrated discovery approach is implemented as a plugin to ProM, the most widely used open-source process mining framework. As a pre-requisite, BPMN Data Model API must be deployed to Docker before running this plugin. Our plugin is available in a new package called Multi-Perspective Chain Miner (MPCM) which is adaptable to ProM. It is aimed to contribute to the body of solutions for multi-perspective process mining. With this solution, the process model mined from the event logs for multiple perspectives can be integrated and stored in a single BPMN-extended data file in blockchain, and be visualized including the information of control-flow, resource, data, and performance. While developing MPCM, perspective algorithms used in process mining have been examined, as reported in Section 3. In the light of these algorithms, it has been investigated how these perspectives could be integrated with each other. In this context, the algorithms supported by the framework are given in Figure 2.
In the scope of the MPCM*, the process is mainly analysed from three perspectives. These are the control-flow, data, and resource perspectives. From the control-flow perspective, the skeleton of a process model can be generated using different algorithms/plugins, namely the Alpha Algorithm [15], IMPetriNet [7], HybridILPMinerPlugin [53], FlexibleHeuristicsMinerPlugin [54], CNetMiner [55], IMProcessTree [7], and FlowerMiner [56]. User can experience how the outputs of these algorithms are integrated with the outputs of other perspectives by selecting and trying different control-flow algorithms. The process skeleton discovered by the control-flow perspective can be extended with the data or resource perspective. Data perspective helps to understand the data inputs to the branches in the process skeleton. For the data perspective, Data Aware Explorer plugin [16] is run and the process skeleton is enriched with information such as average time, percentage of cases that followed the transition, and instance count. In other words, this information can be added to the process model while mining from the data perspective, if selected by the user. The resource perspective that allows to see the roles who perform the activities can also be added to the process skeleton (or to the skeleton previously enriched by the data perspective) by executing Organizational Miner Algorithm [18].
*https://github.com/mervemisin/MultiperspectiveChainMiner
In the control-flow analysis, the output of the mining is converted to a PNML file, while a DataPNML file is created in the data perspective analysis. In the resource perspective analysis, the OrgMiner file, in which activate-resource mapping is made, is created as an XML file. These files are used to obtain a BPMN diagram (e.g., the one shown in Figure 7 which puts together the outputs of the control-flow, data, and resource perspectives.
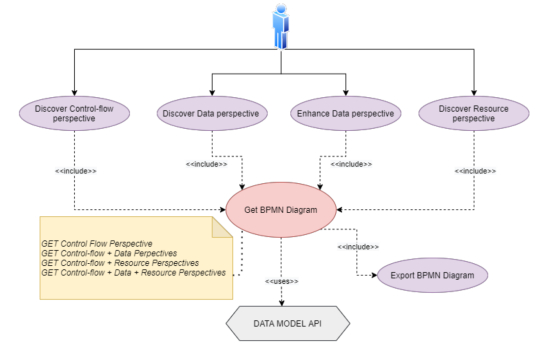
The use-case diagram given in Figure 3 illustrates the main interactions between the user and the MPCM framework. Once event logs include data, resource attributes at the event level, we can combine control-flow, data, and resource perspectives into a single BPMN diagram. In the first part, after importing an event log (typically including the fields of activity, timestamp, data, and resources), the user selects the control-flow algorithm. Then, data and resources perspectives to be explored are selected. If the data perspective is selected, the information about the percentage of transition, average time, and instance count can also be added in front of the data guards and branches displayed in the Data Petri-net. In the second part, the user can proceed with the creation of a BPMN diagram with regard to the process perspectives mined. The framework allows the user to visualize the intermediate models in the control-flow and data perspectives, or in the control-flow and resource perspectives, depending on the user's selection. Finally, the user can export the integrated process model in the format of BPMN or Data Petri-net.
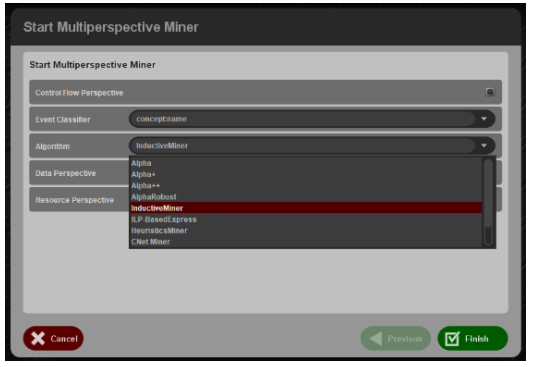
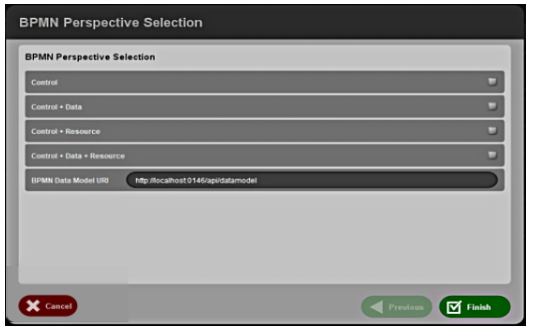
MPCM plugin is designed on ProM plugin infrastructure. As seen in Figure 4, first of all, the user is requested to select control-flow, data, and/or resource perspectives to represent in the BPMN model. The plugin also includes an area for algorithm selection for the control-flow perspective. After selecting the relevant fields, the hybrid or single perspective BPMN output, for which perspectives will be marked by checkboxes in Figure 5 and the BPMN Data Model API addresses input field, is also displayed on this screen. In this way, it is aimed to use BPMN Data Model API with the same interface in a dynamic structure. However, for this research, the value seen in Figure 5 is given as default.
6.
Example application of framework in medical domain
This section explains how the framework can be used to generate a holistic process model for a case in medical domain.
Sepsis data [57] is analysed from different perspectives and represented in an integrated and automatically generated BPMN diagram by examining the results of different control-flow algorithms. The applicability of the plugin developed within the scope of this study can be seen with this dataset, because it contains resource information that performs activities and some data fields (e.g., DiagnosticXthorax, DiagnosticECG etc.) that relate to these activities, in addition to the mandatory fields of case id, activity and timestamp information. This anonymized event log covers traces of 1050 patients' trajectories that are admitted to the emergency ward by displaying symptoms of Sepsis, over the course of 1.5 years in the hospital information systems [57]. It contains 15,214 events for 16 activities which are categorized into medical activities and logistic activities. There are 846 process variants, which indicates the inherited complexity and flexibility problems of healthcare processes [58], although the dataset focuses on a specific sub-group of patients.
The steps required to put together the results from the control-flow, data and resources perspectives to the BPMN Data Model are shown in Figure 6. The user needs to deploy the BPMN Model API [9] before using MPCM framework in order to keep the multi-perspective process model in blockchain. With respect to the steps shown in the Figure 6, multi-perspective process mining starts with the control-flow analysis, and continues with the data perspective analysis and resource analysis.
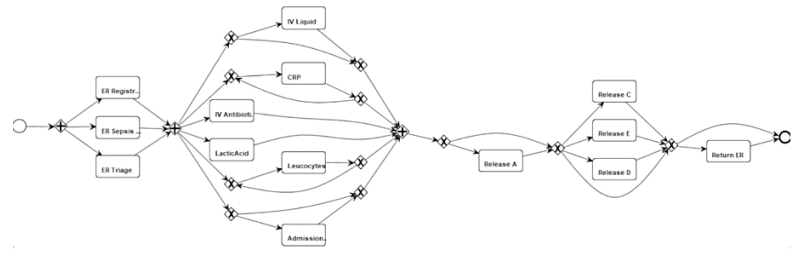
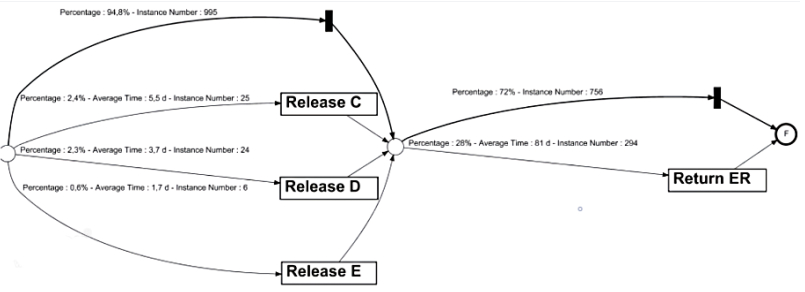
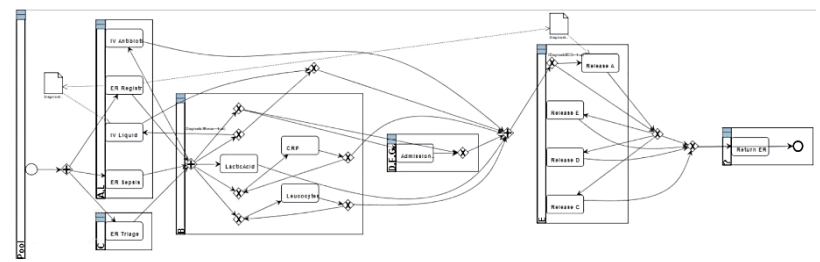
Discover Control-flow Perspective: This analysis starts with selecting control-flow algorithms. According to the comparison of the algorithm metrics on ProM 6.10 as given in Table 4, it was decided that the best alternative to be chosen for Sepsis data was the Inductive Miner algorithm. So, for the Sepsis case, we selected Inductive Miner (IMPetriNet) and discovered the process model from the control-flow perspective. IMPetriNet generates a Petri-net which can be difficult to understand and evaluate by the medical professionals. The discovered Petri-net is automatically converted to a BPMN diagram as shown in Figure 7. According to the figure, the Sepsis Process starts with registration or triaging activities; continues with measuring of leukocytes, CRP, and lactic acid; and ends with some types of discharge (Release C-D) or Return ER activities.
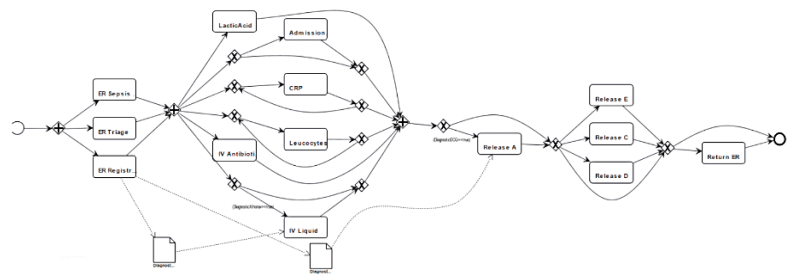
Discover Data Perspective: In multi-perspective process mining, discovered process model in BPMN or Petri-net can be extended with the data perspective and represented in a Data Petri-net. When the user checks the data perspective, Data Aware Explorer Plugin is executed by MPCM plugin. Data guards are added to the previously discovered process model that is a skeleton for other perspectives. The discovered model of Sepsis Process in Data Petri-net is seen in Figure 8.
Enhance Data Perspective: The Data Petri-net created by the data perspective can be enhanced if the user wants to add information from the performance perspective, such as percentage of transition, average time and instance count, to the discovered model. The enhanced process model in Data Petri-net is shown in Figure 9.
Discover Resource Perspective: As an alternative, the framework integrates resources information to the BPMN Data Model, and visualizes the roles that perform the activities in addition to the information from the control-flow and data perspectives. Organizational Miner Plugin (in ProM 5) is used for the exploration of the resource perspective. We discovered the roles in the Sepsis Process and visualize the multi-perspective process in the BPMN diagram in Figure 10.
Get BPMN Diagram: The outputs of the control-flow, data and resource perspectives are integrated using the BPMN Data Model API according to the user selections. The multi-perspective process model is stored in the BPMN Data Model in blockchain in a secure and immutable way. Then, the process model in BPMN can be accessed, viewed, and exported from the Import tab in ProM.
7.
Conclusion and future work
In this article, process mining algorithms have been examined from different perspectives, and a framework called Multi-Perspective Chain Miner (MPCM) has been proposed as a plugin to ProM tool. While the plugin has been developed, open-source algorithms in ProM have been used, and with additional improvements in the Data Aware Explorer plugin, performance and time information have been added in the Petri-net file with the data expression generated in the branches. After the application of the algorithms, it has been ensured that the outputs generated by the control-flow, data, and resource perspectives have been combined in a single process model in BPMN using an API that has generated the BPMN Data Model in blockchain. Then, the BPMN process model has been exported with the plugin developed within the scope of this study.
In this work, it has been observed that the difference of control-flow algorithms applied according to the event logs is important and affects the results. The selected algorithm for the control-flow perspective directly affects the results in terms of quality metrics. The quality of the skeleton obtained by the control-flow algorithm also affects the quality of the model enriched with data and resource perspectives. For this reason, before using the MPCM plugin on an example Sepsis data in medical domain, the algorithm and metric comparisons were made for the control-flow perspective and thus, the most suitable algorithm was chosen for the creation of the skeleton model. Since other perspectives were based on this skeleton, their quality was also positively affected in this way. In future studies, it is planned to work on determining bottlenecks in process models with the help of Smart Contracts to be implemented in blockchain.
Acknowledgments
Authors are grateful to ASELSAN Inc. for the support of the publication process.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: