Superquadratic stochastic processes and their fractional perspective with applications in information theory

1.   Introduction

The mathematical concept of convexity plays a fundamental role in mathematics and engineering, as it offers a solid foundation for analyzing and solving a wide variety of problems. In this theory, convex sets and convex functions are especially important because they help simplify otherwise complex mathematical models and enhance optimization processes. One of the key advantages of convex problems is that they typically have a single global minimum, which means they can be solved efficiently and reliably unlike non-convex problems that may have multiple local minima. This makes convexity crucial in many real-world applications where optimal solutions are desired. Convexity also finds significant applications in various applied disciplines, including control theory, economics, and optimization. In control theory, for instance, convex models make systems stable in a range of conditions and thus stronger and more reliable. Convexity in economics also aids in analyzing consumer attitudes and trends in the market and then assists in optimal resource allocation and sound decision-making. Additionally, convexity is closely related to the field of integral inequalities, a recognized field of mathematical study. Integral inequalities are used for the establishment of bounds on integrals, and convex functions recur whenever such inequalities hold. An immediate example here is the Hermite-Hadamard inequality, which provides bounds for the average value of a convex function on an interval. Such inequalities are not just theoretically significant, but are also of immense practical use in real analysis, numerical analysis, and applied mathematics. References such as ^{[1, 2, 3]} provide further insight into the applications and development of such inequalities, showing that there is a rich interplay between convexity and integral analysis.

Fractional calculus has emerged as a powerful and versatile mathematical tool, finding applications across a wide spectrum of disciplines, including physics, engineering, and, somewhat unexpectedly, computer science ^[4]. The extension of classical calculus to include derivatives and integrals of arbitrary (non-integer) order enables the modeling of complex systems that exhibit memory, non-locality, and hereditary properties that cannot be adequately captured by traditional integer-order models. These features are particularly valuable in viscoelasticity, electromagnetics, control systems, bioengineering, and signal and image processing, where the system's future behavior depends not only on its present state but also on its history. The recent surge in interest in fractional calculus is driven in part by its ability to bridge the gap between discrete and continuous phenomena, and to offer improved mathematical modeling for anomalous diffusion, chaotic systems, and fractional-order filters, among others. Its relevance in computer science has become increasingly apparent in the context of machine learning, network analysis, and complex system simulation, where memory effects and long-range interactions are critical. Beyond these applied domains, fractional calculus has significantly influenced the development of inequality theory, especially through the formulation of fractional integral inequalities. These inequalities generalize classical results by incorporating fractional integral operators, thereby extending their applicability and deepening their theoretical underpinnings. In the last ten years, hectic development in this field has been witnessed, where researchers have produced new forms of traditional inequalities, such as $\mathbb{HH}$, Jensen, Ostrowski, and Grüss inequalities, in fractional integrals. One of the outstanding contributions in this direction is the work by Sarikaya et al. in 2013. ^[5] The authors developed a fractional counterpart of the $\mathbb{HH}$ inequality via $\mathbb{R.L}$ fractional integrals. This result not only generalizes the classical $\mathbb{HH}$ inequality but also opens new chains of research toward finding integral bounds of the convex and generalized convex functions through fractional operators. Since then, many researchers have built on this foundation, formulating new fractional inequalities in different directions, such as Hadamard-type, midpoint-type, and Fejér-type inequalities, with numerous applications in numerical analysis, optimization theory, and differential equations.

Since the seminal introduction of the $\mathbb{HH}$ inequality in the context of $\mathbb{R.L}$ fractional integrals, there has been a surge in interest in developing $\mathbb{HH}$-type inequalities for various generalized fractional integral operators. This foundational result sparked a wave of advancements, wherein researchers have extended the classical Hermite-Hadamard framework to an array of novel fractional operators, each tailored to address different analytical and applied challenges. Some of the prominent fractional integrals explored in this context include the Sarikaya fractional integrals ^[6], the generalized proportional fractional integrals ^[7], the $(k-p)$ fractional integrals ^[8], and the $k$-fractional integrals ^[9]. Other significant contributions have utilized operators such as the Katugampola fractional integrals ^[10], generalized $\mathbb{R.L}$ fractional integrals ^[11], and the $\psi$-$\mathbb{R.L}$ fractional integrals ^[12], which introduce kernel flexibility via auxiliary functions. More recently, conformable fractional integrals ^[13] have gained traction for their local nature and compatibility with classical calculus, further enriching the analytical toolbox. In parallel, generalizations of integral inequalities have been proposed for these operators, extending beyond $\mathbb{HH}$-type bounds. Notable developments include Simpson-type inequalities ^[14], Euler-Maclaurin-type inequalities ^[15], Bullen-type inequalities ^[16], and Ostrowski-type inequalities ^[17], each tailored to estimate functionals under different assumptions of convexity, differentiability, or structural properties of the integrand. To readers who are interested in acquiring an overall impression of recent developments on fractional integral inequalities, e.g., more refined methods, applications, and operator-specific results, we recommend reading surveys and research articles like ^{[18, 19, 20]}, and the references therein. Overall, these articles demonstrate the dynamic and active role of fractional inequality theory and its far-reaching impact on mathematical analysis and its applications.

A stochastic process is a sequence of changing random variables in statistics and probability theory. They describe how a system evolves in what appears to be a random fashion but typically over discrete intervals of time or space. "Stochastic" is employed as an adjective to refer to processes that are at random or irregular rates. Stochastic processes can be utilized in order to model random change in systems over time. For instance, there are many random parameters that may cause fluctuation in bacterial growth, yet long-term prediction is not impossible. Similar to electrical systems' thermal noise generating random fluctuations in voltage or current, this seemingly random activity can be modeled using basic stochastic processes, and these can provide insight into the system's dynamics.

Stochastic processes are mathematical representations developed by physicists and mathematicians over the decades to explain a wide range of events, from fluctuation of the stock market to randomly diffusing gas molecules or the growth of population within ecosystems. Wherever there is an uncertainty, these processes along with other aspects such as molecular interactions could be represented by the stochastic models and have applications far-reaching in engineering as well as research. They are models from the mobility of different molecules in physics and are used to simulate population dynamics or disease spread in biology. Stochastic processes are important since they can describe systems that behave randomly coherently. They have applications in fields such as computer science, data transfer, cryptography, and signal processing where randomness or a desired state at each step is important. As such, they play an essential role in research and in discovering real-world applications. By numerical modeling of the processes, scientists and engineers can model future trends, system optimization, and design solutions that account for uncertainties within the environment. Some other notable applications include secure communication with cryptography, data compression schemes, and system state estimation.

Convex stochastic processes, which extend the definition of traditional convex functions to stochastic process systems involving randomness, were first introduced by Nikodem ^[21] in 1980. Further, he discovered that stochastic processes share several properties with classical convex functions. Jensen convex mapping, which plays a pivotal role in inequality theory, is an effective tool in this area. Several of the important inequalities can be derived based on this correspondence, and how they relate to stochastic processes was demonstrated by Skowronski ^[22] in 1992. Based on these concepts, Kotrys ^[23] demonstrated that, particularly for convex stochastic processes, upper and lower limits of the $\mathbb{HH}$ inequality can be determined using integral operators. Kotrys's work illustrated how the $\mathbb{HH}$ inequality, a basic convex analysis result, could be extended to be used on stochastic processes. In the last few years, papers on stochastic processes of different convexity types are found in the literature. Okur et al. ^[24] used the idea of p-convexity, a particular type of convexity, to construct the $\mathbb{HH}$ inequality for stochastic processes. Erhan ^[25] added more by building these inequalities using another convexity called s-convexity. Budak et al. ^[26] added more to other contributors' work by expressing these inequalities based on the concept of $h$-convexity. As mentioned in the sources ^{[27, 28, 29]}, there have been many research investigating different kinds of convexity for individuals who are interested in the most recent developments in stochastic processes. Further broadening the applicability of these mathematical ideas, Tunç in ^[30] made a substantial contribution by developing the Ostrowski-type inequality particularly for h-convex functions. Zhao et al. ^[31] connected inequality to interval mathematics, putting these inequalities within the context of interval analysis. Using interval analysis as a foundation, Afzal et al. ^[32] presented the notion of stochastic processes before the end of 2022. They also created new versions of the Jensen and $\mathbb{HH}$ inequalities that are designed for stochastic processes, fusing these two mathematical ideas in an innovative way. A novel mathematical framework called the $(\mathrm{m}, h_{1}, h_{2})$-G-convex stochastic process was presented by Eliecer et al. ^[33]. It incorporates functions $h_{1}$ and $h_{2}$ together with a parameter $\mathrm{m}$ to extend classical convexity to stochastic processes. Using this method, they derived certain inequalities related to stochastic analysis. Using fractional operators to apply fractional calculus to the $(\mathrm{m}, h_{1}, h_{2})$-convex stochastic process, Cortez ^[34] expanded on this work and produced additional inequalities. These developments improve mathematical models in many domains by offering strong instruments for assessing systems affected by fractional dynamics and unpredictability. Hafiz ^[35] explored the application of fractional calculus to stochastic processes, establishing a foundation for modeling memory dependent random phenomena. Kotrys ^[36] extended classical inequalities such as Jensen, $\mathbb{HH}$, and Fejér inequalities to strongly convex stochastic processes, providing valuable insights into probabilistic convexity theory. Further developments were made by Agahi and Babakhani ^[37], who introduced fractional-order extensions of Jensen and $\mathbb{HH}$ inequalities in the context of convex stochastic processes, enhancing their applicability in stochastic modeling. Fu et al. ^[38] investigated n-polynomial convex stochastic processes and established $\mathbb{HH}$-type inequalities for such functions, contributing to the growing field of stochastic optimization and uncertainty modeling. These studies collectively highlight the importance of convexity in stochastic settings and its impact on mathematical inequalities, probability theory, and applied optimization.

Superquadraticity is a generalization of convexity that permits more precise and sharper integral inequalities to be formulated. Such greater precision is especially essential in optimization, where tighter bounds are important in finding optimal solutions, and in applied mathematics, where tighter approximations contribute significantly towards the accuracy and reliability of mathematical models. In summary, the superquadratic theory does not only strengthen the theoretical foundation of integral inequalities but also broadens their applicability in analytical works and problem-solving situations.

The concept of superquadratic functions, extending the family of convex functions, was initially introduced in ^[39], further elaborated by Abramovich et al. in ^[40], and laying down principal definitions along with basic properties. Taking this as a premise, Li and Chen ^[41] explored fractional analogs of $\mathbb{HH}$-type inequalities via $\mathbb{R.L}$ fractional integrals, making a bridge between fractional calculus and superquadraticity. Further generalizations were extended by Alomari and Chesneau through the introduction of $h$-superquadratic functions ^[42], whose structural features and their usage in extending classical inequalities were studied. Later, Khan and Butt ^[43] generalized a new class in the form of center-radius $cr$-order interval-valued superquadratic functions, as well as their fractional versions and numerous applications. In addition, Butt and Khan ^[44] proved Fejér-type and $\mathbb{HH}$-type inequalities under the framework of $h$-superquadratic functions and applied. In another extension, Khan et al. ^[45] proposed the $(P, m)$-superquadratic function, offering examples, key properties, and associated inequalities, along with practical applications. The integration of interval calculus with superquadratic functions in the context of information inequalities was explored by Butt and Khan ^[46], while Butt et al. ^[47] addressed fractional Fejér and $\mathbb{HH}$ inequalities using the Atangana-Baleanu fractional operators. Contributing to the expansion into fuzzy environments, the authors in ^[48] introduced the fuzzy interval-valued superquadratic function, establishing a framework for associated results. A pivotal contribution was made by Banić et al. ^[49], who refined classical inequalities through superquadratic functions, laying the groundwork for subsequent theoretical exploration. Further research by Khan et al. ^[50] addressed multiplicatively $(P, m)$-superquadratic functions, deriving fractional integral inequalities that offer multiplicative analogues to classical results. In another important development, Khan et al. ^[51] studied $P$-superquadratic functions using multiplicative calculus, achieving sharper bounds and broader applicability. Moreover, Butt et al. ^[52] presented a fractal interpretation of superquadratic functions, enhancing their utility in stochastic processes through generalized probability estimations. Collectively, these contributions highlight the significant role of superquadraticity in advancing the theory of inequalities, particularly within fractional calculus, multiplicative calculus, and stochastic analysis, thereby opening up new avenues for both theoretical and applied mathematical research.

Following advances in convexity, fractional calculus, stochastic processes, and superquadraticity, we complete the missing link in research: The investigation of superquadratic stochastic processes, their inequalities, and information theory applications. Following the extension of convex functions, superquadratic functions provide improved accuracy and broader applications in mathematical inequalities. Our findings are hence a major improvement over earlier results on convex stochastic processes. For the first time, we establish our theoretical findings by elaborate examples, supported by elaborate graphical representations. We also carry out our analysis to information theory applications, broadening the boundaries of theoretical understanding and operational applicability.

The paragraph that follows provides an explanation of the paper's structure:

Following the review of the required background knowledge and pertinent data regarding convexity, superquadraticity, convex stochastic processes, and their inequalities in Sections 1 and 2, we use 2D and 3D graphical representations to investigate superquadratic stochastic processes and their properties. Moreover, we create new Jensen's and $\mathbb{HH}$-type inequalities in Section 3. Following that, $\mathbb{HH}$-type inequalities are derived in fractional form in Section 4. Graphical explanations and examples of the results are also taken into consideration in order to assess whether the results are beneficial. In Section 5, we discuss how the results may be used in information theory. A brief conclusion and potential study directions pertaining to the work's findings are examined in Section 6.

2.   Preliminaries

The key terms for fractional integrals, convexity, and superquadraticity are defined in this section along with the associated inequalities.

Definition 2.1. ^[1] Let the function $\Psi:\big[{{\mathrm{m}_{o}}}, {\mathrm{n}_{o}}]\subset\mathbb{R}\longrightarrow\mathbb{R}$ be convex, then subsequent inequality

is valid $\forall$ ${{\tau}}_1$, ${{\tau}}_2$ $\in[{{\mathrm{m}_{o}}}, {\mathrm{n}_{o}}]$ and ${{\ell}}$ $\in[0, 1].$

The $\mathbb{HH}$'s inequality is a fundamental mathematical result that establishes lower and upper bounds for mean values. In inequality theory, it is among the first types of inequality to use convex functions. For error calculations that use numerical integration, such as the trapezoidal and midpoint formulae, this inequality is an essential tool. This well-known finding is defined as follows.

Theorem 2.2. ^[1] $\mathbb{HH}$'s inequality states that if the function $\Psi:\mathfrak{I}\subseteq\mathbb{R}\longrightarrow\mathbb{R}$ is convex in $\mathfrak{I}\subseteq \mathbb{R}$, where ${\mathrm{n}_{o}} > {{\mathrm{m}_{o}}}$. The following statement satisfies:

$\forall$ ${{\mathrm{m}_{o}}}, {\mathrm{n}_{o}}\in \mathfrak{I}$.

Definition 2.3. $\mathbb{R.L}$ fractional integrals of fractional order ${{{\ell}}}\geq0$ with ${{\mathrm{m}_{o}}}\geq0$ are stated as

and

the notations $\mathfrak{I}^{{{\ell}}}_{\mathrm{n}_{o}^-}\Psi({{\tau}})$ is the right and $\mathfrak{I}^{{{\ell}}}_{{\mathrm{m}_{o}}^+}\Psi({{\tau}})$ is the left-sided operators. Where $\Gamma({{\ell}}) = \int_{0}^{\infty}{\mathrm{y}_{o}}^{{{\ell}}-1}e^{-{\mathrm{y}_{o}}}d{\mathrm{y}_{o}}$ is defined as the gamma function.

Definition 2.4. A function $\Psi:[0, \infty)\longrightarrow\mathbb{R}$ is said to possess superquadraticity if the inequality (2.3) holds, $\forall$ $\mathbf{\mathfrak{C}}_{{{\tau}}}\in\mathbb{R}$, where ${{\tau}}\geq 0$ and $\mathfrak{C}_{{{\tau}}}$ is a constant such that

Remark 2.5. Function $\Psi$ is said to possess subquadraticity if "$\leq$" is reversed in (2.3). Function $-\Psi$ is superquadratic in the case $\Psi$ is subquadratic.

Using $\Psi({{\tau}}) = {{\tau}}^\mathfrak{q}$ as an example, function $\Psi$ for ${{\tau}}\geq0$ and $\mathfrak{q} \geq 2$ is superquadratic, but for $0\leq\mathfrak{q} < 2$ is subquadratic. In this case, $\mathfrak{C}_{{\tau}} = \mathfrak{q}{{\tau}}^{\mathfrak{q}-1}$. In addition, equality is maintained in (2.3) when $\mathfrak{q} = 2$.

More specifically, a superquadratic function chosen at random meets the three further conditions specified by Lemma 2.6:

Lemma 2.6. If function $\Psi:[0, \infty)\longrightarrow\mathbb{R}$ is superquadratic, then:

● $\Psi(0)\leq0$.

● $\Psi'({{\tau}}) = \mathbf{\mathfrak{C}}_{{{\tau}}}$, provided $\Psi$ exhibits differentiability at ${{\tau}} > 0$ and $\Psi(0) = \Psi'(0) = 0$.

● If $\Psi$ is positive and $\Psi(0) = \Psi'(0) = 0$, then $\Psi$ is convex.

Definition 2.4, is the line of support definition of superquadraticity. In the following, we provide another definition

Definition 2.7. ^[39] If $\Psi$ is superquadratic, then $\Psi$ must fulfil condition (2.4).

$\forall$ ${{\tau}}_1, {{\tau}}_2 \geq 0$ and $0 < {{\ell}} < 1$.

Remark 2.8. $\Psi$ is referred to be subquadratic when symbol $\leq$ is inverted in (2.4). Condition (2.4) is obtained by setting $\mathfrak{n} = 2$ in the Jensen's inequality for superquadratic function.

Jensen's and $\mathbb{HH}$'s integral inequalities are the two major inequalities that make superquadraticity broader and more vast. Both of these are the most significant and most used findings pertaining to superquadratic functions.

Theorem 2.9. ^[40] For a superquadratic function $\Psi$, the below mentioned inequality

holds $\forall\; {{\tau}}_i \geq 0$ and $0\leq{{\ell}}_i\leq1$, where $\overline{{{\tau}}}$ = $\sum^{\mathfrak{n}}_{i = 1}{{\ell}}_{i}{{\tau}}_{i}$ and $\sum^{\mathfrak{n}}_{i = 1}$${{\ell}}_{i} = 1$.

In ^[49], Banić et al. developed $\mathbb{HH}$-type inequalities in the realm of superquadraticity.

Theorem 2.10. If $\Psi\colon I\subset[0, \infty[\longrightarrow\mathbb{R}$ is assumed to be a superquadratic on I = $[{{\mathrm{m}_{o}}}, {\mathrm{n}_{o}}]$, where $0\leq{{\mathrm{m}_{o}}} < {\mathrm{n}_{o}}$, then

Lemma 2.11. ^[39] If function $\Psi^{'}$ is convex and $\Psi(0) = \Psi^{'}(0) = 0$, then $\Psi$ is superquadratic. The converse of the statement is not true.

Theorem 2.12. ^[41] Let $\Psi\colon I\subset[0, \infty[\longrightarrow\mathbb{R}$ be a superquadratic and integrable on I = $[{\mathrm{m}_{o}}, {\mathrm{n}_{o}}]$ with $0\leq{\mathrm{m}_{o}} < {\mathrm{n}_{o}}$, then

Here, $\mathfrak{J}^{{{{\ell}}}}_{{{\mathrm{m}_{o}}}^{+}}$ and $\mathfrak{J}^{{{{\ell}}}}_{{\mathrm{n}_{o}}^{-}}$ are defined by Definition 2.3.

Definition 2.13. ^[42] If $\mathrm{h}$: $\mathfrak{J}\longrightarrow\mathbb{R}$ is a non-negative function, then $\Psi$: $\mathbf{\mathfrak{I}}\longrightarrow\mathbb{R}$ is $h$-superquadratic on $\mathbf{\mathfrak{I}}$, provided it satisfies the inequality (2.8).

$\forall\; {{\ell}}\in (0, 1)$ and ${\mathrm{m}_{o}}, {\mathrm{n}_{o}}\in \mathbf{\mathfrak{I}}$. It is to be noted that $\mathrm{h}({{\ell}})$ and $\mathrm{h}(1-{{\ell}})$ are not zero simultaneously.

Remark 2.14. If inequality (2.8) is inverted, then $\Psi$ is said to be h-subquadratic.

Theorem 2.15. ^[42] If the nonnegative function $\Psi$ is $h$-superquadratic on $\mathbf{\mathfrak{I}}$, then the inequality (2.9) holds

$\forall\; {{\tau}}_i \geq 0$, $0\leq{{\ell}}_i\leq1$, where

$sum^{\mathfrak{n}}_{i = 1}$${{\ell}}_{i} = 1$ and $\overline{{{\tau}}}$ = $\sum^{\mathfrak{n}}_{i = 1}{{\ell}}_{i}{{\tau}}_{i}$.

Remark 2.16. In case $h$ is a non-negative submultiplicative function and $\Psi$ is $h$-subquadratic, then the inequality symbols reverses in (2.9).

Definition 2.17. A mapping $\chi:\Pi\rightarrow \mathbb{R}$ stated on the space $(\Pi, \textbf{A}, \mathrm{P})$ is termed a random variable, provided it is $\textbf{A}$-measurable. The space $(\Pi, \mathrm{A}, \mathrm{P})$ is called probability space, in which $\Pi$ is the set of all possible outcomes, $\textbf{A}$ is a collection of events in other words subsets of $\Pi$, and $\mathrm{P}$ is a probability measure that gives these occurrences probabilities.

Example 2.18. Think of a coin toss where $\Pi = \{H (Head), T (Tail)\}$, $"\textbf{A}"$ contains whole subsets of $\Pi$ and $"\mathrm{P}"$ gives each possible event a probability of $\frac{1}{2}$. Then a random variable $"\chi"$ would be defined as $\chi(T) = 1$ and $\chi(H) = 0.$

Definition 2.19. A mapping $\chi:I\times\Pi\rightarrow \mathbb{R}$ is termed as a stochastic process provided, $\forall$ ${{\tau}}\in I$, $\chi({{\tau}}, \cdot)$ is a random variable.

Example 2.20. Consider spending a week monitoring the temperature at noon every day. In this case, $\Pi$ may stand for all potential weather scenarios, $I = \{1, 2, ..., 7\}$ denotes each day of the week, and $\chi({{\tau}}, \omega)$ provides the temperature on day ${{\tau}}$ under the condition $\omega$. For each fixed day ${{\tau}}$, $\chi({{\tau}}, \cdot)$ as a random variable, represents how the temperature changes with various meteorological circumstances. $\chi({{\tau}}, \cdot)$ represents the stochastic process that describes the temperature over time as ${{\tau}}$ varies.

Definition 2.21. A stochastic process $\chi:I\times\Pi\rightarrow \mathbb{R}$ is said to possess continuity over $I\subset\mathbb{R}$, if $\forall$ ${{\tau}}\in I$, we have

where $\mathrm{P}-\lim$ displays the limit in the probability space.

Definition 2.22. A stochastic process $\chi:I\times\Pi\rightarrow \mathbb{R}$ is said to possess mean-square continuity over $I\subset\mathbb{R}$, if $\forall$ ${{\tau}}\in I$, we have

where $E\big[\chi({{\tau}}, \cdot)\big]$ represents expectation of the random variable.

Remark 2.23. Mean-square continuity clearly indicates probability continuity, while the opposite conclusion is false.

Definition 2.24. A stochastic process $\chi:I\times\Pi\rightarrow \mathbb{R}$ is said to possess mean-square differentiability over $I\subset\mathbb{R}$ at $\mathrm{k}$ if $\exists$ a random variable ${\chi}^{\prime}:I\times\Pi\rightarrow \mathbb{R}$, such that

Definition 2.25. A stochastic process $\chi:I\times\Pi\rightarrow \mathbb{R}$ is said to possess mean-square integrability over $I\subset\mathbb{R}$, if $\forall$ ${{\tau}}\in I$ with $E\big[\chi({{\tau}}, \cdot)\big] < \infty$, $\big[{{\tau}}_{1}, {{\tau}}_{2}\big]\subseteq I$, ${{\tau}}_{1} = \mathfrak{k}_{0} < \mathfrak{k}_{1} < \mathfrak{k}_{2}... < \mathfrak{k}_{n} = {{\tau}}_{2}$, partitions the interval $\big[{{\tau}}_{1}, {{\tau}}_{2}\big]$, and ${{\tau}}_{i} \in \big[\mathfrak{k}_{i-1}, \mathfrak{k}_{i}\big], \forall i = 1, ..., n$, the subsequent condition holds

it implies that $S:I\times\Pi\rightarrow \mathbb{R}$ is a mean-square integral of the stochastic process $\chi:I\times\Pi\rightarrow \mathbb{R}$ and it can be written as

Remark 2.26. It is sufficient to presuppose the mean-square continuity of the stochastic process $\chi$ in order for the mean-square integral to exist.

Remark 2.27. Monotonicity of the mean-square-integral

It claims that if $\chi({{\tau}}, \cdot)\leq S({{\tau}}, \cdot)$, $\forall$ ${{\tau}}\in\big[{{\tau}}_{1}, {{\tau}}_{2}\big]$, then

Lemma 2.28. ^[23] If a stochastic process $\chi:I\times\Pi\rightarrow \mathbb{R}$ is given by $\chi({{\tau}}, \cdot) = \mathrm{M}(\cdot){{\tau}}+\mathrm{N}(\cdot)$, where $\mathrm{M}, \mathrm{N}:\Pi\rightarrow \mathbb{R}$ such that $E(\mathrm{M}^2), E(\mathrm{N}^2) < \infty$ and $\big[{{\tau}}_{1}, {{\tau}}_{2}\big]\subset I$, then

where $\mathrm{M}$ and $\mathrm{N}$ are random variables.

Definition 2.29. ^[23] A stochastic process $\chi:I\times\Pi\rightarrow \mathbb{R}$ is said to be convex over $I\subset\mathbb{R}$, $\forall {\ell} \in [0, 1]$, if

holds $\forall \mathfrak{m}_{o}, \mathfrak{n}_{o}\in I$.

If ${\ell} = \frac{1}{2}$ is picked in (2.13), then the process $\chi$ is termed the Jensen convex. If the process $\chi$ is convex, then $(-\chi)$ is termed the concave stochastic process. For more intriguing properties, one can see ^{[21, 22]}.

Lemma 2.30. ^[22] For any ${{\tau}}_{1}, {{\tau}}_{2}\in I_{o}$ such that ${{\tau}}_{1} < {{\tau}}_{2}$, then the subsequent inequalities

where $\chi^{\prime}_{-}$ and $\chi^{\prime}_{+}$ are the left and right derivatives of $\chi$.

Theorem 2.31. $\mathbb{HH}$ inequality for convex stochastic process:

This claims that if a convex stochastic process $\chi:I\times\Pi\rightarrow \mathbb{R}$ is possessing mean-square continuity and Jensen's convexity on I, then the subsequent inequality

holds $\forall$ ${{\tau}}_{1}, {{\tau}}_{2}\in I$

Definition 2.32. ^[35] Mean-square stochastic $\mathbb{R.L}$ fractional integrals:

If we have a stochastic process $\chi:I\times\Pi\rightarrow \mathbb{R}$ fulfilling the conditions given by Definitions 2.25, then mean-square stochastic $\mathbb{R.L}$ fractional integrals $I^{{\ell}}_{\mathfrak{m}_{o}^{+}}$ and $I^{{\ell}}_{\mathfrak{n}_{o}^{-}}$ of $\chi$ of order ${{\ell}} > 0$ are given by

and

3.   The superquadratic stochastic process and integral inequalities

In this part, we begin by presenting the definition of a superquadratic stochastic process, which is a generalization of convex stochastic process, so that the results developed from the superquadratic stochastic process are more refined compared to the convex stochastic process. On the basis of this definition, we explore its properties and formulate its integral inequalities.

Definition 3.1. A stochastic process $\chi:I\times\Pi\rightarrow \mathbb{R}$ is said to be superquadratic over $I\subset\mathbb{R}$, if

holds $\forall \; \mathfrak{m}_{o}, \mathfrak{n}_{o}\in I$, and ${\ell} \in [0, 1]$.

If ${\ell} = \frac{1}{2}$ is picked in (3.1), then the process $\chi$ is termed as Jensen-superquadratic. If process $\chi$ is superquadratic, then $-\chi$ is termed the subquadratic stochastic process.

Proposition 3.2. Let $\chi:I\times\Pi\rightarrow \mathbb{R}$ be a superquadratic stochastic process, then for $\mathrm{k}\in I_{o}$(Interior of I) and $\chi(0, \cdot) = 0$, there is, a random variable $\mathrm{A}:\Pi\rightarrow \mathbb{R}$, such that $\chi$ is supported at $\mathrm{k}$ by the process $\mathrm{A}(\cdot)({{\tau}}-\mathrm{k})+\chi(\mathrm{k}, \cdot)+\chi(|{{\tau}}-\mathrm{k}|, \cdot)$ that is $\forall {{\tau}} \in I$

Proof. We pick $\mathfrak{r}, \mathfrak{s}, \mathfrak{u}, \mathfrak{v}, \mathrm{k} \in I_{o}$ such that $\mathfrak{r} < \mathfrak{s} < \mathrm{k} < \mathfrak{u} < \mathfrak{v}$. First considering $\mathfrak{r} < \mathfrak{s} < \mathrm{k}$, we have

which is a convex combination of $\mathrm{k}$ and $\mathfrak{r}$. Thus, using the superquadraticity of $\chi$, we attain

after simple calculation, we achieve the following expression

taking limit $\mathfrak{s}\rightarrow {\mathrm{k}}^{-}$ on both sides of (3.5), we get

Similarly, for $\mathrm{k} < \mathfrak{u} < \mathfrak{v}$ and utilizing the superquadraticity of $\chi$, we get

taking limit $\mathfrak{u}\rightarrow {\mathrm{k}}^{+}$ on both sides of (3.7), we arrive at

From inequalities (3.6), (3.8), and utilization of Lemma 2.30, it implies that

Now, if $\mathrm{A}:\Pi\rightarrow \mathbb{R}$ is any random variable fulfilling the condition $\chi^{\prime}_{-}(\mathrm{k}, \cdot)\leq\mathrm{A}(\cdot)\leq\chi^{\prime}_{+}(\mathrm{k}, \cdot)$ and setting it into (3.9) as well as setting $\mathfrak{v} = {{\tau}}$, we obtain

Hence, the proof. □

Next, we provide the proof of an inequality of Jensen's type for superquadratic stochastic processes.

Theorem 3.3. Let $\chi:I\times\Pi\rightarrow \mathbb{R}$ be a superquadratic stochastic process, then $\forall \quad {{\tau}}_{1}, ..., {{\tau}}_{n}\in I, {\ell}_{1}, ..., {\ell}_{\mathfrak{n}} > 0$ such that $\sum^{\mathfrak{n}}_{i = 1}{\ell}_{i} = 1$ and $\bar{{{\tau}}} = \sum^{\mathfrak{n}}_{i = 1}{\ell}_{i}{{\tau}}_{i}$, the inequality

holds.

Proof. Let us take ${{\tau}}_{i}\in I, {\ell}_{i} > 0$ such that $\sum^{\mathfrak{n}}_{i = 1}{\ell}_{i} = 1$ and $\bar{{{\tau}}} = \sum^{\mathfrak{n}}_{i = 1}{\ell}_{i}{{\tau}}_{i}$. According to Proposition 3.2, we have a support

at $\bar{{{\tau}}}$. Then, for every $i\in\{1, ..., n\}$, one has

multiplying the inequality (3.13) by ${\ell}_{i}$ and then summing up to $\mathrm{n}$, we obtain

as we know that $\sum^{n}_{i = 1}{\ell}_{i}({{\tau}}_{i}-\bar{{{\tau}}}) = 0$ and $\sum^{n}_{i = 1}{\ell}_{i}\chi(\bar{{{\tau}}}, \cdot) = \chi(\bar{{{\tau}}}, \cdot) \sum^{n}_{i = 1}{\ell}_{i} = \chi(\bar{{{\tau}}}, \cdot)$ therefore (3.14) becomes

Hence, the proof. □

Next, we offer the $\mathbb{HH}$'s inequality for superquadratic stochastic processes.

Theorem 3.4. Let $\chi:I\times\Pi\rightarrow \mathbb{R}$ be a superquadratic and mean-square continuous stochastic process on $I$, then for every $\mathfrak{m}_{o}, \mathfrak{n}_{o} \in I$, we have

Proof. Since $\chi$ is a mean-square continuous superquadratic stochastic process, Proposition 3.2, $\chi$ has a supporting process, $\forall$ $\mathrm{k}\in I_{o}$. Let us pick $\mathrm{k} = \frac{{\mathfrak{m}_{o}}+{\mathfrak{n}_{o}}}{2}$ in a support, so we have

Integrating over $[\mathfrak{m}_{o}, \mathfrak{n}_{o}]$ and then using Lemma 2.28, we attain

Next, utilizing Definition 3.1 and setting ${\ell}\mathfrak{m}_{o}+(1-{\ell})\mathfrak{n}_{o} = {{\tau}}$ in (3.1), we get

integrating over $[\mathfrak{m}_{o}, \mathfrak{n}_{o}]$ and again using Lemma 2.28, we attain

this implies that

merging inequalities (3.18) and (3.21), we get the required result. □

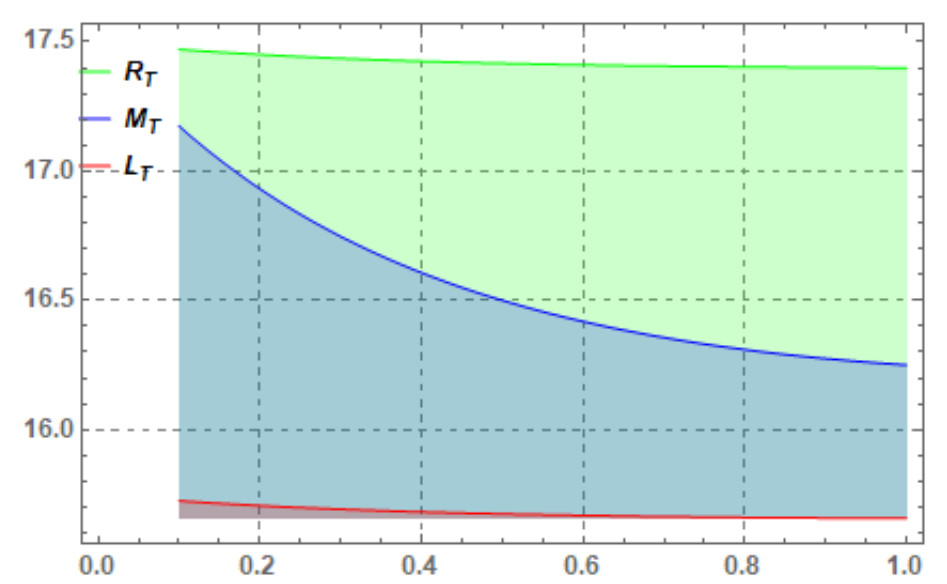
Example 3.5. Since the function $\chi({{\tau}}, \cdot) = {{\tau}}^3$ is a superquadratic stochastic processes on $I = [2, \infty)$, then we have Figure 1 for the right $(R_T)$, left $(L_T)$, and middle $(M_T)$ terms for Theorem 3.4 and confirm the veracity of Theorem 3.4.

4.   Stochastic fractional integral inequalities of $\mathbb{HH}$-type

In this section, we provide the stochastic fractional integral inequalities of $\mathbb{HH}$-type using the stochastic $\mathbb{R.L}$ fractional integral operators mentioned in Definition 2.32.

Theorem 4.1. Let $\chi:I\times\Pi\rightarrow \mathbb{R}$ be a superquadratic and mean-square continuous stochastic process on $I$, then

holds $\mathfrak{m}_{o}, \mathfrak{n}_{o} \in I$, and ${{{\ell}}} > 0$.

Proof. Since $\chi$ is a mean-square continuous superquadratic stochastic process, Proposition 3.2 $\chi$ has a supporting process, $\forall$ $\mathrm{k}\in I_{o}$. Let us pick $\mathrm{k} = \frac{{\mathfrak{m}_{o}}+{\mathfrak{n}_{o}}}{2}$ in a support, therefore, we have

Thus, we can obtain that

Finally, we attain

inequality (4.4) represents the first part of the proof.

Next, utilizing Definition 3.1 and setting ${\ell}\mathfrak{m}_{o}+(1-{\ell})\mathfrak{n}_{o} = {{\tau}}$ in (3.1), we get

Therefore, we have

this implies that

merging inequalities (4.4) and (4.7), we get the required result. □

Remark 4.2. If ${{{\ell}}} = 1$ is picked in (4.1), then we get the result of Theorem 3.4, which is known as $\mathbb{HH}$'s inequality for superquadratic stochastic processes.

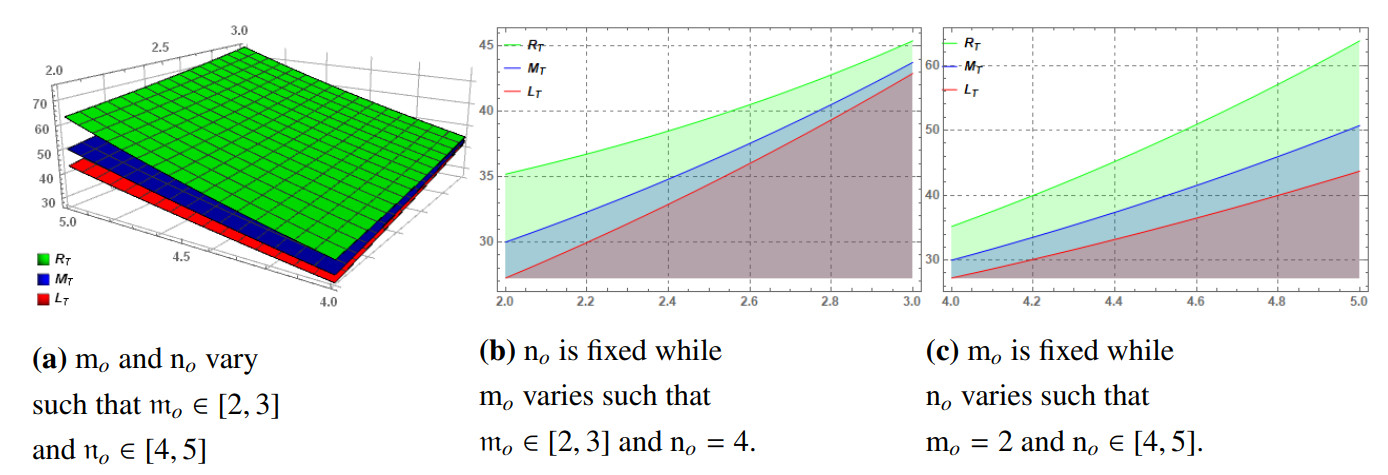
Example 4.3. Since the function $\chi({{\tau}}, \cdot) = {{\tau}}^3$ is a superquadratic stochastic processes on $I = [2, \infty)$, then we have Figure 2 for the $R_T$, $L_T$, and $M_T$ terms for Theorem 4.1 and confirms the veracity of Theorem 4.1. The values for the $R_T$, $L_T$, and $M_T$ terms are as follows:

5.   Applications in the information theory

A crucial aspect of many fields, including information theory, machine learning, and statistics, is the discrimination between two probability distributions. Divergence measures are essentially numbers that may be used to evaluate the "distance" or difference between two probability distributions. In 1991, Lin ^[53] introduced a new class of divergence measures based on Shannon entropy, a concept that forms the very foundation of information theory and quantifies uncertainty or information content in a probability distribution. The Lin divergence provided a systematic way of assessing the discrepancy between two distributions based on information-theoretic principles. Later, Shioya and Da-te in 1995 generalized the method developed by Lin ^[54]. They developed a generalized measure called HH $\Psi$-divergence. They derived a divergence measure that used H.H inequality as the base result from mathematics to work with convex functions. Thus, it became more general, applicable, and opened avenues of greater flexibility to work in probability distribution comparisons for more novel insights and applications.

Below, we provide only the definitions that are essential for the proof of our results.

Definition 5.1. Csiszár $\Psi$-divergence ^[55]:

where $\Psi$ is a convex function defined on $(0, +\infty)$, $\Omega$ is a nonempty set, $\mu$ is a $\sigma$-finite measure, and $\mathrm{\textbf{P}}$ is the set of all probability densities on $\mu$ which is given by

Remark 5.2. Csiszár $\Psi$-divergence for strongly convex function and superquadratic function are obtained by taking function $\Psi$ as a strongly convex function and superquadratic function.

Definition 5.3. $\mathbb{HH}$ $\Psi$-divergence ^[56]:

Definition 5.4. $\mathbb{R.L}$ fractional $\mathbb{HH}$ $\Psi$-divergence ^[57]:

where the fractional operators involved in (5.2) are given by the Definition 2.3.

Remark 5.5. If ${\ell} = 1$ is set in (5.2), then we get (5.1).

Definition 5.6. $\mathbb{R.L}$ fractional $\mathbb{HH}$ $\Psi$-divergence ^[57]:

where the fractional operators involved in (5.3) are given by the Definition 2.3.

Definition 5.7. Stochastic divergence ^[58]:

For a convex stochastic process $\chi:I\times\Pi\rightarrow \mathbb{R}$ on $\mathrm{I}\subseteq (0, \infty)$ such that $\chi(1, .) = 0$, the stochastic divergence for $\mathfrak{p}, \mathfrak{q}\in \mathrm{\textbf{P}}$ is defined as

Remark 5.8. When the convex stochastic process is replaced by the superquadratic stochastic process in (5.4), we obtain stochastic divergence for the superquadratic stochastic process.

Definition 5.9. Stochastic $\mathbb{HH}$-divergence ^[58]:

For a convex stochastic process $\chi:I\times\Pi\rightarrow \mathbb{R}$ on $\mathrm{I}\subseteq (0, \infty)$, the stochastic $\mathbb{HH}$-divergence for $\mathfrak{p}, \mathfrak{q}\in \mathrm{\textbf{P}}$ is defined as

Remark 5.10. When the convex stochastic process is replaced by the superquadratic stochastic process in (5.5), we obtain stochastic $\mathbb{HH}$-divergence for the superquadratic stochastic process.

Definition 5.11. $\mathbb{R.L}$ fractional stochastic $\mathbb{HH}$-divergence ^[58]:

For a convex stochastic process $\chi:I\times\Pi\rightarrow \mathbb{R}$ on $\mathrm{I}\subseteq (0, \infty)$, the $\mathbb{R.L}$ fractional $\mathbb{HH}$-divergence for $\mathfrak{p}, \mathfrak{q}\in \mathrm{\textbf{P}}$ of order ${\ell} > 0$ is defined as

Here, the fractional operators involved in (5.6) are given by Definition 2.32.

Remark 5.12. When the convex stochastic process is replaced by the superquadratic stochastic process in (5.6), we obtain $\mathbb{R.L}$ fractional stochastic $\mathbb{HH}$-divergence for the superquadratic stochastic process.

In the following, we offer the proofs of the results related to stochastic $\mathbb{HH}$-divergence and $\mathbb{R.L}$ fractional stochastic $\mathbb{HH}$-divergence for superquadratic stochastic processes.

Theorem 5.13. Let $\chi:I\times\Pi\rightarrow \mathbb{R}$ on $\mathrm{I}\subseteq (0, \infty)$ be a superquadratic stochastic process and $\chi(1, .) = 0$, then

$\forall$ $\mathfrak{p}, \mathfrak{q}\in \mathrm{\textbf{P}}$, where

and

Proof. Consider the $\mathbb{HH}$'s inequalities for superquadratic stochastic processes, from Theorem 3.4:

Now, setting $\mathrm{m}_{o} = 1$ and $\mathrm{n}_{o} = \frac{\mathfrak{p}({{\tau}})}{\mathfrak{q}({{\tau}})}$ in (5.8), we obtain

since $\chi(1, .) = 0$, we have

multiplying (5.9), both sides by $\mathfrak{q}({{\tau}})\geq0$, where ${{\tau}}\in \Omega$ and then integrating the result on $\Omega$, we obtain

Employing the definitions of stochastic divergence and stochastic $\mathbb{HH}$-divergence, we obtain the required result. □

Theorem 5.14. Let $\chi:I\times\Pi\rightarrow \mathbb{R}$ on $\mathrm{I}\subseteq (0, \infty)$ be a superquadratic stochastic process and $\chi(1, .) = 0$, then

$\forall$ $\mathfrak{p}, \mathfrak{q}\in \mathrm{\textbf{P}}$ and ${\ell} > 0$, where

and

Proof. Consider the fractional $\mathbb{HH}$'s inequalities via $\mathbb{R.L}$ integral operators of order ${\ell} > 0$ for superquadratic stochastic processes, from Theorem 4.1:

Now, setting $\mathrm{m}_{o} = 1$ and $\mathrm{n}_{o} = \frac{\mathfrak{p}({{\tau}})}{\mathfrak{q}({{\tau}})}$ in (5.12), we obtain

since $\chi(1, .) = 0$, we have

multiplying (5.13) both sides by $\mathfrak{q}({{\tau}})\geq0$, where ${{\tau}}\in \Omega$ and then integrating the result on $\Omega$, we obtain

Employing the definitions of Stochastic divergence, Stochastic $\mathbb{HH}$-divergence and $\mathbb{R.L}$ fractional stochastic $\mathbb{HH}$-divergence, we obtain the required result. □

Remark 5.15. If we set ${\ell} = 1$ in Theorem 5.14, we get the result of Theorem 5.13.

6.   Conclusions

In this paper, we introduced and formalized the concept of superquadratic stochastic processes as a generalization of convexity, leading to refined inequalities in the stochastic setting. By leveraging the properties of superquadraticity, we established Jensen's and $\mathbb{HH}$ type inequalities for these processes. Furthermore, we extended these inequalities to their fractional versions using mean-square stochastic $\mathbb{R.L}$ fractional integrals. The theoretical results were validated through graphical representations, which provided insights into the behavior of these inequalities under various stochastic conditions. Additionally, we demonstrated the relevance of our findings in information theory by deriving novel stochastic divergence measures. These results offer new perspectives on the interplay between superquadraticity, stochastic processes, and fractional calculus. Future research could explore further generalizations, such as extending these inequalities to other fractional operators, incorporating different stochastic integral definitions, and investigating applications in machine learning and financial mathematics.

Author contributions

Mohsen Ayyash: Conceptualization, investigation, supervision; Dawood Khan: Formal analysis, writing-original draft & editing, methodology; Saad Ihsan Butt: Software, writing-review, supervision; Youngsoo Seol: Formal analysis, supervision, funding acquisition. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This study is funded by a research grant from Dong-A University.

Conflict of interest

All authors declare no conflict of interest in this paper.