Airplane designing using Quadratic Trigonometric B-spline with shape parameters

Abdul Majeed; Muhammad Abbas; Amna Abdul Sittar; Md Yushalify Misro; Mohsin Kamran; Abdul Majeed; Muhammad Abbas; Amna Abdul Sittar; Md Yushalify Misro; Mohsin Kamran

doi:10.3934/math.2021445

AIMS Mathematics

2021, Volume 6, Issue 7: 7669-7683. doi: 10.3934/math.2021445

Previous Article Next Article

Research article Special Issues

Airplane designing using Quadratic Trigonometric B-spline with shape parameters

1.
Department of Mathematics, Division of Science and Technology, University of Education, 54770 Lahore, Pakistan
2.
Department of Mathematics, University of Sargodha, 40100 Sargodha, Pakistan
3.
School of Mathematical Sciences, Universiti Sains Malaysia, 11800 Penang, Malaysia

Received: 23 January 2021 Accepted: 08 April 2021 Published: 12 May 2021
MSC : 65D10, 65D17, 65D18, 68U07

The B-spline curves have been grasped tremendous achievements inside the widely identified field of Computer Aided Geometric Design (CAGD). In CAGD, spline functions have been used for the designing of various objects. In this paper, new Quadratic Trigonometric B-spline (QTBS) functions with two shape parameters are introduced. The proposed QTBS functions inherit the basic properties of classical B-spline and have been proved in this paper. The proposed scheme associated with two shape parameters where the classical B-spline functions do not have. The QTBS has been used for designing of different parts of airplane like winglet, airfoil, turbo-machinery blades and vertical stabilizer. The designed part can be controlled or changed using free parameters. The effect of shape parameters is also expressed.

Keywords:

Quadratic Trigonometric B-spline functions,
shape parameters,
airplane parts,
uniform knots,
curve designing,
open curves,
closed curves

Citation: Abdul Majeed, Muhammad Abbas, Amna Abdul Sittar, Md Yushalify Misro, Mohsin Kamran. Airplane designing using Quadratic Trigonometric B-spline with shape parameters[J]. AIMS Mathematics, 2021, 6(7): 7669-7683. doi: 10.3934/math.2021445

Related Papers:

[1]	Tian Xu, Jin-E Zhang . Intermittent control for stabilization of uncertain nonlinear systems via event-triggered mechanism. AIMS Mathematics, 2024, 9(10): 28487-28507. doi: 10.3934/math.20241382
[2]	Tao Xie, Xing Xiong . Finite-time synchronization of fractional-order heterogeneous dynamical networks with impulsive interference via aperiodical intermittent control. AIMS Mathematics, 2025, 10(3): 6291-6317. doi: 10.3934/math.2025287
[3]	Siyue Yao, Jin-E Zhang . Exponential input-to-state stability of nonlinear systems under impulsive disturbance via aperiodic intermittent control. AIMS Mathematics, 2025, 10(5): 10787-10805. doi: 10.3934/math.2025490
[4]	Huiling Li, Jin-E Zhang, Ailong Wu . Finite-time stabilization of nonlinear systems with partially known states via aperiodic intermittent control and event-triggered impulsive control. AIMS Mathematics, 2025, 10(2): 3269-3290. doi: 10.3934/math.2025152
[5]	Linni Li, Jin-E Zhang . Input-to-state stability of nonlinear systems with delayed impulse based on event-triggered impulse control. AIMS Mathematics, 2024, 9(10): 26446-26461. doi: 10.3934/math.20241287
[6]	Zhaohui Chen, Jie Tan, Yong He, Zhong Cao . Decentralized observer-based event-triggered control for an interconnected fractional-order system with stochastic Cyber-attacks. AIMS Mathematics, 2024, 9(1): 1861-1876. doi: 10.3934/math.2024091
[7]	Yidan Wang, Li Xiao, Yanfeng Guo . Finite-time stability of singular switched systems with a time-varying delay based on an event-triggered mechanism. AIMS Mathematics, 2023, 8(1): 1901-1924. doi: 10.3934/math.2023098
[8]	Jiaqi Liang, Zhanheng Chen, Zhiyong Yu, Haijun Jiang . Fixed-time consensus of second-order multi-agent systems based on event-triggered mechanism under DoS attacks. AIMS Mathematics, 2025, 10(1): 1501-1528. doi: 10.3934/math.2025070
[9]	Zuo Wang, Hong Xue, Yingnan Pan, Hongjing Liang . Adaptive neural networks event-triggered fault-tolerant consensus control for a class of nonlinear multi-agent systems. AIMS Mathematics, 2020, 5(3): 2780-2800. doi: 10.3934/math.2020179
[10]	Biwen Li, Yujie Liu . Quasi-synchronization of nonlinear systems with parameter mismatch and time-varying delays via event-triggered impulsive control. AIMS Mathematics, 2025, 10(2): 3759-3778. doi: 10.3934/math.2025174

Abstract

1. Introduction

The surface theory is an indispensable research topic for scientists in the fields of differential geometry, physics, engineering, and designation. One type of well-known surfaces is the ruled surfaces which are obtained by the continuous movement of a line along the curve ^[1,2]. Various approaches have been put forward on ruled surfaces considering the characterizations, geometric and algebraic properties of ruled the surfaces. Ruled surfaces have applications in a number of domains including geometric modeling ^[5] or computer aided geometric designing ^[3,4]. Further, the technical advantages of ruled surfaces in the realization of free-form architecture and complex shapes can be seen in ^[6]. Such as surfaces, the theory of curves is also an important research topic regarding various disciplines. A lot of investigation has been done on the motion, evolution, and integrability of curves. Moreover, the geometric characterizations for these integrable curves and the evolution of inelastic plane curves have been studied widely ^{[7,8,9,10,11]}. Hasimoto ^[12] handled the motion of the vortex filament equation has been studied by and the time evolution of the curves has been obtained. It also has been proved that the vortex filament equation (smoke ring) is equal to the nonlinear Schrödinger equation. The motion of the curves is a predecessor part of soliton theory. The geometric applications of Bäcklund and Darboux transformations between curves have been discussed in soliton theory ^[12,13,14]. Many researchers have examined the surfaces obtained from these curves. For instance, the evolution of translation surfaces has been studied by ^[15]. Additionally, by considering the inextensible flows of curves, the developable surfaces and tangent developable surfaces have been considered in ^{[16,17,18,19]} and the evolution of special ruled surfaces according to the Serret-Frenet frame has been clarified in ^[20]. On the other hand, the Serret-Frenet frames are inadequate for studying analytic space curves of which curvatures have discrete zero points since the principal normal and binormal vectors may be discontinuous at zero points of the curvature. For the solution of this problem, Sasai ^[21] has introduced an orthogonal frame and obtained a formula, which corresponds to the Frenet-Serret equation. Recently, in Minkowski 3-space, the modified orthogonal frame with non-zero curvature and torsion of a space curve has been described by Bukcu and Karacan ^[22]. Then, using this the modified orthogonal frame, spherical curves, Mannheim curves and some special curves have been reconsidered ^[23,24,25]. In the light of recent events given above, the aim of this study is to study the evolution of analytic space curve according to the modified orthogonal frame and the geometric properties of special ruled surfaces generated by the motion of these curves.

2. Preliminaries

In Euclidean 3-space, Euclidean inner product is given by $< , > = dx_1^2 + dx_2^2 + dx_3^2$ where $x = \left({{x_1}, {x_2}, {x_3}} \right) \in {E^3}$ . The norm of a vector $x \in {E^3}$ is $\left\| x \right\| = \sqrt {\left| { < x, x > } \right|}$ . For any $\alpha$ curve, if $\left\| {\alpha '(s)} \right\| = 1$ , then $\alpha$ curve is unit speed curve in Euclidean space. The most well-known and used Frenet frame on a curve plays an important role in differential geometry. Let $\alpha$ be a space curve with respect to the arc-length $s$ in Euclidean 3-space ${E^3}$ . $t$ , $n$ and $b$ are tangent, principal normal and binormal unit vectors at each point $\alpha (s)$ of a curve $\alpha$ , respectively. Then there exists an orthogonal frame $\left\{ {t, n, b} \right\}$ which satisfies the Frenet-Serret equation

$\begin{equation} \begin{array}{l} t' = \kappa n, \\ n' = - \kappa t + \tau b, \\ b' = - \tau n \end{array} \end{equation}$

(2.1)

where $\kappa$ is the curvature, $\tau$ is the torsion.

The fundamental theorem of regular curves states that if $\kappa > 0$ and $\tau$ are differentiable functions then there exists a unit speed curve whose curvature and torsion are $\kappa$ and $\tau$ , respectively ^[1]. However, the principal normal and binormal vectors are discontinuous at zero points of the curvature in general and the curvature is not always differentiable even if the curve is analytic. In that case, the formulation of the Frenet frame of a space curve generally established causes ambiguity for an analytical space curve at a point where the curvature vanishes, see Example 2.1.

This problem was considered by Hord ^[26] and Sasai ^[21,27] for analytic space curves of which the curvatures have discrete zero points. With a simple but convenient approach, an orthogonal frame was introduced by Sasai ^[21]. Although this modified orthogonal frame seems like a Frenet frame with scaled normal and binormal vectors, it allows to use a new formula corresponding to the Frenet-Serret equation for the aforementioned case and is also useful for investigating analytic curves with singularities.

Let $\alpha$ be an analytic curve of which curvature has discrete zero points in Euclidean 3-space. Under the assumption $\kappa \left(s \right)$ of $\alpha$ is not identically zero, the elements of modified orthogonal frame are given by

$T = \frac{{d\alpha }}{{ds}}, \quad N = \frac{{dT}}{{ds}}, \quad B = T \wedge N$

where $s$ is the arc-length parameter and $T \wedge N$ is the vector product of $T$ and $N$ .

The relations between the Frenet frame $\left\{ {t, n, b} \right\}$ and modified orthogonal frame $\left\{ {T, N, B} \right\}$ at non-zero points of $\kappa$ are

$T = t, \quad N = \kappa n, \quad B = \kappa b.$

In the course of time, this orthogonal frame is called the modified orthogonal frame ^[22]. The modified orthogonal frame $\left\{ {T, N, B} \right\}$ satisfies

$\left\langle {T, T} \right\rangle = 1, {\rm{ }}\left\langle {N, N} \right\rangle = \left\langle {B, B} \right\rangle = {\kappa ^2}, {\rm{ }}\left\langle {T, N} \right\rangle = \left\langle {T, B} \right\rangle = \left\langle {N, B} \right\rangle = 0.$

such that $\left\langle, \right\rangle$ is the Euclidean inner product. From these equations, the differentiation formula for the modified orthogonal frame $\left\{ {T, N, B} \right\}$ is given by

$\begin{equation} \begin{array}{l} T'\left( s \right) = N\left( s \right), \\ N'\left( s \right) = - {\kappa ^2}T\left( s \right) + \frac{{{\kappa _s}}}{\kappa }N\left( s \right) + \tau B\left( s \right), \\ B'\left( s \right) = - \tau N\left( s \right) + \frac{{{\kappa _s}}}{\kappa }B\left( s \right), \end{array} \end{equation}$

(2.2)

where ${\kappa _s}$ denotes the differentiation with respect to $s$ and $\tau = \frac{{\det \left({\alpha ', \alpha '', \alpha '''} \right)}}{{{\kappa ^2}}}$ is the torsion of $\alpha$ . Here, the essential quantities ${\kappa ^2}$ and $\tau$ are analytic in ^[21,22].

Example 2.1. Let us consider a curve given by the parametric equation

$\alpha \left( s \right) = \left( {\frac{1}{{\sqrt 2 }}\int\limits_0^s {\cos \left( {\frac{{\pi {t^2}}}{2}} \right)dt} , \frac{1}{{\sqrt 2 }}\int\limits_0^s {\sin \left( {\frac{{\pi {t^2}}}{2}} \right)dt} , \frac{s}{{\sqrt 2 }}} \right)$

which is a helical curve over clothoid (Cornu spiral or Euler spiral) ^[2] and has various applications in real life such as the highway, railway route design or roller coasters, etc. Here the components $\int\limits_0^s {\cos \left({\frac{{\pi {t^2}}}{2}} \right)dt}$ and $\int\limits_0^s {\sin \left({\frac{{\pi {t^2}}}{2}} \right)dt}$ are called Fresnel integrals. The elements of the Frenet trihedron of the curve $\alpha$ are obtained as

$t\left( s \right) = \left( {\frac{1}{{\sqrt 2 }}\cos \left( {\frac{{\pi {s^2}}}{2}} \right), \frac{1}{{\sqrt 2 }}\sin \left( {\frac{{\pi {s^2}}}{2}} \right), \frac{1}{{\sqrt 2 }}} \right),$

$n\left( s \right) = \left( { - \frac{s}{{\left| s \right|}}\sin \left( {\frac{{\pi {s^2}}}{2}} \right), \frac{s}{{\left| s \right|}}\cos \left( {\frac{{\pi {s^2}}}{2}} \right), 0} \right),$

$b\left( s \right) = \left( { - \frac{s}{{\sqrt 2 \left| s \right|}}\cos \left( {\frac{{\pi {s^2}}}{2}} \right), - \frac{s}{{\sqrt 2 \left| s \right|}}\sin \left( {\frac{{\pi {s^2}}}{2}} \right), \frac{s}{{\sqrt 2 \left| s \right|}}} \right)$

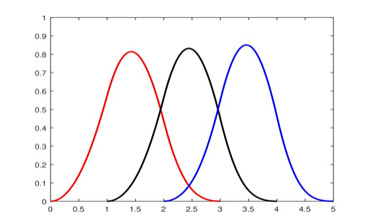
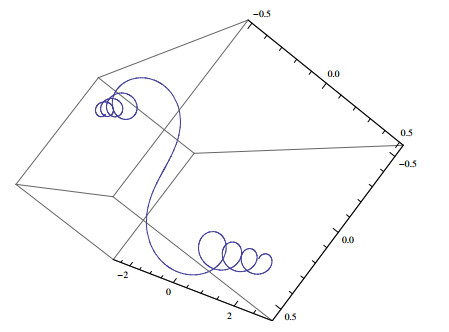
and the curvature is $\kappa \left(s \right) = \frac{{\pi \left| s \right|}}{{\sqrt 2 }}$ . Besides the curvature is not differentiable, the principal normal and binormal vectors are discontinuous at $s = 0$ since ${n_ + } \ne {n_ - }$ and ${b_ + } \ne {b_ - }$ for ${{n}_{+}} = \lim\limits_{s\to {{0}^{+}}}\lim\limits_\, n\left(s \right)$ , ${{n}_{-}} = \lim\limits_{s\to {{0}^{-}}}\lim\limits_\, n\left(s \right)$ and ${{b}_{+}} = \lim\limits_{s\to {{0}^{+}}}\, b\left(s \right)$ , ${{b}_{-}} = \lim\limits_{s\to {{0}^{-}}}\lim\limits_\, b\left(s \right)$ .

Whenever the curvature is considered as a signed quantity $\kappa \left(s \right) = \mp \frac{{\pi s}}{{\sqrt 2 }}$ , the curve forms a symmetrical double spiral, see Figure 1.

Figure 1. Helical Curve over Clothoid.

DownLoad: Full-Size Img PowerPoint

To prevent the occurrence of two reverse oriented principal normal vectors and binormal vectors, it is useful to refer to the modified orthogonal frame with unique elements

$T\left( s \right) = \left( \frac{1}{\sqrt{2}}\cos \left( \frac{\pi {{s}^{2}}}{2} \right), \frac{1}{\sqrt{2}}\sin \left( \frac{\pi {{s}^{2}}}{2} \right), \frac{1}{\sqrt{2}} \right),$

$N\left( s \right) = \left( -\frac{\pi s}{\sqrt{2}}\sin \left( \frac{\pi {{s}^{2}}}{2} \right), \frac{\pi s}{\sqrt{2}}\cos \left( \frac{\pi {{s}^{2}}}{2} \right), 0 \right),$

$B\left( s \right) = \left( -\frac{\pi s}{2}\cos \left( \frac{\pi {{s}^{2}}}{2} \right), -\frac{\pi s}{2}\sin \left( \frac{\pi {{s}^{2}}}{2} \right), \frac{\pi s}{2} \right),$

under the assumption that the curvature $\kappa \left(s \right)$ of $\alpha$ is not zero. Here the essential quantities are obtained as ${\kappa ^2} = \frac{{{\pi ^2}{s^2}}}{2}$ and $\tau \left(s \right) = \frac{\pi s}{\sqrt{2}}$ .

3. Evolution of space curve with modified orthogonal frame

A curve $\alpha$ in Euclidean 3-space is a vector-valued function $\alpha \left({s, t} \right) \in {E^3}$ where $s$ is the arc-length parameter and $t$ is the time parameter, then the equation of the vortex filament (smoke ring equation) is given by

$\begin{equation} {\alpha _t} = {\alpha _s} \wedge {\alpha _{ss}, } \end{equation}$

(3.1)

where the subscripts indicate the partial differential. Let $\alpha$ be an analytic curve with curvature having discrete zero points. To at non-zero points of the curve, the time evolution of the modified orthogonal frame $\left\{ {T, N, B} \right\}$ can be written in matrix form as follows:

$\begin{equation} {\left[ {\begin{array}{*{20}{c}} T\\ N\\ B \end{array}} \right]_t} = \left[ {\begin{array}{*{20}{c}} 0&\eta &\beta \\ { - \eta }&{\kappa {\kappa _t}}&\gamma \\ { - \beta }&{ - \gamma }&{\kappa {\kappa _t}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} T\\ N\\ B \end{array}} \right] \end{equation}$

(3.2)

where $\alpha$ , $\beta$ and $\gamma$ are smooth functions. By considering the curvature $\kappa$ of the curve $\alpha$ is not identically zero and using the equations ${T_{st}} = {T_{ts}}, {\rm{ }}{N_{st}} = {N_{ts}}, {\rm{ }}{B_{st}} = {B_{ts}}$ , we obtain

$\begin{equation} \begin{array}{l} {\eta _s} = \tau \beta - \frac{{{\kappa _s}}}{\kappa }\eta + \kappa {\kappa _t}, \\ {\beta _s} = \gamma - \tau \eta - \frac{{{\kappa _s}}}{\kappa }\beta , \\ {\gamma _s} = {\tau _t} - \beta . \end{array} \end{equation}$

(3.3)

We suppose that the velocity according to the curve $\alpha$ is given by

$\begin{equation} {\alpha _t} = \frac{{d\alpha }}{{dt}} = aT + bN + cB. \end{equation}$

(3.4)

From equation ${\alpha _{st}} = {\alpha _{ts}}$ , we find the following equations

$\begin{equation} \begin{array}{l} 0 = {a_s} - b{\kappa ^2}, \\ \eta = a + {b_s} + \frac{{{\kappa _s}}}{\kappa }b - \tau c, \\ \beta = \tau b + {c_s} + \frac{{{\kappa _s}}}{\kappa }c \end{array} \end{equation}$

(3.5)

where $a$ , $b$ and $c$ are the coefficients of the tangent, normal and binormal vectors of the velocity, respectively. Substituting the Eq. (3.5) into the second Equation of (3.3), we get

$\begin{equation} \gamma = {\left( {\tau b + {c_s} + \frac{{{\kappa _s}}}{\kappa }c} \right)_s} + \tau \left( {a + {b_s} + \frac{{{\kappa _s}}}{\kappa }b - \tau c} \right) + \frac{{{\kappa _s}}}{\kappa }\left( {\tau b + {c_s} + \frac{{{\kappa _s}}}{\kappa }c} \right). \end{equation}$

(3.6)

For a solution of smoke ring equation, the velocity vector is given by

$\begin{equation} {\alpha _t} = {\alpha _s} \wedge {\alpha _{ss}} = B. \end{equation}$

(3.7)

Thus, from the Eqs. (3.4) and (3.7), we get

$\begin{equation} a = 0, {\rm{ }}b = 0, {\rm{ }}c = 1. \end{equation}$

(3.8)

Substituting the Eq. (3.8) into the Eqs. (3.5) and (3.6), we get

$\begin{equation} \begin{array}{l} \eta = - \tau , \\ \beta = \frac{{{\kappa _s}}}{\kappa }, \\ \gamma = \frac{{{\kappa _{ss}}}}{\kappa } - {\tau ^2}. \end{array} \end{equation}$

(3.9)

Thus, according to the modified orthogonal frame, the Eq. (3.9) represents the time evolution of the curve and the motion of the curve

4. Properties of evolution of special ruled surfaces with modified orthogonal frame

In this section, we study the tangent, normal and binormal ruled surfaces using the modified orthogonal frame along an analytic space curve. The parametric equation of the ruled surface is given by

$X\left( {s, v} \right) = \alpha (s) + vl\left( s \right),$

where $\alpha (s)$ is called the base curve and $l(s)$ is the director curve. If the curves $\alpha (s)$ and $l(s)$ move with time $t$ , then the equation of the ruled surface is as follows

$\begin{equation} X\left( {s, v, t} \right) = \alpha (s, t) + vl\left( {s, t} \right). \end{equation}$

(4.1)

4.1. Tangent ruled surface

The ruled surface generated by the motion of the tangent vector $T$ of a curve $\alpha$ is called the tangent ruled surface and the equation of this surface is represented by

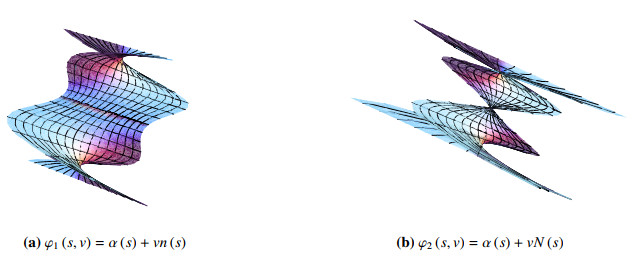
$\begin{equation} X\left( {s, v, t} \right) = \alpha (s, t) + vT\left( {s, t} \right). \end{equation}$

(4.2)

Example 4.1. Let us consider the helical curve over clothoid given in Example 2.1. Then the parametric equation of tangent ruled surface is

$\varphi \left( {s, v} \right) = \left( {\frac{1}{{\sqrt 2 }}\left( {\int\limits_0^s {\cos \left( {\frac{{\pi {t^2}}}{2}} \right)dt} + v\cos \left( {\frac{{\pi {s^2}}}{2}} \right)} \right), \frac{1}{{\sqrt 2 }}\left( {\int\limits_0^s {\sin \left( {\frac{{\pi {t^2}}}{2}} \right)dt + v\sin \left( {\frac{{\pi {s^2}}}{2}} \right)} } \right), \frac{{s + v}}{{\sqrt 2 }}} \right),$

see Figure 2.

Figure 2. Tangent Ruled Surface.

DownLoad: Full-Size Img PowerPoint

The partial differentiations of the equations of the tangent ruled surface are

$\begin{equation} \begin{array}{l} {X_s}\left( {s, v, t} \right) = T + vN, \\ {X_v}\left( {s, v, t} \right) = T, \end{array} \end{equation}$

(4.3)

By using the Eq. (4.3), we get the unit normal field of this surface as

$\begin{equation} U = \frac{{{X_s} \wedge {X_v}}}{{\left\| {{X_s} \wedge {X_v}} \right\|}} = \frac{{ - B}}{\kappa }. \end{equation}$

(4.4)

The first fundamental form of the tangent ruled surface in Euclidean space is given by

$I = \left\langle {dX, dX} \right\rangle = \left\langle {{X_s}ds + {X_v}dv, {X_s}ds + {X_v}dv} \right\rangle = Ed{s^2} + 2Fdsdv + Gd{v^2}$

where the coefficients of the first fundamental form are

$\begin{equation} \begin{array}{l} E = \left\langle {{X_s}, {X_s}} \right\rangle = 1 + v{\kappa ^2}, {\rm{ }}\\ {\rm{F}} = \left\langle {{X_s}, {X_v}} \right\rangle = 1, \\ {\rm{G}} = \left\langle {{X_v}, {X_v}} \right\rangle = 1. \end{array} \end{equation}$

(4.5)

From Eq. (4.3), the second derivatives are found and given as

$\begin{equation} \begin{array}{l} {X_{ss}}\left( {s, v, t} \right) = - v{\kappa ^2}T + \left( {1 + v\frac{{{\kappa _s}}}{\kappa }} \right)N + v\tau B, \\ {X_{sv}}\left( {s, v, t} \right) = N, \\ {X_{vv}}\left( {s, v, t} \right) = 0. \end{array} \end{equation}$

(4.6)

The second fundamental form of the normal surface is given by

$II = \left\langle {dX, dU} \right\rangle = - \left\langle {dX, dU} \right\rangle = \left\langle {{X_s}ds + {X_v}dv, {U_s}ds + {U_v}dv} \right\rangle = ed{s^2} + 2fdsdv + gd{t^2}$

where the coefficients of the second fundamental form are

$\begin{equation} \begin{array}{l} e = \left\langle {{X_{ss}}, U} \right\rangle = - v\tau \kappa , \\ f = \left\langle {{X_{sv}}, U} \right\rangle = 0, \\ g = \left\langle {{X_{vv}}, U} \right\rangle = 0. \end{array} \end{equation}$

(4.7)

Corollary 4.1. The Gaussian and mean the curvatures of the tangent ruled surface $X = X\left({s, v, t} \right)$ are

$\begin{equation} K = 0, \end{equation}$

(4.8)

$\begin{equation} H = \frac{{ - \tau }}{{2v\kappa }}, \end{equation}$

(4.9)

respectively.

Proof. From the Eqs. (4.5) and (4.7), we easily obtain the Gaussian curvature and the mean curvature, respectively, as follows

$K = \frac{{eg - {f^2}}}{{EG - {F^2}}} = 0,$

$H = \frac{1}{2}\frac{{Eg - 2Ff + Ge}}{{EG - {F^2}}} = \frac{{ - \tau }}{{2v\kappa }}$

From the Eqs. (4.8) and (4.9) the followings are obvious.

Corollary 4.2.

ⅰ. The tangent ruled surface is developable.

ⅱ. The tangent ruled surface is minimal surface if $\tau = 0$ .

4.2. Normal ruled surface

The ruled surface generated by the motion of the normal vector $N$ of the curve $\alpha$ is called the normal ruled surface and the equation of this surface is

$\begin{equation} X\left( {s, v, t} \right) = \alpha (s, t) + vN\left( {s, t} \right). \end{equation}$

(4.10)

Example 4.2. If we take the curve given in Example 2.1, then the parametric equations of normal ruled surfaces generated by normal vectors of Frenet frame and modified orthogonal frame are

${\varphi _1}\left( {s, v} \right) = \left( {\frac{1}{{\sqrt 2 }}\int\limits_0^s {\cos \left( {\frac{{\pi {t^2}}}{2}} \right)dt} - v\frac{s}{{\left| s \right|}}\sin \left( {\frac{{\pi {s^2}}}{2}} \right), \frac{1}{{\sqrt 2 }}\int\limits_0^s {\sin \left( {\frac{{\pi {t^2}}}{2}} \right)dt + v} \frac{s}{{\left| s \right|}}\cos \left( {\frac{{\pi {s^2}}}{2}} \right), \frac{s}{{\sqrt 2 }}} \right)$

and

${\varphi _2}\left( {s, v} \right) = \left( {\frac{1}{{\sqrt 2 }}\left( {\int\limits_0^s {\cos \left( {\frac{{\pi {t^2}}}{2}} \right)dt} - v\pi s\sin \left( {\frac{{\pi {s^2}}}{2}} \right)} \right), \frac{1}{{\sqrt 2 }}\left( {\int\limits_0^s {\sin \left( {\frac{{\pi {t^2}}}{2}} \right)dt + v} \pi s\cos \left( {\frac{{\pi {s^2}}}{2}} \right)} \right), \frac{s}{{\sqrt 2 }}} \right),$

respectively. The first normal ruled surface is generated by the normal vector of Frenet frame and it is discontinuous at $s = 0$ and the second one is generated by the normal vector of the modified orthogonal frame, see Figure 3.

Figure 3. Normal Ruled Surfaces.

DownLoad: Full-Size Img PowerPoint

The derivatives of the normal ruled surface with respect to $s$ and $v$ are

$\begin{equation} \begin{array}{l} {X_s}\left( {s, v, t} \right) = (1 - v{\kappa ^2})T + v\frac{{{\kappa _s}}}{\kappa }N + v\tau B, \\ {X_v}\left( {s, v, t} \right) = N, \end{array} \end{equation}$

(4.11)

respectively. Using Eq. (4.11), we get the unit normal field of this surface is found as

$\begin{equation} U = \frac{{{X_s} \wedge {X_v}}}{{\left\| {{X_s} \wedge {X_v}} \right\|}} = \frac{{ - v\tau T + (1 - v{\kappa ^2})B}}{{\sqrt {{{(1 - v{\kappa ^2})}^2}{\kappa ^2} + {{\left( {v\tau } \right)}^2}} }}. \end{equation}$

(4.12)

The first fundamental form of the normal ruled surface in Euclidean space is given by

$I = \left\langle {dX, dX} \right\rangle = \left\langle {{X_s}ds + {X_v}dv, {X_s}ds + {X_v}dv} \right\rangle = Ed{s^2} + 2Fdsdv + Gd{v^2}$

where the coefficients of the first fundamental form are

$\begin{equation} \begin{array}{l} E = \left\langle {{X_s}, {X_s}} \right\rangle = {\left( {1 - v{\kappa ^2}} \right)^2} + {v^2}{\kappa _s}^2 + {v^2}{\tau ^2}{\kappa ^2}, {\rm{ }}\\ {\rm{F}} = \left\langle {{X_s}, {X_v}} \right\rangle = v{\kappa _s}\kappa , \\ {\rm{G}} = \left\langle {{X_v}, {X_v}} \right\rangle = {\kappa ^2}. \end{array} \end{equation}$

(4.13)

From Eq. (4.11), the second derivative is found as

$\begin{equation} \begin{array}{l} {X_{ss}}\left( {s, v, t} \right) = - 3v\kappa {\kappa _s}T + \left( {1 - v{\kappa ^2} + v\frac{{{\kappa _{ss}}}}{\kappa } - v{\tau ^2}} \right)N + \left( {v{\tau _s} + 2v\tau \frac{{{\kappa _s}}}{\kappa }} \right)B, \\ {X_{sv}}\left( {s, v, t} \right) = - {\kappa ^2}T + \frac{{{\kappa _s}}}{\kappa }N + \tau B, \\ {X_{vv}}\left( {s, v, t} \right) = 0. \end{array} \end{equation}$

(4.14)

The second fundamental form of the normal surface is given by

$II = \left\langle {dX, dU} \right\rangle = - \left\langle {dX, dU} \right\rangle = \left\langle {{X_s}ds + {X_v}dv, {U_s}ds + {U_v}dv} \right\rangle = ed{s^2} + 2fdsdv + gd{t^2}$

where the coefficients of the second fundamental form are

$\begin{equation} \begin{array}{l} e = \left\langle {{X_{ss}}, U} \right\rangle = \frac{{v\kappa \left( {3v\tau {\kappa _s} + \left( {1 - v{\kappa ^2}} \right)\left( {\kappa {\tau _s} + 2\tau {\kappa _s}} \right)} \right)}}{{\sqrt {{{\left( {\kappa \left( {1 - v{\kappa ^2}} \right)} \right)}^2} + {{\left( {v\tau } \right)}^2}} }}, \\ f = \left\langle {{X_{sv}}, U} \right\rangle = \frac{{{\kappa ^2}\tau \left( {1 + v - v{\kappa ^2}} \right)}}{{\sqrt {{{\left( {\kappa \left( {1 - v{\kappa ^2}} \right)} \right)}^2} + {{\left( {v\tau } \right)}^2}} }}, \\ g = \left\langle {{X_{vv}}, U} \right\rangle = 0. \end{array} \end{equation}$

(4.15)

Corollary 4.3. The Gaussian and mean the curvatures of a normal ruled surface $X = X\left({s, v, t} \right)$ are

$\begin{equation} K = \frac{{ - {\tau ^2}{\kappa ^2}{{\left( {1 + v - v{\kappa ^2}} \right)}^2}}}{{\left( {{{\left( {\kappa \left( {1 - v{\kappa ^2}} \right)} \right)}^2} + {{\left( {v\tau } \right)}^2}} \right)\left( {{{\left( {1 - v{\kappa ^2}} \right)}^2} + {{\left( {v\tau \kappa } \right)}^2}} \right)}}, \end{equation}$

(4.16)

$\begin{equation} H = \frac{{v\kappa \left( {v\tau {\kappa _s} + \left( {1 - v{\kappa ^2}} \right)\kappa {\tau _s}} \right)}}{{2{{\left( {{{\left( {\kappa \left( {1 - v{\kappa ^2}} \right)} \right)}^2} + {{\left( {v\tau } \right)}^2}} \right)}^{\frac{1}{2}}}\left( {{{\left( {1 - v{\kappa ^2}} \right)}^2} + {{\left( {v\tau \kappa } \right)}^2}} \right)}}, \end{equation}$

(4.17)

respectively.

Proof. From the Eqs. (4.13) and (4.15), we easily obtain the Gaussian curvature and the mean curvature respectively as follows

$K = \frac{{eg - {f^2}}}{{EG - {F^2}}} = \frac{{ - {\tau ^2}{\kappa ^2}{{\left( {1 + v - v{\kappa ^2}} \right)}^2}}}{{\left( {{{\left( {\kappa \left( {1 - v{\kappa ^2}} \right)} \right)}^2} + {{\left( {v\tau } \right)}^2}} \right)\left( {{{\left( {1 - v{\kappa ^2}} \right)}^2} + {{\left( {v\tau \kappa } \right)}^2}} \right)}},$

$H = \frac{1}{2}\frac{{Eg - 2Ff + Ge}}{{EG - {F^2}}} = \frac{{v\kappa \left( {v\tau {\kappa _s} + \left( {1 - v{\kappa ^2}} \right)\kappa {\tau _s}} \right)}}{{2{{\left( {{{\left( {\kappa \left( {1 - v{\kappa ^2}} \right)} \right)}^2} + {{\left( {v\tau } \right)}^2}} \right)}^{\frac{1}{2}}}\left( {{{\left( {1 - v{\kappa ^2}} \right)}^2} + {{\left( {v\tau \kappa } \right)}^2}} \right)}}.$

From the Eqs. (4.16) and (4.17), the following result is obvious.

Corollary 4.4. The normal ruled surface is developable iff $\tau = 0$ and minimal iff $v\tau {\kappa _s} + \left({1 - v{\kappa ^2}} \right)\kappa {\tau _s} = 0.$

4.3. Binormal ruled surface

The ruled surface generated by the motion of the binormal vector $B$ of the curve $\alpha$ is called the binormal ruled surface and the equation of this surface is

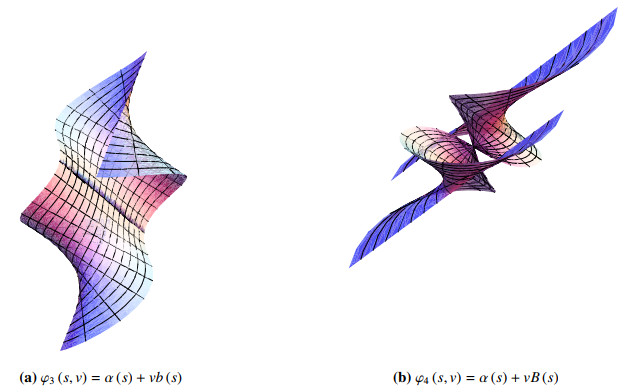
$\begin{equation} X\left( {s, v, t} \right) = \alpha (s, t) + vB\left( {s, t} \right). \end{equation}$

(4.18)

Example 4.3. The parametric equations of binormal ruled surfaces generated by binormal vectors of Frenet frame and modified orthogonal frame the curve given in Example 2.1 are

${\varphi _3}\left( {s, v} \right) = \left( {\frac{1}{{\sqrt 2 }}\left( {\int\limits_0^s {\cos \left( {\frac{{\pi {t^2}}}{2}} \right)dt} - v\frac{s}{{\left| s \right|}}\cos \left( {\frac{{\pi {s^2}}}{2}} \right)} \right), \frac{1}{{\sqrt 2 }}\left( {\int\limits_0^s {\sin \left( {\frac{{\pi {t^2}}}{2}} \right)dt - v} \frac{s}{{\left| s \right|}}\cos \left( {\frac{{\pi {s^2}}}{2}} \right)} \right), \frac{1}{{\sqrt 2 }}\left( {s + v\frac{s}{{\left| s \right|}}} \right)} \right)$

and

${\varphi _4}\left( {s, v} \right) = \left( {\frac{1}{{\sqrt 2 }}\int\limits_0^s {\cos \left( {\frac{{\pi {t^2}}}{2}} \right)dt} - v\frac{{\pi s}}{2}\cos \left( {\frac{{\pi {s^2}}}{2}} \right), \frac{1}{{\sqrt 2 }}\int\limits_0^s {\sin \left( {\frac{{\pi {t^2}}}{2}} \right)dt - v} \frac{{\pi s}}{2}\sin \left( {\frac{{\pi {s^2}}}{2}} \right), \frac{s}{{\sqrt 2 }}\left( {1 + \frac{{v\pi }}{{\sqrt 2 }}} \right)} \right),$

respectively. The first surface (generated by binormal vector of Frenet frame) is discontinuous at $s = 0$ and the second one is generated by binormal vector of modified orthogonal frame, see Figure 4.

Figure 4. Binormal Ruled Surfaces.

DownLoad: Full-Size Img PowerPoint

The tangent vectors for the binormal ruled surface are

$\begin{equation} \begin{array}{l} {X_s}\left( {s, v, t} \right) = T - v\tau N + v\frac{{{\kappa _s}}}{\kappa }B, \\ {X_v}\left( {s, v, t} \right) = B, \end{array} \end{equation}$

(4.19)

where the subscripts $s$ and $v$ represent partial derivatives of the binormal ruled surface. Using Eq. (4.19), we get the unit normal field of this surface is found as

$\begin{equation} U = \frac{{{X_s} \wedge {X_v}}}{{\left\| {{X_s} \wedge {X_v}} \right\|}} = \frac{{ - v\tau T - N}}{{\sqrt {{\kappa ^2} + {{\left( {v\tau } \right)}^2}} }}. \end{equation}$

(4.20)

The first fundamental form of the normal ruled surface in Euclidean space is given by

$I = \left\langle {dX, dX} \right\rangle = \left\langle {{X_s}ds + {X_v}dv, {X_s}ds + {X_v}dv} \right\rangle = Ed{s^2} + 2Fdsdv + Gd{v^2}$

where the coefficients of the first fundamental form are

$\begin{equation} \begin{array}{l} E = \left\langle {{X_s}, {X_s}} \right\rangle = 1 + {v^2}{\tau ^2}{\kappa ^2} + {v^2}{\kappa _s}^2, {\rm{ }}\\ {\rm{F}} = \left\langle {{X_s}, {X_v}} \right\rangle = v{\kappa _s}\kappa , \\ {\rm{G}} = \left\langle {{X_v}, {X_v}} \right\rangle = {\kappa ^2}. \end{array} \end{equation}$

(4.21)

From the Eq. (4.19), the second derivative is found and given as

$\begin{equation} \begin{array}{l} {X_{ss}}\left( {s, v, t} \right) = \left( {v\tau {\kappa ^2}} \right)T + \left( {1 - v{\tau _s} - 2v\tau \frac{{{\kappa _s}}}{\kappa }} \right)N + \left( { - v{\tau ^2} + v\frac{{{\kappa _{ss}}}}{\kappa }} \right)B, \\ {X_{sv}}\left( {s, v, t} \right) = - \tau N + \frac{{{\kappa _s}}}{\kappa }B, \\ {X_{vv}}\left( {s, v, t} \right) = 0. \end{array} \end{equation}$

(4.22)

The second fundamental form of the normal surface is given by

$II = \left\langle {dX, dU} \right\rangle = - \left\langle {dX, dU} \right\rangle = \left\langle {{X_s}ds + {X_v}dv, {U_s}ds + {U_v}dv} \right\rangle = ed{s^2} + 2fdsdv + gd{t^2}$

where the coefficients of the second fundamental form are

$\begin{equation} \begin{array}{l} e = \left\langle {{X_{ss}}, U} \right\rangle = \frac{{{\kappa ^2}\left( { - {v^2}{\tau ^2} - 1 + v{\tau _s} + 2v\tau \frac{{{\kappa _s}}}{\kappa }} \right)}}{{\sqrt {{\kappa ^2} + {{\left( {v\tau } \right)}^2}} }}, \\ f = \left\langle {{X_{sv}}, U} \right\rangle = \frac{{{\kappa ^2}\tau }}{{\sqrt {{\kappa ^2} + {{\left( {v\tau } \right)}^2}} }}, \\ g = \left\langle {{X_{vv}}, U} \right\rangle = 0. \end{array} \end{equation}$

(4.23)

Corollary 4.5. For the binormal ruled surface $X = X\left({s, v, t} \right)$ the Gaussian and mean the curvatures are

$\begin{equation} K = - \frac{{{\tau ^2}}}{{\left( {{\kappa ^2} + {{\left( {v\tau } \right)}^2}} \right)\left( {1 + {{\left( {v\tau \kappa } \right)}^2}} \right)}}, \end{equation}$

(4.24)

$\begin{equation} H = \frac{{{\kappa ^2}\left( {v{\tau _s} - {{\left( {v\tau } \right)}^2} - 1} \right)}}{{2{{\left( {{\kappa ^2} + {{\left( {v\tau } \right)}^2}} \right)}^{\frac{1}{2}}}\left( {1 + {{\left( {v\tau \kappa } \right)}^2}} \right)}}, \end{equation}$

(4.25)

respectively.

Proof. From the Eqs. (4.21) and (4.23), we easily obtain the Gaussian curvature and the mean curvature respectively as follows

$K = \frac{{eg - {f^2}}}{{EG - {F^2}}} = - \frac{{{\tau ^2}}}{{\left( {{\kappa ^2} + {{\left( {v\tau } \right)}^2}} \right)\left( {1 + {{\left( {v\tau \kappa } \right)}^2}} \right)}},$

$H = \frac{1}{2}\frac{{Eg - 2Ff + Ge}}{{EG - {F^2}}} = \frac{{{\kappa ^2}\left( {v{\tau _s} - {{\left( {v\tau } \right)}^2} - 1} \right)}}{{2{{\left( {{\kappa ^2} + {{\left( {v\tau } \right)}^2}} \right)}^{\frac{1}{2}}}\left( {1 + {{\left( {v\tau \kappa } \right)}^2}} \right)}}.$

Corollary 4.6. From the Eqs. (4.16) and (4.17), the normal ruled surface is developable iff $\tau = 0$ and minimal iff $v{\tau _s} - {\left({v\tau } \right)^2} - 1 = 0$ .

Conflict of interest

The authors declare no conflict of interest.

References

[1]	B. Kulfan, J. Bussoletti, Fundamental parameteric geometry representations for aircraft component shapes, 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, The modeling and simulation frontier for multidisciplinary design optimization, Portsmouth, Virginia, 2006.
[2]	J. J. Maisonneuve, D. P. Hills, P. Morelle, C. Fleury, A. J. G. Schoofs, A shape optimisation tool for multi-disciplinary industrial design, In: Computational methods in applied sciences 96: proceedings of the 2nd ECCOMAS conference, Paris, France, 1996,516-522.
[3]	U. Bashir, M. Abbas, M. N. H. Awang, J. M. Ali, A class of quasi-quintic trigonometric Bézier curve with two shape parameters, Science Asia, 39S (2013), 11-15. doi: 10.2306/scienceasia1513-1874.2013.39S.011
[4]	U. Bashir, M. Abbas, J. M. Ali, The G2 and C2 rational quadratic trigonometric Bezier curve with two shape parameters with applications, Appl. Math. Comput., 219 (2013), 10183-10197.
[5]	S. BiBi, M. Abbas, M. Y. Misro, G. Hu, A novel approach of hybrid trigonometric Bézier curve to the modeling of symmetric revolutionary curves and symmetric rotation surfaces, IEEE Access, 7 (2019), 165779-165792. doi: 10.1109/ACCESS.2019.2953496
[6]	S. Maqsood, M. Abbas, G. Hu, A. L. A. Ramli, K. T. Miura, A novel generalization of trigono-metric Bézier curve and surface with shape parameters and its applications, Math. Probl. Eng., 2020 (2020), 4036434.
[7]	M. Usman, M. Abbas, K. T. Miura, Some engineering applications of new trigonometric cubic Bézier-like curves to free-form complex curve modeling, J. Adv. Mech. Des. Syst., 14 (2020), 1-15.
[8]	X. Z. Hu, G. Hu, M. Abbas, M. Y. Misro, Approximate multi-degree reduction of Q-Bézier curves via generalized Bernstein polynomial functions, Adv. Differ. Equ., 2020 (2020), 413. doi: 10.1186/s13662-020-02871-y
[9]	F. H. Li, G. Hu, M. Abbas, K. T. Miura, The generalized H-Bézier model: Geometric continuity conditions and applications to curve and surface modeling, Mathematics, 8 (2020), 924. doi: 10.3390/math8060924
[10]	A. Majeed, M. Abbas, K. T. Miura, M. Kamran, T. Nazir, Surface modeling from 2D contours with an application to craniofacial fracture construction, Mathematics, 8 (2020), 1246. doi: 10.3390/math8101793
[11]	G. Hu, H. N. Li, M. Abbas, K. T. Miura, G. L. Wei, Explicit continuity conditions for G1 connection of S- $\lambda$ curves and surfaces, Mathematics, 8 (2020), 1359. doi: 10.3390/math8081359
[12]	B. M. Kulfan, Universal parametric geometry representation method, J. Aircraft, 45 (2008), 142-158. doi: 10.2514/1.29958
[13]	A. Majeed, A. R. M. Piah, Image reconstruction using rational Ball interpolant and genetic algorithm, Appl. Math. Sci., 8 (2014), 3683-3692.
[14]	A. Majeed, A. R. M. Piah, Reconstruction of craniofacial image using rational cubic Ball interpolant and soft computing technique, In: AIP Conference Proceedings, 1682 (2015), 030001.
[15]	W. P. Henderson, The effect of canard and vertical tails on the aerodynamic characteristics of a model with a 59 deg sweptback wing at a Mach number of 0.30, 1974.
[16]	M. Maughmer, The design of winglets for low-speed aircraft, Technical Soaring, 30 (2016), 6173.
[17]	J. M. Grasmeyer, Multidisciplinary design optimization of a strut-braced wing aircraft, Ph.D. dissertation, Virginia Polytechnic Institute and State University, Blacksburg, USA, 1998.
[18]	S. Rajendran, Design of Parametric Winglets and Wing tip devices: A conceptual design approach, Ph.D. dissertation, Linkoping University, SE-58183 Linkoping, Sweden, 2012.
[19]	A. Majeed, M. Kamran, M. K. Iqbal, D. Baleanu, Solving time fractional Burgers and Fishers equations using cubic B-spline approximation method, Adv. Differ. Equ., 2020 (2020), 175. doi: 10.1186/s13662-020-02619-8
[20]	A. Majeed, M. Abbas, F. Qayyum, K. T. Miura, M. Y. Misro, T. Nazir, Geometric modeling using new Cubic trigonometric B-Spline functions with shape parameter, Mathematics, 8 (2020), 2102. doi: 10.3390/math8101793
[21]	A. Majeed, F. Qayyum, New rational cubic trigonometric B-spline curves with two shape parameters, Comput. Appl. Math., 39 (2020), 1-24. doi: 10.1007/s40314-019-0964-8
[22]	X. L. Han, Quadratic trigonometric polynomial curves with a shape parameter, Comput. Aided Geom. D., 21 (2004), 535-548. doi: 10.1016/j.cagd.2004.03.001
[23]	X. L. Han, Piecewise quadratic trigonometric polynomial curves, Math. Comput., 72 (2003), 1369-1377. doi: 10.1090/S0025-5718-03-01530-8
[24]	J. Lin, S. Reutskiy, A cubic B-spline semi-analytical algorithm for simulation of 3D steady-state convection- diffusion-reaction problems. Appl. Math. Comput., 371 (2020), 124944.
[25]	S. Reutskiy, Y. H. Zhang, J. Lin, H. G. Sun, Novel numerical method based on cubic B-splines for a class of nonlinear generalized telegraph equations in irregular domains, Alex. Eng. J., 59 (2020), 77-90. doi: 10.1016/j.aej.2019.12.009
[26]	S. Reutskiy, J. Lin, B. Zheng, J. Y. Tong, A novel B-Spline method for modeling transport problems in anisotropic inhomogeneous Media, Adv. Appl. Math. Mech., 13 (2021), 590-618. doi: 10.4208/aamm.OA-2020-0052
[27]	G. Hu, J. L. Wu, X. Q. Qin, A novel extension of the Bezier model and its applications to surface modeling, Adv. Eng. Softw., 125 (2018), 27-54. doi: 10.1016/j.advengsoft.2018.09.002
[28]	G. Hu, J. L. Wu, Generalized quartic H-Bezier curves: Construction and application to developable surfaces, Adv. Eng. Softw., 138 (2019), 102723. doi: 10.1016/j.advengsoft.2019.102723
[29]	G. Hu, C. C. Bo, G. Wei, X. Q. Qin, Shape-adjustable generalized Bezier surfaces: Construction and it is geometric continuity conditions, Appl. Math. Comput., 378 (2020), 125215.

Reader Comments

Your name:*

Email:*
© 2021 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)