1.
Introduction
Historically, the exponential distribution has been widely applied to model lifetime data due to its analytical simplicity and the availability of its simple statistical methods such as the existence of its closed-form solutions of the cumulative distribution function (CDF) [1]. Notably, the exponential distribution is the only known continuous distribution characterized by a constant hazard (failure) rate as well as a memoryless property [2]. Due to the limitations of the hazard rate function (HRF) of the exponential distribution, its applicability to modeling survival data is somewhat limited, as the available data exhibit varying hazard shapes. As a result, in recent years, the Weibull, the log-normal, the log-logistic, and the gamma distributions have become the most popular distributions applied in survival analysis, particularly for time-to-event data analysis. The popularity of the wide range of applications has been motivated by the nature of their HRFs which range from monotonic to non-monotonic shapes; see, e.g., [1,3,4].
Lately, researchers have become extremely interested in extending distributions to realize more flexible distributions that can accommodate different hazard shapes; see e.g., [5,6,7]. Due to the availability of various methods of distribution modification, the exponential distribution has been modified by several researchers to achieve a better fit for real data. Some of these extensions include the exponentiated exponential [8] as an alternative to the gamma distribution and the generalized exponential distribution [9], which outperformed the Weibull and gamma distributions. As well as the odd exponentiated half-logistic exponential distribution [10] whose hazard rate can assume increasing, decreasing, or bathtub shapes, The exponentiated exponential [11], beta-exponential [12], generalized gull alpha-power exponential [13], and exponentiated generalized alpha-power exponential [14], among others.
Furthermore, many researchers have been focused on finding the association between the survival time or HRF and the covariates for the analysis of uncensored time-to-event data. From this, this relationship can be quantified and these covariates can be employed in fields such as medicine for disease management and prevention see [15,16,17,18]. These covariates can be classified into either time-dependence covariates or covariates that do not change with time. Thus, they accommodate sophisticated lifetime models that are acceptable in various industrial and medical settings. For instance, in a medical setup, gender and the type of treatment can be classified as time-independent covariates while calorie intake, age, and the level of dosage are all examples of covariates that may depend and even change with time [19].
This idea of finding and quantifying the association between the survival time and the covariates has led to the development of hazard-based regression models, with the main aim of estimating the regression coefficients for the corresponding covariate components. Moreover, the extended distributions have actively been used as baseline distributions in the development of hazard-based regression models to realize more accurate survival predictions. For instance, [20] extended the Weibull distribution by using the generalized Topp-Leone generator and used it as a baseline distribution in the formulation of an accelerated failure time (AFT) model. The log-logistic distribution has been generalized by Muse et al. [7] who developed a hazard-based regression model with the extended model as the baseline distribution. A multi-parametric hazard-based regression model called the extended exponential-Weibull AFT model has been proposed in [21]. This model performed effectively modeled right-censored time-to-event data.
In recent years, a tremendous shift from non-parametric to parametric regression models for survival analysis has resulted in the provision of attractive and flexible methods for the analysis of time-to-event data from different disciplines such as population health, medicine, and disease modeling [22]. There are several parametric regression models among which, the proportional hazard (PH) model and the AFT model are the most commonly used in the analysis of censored time-to-event data; see [7,23]. Others include the proportional odds model and the accelerated hazard model.
The AFT models are a type of statistical model that is used to analyze time-to-event data [24,25]. These models assume that the time to an event (such as death, failure, or disease onset) follows a particular probability distribution and that certain factors (such as age, sex, and treatment group) may influence the rate at which the event occurs [26]. When the distribution of the model's error component is well known, the AFT model is said to be parametric; otherwise, it is called a semi-parametric model; see [27,28]. The parametric AFT models have different advantages over the semi-parametric AFT models in survival analysis. Some of the significant advantages are as follows:
(1) Efficiency: Parametric AFT models estimate fewer parameters than semi-parametric models. This frequently results in more efficient calculations, particularly when the underlying distributional assumptions are roughly true. Parametric models can provide more accurate estimates of the survival distribution since are required for estimation [29].
(2) Flexibility: Parametric AFT models provide additional flexibility in the simulation of the structure of the survival distribution. Researchers can capture a broader range of survival patterns and perhaps increase model fit by specifying a parametric form for the survival function (SF) (such as Weibull, exponential, log-normal, etc.) as opposed to semi-parametric models, which assume fewer distributional features [29].
(3) Interpretability: The parameters of parametric AFT models are frequently interpreted in terms of the underlying survival timescale. For example, in the Weibull distribution, the shape parameter controls whether the hazard rises, falls, or stays constant over time. This interpretability is useful for gaining insight into the elements that determine survival [30].
Furthermore, parametric AFT models, such as those using proportional hazard metrics, allow variables to accurately predict survival outcomes [28]. Parametric AFT models are used to estimate the effects of these factors on the event time and to make predictions about future events. They are commonly used in fields such as biostatistics, reliability engineering, and survival analysis.
The AFT model has been considered to be more applicable and realistic than the PH model. Additionally, more distributions together with their generalizations have been proven to be closed under the AFT but not under the PH model [24]. Furthermore, according to [23,31], the covariates of the AFT model directly influence the time to event while those of the PH model only affect the HRF. Also, the constant acceleration assumption made by both the PH and the AFT models is open for relaxation in the AFT allowing for time dependency related to modeling non-PH sytems [32].
The AFT model is said to be a parametric model if the error component in the model follows a well-known distribution. The model considers the regression of survival time on one or more covariates; hence, the model is mainly applied to elucidate the effects of the covariates that either decelerate or accelerate the survival time; see e.g., [20,33].
Based on the above discussion, we propose a fully parametric AFT regression model under the baseline extended alpha-power exponential (EAPE) distribution. The proposed regression model aims to expand the scope of the exponential distribution in the analysis of time-to-event data and also to introduce an alternative model that can compete with the most commonly used classical Weibull, log-logistic, and gamma regression models. The primary motivation for this research was to broaden the application of the exponential distribution in the analysis of survival data. The proposed AFT regression model is quite versatile and can be used for a variety of survival analysis applications.
The proposed EAPE-AFT model is useful in survival analysis because of its adaptability, interpretability, and efficiency. The model explicitly describes the survival time distribution, allowing for a broader range of hazard functions and more flexible modeling of covariate effects. This direct parameterization allows for easy reading of the model's parameters, resulting in a better understanding of how covariates influence survival time. Overall, the parametric EAPE-AFT model developed in this study is a useful and accessible tool for studying survival data, providing insights that may be used to make decisions in a variety of situations.
The rest of this article is organised as follows: Section 2 gives the formulation of the proposed model. The maximum likelihood (ML) estimation methodology for the parameters of the proposed model is described in Section 3. In Section 4, a simulation study to assess the performance of the estimates is given. Section 5 gives a practical illustration of the model through the use of real data while a discussion is given in Section 6. Finally, conclusions and recommendations are given in Section 7.
2.
Model formulation
AFT models are typically formulated by using a parametric approach. The basic idea is to model the logarithm of the event time as a linear function of the predictor variables, with the assumption that the error term follows a probability distribution. The most commonly used probability distributions in AFT models are the Weibull and log-normal distributions.
For instance, the Weibull AFT model can be formulated as follows:
where T is the event time, X is a matrix of the predictor variables, β is a vector comprising the coefficients to be estimated, and e is the error term, which follows an extreme value distribution if the survival times follow a Weibull distribution.
Once the model is formulated, it can be fit to the data by using ML estimation or other methods. The coefficients estimated from the model can be used to make predictions about future event times and assess the effects of predictor variables on the event time.
2.1. The EAPE distribution
In this study, we consider the EAPE distribution [34] as a baseline model. The CDF of the EAPE distribution can be expressed as follows
where α and b>0 are shape parameters and λ is a scale parameter. By manipulating these parameters, one can customize the EAPE distribution to accurately represent diverse patterns and characteristics observed in lifetime data.
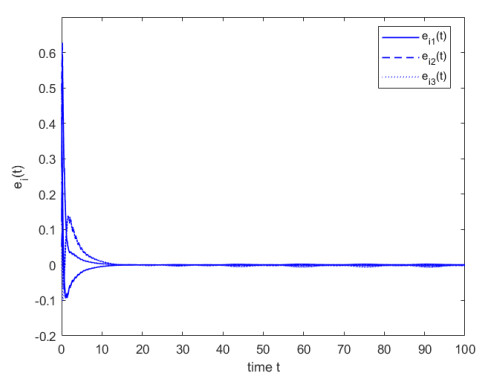
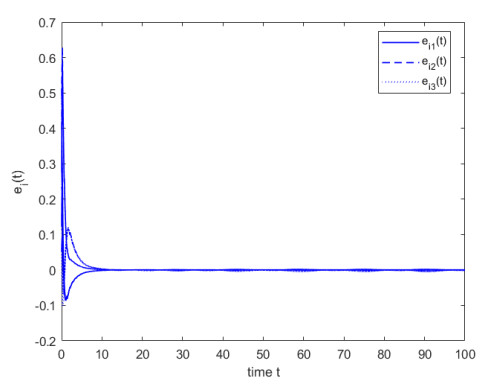
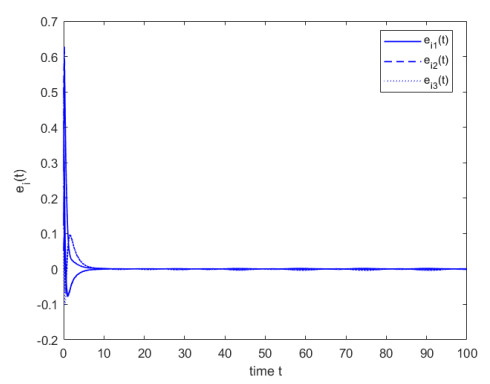
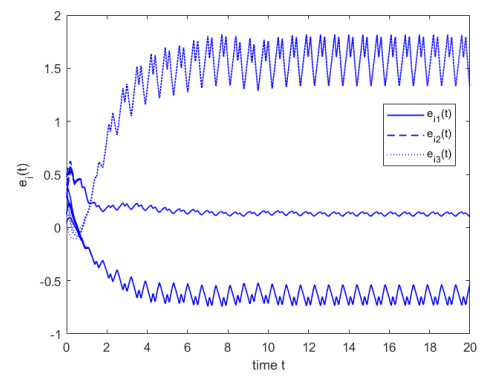
Figure 1 gives a visual display of the HRF shapes for the EAPE model indicating that the EAPE HRF can take four shapes including constant, unimodal, monotonically increasing, and monotonically decreasing. The HRF is a crucial term in survival analysis which is a field of statistics that examines the time until a specific event occurs, such as the death or failure of an item. The shape of the HRF might reveal vital information about the survival of the item or population under consideration. In the case of an unimodal HRF, the hazard rate is initially low, then rises to a peak, and then falls again. This form is frequently observed in biological systems, such as the aging of living organisms. The inflection point or mode is the highest point in the HRF and it reflects the moment when the HRF is at its peak. In practice, this shape facilitates identification of the most susceptible phase for an item or population. For example, in a medical study, the inflection point may represent the age at which a person is most likely to encounter a specific health event, such as a heart attack or stroke. Understanding the shape of the HRF can assist researchers and practitioners in making sound decisions regarding preventative actions or treatments to reduce the risk of such incidents [35].
The probability density function (PDF) of the EAPE model reduces to
The S of the EAPE distribution is given by
Hence, the HRF and the cumulative-HRF (CHRF) have the following respective forms
and
2.2. The AFT model and its assumptions
If the random variable T is the event time, x is a vector of covariates (also known as regressor variables), β is a vector of regressor coefficients, and ψ(x′β) is a link function for the regressor variables, then we have the following assumptions:
(i) ψ(0)=1;
(ii) ψ(x′β)>0;
(iii) ψ(x′β) is a one-to-one monotonic function.
Then, the HRF of the AFT model is described as follows:
Using the assumption that
the HRF of the AFT model is given by
The corresponding SF reduces to
Hence, the CHRF can be derived as follows:
Further, the PDF and CDF of the AFT model are respectively derived as follows:
and
2.3. The proposed EAPE-AFT model
Considering the EAPE distribution and the AFT models, the HRF and the SF of the proposed EAPE-AFT model respectively have the following forms
and
Clearly, by taking
the HRF and SF in Eqs (2.12) and (2.13) can respectively be rewritten as
and
Equations (2.12) and (2.13) represent the HRF and SF of the EAPE distribution, respectively. This means that the EAPE distribution is closed under the AFT model.
The corresponding CHRF, PDF, and CDF of the EAPE-AFT model are given, respectively, as follows:
and
3.
The ML estimation
In this section, the parameters of the EAPE-AFT regression model are estimated by using the ML estimation approach under a right-censoring scheme. The ML method is known to produce unique and asymptotically efficient estimators [36]. Other properties include asymptotic bias, asymptotic normality, and consistency.
Consider the lifetimes, T1,T2,...,Tn, of n individuals. If the data are subject to right censoring and the component Cj>0 is the possible censoring time for the j individual, then
Further, let
Let (tj,σj and xj) be a set of right-censored sample data with
be an n×1 vector of regressor variables for the j individual depending on the value of σj, and tj be the censoring time for the j individual. Furthermore, the assumption of non-informative censoring, which means that the survival time distribution provides no information on the censoring time distribution and vice versa, is considered. More details on non-informative censoring are explored in [1,37]. Under this assumption, σj and tj are considered to be random variables with a joint probability distribution function given by
Therefore, if the event of interest occurs at time tj, the j individual contributes f(tj) to the likelihood function and S(tj) if censored at time tj. Hence, we obtain the likelihood function by incorporating the information obtained from the censored observations, as follows:
where Θ is the baseline vector of parameters. In our case, Θ=(α,λ,b,β).
We have that
thus, the likelihood function takes the following form:
Hence, the log-likelihood function reduces to
Therefore, the log-likelihood of the EAPE-AFT regression model becomes
Hence
where
The ML estimates can be obtained directly by optimizing the log-likelihood function or by solving a system of equations that has been derived by equating the first partial derivatives of the log-likelihood function with respect to the parameters to zero. In this study, we employed the Broyden-Fletcher-Goldfarb-Shanno (BFGS) method in the optimization of the log-likelihood function given in Eq (3.3) to obtain the ML estimators of the EAPE-AFT parameters. The BFGS algorithm was independently introduced by the authors of [38,39,40,41]. The BFGS algorithm is one of the most efficient algorithms for solving unconstrained optimization problems. It is an iterative technique that begins with an initial guess value Θ0 and an initial Hessian matrix H0 to provide a solution to a given function. The following steps are followed such that for k=(0,1,...) an approximation point Θk and an mXm matrix Hk are obtained on the k iteration.
Given parameters: Θ0, H0>0 and unconstrained optimization problem ℓ(Θ).
(1) First, the quasi-Newton direction is obtained as follows:
(2) The step length dk is obtained such that it meets certain line search conditions.
(3) The next iteration is obtained as follows:
(4) An important feature of the algorithm is the choice of Hk. That is, it must be positive definite and satisfy the quasi-Newton formula given by
where
(5) Finally, the matrices denoted by Hk are updated in accordance with the following BFGS formula
where Θ=(α,λ,b,β) is a vector of parameters of the EAPE distribution.
4.
Simulation study
In this section, we show the ability of the proposed model to make inferences by presenting simulation results. Specifically, we demonstrate how the model can estimate parameters accurately by using the absolute bias (AB), mean square error (MSE), and relative bias (RB) measures. We check the ability of the model to recover the baseline HRF shapes. Moreover, we obtain the Akaike information criteria (AIC) to choose models that accurately describe the underlying HR shape. We also investigate how the model's inferential capabilities are affected by different proportions of censoring.
The AFT regression framework given in Eq (2.6) was assumed for data generation and simulation design. We generated samples of sizes n=2000 and n=5000. The covariate vector,
was considered in the simulation study where x1 and x2 are binary variables derived from a Bernoulli(0.5) distribution whereas x3 and x4 are continuous variables derived from a standard Gaussian distribution. The vector corresponds to the following coefficients of the AFT regression
whose initial values were chosen to be (−2.5,0.5,−0.75,0.5,−0.75).
In simulating lifetime censored data from the AFT framework, we used the technique of the inverse transform as explained in [19]. Further, because the main aim of the study was to test the robustness of the proposed model when applied to model different types of time-to-event data, we considered the inverse transform of the exponentiated Weibull (EW) distribution under the assumption of the presence of a regression intercept and covariate effects [3,5,21,42]. Also, the assumption of non-informative censoring has been incorporated for the generation of censored data.
If a random variable T comes from the EW distribution with parameters α,b and λ, the PDF of T is given by
This distribution accommodates all of the most basic HRF shapes which include constant, monotonic (increasing and decreasing), and non-monotonic (unimodal and bathtub), and it is also closed under the AFT regression models. It follows that the CHRF for the EW distribution is defined as follows:
The inverse CHRF is given by
4.1. Simulated scenarios
This study was conducted for three simulation scenarios based on monotonically increasing, monotonically decreasing, and unimodal hazard shapes to assess how well the proposed EAPE-AFT model performs in comparison with some selected competing distributions, i.e., the log-logistic-AFT (LL-AFT) and Weibull-AFT (W-AFT). The simulations were also conducted to explore the effects of the baseline HRF on the inferential properties of the hazard-based regression models.
First scenario: monotonically increasing HRF
In this scenario, we generated lifetime data from the EW distribution with (α=1.5,b=1.4,λ=1.1) and two censoring percentages, i.e., 14.45%≈15% and 22.15%≈22% which were determined from the censoring times derived from an exponential distribution by using the rate parameter θ=0.26 and θ=0.15, respectively.
Second scenario: monotonically decreasing HRF
In this scenario, we generated lifetime data from the EW distribution with α=1.2,b=1.2,λ=0.8 and two censoring percentages, i.e., 15% and 22% which were determined from the censoring times derived from an exponential distribution by using the rate parameter θ=0.56 and θ=0.31, respectively.
Third scenario: unimodal HRF
In this scenario, we generated lifetime data from the EW distribution with α=0.9,b=3.5,λ=1.2 and two censoring percentages, i.e., 14.75%≈15% and 22% which were determined from the censoring times derived from an exponential distribution using the rate parameter θ=0.27 and θ=0.19, respectively.
Using the different parameter combinations, the plots of hazard shapes of the EW distribution were constructed as reported in Figure 2 for the cases of monotonically increasing, monotonically decreasing, and unimodal. Figure 3 gives the total time on test (TTT) plots for the lifetime data generated for each of the three scenarios.
4.2. Analysis of simulated data
To evaluate the predictive and analytical capabilities of the proposed model in each scenario, the EAPE-AFT model is was fit to the lifetime data that were generated based on the EW distribution as was the case for the W-AFT and LL-AFT models. Additionally, for all the fitted models, the AB, RB, and MSE were calculated to evaluate the stability of the regression coefficient estimators. Finally, the AIC was computed for model comparison.
Given that our main objective was to evaluate the accuracy of the estimates (or stability of the estimators) of the covariate coefficients, rather than analyze the characteristics of the optimization process, we utilized the parameter values from the generating model to initiate the optimization procedure in every scenario. We conducted the analysis by using the R programming language, and the optimization step was executed by using the "nlminb" function in the R software.
4.3. Simulation results
Simulation results for the first scenario are presented in Tables 1–4. Based on these results, it can be inferred that the proposed EAPE-AFT model performs better than the EW-AFT, the W-AFT, and the LL-AFT models, as it achieved the lowest AIC. Additionally, the AIC values for the EW-AFT, EAPE-AFT and W-AFT distributions can be seen as close to each other but they are superior to those for the LL-AFT model. When the censoring percentage was increased to 22% and the sample size was increased, the EAPE-AFT model consistently outperformed all of the considered models with the lowest AIC values. For the covariates, x1,x2,x3,x4, and the intercept, all models indicated low values of the AB, MSE, and RB. Increasing the sample size from 2000 to 5000, the values of AB, MSE, and RB decreased indicating consistency of the estimates. Moreover, the AB, MSE, and RB values for the covariates of the EAPE-AFT, EW-AFT, and W-AFT models dominated those of the LL-AFT model. However, increasing the censoring percentage resulted in increased estimation error.
In Scenario 2 as presented in Tables 5–8, all competing models could account for the diminishing HRF shape, but the EAPE-AFT model was found to be the best in terms of the value of the AIC. The EAPE-AFT, EW-AFT, W-AFT, and LL-AFT had similar AIC.
The results for Scenario 3 are presented in Tables 9–12. These results show that the EAPE-AFT model outperformed all of the considered models with the lowest AIC values, and that the EW-AFT, and LL-AFT models had the lowest values for the AIC. On the other hand, the W-AFT model generates the least accurate estimates in terms of the AB, MSE, and RB.
In conclusion, the study has revealed that both sample size and censoring percentage impact the performance of the considered models. When the censoring and sample size were increased, the EAPE-AFT model consistently outperformed the EW-AFT, W-AFT and LL-AFT models.
5.
Survival analysis
In survival analysis, the right censored data are the most common type of censored data available. The time to event in these analyses is commonly taken to be the time between survival and death. In this section, we focus on the use of multi-parametric (more than one covariate) hazard-based regression models. Hence, the EAPE-AFT regression model has been adopted to analyze real-world right-censored survival data. The main goal of this part of the study was to compare the EAPE-AFT model with its sub-models which include the alpha-power exponential AFT (APE-AFT), exponentiated exponential AFT (EE-AFT), and exponential AFT (E-AFT) distributions.
5.1. Data description
Breast cancer is a disease characterized by the abnormal growth of cells in breast tissue, affecting both men and women and constituting the most common type of cancer among women worldwide. According to the World Health Organization, it is responsible for over two million new cases and more than 600,000 deaths annually across the globe. This study utilized data previously analyzed by the authors of [43] on breast cancer patients from the Rotterdam tumor bank which contained records of 2982 primary breast cancer patients, and which formed the original data set. A full description of the data can be found in [43].
The following covariates were taken into account for the illustrations of this study. We considered the following for each patient:
(1) t: days to death or last follow-up; death: used for censoring.
(2) x1: hormon (hormonal treatment).
(3) x2: meno (menopausal status).
(4) x3: age (age at surgery).
We begin with the exploration of the data and Table 13 gives the summary statistics for the data. In the sample of the study, approximately 57.383% of the data was censored, indicating that the exact observational lifetimes for those individuals are not known. The explanatory variable "age" represents the age of patients at the time of surgery and it was recorded as a continuous variable. The average age in the breast cancer patients' data set from the Rotterdam bank was 44.507 years, with a standard deviation of 29.620.
The variable "meno" describes the status of menopause referring to the classification of women based on their hormonal status as related to menopause. It is a categorical variable with two levels:
Premenopausal (0): This level indicates that women in the data set are still in their reproductive phase and have not yet experienced menopause.
Postmenopausal (1): This level indicates that women in the data set have gone through menopause, which is the permanent cessation of menstruation. Postmenopausal women can no longer conceive naturally as their ovaries have stopped releasing eggs. The data set consisted of 1312(44.027%) premenopausal patients and 1670(55.973%) postmenopausal patients. The variable "hormon" indicates whether the patients received hormonal treatment.
It is a categorical variable with two levels:
No (0): This level signifies that individuals in the data set have not undergone hormonal treatment.
Yes (1): This level indicates that individuals in the data set have received hormonal treatment. They have undergone medical intervention involving hormonal therapy or medication aimed at altering or regulating their hormone levels. There were 339 (11.309%) patients who received hormonal treatment.
The Cox PH plot is given in Figure 4, where panel (a) illustrates that the survival probabilities deviate from linearity at later time points, indicating an increasing HRF.
The shape of the HRF is affirmed by the shape of the Kaplan-Meier plot in Figure 4. This plot shows a steep initial decrease in survival probability followed by a more steady decline over time reflecting an increasing HRF [31].
As depicted by the histogram and the non-parametric kernel density estimation results in Figure 5. The distribution of the data was asymmetrical and positively skewed, which is a common characteristic of survival data.
Furthermore, to identify extreme observations, we constructed box plots and violin plots as in Figure 5 which revealed the presence of some extreme observations.
5.2. The Cox PH model
To investigate the association between survival time and the factors believed to influence it, we simulated a Cox PH model. The Cox PH model was used to estimate the parameters. Table 14 presents the results of the regression analysis for the Cox PH model, displaying the regression coefficients, standard errors (SEs), and p-values. Notably, all covariates except the menopausal status yielded a significant impact on the days to the death for breast cancer patients at a 5% level of significance.
Schoenfeld residuals are useful for assessing the PH assumption in the Cox model. In this study, we applied the global test, which is a statistical test that is used to evaluate the overall PH assumption in a Cox PH model. It assesses whether there is a significant departure from proportionality across all covariates in the model. Table 15 provides evidence that the PH models do not adequately fit the breast cancer data. Additionally, Figure 6 clearly demonstrates the rejection of the assumption of PH for all covariates included. In other words, the PH models do not adequately capture the patterns observed in the breast cancer patient data set.
5.3. Analysis of AFT model
Table 16 gives the values of the ML estimates and their corresponding Ses for the parameters of all considered regression models. Note that all of the coefficients were significant except for ^β2. This is consistent with the results for the Cox PH model which indicated that the covariate hormon does not influence the remaining days to the death for breast cancer patients.
Moreover, Table 17 provides the p-values and confidence intervals for each parameter, as they are measures that aid in determining the statistical significance of a parameter, and, together with information criterion measures, they were used for model comparison. The measures include the Akaike information criterion (AIC), the consistent Akaike's information criterion (CAIC), and the Bayesian information criterion (BIC). A p-value less than the level of significance indicates that the parameter is statistically significant and has a considerable influence on the outcome. The confidence interval defines a range within which we can be confident that the parameter's true value lies. If this interval excludes 0, it indicates that the parameter is statistically significant. The results given in Table 17 confirm that at 5% level of significance, all parameters were significant except for β2 for all for the considered models.
The Kaplan-Meier survival curve is depicted in Figure 7, and it demonstrates a statistically significant differentiation in survival durations between the menopausal status group and the hormonal treatment, as evidenced by a p-value below 0.0001. Additionally, the Kaplan-Meier plot confirms the violation of the Cox PH assumption when considering the covariate hormon; it also affirms that under the AFT model, the covariate meno does not influence the outcome variable.
In the analysis of the proposed model, we have compared the fit of the EAPE-AFT model with the APE-AFT, EE-AFT, and E-AFT sub-models whose PDFs are respectively given by
To compare the fit of our model with its sub-models, three information criteria have been utilized. These include the AIC, CAIC, and BIC. The values of the information criteria are provided in Table 17 which shows that the EAPE-AFT model outperformed all AFT regression models. Additionally, the HRFs for all considered competing AFT models were fit to the data and are displayed in Figure 8.
6.
Discussion
The main goal of this study was to develop a more adaptable model than the Cox model to improve the ability of the exponential distribution to model real-life data. An extensive Monte Carlo simulation was utilized to evaluate the estimators of the EAPE-AFT parameters. Finally, the proposed model was validated on breast cancer data and the choice of the AFT model was justified by the simulation results confirming a direct relationship between covariates and time to event, which improved interpretability.
Regarding the three hazard rate shapes, i.e., the increasing, decreasing, and unimodal shapes, the simulation results revealed that the extended EAPE-AFT model outperformed other existing AFT models, i.e., the W-AFT and LL-AFT models, in terms of ability to different HRFs. The values of the performance metrics such as the AB, RB, and MSE indicate the usefulness of the proposed EAPE-AFT model.
While the proposed model facilitates modeling and the interpretation of survival data, it is limited to data that exhibit bathtub hazard shapes. Additionally, the model is unable to handle crossing survival curves.
7.
Conclusions and recommendation
In this paper, we have proposed a new survival regression model for analyzing and modeling censored survival data, called the EAPE-AFT model. The new model outperformed other existing AFT models. We have developed methods for estimating the EAPE-AFT parameters by using the ML estimation technique. We have conducted simulation studies to compare the performance of the proposed model with that of other models, such as the W-AFT and the LL-AFT models. Based on our study, we have found out that the new AFT model provides a more accurate fit for various shapes of hazard rates and different levels of censoring. We have also applied the model to breast cancer patients data and found that it provides a better fit than its sub-models. In conclusion, the EAPE-AFT regression model has the potential to be a useful tool for analyzing various forms of survival data, as it can be applied to several widely known AFT models as special cases.
Future research should investigate residual analysis methodologies, diagnostic criteria for model fit, and model extension to improve the handling of diverse censoring processes.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors extend their appreciation to the Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia for funding this research work through project number 445-9-876. The authors would also like to thank the Editor and the reviewers for their constructive comments and suggestions which have greatly improved the paper.
Conflict of interest
The authors of this paper declare no conflicts of interest that might have interfered with the findings or development of this study.










 DownLoad:
DownLoad: