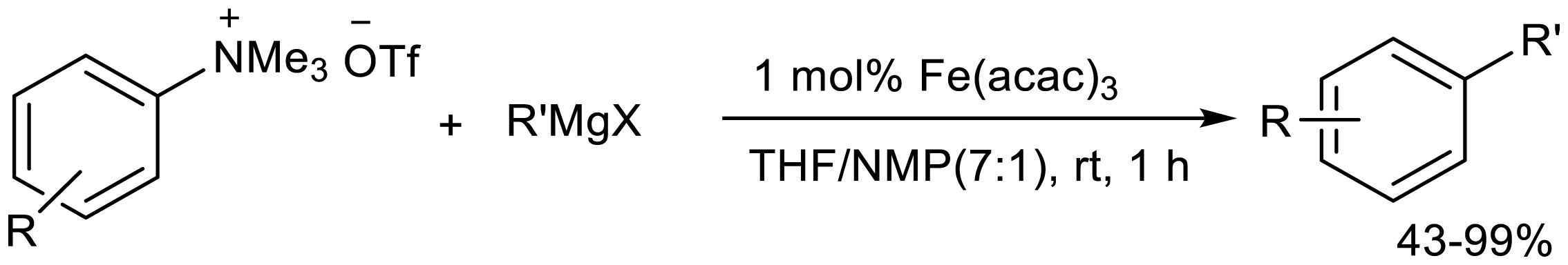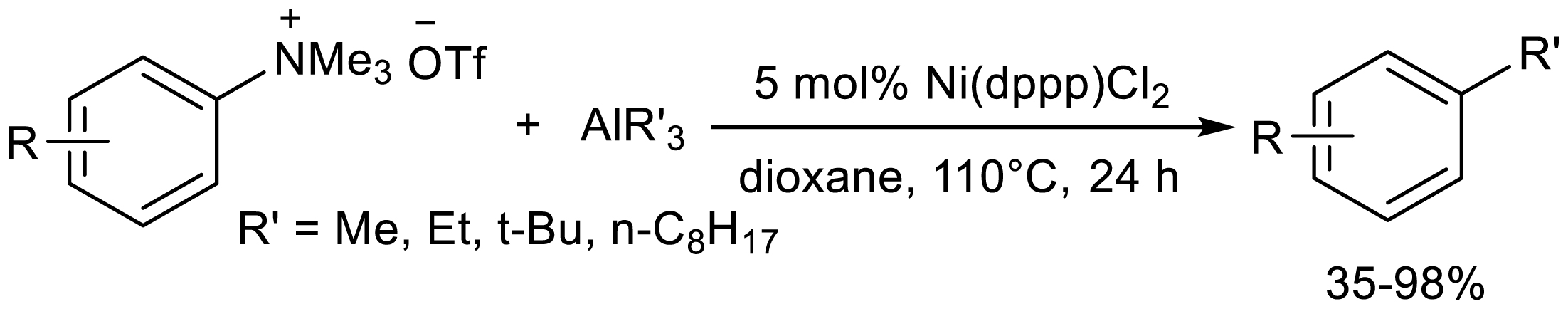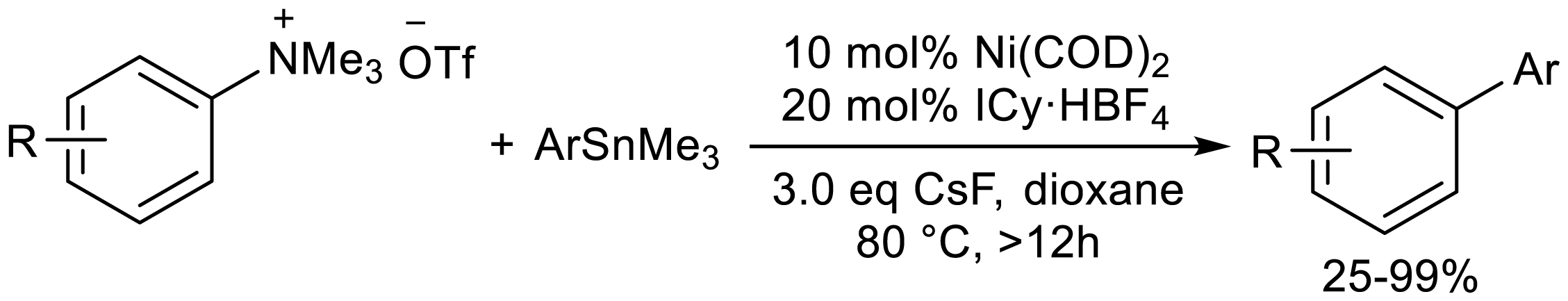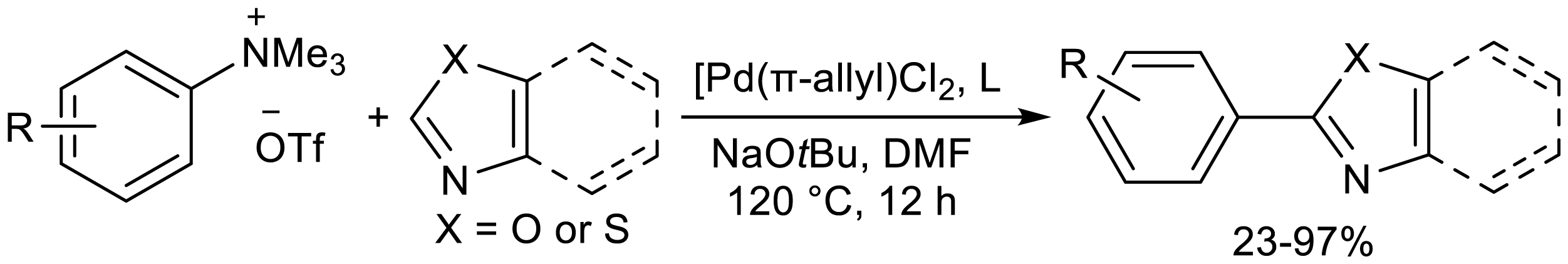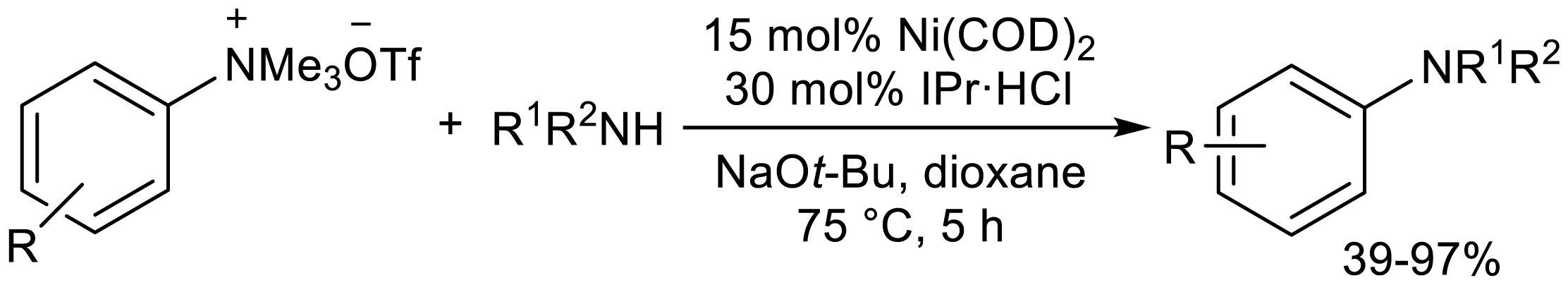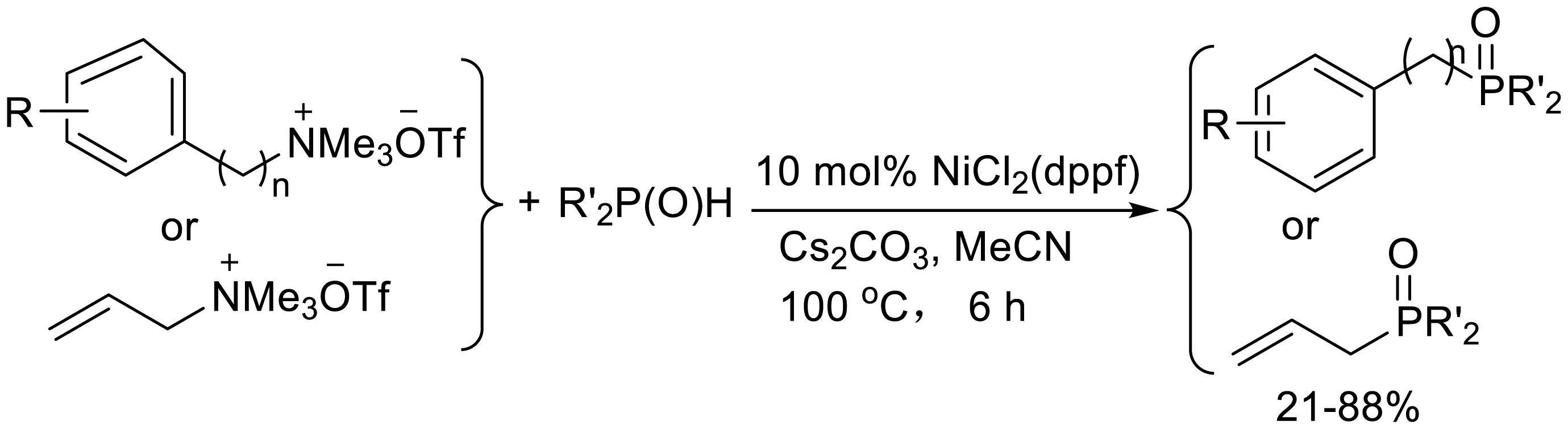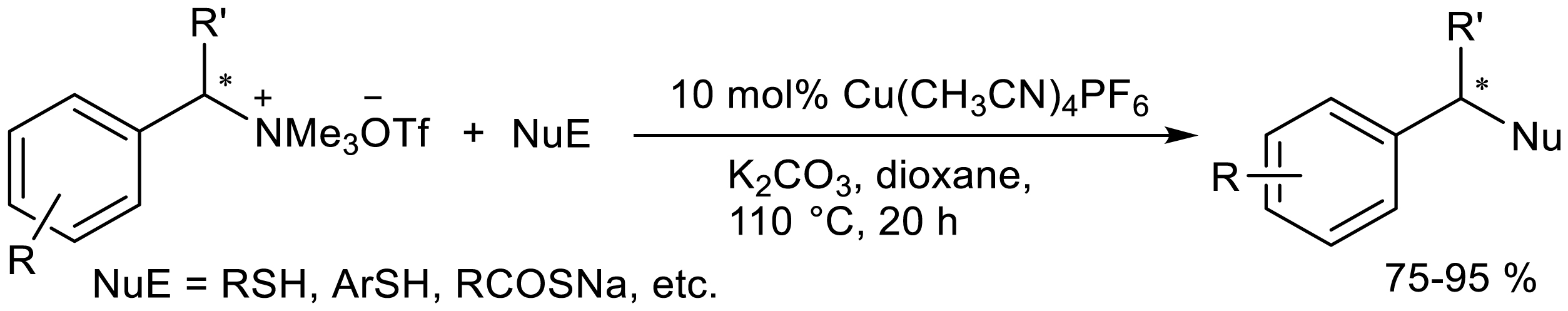1.
Introduction
There are many types of amines which are widely used in pharmaceuticals, agrochemicals, fine chemicals, dyes and functional materials. The formation and conversion of carbon-nitrogen bonds is a key issue in organic chemistry [1],[2]. However, carbon-nitrogen bonds have high bond dissociation energies, resulting in difficulties in direct conversion. At present, the conversion of carbon-nitrogen bonds is mainly achieved by activating carbon-nitrogen bonds, generally converting amines into compounds such as amides, sulfonamides, triazene, diazo salts and quaternary ammonium salts and then further realizing the breaking of carbon-nitrogen bonds and the formation of new bonds [3],[4].
As early as 1988, Wenkert of the University of California, San Diego reported the groundbreaking study of quaternary ammonium salt, and since then the carbon-nitrogen bond conversion reaction of various metal-catalyzed quaternary ammonium salts has been studied one after another [5]. The reagents participating in the coupling reaction range from the very beginning of organometallic reagents to later organoboronic reagents, organosilicate reagents, alkynes and other active carbon-hydrogen bonds and even inorganic substances such as carbon dioxide, carbon monoxide, etc.
Quaternary ammonium salts are easily prepared by the reaction of amines and alkyl electrophiles and are chemically stable and can be stored for a long time. In recent years, great progress has been made in the chemical transformation of quaternary ammonium salts to form new C-X bonds through cleavage of C-N bondage. Combined with the relevant research work of our group, this review provides a comprehensive introduction to the research progress of chemical conversion of quaternary ammonium salts in recent years. For more information about recent advances in electro- or photochemical driven transformations via cleavage of the C-N bond of quaternary ammonium salts, the readers may also refer the recent review [6]. The advances in photochemical construction of aromatic C-P bonds via C-hetero bond cleavage was reported recently [7] and the readers may get some ideas from this review.
2.
Transition metal-catalyzed C–B bond construction involving quaternary ammonium salts
Arylboronic acids are gaining more and more attention in the field of organic chemistry. They play an important role in the fields of catalysis, molecular self-assembly, carbohydrate analysis, molecular sensing, materials science and medicinal chemistry. The method of constructing C-B bonds by transition metal catalyzed C-N bond breaking of quaternary ammonium salts has great value in the preparation of some organoborate ester intermediates.
In 2015, Itami's group reported nickel-catalyzed cross-coupling of aryl and benzyl quaternary ammonium salts to diborates (Scheme 1) [8]. The reaction used Ni(COD)2 as a catalyst and dioxane as a solvent when using aryl quaternary ammonium salts; Ni(NO3)2·6H2O as a catalyst and 1,2-dimethoxyethane (DME) as a solvent when using benzyl quaternary ammonium salts. The authors also performed a variety of transformations on the C-B bonds of the products and obtained the products after oxidation, cross-coupling, carbonylation and oxidative cyclization, respectively, which proved the practicability of the synthetic products of this method.
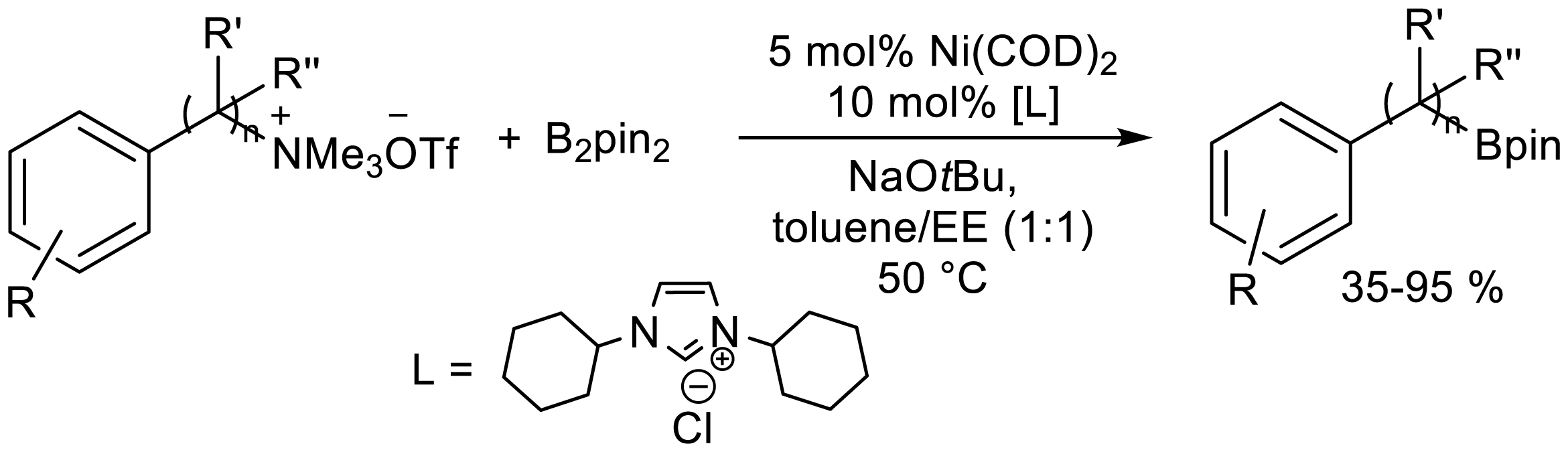
Shi's group reported highly chemically selective and regionally selective C-N bond boronation of activated ammonium salts catalyzed by nickel under mild and scalable conditions (Scheme 2) [9]. The system is effective not only for multiple functional groups of arylamines but also for primary, secondary and tert-benzylamines. The authors proposed that the main advantage of this mild and highly selective C-N bond boronation method was benefit for its application in post-synthesis modification.
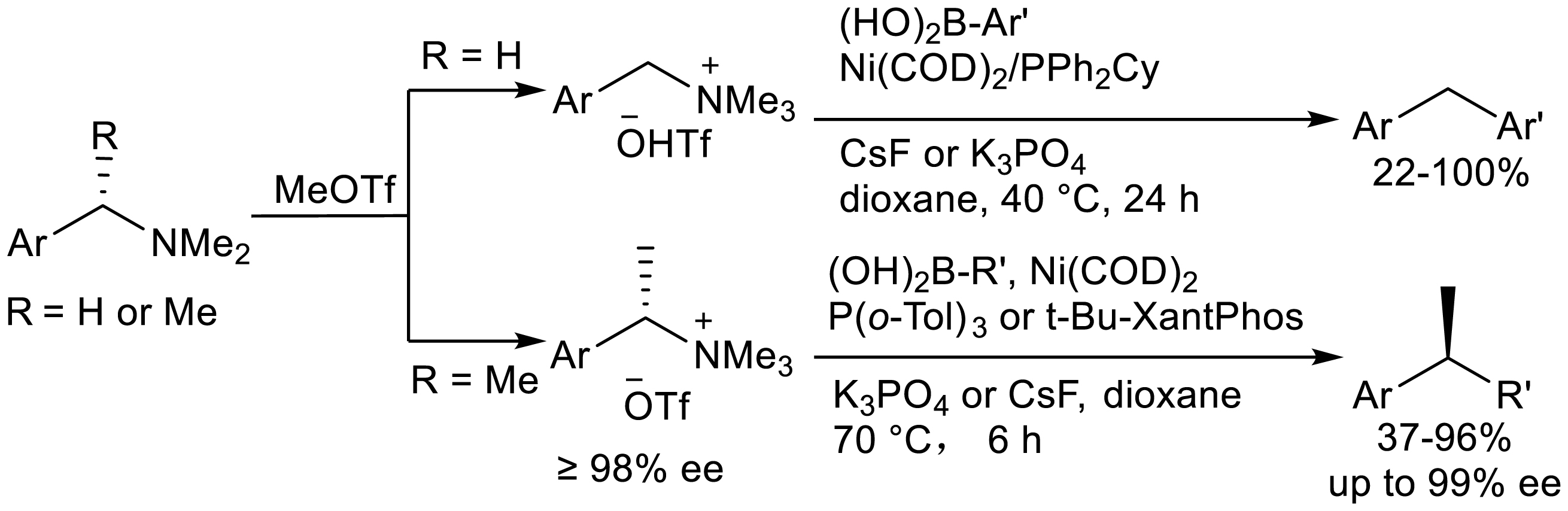
The Watson group discovered the cross-coupling of para-benzylammonium salts and diborates with stereospecificity under nickel catalysis to provide highly enantiomeric-enriched benzylborates (Scheme 3) [10]. The reaction uses an electrophilic agent derived from an amine of high enantiomeric purity, using a simple and inexpensive nickel catalyst (Ni(COD)2 or Ni(OAc)2·4H2O) to give highly enantiomeric pure products under mild conditions. The wide range of reactions enables the synthesis of a variety of para-benzyl paraborates with moderate to high yields (44–83%) and excellent enantiomeric excess (ee) values.
3.
Transition metal-catalyzed C-C bond construction involving quaternary ammonium salts
3.1. Reaction with Grignard reagents
The representative of the reaction of quaternary ammonium salts with organometallic reagents is the reaction with Grignard reagents. Wenkert's group reported a nickel-catalyzed Kumada-Corriu coupling reaction of aryl trimethylammonium iodide with aryl and alkyl Grignard reagents (Scheme 4) [5]. In the presence of Ni[dppp]Cl2 and Et3N, aryl trimethylammonium iodides react with phenyl, benzyl, methyl and isopropyl Grignard reagents in benzene to provide corresponding cross-coupling products at yields of up to 63%. Through this pioneering work, the feasibility of cleaving C-N bonds by adding Ni(0) to the C-N bonds of aryl trimethylammonium salts was demonstrated.
The Boehringer Ingelheim pharmaceutical Reeves team reported palladium-catalyzed cross-coupling of arytrimethylammonium trifluoromethanesulfonate with the aryl Grignard reagent (Scheme 5). The reaction is performed at room temperature and yields a cross-coupling product with a yield of 84–94% [11].
Wang's group reported the cross-coupling of iron-catalyzed aryltrimethylammonium trifluoromethanesulfonate with alkyl Grignard reagent at room temperature, at which the reaction proceeded smoothly in a mixed solvent of THF and NMP (7:1), resulting in a target product with a yield of 43–99% (Scheme 6) [12].
3.2. Reaction with organozinc reagents
In addition to Grignard's reagents, other organometallic reagents have also been used to react with quaternary ammonium salts. In 2011, Wang's group reported the cross-coupling of nickel-catalyzed arytrimethylammonium salts with organozinc reagents [13]. In the presence of Ni(PCy3)2Cl2, the reaction was carried out at 90 °C in a mixed solvent of THF and NMP (1:1), providing the corresponding cross-coupling product at a yield of 25–99% (Scheme 7).
3.3. Reaction with organoaluminum reagents
The Uchiyama group at the University of Tokyo in Japan demonstrated that Ni(dppp)Cl2 catalyzed the alkylation of organoaluminum reagents and aryltrimethylammonium trifluoromethanesulfonates (Scheme 8) [14]. This catalyst and reaction conditions also apply to the coupling reaction of triaryl aluminum reagents. However, only a limited amount of aryltrimethylammonium trifluoromethanesulfonates can successfully fulfill this conversion. When Ni(PCy3)2Cl2-catalyzed i-Bu2AlAr reacts with aryltrimethylammonium trifluoromethanesulfonates, the reaction can adapt to a wide range of aryl ammonium salts, providing a biaryl group with good to excellent yields.
3.4. Reaction with organotin reagents
Uchiyama's group further reported the nickel-catalyzed cleavage of quaternary ammonium salts by C-N bonds and the Stille cross-coupling reaction with organotin reagents (Scheme 9) [15]. In the presence of a commercially available amount of Ni(COD)2, the imidazole ligand and 3.0 equivalent CsF, aryltrimethylammonium salts reacted smoothly with arylstanlenes at a molar ratio of 1:1, providing a corresponding biaryl group with broad functional group compatibility (yield 25–99%).
3.5. Reaction with organolithium reagents
Uchiyama's group discovered that the Pd(PPh3)2Cl2 catalyst can be used to couple aryl lithium compounds with aryl ammonium salts via the cleavage of C-N bonds under mild conditions, yielding biaryl compounds at yields of 46–91% (Scheme 10) [16].
3.6. Reaction with organic boron reagents
Suzuki coupling reaction between quaternary ammonium salts and organic boron reagents forms C-C bonds. MacMillan's group first reported the Suzuki coupling reaction with quaternary ammonium salts which reacted with organic boron reagents catalyzed by nickel (Scheme 11) [17]. During this reaction, the various electron-withdrawing and electron-donating substituents on the arytrimethylammonium trifluoromethanesulfonates and organoboronic reagents are not affected. In addition to arylboronic acids, the scope of the substrates also covers borates and alkenylboranes. This method provides a novel and mild method to activate anilines and realize Ni-catalyzed cross-coupling reaction.
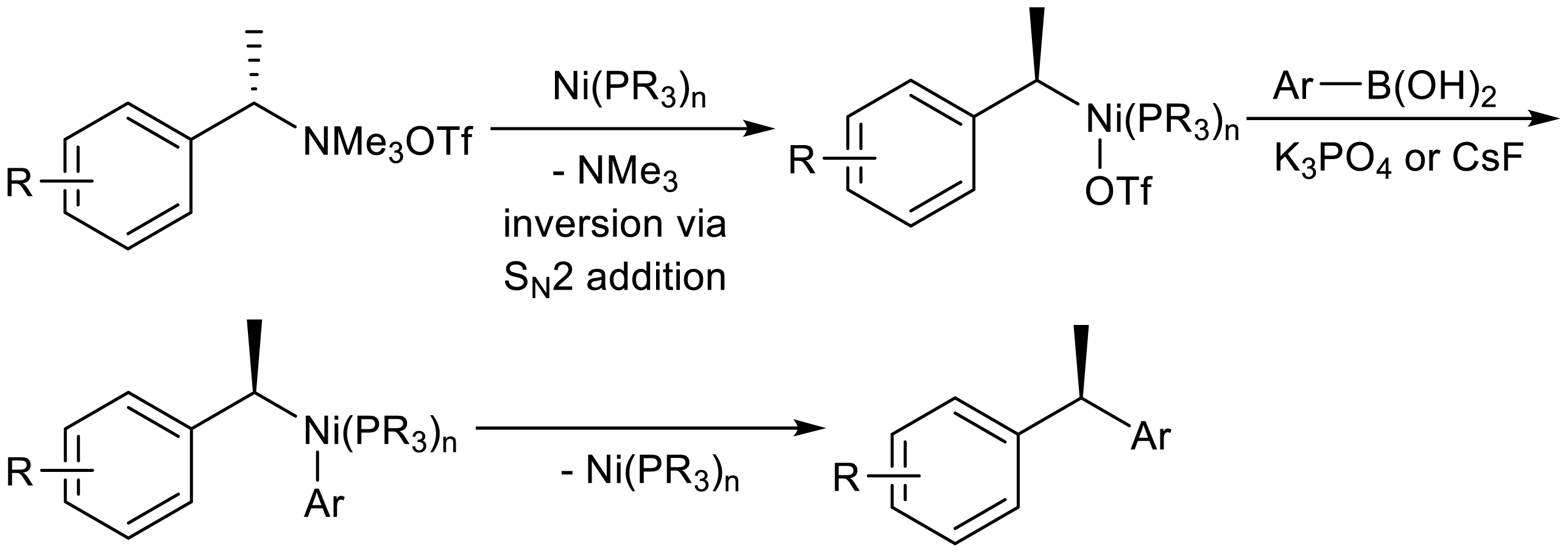
In 2013, Watson of the University of Delaware developed a nickel-catalyzed cross-coupling reaction of benzyl ammonium trifluoromethanesulfonates with arylboronic acids to prepare diarylmethanes and diarylethanes (Scheme 12) [18]. The reaction was carried out under mild reaction conditions and has excellent functional group tolerance. In addition, it converts branched-chain benzyl ammonium salts into diaryl ethanes and the chiralities of the raw quaternary ammonium salts were excellently transferred to the products during the reaction, providing a new synthesis strategy for the synthesis of highly enantiomer-enriched diaryl ethanes.
This paper proposed that the nickel catalyst may carried out oxidation-addition with the carbon-nitrogen bond through the SN2 mechanism, resulting in a reversal of the configuration. Then, under the action of the base the aryl group replaces the trifluoromethanesulfonate group coordinated with the nickel catalyst in the transition state and finally the nickel catalytic reaction intermediate releases the final product chiral diaryltethanes through reduction elimination and the nickel catalyst is recycled (Scheme 13).
3.7. Reaction with terminal alkynes
Quaternary ammonium salts can also be coupled to some compounds with active hydrogen atoms such as terminal alkynes and some heterocyclic compounds with active hydrogen. In 2019, Cao's research group developed a palladium-catalyzed cross-coupling reaction between arylammonium trifluoromethanesulfonates and terminal alkynes (Scheme 14) [19]. The reactants were stoichiometric under mild conditions and the reaction has a wide range of substrates, allowing the use of alkyne substrates with alkyl, aryl and heteroaryl substituents with yields of up to 93%. In 2022, [Pd(IPr)(3-CF3-An)Cl2] was reported as a new efficient catalyst. In the presence of this new catalyst, the yields increased under a similar reaction condition [20].
In the same year, Zhao et al. developed a cross-coupling reaction of benzyltrimethylammonium trifluoromethanesulfonates with terminal alkynes (Scheme 15) [21]. The reaction used Pd(PPh3)4 as the catalyst, does not require additional ligands and the catalyst could easily prepare a series of aryl alkyne derivatives using only the weak base K2CO3. Aryl, heteroaryl, alkyl and silyl acetylenes were adapted to this system. In addition, benzyl trimethylammonium salts with electron-donating groups or weakly electron-withdrawing groups on the benzene ring could also react smoothly with phenylacetylene.
3.8. Reaction with heterocycles with activated sp2 C-H
In 2015, Wang and his collaborators reported palladium-catalyzed reaction of (benzo)oxazoles or (benzo)thiazoles with arytrimethylammonium trifluoromethanesulfonates to produce a series of 2-aryl(benzo)oxazoles or 2-aryl(benzo)thiazoles (Scheme 16) [22]. The reaction used sodium tert-butoxide as base and DMF as solvent and reacted at 120 °C for 12 hours. The reaction of arytrimethylammonium trifluoromethanesulfonates with electron-withdrawing group and electron-donating group with (benzo)oxazoles or (benzo)thiazoles achieved good results.
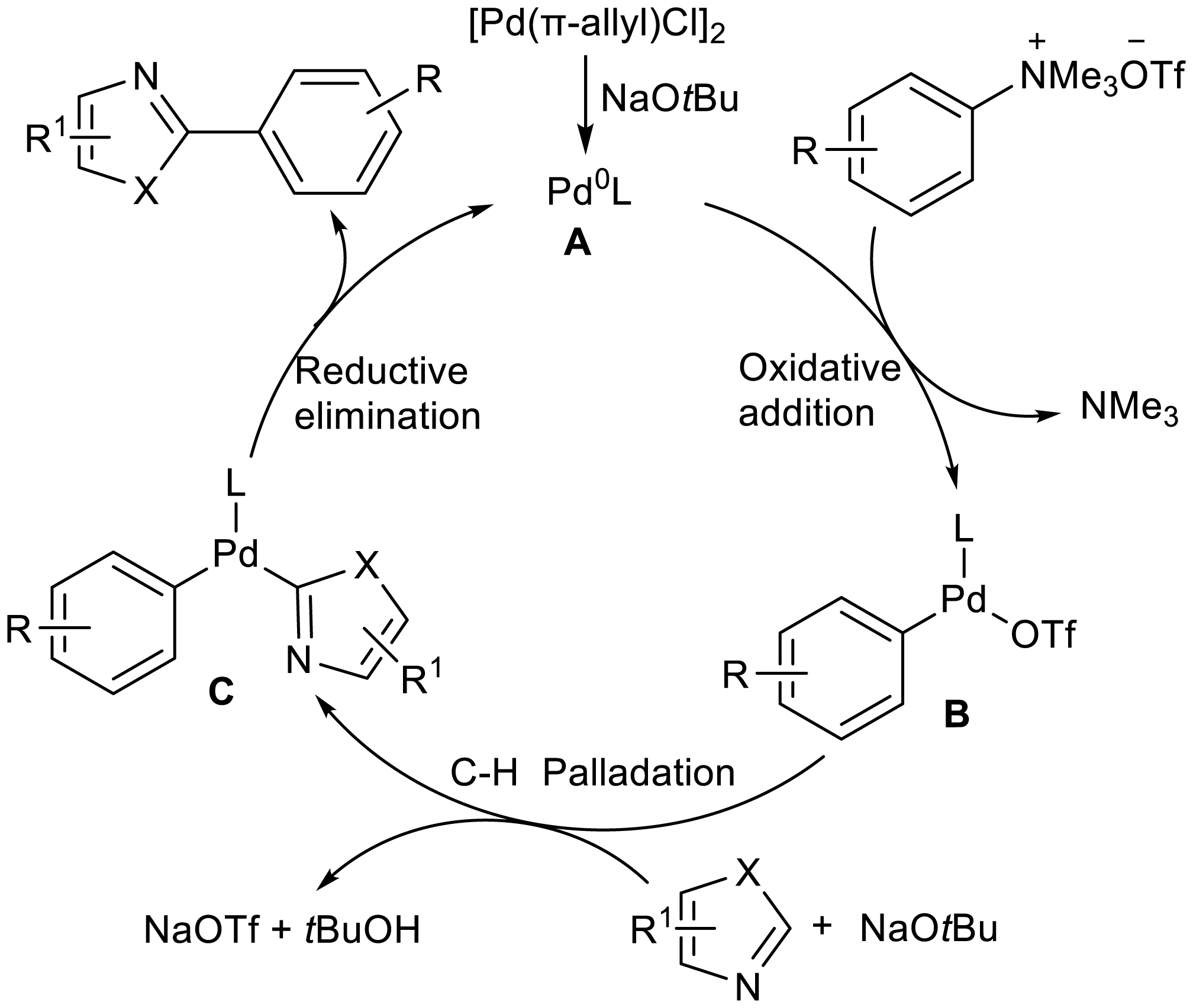
Wang proposed the following mechanism (Scheme 17): The in situ formed zero-valent palladium A carries out oxidative addition with the aryl ammonium salts to form the intermediate palladium complexes B and trimethylamine is eliminated. Under the action of alkali, azoles and intermediate B perform C-H bond palladation to form aryl heteroaryl palladium intermediates C and finally C carry reductive elimination to afford cross-coupling products while the Pd(0) complex is regenerated.
3.9. Reaction with organosilicates
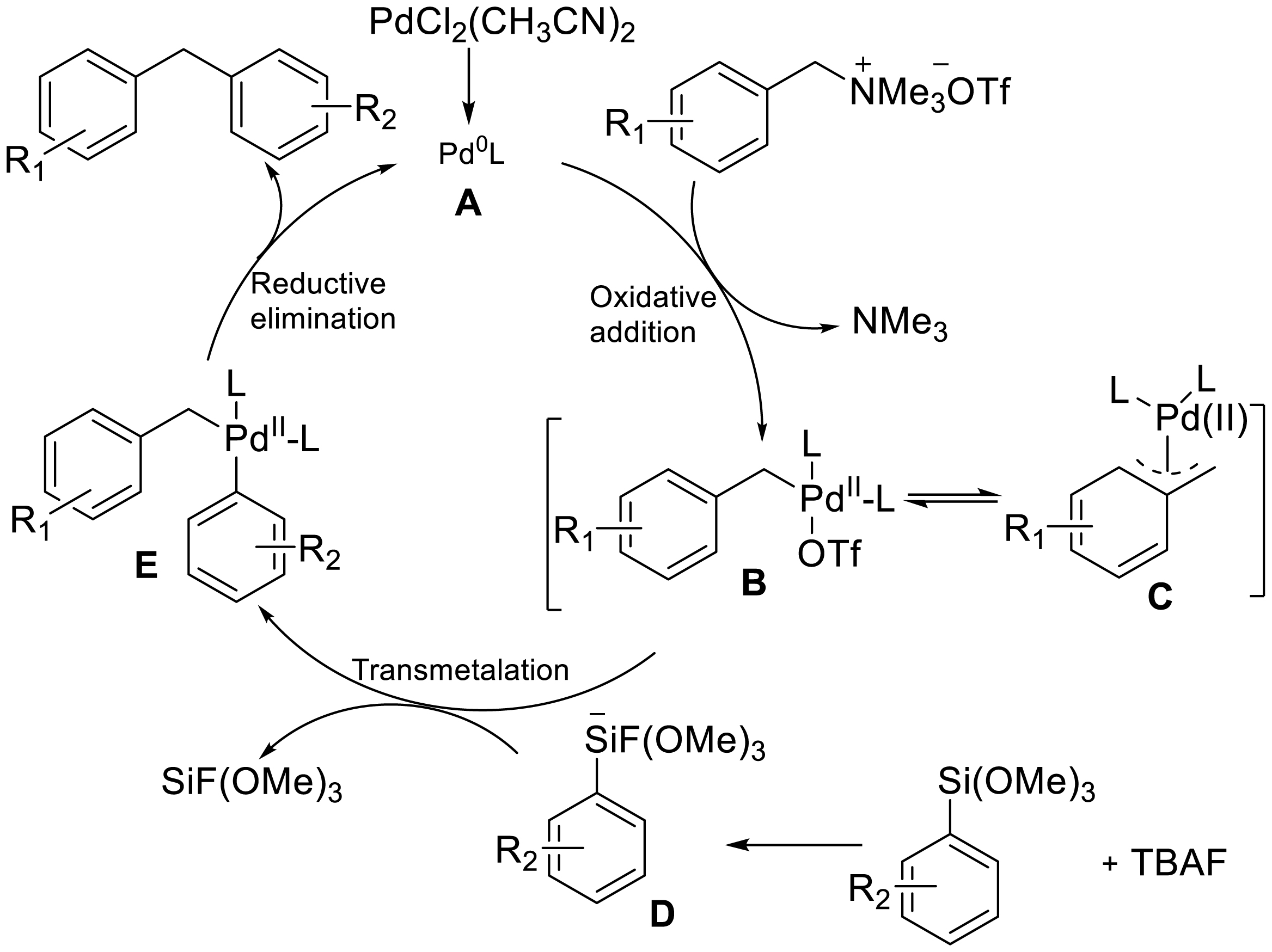
Quaternary ammonium salts can also cross couple with aromatic organosilicates. Zhao's group first reported the Hiyama cross-coupling reaction between aromatic organosilicates and benzyltrimethylammonium salts catalyzed by palladium (Scheme 18) [23]. The reaction yielded the product diarylmethanes at good yields and the products had broad functional group tolerance.
Zhao believed that the reaction proceeds as follows (Scheme 19): Under optimized reaction conditions, Pd(0) source A is formed in situ from PdCl2(CH3CN)2. Subsequently, A is oxidized with benzyltrimethylammonium salts to produce C(sp3)–Pd complex B by cleavage of C-N bond, releasing the by-product trimethylamine. Palladium complex E is then prepared by metal transfer reaction of C(sp3)–Pd complex B with arylsilane D. Finally, the coupling product is released when the palladium complex E is reduced and eliminated and the Pd(0) catalyst is regenerated to complete the catalytic cycle.
3.10. Reaction with carbon dioxide
Carbon dioxide and carbon monoxide can also react with quaternary ammonium salts to form products containing carboxyl or carbonyl groups. In 2016, Martin's group reported nickel-catalyzed reactions of quaternary ammonium salts with carbon dioxide (Scheme 20) [24]. The reaction undergoes carbon-nitrogen bond cleavage of quaternary ammonium salts and reduced carboxylation of carbon dioxide and the method is suitable for a variety of substrates including sec-benzylammonium salts with β-hydrogen and avoids the dimer or elimination products typically observed in carboxylation reactions with benzyl electrophiles.
In 2018, Yu's group reported an iridium-catalyzed electrophilic cross coupling reaction without an external reducing agent through visible light redox (Scheme 21) [25]. Carbon dioxide is selectively coupled using benzylamine quaternary ammonium salts with primary, secondary and tertiary carbons. Of note, the in situ by-product of this reaction, trimethylamine, is effectively used as an electron donor. Moreover, this protocol exhibits mild reaction conditions, low catalyst loading, wide substrate range, good functional group tolerance and easy scalability. Unfortunately, since this reaction may involve the photocatalytic single-electron reduction of benzyl quaternary ammonium salts, this reaction can only obtain racemic carboxylic acid products even for optically pure quaternary ammonium salts [25].
3.11. Reaction with carbon monoxide
In the same year, Wang and his collaborators reported a palladium-catalyzed three-component reaction of benzyltrimethylammonium trifluoromethanesulfonates, carbon monoxide and corresponding nucleophiles to form arylacetamides and aryl esters (Scheme 22) [26]. This method has mild reaction conditions, is suitable for carbon monoxide conditions at one atmospheric pressure and does not require redox additives. The reaction is suitable for a variety of substituted benzyltrimethylammonium salt substrates and alkyl and aryl amines, alcohols and phenols can be used as nucleophiles.
4.
Transition metal-catalyzed C-N bond construction involving quaternary ammonium salts
Compounds containing C-N bonds have a wide range of uses in biomedicine, pesticides, functional materials and other fields. Amines may be synthesized by cleavage of C-N bond of quaternary ammonium salts and C-N cross coupling reaction with amino-containing compounds.
Wang's group found that aromatic quaternary ammonium salts could react with amines in the presence of nickel catalysts for C-N cross-coupling reactions (Scheme 23) [27]. This reaction enables the conversion of simple aromatic amines to new higher aromatic amines. The range of substrates for electrophilic reagents is suitable for both activated and unactivated aryl trimethylammonium trifluoromethanesulfonates. The range of substrates for amines includes aliphatic, aromatic primary and secondary amines, cyclic amines and sterically hindered amines.
Zeng's group reported the Buchwald-Hartwig-type cross-coupling reaction of aromatic quaternary ammonium salts and benzyl quaternary ammonium salts with NH-containing heteroaromatics catalyzed by palladium (Scheme 24) [28]. In the presence of Pd(OAc)2 and t-BuXPhos, cross coupling reaction of aryl or benzyltrimethylammonium trifluoromethanesulfonates with NH-heteroaromatics by cleavage of C–N bond yielded nitrogenous heteroaromatics at yields of 30–89%. The reaction substrate ranges from a wide range of nitrogenous aromatics including indole, benzimidazole, benzotriazole, carbazole, pyrrole and pyrazole. This method is an important complement to the Buchwald-Hartwig cross-coupling reaction.
5.
Transition metal-catalyzed C-Si bond construction involving quaternary ammonium salts
The cross-coupling reaction of quaternary ammonium salts with silane reagents can also provide compounds with C-Si bond which have good potential applications because C-Si bond are easily converted to other carbon hetero bonds. The Montgomery group at the University of Michigan proposed a nickel-catalyzed method for converting arylammonium salts to arylsilanes (Scheme 25) [29]. The nitrogen heterocyclic carbene (NHC) ligand used in this method has excellent reaction effect. This method has mild reaction conditions, is resistant to a wide range of functional groups and can obtain arylsilanes from simple aniline building blocks (15–98% yields).
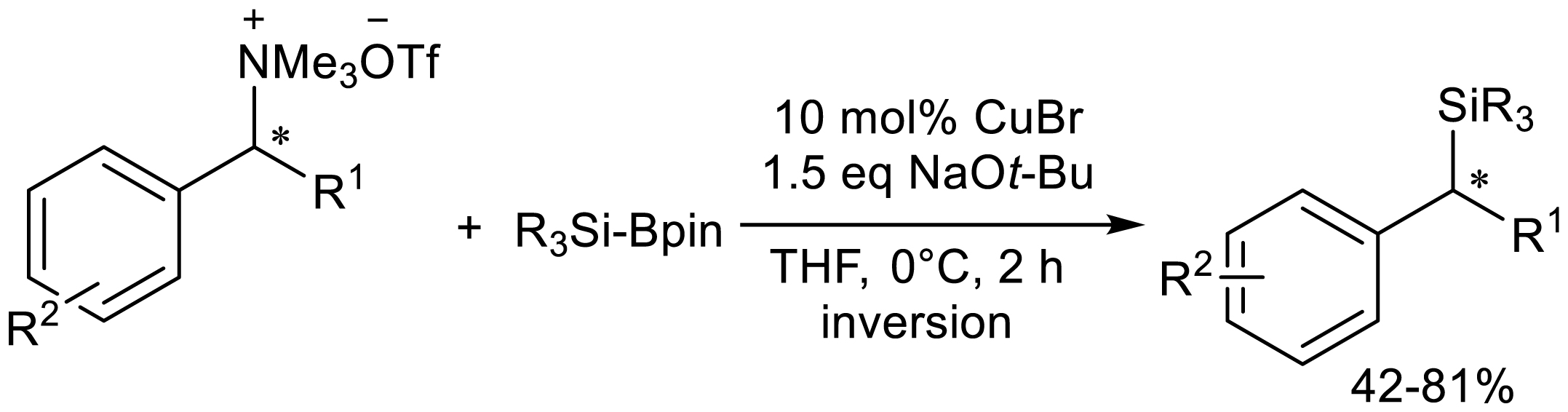
The Oestreich group at the Technical University of Berlin, Germany reported a method for synthesizing benzylsilane starting with the corresponding quaternary ammonium trifluoromethanesulfonates (Scheme 26) [30]. The reaction was catalyzed by copper (I) salt, tetrahydrofuran as solvent, silyl borate as silicon pronucleophile and the corresponding benzyl silane could be obtained by reacting at 0 °C for 2 h with yields of 42–81%. Some enantiomeric-rich benzylammonium salts undergo stereotactic reactions by SN2 substitution of ammonium groups, resulting in α-chiral silanes with reverse configurations. Cyclopropyl substituted substrates do not open the ring. Thus, indicating an ionic reaction mechanism without benzyl intermediates.
6.
Transition metal-catalyzed C–P bond construction involving quaternary ammonium salts
Wang et al. found that quaternary ammonium salts underwent a C–P bond cross-coupling reaction with dialkyl phosphine oxide. This reaction underwent phosphonylation with quaternary ammonium salts with appropriate phosphorus-containing nucleophiles catalyzed by NiCl2 under the action of cesium carbonate (Scheme 27) [31]. The phosphine nucleophiles used include diaryl/dibutylphosphine oxides, dialkylphosphonates and ethyl phenylphosphinates and the quaternary ammonium salts used include aryl/benzyl quaternary ammonium salts, heteroaromatic quaternary ammonium salts and allyl quaternary ammonium salt (Scheme 11). The reaction conditions are mild and the reaction substrates are extensive. However, some substrates gave low yields.
Zeng and his collaborators found that copper-catalyzed cleavage of the C-N bond and cross coupling of C–P bond between quaternary ammonium salts and diarylphosphine oxides or dicycloalkyl phosphine oxides could be achieved in moderate to good yields without strict protection with an inert gas (Scheme 28) [32].
7.
Transition metal-catalyzed C-S bond construction involving quaternary ammonium salts
Organosulfur compounds are widely used in various fields, especially in the pharmaceutical industry and sulfur-containing drugs are used to treat a variety of diseases [33],[34]. In this context, our group completed the construction of multiple C-S bonds based on the participation of quaternary ammonium salts under transition metal catalysis on the basis of long-term study of sulfur chemistry [35],[36] (Scheme 29).
Our research group fulfilled Cu(I)-catalyzed cleavage of C-N bond and C-S cross coupling reaction of chiral benzyl quaternary ammonium salts in situ prepared from enantiomer-enriched chiral benzylamines and methyl trifluoromethanesulfonate and a variety of nucleophilic sulfur sources (such as mercaptans, thiols, sodium thioacetate, etc.). A series of highly enantiomeric pure chiral benzyl sulfides, chiral benzyl sulfones, chiral benzyl thioacetates were obtained (Scheme 12) [37]. The reaction substrate has a wide range (55 products) and can be applied to a variety of enantiomer-enriched benzyl quaternary ammonium salts among which benzyl α-amino acid ester-derived quaternary ammonium salts can also react and provide the corresponding product chiral α-phenylthiophenylacetate methyl ester with a yield of 85%. Notably, all reactions produced highly diastereomerically pure products with Walden inversion in configuration with ee values of 94–99%.
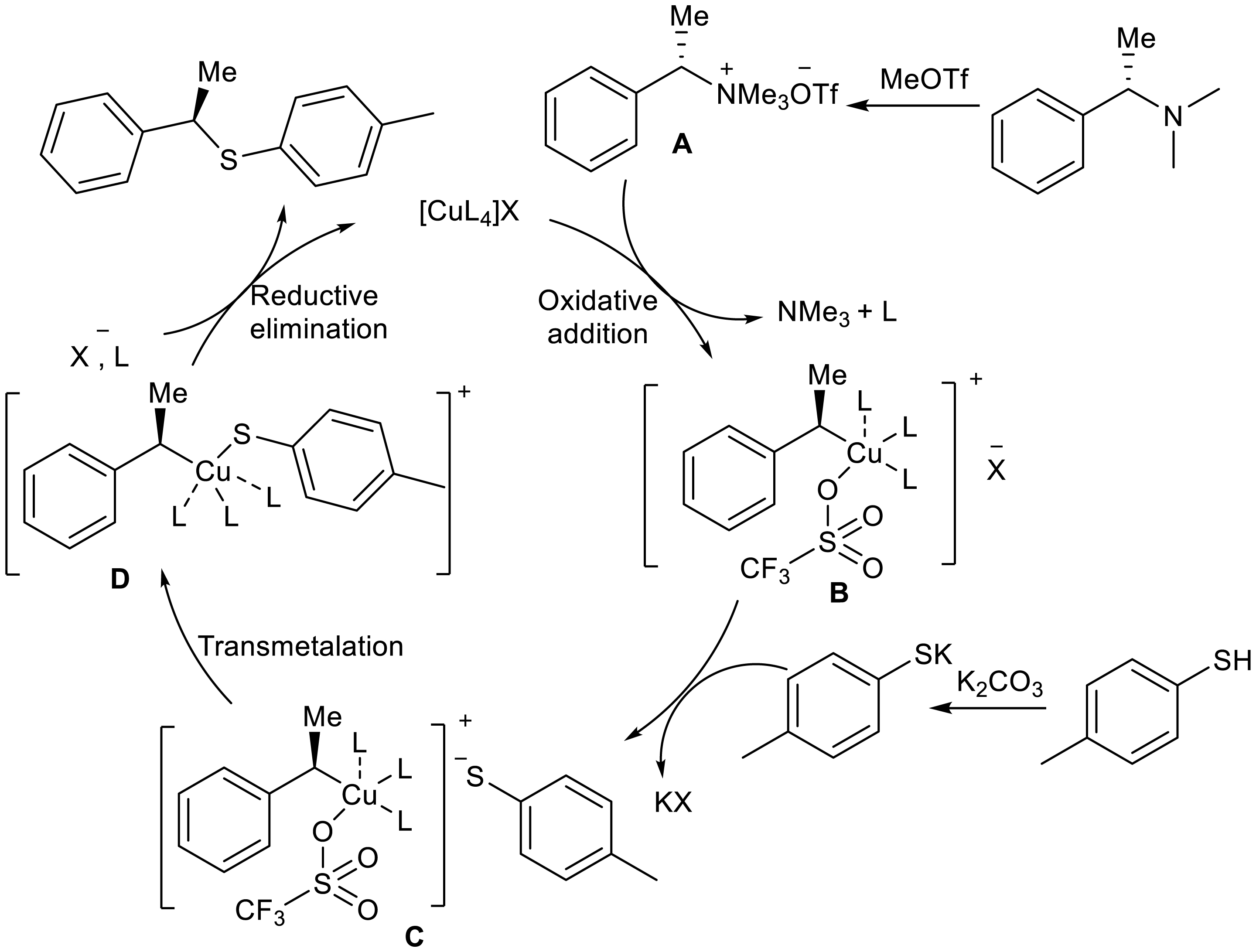
The reaction mechanism is speculated as follows (Scheme 30): Benzyl quaternary ammonium A and the copper catalyst undergo oxidative addition. While trimethylamine is removed, intermediate B is formed. Then, the anion group is exchanged with potassium p-toluenethiolate to form intermediate C. Then, the key complex D is obtained by the transfer metallization of the inner and outer anion groups. Then, D is reduced and eliminated to give the target product chiral benzyl sulfide and the catalyst is restored. The Walden inversion should occur when the copper catalyst and benzyl quaternary ammonium salts undergo oxidative addition.
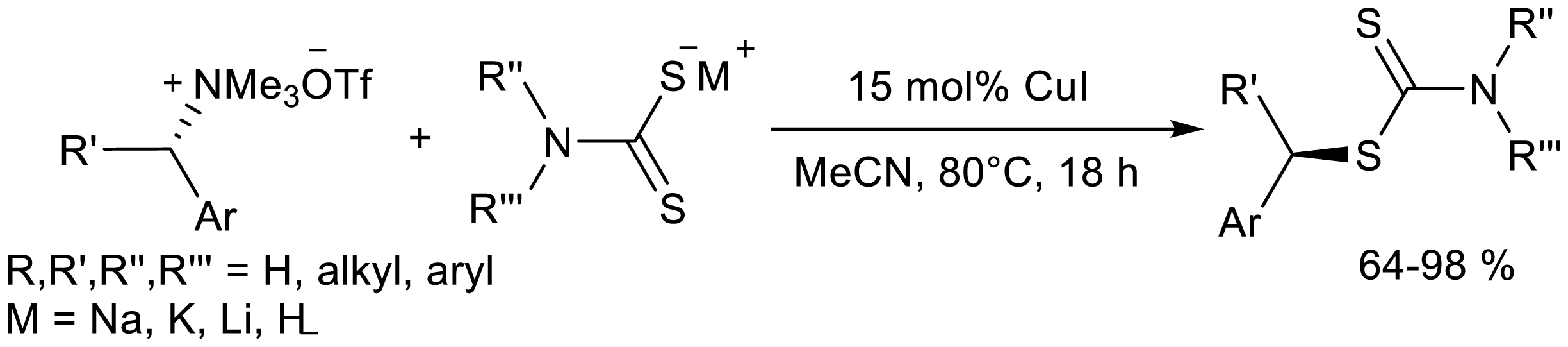
Zeng's group provided a copper-catalyzed method for cross-coupling quaternary ammonium salts with alkyl dithiocarbamates to provide the corresponding products with C-S bond (Scheme 31) [38]. The yields of this reaction were generally high and the product can be easily converted into sulfur-containing organic compounds such as thioether, thiols and thiols which provides a new synthesis strategy of organic sulfur molecules. A wide range of common benzyl quaternary ammonium salts, allyl quaternary ammonium salts, phenethyl quaternary ammonium salts and amino acid ester quaternary ammonium salts can be applied to this system. For alkyl dithiocarbamates, both monoalkyl substituted and dialkyl-substituted dithiocarbamates could carry out this reaction. For enantiomeric pure benzyl quaternary ammonium salts, the target products with configuration inversion can be obtained with excellent ee values (93–99%).
8.
Conclusions and outlook
The study of C-N bond activation and cleavage of amines is a research hotspot. This review mainly introduces the research progress of transition metal-catalyzed cleavage of C-N bond of aromatic amines- and benzylamine-derived quaternary ammonium salts and construction of new C-X bonds in recent years. Through the cleavage of C-N bond, quaternary ammonium salts are suitable for synthesis of borates, aromatics, alkanes, ethers, amines, silanes, phosphine, sulfides, disulfides, selenium ethers, diselenoides and other organic compounds.
Tremendous progress has been made in the study of quaternary ammonium salts constructing new C-X bonds through cleavage of C-N bonding, but there are still many development opportunities. Photoinduction or photocatalysis and electrochemistry have made gratifying progress, but it may be that because the reaction process is a free radical reaction, enantiomeric-enriched chiral products cannot be obtained even with optically pure chiral benzyl quaternary ammonium salts as substrates which needs further research. The use of new experimental methods such as photocatalysis or light induction, electrochemistry, ultrasound, microwave, etc., is also a worthy field for development in this field.
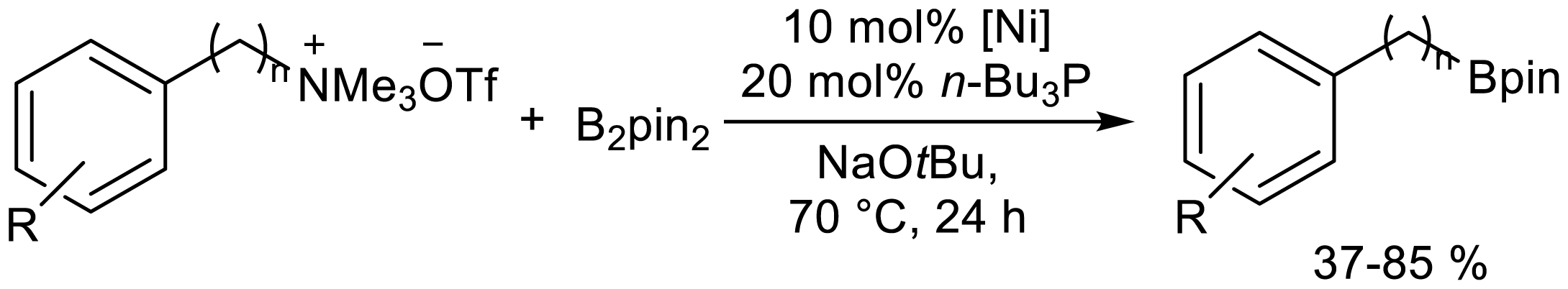









 DownLoad:
DownLoad: