Two-grid method for semiconductor device problem by mixed finite element method and characteristics finite element method

1.   Introduction

In this study, we consider the following mathematical model of a semiconductor device, which consists of three quasilinear partial differential equations [1,15]:

where (1) is an elliptic-type partial differential equation for the electric potential, and (2) and (3) are parabolic-type partial differential equations for the electron and hole concentrations. The unknown functions are the electrostatic potential $\psi$, the electron concentration $e$, and the hole concentration $p$. $\Omega$ is a polygonal domain in $\mathbb{R}^{d}(d = 2,3)$. The value of $\alpha$ is $q/{\epsilon}$, $q$ is the electron charge, and ${\epsilon}$ is the dielectric permittivity. These are all positive constants. $N(x) = N_{D}(x)-N_{A}(x)$ is a given function of $N_{D}(x)$ and $N_{A}(x)$ that represents the donor and acceptor impurity concentrations. The diffusion coefficients $D_{s}(x)(s = e,p)$ and the mobilities $\mu_{s}(x)(s = e,p)$ obey the Einstein relation $D_{s}(x) = U_{T}\mu_{s}(x)$, where $U_{T}$ is the thermal voltage. $R(e,p)$ is a recombination term.

It is assumed that the boundary and initial conditions are as follows:

In addition, we need the compatibility condition

The study of the transient behaviors of semiconductor devices plays an important role in modern computational mathematics. Since Gummel [14] first presented sequence iterative computation methods for this kind of problem in 1964, a variety of numerical approaches have been introduced to obtain better approximations for (1)–(3). The main techniques include the difference method [13], finite element method [27], mixed finite element method [25], characteristics finite element method [26], characteristics finite difference method [24], upwind finite volume method [21], and characteristics mixed finite element method [22].

The semiconductor device problem becomes a large system of non-linear equations when using the finite element method to solve (1)–(5). Thus, we will consider a highly efficient and accurate algorithm for this large system. It is well known that the two-grid algorithm is a simple but effective algorithm. This method was first proposed by Xu for non-linear elliptic equations [18,19] and has been widely used in many kinds of problems. Dawson [10] applied a two-grid finite difference scheme for non-linear parabolic equations. Chen [6,5] presented an efficient two-grid scheme for semi-linear reaction–diffusion equations and miscible displacement problems. Dai [9] used a two-grid method based on Newton iteration for the Navier–Stokes equations. Chen and Yang [4] introduced this method for finite volume element approximations of nonlinear parabolic equations. Yu [23] presented a two-grid algorithm for mixed Stokes–Darcy problem. Wang investigated this method for semilinear elliptic interface problem [16]. Xu and Hou recently used this method for semilinear parabolic integro–differential equations [20]. Thus, it would be natural to use the two-grid method for the equations of a semiconductor device.

The electric field intensity ${\boldsymbol{u}} = -\nabla \psi$ is very important in production, and the numerical behavior of (2) and (3) strongly depends on the accuracy of the approximation of ${\boldsymbol{u}}$. To improve the accuracy of $e$ and $p$, we apply the mixed finite element method, which gives direct approximations of $\psi$ and ${\boldsymbol{u}}$ simultaneously for the electric potential equation (1). The direct approximation of the electric field intensity, rather than one that requires differentiation of $\psi$, can provide improved accuracy for the same computational effort.

We use the characteristics finite element method for the electron and hole concentration equations, (2) and (3), respectively. In reality, the values of $D_{s}(s = e,p)$ are quite small in the concentration equations, and thus, (2) and (3) are strongly convection dominated. The standard finite element method produces unacceptable numerical diffusion or nonphysical oscillations in the concentration approximation. The characteristics finite element method was introduced and analyzed by Douglas and Russell [12] in 1982. Using this method to treat the hyperbolic parts of the concentration equation, the procedure is simple, the time-truncation errors are smaller, and lastly and most importantly, nonphysical oscillations are avoided.

We determine the $L^q$ error estimates for the mixed finite element solutions and the characteristics finite element solutions. We then present an efficient two-grid method based on the idea of Newton iteration. To the best of our knowledge, few results about the application of the two-grid algorithm to semiconductor device problems have been reported. The main idea of this algorithm is to solve the nonlinear coupled equations on a coarse grid, and then to solve the linear equations on a fine grid rather than solving the coupled nonlinear equations on the fine grid. Finally, we obtain the $L^{q}$ error estimates for this algorithm and give the numerical experiment to illustrate the theoretical results. The two-grid algorithm achieves asymptotically optimal approximations but requires less time.

An outline of this paper is as follows. In Section 2, we present the weak formulation and full discrete scheme of this model. In Section 3, we present the $L^q$ error estimates of the finite element solutions. In Section 4, we introduce a two-grid algorithm and analyze its convergence. Finally, the numerical experiment is presented in Section 5.

2.   Weak formulation and full discrete scheme

2.1.   Notation and assumptions

In this paper, we denote $L^q(\Omega) = \{f:\|f\|_{L^q(\Omega)} <\infty\}$, where

$(L^2(\Omega))^2$ is the space of vectors that contains each component in $L^2(\Omega)$. We define the Sobolev spaces as $W^{m,q}(\Omega) = \{f\in L^{1}_{loc}(\Omega):\|f\|_{W^{m,q}(\Omega)}<\infty\}$, whose norms are

To simplify the notation, we write $H^m(\Omega) = W^{m,2}(\Omega),$ $\|\cdot\|_m = \|\cdot\|_{m,2}$ and $\|\cdot\| = \|\cdot\|_{0,2}$. Let $X$ be any of the spaces just defined. If $f(x,t)$ represents functions on $\Omega \times J$, we set

For convenience, we drop $\Omega$ from the notations. Thus, we write $L^{\infty}(J;H^{k+3})$ for $L^{\infty}(J;H^{k+3}(\Omega))$.

We let $(\cdot,\cdot)$ be the $L^2(\Omega)$ inner product. Furthermore, $H^1_0(\Omega) = \{f\in H^1(\Omega):f|_{\partial\Omega} = 0\}$, and $H(\mathrm{div};\Omega)$ is the set of vector functions in $(L^2(\Omega))^2$ that have $\nabla\cdot {\boldsymbol{v}} \in L^2(\Omega)$. We also define

We provide some rational assumptions about the coefficients and the solutions of (1)–(3). These assumptions are reasonable in physics [15,14].

(1) For integers $l,k\geq0$, the solution functions have the following regularity (A)

(2) The problem is positive definite, such that

where $D_*$, $D^*$, $\mu_*$, and $\mu^*$ are positive constants.

(3) $|\nabla\mu_{s}(x)|\leq C,\quad s = e,p.$

(4) $R(e,p)$ is Lipschitz continuous in an $\varepsilon$-neighborhood of the solutions.

2.2.   Characteristics method for the concentration equations

For the electron and hole concentration equations, (2) and (3), respectively, convection is dominant over diffusion, so we use the characteristics finite element method to solve them.

We rewrite (2) and (3) in the form

where ${\boldsymbol{u}} = -\nabla\psi$.

We let ${\boldsymbol{u}} = (u_{1}, u_{2})^{T}$, $\tau_{e}$ be the unit vector in the direction $(-\mu_{e}u_{1}, -\mu_{e}u_{2},1)$, $\tau_{p}$ be the unit vector in the direction $(\mu_{p}u_{1}, \mu_{p}u_{2},1)$, and $\phi_{s} = \sqrt{1+\mu^{2}_{s}(u^{2}_{1}+u^{2}_{2})}$ $(s = e,p)$. The characteristic derivatives in the $t$ direction are given by

Associated with the equations above, (7) and (8) can be rewritten as follows:

We partition $J$ into $\triangle t = T/N$ and $t^n = n\triangle t$. Furthermore, we denote $f^{n}(x)$ as $f(x,t^{n})$ and $(\partial e^n/\partial \tau_{e})(x)$ as $(\partial e/\partial \tau_{e})(x,t^n)$. The backward difference quotient in the $\tau_{e}$-direction is as follows:

Defining $\hat{x}^{n-1}_{e} = x+\mu_{e}{\boldsymbol{u}}^{n}(x)\triangle t$ and $\hat{e}^{n-1}(x) = e^{n-1}(\hat{x}^{n-1}_{e})$, then

Similarly,

Defining $\hat{x}^{n-1}_{p} = x-\mu_{p}{\boldsymbol{u}}^{n}(x)\triangle t$ and $\hat{p}^{n-1}(x) = p^{n-1}(\hat{x}^{n-1}_{p})$, then

2.3.   Weak form and full discrete procedure

The weak forms of (1), (9) and (10) are equivalent to the following problem: for $t\in J$, find a map $\{\psi,{\boldsymbol{u}},e,p\}:J\rightarrow W\times {\boldsymbol{V}}\times H_{0}^1(\Omega)\times H_{0}^1(\Omega)$ such that $e(x,0) = e_0(x)$, $p(x,0) = p_0(x)$:

We let $\mathcal{T}_{h_{\psi}}$ and $\mathcal{T}_{h_c}$ be a quasi-uniform mesh of $\Omega$ comprising triangles or rectangles such that the elements have diameters bounded by $h_{\psi}$ and $h_{c}$. We denote $W_{h}\times {\boldsymbol{V}}_{h}\subset W\times {\boldsymbol{V}}$ as the Raviart–Thomas mixed finite element spaces with order $k$. The approximation properties are given as follows:

We denote $M_{h}\subset H_{0}^1(\Omega)$ as a piecewise polynomial space of degree $l$, and

Using (11) and (12), the full discrete scheme of the weak form, (13)–(16), consists of $\{\psi^n_h, {\boldsymbol{u}}^n_h,e^n_h,p^n_h\}\in W_{h} \times {\boldsymbol{V}}_{h}\times M_{h}\times M_{h}$, given by

where $\partial_{\tau_{e}}e_{h}^n = \frac{e_{h}^n-\hat{e}_{h}^{n-1}}{\triangle t}$ and $\partial_{\tau_{p}}p_{h}^n = \frac{p_{h}^n-\hat{p}_{h}^{n-1}}{\triangle t}$. In addition, the initial approximations $e^0_h$ and $p^0_h$ must be determined by the elliptic projections of $e_0$ and $p_0$.

3.   $L^q$ error estimate of finite element solution

In this section, we present the $L^q$ error estimate of the mixed finite element method for the electrostatic potential and electric field intensity and the characteristics finite element method for the concentrations.

3.1.   Convergence analysis of mixed finite element solution

First, it is useful to introduce an elliptic mixed method projection $(R_h \psi, R_h {\boldsymbol{u}}): J \rightarrow W_{h}\times {\boldsymbol{V}}_{h}$, which satisfies

Following Brezzi [3], we have

The estimations of $\psi^n_h-R_h\psi^n$ and ${\boldsymbol{u}}^n_h-R_h{\boldsymbol{u}}^n$ are derived as follows. By subtracting (21) and (22) from (17) and (18), respectively, at time $t = t^n$, we determine that

Following Brezzi [3], we have

3.2.   $L^q$ error estimate of characteristics finite element method

We introduce an elliptic method projection $(R_h e,R_h p): J \rightarrow M_{h}\times M_{h}$ such that

where the positive constants $\lambda_{s}(s = e,p)$ will be chosen to ensure the coercivity of the forms. Based on the theory of the Galerkin method for elliptic problems [8,17], we have

To obtain the convergence estimations of $\|s^n-s^n_h\|_{0,q}(s = e,p)$, we divide them as follows:

For the concentration, we only discuss the electron concentration equation, as the results were similar for the hole concentration equation. First, we obtain the convergence results of $\|s^n-R_h s^n\|_{0,q}(s = e,p)$ with help of an elliptic problem.

Lemma 3.1. If $(e^{n}, p^{n})$ is the solution of (15)–(16) at $t = t^{n}$, and $(R_he^{n},R_hp^{n})$ is the elliptic projection solution of (27)–(28) at $t = t^{n}$, then for $1\leq n \leq N$, $2\leq q < \infty$ and $l\geq1$, we have the following:

Proof. We let $L$ denote an elliptic operator such that

and it has a bilinear form

where $\lambda$ will be chosen to ensure the coercivity of $a(e^n,z)$. From (27), it is clear that $R_he^n$ is the finite element solution of this elliptic problem. We consider the auxiliary problem

This problem is uniquely solvable for $\omega \in L^p(\Omega)$, and

where $\frac{1}{p}+\frac{1}{q} = 1$. We use a duality argument. Based on (27), Hölder's inequality, and (33), we denote $I_h$ as an interpolation operator and obtain

From [2,Theorem 8.5.3] and the approximation property, we have

Using (34) and (35), we have

Lastly, we obtain similar results for the hole concentration equation.

Next, we obtain the convergence property for $\|R_hs^n-s^n_h\|_{0,q}(s = e,p)$.

Lemma 3.2. Let $(R_h e^n, R_h p^n)$ be the elliptic projection solution of (27)–(28) at $t = t^n$, and $(e_h^{n}, p_h^{n})$ be the finite element solution of (19)–(20). If the regularity assumptions (A) hold, and the initial functions $e_h^{0} = R_h e^0$ and $p_h^{0} = R_h p^0$, then for $1\leq n \leq N$, $2\leq q < \infty$ and $l,k\geq1$, we have

Proof. The proof process is similar to the analysis presented by [25] and [26], but with some changes. First, we subtract (15) and (27) from (19) at $t = t^n$ to have

We let $\xi_{e}^n = e^n-R_he^n$, $\zeta_{e}^n = e^n_h-R_he^n$, $\xi_{p}^n = p^n-R_hp^n$, $\zeta_{p}^n = p^n_h-R_hp^n$, and select $z = \zeta_{e}^n-\zeta_{e}^{n-1} = \partial_{t}\zeta_{e}^{n}\Delta t$. Summing over $1\leq n \leq m$, from (38), we have the following:

where

Now we estimate each term on the right hand of (39). First, using a second-order Taylor expansion at point $(e_h^n,p_h^n)$ for $R(e^n,p^n)$, Young's inequality, and (29), we have

where $R_{e}$ and $R_{p}$ are the partial derivatives for each variable.

For $F_2$, we have

For the estimation of $F_3$, using (29), we get

As to $F_4$, we obtain similar estimate:

For $F_5$, we obtain

where the calculations of (41), (42), and (44) are presented in detail elsewhere [25,26].

For $F_6$, from (29) we have

Next, we obtain an error estimate for $F_7$. Using (26), (29), and (23), we have

Hence, we conclude that

Finally, for $F_8$, we have

From (29), we can determine the following:

Thus, we have

Combining (39) with (40)–(47) and noting that $e_h^{0} = R_h e^0$ and $p_h^{0} = R_h p^0$, we have

To obtain the $H^1$ norm of $\nabla\zeta_{e}^m$, we add $\|\zeta_{e}^m\|^2$ to the above equation. Note that

The both sides of the above inequality are sum from $n = 1$ to $m$, then we have

Similarly, for the $L^{2}$ estimates of $\nabla\zeta_{p}$ and $\zeta_{p}$, we find that

Combining (48)–(51) and selecting sufficiently small values of $\Delta t$ and $\varepsilon$, we obtain

where $C = C(\varepsilon)$ is a constant that depends on $\varepsilon$. An application of the discrete Gronwall Lemma yields the following:

Then, for $1\leq m\leq N$, we determine that

Similar to the proof process of Theorem 3.4 in [19], we determine that

We apply a duality argument to estimate $\|e_{h}^n-R_{h}e^n\|_{0,q}$ by considering an auxiliary problem: find $\omega\in H^1_0(\Omega)$ such that

This problem is uniquely solvable for $\omega \in L^q(\Omega)$, and

where $p = q/(q-1)\in [1,2]$ for $2\leq q\leq \infty$. If $s = 2q/(q + 2)$, applying the Sobolev embedding theorem, we have

By Lemma 3.1 of [19] and (53), we have

For $q = 2$, since $s = 1$, from (52), we have the following:

For $2<q<\infty$, since $2s<q$, we have

which yields (36). Similarly, we can obtain (37).

From Lemmas 3.1 and 3.2, we obtain the following important theorem:

Theorem 3.3. Let $(e^{n}, p^{n})$ be the solution of (15)–(16) at $t^n$, and $(e_h^{n}, p_h^{n})$ be the finite element solution of (19)–(20). If the regularity assumptions (A) hold, and the initial functions $e_h^{0} = R_h e^0$ and $p_h^{0} = R_h p^0$, then for $1\leq n \leq N$, $2\leq q < \infty$ and $l,k\geq1$, we have

3.3.   $L^q$ error estimate of mixed finite method

First, it is useful to denote the $L^2$ projection $Q_h$ as follows. For $\boldsymbol {\rho}\in (L^2(\Omega))^{2}$,

For $\boldsymbol {\rho}\in ( W^{k+1,q}(\Omega))^2$, the $L^2$ projection operator has approximation property [11]:

Next, the $L^q$ error estimate of the electrostatic potential will be obtained. We obtain the following error equations by subtracting (13) and (14) from (21) and (22), respectively:

Let $D_h$ be the $L^2$-projection onto the space

$D_h$ has the following stability property [7]:

Lemma 3.4. If ${\boldsymbol{u}}^n$ and $R_h{\boldsymbol{u}}^n$ are the solutions of (13)–(14) and (21)–(22), respectively, at $t = t^n$. For $1\leq n\leq N$, $2\leq q <\infty$ and $k\geq 1$, we have

Proof. This Lemma can be easily derived from (58) and (60). More details of the proof can be found in [6,Lemma 3.2] and [5,Lemma 4.1].

For (25), if $1/p+1/q = 1$, we have

Lastly, we obtain the $L^q$ error estimate of the electric field intensity:

4.   Two-grid algorithm and error estimate

The two-grid algorithm and its convergence analysis are presented in this section. The fundamental ingredient of the scheme is a new finite element space ${\boldsymbol{V}}_H\times W_H\times M_H\times M_H \subset {\boldsymbol{V}}_h\times W_h\times M_h\times M_h(h< H<1)$ defined on a coarser quasi-uniform triangulation or rectangulation of $\Omega$. The non-linear equations can be solved by applying the Newton iteration procedure on the fine grid to linearize the non-linear system. The solutions of the original non-linear system will be reduced to the solutions of a small-scale non-linear system on the coarse space and a linear system on the fine space. First, we provide the two-grid algorithm.

Step 1. Solve the non-linear coupled system for $({\boldsymbol{u}}^n_H, \psi^n_H, e^n_H, p^n_H) \in {\boldsymbol{V}}_H\times W_H\times M_H\times M_H$ on the coarse grid $\mathcal{T}_H$:

Step 2. Solve the linear coupled system for $({\boldsymbol{U}}^n_h, \Psi^n_h, E^n_h, P^n_h) \in {\boldsymbol{V}}_h\times W_h\times M_h\times M_h$ on the fine grid $\mathcal{T}_h$:

where $\mathcal{R}(E^n_h, P^n_h) = R(e_H^n,p_H^n)+R_e(e_H^n,p_H^n)(E_h^n-e_H^n)+R_p(e_H^n,p_H^n)(P_h^n-p_H^n)$.

Next, we present an error estimation analysis of the exact solutions $({\boldsymbol{u}}^n,\psi^{n},e^n, p^n)$ and two-grid solutions $({\boldsymbol{U}}^n_h, \Psi^n_h, E^n_h, P^n_h)$. We note that $({\boldsymbol{U}}^n_h, \Psi^n_h)$ are the two-grid solutions defined in (69) and (70). Using (23), (26), and triangle inequality, we can analyze the electrostatic potential and electric field intensity:

Next, we prove $\|e^n-E^n_h\|_{0,q}$ and $\|p^n-P^n_h\|_{0,q}$. The elliptic projection will be used as an intermediate variable to assist this proof, and the main results are as follows:

Lemma 4.1. Let $(R_h e^n, R_h p^n)$ be the elliptic projection solution of (27)–(28) at $t = t^n$, $(E^n_h, P^n_h)$ be the two-grid solution of (71)–(72). If we choose $E_h^{0} = R_h e^0$ and $P_h^{0} = R_h p^0$, the regularity assumptions (A) hold, then for $1\leq n\leq N$, $2\leq q <\infty$ and $l,k\geq 1$, we have

Proof. We subtract (15) and (27) from (71) at $t = t^n$ to obtain the following error equation:

We let $\eta_{e}^n = E^n_h-R_he^n$ and $\eta_{p}^n = P^n_h-R_hp^n$ and select $z = \eta_{e}^n-\eta_{e}^{n-1} = \partial_{t}\eta_{e}^{n}\Delta t$. Summing over $1\leq n \leq m$, from (76), we have

where

Now we estimate each term on the right hand of (77) as follows. First, using a second-order Taylor expansion at point $(e_H^n,p_H^n)$ for $R(e^n,p^n)$, (29), (54) and (55), we have

where $e^{\ast}$ is a point between $e^n$ and $e_H^n$, $p^{\ast}$ is a point between $p^n$ and $p_H^n$.

Similar to the proof process of Lemma 3.2, we give the following error estimations directly,

For $K_7$, we have

Using (73) and (29), we have

Using (64), (54), and (31), we have

From (84)–(86), we obtain

For $K_8$, we have

Related to $J_{1}$, we have

Related to $J_{2}$, we have

Using (54), (55), and (31), we have

Similar to $J_{21}$, we have the same estimation of $J_{22}$. Finally, for $J_{3}$ we have

From (88)–(90), we obtain

Combining (77) with estimates (78)–(83), (87) and (91), and noting that $E_h^{0} = R_h e^0$ and $P_h^{0} = R_h p^0$, we have

Similar to the proof process of Lemma 3.2, we determine that

which yields (74). Similarly, we can obtain (75).

Using the triangle inequality, (31), (32), and Lemma 4.1, we have the following results:

Theorem 4.2. Let $(e^n, p^n)$ be the solution of (15)–(16) at $t = t^n$, and $(E^n_h, P^n_h)$ be the two-grid solution of (71)–(72). If the regularity assumptions (A) hold, and the initial functions $E_h^{0} = R_h e^0$ and $P_h^{0} = R_h p^0$, then for $1\leq n\leq N$, $2\leq q <\infty$ and $l,k\geq 1$, we have

Lastly, from Theorem 4.2 and (73), we obtain

Theorem 4.3. Let $(\psi^n, {\boldsymbol{u}}^n)$ be the solution of (13)–(14) at $t = t^n$, and $(\Psi^n_h, {\boldsymbol{U}}^n_h)$ be the two-grid solution of (69)–(70). If the regularity assumptions (A) hold, and the initial functions $E_h^{0} = R_h e^0$ and $P_h^{0} = R_h p^0$, then for $1\leq n\leq N$ and $l,k\geq 1$, we have

5.   Numerical experiment

In this section, the numerical experiment is presented to illustrate the efficiency of the two-grid method for solving the semiconductor device problem in Section 4.

We consider the following equations with Dirichlet boundary condition:

where $\Omega = (0,1)^2$, $t\in[0,T]$. We take the exact solutions of (97)–(99) are

The right hand sides $f_{1}$ and $f_{2}$ are determined by the above exact solutions.

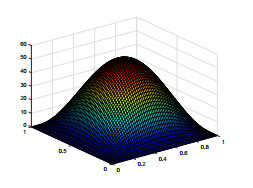
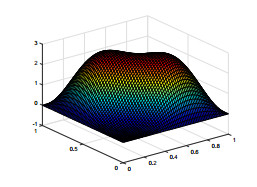
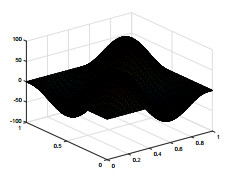
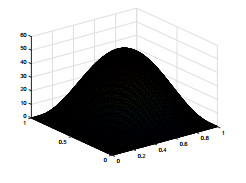
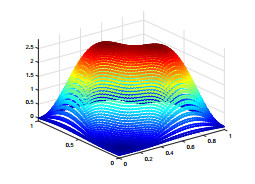
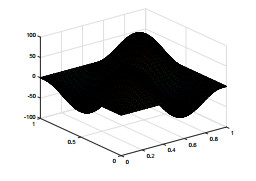
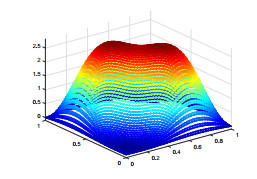
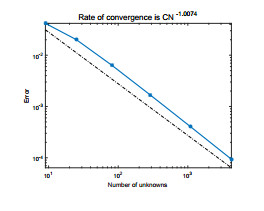
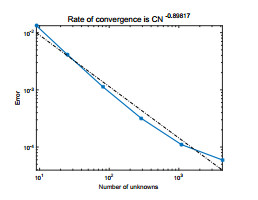
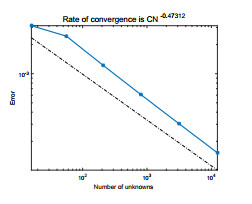
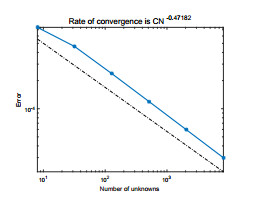
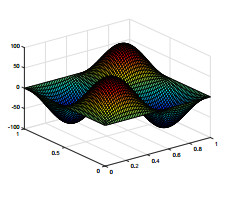
We use piecewise constant for $\psi$, the lowest Raviart–Thomas element for ${\boldsymbol{u}}$ and piecewise linear continuous function for $e$, $p$. We select the time step $\tau = 1.0e-2$ and $T = 1$. For the sake of simplicity, we assume $h_{\psi} = h_c = h$, $H_{\psi} = H_c = H$. The exact solutions $e^{n}$, $p^{n}$, $\psi^{n}$, the characteristics finite element and the mixed finite element method solutions $e^{n}_{h}$, $p^{n}_{h}$, $\psi^{n}_{h}$ and the two-grid method solutions $E^{n}_{h}$, $P^{n}_{h}$, $\Psi^{n}_{h}$ are shown in Figs. 1-9. To compare these pictures, we can see that the solutions of finite element method and two-grid method are identical with the exact solutions. From Figs. 10-13, we can observe that the convergence rate of the error for $\|e^{n}-e^{n}_{h}\|$, $\|p^{n}-p^{n}_{h}\|$, $\|\psi^{n}-\psi^{n}_{h}\|$, and $\|{\boldsymbol{u}}^n-{\boldsymbol{u}}^n_h\|$, respectively. In Tables 1–3, we present the numerical results for error estimates and CPU time cost of the finite element method and the two-grid method. As shown in Tables 1–3, we can know that when the coarse grid and the fine grid satisfy $H = h^{\frac{1}{2}}$, the two-grid method achieves the same accuracy as the finite element method but requires less time.

6.   Conclusion

This paper has presented a two-grid algorithm for coupled semiconductor device equations discretized by the mixed finite element method and the characteristics finite element method. The fundamental idea of the two-grid method is that we can solve non-linear equations by applying the Newton iteration procedure on the fine grid to linearize the non-linear system. It was shown that the two-grid method still achieves asymptotically optimal approximations as long as a mesh size between those of coarse and fine grids satisfies $H = O(h^{1/2})$. From the numerical experiment, we can find that less time will be required for the two-grid algorithm since only a small-scale non-linear problem must be solved. Hence, the two-grid method is an effective method for solving the semiconductor device problem. In our future work, we will consider more complicated two-grid algorithms for the semiconductor device problem by the mixed finite element method of characteristics.

Acknowledgments

We would like to express our gratitude to the anonymous referees for their helpful suggestions.