An adaptive edge finite element method for the Maxwell's equations in metamaterials

1.   Introduction

In this paper, we consider the following two-dimensional time harmonic Maxwell's equations

where $\Omega \subset \mathbb{R}^2$ is a bounded domain with Lipschitz boundary $\partial\Omega$, $\boldsymbol{E} = [E_1, E_2]^t$ denotes electric field and $\boldsymbol{F} = [F_1, F_2]^t \in [L_2(\Omega)]^2$ represents the given wave source term, where $[L_2(\Omega)]^2$ is denoted as the two-dimensional vector space of square integrable functions. The parameters $\mu$ and $\varepsilon$ are the permeability and permittivity of the material medium, which may be functions of position. And $k$ is the wavenumber. The curl $\nabla\times$ of $v = [v_i]_{i = 1}^d$ is defined differently depending on the space dimension $d$. For $d = 1$, the curl of a scalar $v$ is defined as the vector $\nabla\times v = [\partial_yv_1, -\partial_xv_1]$. For $d = 2$, it is the number $\nabla\times v = \partial_xv_2-\partial_yv_1$.

Solutions of many problems of interest require computation of phenomena occurring in a physical domain of infinite extent. In such an infinite domain, electromagnetic sources are all considered to be at the origin, and to scatter energy to infinity. A condition is required to prevent the nonphysical inverse process, where energy is transferred by radiation from infinity to the origin, and ensure uniqueness of the solution in an infinite domain. For the two-dimensional case, the following condition, known as the Silver-Müller radiation condition [5], must be satisfied

The numerical approximations of the Maxwell's equations have been extensively investigated in the last many years, such as finite element method (FEM) [6,7,15,18,23,36], finite difference time domain method (FDTD) [14,30], interior penalty discontinuous Galerkin method (IPDG) [17], hybridizable discontinuous Galerkin method (HDG) [27], nodal discontinuous Galerkin method (NDG) [22] and multigrid method (MG) [11], etc. In recent years, metamaterials as a new type of material have attracted people's attention because of their potential applications in many fields [14,28], such as cloaking devices [2,12,24], sub-wavelength imaging and perfect lens. We mention in passing some related mathematical research on metamaterials in the literature [1,4,20,21], and some related finite element methods designed for simulating the electromagnetic wave in metamaterlals [33,34,35]. The advantage of adaptive finite element method in metamaterials, which will be considered in this paper, is to make possible, with reasonable computational cost, the local mesh adjustment of the computational domain according to a-posteriori error estimator.

The adaptive method can improve the efficiency of electromagnetic field calculation, and it is simple and and accurate [6,7,23]. In this paper, we develop the adaptive finite element method of Maxwell's equation in metamaterials. Because many electromagnetic problems are actually interface problems, we need to deal with them carefully. Some parts of the interface problems do not need to be refined near the interface, but they are still refined by using the usual indicators. So the more efficient a-posteriori error estimator should be considered without regard to the particularity of the examples and make the meshes match the images of the numerical solution better, which is the purpose of this article. In view of such problems, the recovery technique is used in each sub-area and the corresponding error is calculated. Errors of all sub-areas constitute errors of the domain of interest to guide the grid refinement.

The rest of this paper is organized as follows. In Section 2, we introduce the finite element scheme for the Maxwell's equations. A-posteriori error estimators are proposed, which include two types: one is the residual-based and the other is the recovery-based in Section 3. Afterwards in Section 4, several numerical examples are presented to compare the realization effect of the different posteriori error indicators. In Section 5, we give a conclusion.

2.   Finite element scheme

Let $L_2(\Omega)$ be the Hilbert space of square integrable functions on $\Omega$ equipped with the standard $L_2$-norm: $||w|| = \sqrt{(w, w)}$, where $(\cdot, \cdot)$ is standard $L_2$-inner product. Consider the following Hilbert space

and the subspace

equipped with the norm

where $\boldsymbol{n}$ is the unit outward normal vector to $\partial\Omega$.

The Berenger PML [3] is applied to approximate the Silver-Müller radiation condition with the perfect electric conductor (PEC) boundary conditions

The variational formulation of Eq.(1) reads: Given $\boldsymbol{F}\in [L_2(\Omega)]^2$, find $\boldsymbol{E} \in H_0( \text{curl}; \Omega)$ such that

where

Let $\mathcal{T}_h = \{ K\}$ be a regular triangle partition of the domain $\Omega$ with mesh size $h$, define the lowest order edge elements space [25]

A basis for $\boldsymbol{V}_h$ is given by the set of Nédélec's shape functions $\{\phi_i\}_{i = 1}^{n_e}$ with $n_e$ the number of triangle edges in the mesh, the simple formula for local shape functions is defined as

for any triangle $K\in\mathcal{T}_h$, $E = [v_i, v_j] \subset \overline{K}$ with vertices $\{v_i = (x^i, y^i)\}_{i = 1}^3$, and associated with linear Lagrangian basis functions $\{\lambda_i\}_{i = 1}^3$, where the explicit expressions for the basis $\lambda_i$ of the triangle $K$ is given by

with cyclic permutation of the indices $\{i, j, k\}$ over $\{1, 2, 3\}$ and $|K|$ is the area of $K$. It can be shown that edge finite elements guarantee the continuity of the tangential component across faces shared by adjacent triangles; they thus fit the continuity properties of the electric field.

With the choice of discrete space $\boldsymbol{V}_h$, the curl-conforming finite element scheme of Eq.(4) takes the form as follows: Given $\boldsymbol{F}\in [L_2(\Omega)]^2$, seek $\boldsymbol{E}_h \in \boldsymbol{V}_h$ such that

3.   A-posteriori error estimations

Having computed a finite element solution, it is possible to obtain a-posteriori error estimations. These estimations accomplish two main goals. Firstly, they are able to quantify the actual error numerically. Secondly, they can be used to perform the adaptive mesh refinement, which solves the problem iteratively. The method uses a-posteriori error estimators to indicate where errors are particularly high, and more mesh intervals are then placed in those locations. This process

can be repeated until a satisfactory error tolerance or result is reached. In this section, we propose a-posteriori error estimations including not only a residual type but also a recovery type. A Dörfler marking strategy [13] is used in the adaptive process.

3.1.   The residual-based a-posteriori error estimation

The residual type a-posteriori error estimator $\eta^{r0}_{K_l}$ [15] for the element $K_l$ is defined as

where $\mathcal{E}$ denotes the set of all interior edges, $h_{K_l} = |K_l|^{1/2}$ is the the diameter of $K_l$, and the local contributions $R^1_{K_l}, R^2_{K_l}$ and $J^1_{E}, J^2_{E}$ are defined, respectively, as

and

where $[\boldsymbol{F}\cdot\boldsymbol{v}]_E : = \boldsymbol{F}\cdot\boldsymbol{v}|_{K_m} - \boldsymbol{F}\cdot\boldsymbol{v}|_{K_n}$ on the edge $E$ for $E = K_m \cap K_n$, $K_m, K_n \in \mathcal{T}_h$.

3.2.   The recovery-based a-posteriori error estimations

The recovery type a-posteriori error estimators $\eta^{r1}_{K_l}$ [23] and $\eta^{r2}_{K_l}$ are considered, respectively, as

and

for $K_l \in \mathcal{T}_h$, here $R$ denotes the recovery operator. The specific recovery algorithm see the Algorithm 1.

Remark 1. Recovery operator can be built in a variety of ways such as gradient recovery [19,26,37], functional recovery [29], flux recovery [8,9,10,31] and so on. Two quantities related to $\mu^{-1}\nabla\times\boldsymbol{E}$ and $\varepsilon \boldsymbol{E}$ are recovered in the respective H(curl)-and H(Div)-conforming finite element spaces in [9,10]. It is different that we take average of flux to construct the flux recovery operator, which is easy to implement with superconvergence.

Theorem 3.1. Assume that the domain $\Omega$ is covered by a triangular mesh formed by parallelograms, and under the assumption [23,Lemma 2.6]:

(1) Assume that $|\mu^{-1}|< C_1$, for any function $\boldsymbol{u} = (u_1, u_2)^T\in(W^{3, \infty}(\Omega))^2$ and any parallelogram center $\boldsymbol{x}_e$, we have

(2) Assume that $|\varepsilon_i|< C_2 (i = 1, 2, 3, 4$) with $\varepsilon = [\varepsilon_1, \varepsilon_2;\varepsilon_3, \varepsilon_4]$, for $\boldsymbol{E}\in(W^{2, \infty}(\Omega))^2$ and $h$ is enough small with any parallelogram center $\boldsymbol{x}_e$, we have

(3) Under the assumption of (1) and (2) above, $\boldsymbol{E}$ and $\boldsymbol{E}_h$ satisfy Eqs.(4) and (6), respectively. If $\boldsymbol{E}\in(W^{3, \infty}(\Omega))^2$ and $h$ is enough small, then we have

Remark 2. The proof of Theorem 3.1 is similar to the reference of [23,Lemma 2.7], [16,Theorem 3.3] and [23,Theorem 2.2].

4.   Numerical examples

This section is devoted to numerical examples to illustrate the efficiency and reliability of the proposed a-posteriori error indicators. The wave source term is given by $\boldsymbol{F} = k^2 \boldsymbol{P} \exp(ik\boldsymbol{d} \cdot\boldsymbol{x}) q(\boldsymbol{x})$, where $i = \sqrt{-1}$ is the imaginary unit. For simplicity, we use the Ndof and $I$ to denote the number of degrees of freedom and the identity matrix, respectively.

Example 4.1. Let $\Omega = [-1, 1] \times [-1, 1]$ and take the coefficients as follows

We choose the analytic solution

and compute $\boldsymbol{F}$ accordingly.

The Example 4.1 is aimed to test the convergence result stated in Theorem 3.1. Clearly, the results shown in Table 1 are consistent with Theorem 3.1.

Example 4.2. Let $\Omega$ be the rectangular domain $[-2, 2] \times [-5, 2]$, the parameters $\mu$ and $\varepsilon$ are taken, respectively, as

and

where the negative index metamaterial medium area $\Omega_1 = [-2, 2]\times[-2.5, -0.5]$. We choose $k = 10, \boldsymbol{P} = [1, 0]^t, \boldsymbol{d} = [0, 1]^t$ and $q(\boldsymbol{x}) = 1-4(x^2+(y-1.45)^2)$ in the ball with a center $(0, 1.45)$ of radius $1/2$ and $q(\boldsymbol{x}) = 0$ outside. In our simulation, we choose a uniform mesh with $h = 0.1$ and use a PML with $5$ cells in thickness around the rectangular domain.

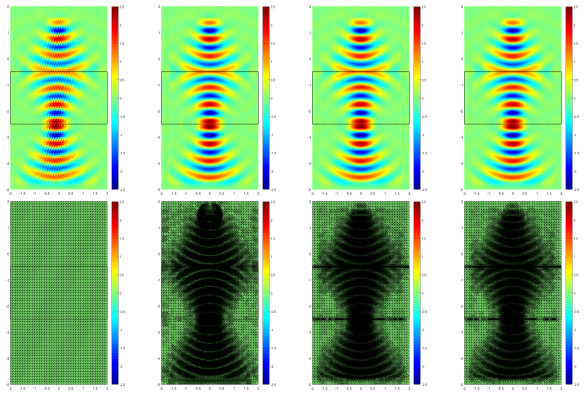
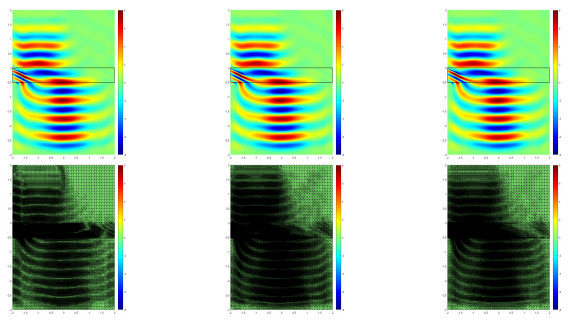
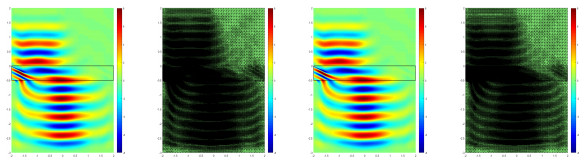
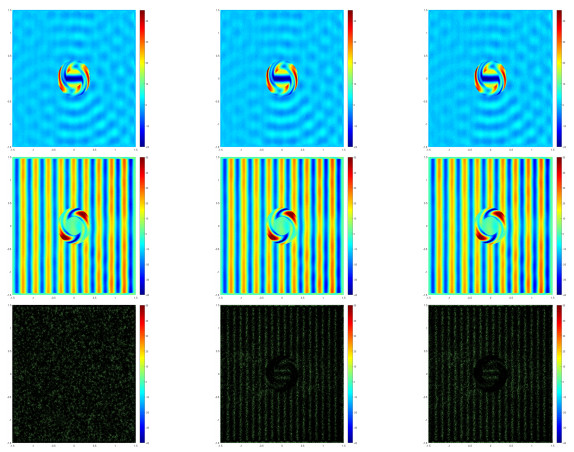
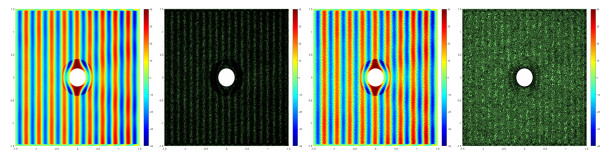
Example 4.2 simulates the backward wave propagation phenomenon illustrated in Fig. 1, which is based on the three types a-posteriori error indicators mentioned above. It can see that wave propagates as usual before it enters the metamaterial region. Once the wave enters into the metamaterial, wave propagates backward inside the metamaterial slab. And that wave propagates as usual again when leaves the metamaterial slab.

From the point of view of suitability between the grid and the numerical solution, it can be seen that the residual type is better than the others in Fig. 1. From the numerical solution of the images, some parts of the horizontal interfaces between the two media do not need to be refined, but in fact, these places are still refined when using the recovery a-posteriori error indicators.

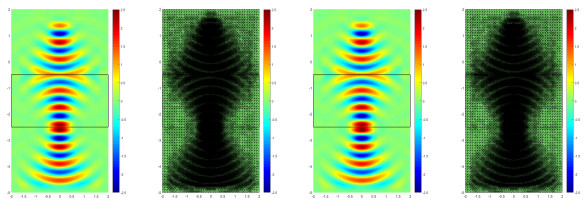
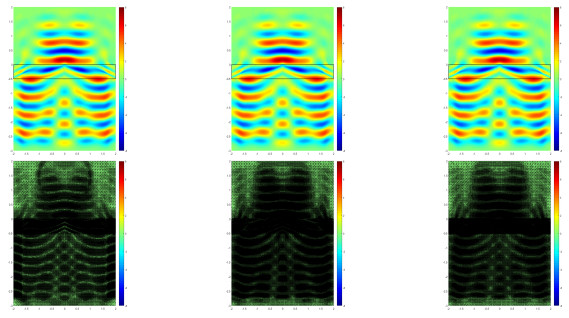
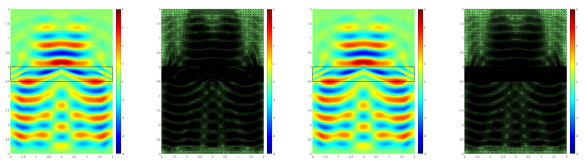
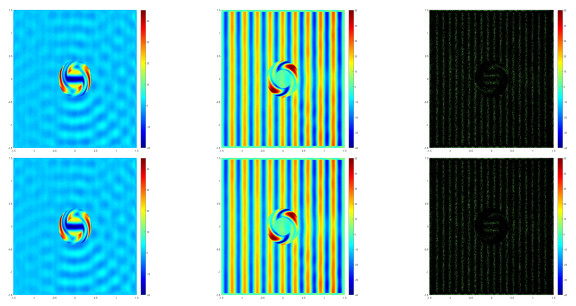
Thus according to two horizontal interfaces formed between the media, we divide the whole area into three sub-areas, and the recovery type a-posteriori error of the whole area is consisted of these sub-areas, which are shown in Fig. 2. Compared with the direct recovery type a-posteriori error of the whole area in Fig. 1, adaptive meshes by using the recovery type a-posteriori error of the whole area consisted of the error for these sub-areas perform better on the interfaces during the refinement process, which achieves the expected effect.

Remark 3. In Example 4.3-4.6, we also first consider the three types a posteriori error indicators mentioned above on the whole area and then consider that according to the number of interfaces $n$ formed between the media, the entire area can be divided into $n+1$ sub-areas, which each sub-area is independent and parallel computing can be considered, the recovery type a posteriori error of the whole area is consisted of the error for these sub-areas.

Example 4.3. Let $\Omega = [-2, 2] \times [-3, 2]$ be a rectangular domain with $k = 10, \boldsymbol{P} = [1, 0]^t, \boldsymbol{d} = [0, 1]^t$ and $q(\boldsymbol{x}) = {\rm{erfc}}(5((x-x_0)^2+(y-y_0)^2-1))/2$, where ${\rm{erfc}}(x) = \frac{2}{\sqrt{\pi}}\int_{x}^{\infty} \exp(-t^2) dt$. The parameters $\mu$ and $\varepsilon$ are defined as follows

and

which can be easily derived according to the theory of article [36] while the wave propagates along the $y$-axis. The constant $m_p$ is called "moving parameter" and the symbol "$\ast$" denotes as the symmetric part of the matrix. In our simulation, we choose a uniform mesh with $h = 0.1$ and use a PML with $5$ cells in thickness around the rectangular domain.

In Example 4.3, the moving medium area is fixed in $\Omega_1 = [-2, 2] \times [-0.5, 0]$, which can be denoted as the union of $\Omega_2 = [-2, 0] \times [-0.5, 0]$ and $\Omega_3 = [0, 2] \times [-0.5, 0]$. We achieve the different moving effects by the different choices of the center point $(x_0, y_0)$ and the parameter $m_p$.

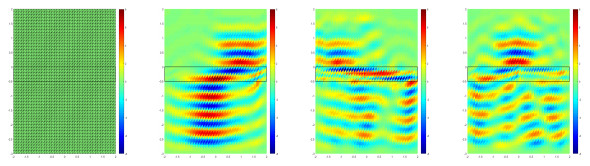
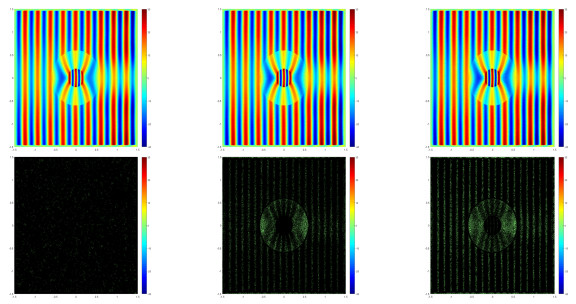
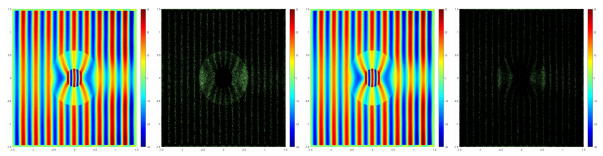
Firstly, we choose the center point $(x_0, y_0) = (1, 1.45)$ with $m_p = 2$ for the domain $\Omega_1$, i.e., the wave source is fixed in the upper right. Clearly, we can see that the wave moves from right to left after wave passes the moving medium area shown in Figs. 4 and 5.

Then, the center point $\boldsymbol{x}_0 = (x_0, y_0)$ are chosen as $(-1, 1.45)$ with $m_p = -2$ for the domain $\Omega_1$, i.e., the wave source is fixed in the upper left. Obviously, we can see that the wave moves from left to right after wave passes the moving medium area shown in Figs. 6 and 7.

Finally, the constant $m_p$ is taken as $2$ for domain $\Omega_2$ and $-2$ for domain $\Omega_3$ with the center point $\boldsymbol{x}_0 = (0, 1.45)$, i.e., the wave source is fixed in the upper middle. Evidently, we can see that the wave moves from the middle to left and right after wave passes the moving medium area shown in Figs. 8 and 9.

Overall, it can be seen that the recovery type a-posteriori error indicators perform better.

For Example 4.4-4.5, we consider the square domain $\Omega = [-1.5, 1.5]\times[-1.5, 1.5]$ with $k = 20, \boldsymbol{P} = [0, 1]^t, \boldsymbol{d} = [-1, 0]^t, q(\boldsymbol{x}) = 1$ and use a PML with $1/60$ of the region in thickness.

Example 4.4. The parameters $\mu$ and $\varepsilon$ are taken, respectively, as

and

where $m = \frac{\theta_0r}{R_2- R_1}$. Here, we choose the initial mesh with $167744$ Ndof and take $R_1 = 0.2$, $R_2 = 2R_1$, $\theta_0 = \frac{\pi}{2}$ in the simulation.

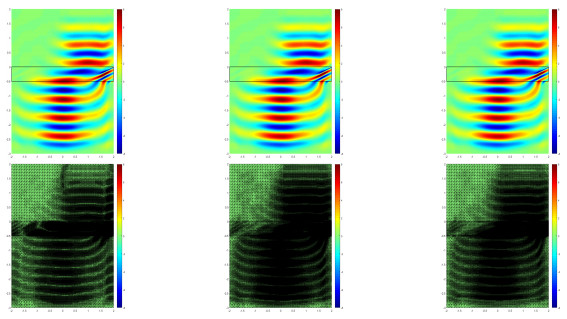
In Example 4.4, we simulate the cylindrical rotation cloak. To see how wave propagates in the rotator, we plot the electric fields $\boldsymbol{E}$ in Figs. 10 and 11. Clearly, it can be observed that the wave gets distorted in the metamaterial region and note that the parameter $\theta_0$ determines the degree of distortion of the wave. Although the residual type a-posteriori error estimator achieves the rotation effect, the corresponding grid does not match the graphs of the numerical solution at all. In contrast, the recovery type a-posteriori error indicators are always good and meshes are more refined in the metamaterial region.

Example 4.5. We consider the parameters

and

where the constants are denoted, respectively, as,

In our simulation, the parameters a, b and c are taken as $0.2$, $0.4$ and $0.6$, respectively. There is $167744$ Ndof in the initial mesh.

Example 4.5 simulates the electromagnetic concentration effect, which are shown in Figs. 12 and 13. As in the previous example, although the residual type a-posteriori error estimator achieves the concentration effect, the pattern of the corresponding grid is not matched with the graph of the numerical solution. The advantage of recovery type a-posteriori errors is prominent again.

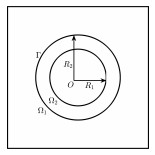
Example 4.6. Let $\Omega$ be the part of the square domain $[-1.5, 1.5] \times [-1.5, 1.5]$ outside the circle centered at origin with radius $R_1$. The computational areas $\Omega_1$ and $\Omega_2$ $(\Gamma = \Omega_1\cap\Omega_2)$ are shown in Fig. 14. Here, we take $R_1 = 0.2$, $R_2 = 2R_1$ and the initial mesh with $20287$ Ndof. We choose $k = 20, \boldsymbol{P} = [0, 1]^t, \boldsymbol{d} = [-1, 0]^t$ and $q(\boldsymbol{x}) = 1$. The parameters $\mu$ and $\varepsilon$ are given as follows

and

In Example 4.6, the colaking simulation is displayed in Figs. 15 and 16. It is obvious that the recovery-based a-posteriori error estimation $\eta^{r1}_{K_l}$ works well and the implementation is faster. Note that neither the permeability $\mu^{-1}$ nor the permittivity $\varepsilon$ belongs to $L^\infty(\Omega)$, which is not under assumptions in Theorem 3.1. In spite of this, recovery-based a-posteriori error estimation $\eta^{r2}_{K_l}$ still works for this example.

Remark 4. The relationship between the direction of wave source and the position of metamaterial plays a very important role in the actual simulation.

5.   Conclusions

In this paper, we used adaptive edge element method for the time-harmonic Maxwell's equation, which was not only based on the residual type a-posteriori estimation, but also based on the recovery type. And we presented the numerical examples to illustrate the reliability and efficiency of the proposed a-posteriori error estimations. By adding the different wave source terms, the results were similar to those obtained by the time domain Maxwell's equations simulations [18,36]. Through the results of these examples, it can see that the recovery type a-posteriori error indicator deserves to be considered and recommended on the each sub-area.

Acknowledgments

Wang's research was supported by Hunan Provincial Innovation Foundation for Postgraduate(CX20190464). Yang's research was supported by NSFC Projects 11771371, Key Project of Hunan Education Department, China 18A056 and Project of Scientific Research Fund of Hunan Provincial Science and Technology Department(No: 2018WK4006). Huang's reserach was supported by NSFC Projects 11971410.