1. Introduction
The brain is a large network system that transmits information through spikes, which are short electrical signals in neurons. An action potential is transmitted to neurons with a time delay compared with the action potential in the preceding neuron. Over 0.5 msec passes before change occurs in the potential in the neuron receiving the input, and this is called synaptic propagation delay [1]. When a neuron fires, it is not able to fire for a certain length of time, and this is called a refractory period [2]. Synaptic propagation delays and refractory periods vary in different neurons. In addition, these times can fluctuate and are considered as a kind of noise. Information processing in brain activity might be conducted with spike propagation. In actuality information processing in the brain is rather stable despite the possible variabilities. Spike propagation and information transmission mechanisms are important research targets.
The first theory of information architecture was the cell-assembly theory proposed by Hebb in 1949 [3,4]. This theory was based on previous findings in associative memory and cell assembly. Okada et al. examined the relationship between associative memory and sparse coding [5]. The second theory involves the synfire chain model proposed by Abel [6]. This theory states that neuronal groups fire in a synchronous time pattern. However, the transfer of information between neurons and the function of the communication have not been fully elucidated. A question that remains is how neural activity propagates through cortical networks that are connected through synapses. Tanaka et al. showed that cortical networks use recurrent circuits in which a large number of neurons are bound to each other [7]. We developed a time-shift diagramming method that can be used to visualize the propagation of brain waves that communicate information [8,9,10].
The questions of how information communication is controlled, what constructs the information, and how the controlled information communication is constructed are unanswered. The answers to these questions are essential in investigations of the mechanisms underlying information communication. In order to resolve this question, we need to decode the sequence pattern of spike activity (analyses of the time-series patterns of firing) rather than examining the rate of spikes or action potential waveforms. In this study, we conducted a physiological experiment in cultured neurons from the rat hippocampus and recorded the spike trains. A significantly increased percentage of M-sequences spikes were recorded in the spike trains [11]. The raster plot analyses showed that linear-feedback shift-register circuits generated pseudo-random sequences including M-sequences [12]. However, we were unable to elucidate the meaning of the codes. In addition, we have shown that spikes propagate in neural networks because spike waves can be observed as code flow [13]. We then showed that cultured neuronal networks can be used in simulations with mesh-type two-dimensional neural network models composed of neurons that are modeled by integration and firing without leakage. In order to understand information processing in the brain, we simulated the firing activity of a large number of neurons in a neural network [14]. In our study, we found that stimulations at different sites were associated with the detection of different waves. In our previous study, we observed the generation of a number of spatiotemporal forms of spike wave propagations by various stimulated neurons in a cultural neuronal network [15]. We stimulated one of the two transmission neuron groups, and used the Dynamic Time Warping (DTW) method [16] to determine whether remote neurons receiving inputs can be used to identify the transmission neuronal group that was stimulated. We then confirmed the existence of two types of neurons: one that can identify the stimulated neuron and one that cannot. However, in that study, we were unable to elucidate the mechanisms underlying the results. With culture, parameters such as connection weights and synaptic delays are fixed and cannot be manipulated. In contrast, we can change the parameters in simulations. By changing the parameters and analyzing the different results obtained with different conditions, we can elucidate the mechanisms underlying the identification of the stimulated group of neurons.
In this study, we simulated spike responses to stimulations with various synaptic propagation delays and refractory periods. The simulation was conducted under the condition that the weights of the synapses were all fixed because we were only interested in examining the effects of fluctuations in the synaptic propagation delays and refractory periods without any confounding influence of variations in the synaptic weights. In order to focus on communication, we analyzed the information-flow of the network.
2. Methods
2.1. Specification of the simulated neural network
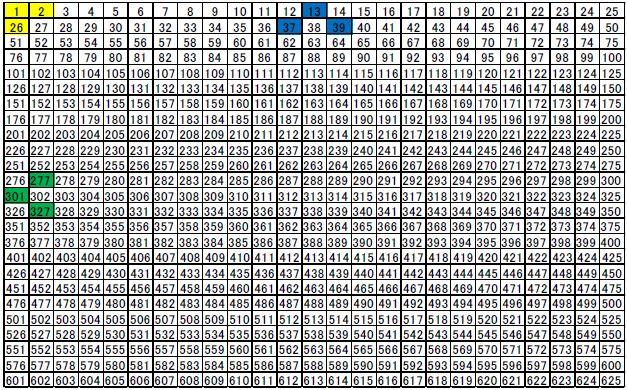
A 25 × 25 two-dimensional neural network was implemented (Figure 2). We used an integrate-and-fire model without any leakage as the neuronal model [17,18,19]. As well known, neurons have the property of all-or-none. Therefore, we implement an accepting period which is more stringent than the leak in the model. Accepting periods randomly accept input spikes or ignore. We will verify that neurons can communicate under such condition. The leak was ignored for simplicity. Each neuron had connection weights to and from eight neighboring neurons. We generated random weights of the synapses in the beginning of the experiment, and these weights were fixed through the experiment because we were only interested in examining the effects of fluctuations in the synaptic propagation delays and refractory periods. Therefore, any potential effects of synaptic weight variations were excluded. Three neurons were simultaneously stimulated at 0.1 msec, as shown in Figure 2, because we found in a number of preliminary simulations that the stimulation of three or more neurons stabilizes information propagation. We characterized the three neurons as being in the stimulated neuron group or transmitting neuron group. Spike waves were propagated from the stimulated neuron group to the other neurons. In our previous wet-lab experiments, we applied a time sampling rate of 0.1 msec, which was considered a bin. Thus, the time unit of a bin was 0.1 msec. The instantaneous variances in the synaptic propagation delays and refractory periods were both set to 0.167, 0.333, 0.500, 0.667, 1.000, or 2.000 [bin2] (bin = 0.1 msec) [17,18]. The stimulations (T, L, and D) were applied, as shown in Figure 2.
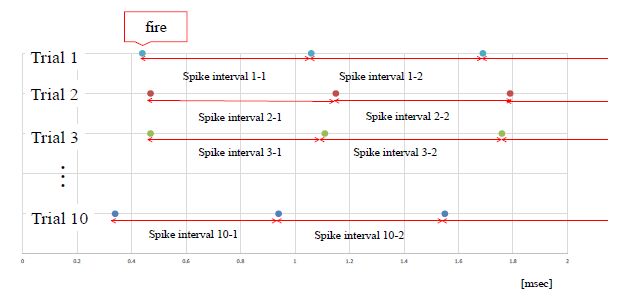
We calculated the spike-interval sequences of one neuron between 0-120 msec for 10 trials (Figure 3).
2.2. Analysis procedure
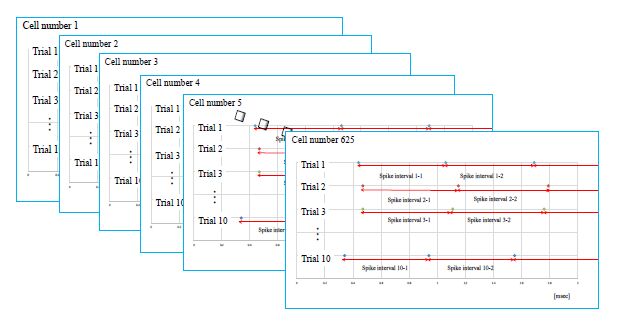
We obtained the spike-interval sequences for 625 neurons (total, 6, 250 sequences) with stimulation T (Figure 4) and stimulation L.
2.3. Local DTW
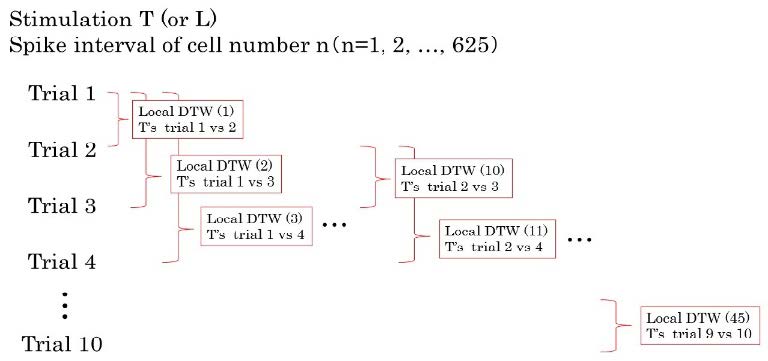
We calculated DTW in a combination of 10 trials (total, 45 sets) to calculate the spike-interval time differences between the trial sets of stimulation T (Figure 5). DTW was calculated among 10 trials for each neuron. In addition, we conducted DTW in a combination of 10 trials (total, 45 sets) to calculate the spike-interval time differences between the trial sets of stimulation L. DTW is an algorithm that is used to measure the differences between two signal sequences with different time scales or expansions. When the difference is large, the value approaches 1, while the value approaches 0 when the difference is small. We measured the DTW values in a combination of 10 trials with the same stimulated groups (T or L) and calculated the average of the 90 sets (two trials of 45 sets). We refer to these calculations as Local DTW (See Figure 5).
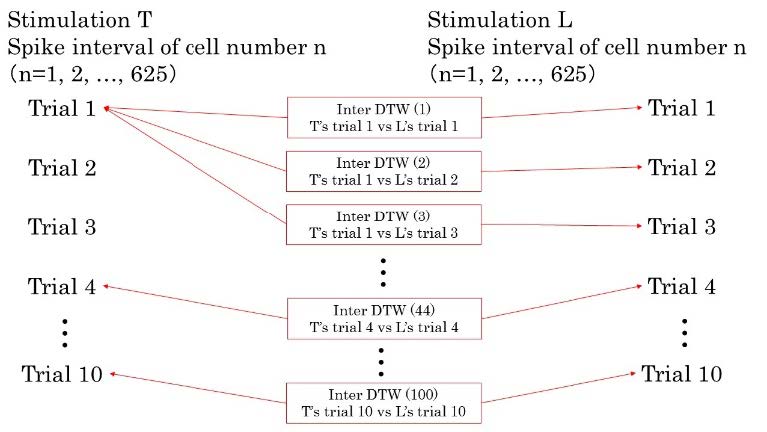
2.4. Inter DTW
We calculated DTW for the combination of the 10 trials (total, 100 sets) in stimulations L and T in order to calculate the spike-interval time differences between the trial sets (Figure 6). We calculated the average of the 100 sets. We refer to these calculations as Inter DTW.
2.5. T-test
We used two-sided t-tests at the 5% significance level to compare the Local DTW and Inter DTW results. We determined the number of neurons in which the Inter DTW was significantly larger than the Local DTW. The neurons with significantly larger test statistics were considered able to identify stimulations T or L.
3. Results
3.1. Spike propagation
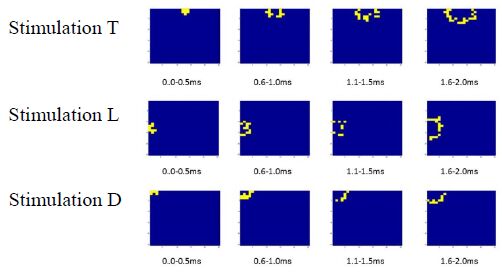
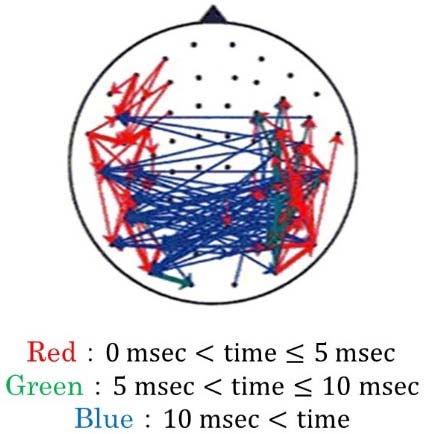
Figure 7 shows the results of a simulation of spike propagation in 10 msec. The transmitting neurons were stimulated at 0.0 msec. In all of the stimulations (T, L, and D), the spike waves spread in all directions. The propagation route was changed in each trial.
3.2. Positions of the firing neurons with different variances
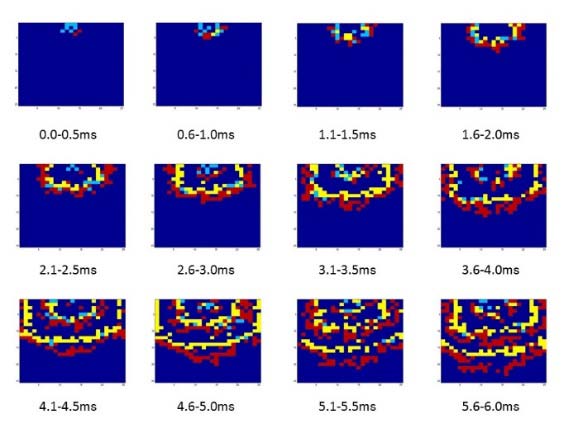
Figure 8 shows the results of the positions of the firing neurons with different variances. We set the variances of the synaptic delay and refractory period as 0.167 (yellow in Figure 8) and 2.0 (red in Figure 8), respectively. The blue in Figure 8 indicates the results with both 0.167 and 2.0 variances. Figure 8 shows the positions 0.0-6.0 msec after the stimulation. The propagation speed for a variance of 2.0 (red) was faster than the speed for a variance of 0.167 (yellow). Thus, when the synaptic delays and refractory periods were changed, the propagation speeds increased as the variances increased.
3.3. Classification of the stimulated neuron groups
In order to ascertain whether the difference between the mean value of Local DTW (90 set of trial combination) and the mean value of Inter DTW (100 set of trial combination) is statistically significant or not, a two-tailed t-test was conducted with a significance level of 5% at each cell. Among them, we picked up and showed the value of Local DTW and Inter DTW (mean ± SD) at cell number 98, 132, 313, 504 and 590 in Table 1. As results, the mean value of Inter DTW was significantly greater than that of Local DTW (p = 0.03) at cell number 590, while no significant difference was observed (p = 0.79) at cell number 313.
Table 1. The value of Local DTW and Inter DTW (mean ± SD) and Significance between them (at cell No. 98, 132, 313, 504 and 590). S indicates Significance and NS indicates No Significance
| Cell No. | Inter DTW | Local DTW | Significance |
| 98 | 0.029 ± 0.026 | 0.020 ± 0.020 | S |
| 132 | 0.037 ± 0.023 | 0.039 ± 0.023 | NS |
| 313 | 0.022 ± 0.018 | 0.023 ± 0.018 | NS |
| 504 | 0.029 ± 0.025 | 0.021 ± 0.016 | S |
| 590 | 0.020 ± 0.018 | 0.014 ± 0.014 | S |
As described in Section 2.5, the neurons with significantly larger test statistics were considered able to identify stimulations T or L (Identifiable neurons).
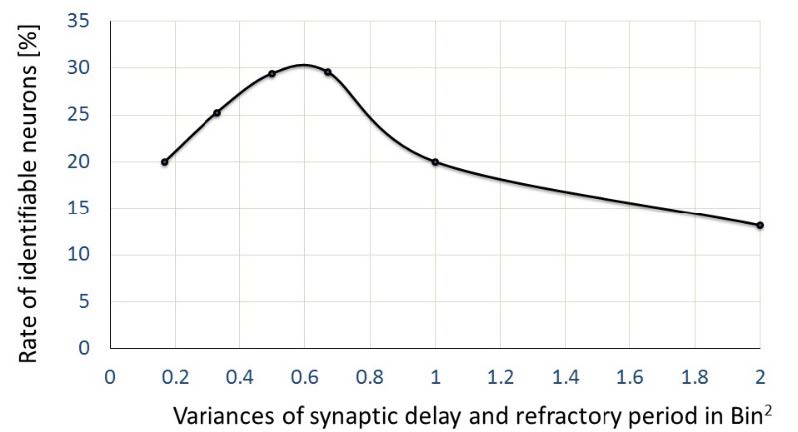
Figure 9 shows the percentages of neurons that could identify the stimulated neurons for neurons with significantly larger test statistics vs. neurons with variances in the synaptic delay and refractory period. The vertical axis shows the percentage of identifying neurons among the 625. The horizontal axis shows the variances of the synaptic delay and refractory period in bin2. When the variances of the synaptic delay and refractory period increased from 0.167 to 0.667, the percentage of identifiable neurons with different firing time profiles for stimulations T and L increased. However, when the variance was over 0.667, the percentage of neurons that could identify the stimulated neurons decreased. In the case of the variances of the synaptic delay and refractory being 0, the t-test can’t be performed because the variance is 0. Therefore, the result is not described. Since when variance is around 0.6, there was no special difference in the spike waves, we didn’t show them in figure 8.
We examined whether it is possible to discriminate between stimulus T and stimulus L individually for each neuron. We should have multiply compared at the stage of raw data. However, for the sake of simplicity, we only t-tested the difference between the mean values of Local DTW and Inter DTW for stimulus T and stimulus L, respectively. In order to integrate them, we evaluated the rate of Identifiable neurons as Figure 9.
4. Discussion
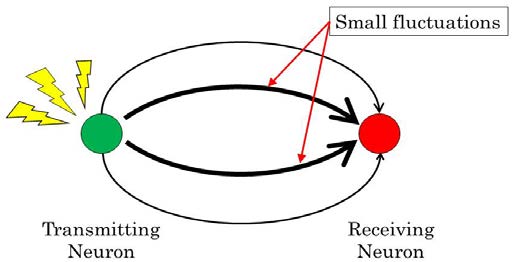
The spike propagation results showed that the propagation route and velocity changed in response to alterations in the variances of the synaptic propagation delay and refractory period. This occurred because the synaptic delays and refractory periods with larger variances resulted in faster propagation of the spikes. As a result, the stimulus arrived earlier. The DTW results showed many signaling routes that were spatially different compared with the route for the transmitting neurons to the receiving neurons. They were transmitted in parallel (Figure 10).
The spikes that reach a neuron first result in firing of the neuron. Thus, the approximate flow of information is through this spatially representative route. When the variances in the synaptic propagation delays and refractory periods were small, the information passed through the thick route in each trial of Figure 10.
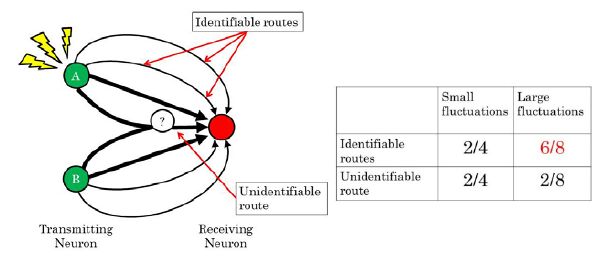
The routes to each transmission neuron from the receiving neuron often overlapped from the half-way point. In that case, the receiving neuron was difficult to use to identify the transmitting neurons (Figure 11). If there is large instantaneous variation in the synaptic propagation delays and refractory periods, the information is thought to pass through temporally various representative routes (Figure 11).
Thus, if the variations in the synaptic propagation delays and refractory periods increase, the spike wave will pass through the various representative routes. This then increases the probability of identification. When the variance is too large with a large bin2, the receiving neuron will receive spike profiles with too much disturbance, which makes identification of the spike wave itself difficult. These results suggested that changes in the propagation routes of the firing of neurons required a little variance in the synaptic propagation delays and refractory periods. Thus, variation may stabilize multiplex communication. In this paper, we simulated the case where the variances in synaptic propagation delays and refractory periods are the same. In that case, we explained a reason that the curve of figure 9 has a peak, which seems having high possibility. However, it is necessary to evaluate it by changing the variances in synaptic propagation delays and refractory periods, separately. We like to explain that in another paper.
5. Conclusion
Many previous studies have examined neural networks based on their firing patterns from a macro point of view, while we studied neural networks from the point of view of communication [3,4,5,6,7]. In order to understand information processing in the brain, we conducted simulations that assumed interactions of the firing activities of a large number of neural networks in the present study. We used an integrate-and-fire neuronal model without leakage and a 25 × 25 two-dimensional neural network. We showed how stimulation of the neurons was transmitted to the required neurons in the simulation as spike propagation occurred in 10 msec after the transmitting neurons were stimulated at 0.1 msec in the simulation. The two neuron groups were also stimulated with synaptic propagation delays and refractory periods with different variances. When the fluctuations in the synaptic delays and refractory periods were changed, the propagation speed increased as the variance increased. These results suggested that to change the propagation route of the firing of the neurons, some variance in the synaptic propagation delays and refractory periods is required. We examined the percentages of neurons with significantly larger test statistics vs. those with variances in the synaptic delays and refractory periods. The results suggested that variations in the synaptic delays and refractory periods improved the stability of multiplex communication.
In future studies, we need to examine whether multi-directional spike waves can be identified in more than two directions and the three-dimensional structure of the network. The present culture experiment examined not just one stimulated neurons and receiving neuron, but plural. Thus, several neurons were simultaneously recorded because an external electrode was used in the culture experiment. The simulation in the present study was used to examine neuron identification. It is possible to analyze the simulation with more detail. Thus, future studies need to examine the raw characteristics of each neuron.
Acknowledgements
This study was supported in part by the Grant-in-Aid for Scientific Research of Exploratory Research JP21656100, JP25630176, JP16K12524 and Scientific Research (A) JP22246054 of Japan Society for the Promotion of Science.
Conflict of Interest
The authors declare that there is no conflict of interest regarding the publication of this paper.









 DownLoad:
DownLoad: