First of all, we establish an identity for higher-order differentiable functions. Then, we prove some integral inequalities for mappings that have continuous derivatives up to the order n−1 with n≥1 and whose n-th derivatives are the element of L1, Lr, and L∞. In addition, estimates of new composite quadrature rules are examined. Finally, natural applications for exponential and logarithmic functions are given.
This paper is dedicated to S. Salsa, as the expression of our friendship and respect.
1.
Introduction
1.1. Model and question
Consider the following system, with unknowns u(t,x) and v(t,x,y), where (t,x,y)∈R+×R×R+
The real number μ is a positive given parameter, and the nonlinear term f is chosen as
with a>0 and g of class C2, with g≥0, convex, g(0)=g′(0)=0, g′(+∞)>a. The equation for v in the upper half-plane is therefore a variant of the Fisher-KPP equation, in reference to the pioneering works of Fisher [11] and of Kolmogorov, Petrovskii and Piskunov [14]. The operator (−∂xx)α is the fractional Laplacian of order α∈(0,1):
the constant cα>0 being chosen so that the symbol of (−∂xx)α is |ξ|1+2α. By P. V. we mean
an expression that is well defined as soon as u is bounded on R, and smooth enough.
The initial datum is chosen as
where x0 and δ0 are given positive constants. Their value is not relevant for the discussion, one may think them as small. Under the listed assumptions, system (1.1) has a unique global smooth solution, that is also globally bounded as well as its derivatives, see [2]. The question under study is the behaviour of (u(t,x),v(t,x,y)) for large t.
1.2. Motivation, context, known results
System (1.1) is relevant in the study of the influence of a line having a fast diffusion of its own, that exchanges with an adjacent domain of the plane (here, the upper half plane), in which reactive and diffusive phenomena occur. The application is the modelling of how biological invasions can be enhanced by transportation networks, see [4] for an overview. In this context, u(t,x) represents the density of individuals on the line, and v(t,x,y) represents the density of individuals in the upper half-plane. Exchanges occur through the Robin condition −∂yv(t,x,0)=μu(t,x)−νv(t,x,0).
System (1.1) was first introduced by H. Berestycki, L. Rossi and the second author in [7]. There, the diffusion on the line (that we called "the road", while the upper half plane was called "the field") took the form −D∂xx, with D>0, possibly large. The effect of the line may be accounted for as follows: when not present, the model amounts to the single Fisher-KPP equation with unknown v(t,X), X∈R2:
Note that here, we need to shift the mass from the line to the plane in order to avoid the trivial solution v≡0. We have (Aronson, Weinberger [1])
where c∗=2√a, and v0 is the unique positive zero of f, whose existence is granted by the assumptions. In other words, the stable state v0 invades the whole space at speed c∗. Reverting to (1.1), and concentrating on what happens on the line (or its vicinity), first when the diffusion is −D∂xx, then when it is (−∂xx)α. In the first case, the main result of [7] is the existence of c∗(D)>0, with lim infc∗(D)√D>0, such that invasion occurs at speed c∗(D) on the line and in the upper half plane, at finite distance from the line. This shows the importance of the line on the overall propagation. The limiting states for u and v are u∞≡νv0μ, v∞≡v0, a property that is not entirely trivial, and also proved in [7].
The effect of the nonlocal diffusion (−∂xx)α was studied for the first time in [2] by H. Berestycki, L. Rossi and the two authors of the present paper. The main result of [2] is the following.
Theorem 1.1. Define λ∗=a1+2α. Then we have
In (1.5), the limits of v should be understood pointwise in y.
Let us note that this result may be parallelled by the following one: let us bluntly replace the exchange term μu−νv in the equation for u by the reaction term f(u) (so that we shift the whole weight of the reaction from the upper half plane to the line), so as to obtain
Then, Cabré and the second author [8] proved that invasion at the same rate as in Theorem 1.1 occurs. Thus, u(t,x) actually behaves just as in equation (1.6) at the leading order.
While Theorem 1.1 captures the essence of the main features of the invasion phenomenon, it is interesting to ask whether the asymptotics can be made a little more precise. Indeed there is, in Theorem 1.1, a lot of room between the upper and lower bound. For instance the level sets of u may advance like tpeλ∗t, where p could be any real number. This question can also be asked for the simpler model (1.6), all the more as one may give the following heuristics: the dynamics of (1.6) being driven by the small values of u (given the concavity of u they are, loosely speaking, the most unstable ones in the range of f), so that the dynamics of the level sets is really given by the linear equation
Call Gα(t,x) the fractional heat kernel, we have Gα(t,x)≲t|x|1+2α for large t and x, see [15] for instance. Then we have
still for large t and x. So, a level set of u will move like t11+2αeat1+2α. This heuristics does not give the correct sharper behaviour, as was proved by Cabré and the two authors of the paper [9]: a level set {x(t)} of u will in fact be such that |x(t)|e−at1+2α is bounded, that is, there is no polynomial correction in the expansion of x(t).
Consider now the linearised version of (1.1):
Let us call this time Gα(t,x) the solution u(t,x) with the initial datum δx=0, that is, the u-component of the fundamental solution. Then the first author proved [10] (a more precise estimate will be stated later).
And so, a level set {x(t)} of the solution u(t,x) of (1.7) will move like t−32(1+2α)eat1+2α. The question that we want to address in this paper is whether a discrepancy of the same kind holds between the linear and nonlinear equation.
1.3. Result and organisation of the paper
Surprisingly, and in contrast to what happens with (1.6), the linear equation (1.7) mimicks the behaviour of the nonlinear one (1.1) in a better fashion than for the fractional Fisher-KPP equation. The result that we are going to prove is the following.
Theorem 1.2. Consider any λ∈(0,νv0μ). Let xλ(t) be the largest x such that u(t,x)=λ or u(t,−x)=λ. Then, for all δ>0, there is Tλ,δ>0 such that, for all t≥Tλ,δ we have
In fact, the upper bound is more precise, as we may choose δ=0 there. To improve the lower bound seems to us more challenging, and will be addressed in a future work.
The paper is organised as follows. In Section 2, we explain the strategy of the proof of Theorem 1.2 and discuss some perspectives that our work has opened. In Section 3 we address the underlying mechanism of Theorem 1.2, namely, the transients of the one-dimensional Fisher-KPP equation with Dirichlet boundary conditions, this is a result of independent interest for the Fisher-KPP equation. We then devote a short section to quantify how the exchanges between the road and the field are organised. The proof of Theorem 1.2 is then displayed in Section 5. In the whole paper, the computations will be greatly simplified when we take a function g≥0, smooth, convex, supported in (θ,1] for some θ∈(0,1), with g(1)=1. Therefore, the computations will sometimes be carried out with this type of nonlinearity in order to highlight the main ideas, before being extended to the general Fisher-KPP nonlinearity. Also, from now on we will assume, without loss of generality, that a=1.
2.
The underlying mechanism of Theorem 1.2, discussion
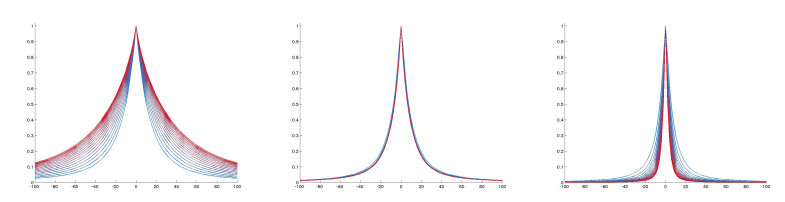
The starting point of this paper was the following numerical simulations, carried out in the PhD thesis of the first author [10]. We take a=1. The Figure 1, taken from [10], represents the graph, at various times, of the function
that is, the solution u(t,x) with different renormalisations. From left to right, the value of m is m=0, m=32(1+2α) and m=31+2α. The gradation of colours from blue to red represents the advance in time, blue standing for the earlier stages of the development.
One sees that, on the left, the graph of the renormalised solution tends to spread, whereas, on the right, it becomes a peak at x=0. In the middle, it converges to a nontrivial graph. This indicates a stabilisation mechanism for the middle value of m, and this came to us as a surprise. However, this suggests the following idea: the t−3/2 term being typical of the one-dimensional Dirichlet heat equation, we thought that it was interesting to understand this feature in a little more depth.
Assuming – which will turn out to be a good approximation – that ∂xxv is small, this suggests in fact that, for a fixed x, the function v(t,x,y) behaves like a solution of the one dimensional Fisher-KPP equation
This is even more evident when one takes f(v)=av−g(v), g vanishing on a small interval to the right of 0. The initial value (or, at least, the value of v at any small positive time) is small, dictated by the size of u(1,x). The Dirichlet boundary condition is the most convenient one that allows to put below the solution v(t,x,y) of (1.1) a barrier devised on the model of w(t,y), with an initial datum suitably dictated by the behaviour of u(t,x) (the solution of (1.1) on the line) at infinity. Of course, with this particular condition, the role of the line seems to be forgotten, such is not exactly the case, as long as we prove – as will be done in the course of this work – some easy lemmas that describe how the communication between the road and the field is organised.
Let us briefly discuss the optimality of our estimates. Of course, the corrections of the exponents in (1.8) by a small δ>0 shows that there is still a room for improvement. In particular, one could ask whether replacing the Dirichlet boundary condition by the exchange condition −∂yv+νv=μu in the 1D Fisher-KPP equation would lead to the optimal bounds. In fact, the best strategy would probably be to investigate the full one-dimensional problem with unknowns (u(t),v(t,y))
We choose no to do it here, as it would involve, in our opinion, heavier computations with possibly no real further understanding of the mechanisms at work. So, we leave this task for a future contribution.
3.
The transients for 1D Fisher-KPP propagation with small initial data
In this section we consider a function g≥0, smooth, convex, supported in (θ,1], with g(1)=1 (this last assumption is in fact unnecessary). Pick a small ε>0 with ε<θ. The goal of this section is to understand how much time it will take to the solution of the model Fisher-KPP equation
to reach the value θ at finite distance from y=0. First, let us note that the value θ will eventually be reached at a distance that remains bounded and bounded away from y=0, uniformly with respect to t and ε. Indeed, a classical sub-solution argument (see for instance Berestycki-Hamel-Roques [6]) implies that v will converge to the unique nontrivial solution v∞ of
which satisfies v′∞(0)>0, hence uniformly bounded from below on every set of the form [y0,+∞), y0>0. On the other hand, as ε→0, the time that it will take to v to come close to v∞ will grow infinitely, and our aim is to devise an upper bound that will be precise up to algebraic powers of ε.
Theorem 3.1. Let vε be the solution to (3.1), and ε<λ<v∞(1). Define Tε as the first time t such that
Then, for all δ>0, there is Qδ>0, possibly blowing up as δ→0, such that
It is worth saying a word on the scenario leading to (3.4), and the special structure of the nonlinearity f(v)=v−g(v) will make it especially obvious: the region where the solution will first reach a nontrivial value is not close to 0, but at a large distance from 0. At this stage, one could think of invoking classical results on Fisher-KPP propagation for studying how much more time vε will take to be nontrivial near y=0. This is not the correct intuition, because it would lead to a Tε that would be largely over-estimated. The mechanism is in fact closer to that of nonlocal Fisher-KPP propagation [8,9]. It is also not so far from what happens with the classical Fisher-KPP with slowly decreasing initial data, [12,13].
Proof of Theorem 3.1. For small, or, even, finite t, (for instance t∈[1,2]) we have vε(t,y)<θ as soon as ε>0 is small enough. Let us make this assumption; as soon as vε≤θ everywhere we have g(vε)≡0 and, thus:
For t≥1 and y′∈[12,1] we have for all y>1
C>0 universal. So we have, for a possibly different C>0:
For all fixed t≥2, the maximum in y of the right handside of (3.6) is taken at
where z0 is the point of maximum of m(z):=ze−z2/5. Call m0 the (easily computable) maximum of m, a sufficient condition to have vε(t,y)≤θ everywhere is to have, from (3.6):
Define T1ε≥2 as
So, we have easily proved that vε reaches a nontrivial value in a time of (roughly) the order of ln(ε−1), but this value is reached at y∼(lnε−1)1/2. To study what happens at finite distance to y=0, consider L>0 large. There is cL>0, with, in the worst case scenario
such that, in the limit ε→0, we have, from (3.5):
Let eL(y) be the first Dirichlet eigenfunction of −∂xx on (1,L), we normalise so that its maximum is 1. Thus we have
with first eigenvalue
Let v_ε,L(t,y) solve
On the one hand, we have
On the other hand we have v_ε,L(t,y)≤vε(t,y) for t≥T1ε, as long as v_ε,L(t,y) is globally less than θ. This last condition is fulfilled as long as
and the maximum is exactly θ at equality. Note that it is attained far away from the origin, that is, at yL=L−12+1. However, the situation is not as bad as before, because we now have
This is certainly a small quantity, but it is independent of ε. Let us set
We have now, from (3.11):
From now on, once again by a classical sub-solution argument, there is ˜TL>0 (independent of ε), blowing up as L→+∞, such that
This is not exactly (3.3), but we are now quite close to it: from the Harnack inequality we have
for some universal q>0, and the same sub-solution argument yields the (3.3), at a time of the form T1ε+T2ε+˜TL+˜T′L, the new constant ˜T′L being ε-indeendent. Set Tε=T1ε+T2ε+˜TL+˜T′L; it now suffices to notice that (3.11) implies that
which, combined to (3.7), implies
Let us denote by μL a common bound for the two O(1L2) appearing in the above expression. We now pick a small δ and choose L>0, denoted by Lδ, such that
which is exactly (3.4).
Remark 3.2 Using f(v)≤v, and the solution ¯v(t,x) of (3.1) with f(v)=v−g(v) replaced by v, we obtain the (sharper) converse inequality
thus an asymptotic expansion of Tε:
4.
Communications between the road and the field
The goal of this section is to prove that, if the solution on the road is of a certain order at some time and on a certain interval, then the solution in the field will be of the same order, possibly in a square with a smaller size and a little later in time. We also want to prove that the converse holds: if the solution is of some order at some time and some point in the field, this is transmitted to the road. Such results can be seen as weak versions of the Harnack inequality (a bound at a certain time and point would entail the same bound in a whole neighbourhood, possibly at later times) but this will be sufficient for our purpose. See [5] for estimates that are more in the spirit of the Harnack inequality.
Lemma 4.1. Consider t0≥1, x0∈R, L≥1 and ε>0 (not necessarily small) such that
There is cL>0 (universal otherwise) such that
Proof. Without loss of generality, we may translate time and space so as to have t0=1, x0=0. Notice then that, because v(t,x,0)≥0 we have
Recall that the fundamental solution of the fractional heat equation of order α, that we call Gα(t,x), is uniformly bounded away from 0 on [1,2]×[−L−1,L+1]. Thus
This implies
Then, recall that f(v)v is bounded from below - say, by −Λ>0, with Λ>0, and that
is a super-solution to the heat equation, while the boundary condition reads
for a possibly different cL. Thus we have ˜v≥v_, where
By parabolic regularity we have, for some universal C>0:
Thus, there is y0∈(0,1), independent of x0 - and thus of ε such that
And the classical parabolic Harnack inequality implies the lemma. Note that, due to [3], Section 3, one may push it to the boundary thanks to the Robin condition, at the expense of considering ˜v_(t,x,y):=eνyv_(t,x,y).
Lemma 4.2. Consider t0≥1, x0∈R, and ε>0 such that
For all L>0, there is cL>0 (universal otherwise) such that
Proof. Once again there is no loss in generality by assuming t0=1, x0=0. The classical Harnack inequality applied to v entails a lower bound of the order ε at least for v(t,x,1) for t∈[1,2] and −2L≤x≤2L. Fix now L>0, for all δ∈(0,1) there is cδ>0 (we omit the dependence in L) such that
Assume the existence of x1∈[−L,L] and t1∈[1,2] such that v(t1,x1,0) is much smaller than its order of magnitude in the field. This is equivalent to assuming the existence of a sequence of solutions (un,vn) of (1.1), such that the following situation holds:
● for t∈[1,2], x∈[x1−L/2,x1+L/2] and y=1, then vn(t,x,y)≥cε (dependence on L omitted),
● there is t1∈[1,2] such that vn(t1,x1,0)≤1/n.
Remember that vn is uniformly bounded from above. So, by parabolic regularity, (a subsequence of) the sequence (un,vn)n converges, on [1,2]×[x1−L/2,x1+L/2]×[0,1] to a limiting function (u∞,v∞) which is not identically equal to 0 due to the first assumption on vn. The Hopf Lemma implies ∂yv∞(t,x,0)>0, thus the exchange condition yields
This contradicts the fact that v∞(t1,x1,0)=0. Now, we have u(t,x)≥u_(t,x), with
Thus, for t∈[1,2] we have
for a constant c′ that only depends on L.
5.
Bounds to the full model
The starting point of the analysis is the (computationally non trivial) result, whose main line of the proof are given in [2], and proved in full length in [10]. From now on we will assume, for simplicity, that ν=1.
Theorem 5.1 ([10], Chapter 4). Let (¯u(t,x),¯v(t,x,y)) solve
with (¯u(0,x),¯v(0,x,y))=(u0(x),0) and u0≢0 nonnegative and compactly supported. There exists a function R(t,x) and constants δ>0, C>0 such that
1). we have, for large x:
2). and the function R(t,x) is estimated as
Note that this result readily entails the upper bound in Theorem 1.2, so that it suffices to prove the lower bound. We first prove it when g is compactly supported in (0,1], then indicate the necessary changes for a general g.
5.1. Proof of Theorem 1.2 when g is compactly supported in (0,1]
Assume g to be supported in (θ,1). Let us pick λ∈(ε,1/μ) and x0>0 (the same argument would apply for x0<0) very large, we set
From Theorem 5.1, applied at time t=1, the function u(1,x) is of the order ε (and also of the order 1/x1+2α0) on any interval around x0 whose length will not exceed, say, √x0. Thus, from Lemma 4.1, applied on every sub-interval of [x0−√x0,x0+√x0] of length 1 we have
Note that the constant c does not depend on x0, Lemma 4.1 being purely local.
We ask how much time it will take for u to reach the value λ at x0. From (5.2) we have, as soon as ε<θ is small enough - that is, if x0 is large enough - and for all L>0:
Then, translate the point (x0,0) to the origin, and let this time v_(t,x,y) solve the two-dimensional Fisher-KPP equation with Dirichlet conditions on the road:
As long as v_≤θ everywhere, it solves the linear equation, that is, with g(v)=0. In such a case it consists of the product of two solutions of the heat equation times the exponential:
where v_1D(t,y) is the solution of the Dirichlet heat equation in y, and is exactly given by (3.5). The function v1D reaches θ in a time T1ε given by equation (3.7), in other words
This time is too short for the solution of the heat equation in x to decay significantly on, say, the interval [−L,L] with L large but finite (any size L which is an o(√x0) will do). We have indeed, for |x|≤L and t≤T1ε:
simply because x0∼ε−1/(1+2α) and T1ε is of the order ln(1ε). Thus, the function y↦v_(T1ε,0,y) reaches a maximum of the order θ, at a point of the order √T1ε, while it is of the order 1√T1ε for y∼1. Then, we run (5.4) again, from T1ε, with
the function eL′(x,y) being the first eigenfunction of the Dirichlet Laplacian in the rectangle (−L′,L′)×(1,L′), and L′ a large number (in fact we could take L′=L). We have
the first eigenvalue being still an O(1L′2). And so, for a time Tε given by (3.12), there is q>0 independent of ε such that v_(Tε,0,1)≥q.
To conclude the proof, it remains to prove the existence of q′>0 universal such that u(Tε,0)≥q′. This is, however, easy: because x0 is arbitrary, we have
and Lemma 4.2 implies the desired bound for u.
5.2. The lower bound for a general concave nonlinearity
We write again
Thus we have, for all v∈[0,1]: g(v)=O(v2), and this is what we will really use. In view of what we have already done when g vanishes in a vicinity of 0, what we really have to do is study the function v(t,x,y) solving
with ε=11+x1+2α0. In view of the proof of Theorem 3.1, and Section 4, the main property that we have to prove is the following.
Lemma 5.2. Let T1ε be given by (3.7). There is q>0 universal such that
It then suffices, as in the preceding section, to put v above the solution v_δ,L,L′ of
with δ small, and eL,L′(y) the first eigenfunction of the Dirichlet Laplacian in (−L,L)×(1,L′). At time
we have v_δ,L,L′(t,x,y)≥Cδ on (−L,L)×(1,L′), and one finishes the proof of Theorem 1.2 by Lemmas 4.1 and 4.2.
Let us therefore present the
Proof of Lemma 5.2. Call X=(x,y)∈R×R+ a generic point of the upper half-plane R×R−. Let G(t,X,X′) be the fundamental solution of the Dirichlet heat equation in the upper half-plane, we have
the function G0 being the Dirichlet fundamental solution (see (3.5)) whereas G1 is the standard Gaussian G1(t,x)=e−x2/4t√4πt. The Duhamel formula yields
We have
We call et−sD(t−s,s,X,X′) the integrand of the second integral in the right handside of (5.8). Because g(v)=O(v2) we get, taking (5.5) and (3.6) into account:
C>0 universal. Note that we have only estimated the integral for s≥1, the integral for s≤1 being negligible. Integrating in x′ and specialising at x=0 we get
where
We are going to prove the inequality
C>0 universal. There is nothing special about the point X=(0,1) the inequality would be valid for all neighbouring points, at the expense of increasing C. Recall the inequality (see Sections 2 and 3) for v:
This, combined to (5.10), will imply the lemma. As we will set, eventually, t=Tε1, we will always assume t large, and
we cut the time interval (0,t) into two.
1). s∈(0,κt), κ>0 small. We will use the factor e−y′2/3s to make the integral convergent, and make the change of variables y′↦z′=y′/√s.Thus we have
using et+s≤e(1+κ)t, the fact that t≤Tε1 and the definition of Tε1, we end up with
And so letting t−Tε1 we obtain
2). The range s≥κt. This time we rely on the part e−(1+y′)24(t−s) to make the spatial integral convergent, and we will have to be a little careful about the et+s factor. As for the powers y′2, we dominate them by 1+|1+y′|2. We make the change of variables y′↦z′√t−s and we have
We integrate on (κt,t)×R×R+. This yields
Making sure that κ∈(0,1/4) and putting everything together yields (5.10), hence the lemma.
Acknowledgements
The research leading to these results has received funding from the ERC under the European Union's Seventh Frame work Programme (FP/2007-2013) / ERC Grant Agreement 321186 - ReaDi.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad:



