1. Introduction

Magnetic nanoparticles are of great interest in recent research due to their possible applications in magnetic storage devices, MRAM (magnetoresistive random access memory), logical circuits, or magnetic quantum cellular automata ^[1,2,3,4,5]. For higher memory capacity, bit-patterned media with self-assembled magnetic particle arrays can be used instead of conventional thin film systems ^[6]. Amongst these nanostructures, rings are of special interest due to stray fields being minimized in them. The flux-closed vortex states occurring in such rings can represent different information ^[7,8,9]; however, differentiating between them usually necessitates new technologies ^{[8,10,11,12,13]}.

In former publications, we have thus reported in detail the magnetic properties and magnetization reversal processes in fourfold or higher-order nanostructured rings from magnetic material, represented by nanowires building squares ^{[14,15,16,17,18]} or “walls” as they can be produced by lithographic processes ^[19]. Depending on shape and dimension as well as material and angular orientation of the external magnetic field, such nanoparticles can show four or even more stable magnetic states at remanence, correlated with exotic magnetic states, such as different onion states, horseshoe or vortex states. Such stable intermediate states are often found in exchange bias systems in simulation and experiment ^[20,21] but can also occur in ferromagnetic nanoparticles of special shapes. It was found, e.g., that square nanowire rings of four iron (Fe) wires with diameter 10 nm and length 70 nm and with overlapping ends showed magnetization reversal processes via stable intermediate onion states over a broad angular range ^[17]. By varying the diameters of the crossed wires between 6 nm and 20 nm and the lengths between 30 nm and 70 nm, simulations showed different horseshoe and vortex states ^[14]. The influence of the relative orientation of the nanowires, especially the amount and place of crossing, was also investigated. Both parameters were found to be crucial for the possible existence of stable intermediate states ^[16]. In a sixfold wire system with half-balls as corner connections, even more possible magnetic states were found, correlated with one or two steps in the hysteresis loop; however, most of these states were instable so that this approach was not followed further ^[15]. Changing the material from iron to cobalt, a much broader variety of magnetization reversal mechanisms and magnetic states was found especially in an angular region around 0°, combined with the frequent existence of domain-wall states ^[18]. These states, however, were less stable than those simulated in iron systems. Stability of lithographically produced open squares with different corner solutions was also modelled for Fe particles of diameter 400 nm. It was found that typical rounded corners, occurring naturally in the lithography process, resulted in strong deviations of the coercive fields ^[19]. In spite of these problems, square nanowall or nanowire particles are of high interest for the development of magnetic data storage media since they offer the possibility to create quaternary magnetic memories, with each storage position storing two or more bits ^[17] and thus increased overall storage capacity.

While this finding has been proven for a broad range of parameters for single nanoparticles, the question arose how clustering several nanoparticles would influence the magnetic properties of these special magnetic particles. This is why in the recent paper simulations of fourfold magnetic nanoparticles of different dimensions are analyzed, separately as single objects and additionally as clusters, allowing comparing their coercive fields and magnetization reversal mechanisms.

---

2. Materials and Method

Magnetic nanostructures were investigated using the micromagnetic simulator OOMMF (Object Oriented MicroMagnetic Framework) ^[22], based on finite differences (i.e., discretizing space into small cuboids) and the Landau-Lifshitz-Gilbert (LLG) equation of motion ^[23]. The simulation parameters were: material Py (permalloy), mesh size 5 nm, damping coefficient 0.05, anisotropy constant K₁ = 0.5 × 10³ J/m³, exchange constant A = 1.05 × 10⁻¹¹ J/m, and saturation magnetization M_s = 796 × 10³ A/m ^[24,25,26]. The external field is varied between −200 mT and 200 mT parallel to the sample plane. The sample orientation is varied between 0° (i.e., the external magnetic field parallel to the x-axis of the sample) and 180° in steps of 5°.

The samples under simulation are depicted in Figure 1, showing a single particle as well as a cluster of 4 × 4 particles interacting with each other through their demagnetization fields. Lateral dimensions for the single particles were chosen as 120 nm, 200 nm and 400 nm, identically to real samples investigated in former projects ^[27,28] and being typical in recent lithographic approaches ^[27]. The free space between the particles in the clusters was chosen identical to the respective particle width. For a cluster of 4 × 4 objects, the whole structured areas had thus lateral dimensions between 960 nm and 3200 nm side length. The sample height was always 5 nm which is not too high for lithography processes and thus a usual layer thickness for such nanoparticles.

---

3. Results and Discussion

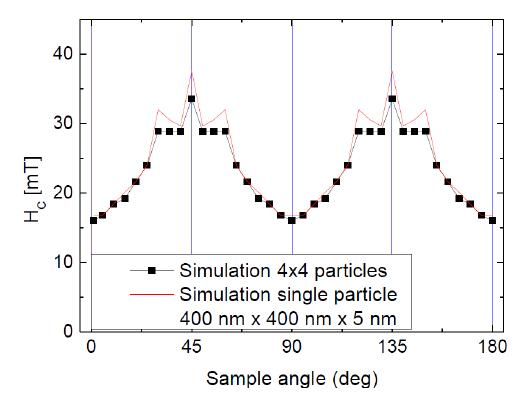
For the largest particle under investigation with 400 nm width, Figure 2 depicts the results of simulations for a single object and a cluster of 4 × 4 particles. Comparing both graphs, it is visible that for most in-plane angles, the coercive fields are approximately equal, while around the easy axes at 45° and 135°, deviations between both situations occur. For applications in bit-patterned media, however, utilizing the doubled amount of stable states at remanence is only possible in an angular region between max. 5° and 20° ^[29]. The particle interactions around 45° do thus not raise difficulties in the technologically interesting area. They can be attributed to starting magnetization reversal in the corners of the single magnetic particles, triggered by the interactions with neighboring particles, allowing for easier reversal of a complete side of the nanoparticles. These states with one or two of the corner regions already changing magnetization orientations can only be found in the largest particles due to the necessary area to show coherent magnetization orientation.

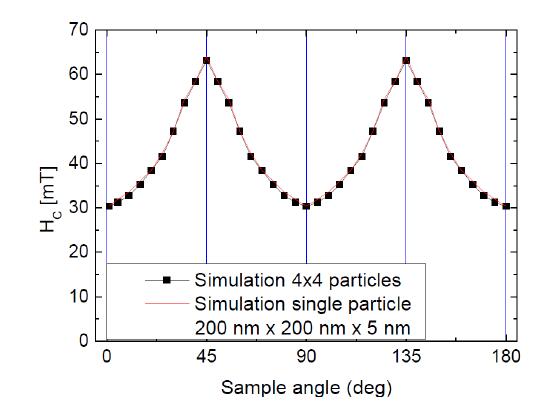
Smaller particles may nevertheless be influenced more significantly by interactions between neighboring magnetic objects due to the reduced distances between them. Figure 3 shows the simulated coercive fields for a single particle of 200 nm side length and the respective 4 × 4 cluster.

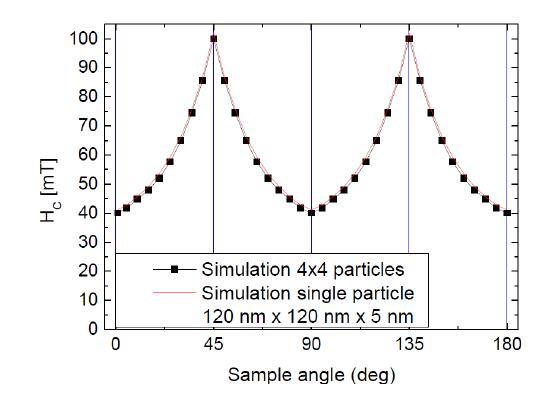
Interestingly, nearly no difference occurs between single object and cluster for this particle dimension. The same finding occurs for the smallest dimension, as visible in Figure 4. For a single particle of 120 nm side length and the respective 4 × 4 cluster, the coercive fields are nearly identical.

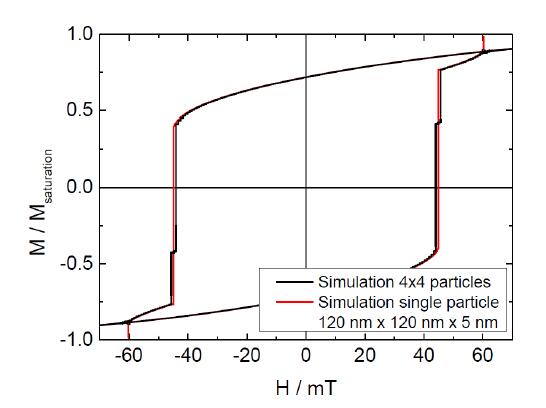
The fact that the coercive fields are approximately equal in most cases, especially for the smaller particles, is not sufficient for proving that additional stable states at remanence also occur in the particle clusters under similar conditions as in the single particles. Figure 5 shows hysteresis loops, simulated for a single nanoparticle of 120 nm side length and the respective 4 × 4 cluster, at an angle of 10° between the particle edge and the external magnetic field. Apparently, the cluster starts reversing its magnetization at smaller fields and finishes this process at larger fields, i.e., the different particles within the cluster switch to another magnetic state at slightly different external magnetic fields. Nevertheless, the plateau between approx. −45 mT and −60 mT, which corresponds to one of the stable intermediate states and leads to one of the additional stable states at remanence when the external magnetic field is reduced to zero ^[17] is approximately identical.

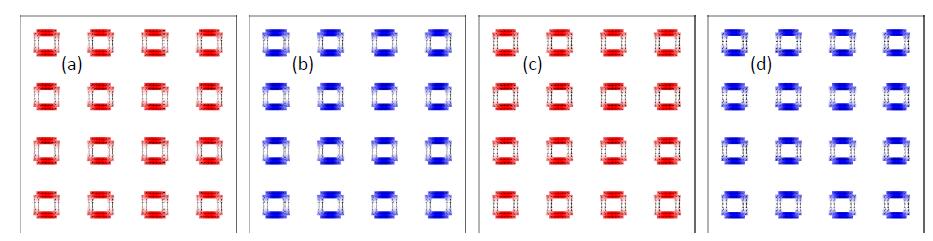
This means that while small deviations of the coercive fields may occur, the most important feature of these particles, i.e., the existence of four stable states at vanishing magnetic field, is not impeded by clustering the single nanoparticles. This finding is supported by the snapshots of the four magnetization states at zero external magnetic field, depicted in Figure 6. The dimension and angular orientation were chosen identical to Figure 5. The magnetic states shown here were reached by the following field sequences: positive saturation ®0 mT (a), positive saturation ® step around −55 mT ® 0 mT (b), negative saturation ® step around +55 mT ® 0 mT (c), and negative saturation ® 0 mT (d).

The same result was found for all other angles of the three particle sizes in which stable intermediate states occurred.

As these micromagnetic simulations have shown, previous findings of stable magnetic states at remanence can be expanded unambiguously from single magnetic particles to particle clusters. Due to the broadened slopes of the hysteresis loop around the coercive fields, the area of the stable intermediate state (in Figure 5 approx. between −45 mT and −60 mT as well as in the identical positive field range) is slightly reduced which has to be taken into account in technological applications. However, the usual shape deviations in the lithography process results in much stronger limitations of the utilizable field and angular region ^[19].

---

4. Conclusions

We have compared magnetic properties and magnetization reversal mechanisms of single magnetic particles of different sizes with clusters prepared from these particles. While the coercive fields near the easy axes of the largest particle showed deviations between single object and cluster, the hysteresis loops of both situations were found to be approximately equal in all other dimensions and angular regions. Especially the possibility to reach a stable magnetic state at remanence from an intermediate “plateau” state is nearly unaltered. This finding ensures that the technological application of such nanoparticles in quaternary memory devices, storing two bits per nanoparticle, can be expanded from single particles to large-area bit-patterned media.

---

Conflict of Interest

All authors declare no conflicts of interest in this paper.

---