State of the art in carbon taxes: a review of the global conclusions

Tadhg O'Mahony; Tadhg O'Mahony

doi:10.3934/GF.2020022

Green Finance

2020, Volume 2, Issue 4: 409-423. doi: 10.3934/GF.2020022

Previous Article Next Article

Review

State of the art in carbon taxes: a review of the global conclusions

Tadhg O'Mahony ^,

Finland Futures Research Centre, University of Turku, Tampere, Finland

Received: 28 September 2020 Accepted: 20 November 2020 Published: 24 November 2020
JEL Codes: H23, P48, Q01, Q38, Q50, Q54

Carbon taxes have been advocated as a key economic measure for the reduction of greenhouse gas emissions. The basis of this proposition,is the economic theory that applying a tax on carbon dioxide emissions is the "optimal" solution to addressing the market failure of externalities. In moving from theory to practice,the evidence from comprehensive global assessments,over the last three decades,covering actual policy experience and empirical study of policy effects,requires evolution and refinement of the theory. Carbon taxes are not adopted at the scale,coverage or price level necessary to effectively reduce emissions in line with the Paris Agreement. A persistent "implementation gap" has arisen,largely due to the political and social challenges that accompany taxation. Assessments of policy experience in key sectors of built environment,transport and industry,highlight the critical role of regulation,standards and technology among broader policy programmes. While a carbon tax can provide simplicity and scope,it is not sufficient on its own. Consistent with this finding,recent modelling innovations show that taxes can be employed as part of a portfolio of best practice policies and measures,for deep reduction of emissions. Portfolios can facilitate application of a lower,more "moderate" carbon tax,which enhances the social acceptability and political feasibility of the tax itself. When designing a tax,revenue recycling can help with policy resistance,delivering the "double dividend" of economic and climate gains,and addressing distributional considerations. A carbon tax may be useful to complement the broader portfolio of policies and measures accepted as necessary for long-term transition and transformation. It can offer support and prevent rebounds,but is not a substitute for the fundamental systems change that is at the core of addressing urgent sustainability crises.

Keywords:

Citation: Tadhg O'Mahony. State of the art in carbon taxes: a review of the global conclusions[J]. Green Finance, 2020, 2(4): 409-423. doi: 10.3934/GF.2020022

Related Papers:

[1]	Luca Spiridigliozzi, Grazia Accardo, Emilio Audasso, Barbara Bosio, Sung Pil Yoon, Gianfranco Dell’Agli . Synthesis of easily sinterable ceramic electrolytes based on Bi-doped 8YSZ for IT-SOFC applications. AIMS Materials Science, 2019, 6(4): 610-620. doi: 10.3934/matersci.2019.4.610
[2]	Muhammad Awwaluddin, Sri Hastuty, Djoko Hadi Prajitno, Makmuri, Budi Prasetiyo, Yudi Irawadi, Jekki Hendrawan, Harry Purnama, Eko Agus Nugroho . Effect of Yttrium on corrosion resistance of Zr-based alloys in Ringer's lactate solution for biomaterial applications. AIMS Materials Science, 2024, 11(3): 565-584. doi: 10.3934/matersci.2024028
[3]	ME Makhatha . Effect of titanium addition on sub-structural characteristics of low carbon copper bearing steel in hot rolling. AIMS Materials Science, 2022, 9(4): 604-616. doi: 10.3934/matersci.2022036
[4]	Hung Nguyen Manh, Oanh Le Thi Mai, Chung Pham Do, Mai Vu Thanh, Anh Nguyen Thi Diep, Dao La Bich, Hang Lam Thi, Duyen Pham Thi, Minh Nguyen Van . Effect of monobasic/dibasic phosphate salts on the crystallinity, physical properties and photocatalytic performance of Ag₃PO₄ material. AIMS Materials Science, 2022, 9(5): 770-784. doi: 10.3934/matersci.2022047
[5]	Tim Slawik, Anne Günther, Tassilo Moritz, Alexander Michaelis . Co-Sintering behaviour of zirconia-ferritic steel composites. AIMS Materials Science, 2016, 3(3): 1160-1176. doi: 10.3934/matersci.2016.3.1160
[6]	Nuriya Mukhamedova, Yernat Kozhakhmetov, Mazhyn Skakov, Sherzod Kurbanbekov, Nurzhan Mukhamedov . Microstructural stability of a two-phase (O + B2) alloy of the Ti-25Al-25Nb system (at.%) during thermal cycling in a hydrogen atmosphere. AIMS Materials Science, 2022, 9(2): 270-282. doi: 10.3934/matersci.2022016
[7]	Marek Konieczny . Transformation superplasticity of laminated CuAl₁₀Fe₃Mn₂ bronze-intermetallics composites. AIMS Materials Science, 2020, 7(3): 312-322. doi: 10.3934/matersci.2020.3.312
[8]	Toshio Ogawa, Hiroyuki Dannoshita, Yoshitaka Adachi . Evaluation of tensile properties of ferrite single-phase low-carbon steel with different initial microstructures. AIMS Materials Science, 2019, 6(5): 798-805. doi: 10.3934/matersci.2019.5.798
[9]	Stefan Wagner, Astrid Pundt . Hydrogen as a probe for defects in materials: Isotherms and related microstructures of palladium-hydrogen thin films. AIMS Materials Science, 2020, 7(4): 399-419. doi: 10.3934/matersci.2020.4.399
[10]	Ravinder Kataria, Ravi Pratap Singh, Jatinder Kumar . An experimental study on ultrasonic machining of Tungsten carbide-cobalt composite materials. AIMS Materials Science, 2016, 3(4): 1391-1409. doi: 10.3934/matersci.2016.4.1391

Abstract

1. Introduction

Hirota and Ito ^[1] proposed the following Sawada-Kotera equation to theoretically study the resonances of solitons in one dimension,

$\begin{equation} u_{t}+ b(15u^3+15 uu_{xx}+u_{xxxx})_x = 0, \end{equation}$

(1.1)

which has a non-vanishing boundary condition

$\begin{equation} u|_{x = \infty} = constant. \end{equation}$

(1.2)

Replace $u$ by $u+\frac{a}{15b}$ and apply the Galilei transformation to remove $u_x$ , then Eq (1.1) changes to the KdV-Sawada-Kotera equation ^[2]

$\begin{equation} u_{t}+a(3 u^2+u_{xx})_x+ b(15u^3+15 uu_{xx}+u_{xxxx})_x = 0, \end{equation}$

(1.3)

where $a$ , $b$ are constants. It is a linear combination of the Sawada-Kotera equation and the KdV equation, with considering $a = 0$ , Eq (1.3) reduces to the Sawada-Kotera equation, when $b = 0$ , Eq (1.3) reduces to the KdV equation. In the past few years, many achievements have been made in the study of KdV-Sawada-Kotera equation. About this equation, conservation laws are investigated by Konno ^[3], and traveling wave solutions are discovered in ^[4]. Quasi-periodic wave and exact solitary wave solutions to the KdV-Sawada-Kotera equation are obtained ^[5].

As we know, nonlinear differential equations (NLDEs) are widely utilized in fluid dynamics, solid state physics, plasma physics, biology, nonlinear optics, chemistry and so on. The study to exact solutions of various NLDEs is extremely important in modern mathematics with ramifications to some areas of physics, mathematics and other sciences. There are many systematic methods to seek exact solutions of NLDEs, for example, Hirota bilinear method ^[6,7], modified simple equation method ^[8], generalized $(G'/G)$ -expansion method ^[9,10], modified Kudryashov method ^[11,12], exp function method ^[13,14], modified extended tanh method ^[15,16], sine-Gordon expansion method ^[17,18], extended sine-Gordon expansion method ^[19,20], complex method ^{[21,22,23,24]} and exp $(-\psi(z))$ -expansion method ^{[25,26,27,28]}.

Eremenko showed that all meromorphic solutions of the Kuramoto Sivashinsky equation are elliptic function and its degeneration in ^[29]. After that, Laurent series were applied by Kudryashov et al. ^[30,31] to obtain meromorphic exact solutions to certain nonlinear differential equations. On the basis of their work, Yuan et al. ^[32,33] established the complex method combining the theories of complex analysis and complex differential equations. It is a powerful approach to obtain exact solutions for NLDEs that admit $\langle p, q \rangle$ condition or are Briot-Bouquet (BB) equations ^[34]. Following their work, we propose the extended complex method to get meromorphic exact solutions for NLDEs which neither admit $\langle p, q \rangle$ condition nor BB equations. Therefore, the extended complex method is an enhancement of the complex method and should deal with more NLDEs in applied sciences.

The exp $(-\psi(z))$ -expansion approach is an effectual technique to seek analytical solutions for NLDEs. A lot of researchers, for instance, Jafari, Khan, Roshid, etc ^{[25,26,27,28]}, made good use of this method to study NLDEs. In this article, we utilize two different systematic methods mentioned above to seek meromorphic exact solutions of the KdV-Sawada-Kotera equation. Dynamic behaviors of the solutions are shown by some graphs in which the profiles of Weierstrass elliptic function solutions have never been shown in former literatures.

2. Description of the exp $(-\psi(z))$ -expansion method

Consider the following nonlinear PDE:

$\begin{equation} P(u, u_x, u_t, u_{xx}, u_{tt}, \cdots) = 0, \end{equation}$

(2.1)

where $P$ is a polynomial consisted by the unknown function $u(x, t)$ as well as its partial derivatives.

Step 1. Reduce Eq (2.1) to the ODE

$\begin{equation} F(u, u', u'', u''', \cdots) = 0, \end{equation}$

(2.2)

by traveling wave transform

$u(x, t) = u(z), \quad z = kx+r t.$

Step 2. Assume that Eq (2.2) has exact solutions as follows:

$\begin{equation} u(z) = \sum\limits_{\tau = 0}^{m}B_\tau(\exp(-\psi(z)))^\tau, \end{equation}$

(2.3)

where $B_\tau (0\leq \tau\leq m)$ are constants to be determined latter, such that $B_m\neq 0$ and $\psi = \psi(z)$ admits the following ODE:

$\begin{equation} \psi'(z) = \gamma+\exp(-\psi(z))+\mu \exp(\psi(z)). \end{equation}$

(2.4)

The solutions of Eq (2.4) are given in the following.

When $\gamma^2-4\mu > 0$ , $\mu\neq0$ ,

$\begin{equation} \psi(z) = \ln\left(\frac{-\sqrt{(\gamma^2-4\mu)}\tanh(\frac{\sqrt{\gamma^2-4\mu}}{2}(z+c))-\gamma}{2\mu}\;\right), \end{equation}$

(2.5)

$\begin{equation} \psi(z) = \ln\left(\frac{-\sqrt{(\gamma^2-4\mu)}\coth(\frac{\sqrt{\gamma^2-4\mu}}{2}(z+c))-\gamma}{2\mu}\;\right). \end{equation}$

(2.6)

When $\gamma^2-4\mu < 0$ , $\mu\neq0$ ,

$\begin{equation} \psi(z) = \ln\left(\frac{\sqrt{(4\mu-\gamma^2)}\tan(\frac{\sqrt{(4\mu-\gamma^2)}}{2}(z+c))-\gamma}{2\mu}\;\right), \end{equation}$

(2.7)

$\begin{equation} \psi(z) = \ln\left(\frac{\sqrt{(4\mu-\gamma^2)}\cot(\frac{\sqrt{(4\mu-\gamma^2)}}{2}(z+c))-\gamma}{2\mu}\;\right). \end{equation}$

(2.8)

When $\gamma^2-4\mu > 0$ , $\gamma\neq0$ , $\mu = 0$ ,

$\begin{equation} \psi(z) = -\ln\left(\frac{\gamma}{\exp(\gamma(z+c))-1}\;\right). \end{equation}$

(2.9)

When $\gamma^2-4\mu = 0$ , $\gamma\neq0$ , $\mu\neq0$ ,

$\begin{equation} \psi(z) = \ln\left(-\frac{2(\gamma(z+c)+2)}{\gamma^2(z+c)}\;\right). \end{equation}$

(2.10)

When $\gamma^2-4\mu = 0$ , $\gamma = 0$ , $\mu = 0$ ,

$\begin{equation} \psi(z) = \ln(z+c). \end{equation}$

(2.11)

In Eqs (2.5)–(2.11), $B_m\neq0, \gamma, \mu, c$ are constants. Taking the homogeneous balance between nonlinear terms and highest order derivatives of Eq (2.2) yields the positive integer $m$ .

Step 3. Insert Eq (2.3) into Eq (2.2) and collect the function exp $(-\psi(z))$ to yield the polynomial to exp $(-\psi(z))$ . Letting all coefficients with same power of exp $(-\psi(z))$ be zero to obtain a system of algebraic equations. Solving these equations, we achieve the values of $B_m\neq0, \gamma, \mu$ and substitute them into Eq (2.3) as well as Eqs (2.5)–(2.11) to accomplish the determination for analytical solutions of the original PDE.

3. Utilization of the exp $(-\psi(z))$ -expansion method to the KdV-Sawada-Kotera equation

Substituting

$u(x, t) = u(z), \quad z = kx+r t,$

into Eq (1.3) and then integrating it we obtain

$\begin{equation} ru+3kau^2+k^3au''+15kbu^3+15k^3b u u'' +k^5b u''''+\zeta = 0. \end{equation}$

(3.1)

where $\zeta$ is the integration constant.

Taking the homogeneous balance between $u''''$ and $uu''$ in Eq (3.1) to yields

$\begin{equation} u(z) = B_0+B_1\exp(-\psi(z))+B_2(\exp(-\psi(z)))^2, \end{equation}$

(3.2)

where $B_2\neq0$ , $B_1$ and $B_0$ are constants.

Substituting $u'''', uu'', u'', u^3, u^2, u$ into Eq.(3.1) and equating the coefficients about $\exp(-\psi(z))$ to zero, we obtain

$e^{0(-\psi(z))}:$

${k}^{5}bB_{1}\, {\gamma}^{3}\mu+14\, {k}^{5}bB_{2}\, {\gamma}^{2}{\mu}^{2 }+8\, {k}^{5}bB_{1}\, \gamma\, {\mu}^{2}+16\, {k}^{5}bB_{2}\, {\mu}^{3}+15 \, {k}^{3}bB_{0}\, B_{1}\, \mu\, \gamma$

$+30\, {k}^{3}bB_{0}\, B_{2}\, {\mu}^{2 }+a{k}^{3}B_{1}\, \mu\, \gamma+2\, a{k}^{3}B^{2}_{2}\, {\mu}+15\, kb{B_{0}} ^{3}+3\, ka{B^{2}_{0}}+rB_{0}+\zeta = 0,$

$e^{1(-\psi(z))}:$

$B_{1}\, b{\gamma}^{4}{k}^{5}+30\, B_{2}\, b{\gamma}^{3}{k}^{5}\mu+22\, B_{ 1}\, b{\gamma}^{2}{k}^{5}\mu+120\, B_{2}\, b\gamma\, {k}^{5}{\mu}^{2}+30\, {k}^{3}bB_{0}\, B_{1}\, \mu$

$+15\, B_{0}\, B_{1}\, b{\gamma}^{2}{k}^{3}+90\, B_ {0}\, B_{2}\, b\gamma\, {k}^{3}\mu+15\, {B_{1}}^{2}b\gamma\, {k}^{3}\mu+30 \, B_{1}\, B_{2}\, b{k}^{3}{\mu}^{2}+16\, B_{1}\, b{k}^{5}{\mu}^{2}$

$+B_{1}\, a{\gamma}^{2}{k}^{3}+6\, B_{2}\, a\gamma\, {k}^{3}\mu+2\, a{k}^{3}B_{1} \, \mu+45\, {B^{2}_{0}}B_{1}\, bk+6\, B_{0}\, B_{1}\, ak+B_{1}\, r = 0,$

$e^{2(-\psi(z))}:$

$16\, B_{2}\, b{\gamma}^{4}{k}^{5}+15\, B_{1}\, b{\gamma}^{3}{k}^{5}+232\, B _{2}\, b{\gamma}^{2}{k}^{5}\mu+60\, B_{1}\, b\gamma\, {k}^{5}\mu+136\, B_{2 }\, b{k}^{5}{\mu}^{2}$

$+60\, B_{0}\, B_{2}\, b{\gamma}^{2}{k}^{3}+15\, {B_{1} }^{2}b{\gamma}^{2}{k}^{3}+105\, B_{1}\, B_{2}\, b\gamma\, {k}^{3}\mu+30\, { B_{2}}^{2}b{k}^{3}{\mu}^{2}+45\, B_{0}\, B_{1}\, b\gamma\, {k}^{3}$

$+120\, B_{0}\, B_{2}\, b{k}^{3}\mu+30\, {B^{2}_{1}}b{k}^{3}\mu+4\, B_{2}\, a{\gamma} ^{2}{k}^{3}+3\, B_{1}\, a\gamma\, {k}^{3}+8\, B_{2}\, a{k}^{3}\mu+45\, {B^{2}_{0}}B_{2}\, bk$

$+45\, B_{0}\, {B^{2}_{1}}bk+6\, B_{0}\, B_{2}\, ak+3\, {B^{2}_{1}}ak+B_{2}\, r = 0,$

$e^{3(-\psi(z))}:$

$130\, B_{2}\, b{\gamma}^{3}{k}^{5}+50\, B_{1}\, b{\gamma}^{2}{k}^{5}+440\, B_{2}\, b\gamma\, {k}^{5}\mu+75\, B_{1}\, B_{2}\, b{\gamma}^{2}{k}^{3}+40\, B_{1}\, b{k}^{5}\mu$

$+90\, {B^{2}_{2}}b\gamma\, {k}^{3}\mu+150\, B_{0}\, B_{2 }\, b\gamma\, {k}^{3}+45\, {B^{2}_{1}}b\gamma\, {k}^{3}+30\, B_{0}\, B_{1}\, b{k}^{3}+10\, B_{2}\, a\gamma\, {k}^{3}$

$+150\, B_{1}\, B_{2} \, b{k}^{3}\mu+90\, B_{0}\, B_{1}\, B_{2}\, bk+15\, {B^{3}_{1}}bk+2\, B_{1}\, a{k}^{3}+6\, B_ {1}\, B_{2}\, ak = 0,$

$e^{4(-\psi(z))}:$

$330\, B_{2}\, b{\gamma}^{2}{k}^{5}+60\, B_{1}\, b\gamma\, {k}^{5}+60\, {B^{2}_{2 }}b{\gamma}^{2}{k}^{3}+240\, B_{2}\, b{k}^{5}\mu+195\, B_{1}\, B_{2}\, b\gamma\, {k}^{3}$

$+90\, B_{0}\, B_{2}\, b{k}^{3 }+30\, {B^{2}_{1}}b{k}^{3}+45\, B_{0}\, {B^{2}_{2}}bk+45\, {B^{2}_{1}}B_{2 }\, bk+6\, B_{2}\, a{k}^{3}+3\, {B^{2}_{2}}ak$

$+120\, {B^{2}_{2}}b{k}^{3}\mu = 0,$

$e^{5(-\psi(z))}:$

$336\, B_{2}\, b\gamma\, {k}^{5}+24\, B_{1}\, b{k}^{5}+150\, {B^{2}_{2}}b \gamma\, {k}^{3}+120\, B_{1}\, B_{2}\, b{k}^{3}+45\, B_{1}\, {B^{2}_{2}}bk = 0,$

$e^{6(-\psi(z))}:$

$120\, B_{2}\, b{k}^{5}+90\, {B^{2}_{2}}b{k}^{3}+15\, {B^{3}_{2}}bk = 0.$

We solve the above algebraic equations and derive two different families:

Family 1:

$\begin{equation} B_2 = -4k^2, B_1 = -4\gamma k^2, B_0 = -{\frac {5k^2b({\gamma}^{2}+8\mu)+a}{15b}}, r = -\frac{k(5k^4b^2({\gamma}^{2}-4\mu)^2-a^2)}{5b}, \end{equation}$

(3.3)

where $\gamma$ and $\mu$ are arbitrary constants.

Substituting Eq (3.3) into Eq (3.2) yields

$\begin{equation} u(z) = -{\frac {5k^2b({\gamma}^{2}+8\mu)+a}{15b}}-4k^2\gamma\exp(-\psi(z))-4k^2(\exp(-\psi(z)))^2. \end{equation}$

(3.4)

Applying Eqs (2.5)–(2.11) into Eq (3.4) respectively, we get the following exact solutions of the KdV-Sawada-Kotera equation.

Family 1.1: When $\gamma^2-4\mu > 0$ , $\mu\neq0$ ,

$u_{11}(z) = -{\frac {5k^2b({\gamma}^{2}+8\mu)+a}{15b}}+ \frac{8k^2\gamma\mu}{\sqrt{(\gamma^2-4\mu)}\tanh\left(\frac{\sqrt{\gamma^2-4\mu}}{2}(z+c)\right)+\gamma}$

$- \frac{16k^2\mu^2}{\left(\sqrt{(\gamma^2-4\mu)}\tanh\left(\frac{\sqrt{\gamma^2-4\mu}}{2}(z+c)\right)+\gamma\right)^2},$

$u_{12}(z) = -{\frac {5k^2b({\gamma}^{2}+8\mu)+a}{15b}}+ \frac{8k^2\gamma\mu}{\sqrt{(\gamma^2-4\mu)}\coth\left(\frac{\sqrt{\gamma^2-4\mu}}{2}(z+c)\right)+\gamma}$

$- \frac{16k^2\mu^2}{\left(\sqrt{(\gamma^2-4\mu)}\coth\left(\frac{\sqrt{\gamma^2-4\mu}}{2}(z+c)\right)+\gamma\right)^2}.$

Family 1.2: When $\gamma^2-4\mu < 0$ , $\mu\neq0$ ,

$u_{13}(z) = -{\frac {5k^2b({\gamma}^{2}+8\mu)+a}{15b}}- \frac{8k^2\gamma\mu}{\sqrt{(4\mu-\gamma^2)}\tan\left(\frac{\sqrt{4\mu-\gamma^2}}{2}(z+c)\right)-\gamma}$

$-\frac{16k^2\mu^2}{\left(\sqrt{(4\mu-\gamma^2)}\tan\left(\frac{\sqrt{4\mu-\gamma^2}}{2}(z+c)\right)-\gamma\right)^2},$

$u_{14}(z) = -{\frac {5k^2b({\gamma}^{2}+8\mu)+a}{15b}}- \frac{8k^2\gamma\mu}{\sqrt{(4\mu-\gamma^2)}\cot\left(\frac{\sqrt{4\mu-\gamma^2}}{2}(z+c)\right)-\gamma}$

$-\frac{16k^2\mu^2}{\left(\sqrt{(4\mu-\gamma^2)}\cot\left(\frac{\sqrt{4\mu-\gamma^2}}{2}(z+c)\right)-\gamma\right)^2}.$

Family 1.3: When $\gamma^2-4\mu > 0$ , $\gamma\neq0$ , $\mu = 0$ ,

$u_{15}(z) = -{\frac {5k^2b{\gamma}^{2}+a}{15b}}- \frac{4k^2\gamma^2}{\exp(\gamma(z+c))-1} - \frac{4k^2\gamma^2}{\left(\exp(\gamma(z+c))-1\right)^2}.$

Family 1.4: When $\gamma^2-4\mu = 0$ , $\gamma\neq0$ , $\mu\neq0$ ,

$u_{16}(z) = -{\frac {60k^2b\mu+a}{15b}}+ \frac{2k^2\gamma^3(z+c)}{\gamma(z+c)+2} -\frac{k^2\gamma^4(z+c)^2}{(\gamma(z+c)+2)^2}.$

Family 1.5: When $\gamma^2-4\mu = 0$ , $\gamma = 0$ , $\mu = 0$ ,

$u_{17}(z) = -{\frac {a}{15b}}-\frac{4k^2}{(z+c)^2}.$

Family 2:

$\begin{equation} B_2 = -2k^2, B_1 = -2\gamma k^2, B_0 = -{\frac {2a +5k^2b({\gamma}^{2}+8\mu)}{30b}}, r = -\frac{k(4a^2+5k^4b^2({\gamma}^{2}-4\mu)^2)}{20b}, \end{equation}$

(3.5)

where $\gamma$ and $\mu$ are arbitrary.

Substituting Eq (3.5) into Eq (3.2) yields

$\begin{equation} u(z) = -{\frac {2a +5k^2b({\gamma}^{2}+8\mu)}{30b}}-2k^2\gamma\exp(-\psi(z))-2k^2(\exp(-\psi(z)))^2. \end{equation}$

(3.6)

Applying Eqs (2.5)–(2.11) into Eq (3.6) respectively, we get the following exact solutions of the KdV-Sawada-Kotera equation.

Family 2.1: When $\gamma^2-4\mu > 0$ , $\mu\neq0$ ,

$u_{21}(z) = -{\frac {2a +5k^2b({\gamma}^{2}+8\mu)}{30b}}+ \frac{4k^2\gamma\mu}{\sqrt{(\gamma^2-4\mu)}\tanh\left(\frac{\sqrt{\gamma^2-4\mu}}{2}(z+c)\right)+\gamma}$

$- \frac{8k^2\mu^2}{\left(\sqrt{(\gamma^2-4\mu)}\tanh\left(\frac{\sqrt{\gamma^2-4\mu}}{2}(z+c)\right)+\gamma\right)^2},$

$u_{22}(z) = -{\frac {2a +5k^2b({\gamma}^{2}+8\mu)}{30b}}+ \frac{4k^2\gamma\mu}{\sqrt{(\gamma^2-4\mu)}\coth\left(\frac{\sqrt{\gamma^2-4\mu}}{2}(z+c)\right)+\gamma}$

$- \frac{8k^2\mu^2}{\left(\sqrt{(\gamma^2-4\mu)}\coth\left(\frac{\sqrt{\gamma^2-4\mu}}{2}(z+c)\right)+\gamma\right)^2}.$

Family 2.2: When $\gamma^2-4\mu < 0$ , $\mu\neq0$ ,

$u_{23}(z) = -{\frac {2a +5k^2b({\gamma}^{2}+8\mu)}{30b}}- \frac{4k^2\gamma\mu}{\sqrt{(4\mu-\gamma^2)}\tan\left(\frac{\sqrt{4\mu-\gamma^2}}{2}(z+c)\right)-\gamma}$

$-\frac{8k^2\mu^2}{\left(\sqrt{(4\mu-\gamma^2)}\tan\left(\frac{\sqrt{4\mu-\gamma^2}}{2}(z+c)\right)-\gamma\right)^2},$

$u_{24}(z) = -{\frac {2a +5k^2b({\gamma}^{2}+8\mu)}{30b}}- \frac{4k^2\gamma\mu}{\sqrt{(4\mu-\gamma^2)}\cot\left(\frac{\sqrt{4\mu-\gamma^2}}{2}(z+c)\right)-\gamma}$

$-\frac{8k^2\mu^2}{\left(\sqrt{(4\mu-\gamma^2)}\cot\left(\frac{\sqrt{4\mu-\gamma^2}}{2}(z+c)\right)-\gamma\right)^2}.$

Family 2.3: When $\gamma^2-4\mu > 0$ , $\gamma\neq0$ , $\mu = 0$ ,

$u_{25}(z) = -{\frac {2a +5k^2b{\gamma}^{2}}{30b}}- \frac{2k^2\gamma^2}{\exp(\gamma(z+c))-1} - \frac{2k^2\gamma^2}{\left(\exp(\gamma(z+c))-1\right)^2}.$

Family 2.4: When $\gamma^2-4\mu = 0$ , $\gamma\neq0$ , $\mu\neq0$ ,

$u_{26}(z) = -{\frac {a +30k^2b\mu}{15b}}+ \frac{k^2\gamma^3(z+c)}{\gamma(z+c)+2} -\frac{k^2\gamma^4(z+c)^2}{2(\gamma(z+c)+2)^2}.$

Family 2.5: When $\gamma^2-4\mu = 0$ , $\gamma = 0$ , $\mu = 0$ ,

$u_{27}(z) = -{\frac {a}{15b}}-\frac{2k^2}{(z+c)^2}.$

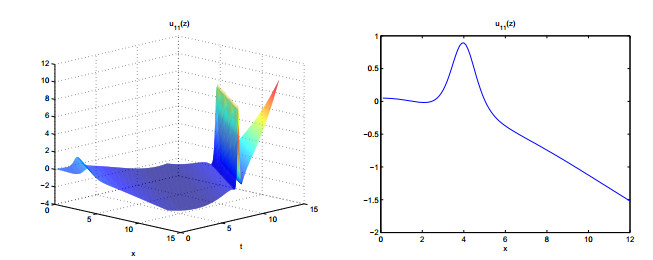
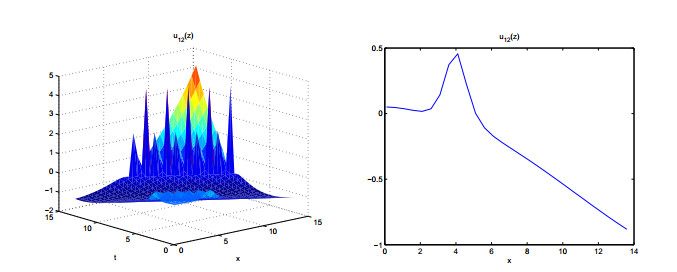
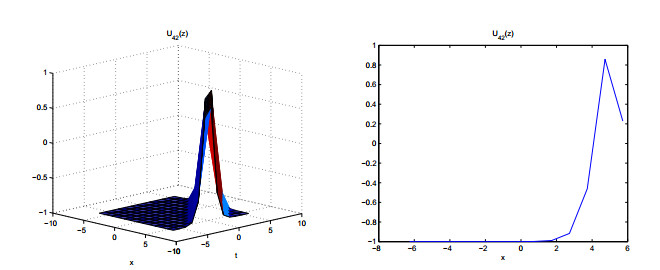
Figures 1–6 show the properties of the solutions.

Figure 1. The 3D and 2D surfaces of

$u_{11}(z)$ by considering the values

$\gamma = 4$ ,

$\mu = 3$ ,

$k = 1$ ,

$r = 1$ ,

$c = 1$ ,

$b = 1$ ,

$a = -215$ and

$t = 0$ for the 2D graphic.

DownLoad: Full-Size Img PowerPoint

Figure 2. The 3D and 2D surfaces of

$u_{12}(z)$ by considering the values

$\gamma = 4$ ,

$\mu = 3$ ,

$k = 1$ ,

$r = 1$ ,

$c = 1$ ,

$b = 1$ ,

$a = -215$ and

$t = 0$ for the 2D graphic.

DownLoad: Full-Size Img PowerPoint

Figure 3. The 3D and 2D surfaces of

$u_{13}(z)$ by considering the values

$\gamma = 4$ ,

$\mu = 5$ ,

$k = 1$ ,

$r = 1$ ,

$c = 1$ ,

$b = 1$ ,

$a = -295$ and

$t = 0$ for the 2D graphic.

DownLoad: Full-Size Img PowerPoint

Figure 4. The 3D and 2D surfaces of

$u_{14}(z)$ by considering the values

$\gamma = 4$ ,

$\mu = 5$ ,

$k = 1$ ,

$r = 1$ ,

$c = 1$ ,

$b = 1$ ,

$a = -295$ and

$t = 0$ for the 2D graphic.

DownLoad: Full-Size Img PowerPoint

Figure 5. The 3D and 2D surfaces of

$u_{15}(z)$ by considering the values

$\gamma = 1$ ,

$\mu = 0$ ,

$k = 1$ ,

$r = 1$ ,

$c = 1$ ,

$b = 1$ ,

$a = -20$ and

$t = 0$ for the 2D graphic.

DownLoad: Full-Size Img PowerPoint

Figure 6. The 3D and 2D surfaces of

$u_{16}(z)$ by considering the values

$\gamma = 1$ ,

$\mu = \frac{1}{4}$ ,

$k = 1$ ,

$r = 1$ ,

$c = 1$ ,

$b = 1$ ,

$a = -30$ and

$t = 0$ for the 2D graphic.

DownLoad: Full-Size Img PowerPoint

4. The extended complex method

Step 1. Substitute the transformation $I: u(x, t)\rightarrow U(z)$ , $(x, t)\rightarrow z$ into a nonlinear PDE to yield an ODE

$\begin{equation} G(U, U', U'', \cdots) = 0. \end{equation}$

(4.1)

Step 2. Determination of the weak $\langle p, q \rangle$ condition.

Assume that the meromorphic solutions $U$ of Eq (4.1) have at least one pole and let $q, \; p\in {\mathbb N}$ . Substitute the Laurent series

$\begin{equation} U(z) = \sum\limits_{k = -q}^{\infty}T_{k}z^{k}, T_{-q}\neq 0, q \gt 0, \end{equation}$

(4.2)

into Eq (4.1) to determine $p$ distinct Laurent principal parts

$\sum\limits_{k = -q}^{-1}T_{k}z^{k},$

then we say that the weak $\langle p, q \rangle$ condition of Eq (4.1) holds.

It is know that Weierstrass elliptic function $\wp(z): = \wp(z, g_2, g_3)$ has double periods and satisfies:

$(\wp'(z))^2 = 4 \wp(z)^3-g_2 \wp(z)-g_3,$

and it admit an addition formula ^[35] as follows:

$\wp(z-z_0) = -\wp(z)+ \frac{1}{4}\left[\frac{\wp'(z)+\wp'(z_0)}{\wp(z)-\wp(z_0)}\right]^2-\wp(z_0).$

Step 3. Substituting the indeterminate forms

$U(z) = \sum\limits_{i = 1}^{h-1}\sum\limits_{j = 2}^{q}\frac{(-1)^j\beta_{-ij}}{(j-1)!}\frac{d^{j-2}}{dz^{j-2}} \left(\frac{1}{4}\left(\frac{\wp'(z)+D_i}{\wp(z)-C_i}\right)^2 -\wp(z)\right) +\sum\limits_{i = 1}^{h-1}\frac{\beta_{-i1}}{2}\frac{\wp'(z)+D_i}{\wp(z)-C_i}$

$\begin{equation} +\sum\limits_{j = 2}^{q}\frac{(-1)^j\beta_{-hj}}{(j-1)!}\frac{d^{j-2}}{dz^{j-2}}\wp (z)+\beta_0, \end{equation}$

(4.3)

$\begin{equation} U(z) = \sum\limits_{i = 1}^{h}\sum\limits_{j = 1}^{q}\frac{\beta_{ij}}{(z-z_{i})^{j}}+ \beta_0, \end{equation}$

(4.4)

$\begin{equation} U(e^{\alpha z}) = \sum\limits_{i = 1}^{h}\sum\limits_{j = 1}^{q}\frac{\beta_{ij}}{(e^{\alpha z}-e^{\alpha z_{i}})^{j}}+ \beta_0, \end{equation}$

(4.5)

into Eq (4.1) respectively yields a set of algebraic equations, and then solving these equations, we achieve elliptic function solutions, simply periodic solutions and rational function solutions with a pole at $z = 0$ , in which $D_i^2 = 4C_i^3-g_2C_i-g_3$ , $\beta_{-ij}$ are determined by (4.2), and $\sum\limits_{i = 1}^h\beta_{-i1} = 0$ , and $R(z)$ , $R(e^{\alpha z}) (\alpha \in {\mathbb C})$ have $h(\leq p)$ distinct poles of multiplicity $q$ .

Step 4. Derive the meromorphic solutions at arbitrary pole, and insert the inverse transform $I^{-1}$ back to the meromorphic solutions to obtain exact solutions of the given PDE.

5. Utilization of the extended complex method to the KdV-Sawada-Kotera equation

Inserting (4.2) into Eq.(3.1) yields

$T_{-2} = -4k^2, T_{-1} = 0, T_{0} = -\frac{a}{15b}, T_{1} = 0, T_{2} = \frac{5r b-ka^2}{300k^3b^2}, \cdots$

and

$T_{-2} = -2k^2, T_{-1} = 0, T_{0} = -\frac{a}{15b}, T_{1} = 0, T_{2} = \frac{ka^2-5r b}{150k^3b^2}, \cdots$

Therefore we know that $p = 2, \; q = 2$ , then the weak $\langle 2, 2 \rangle$ condition of Eq (3.1) hold.

By the weak $\langle 2, 2 \rangle$ condition and (4.3), we have the form of the elliptic solutions of Eq (3.1)

$U_{10}(z) = \beta_{-2}\wp(z)+\beta_{20},$

with pole at $z = 0$ .

Substituting $U_{10}(z)$ into Eq (3.1) yields

$\begin{equation} \sum\limits_{i = 1}^{4}c_{{1i}}\wp^{i-1}(z) = 0, \end{equation}$

(5.1)

where

$c_{{11}} = -12\, {k}^{5}b\beta_{{-2}}g_{{3}}-\frac{15}{2}\, {k}^{3}b\beta_{{-2}}\beta_{{20} }g_{{2}}+15\, kb{\beta^{3}_{{20}}}+3\, ka{\beta^{2}_{{20}}}-\frac{1}{2}\, a{k}^{3}\beta_{{-2}}g_{{2}}+r\, \beta_{{20}}+\zeta,$

$c_{{12}} = -18\, {k}^{5}b\beta_{{-2}}g_{{2}}-\frac{15}{2}\, {k}^{3}b{\beta^{2}_{{-2}}}g_{{2 }}+45\, kb\beta_{{-2}}{\beta^{2}_{{20}}}+6\, ka\beta_{{-2}}\beta_{{20}}+r\, \beta_{{-2}},$

$c_{{13}} = 90\, {k}^{3}b\beta_{{-2}}\beta_{{20}}+6\, a{k}^{3}\beta_{{-2}}+45\, bk{ \beta^{2}_{{-2}}}\beta_{{20}}+3\, ak{\beta^{2}_{{-2}}},$

$c_{{14}} = 120\, b{k}^{5}\beta_{{-2}}+90\, b{k}^{3}{\beta^{2}_{{-2}}}+15\, bk{\beta^{3}_{{-2}}}.$

Equate the coefficients of all powers of $\wp(z)$ in Eq (5.1) to zero to achieve one set of algebraic equations:

$c_{{11}} = 0, c_{{12}} = 0, c_{{13}} = 0, c_{{14}} = 0.$

Solve the above equations, then

$\beta_{{-2}} = -4k^2, \beta_{{20}} = -\frac{a}{15b}, g_2 = {\frac {{a}^{2}k-5\, br}{60\, {b}^{2}{k}^{5}}}, g_3 = -{\frac {2\, {a}^{3}k+225\, \zeta \, {b}^{2}-15\, abr}{10800\, {b}^{3}{k}^{7}}},$

and

$\beta_{{-2}} = -2k^2, \beta_{{20}} = -\frac{a}{15b}, g_2 = {\frac {5\, br-{a}^{2}k}{15\, {b}^{2}{k}^{5}}}, g_3 = -{\frac {2\, {a}^{3}k+225\, \zeta \, {b}^{2}-15\, abr}{5400\, {b}^{3}{k}^{7}}},$

then

$U_{11, 0}(z) = -4k^2\wp(z)-\frac{a}{15b},$

and

$U_{12, 0}(z) = -2k^2\wp(z)-\frac{a}{15b}.$

Thus, elliptic solutions of Eq (3.1) with arbitrary pole are

$U_{11}(z) = -4k^2\wp(z-z_{0})-\frac{a}{15b},$

and

$U_{12}(z) = -2k^2\wp(z-z_{0})-\frac{a}{15b},$

where $z_0\in {\mathbb C}$ .

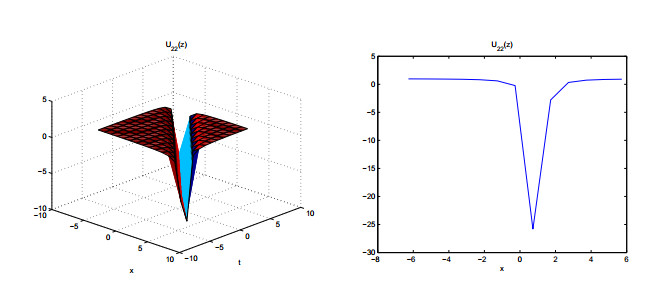
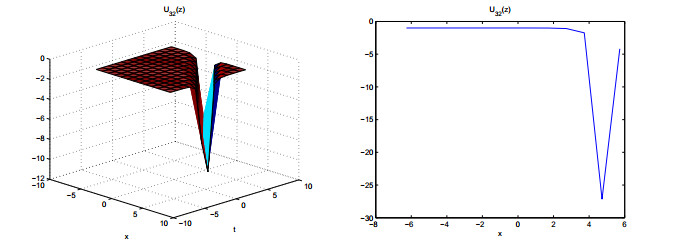
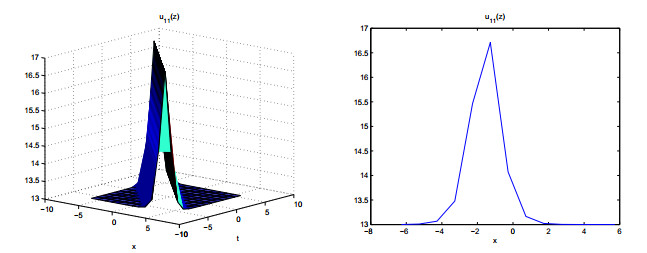
Use the addition formula to $U_{11}(z)$ and $U_{12}(z)$ , then

$U_{11}(z) = 4k^2\wp(z)-k^2\left(\frac{\wp'(z)+D}{\wp(z)-C}\right)^2+\frac{60k^2bC-a}{15b},$

and

$U_{12}(z) = 2k^2\wp(z)-\frac{k^2}{2}\left(\frac{\wp'(z)+D}{\wp(z)-C}\right)^2+\frac{30k^2bC-a}{15b},$

where $C^2 = 4D^3-g_2D-g_3$ . $g_2 = {\frac {{a}^{2}k-5\, b\mu}{60\, {b}^{2}{k}^{5}}}, \; g_3 = -{\frac {2\, {a}^{3}k+225\zeta \, {b}^{2}-15\, ab\mu}{10800\, {b}^{3}{k}^{7}}}$ in the former case, $g_2 = {\frac {5\, br-{a}^{2}k}{15\, {b}^{2}{k}^{5}}}, \; g_3 = -{\frac {2\, {a}^{3}k+225\, \zeta \, {b}^{2}-15\, abr}{5400\, {b}^{3}{k}^{7}}}$ in the latter case.

By (4.4) and the weak $\langle 2, 2 \rangle$ condition, we have the indeterminate form of rational solutions

$U_{20}(z) = \frac{\beta_{12}}{z^2} +\frac{\beta_{11}}{z}+\beta_{10},$

with pole at $z = 0$ .

Substituting $U_{20}(z)$ into Eq (3.1) yields

$\begin{equation} \sum\limits_{i = 1}^{7}c_{{2i}}z^{i-7} = 0, \end{equation}$

(5.2)

where

$c_{{21}} = 120\, b{k}^{5}\beta_{{12}}+90\, b{k}^{3}{\beta_{{12}}}^{2}+15\, bk{\beta_ {{12}}}^{3},$

$c_{{22}} = 24\, b{k}^{5}\beta_{{11}}+120\, b{k}^{3}\beta_{{11}}\beta_{{12}}+45\, bk \beta_{{11}}{\beta_{{12}}}^{2},$

$c_{{23}} = 90\, b{k}^{3}\beta_{{10}}\beta_{{12}}+30\, b{k}^{3}{\beta_{{11}}}^{2}+6 \, a{k}^{3}\beta_{{12}}+45\, bk\beta_{{10}}{\beta_{{12}}}^{2}+45\, bk{\beta_{{11}}}^{2}\beta_{{12}}+3\, ak{\beta_{{12}}}^{2},$

$c_{{24}} = 30\, b{k}^{3}\beta_{{10}}\beta_{{11}}+2\, a{k}^{3}\beta_{{11}}+90\, bk \beta_{{10}}\beta_{{11}}\beta_{{12}}+15\, bk{\beta_{{11}}}^{3}+6\, ak\beta_{{11}}\beta_{{12}},$

$c_{{25}} = 45\, bk{\beta_{{10}}}^{2}\beta_{{12}}+45\, bk\beta_{{10}}{\beta_{{11}}}^ {2}+6\, ak\beta_{{10}}\beta_{{12}}+3\, ak{\beta_{{11}}}^{2}+r\, \beta_{{12}},$

$c_{{26}} = 45\, bk{\beta_{{10}}}^{2}\beta_{{11}}+6\, ak\beta_{{10}}\beta_{{11}}+r \, \beta_{{11}},$

$c_{{27}} = 15\, kb{\beta_{{10}}}^{3}+3\, ka{\beta_{{10}}}^{2}+r\, \beta_{{10}}+\zeta.$

Equate the coefficients of all powers of $z$ in Eq (5.2) to zero to achieve a system of algebraic equations:

$c_{{21}} = 0, c_{{22}} = 0, c_{{23}} = 0, c_{{24}} = 0, c_{{25}} = 0, c_{{26}} = 0, c_{{27}} = 0.$

Solving the above equations, we get

$\beta_{{12}} = -4k^2, \beta_{{11}} = 0, \beta_{{10}} = -\frac{a}{15b},$

and

$\beta_{{12}} = -2k^2, \beta_{{11}} = 0, \beta_{{10}} = -\frac{a}{15b},$

then

$U_{21, 0}(z) = -\frac{4k^2}{z^2} -\frac{a}{15b},$

and

$U_{22, 0}(z) = -\frac{2k^2}{z^2} -\frac{a}{15b},$

where $r = \, {\frac {k{a}^{2}}{5b}}$ , $\zeta = {\frac {k{a}^{3}}{225\, {b}^{2}}}$ .

Insert $U(z) = R(\eta)$ into Eq (3.1) to yield

$k^5b\alpha^4(R^{(4)}\eta^4+6R'''\eta^3+7R''\eta^2+R'\eta)+15k^3b\alpha^2 R(\eta R'+\eta^2R'')$

$\begin{equation} +15kbR^3+3kaR^2+ak^3\alpha^2(\eta R'+\eta^2R'')+rR+\zeta = 0, \end{equation}$

(5.3)

where $\eta = e^{\alpha z}$ ( $\alpha \in {\mathbb C}$ ).

Substituting

$U_{30}(z) = \frac{b_{12}}{(e^{\alpha z}-1)^2} +\frac{b_{11}}{e^{\alpha z}-1}+b_{10},$

into the Eq (5.3), we have

$\begin{equation} \sum\limits_{i = 1}^{7}c_{{3i}}\alpha^2 e^{(7-i)\alpha z}(e^{\alpha z}-1)^{-6} = 0, \end{equation}$

(5.4)

in which

$c_{{31}} = 15\, bk{b^{3}_{{10}}}+3\, ak{b^{2}_{{10}}}+rb_{{10}}+\zeta,$

$c_{{32}} = {\alpha}^{4}b{k}^{5}b_{{11}}+15\, {\alpha}^{2}b{k}^{3}b_{{10}}b_{{11}}+ a{\alpha}^{2}{k}^{3}b_{{11}}-90\, bk{b^{3}_{{10}}}+45\, bk{b^{2}_{{10}}} b_{{11}}-18\, ak{b^{2}_{{10}}}$

$+6\, akb_{{10}}b_{{11}}-6\, rb_{{10}}+rb_{{11}}-6\, \zeta,$

$c_{{33}} = 10\, {\alpha}^{4}b{k}^{5}b_{{11}}+16\, {\alpha}^{4}b{k}^{5}b_{{12}}-30\, {\alpha}^{2}b{k}^{3}b_{{10}}b_{{11}}+60\, {\alpha}^{2}b{k}^{3}b_{{10}}b _{{12}}+15\, {\alpha}^{2}b{k}^{3}{b^{2}_{{11}}}$

$-2\, a{\alpha}^{2}{k}^{3} b_{{11}}+4\, a{\alpha}^{2}{k}^{3}b_{{12}}+225\, bk{b_{{10}}}^{3}-225\, bk {b_{{10}}}^{2}b_{{11}}+45\, bk{b_{{10}}}^{2}b_{{12}}+45\, bkb_{{10}}{b^{2}_{{11}}}$

$+45\, ak{b^{2}_{{10}}}-30\, akb_{{10}}b_{{11}}+6\, akb_{{10}}b_ {{12}}+3\, ka{b^{2}_{{11}}}+15\, rb_{{10}}-5\, rb_{{11}}+rb_{{12}}+15\, \zeta,$

$c_{{34}} = 66\, {\alpha}^{4}b{k}^{5}b_{{12}}-90\, {\alpha}^{2}b{k}^{3}b_{{10}}b_{{ 12}}-15\, {\alpha}^{2}b{k}^{3}{b_{{11}}}^{2}+75\, {\alpha}^{2}b{k}^{3}b_ {{11}}b_{{12}}-6\, a{\alpha}^{2}{k}^{3}b_{{12}}$

$-300\, bk{b^{3}_{{10}}}+ 450\, bk{b^{2}_{{10}}}b_{{11}}-180\, bk{b^{2}_{{10}}}b_{{12}}-180\, bkb_{ {10}}{b^{2}_{{11}}}+90\, bkb_{{10}}b_{{11}}b_{{12}}+15\, kb{b^{3}_{{11}}}$

$+60\, akb_{{10}}b_{{11}}-24\, akb_{{10}}b_{{12}}- 12\, ka{b^{2}_{{11}}}+6\, akb_{{11}}b_{{12}}-20\, rb_{{10}}+10\, rb_{{11}}-4\, rb_{{12}}-20\, \zeta$

$-60\, ak{b^{2}_{{10}}},$

$c_{{35}} = -10\, {\alpha}^{4}b{k}^{5}b_{{11}}+36\, {\alpha}^{4}b{k}^{5}b_{{12}}+30 \, {\alpha}^{2}b{k}^{3}b_{{10}}b_{{11}}-15\, {\alpha}^{2}b{k}^{3}{b^{2}_{{11 }}}-30\, {\alpha}^{2}b{k}^{3}b_{{11}}b_{{12}}$

$+60\, {\alpha}^{2}b{k}^{3}{b^{2}_{{12}}}+2\, a{\alpha}^{2}{k}^{3}b_{{11}}+225\, bk{b^{3 }_{{10}}}-450\, bk{b^{2}_{{10}}}b_{{11}}+270\, bk{b^{2}_{{10}}}b_{{12}}+270\, bkb _{{10}}{b^{2}_{{11}}}$

$-270\, bkb_{{10}}b_{{11}}b_{{12}}+45\, bkb_{{10}}{b^{2} _{{12}}}-45\, kb{b^{3}_{{11}}}+45\, bk{b^{2}_{{11}}}b_{{12}}+45\, ak{ b^{2}_{{10}}}-60\, akb_{{10}}b_{{11}}$

$+36\, akb_{{10}}b_{{12}}+18\, ka{b^{2}_{{11}}}-18\, akb_{{11}}b_{{12}}+3\, ka{b^{2}_{{12}}}+15\, rb_{{10}}-10 \, rb_{{11}}+6\, rb_{{12}}+15\, \zeta,$

$c_{{36}} = -{\alpha}^{4}b{k}^{5}b_{{11}}+2\, {\alpha}^{4}b{k}^{5}b_{{12}}-15\, { \alpha}^{2}b{k}^{3}b_{{10}}b_{{11}}+30\, {\alpha}^{2}b{k}^{3}b_{{10}}b_ {{12}}+15\, {\alpha}^{2}b{k}^{3}{b^{2}_{{11}}}$

$-45\, {\alpha}^{2}b{k}^{3} b_{{11}}b_{{12}}+30\, {\alpha}^{2}b{k}^{3}{b^{2}_{{12}}}-a{\alpha}^{2}{ k}^{3}b_{{11}}+2\, a{\alpha}^{2}{k}^{3}b_{{12}}-90\, bk{b^{3}_{{10}}}+18\, akb_{{11}}b_{{12}}$

$+225\, bk{b^{2}_{{10}}}b_{{11}}-180\, bk{b^{2}_{{10}}}b_{{12}}-180\, bkb_{ {10}}{b^{2}_{{11}}}+270\, bkb_{{10}}b_{{11}}b_{{12}}+45\, kb{b^{3}_{{11}}}-6\, rb_{{10}}$

$-90\, bk{b^{2}_{{11}}}b_{{12}}+45\, bkb_{ {11}}{b^{2}_{{12}}}-18\, ak{b^{2}_{{10}}}+30\, akb_{{10}}b_{{11}}-24\, ak b_{{10}}b_{{12}}-6\, ka{b^{2}_{{12}}}+5\, rb_{{11}}$

$-12\, ka{b^{2}_{{11}}}-90\, bkb_{{10}}{b^{2}_{{12}}}-4\, rb_{{12}}-6\, \zeta,$

$c_{{37}} = 15\, bk{b^{3}_{{10}}}-45\, bk{b^{2}_{{10}}}b_{{11}}+45\, bk{b^{2}_{{10}}} b_{{12}}+45\, bkb_{{10}}{b^{2}_{{11}}}-90\, bkb_{{10}}b_{{11}}b_{{12}}+ 45\, bkb_{{10}}{b^{2}_{{12}}}$

$-15\, kb{b^{3}_{{11}}}+45\, bk{b^{2}_{{11}}} b_{{12}}-45\, bkb_{{11}}{b^{2}_{{12}}}+15\, kb{b^{3}_{{12}}}+3\, ak{b_{{ 10}}}^{2}-6\, akb_{{10}}b_{{11}}+6\, akb_{{10}}b_{{12}}$

$+3\, ka{b^{2}_{{11}}}-6\, akb_{{11}}b_{{12}}+3\, ka{b^{2}_{{12}}}+rb_{{10}}-rb_{{11}}+rb_{ {12}}+\zeta.$

Equate the coefficients of all powers about $e^{\alpha z}$ in Eq (5.4) to zero to achieve a system of algebraic equations:

$c_{{31}} = 0, c_{{32}} = 0, c_{{33}} = 0, c_{{34}} = 0, c_{{35}} = 0, c_{{36}} = 0, c_{{37}} = 0.$

Solving the above equations, we get

$b_{{12}} = -4k^2\alpha^{2}, b_{{11}} = -4k^2\alpha^{2}, b_{{10}} = -\frac{5k^2b\alpha^2+a}{15b},$

$r = \, {\frac { \left( -5\, {\alpha}^{4}{b}^{2}{k}^{4}+{a}^{2} \right) k}{5b}}, \zeta = {\frac { \left( 10\, {\alpha}^{4}{b}^{2}{k}^{4}-5\, a{\alpha}^{2}b{k}^{2 }+{a}^{2} \right) k \left( 5\, {\alpha}^{2}b{k}^{2}+a \right) }{225\, {b}^{2}}},$

and

$b_{{12}} = -2k^2\alpha^{2}, b_{{11}} = -2k^2\alpha^{2}, b_{{10}} = -\frac{5k^2b\alpha^2+a}{15b},$

So simply periodic solutions of Eq (3.1) with pole at $z = 0$ are

$U_{31, 0}(z) = -\frac{4k^2\alpha^{2}}{(e^{\alpha z}-1)^2} -\frac{4k^2\alpha^{2}}{(e^{\alpha z}-1)}-\frac{5k^2b\alpha^2+a}{15b}$

$= -\frac{4k^2\alpha^{2}e^{\alpha z}}{(e^{\alpha z}-1)^2} -\frac{5k^2b\alpha^2+a}{15b}$

$= -k^2\alpha^{2} \coth^2\frac{\alpha z}{2}+\frac{10k^2b\alpha^2-a}{15b},$

and

$U_{32, 0}(z) = -\frac{2k^2\alpha^{2}}{(e^{\alpha z}-1)^2} -\frac{2k^2\alpha^{2}}{(e^{\alpha z}-1)}-\frac{5k^2b\alpha^2+a}{15b}$

$= -\frac{2k^2\alpha^{2}e^{\alpha z}}{(e^{\alpha z}-1)^2} -\frac{5k^2b\alpha^2+a}{15b}$

$= -\frac{k^2\alpha^{2}}{2} \coth^2\frac{\alpha z}{2}+\frac{5k^2b\alpha^2-2a}{30b}.$

Similar to $U_{30}(z)$ , we substitute

$U_{40}(z) = \frac{b_{12}}{(e^{\alpha z}+1)^2} +\frac{b_{11}}{e^{\alpha z}+1}+b_{10},$

into the Eq (5.3) to yield

$b_{{12}} = -4k^2\alpha^{2}, b_{{11}} = 4k^2\alpha^{2}, b_{{10}} = -\frac{5k^2b\alpha^2+a}{15b},$

and

$b_{{12}} = -2k^2\alpha^{2}, b_{{11}} = 2k^2\alpha^{2}, b_{{10}} = -\frac{5k^2b\alpha^2+a}{15b},$

then

$U_{41, 0}(z) = -\frac{4k^2\alpha^{2}}{(e^{\alpha z}+1)^2} +\frac{4k^2\alpha^{2}}{(e^{\alpha z}+1)}-\frac{5k^2b\alpha^2+a}{15b}$

$= \frac{4k^2\alpha^{2}e^{\alpha z}}{(e^{\alpha z}+1)^2} -\frac{5k^2b\alpha^2+a}{15b}$

$= -k^2\alpha^{2} \tanh^2\frac{\alpha z}{2}-\frac{a-10k^2b\alpha^2}{15b},$

and

$U_{42, 0}(z) = -\frac{2k^2\alpha^{2}}{(e^{\alpha z}+1)^2} +\frac{2k^2\alpha^{2}}{(e^{\alpha z}+1)}-\frac{5k^2b\alpha^2+a}{15b}$

$= \frac{2k^2\alpha^{2}e^{\alpha z}}{(e^{\alpha z}+1)^2} -\frac{5k^2b\alpha^2+a}{15b}$

$= -\frac{k^2\alpha^{2}}{2} \tanh^2\frac{\alpha z}{2}-\frac{2a-5k^2b\alpha^2}{30b}.$

Substituting

$U_{50}(z) = \frac{b_{14}}{(e^{\alpha z}-1)^2} +\frac{b_{13}}{(e^{\alpha z}+1)^2}+\frac{b_{12}}{e^{\alpha z}-1} +\frac{b_{11}}{e^{\alpha z}+1}+b_{10},$

into the Eq (5.3) to yield

$b_{{14}}-4k^2\alpha^{2}, b_{{13}} = -4k^2\alpha^{2}, b_{{12}} = -4k^2\alpha^{2}, b_{{11}} = 4k^2\alpha^{2}, b_{{10}} = -\frac{2(5k^2b\alpha^2+a)}{15b},$

and

$b_{{14}}-2k^2\alpha^{2}, b_{{13}} = -2k^2\alpha^{2}, b_{{12}} = -2k^2\alpha^{2}, b_{{11}} = 2k^2\alpha^{2}, b_{{10}} = -\frac{2(5k^2b\alpha^2+a)}{15b},$

then

$U_{51, 0}(z) = -\frac{4k^2\alpha^{2}}{(e^{\alpha z}-1)^2} -\frac{4k^2\alpha^{2}}{(e^{\alpha z}+1)^2}-\frac{4k^2\alpha^{2}}{(e^{\alpha z}-1)} +\frac{4k^2\alpha^{2}}{(e^{\alpha z}+1)} -\frac{2(5k^2b\alpha^2+a)}{15b}$

$= -\frac{4k^2\alpha^{2}e^{\alpha z}}{(e^{\alpha z}-1)^2} + \frac{4k^2\alpha^{2}e^{\alpha z}}{(e^{\alpha z}+1)^2} -\frac{2(5k^2b\alpha^2+a)}{15b},$

and

$U_{52, 0}(z) = -\frac{2k^2\alpha^{2}}{(e^{\alpha z}-1)^2} -\frac{2k^2\alpha^{2}}{(e^{\alpha z}+1)^2}-\frac{2k^2\alpha^{2}}{(e^{\alpha z}-1)} +\frac{2k^2\alpha^{2}}{(e^{\alpha z}+1)} -\frac{2(5k^2b\alpha^2+a)}{15b}$

$= -\frac{2k^2\alpha^{2}e^{\alpha z}}{(e^{\alpha z}-1)^2} + \frac{2k^2\alpha^{2}e^{\alpha z}}{(e^{\alpha z}+1)^2} -\frac{2(5k^2b\alpha^2+a)}{15b}.$

Collecting meromorphic solutions of Eq (3.1) in above procedures, we have the following solutions with arbitrary pole:

$(1)U_{11}(z) = 4k^2\wp(z)-k^2\left(\frac{\wp'(z)+D}{\wp(z)-C}\right)^2+\frac{60k^2bC-a}{15b},$

$(2)U_{12}(z) = 2k^2\wp(z)-\frac{k^2}{2}\left(\frac{\wp'(z)+D}{\wp(z)-C}\right)^2+\frac{30k^2bC-a}{15b},$

where $C^2 = 4D^3-g_2D-g_3$ , $g_2 = {\frac {{a}^{2}k-5\, b\mu}{60\, {b}^{2}{k}^{5}}}, \; g_3 = -{\frac {2\, {a}^{3}k+225\, \zeta \, {b}^{2}-15\, ab\mu}{10800\, {b}^{3}{k}^{7}}}$ in the former case, $g_2 = {\frac {5\, br-{a}^{2}k}{15\, {b}^{2}{k}^{5}}}, \; g_3 = -{\frac {2\, {a}^{3}k+225\, \zeta \, {b}^{2}-15\, abr}{5400\, {b}^{3}{k}^{7}}}$ in the latter case;

$(3)U_{21}(z) = -\frac{4k^2}{(z-z_0)^2} -\frac{a}{15b},$

$(4)U_{22}(z) = -\frac{2k^2}{(z-z_0)^2} -\frac{a}{15b},$

where $r = \, {\frac {k{a}^{2}}{5b}}$ , $\zeta = {\frac {k{a}^{3}}{225\, {b}^{2}}}$ ;

$(5)U_{31}(z) = -k^2\alpha^{2} \coth^2\frac{\alpha (z-z_0)}{2}+\frac{10k^2b\alpha^2-a}{15b},$

$(6)U_{32}(z) = -\frac{k^2\alpha^{2}}{2} \coth^2\frac{\alpha (z-z_0)}{2}+\frac{5k^2b\alpha^2-2a}{30b},$

$(7)U_{41}(z) = -k^2\alpha^{2} \tanh^2\frac{\alpha (z-z_0)}{2}-\frac{a-10k^2b\alpha^2}{15b},$

$(8)U_{42}(z) = -\frac{k^2\alpha^{2}}{2} \tanh^2\frac{\alpha (z-z_0)}{2}-\frac{2a-5k^2b\alpha^2}{30b},$

$(9)U_{51}(z) = -\frac{4k^2\alpha^{2}e^{\alpha (z-z_0)}}{(e^{\alpha (z-z_0)}-1)^2} + \frac{4k^2\alpha^{2}e^{\alpha (z-z_0)}}{(e^{\alpha (z-z_0)}+1)^2} -\frac{2(5k^2b\alpha^2+a)}{15b},$

$(10)U_{52}(z) = -\frac{2k^2\alpha^{2}e^{\alpha (z-z_0)}}{(e^{\alpha (z-z_0)}-1)^2} + \frac{2k^2\alpha^{2}e^{\alpha (z-z_0)}}{(e^{\alpha (z-z_0)}+1)^2} -\frac{2(5k^2b\alpha^2+a)}{15b},$

where $r = \, {\frac { \left(-5\, {\alpha}^{4}{b}^{2}{k}^{4}+{a}^{2} \right) k}{5b}}, \zeta = {\frac { \left(10\, {\alpha}^{4}{b}^{2}{k}^{4}-5\, a{\alpha}^{2}b{k}^{2 }+{a}^{2} \right) k \left(5\, {\alpha}^{2}b{k}^{2}+a \right) }{225\, {b}^{2}}}$ .

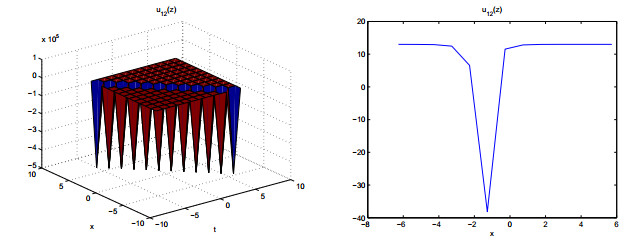
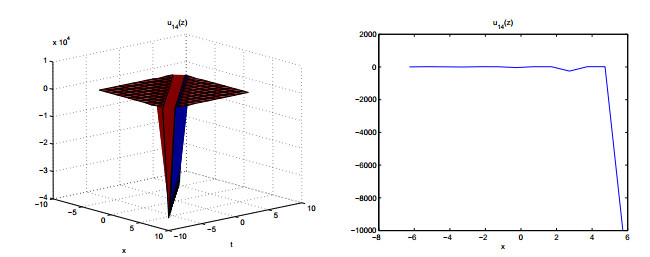
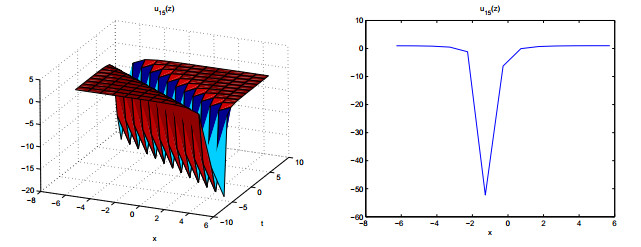
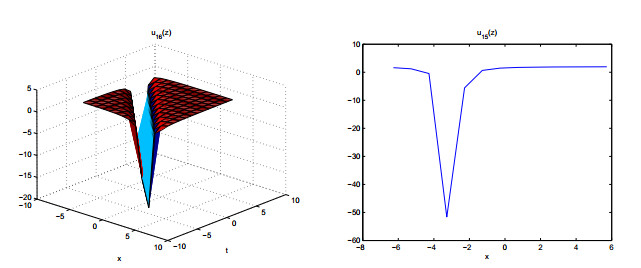
Figures 7–11 show the properties of the solutions.

Figure 7. The 3D and 2D surfaces of

$U_{11}(z)$ by considering the values

$k = 0.28$ ,

$r = 0.42$ ,

$a = -3.79$ ,

$b = 4.97$ ,

$D = -0.032$ ,

$\mu = 1.32$ ,

$\zeta = - 0.071$ and

$t = 0$ for the 2D graphic.

DownLoad: Full-Size Img PowerPoint

Figure 8. The 3D and 2D surfaces of

$U_{12}(z)$ by considering the values

$k = 0.28$ ,

$r = 0.42$ ,

$a = -3.79$ ,

$b = 4.97$ ,

$D = -0.032$ ,

$\mu = 1.32$ ,

$\zeta = - 0.071$ and

$t = 0$ for the 2D graphic.

DownLoad: Full-Size Img PowerPoint

Figure 9. The 3D and 2D surfaces of

$U_{22}(z)$ by considering the values

$k = 1$ ,

$r = 1$ ,

$b = 1$ ,

$a = -15$ ,

$z_0 = -1$ and

$t = 0$ for the 2D graphic.

DownLoad: Full-Size Img PowerPoint

Figure 10. The 3D and 2D surfaces of

$U_{32}(z)$ by considering the values

$k = 1$ ,

$r = 1$ ,

$b = 1$ ,

$a = -5$ ,

$\alpha = 2$ ,

$z_0 = -5$ and

$t = 0$ for the 2D graphic.

DownLoad: Full-Size Img PowerPoint

Figure 11. The 3D and 2D surfaces of

$U_{42}(z)$ by considering the values

$k = 1$ ,

$r = 1$ ,

$b = 1$ ,

$a = -5$ ,

$\alpha = 2$ ,

$z_0 = -5$ and

$t = 0$ for the 2D graphic.

DownLoad: Full-Size Img PowerPoint

6. Conclusions

In this paper, we derive meromorphic exact solutions to the KdV-Sawada-Kotera equation via two different systematic methods. Five types of solutions are constructed, including hyperbolic, trigonometric, exponential, elliptic and rational function solutions. Dynamic behaviors of these solutions are given by some graphs. Observing from the figures, we know that the obtained solutions are soliton solutions. Among of them, , and show multiple soliton solutions, and others show singular soliton solutions. The graphs of Weierstrass elliptic function solutions $U_{11}(z)$ and $U_{12}(z)$ are more interesting and have never been shown in other literatures. We can use the ideas of this study to other differential equations in complexity and nonlinear science.

Acknowledgment

This research is supported by the NSFC (11901111); Visiting Scholar Program of Chern Institute of Mathematics.

Conflict of interest

The authors declare no conflict of interest.

References

[1]	Bertram C, Luderer G, Pietzcker RC, et al. (2015) Complementing carbon prices with technology policies to keep climate targets within reach. Nat Clim Change 5: 235-239. doi: 10.1038/nclimate2514
[2]	Brown MA, Li Y (2018) Carbon pricing and energy efficiency: pathways to deep decarbonization of the US electric sector. Energ Effic 12: 1-19.
[3]	Bruckner T, Bashmakov IA, Mulugetta Y, et al. (2014) Energy Systems, In: Edenhofer O, Pichs-Madruga R, Sokona Y, et al., Climate Change 2014: Mitigation of Climate Change, eds., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
[4]	Chen H, Wang L, Chen W (2018) Modeling on building sector's carbon mitigation in China to achieve the 1.5 ℃ climate target. Energ Effic 12: 483-496. doi: 10.1007/s12053-018-9687-8
[5]	Coase RH (1960) The Problem of Social Cost. J Law Econ 3: 1-44. doi: 10.1086/466560
[6]	Coase RH (1991) The Institutional Structure of Production, Ronald H. Coase Prize Lecture to the memory of Alfred Nobel, December 9, 1991. Available from: https://www.nobelprize.org/prizes/economic-sciences/1991/coase/lecture/.
[7]	de Coninck H, Revi A, Babiker M, et al. (2018) Strengthening and implementing the global response, In: Masson-Delmotte V, Zhai P, Pö rtner HO, et al., Global warming of 1.5 ℃. An IPCC Special Report on the impacts of global warming of 1.5 ℃ above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change, sustainable development, and efforts to eradicate poverty, eds., [In Press].
[8]	EEA (European Environment Agency) (2019) The European Environment—State and Outlook 2020: Knowledge for Transition to a Sustainable Europe. European Environment Agency Copenhagen. Available from: https://www.eea.europa.eu/publications/soer-2020 (accessed 11 November 2020).
[9]	Fleurbaey M, Kartha S, Bolwig S, et al. (2014) Sustainable Development and Equity, In: Edenhofer O, Pichs-Madruga R, Sokona Y, et al., Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, eds., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
[10]	GCEC (2018) Unlocking the Inclusive Growth Story of the 21st Century. Global Commission on the Economy and Climate. Available from: https://newclimateeconomy.report/2018/wp-content/uploads/sites/6/2018/09/NCE_2018_FULL-REPORT.pdf.
[11]	Goulder L (1995) Environmental taxation and the double dividend: A reader's guide. Int Tax Public Financ 2: 157-183. doi: 10.1007/BF00877495
[12]	IMF (2019) Putting a Price on Pollution. Financ Dev 56: 16-19.
[13]	IPCC (Intergovernmental Panel on Climate Change) (1990) IPCC First Assessment Report. Climate Change. The IPCC Response Strategies. Available from: https://www.ipcc.ch/site/assets/uploads/2018/03/ipcc_far_wg_III_full_report.pdf.
[14]	Kirby P, O'Mahony T (2018) The Political Economy of the Low-Carbon Transition: Pathways Beyond Techno-optimism, International Political Economy Series, Palgrave Macmillan, Cham, UK.
[15]	Kolstad C, Urama K, Broome J, et al. (2014) Social, Economic and Ethical Concepts and Methods, In: Edenhofer O, Pichs-Madruga R, Sokona Y, et al., Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovern-mental Panel on Climate Change, eds., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
[16]	Klenert D, Mattauch L, Combet E, et al. (2018) Making carbon pricing work for citizens. Nat Clim Change 8: 669-677. doi: 10.1038/s41558-018-0201-2
[17]	Kriegler E, Bertram C, Kuramochi T, et al. (2018) Short term policies to keep the door open for Paris climate goals. Environ Res Lett 13: 074022.
[18]	Lefèvre J, Wills W, Hourcade JC (2018) Combining low-carbon economic development and oil exploration in Brazil? An energy—economy assessment. Clim Policy 18: 1-10. doi: 10.1080/14693062.2018.1431198
[19]	Lucon O, Ü rge-Vorsatz D, Zain Ahmed A, et al. (2014) Buildings, In: Edenhofer O, Pichs-Madruga R, Sokona Y, et al., Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, eds., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
[20]	Méjean A, Guivarch C, Lefèvre J, et al. (2018) The transition in energy demand sectors to limit global warming to 1.5 ℃. Energ Effic 12: 441-462. doi: 10.1007/s12053-018-9682-0
[21]	Morita T, Robinson J, Adegbulugbe A, et al. (2001) Greenhouse gas emission mitigation scenarios and implications, In: Metz B, Davidson O, Swart R, et al., (Eds.), Climate Change 2001: Mitigation, Contribution of Working Group III to the Third Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, UK, 700.
[22]	Mundaca L, Ü rge-Vorsatz D, Wilson C (2019) Demand-side approaches for limiting global warming to 1.5 ℃. Energ Effic 12: 343-362. doi: 10.1007/s12053-018-9722-9
[23]	Newell P, Paterson M (2010) Climate Capitalism: Global Warming and the Transformation of the Global Economy, Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511761850
[24]	O'Mahony T (2014) Integrated Scenarios for Energy: A Methodology for the Short Term. Futures 55: 41-57. doi: 10.1016/j.futures.2013.11.002
[25]	O'Mahony T, Dufour J (2015) Tracking development paths: Monitoring driving forces and the impact of carbon-free energy sources in Spain. Environl Sci Policy 50: 62-73. doi: 10.1016/j.envsci.2015.02.005
[26]	Rogelj J, Shindell D, Jiang K, et al. (2018) Mitigation pathways compatible with 1.5 ℃ in the context of sustainable development, In: Masson-Delmotte V, Zhai P, Pö rtner HO, et al., Global warming of 1.5 ℃. An IPCC Special Report on the impacts of global warming of 1.5 ℃ above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change, sustainable development, and efforts to eradicate poverty, eds., [In Press].
[27]	Sathaye J, Najam A, Cocklin C, et al. (2007) Sustainable Development and Mitigation, In: Metz B, Davidson OR, Bosch PR, et al., Climate Change 2007: Mitigation. Contribution of Working Group III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, eds., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
[28]	Sims R, Schaeffer R, Creutzig F, et al. (2014) Transport, In: Edenhofer O, Pichs-Madruga R, Sokona Y, et al., Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, eds., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
[29]	Somanathan E, Sterner T, Sugiyama T, et al. (2014) National and Sub-national Policies and Institutions, In: Edenhofer O, Pichs-Madruga R, Sokona Y, et al., Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, eds., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
[30]	Sonnenschein J, Van Buskirk R, Richter JL, et al. (2018) Minimum energy performance standards for the 1.5 ℃ target: an effective complement to carbon pricing. Energ Effic 12: 387-402. doi: 10.1007/s12053-018-9669-x
[31]	Stiglitz JE, Stern N (2017) Report of the High-Level Commission on Carbon Prices, World Bank.
[32]	Wakiyama T, Zusman E (2016) What would be the effects of a carbon tax in Japan: an historic analysis of subsidies and fuel pricing on the iron & steel, chemical, and machinery industries. AIMS Energ 4: 606-632. doi: 10.3934/energy.2016.4.606
[33]	World Bank (2020) State and Trends of Carbon Pricing 2020. Available from: https://openknowledge.worldbank.org/handle/10986/33809.

Reader Comments

Your name:*

Email:*
© 2020 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)