1. Introduction
Pinus L. (pinyon) and Juniperus L. (juniper) (P-J) expansion has become a serious problem for rangeland habitat management in the western United States over the last century [1,2]. As these woodlands expand and infill in shrub-steppe ecosystems, herbaceous understory decreases and soil erosion increases [3,4,5,6]. A reduction in shrub-steppe ecosystems poses a problem for sagebrush (Artemisia L.) obligate species such as sage-grouse (Centrocercus urophasianus Bonaparte) [7], as well as numerous other wildlife species supported by sagebrush. Increased fuel loads can also lead to catastrophic wildfires and subsequent weed dominance [8,9,10,11]. One way land managers mitigate these negative effects is to apply tree reduction treatments. Remote sensing techniques, as opposed to ground measurements (which can be time consuming and labor intensive) may aid land managers in planning and prioritizing tree reduction treatments by providing a way to rapidly assess tree canopy cover across a landscape.
Remote sensing technologies, particularly object-based image analysis (OBIA) has been shown to be an effective alternative to ground measurements in sagebrush ecosystems with P-J encroachment [12,13,14,15], in assessing P-J above ground biomass [16], in evaluating P-J expansion over time [17], and in assessing pretreatment P-J cover in a post-hoc study [18]. OBIA segments pixels within an image into homogenous objects that can then be classified into different land cover categories. There are multiple OBIA software packages, however, studies that compare the efficiency of different packages with ground measurements are limited [19,20].
For this study, three potentially useful OBIA software packages (ENVI Feature Extraction 4.5® (Exelis Visual Information Solutions, Boulder, Colorado), Feature AnalystTM (Visual Learning System’s Inc. 2002) for ArcMAP 10.1® and Trimble eCognition Developer 8.2® (Trimble Germany GmbH, Munich, Germany)) were selected to evaluate their ability to extract P-J canopy cover from NAIP imagery. These packages were selected because of their availability and effectiveness shown in estimating vegetation cover in past studies [12,13,14,15,16,17,20,21,22,23,24]. ENVI Feature Extraction allows the user to extract information about each object from imagery based on spatial, spectral, and textural characteristics. The user selects objects that represent the desired landscape feature to be classified and then the software uses a nearest neighbor algorithm to classify each image [25]. Feature AnalystTM utilizes similar extraction techniques as ENVI Feature Extraction but instead of selecting image objects, the user digitizes around landscape features that represent the desired classification categories [26]. eCognition Developer allows the user to create a list of rules that segment the imagery into objects, and then classifies the objects of interest based on spatial, spectral, and textural characteristics [27].
Although these software packages have many similarities (i.e., classification based on multiple spatial and spectral parameters), they also have substantial differences in affordability and ease of use. Hence, our objective was to evaluate which OBIA software package best extracts P-J canopy cover from National Agricultural Imagery Program (NAIP) imagery, when compared to two ground P-J canopy cover measurements (line-point intercept and crown diameter). NAIP imagery was used because of its extensive coverage, and free availability to land managers and researchers. Because of the variable amounts of P-J woodland canopy cover found across a landscape, we also compared how well the different OBIA techniques extracted P-J canopy cover when broken into categories based on total tree canopy cover (low tree canopy cover < 15%; intermediate tree canopy cover 15-45%; and high tree canopy cover > 45%).
2. Materials and Methods
2.1. Study sites
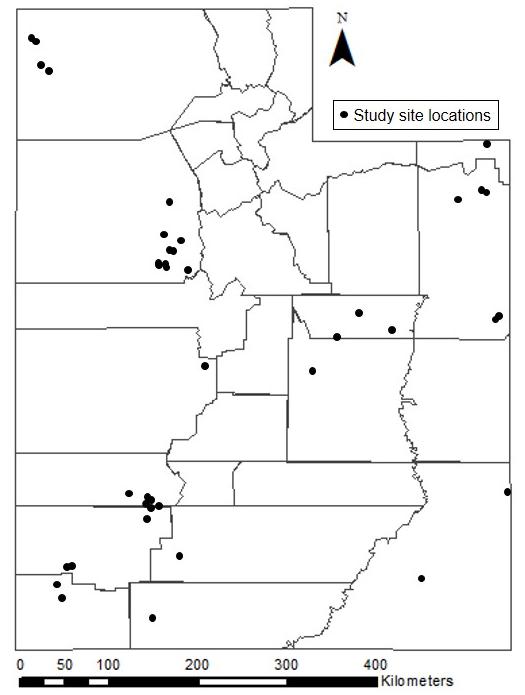
Study sites are located within the state of Utah in the Great Basin and Colorado Plateau physiographic provinces (Figure 1) on lands managed by either the Bureau of Land Management (BLM) or US Forest Service (USFS). Within each of our 44 study sites we systematically selected 3 to 9 plots (0.1-ha or 30 × 33 m2) for sampling that represented a range of P-J tree canopy cover categories: low ( < 15%), intermediate (15-45%), and high ( > 45%) using ArcMap. Plots were then verified in the field to assure that the desired tree cover gradient was achieved. Not all study sites had all tree canopy cover categories, so the number of plots ranged from a minimum of three (1 tree cover category × 3 plots = 3) to 9 (3 tree cover categories × 3 plots = 9). The only exception to this sampling scheme was for three sites originally treated and measured in a previous study known as SageSTEP [28]. On those sites, 61 plots were measured across the range of tree canopy cover categories.
2.2. Ground measurements
Tree canopy cover was measured using the line-point intercept and crown diameter methods on each 0.1-ha plot in 2011 and 2012. For the line-point intercept method, five, 30-m transects were sampled per plot [9,28]; sampling transects were placed on a baseline transect at the 2, 7, 15, 23, and 28 m marks and laid out across the plot. On each 30-m sampling transect, a pin flag was dropped every 0.5-m and the presence/absence of P-J canopy cover was recorded for that point. To calculate tree canopy cover for each plot, the total number of points with P-J canopy cover present were summed and divided by 300 (60 points × 5 transects = 300 points per plot).
The crown diameter method was used to measure every tree > 0.5-m in height that had at least half the tree trunk within the established plot. The longest canopy diameter (or maximum foliage spread: Dia1) and the measurement perpendicular to the longest diameter (Dia2) were measured using a plastic, telescoping measuring rod. Canopies that extended outside the plot boundary were fully measured if the tree trunk was within the established plot. When tree canopies overlapped, individual tree canopy diameters were measured as described above. Measurements were used to calculate the crown area (A) for each tree using the following equation:
Tree canopy cover for each plot was calculated by dividing the total tree canopy cover for a plot by the total area of the plot (1000 m2).
2.3. Imagery acquisition
Digital ortho quarter quad tiles (DOQQs) of the study sites were acquired from the National Agricultural Imagery Program (US Department of Agriculture 2008) in 2010 as part of a retrospective study evaluating vegetation response to pinon and juniper tree shredding treatments [29]. All images were collected in 2006 with the exception of the South Creek site, which was collected in 2009 (2006 imagery was not available). All DOQQs have 1-m spatial resolution. The spectral resolution bands used in our analysis were red, green, and blue for all sites. The 5-6 yearsdifference between ground-measurements (collected in 2011 and 2012) and imagery acquisition (2006) is presumed to be minimal for tree canopy cover; our sites had minimal disturbance within the above stated timeframe, and Juniperus osteosperma (Torr.) Little (Utah juniper) is considered a slow growing tree (http://www.fs.fed.us/database/feis/plants/tree/junost/all.html#126). Of the 44 study sites, NAIP imagery at 4 sites was too blurred to perform the classification. Additionally, 2 sites had shrubs Amelanchier alnifolia (Nutt.) Nutt. ex M. Roem. var. utahensis (Koehne) M.E. Jones (Utah serviceberry) and Quercus gambelii Nutt. (Gambel’s oak) that had similar spectral characteristics as P-J canopies on NAIP imagery. Hence, our study sites were reduced to 38.
2.4. Image processing
We evaluated eCognition, ENVI Feature Extraction, and Feature AnalystTM independently to estimate OBIA P-J canopy cover using DOQQs. Through trial and error, we found better agreements between OBIA and ground-measured cover estimates when we clipped DOQQs into smaller areas based on visual estimates of the P-J tree canopy cover categories described above (Figure 2). Smaller sized imagery led to faster processing times when classifying tree cover for all three OBIA software packages. For each OBIA we distinguished two classes: (1) a “tree” class, consisting of P-J trees, and (2) an “other” class which primarily included all other vegetation types, bare ground, and shadows. These methods are further described below in the corresponding section for each software package.
Prior to extracting P-J canopy cover from DOQQs for our comparisons, global positioning system (GPS) coordinates of each 0.1-ha plot were collected using a Delorme PN-60 GPS unit with accuracy to within 3 meters (http://delorme.com, accessed 5 June 2015). GPS coordinates were collected in the middle and bottom left corner (downslope of the middle point) of each plot. The 2 points collected were used to reference the individual plot locations on the DOQQs; as well as create a shapefile of the individual plots in ArcMap that were used to clip the classified imagery so measurements would be made on the same experimental unit for both OBIA and ground-measured tree canopy cover.
2.5. eCognition developer
Trimble’s eCognition Developer software (Trimble Germany GmbH, Munich, Germany) utilizes OBIA techniques that allow the user to develop rule-sets to classify objects of interest. We used a multiresolution segmentation algorithm [30] and spectral difference algorithm to create image objects with a median scale of 3-m2. The spectral difference algorithm reduces the complexity of the image objects by merging them according to their mean image layer intensity values [27]. After the segmentation was completed, we combined brightness values (spectral parameter) and relative border (a contextual feature which the user can use to enlarge or reduce objects based on neighboring image objects; [27]) to classify P-J canopy cover.
Because of eCognition’s ability to easily refine parameters within a rule-set, we used training plots (32, 0.1-ha plots or 12% of the total sample plots) to create a rule-set to extract P-J canopy cover, and validation plots (239, 0.1-ha plots or 88% of the total sampled plots) to test the accuracy of the rule-set. For each clipped DOQQ, a training plot that best represented the variation found within the clipped image (i.e., had similar vegetation and bare ground cover, and brightness values) was used to define thresholds for each parameter (brightness value and relative border) used to extract P-J canopy cover within the rule-set. Thresholds were refined for each parameter until the extracted P-J canopy cover and ground canopy cover measurements (crown diameter method) were ±1%. Because of the hierarchical nature of eCognition, once P-J canopy cover was classified, all remaining unclassified objects were classified as “other”.
After the thresholds for each parameter were developed using the training plot(s), the rule-set was applied to the DOQQ. The classified DOQQs were then clipped by validation plot in ArcMap, and tree canopy cover was calculated for each plot. To calculate tree canopy cover, the area of each polygon that represented the “tree” class within the plot was divided by the total area of the plot. Only validation plots were used for the statistical analysis. Training and validation plots were an unnecessary step with ENVI Feature Extraction and Feature AnalystTM as they did not use rule-sets, therefore we only used them with eCognition.
2.6. Feature AnalystTM and ENVI Feature Extraction
Feature AnalystTM (Visual Learning System’s Inc. 2002) for ArcMAP® 10.1, and ENVI Feature Extraction (ENVI Zoom 4.5, Exelis Visual Information Solutions, Boulder, Colorado) have similar processing methods and both use an object-based image analysis approach to segment an image into homogenous objects. For each clipped DOQQ, Feature AnalystTM classified “tree” or “other” using 50 image objects per class that were digitized or defined by the user. For ENVI Feature Extraction, objects were automatically created using spectral characteristics and then defined by the user as either “tree” or “other”. The selected image objects (ENVI Feature Extraction) and digitized objects (Feature AnalystTM) captured the variation found within the imagery for these two categories. For example, within the “other” category, shadows, bare ground, and vegetation other than P-J trees were selected. Following the digitization of classes, Feature AnalystTM then uses an automated feature extraction (AFE) model which takes into account the shape, size, color, texture, and pattern of the image objects [26] to classify the imagery. Likewise, ENVI Feature Extraction takes into account spectral values of each defined object and utilizes the Nearest Neighbor algorithm (computes the Euclidean distance from each segment in the segmentation image to every object that was defined [25]) to classify the image. Following classification, we digitized (Feature AnalystTM) or selected (Feature Extraction) 10 examples of errors (or misclassified objects) and re-ran the classification in order to refine the P-J tree canopy cover classification. This correction process was cycled through 5 times - until 100 objects had been digitized/selected for each class. Once the smaller DOQQ had been classified, we clipped the DOQQ by validation plot using ArcMap so all measurements (OBIA and ground) would be made on the same experimental unit. We then extracted the area of each polygon that represented the “tree” class within a plot, and divided that area by the total area of the plot.
2.7. Accuracy assessment
Erdas Imagine 11.0 (Erdas Inc., Atlanta, GA) was used to run an accuracy assessment on each clipped DOQQ, which tested our tree cover classification’s reliability for each OBIA technique. We randomly selected sixty points per clip (30 points per class × 2 classes (“tree” and “other”) × 48 clipped images = 2880), and using the unclassified NAIP imagery and expert knowledge we decided if each point was correctly classified or not. The total points (correct and incorrect) for each class (“tree” or “other”) for all the sites were then summed, and an error matrix was produced which includes a measurement of overall accuracy of the classified images, a kappa statistic (indicating percentage-wise the reliability of the classification in comparison to a randomly assigned cover type for each pixel), and producer’s (omission) and user’s (commission) errors [31].
2.8. Statistical analysis
To assess the relationship between ground measured tree canopy cover and OBIA canopy cover estimates, we used a Pearson Correlation. Additionally, a partial correlation by tree canopy cover category (low, intermediate, and high) was also used to evaluate the relationship between the methods. To determine whether tree canopy cover estimates were different between OBIA methods and ground measurements by tree canopy cover, we used a one-way ANOVA. Mean differences for each tree cover category were compared using the Tukey-Kramer HSD (p < 0.05). Since actual tree canopy cover is unknown, the statistical analysis in this study should be used conservatively.
3. Results and Discussion
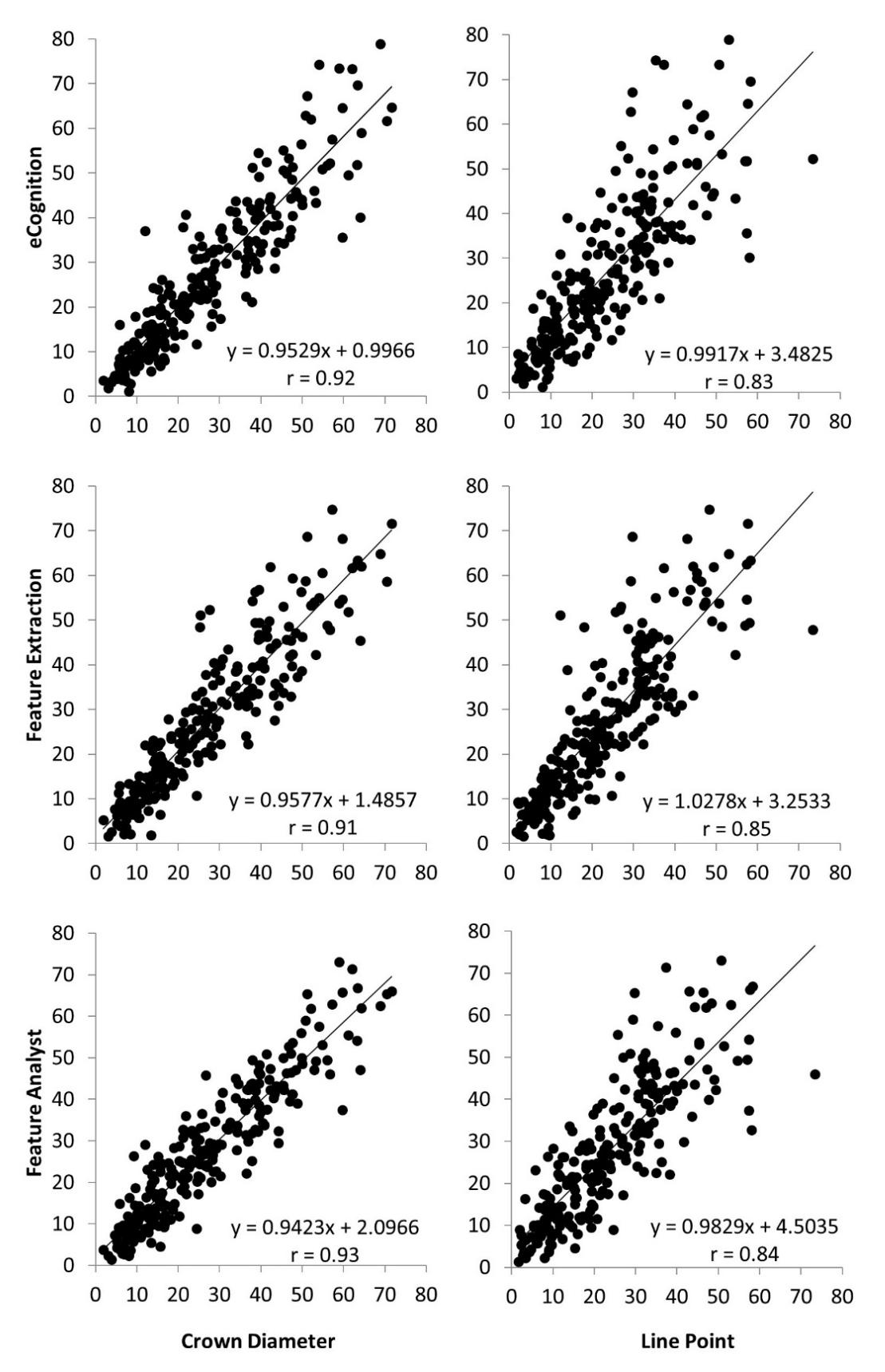
Our study suggests that OBIA techniques and NAIP imagery is a viable method for estimating pinyon and juniper canopy cover across Utah. Strong correlations were found between all OBIA techniques and ground measurements estimating P-J canopy cover (Figure 3). The crown diameter method had stronger correlations with OBIA techniques than those found with the line point intercept method. The correlations between tree canopy cover estimates using Feature AnalystTM, eCognition, and Feature Extraction with the crown diameter method were r = 0.93, r = 0.92, and r = 0.91, respectively. Line point intercept methods were slightly lower with r = 0.85 with Feature Extraction, and r = 0.83 for both eCognition and Feature AnalystTM. Correlation coefficients (r) between all methods can be found in the supplementary material (Table S1, S2, and S3).
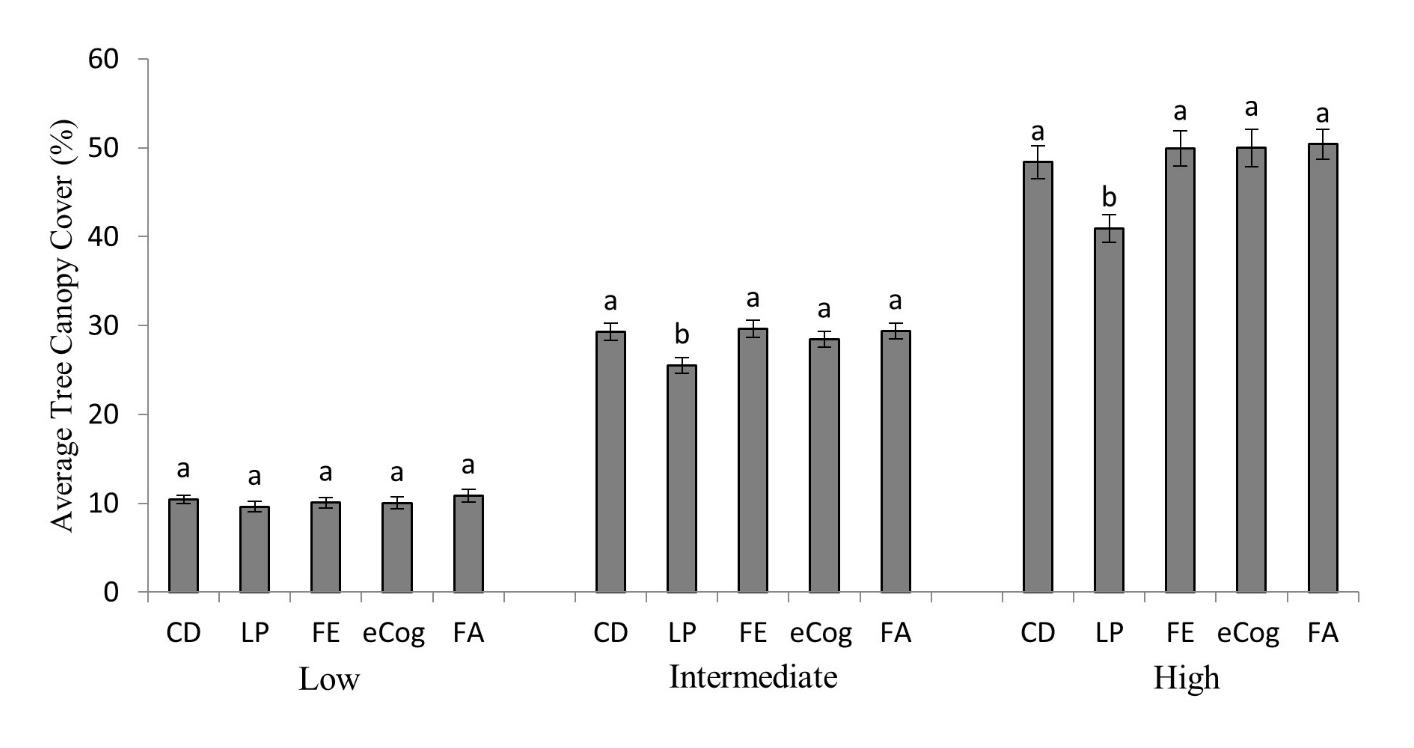
Because tree canopy cover varies greatly across a landscape, tree canopy cover categories (low < 15%, intermediate 15-45%, and high > 45% tree canopy cover) were evaluated to identify potential constraints to OBIA techniques. For low tree canopy cover, the average range of estimated percent tree canopy cover across all methods was between 9.6 and 10.9%, with no significant difference between methods (Figure 4). Average estimated tree canopy cover for the intermediate category ranged from 25.5 to 29.6%. For the high category, the average estimated percent tree canopy cover ranged from 40.9 to 50.4%. The line point intercept method estimated tree canopy cover significantly lower (p < 0.05) than all other methods for both the intermediate and high tree canopy cover category (Figure 4).
This difference between OBIA techniques, the crown diameter method, and the line point intercept method are somewhat expected. The line point intercept method measures trees along a portion of the plot and then is extrapolated for the entire area, which lead to lower tree canopy cover estimates than our other methods. With the crown diameter method, every tree that was rooted within the plot was measured, which may include canopy cover that extended beyond the designated 0.1-h plot that was extracted during our image processing for our OBIA. On the other hand, canopy cover from trees not rooted within the plot, but with canopy that extended within the plot boundary were measured using OBIA techniques, but not with the crown diameter method.
The crown diameter method also measured each tree in its entirety; hence, when tree canopies overlapped this increased the crown diameter method estimations of tree canopy cover, but was not captured in the OBIA techniques or line point intercept method. Lastly, smaller trees ( < 1m canopy diameter) were likely undetected using our OBIA techniques. This limitation is in part due to the pixel resolution of the imagery selected but also, likely due to interference by surrounding shrubs and herbaceous vegetation which theoretically, should make our OBIA tree canopy cover estimates lower than the ground-based measurements. Although OBIA techniques and the crown diameter method were not significant different (p > 0.05), these differences in estimating tree canopy cover may explain some of the variation captured in the Pearson correlations (Figure 3).
Additional variation from plot to plot may be due to imagery limitation (shadows, blurry imagery), and what vegetation was found at each plot. Across all sites, the overall accuracy for our OBIA classified imagery was 94%, 92%, and 91% for ENVI Feature Extraction, Feature AnalystTM, and eCognition, respectively (Table 1). The average kappa statistics were 0.88 for ENVI Feature extraction, 0.84 for Feature AnalystTM, and 0.83 for eCognition 0.83 (Table 1). These kappa statistics indicate a strong agreement between OBIA classification and ground reference data [32]. However, the most common misclassified objects were shadows and patches of darker green shrubs such as Purshia tridentata (Pursh) DC. (antelope bitterbrush) and Cercocarpus ledifolius Nutt. (curl-leaf mountain mahogany). During image processing and OBIA, additional errors likely occurred. The accuracy of the GPS units used to mark plot locations were within 3-m. Although this seems minimal on a landscape scale, 3-m may be substantial when extracting tree canopy cover on a plot level, especially with increasing P-J canopy cover.
Table 1. Error matrix comparing object-based image analysis classification accuracies of cover classes (tree and other) for (A) eCognition, (B) Feature Analyst, and (C) ENVI Feature Extraction.
| (A) eCognition | | | | |
| Classified Data | Tree | Other | Row Totals | User’s Accuracy |
| Tree | 1223 | 29 | 1252 | 98% |
| Other | 217 | 1411 | 1628 | 87% |
| Column Total | 1440 | 1440 | 2880 | |
| Producer’s Accuracy | 85% | 98% | | |
| Overall Accuracy: 91% | Kappa Statistic: 0.83 | | N = 2880 | |
| (B) Feature Analyst | | | | |
| Classified Data | Tree | Other | Row Totals | User’s Accuracy |
| Tree | 1247 | 35 | 1282 | 97% |
| Other | 193 | 1405 | 1598 | 88% |
| Column Total | 1440 | 1440 | 2880 | |
| Producer’s Accuracy | 87% | 98% | | |
| Overall Accuracy: 92% | Kappa Statistic: 0.84 | | N = 2880 | |
| (C) ENVI Feature Extraction | | | | |
| Classified Data | Tree | Other | Row Totals | User’s Accuracy |
| Tree | 1299 | 39 | 1338 | 97% |
| Other | 141 | 1401 | 1542 | 91% |
| Column Total | 1440 | 1440 | 2880 | |
| Producer’s Accuracy | 90% | 97% | | |
| Overall Accuracy: 94% | Kappa Statistic: 0.88 | | N = 2880 | |
N = number of points evaluated.
Bold values indicate correct number of points classified within the cover class |
When evaluating the OBIA software used in this study, no one OBIA program was more accurate at classifying P-J canopy cover than another. ENVI Feature Extraction and Feature AnalystTM were relatively easy to learn and use, and the software was less expensive than eCognition Developer. However, with eCognition Developer the user is able to create rule-sets that can be applied to multiple sites with similar spectral, spatial, and contextual properties with minimal adjustments to feature parameters. Having this ability, it was possible to classify tree canopy cover in each clipped image in as little as 20 minutes, as opposed to 40-45 minutes with the other two software packages. ENVI and Feature AnalystTM require the user to train the program on an image-by-image basis which added the additional time to classify tree canopy cover.
4. Conclusion
OBIA techniques combined with NAIP imagery is an efficient method to extract tree canopy cover on a landscape scale. Although some variations were found on a plot-by-plot level, the overall accuracy of the remotely-sensed cover is acceptable for estimating P-J canopy cover, which may be useful for land management planning. These methods also allow for baseline measurements of P-J canopy cover to be captured and used to evaluate temporal changes due to disturbances and climate regimes.
Acknowledgments
This research was funded by the US Joint Fire Science Program and Brigham Young University. This is contribution number 118 of the Sagebrush Steppe Treatment Evaluation Project (SageSTEP) funded by the US Joint Fire Science Program. We thank the USDI Bureau of Land Management, USDA Forest Service, and Division of Wildlife Resources in Utah for allowing this research on public and state lands. We appreciate the support of the BYU Geospatial Habitat Analysis Lab where research was conducted.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: