Figure 1.
Shape of $ q_1 $ in (3.12), (a) real part and (b) imaginary part.
Citation: Bedr'Eddine Ainseba, Mostafa Bendahmane, Yuan He. Stability of conductivities in an inverse problem in the reaction-diffusion system in electrocardiology[J]. Networks and Heterogeneous Media, 2015, 10(2): 369-385. doi: 10.3934/nhm.2015.10.369
| [1] | Mahmoud A. E. Abdelrahman, Wael W. Mohammed, Meshari Alesemi, Sahar Albosaily . The effect of multiplicative noise on the exact solutions of nonlinear Schrödinger equation. AIMS Mathematics, 2021, 6(3): 2970-2980. doi: 10.3934/math.2021180 |
| [2] | Jalil Manafian, Onur Alp Ilhan, Sizar Abid Mohammed . Forming localized waves of the nonlinearity of the DNA dynamics arising in oscillator-chain of Peyrard-Bishop model. AIMS Mathematics, 2020, 5(3): 2461-2483. doi: 10.3934/math.2020163 |
| [3] | Yongyi Gu, Najva Aminakbari . Two different systematic methods for constructing meromorphic exact solutions to the KdV-Sawada-Kotera equation. AIMS Mathematics, 2020, 5(4): 3990-4010. doi: 10.3934/math.2020257 |
| [4] | P. Veeresha, D. G. Prakasha, Jagdev Singh . Solution for fractional forced KdV equation using fractional natural decomposition method. AIMS Mathematics, 2020, 5(2): 798-810. doi: 10.3934/math.2020054 |
| [5] | M. Hafiz Uddin, M. Ali Akbar, Md. Ashrafuzzaman Khan, Md. Abdul Haque . New exact solitary wave solutions to the space-time fractional differential equations with conformable derivative. AIMS Mathematics, 2019, 4(2): 199-214. doi: 10.3934/math.2019.2.199 |
| [6] | Yunmei Zhao, Yinghui He, Huizhang Yang . The two variable (φ/φ, 1/φ)-expansion method for solving the time-fractional partial differential equations. AIMS Mathematics, 2020, 5(5): 4121-4135. doi: 10.3934/math.2020264 |
| [7] | Weiping Gao, Yanxia Hu . The exact traveling wave solutions of a class of generalized Black-Scholes equation. AIMS Mathematics, 2017, 2(3): 385-399. doi: 10.3934/Math.2017.3.385 |
| [8] | Yousef Jawarneh, Humaira Yasmin, Ali M. Mahnashi . A new solitary wave solution of the fractional phenomena Bogoyavlenskii equation via Bäcklund transformation. AIMS Mathematics, 2024, 9(12): 35308-35325. doi: 10.3934/math.20241678 |
| [9] | S. Owyed, M. A. Abdou, A. Abdel-Aty, H. Dutta . Optical solitons solutions for perturbed time fractional nonlinear Schrodinger equation via two strategic algorithms. AIMS Mathematics, 2020, 5(3): 2057-2070. doi: 10.3934/math.2020136 |
| [10] | Safoura Rezaei Aderyani, Reza Saadati, Javad Vahidi, Nabil Mlaiki, Thabet Abdeljawad . The exact solutions of conformable time-fractional modified nonlinear Schrödinger equation by Direct algebraic method and Sine-Gordon expansion method. AIMS Mathematics, 2022, 7(6): 10807-10827. doi: 10.3934/math.2022604 |
In recent years, nonlinear partial differential equations (NPDEs) are widely used to describe complex phenomena in various fields of sciences, such as fluid mechanics, plasma, chemical reactions, optical fibers, solid state physics, relativity, ecology, gas dynamics physics and optical fiber, [1,2,3,4,5,6,7,8,9,10,11]. Therefore, exploring exact solutions for NPDEs plays an important role in nonlinear science. These solutions might be essential and important for the exploring some physical phenomena. Therefore investigating new technique to solve so many problems is so interesting topic. Thus, many new methods have been introduced, such as the F-expansion method [12,13], $ (\frac{G^{'}}{G})- $ expansion method [14,15], tanh-sech method [16,17,18], exp-expansion method [19,20], the homogeneous balance method [21,22], Jacobi elliptic function method [23,24], sine-cosine method [25,26,27], extended tanh-method [28,29] and the Riccati-Bernoulli sub-ODE method [30,31,32,33] proposed for solving more complicated problems. Indeed, there are recent development in analytical methods for investigation solutions for NPDEs, see [34,35,36,37,38,39,40].
The nonlinear Schrödinger equations (NLSEs) are so important models in nonlinear evolution equations, which come in many areas of applied sciences such as nonlinear optics, quantum mechanics, fluid dynamics, molecular biology, elastic media, hydrodynamics, biology and plasma physics.
This paper is concerned with the unstable nonlinear Schrödinger equation (UNS) [41,42] given by
| $ iqt+qxx+2η∣q∣2q−2γq=0,i=√−1, $ | (1.1) |
where, $ \eta, \gamma $ is a free parameter and $ q = q(x, t) $ is a complex-valued function. Equation (1.1) is a type of nonlinear Schrödinger equation with space and time exchanged. This equation prescribes a time evolution of disturbances in unstable media. The behavior of type occurs for the two-layer baroclinic instability and the lossless symmetric two-stream plasma instability [43]. To the best of our knowledge, no previous research work has been done using the proposed methods for solving the unstable nonlinear Schrödinger equation. Actually, many numerical and analytical methods have been also implemented to get solutions for Eq (1.1) such as modified Kudraysov method, the sine-Gordon expansion approach [41], $ exp_{a} $ method and hyperbolic function method [42], the new Jacobi elliptic function rational expansion method and the exponential rational function method [44], the extended simple equation method[45].
The main aim of this paper is to explore the UNS equation using exp$ (-\varphi(\xi)) $-expansion method, sine-cosine method and Riccati-Bernoulli sub-ODE method. We also show that the Riccati-Bernoulli sub-ODE technique gives infinite solutions. Actually, we introduce new types of exact analytical solutions. Comparing our results with other results, one can see that our results are new and most extensive. Indeed the new solutions presented in this article are so important in the theory of soliton. Moreover these solutions turn out to be very useful for Physicists to explain many interesting physical phenomena.
The rest of the paper is arranged as follows: In Section 2, the exp-function method, sine-cosine method and Riccati-Bernoulli sub-ODE method are briefly reviewed. In Section 3, some new exact solutions of the unstable Schrödinger equation are presented. Discussion of our results and comparing with the results of other authors is in Section 4. Conclusion and future works will appear in Section 5.
We present a brief description about the exp$ (-\varphi(\xi)) $-expansion method, sine-cosine method and Riccati-Bernoulli sub-ODE method to obtain new exact solutions for a given NPDE. For this goal, consider a NPDE in two independent variables $ x $ and $ t $ as
| $ G(ϑ,ϑt,ϑx,ϑtt,ϑxx,....)=0, $ | (2.1) |
where $ G $ is a polynomial in $ \vartheta(x, t) $ and its partial derivatives. The main steps are as follows [30]:
Step 1. Introducing the transformation
| $ ϑ(x,t)=ϑ(ξ),ξ=k(x+ςt), $ | (2.2) |
varies Eq (2.1) to the following ordinary differential equation (ODE):
| $ D(ϑ,ϑ′,ϑ″,ϑ‴,.....)=0, $ | (2.3) |
where $ D $ is a polynomial in $ \vartheta(\xi) $ and its derivatives such that the superscripts denote the ordinary derivatives with respect to $ \xi $.
According to the exp$ (-\varphi(\xi)) $-expansion technique [19,20,31], we assume that the solution of Eq (2.3) can be written in a polynomial form of $ exp(-\varphi(\xi)) $ as follows
| $ ϑ(ξ)=Am(exp(−φ(ξ)))m+....., am≠0, $ | (2.4) |
where $ \varphi(\xi) $ obeys the following ODE
| $ φ′(ξ)=exp(−φ(ξ))+νexp(φ(ξ))+λ. $ | (2.5) |
Eq (2.5) has the following solutions:
1. At $ \lambda^{2}-4\nu > 0, \nu\neq0, $
| $ φ(ξ)=ln(−√λ2−4ν tanh(√λ2−4ν2(ξ+C))−λ2ν), $ | (2.6) |
2. At $ \lambda^{2}-4\nu < 0, \nu\neq0, $
| $ φ(ξ)=ln(√4ν−λ2 tan(√4ν−λ22 (ξ+C))−λ2ν), $ | (2.7) |
3. At $ \lambda^{2}-4\nu > 0, \nu = 0, \lambda \neq0 $
| $ φ(ξ)=−ln(λexp(λ(ξ+C))−1), $ | (2.8) |
4. At $ \lambda^{2}-4\nu = 0, \nu\neq0, \lambda\neq0, $
| $ φ(ξ)=ln(−2(λ(ξ+C)+2)λ2(ξ+C)), $ | (2.9) |
5. At $ \lambda^{2}-4\nu = 0, \nu = 0, \lambda = 0, $
| $ φ(ξ)=ln(ξ+C). $ | (2.10) |
Here $ C $ is an arbitrary constant.
Finally, superseding Eq (2.4) with Eq (2.5) into Eq (2.3) and agammaegating all terms of the same power $ exp\left(-m\varphi(\xi)\right) $, $ m = 0, 1, 2, 3, ... $. After that equating them to zero, we get algebraic equations solved by Mathematica or Maple to obtain the values of $ a_i $. Hence, we get the solutions (2.4), which give the exact solutions of Eq (2.3).
The solutions of Eq (2.3) can be expressed in the form [46,47]
| $ ϑ(x,t)={αsinr(βξ),∣ξ∣≤πβ,0,otherwise,, $ | (2.11) |
or in the form
| $ ϑ(ξ)(x,t)={αcosr(βξ),∣ξ∣≤π2μ,0,otherwise,, $ | (2.12) |
where $ \alpha, \; \beta $ and $ r\neq0 $, are parameters determined in sequel. From (2.11) we have
| $ ϑ(ξ)=αsinr(βξ),ϑn(ξ)=αnsinnr(βξ),(ϑn)ξ=nβrαncos(βξ)sinnr−1(βξ),(ϑn)ξξ=−n2β2rαnsinnr(βξ)+nβ2αnr(nr−1)sinnr−2(βξ), $ | (2.13) |
and from (2.12) we have
| $ ϑ(ξ)=αcosr(βξ),ϑn(ξ)=αncosnr(βξ),(ϑn)ξ=−nβrαnsin(βξ)cosnr−1(βξ),(ϑn)ξξ=−n2β2rαncosnr(βξ)+nβ2αnr(nr−1)cosnr−2(βξ). $ | (2.14) |
Finally, superseding Eq (2.13) or Eq (2.14) into Eq (2.3), then balance the terms of the cosine functions (2.14) or the sine functions (2.13). Then, we sum all terms with the same power in $ cos^{r}(\beta\xi) $ or $ sin^{r}(\beta\xi) $ and equating their coefficients to zero in order to obtain an algebraic equations in the unknowns $ \beta, \; \alpha $ and $ r $. Solving this system yields these unknown constants.
According to description of this method [30,31,32,33,48,49], we assume that Eq (2.3) has the following solution:
| $ ϑ′=aϑ2−n+bϑ+cϑn, $ | (2.15) |
where $ a, b, c $ and $ n $ are constants calculated later. From Eq (2.15), we get
| $ ϑ″=ab(3−n)ϑ2−n+a2(2−n)ϑ3−2n+nc2ϑ2n−1+bc(n+1)ϑn+(2ac+b2)ϑ, $ | (2.16) |
| $ ϑ‴=(ab(3−n)(2−n)ϑ1−n+a2(2−n)(3−2n)ϑ2−2n +n(2n−1)c2ϑ2n−2+bcn(n+1)ϑn−1+(2ac+b2))ϑ′. $ | (2.17) |
The exact solutions of Eq (2.15), for an arbitrary constant $ \mu $ are given as follow:
1. For $ n = 1 $, the solution is
| $ ϑ(ξ)=μe(a+b+c)ξ. $ | (2.18) |
2. For $ n \neq 1 $, $ b = 0 $ and $ c = 0 $, the solution is
| $ ϑ(ξ)=(a(n−1)(ξ+μ))1n−1. $ | (2.19) |
3. For $ n \neq 1 $, $ b\neq0 $ and $ c = 0 $, the solution is
| $ ϑ(ξ)=(−ab+μeb(n−1)ξ)1n−1. $ | (2.20) |
4. For $ n \neq 1 $, $ a\neq 0 $ and $ b^2-4ac < 0 $, the solution is
| $ ϑ(ξ)=(−b2a+√4ac−b22atan((1−n)√4ac−b22(ξ+μ)))11−n $ | (2.21) |
and
| $ ϑ(ξ)=(−b2a−√4ac−b22acot((1−n)√4ac−b22(ξ+μ)))11−n. $ | (2.22) |
5. For $ n \neq 1 $, $ a\neq 0 $ and $ b^2-4ac > 0 $, the solution is
| $ ϑ(ξ)=(−b2a−√b2−4ac2acoth((1−n)√b2−4ac2(ξ+μ)))11−n $ | (2.23) |
and
| $ ϑ(ξ)=(−b2a−√b2−4ac2atanh((1−n)√b2−4ac2(ξ+μ)))11−n. $ | (2.24) |
6. For $ n \neq 1 $, $ a\neq0 $ and $ b^2-4ac = 0 $, the solution is
| $ ϑ(ξ)=(1a(n−1)(ξ+μ)−b2a)11−n. $ | (2.25) |
Bäcklund transformation
When $ \vartheta_{m-1}(\xi) $ and $ \vartheta_{m}(\xi)(\vartheta_{m}(\xi) = \vartheta_{m}(\vartheta_{m-1}(\xi))) $ are the solutions of Eq (2.15), we obtain
| $ \frac{d\vartheta_{m}(\xi)}{d\xi} = \frac{d\vartheta_{m}(\xi)}{d\vartheta_{m-1}(\xi)} \frac{d\vartheta_{m-1}(\xi)}{d\xi} = \frac{d\vartheta_{m}(\xi)}{d\vartheta_{m-1}(\xi)}(a\vartheta_{m-1}^{2-n}+b\vartheta_{m-1}+c\vartheta_{m-1}^{n}), $ |
namely
| $ dϑm(ξ)aϑ2−nm+bϑm+cϑnm=dϑm−1(ξ)aϑ2−nm−1+bϑm−1+cϑnm−1. $ | (2.26) |
Integrating Eq (2.26) once with respect to $ \xi $, we obtain the following Bäcklund transformation of Eq (2.15):
| $ ϑm(ξ)=(−cK1+aK2(ϑm−1(ξ))1−nbK1+aK2+aK1(ϑm−1(ξ))1−n)11−n, $ | (2.27) |
where $ K_1 $ and $ K_2 $ are arbitrary constants. If we get a solution for this equation, we use Eq (2.27) to obtain infinite sequence of solutions of Eq (2.15), as well of Eq (2.1).
In order to solve the Eq (1.1), using exp$ (-\varphi(\xi)) $-expansion method and the Riccati-Bernoulli sub-ODE method, the following solution structure is selected
| $ q(x,t)=eiχ(x,t)u(ξ),χ(x,t)=px+νt,ξ=kx+ωt, $ | (3.1) |
where $ p $, $ \nu $, $ k $ and $ \omega $ are constants. Substituting (3.1) into (1.1), we have the ODE
| $ k2u″−2u3−(p2+ν+2γ)u=0,ω=−2pk,η=−1. $ | (3.2) |
Now we apply exp$ (-\varphi(\xi)) $-expansion and the Riccati-Bernoulli sub-ODE methods for Eq (3.2).
According to the exp$ (-\varphi(\xi)) $-expansion technique, Eq (3.2) has the following solution
| $ u=A0+A1exp(−φ), $ | (3.3) |
where $ A_0 $ and $ A_1 $ are constants and $ A_1 \neq 0 $. It is easy to see that
| $ u″=A1(2exp(−3φ)+3λexp(−2φ)+(2μ+λ2)exp(−φ)+λμ), $ | (3.4) |
| $ u3=A31exp(−3φ)+3A0A21exp(−2φ)+3A20A1exp(−φ)+A30. $ | (3.5) |
Superseding $ u $, $ u'' $, $ u^3 $ into Eq (3.2) and hence equating the coefficients of $ exp{(-\varphi)} $ to zero, we obtain
| $ k2A1λμ−2A30−(p2+ν+2γ)A0=0, $ | (3.6) |
| $ k2A1(λ2+2μ)−6A20A1−(p2+ν+2γ)A1=0, $ | (3.7) |
| $ k2A1λ−2A0A21=0, $ | (3.8) |
| $ k2A1−A31=0. $ | (3.9) |
Solving Eqs (3.6)–(3.9), we get
| $ A_0 = \pm\frac{k\lambda}{2}, A_{1} = \pm k, \nu = -\frac{1}{2}(4\gamma+k^2(\lambda^2-4\mu)+2p^2). $ |
We consider only one case, whenever the other cases follow similarly. In this case, the solution of Eq (3.3) reads as:
| $ u(ξ)=±k2(λ+2exp(−φ(ξ))). $ | (3.10) |
Superseding Eqs (2.6)–(2.7) into Eq (3.10), we obtain:
Case 1. At $ \lambda^{2}-4\mu > 0, \mu\neq0, $
| $ u1,2(x,t)=±k2(λ−4μ√λ2−4μtanh(√λ2−4μ2(ξ+C))+λ). $ | (3.11) |
Using Eqs (3.1) and (3.11) the solutions of equation (1.1) are
| $ q1,2(x,t)=±k2eiχ(λ−4μ√λ2−4μtanh(√λ2−4μ2(ξ+C))+λ). $ | (3.12) |
Case 2. At $ \lambda^{2}-4\mu < 0, \mu\neq0, $
| $ u3,4(x,t)=±k2(λ+4μ√4μ−λ2tan(√4μ−λ22(ξ+C))−λ). $ | (3.13) |
Using Eqs (3.1) and (3.13) the solutions of Eq (1.1) are
| $ q3,4(x,t)=±k2eiχ(λ+4μ√4μ−λ2tan(√4μ−λ22(ξ+C))−λ). $ | (3.14) |
Case 3. At $ \lambda^{2}-4\mu > 0, \mu = 0, \lambda \neq0 $
| $ u5,6(x,t)=±k2(λ+2λexp(λ(ξ+C))−1). $ | (3.15) |
Using Eqs (3.1) and (3.15) the solutions of Eq (1.1) are
| $ q5,6(x,t)=±k2eiχ(λ+2λexp(λ(ξ+C))−1). $ | (3.16) |
Case 4. At $ \lambda^{2}-4\mu = 0, \mu\neq0, \lambda\neq0, $
| $ u7,8(x,t)=±k2(λ−λ2(ξ+C)λ(ξ+C)+2). $ | (3.17) |
Using Eq (3.1) and (3.17) the solutions of Eq (1.1) are
| $ q7,8(x,t)=±k2eiχ(λ−λ2(ξ+C)λ(ξ+C)+2). $ | (3.18) |
Case 5. At $ \lambda^{2}-4\mu = 0, \mu = 0, \lambda = 0, $
| $ u9,10(x,t)=±k2(1ξt+C). $ | (3.19) |
Using Eqs (3.1) and (3.19) the solutions of Eq (1.1) are
| $ q9,10(x,t)=±k2eiχ(1ξt+C). $ | (3.20) |
Here $ k, \lambda, \mu, C $ are constants, $ \xi = k (x -2pt) $ and $ \chi = p x -\frac{1}{2}(4\gamma+k^2(\lambda^2-4\mu)+2p^2)\; t $.
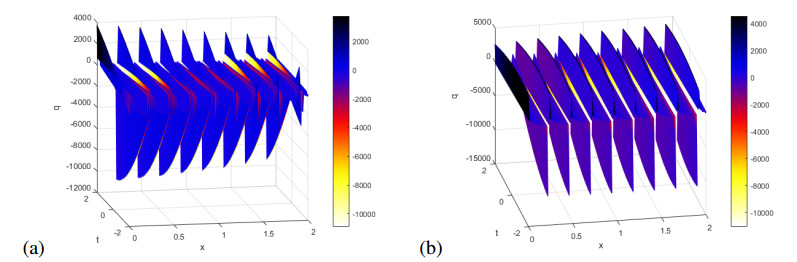
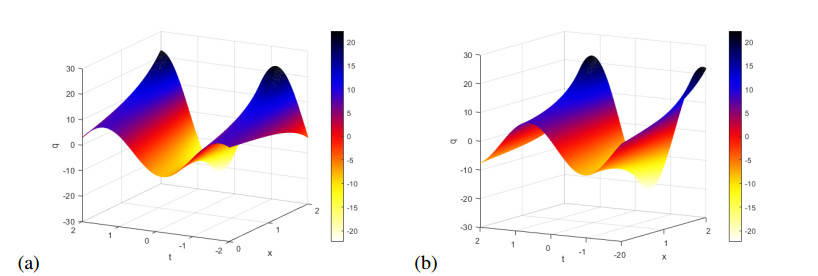
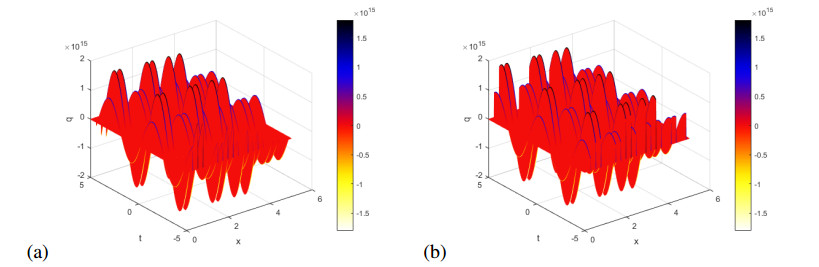
We have plotted these solutions in Figures 1–5. Figure 1(a) shows the real part of $ q = q_1(x, t) $ in (3.12), while Figure 1(b) shows imaginary part of this solution for $ k $ = 1.5, $ p $ = 1.5, $ \gamma $ = 1.3, $ \lambda $ = 2.3, $ \mu = 1 $, $ \omega $ = -4.5, $ \nu $ = -6.3012 and $ C $ = 1.4.
Figure 2(a) shows the real part of $ q = q_3(x, t) $ in (3.14), while Figure 2(b) shows imaginary part of this solution for $ k $ = 1.2, $ p $ = 1.2, $ \gamma $ = 1.8, $ \lambda $ = 1.2, $ \mu = 2 $, $ \omega $ = -2.88, $ \nu $ = -0.3168 and $ C $ = 0.4.
Figure 3(a) shows the real part of $ q = q_5(x, t) $ in (3.16), while Figure 3(b) shows imaginary part of this solution for $ k $ = 0.4, $ p $ = 0.6, $ \gamma $ = 0.3, $ \lambda $ = 1.2, $ \mu = 0 $, $ \omega $ = -0.48, $ \nu $ = -1.0752 and $ C $ = 1.
Figure 4(a) shows the real part of $ q = q_7(x, t) $ in (3.18), while Figure 4(b) shows imaginary part of this solution for $ k $ = 0.5, $ p $ = 0.5, $ \gamma $ = 2.3, $ \lambda $ = 2, $ \mu = 1 $, $ \omega $ = -0.5, $ \nu $ = -4.85 and $ C $ = 4.
Figure 5(a) shows the real part of $ q = q_9(x, t) $ in (3.20), while Figure 5(b) shows imaginary part of this solution $ k $ = -0.7, $ p $ = -0.5, $ \gamma $ = 0.8, $ \lambda = \mu $ = 0, $ \omega $ = -0.7, $ \nu $ = -1.85 and $ C $ = 4.
According to sine-cosine technique, subtitling Eq (2.13) into Eq (3.2), gives
| $ k2(−β2r2αsinr(βξ)+β2αr(r−1)sinr−2(βξ))−2α3sin3r(βξ)−(p2+ν+2γ)λsinr(βξ)=0. $ | (3.21) |
Thus by comparing the coefficients of the sine functions, we get
| $ r−1≠0,r−2=3r, k2β2αr(r−1)−2α3=0, −k2β2r2α−(p2+ν+2γ)α=0. $ | (3.22) |
Solving this system gives
| $ r=−1,α=±√−p2−ν−2γ,β=±√−(p2+ν+2γ)k, $ | (3.23) |
for $ p^{2}+\nu+2\gamma < 0 $ and $ k \neq0 $. We get the same result if we also use the cosine method (2.14). Thus, the periodic solutions are
| $ ˜u1,2(x,t)=±√−p2−ν−2γsec(√−(p2+ν+2γ)k(kx+ωt)),∣√−(p2+ν+2γ)k(kx+ωt)∣<π2 $ | (3.24) |
and
| $ ˜u3,4(x,t)=±√−p2−ν−2γcsc(√−(p2+ν+2γ)k(kx+ωt)),0<√−(p2+ν+2γ)k(kx+ωt)<π. $ | (3.25) |
Using Eqs (3.1) and (3.19) the solutions of Eq (1.1) are
| $ ˜q1,2(x,t)=±√−(p2+ν+2γ)ei(px+νt)sec(√−(p2+ν+2γ)k(kx+ωt)),∣√−(p2+ν+2γ)k(kx+ωt)∣<π2 $ | (3.26) |
and
| $ ˜q3,4(x,t)=±√−p2−ν−2γei(px+νt)csc(√−(p2+ν+2γ)k(kx+ωt)),0<√−(p2+ν+2γ)k(kx+ωt)<π. $ | (3.27) |
However, for $ p^{2}+\nu+2\gamma > 0 $ and $ k \neq0 $. we obtain the soliton and complex solutions
| $ ˜u5,6(x,t)=±√−p2−ν−2γsech(√(p2+ν+2γ)k(kx+ωt)) $ | (3.28) |
and
| $ ˜u7,8(x,t)=±√p2+ν+2γcsch(√(p2+ν+2γ)k(kx+ωt)). $ | (3.29) |
Using Eqs (3.1) and (3.19) the solutions of equation
| $ ˜q5,6(x,t)=±√−p2−ν−2γei(px+νt)sech(√(p2+ν+2γ)k(kx+ωt)) $ | (3.30) |
and
| $ ˜q7,8(x,t)=±√p2+ν+2γei(px+νt)csch(√(p2+ν+2γ)k(kx+ωt)). $ | (3.31) |
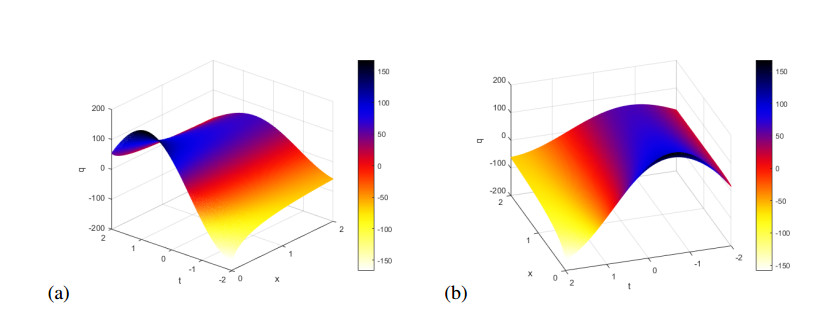
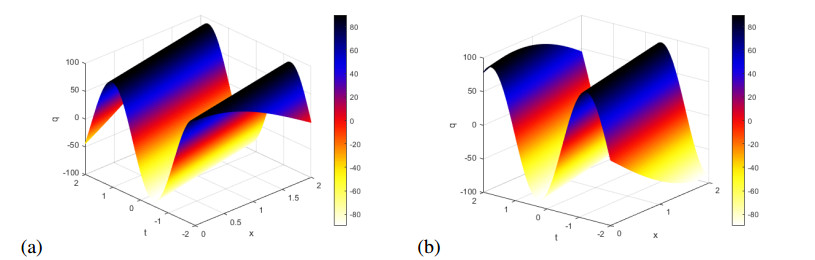
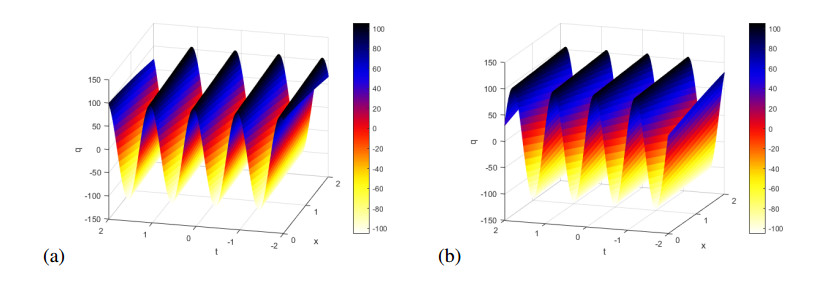
Figure 6(a) shows the real part of $ q = \tilde{q}_1(x, t) $ in (3.26), while Figure 6(b) shows imaginary part of this solution for $ p $ = 2, $ \nu $ = -2, $ \gamma $ = -3, $ k $ = 2 and $ \omega $ = 1.
Figure 7(a) shows the real part of $ q = \tilde{q}_5(x, t) $ in (3.30), while Figure 7(b) shows imaginary part of this solution for $ p $ = 2.6, $ \nu $ = 2.1, $ \gamma $ = 3.1, $ k $ = 1.2 and $ \omega $ = 2.
According to Riccati-Bernoulli Sub-ODE technique, substituting Eq (2.16) into Eq (3.2), we get
| $ k2(ab(3−n)u2−n+a2(2−n)u3−2n+nc2u2n−1+bc(n+1)un+(2ac+b2)u)−2u3−(p2+ν+2γ)u=0. $ | (3.32) |
Putting $ n = 0 $, Eq (3.32) becomes
| $ k2(3abu2+2a2u3+bc+(2ac+b2)u)−2u3−(p2+ν+2γ)u=0. $ | (3.33) |
Putting each coefficient of $ u^i (i = 0, 1, 2, 3) $ to zero, we get
| $ bc=0, $ | (3.34) |
| $ k2(2ac+b2)−(p2+ν+2γ)=0, $ | (3.35) |
| $ 3ab=0, $ | (3.36) |
| $ k2a2−1=0. $ | (3.37) |
Solving Eqs (3.34)–(3.37), we have
| $ b=0, $ | (3.38) |
| $ ac=p2+ν+2γ2k2, $ | (3.39) |
| $ c=±p2+ν+2γ2k, $ | (3.40) |
| $ a=±1k. $ | (3.41) |
Hence, we give the cases of solutions for Eq (3.2) as follows
Rational function solutions: (When $ b = 0 $ and $ c = 0 $, i.e., $ p^{2}+\nu+2\gamma = 0 $)
The solution of Eq (3.2) is
| $ ˆu1(x,t)=(−a(kx+ωt+μ))−1. $ | (3.42) |
Therefore, using Eqs (3.1) and (3.42), the following new explicit exact solution of the unstable nonlinear Schrödinger equation can be acquired
| $ ˆq1(x,t)=ei(px+νt)(−a(kx+ωt+μ))−1, $ | (3.43) |
where $ p, \nu, \gamma, k, \omega, \mu $ are arbitrary constants.
Trigonometric function solution: (When $ p^{2}+\nu+2\gamma > 0 $)
Superseding Eq (3.1) and Eqs (3.38)–(3.41) into Eqs (2.21) and (2.22), then the exact solutions of Eq (1.1) are
| $ ˆu2,3(x,t)=±√p2+ν+2γ2tan(√p2+ν+2γ√2k(kx+ωt+μ)) $ | (3.44) |
and
| $ ˆu4,5(x,t)=±√p2+ν+2γ2cot(√p2+ν+2γ√2k(kx+ωt+μ)). $ | (3.45) |
Consequently, using Eqs (3.1) and (3.42), the following new explicit exact solution for the unstable nonlinear Schrödinger equation can be obtained
| $ ˆq2,3(x,t)=±ei(px+νt)√p2+ν+2γ2tan(√p2+ν+2γ√2k(kx+ωt+μ)) $ | (3.46) |
and
| $ ˆq4,5(x,t)=±ei(px+νt)√p2+ν+2γ2cot(√p2+ν+2γ√2k(kx+ωt+μ)), $ | (3.47) |
where $ p, \nu, \gamma, k, \omega, \mu $ are arbitrary constants.
Hyperbolic function solution : (When $ p^{2}+\nu+2\gamma < 0 $)
Substituting Eq (3.1) and Eqs (3.38)–(3.41) into Eqs (2.23) and (2.24), then the exact solutions of Eq (1.1) are
| $ ˆu6,7(x,t)=±√−(p2+ν+2γ)2tanh(√−(p2+ν+2γ)√2k(kx+ωt+μ)) $ | (3.48) |
and
| $ ˆu8,9(x,t)=±√−(p2+ν+2γ)2coth(√−(p2+ν+2γ)√2k(kx+ωt+μ)). $ | (3.49) |
Subsequently, the following new explicit exact solution to the unstable nonlinear Schrödinger equation can be gained
| $ ˆq6,7(x,t)=±ei(px+νt)√−(p2+ν+2γ)2tanh(√−(p2+ν+2γ)√2k(kx+ωt+μ)) $ | (3.50) |
and
| $ ˆq8,9(x,t)=±ei(px+νt)√−(p2+ν+2γ)2coth(√−(p2+ν+2γ)√2k(kx+ωt+μ)), $ | (3.51) |
where $ p, \nu, \gamma, k, \omega, \mu $ are arbitrary constants.
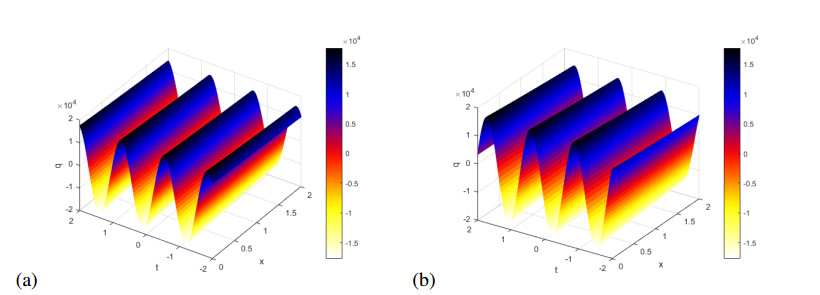
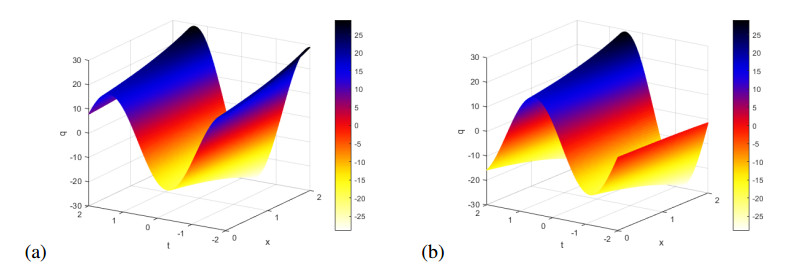
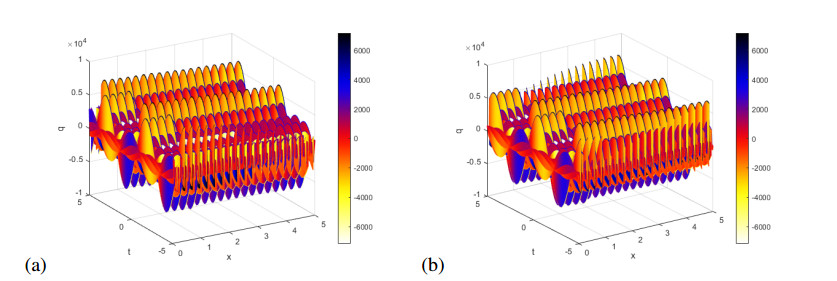
We have plotted these solutions in Figures 8–10. Figure 8(a) shows the real part of $ q = \hat{q}_2(x, t) $ in (3.46), while Figure 8(b) shows imaginary part of this solution for $ k $ = 0.5, $ p $ = -1.3, $ \omega $ = 1.3, $ \nu $ = 1.4, $ \gamma $ = 1.5 and $ \mu $ = 1.
Figure 9(a) shows the real part of $ q = \hat{q}_6(x, t) $ in (3.50), while Figure 9(b) shows imaginary part of this solution for $ k $ = 1.5, $ p $ = 1.3, $ \omega $ = -3.9, $ \nu $ = -2.4, $ \gamma $ = -1.3 and $ \mu $ = 1.
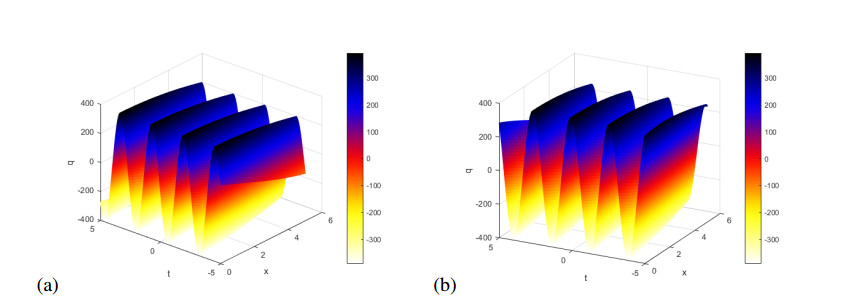
Figure 10(a) shows the real part of $ q = \hat{q}_1(x, t) $ in (3.43), while Figure 10(b) shows imaginary part of this solution for $ k $ = 0.2, $ a $ = 5, $ p $ = 1.2, $ \omega $ = -0.48, $ \nu $ = 1.4 and $ \mu $ = 1.
Remark 1. Using Eq (2.27) for $ u_i(x, y) $, $ i $ = 1, ..., 9, once, then Eq (3.2) as well as for Eq (1.1) has an infinite solutions. In sequence, by applying this process again, we get new families of solutions.
| $ ˆu⋆1(x,t)=B3−aB3(kx+ωt+μ)±1, $ | (3.52) |
| $ ˆu⋆2,3(x,t)=−p2+ν+2γ2±B3√p2+ν+2γ2tan(√p2+ν+2γ√2k(kx+ωt+μ))B3±√p2+ν+2γ2tan(√p2+ν+2γ√2k(kx+ωt+μ)), $ | (3.53) |
| $ ˆu⋆4,5(x,t)=−p2+ν+2γ2±B3√p2+ν+2γ2cot(√p2+ν+2γ√2k(kx+ωt+μ))B3±√p2+ν+2γ2cot(√p2+ν+2γ√2k(kx+ωt+μ)), $ | (3.54) |
| $ ˆu⋆6,7(x,t)=−p2+ν+2γ2±B3√−(p2+ν+2γ)2tanh(√−(p2+ν+2γ)√2k(kx+ωt+μ))B3±√−(p2+ν+2γ)2tanh(√−(p2+ν+2γ)√2k(kx+ωt+μ)), $ | (3.55) |
| $ ˆu⋆8,9(x,t)=−p2+ν+2γ2±B3√−(p2+ν+2γ)2coth(√−(p2+ν+2γ)√2k(kx+ωt+μ))B3±√−(p2+ν+2γ)2coth(√−(p2+ν+2γ)√2k(kx+ωt+μ)), $ | (3.56) |
where $ B_{3}, p, \nu, \gamma, k, \omega $ and $ \mu $ are arbitrary constants.
In this article, the exp$ (-\varphi(\xi)) $-expansion, the sine-cosine and Riccati-Bernoulli sub-ODE techniques have been efficiently applied to construct many new solutions. As an outcome, a number of new exact solutions for the UNS equation were formally derived. Namely, the exp$ (-\varphi(\xi)) $-expansion method gives a first family of ten solutions. Whereas, sine-cosine method give another different second family of eight solutions. Indeed, Riccati-Bernoulli sub-ODE method gives a wide range of new explicit exact solutions including rational functions, trigonometric functions, hyperbolic functions and exponential functions in a straightforward manner. The effectiveness and helpfulness of the exp$ (-\varphi(\xi)) $-expansion, the sine-cosine and Riccati-Bernoulli sub-ODE methods to deal with UNS equation was proved. As a success, a wide range of new explicit exact solutions were obtained in a straightforward manner. Our study shows that the proposed three methods are reliable in handling NPDEs to establish a variety of exact solutions. Finally, we have plotted some 3D graphs of these solutions and we have shown that these graphs can be controlled by adjusting the parameters.
Remark 2.
1. Comparing our results concerning the UNS equation with the results in [41,42,44,45], one can see that our results are new and most extensive. Indeed, choosing suitable values for the parameters similar solutions can be verified.
2. The Riccati-Bernoulli sub-ODE method has an interesting feature, that admits infinite solutions, which has never given for any other method.
3. The three proposed methods in this article are efficient, powerful and adequate for solving other types of NPDEs and can be easily extended to solve nonlinear fractional differential equations, see [32,33,49,50,51,52,53,54,55,56].
The exp$ (-\varphi(\xi)) $-expansion, sine-cosine and Riccati-Bernoulli sub-ODE techniques have successfully been applied for the UNS equation. Many new exact solutions are obtained during the analytical treatment. The availability of computer systems like Matlab or Mathematica facilitates avoids us the tedious algebraic calculations. Indeed, the obtained solutions are of significant importance in the studies of applied science as they help in explaining some interesting physical mechanism for the complex phenomena. The 3D graphs of some exact solutions are plotted for suitable parameters. Finally, the proposed methods can be applied for a wide range of nonlinear partial differential equations arising in natural sciences. Currently, work is in progress on the applications of the proposed methods in this paper in order to solve the other nonlinear partial differential equations. Indeed these methods can be extended to solve fractional partial differential equations.
The authors thank the editor and anonymous reviewers for their valuable comments and suggestions.
The authors declare no conflict of interest.
| [1] | to appear in SIAM Journal on Control and Optimization, arXiv:1106.1788. |
| [2] |
M. Bendahmane and K. H. Karlsen, Analysis of a class of degenerate reaction-diffusion systems and the bidomain model of cardiac tissue, Netw. Heterog. Media, 1 (2006), 185-218. doi: 10.3934/nhm.2006.1.185
|
| [3] |
M. Bendahmane and K. H. Karlsen, Convergence of a finite volume scheme for the bidomain model of cardiac tissue, Appl. Numer. Math., 59 (2009), 2266-2284. doi: 10.1016/j.apnum.2008.12.016
|
| [4] |
M. Bendahmane, R. Bürger and R. Ruiz Baier, A finite volume scheme for cardiac propagation in media with isotropic conductivities, Math. Comp. Simul., 80 (2010), 1821-1840. doi: 10.1016/j.matcom.2009.12.010
|
| [5] | H. Brezis, Functional Analysis, Sobolev Spaces and Partial Differential Equations, Springer, New York, 2011. |
| [6] | A. L. Bukhgeĭm, Carleman estimates for Volterra operators and uniqueness of inverse problems, in Non-classical Problems of Mathematical Physics, Computing Center of Siberian Branch of Soviet Academy of Sciences, Novosibirsk, 1981, 56-64. |
| [7] | A. L. Bukhgeim, Introduction to the Theory of Inverse Problems, VSP, Utrecht, 2000. |
| [8] | A. L. Bukhgeim and M. V. Klibanov, Uniqueness in the large class of multidimensional inverse problems, (Russian) Dokl. Akad. Nauk SSSR, 260 (1981), 269-272. |
| [9] | K. C. Chang, Methods in Nonlinear Analysis, Springer-Verlag Berlin Heidelberg, Netherlands, 2005. |
| [10] | P. Colli Franzone and G. Savaré, Degenerate evolution systems modeling the cardiac electric field at micro- and macroscopic level, in Evolution Equations, Semigroups and Functional Analysis (Milano, 2000), Progr. Nonlinear Differential Equations Appl., 50, Birkhäuser, Basel, 2002, 49-78. |
| [11] |
M. Cristofol, P. Gaitan and H. Ramoul, Inverse problems for a $2 \times 2$ reaction-diffusion system using a Carleman estimate with one observation, Inverse Problems, 22 (2006), 1561-1573. doi: 10.1088/0266-5611/22/5/003
|
| [12] | A. V. Fursikov and O. Yu. Imanuvilov, Controllability of Evolution Equations, Lecture Notes Series, 34, RIM Seoul National University, Korea, 1996. |
| [13] |
O.Yu. Imanuvilov, M. Yamamoto, Lipschitz stability in inverse problems by Carleman estimates, Inverse Problems, 14 (1998), 1229-1245. doi: 10.1088/0266-5611/14/5/009
|
| [14] |
O. Yu. Imanuvilov and M. Yamamoto, Carleman estimates for the non-stationary Lamé system and the application to an inverse problem, ESAIM, COCV, 11 (2005), 1-56. doi: 10.1051/cocv:2004030
|
| [15] |
V. Isakov, Carleman estimates and applications to inverse problems, Milan J. Math., 72 (2004), 249-271. doi: 10.1007/s00032-004-0033-6
|
| [16] | M. V. Klibanov, Carleman estimates and inverse problems in the lasrt two decades, in Surveys on Solution Methods for Inverse Problems, Springer, Vienna, 2000, 119-146. |
| [17] |
M. V. Klibanov and M. Yamamoto, Lipschitz stability of an inverse problem for an acoustic equation, Appl. Anal., 85 (2006), 515-538. doi: 10.1080/00036810500474788
|
| [18] | M. A. Krasnoselskii, Positive Solutions of Operator Equations, Noordhoff, Groningen, 1964. |
| [19] |
G. Lebeau and L. Robbiano, Contrôle exact de l'equation de la chaleur, Comm. Partial Differential Equations, 20 (1995), 335-356. doi: 10.1080/03605309508821097
|
| [20] |
J.-P. Puel and M. Yamamoto, On a global estimate in a linear inverse hyperbolic problem, Inverse Problems, 12 (1996), 995-1002. doi: 10.1088/0266-5611/12/6/013
|
| [21] |
K. Sakthivel, N. Baranibalan, J.-H. Kim and K. Balachandran, Stability of diffusion coefficients in an inverse problem for the Lotka-Volterra competition system, Acta Appl. Math., 111 (2010), 129-147. doi: 10.1007/s10440-009-9455-z
|
| [22] |
Z. Q. Wu, J. X. Yin and C. P. Wang, Elliptic and Parabolic Equations, World Scientific Publishing Co. Pte. Ltd, 2003. doi: 10.1142/6238
|
| [23] |
M. Yamamoto, Uniqueness and stability in multidimensional hyperbolic inverse problems, J. Math. Pures Appl., 78 (1999), 65-98. doi: 10.1016/S0021-7824(99)80010-5
|
| [24] |
G. Yuan and M. Yamamoto, Lipshitz stability in the determination of the principal part of a parabolic equation, ESAIM: Control Optim. Calc. Var., 15 (2009), 525-554. doi: 10.1051/cocv:2008043
|
| 1. | Mostafa M.A. Khater, Mustafa Inc, K.S. Nisar, Raghda A.M. Attia, Multi–solitons, lumps, and breath solutions of the water wave propagation with surface tension via four recent computational schemes, 2021, 20904479, 10.1016/j.asej.2020.10.029 | |
| 2. | Mostafa M. A. Khater, Yu-Ming Chu, Raghda A. M. Attia, Mustafa Inc, Dianchen Lu, On the Analytical and Numerical Solutions in the Quantum Magnetoplasmas: The Atangana Conformable Derivative (1+3)-ZK Equation with Power-Law Nonlinearity, 2020, 2020, 1687-9120, 1, 10.1155/2020/5809289 | |
| 3. | Usman Younas, Muhammad Bilal, Tukur Abdulkadir Sulaiman, Jingli Ren, Abdullahi Yusuf, On the exact soliton solutions and different wave structures to the double dispersive equation, 2022, 54, 0306-8919, 10.1007/s11082-021-03445-2 | |
| 4. | Ghazala Akram, Maasoomah Sadaf, Iqra Zainab, Observations of fractional effects of β-derivative and M-truncated derivative for space time fractional Phi-4 equation via two analytical techniques, 2022, 154, 09600779, 111645, 10.1016/j.chaos.2021.111645 | |
| 5. | Mojtaba Shahraki, Hossein Malekpoor, The effects of polarization on soliton interactions inside optical fibers, 2022, 54, 0306-8919, 10.1007/s11082-022-03514-0 | |
| 6. | Md. Abdul Kayum, Ripan Roy, M. Ali Akbar, M. S. Osman, Study of W-shaped, V-shaped, and other type of surfaces of the ZK-BBM and GZD-BBM equations, 2021, 53, 0306-8919, 10.1007/s11082-021-03031-6 | |
| 7. | Khalid K. Ali, Hadi Rezazadeh, Nauman Raza, Mustafa Inc, Highly dispersive optical soliton perturbation with cubic–quintic–septic law via two methods, 2021, 35, 0217-9792, 10.1142/S0217979221502763 | |
| 8. | Delmar Sherriffe, Diptiranjan Behera, P. Nagarani, Different forms for exact traveling wave solutions of unstable and hyperbolic nonlinear Schrödinger equations, 2024, 38, 0217-9792, 10.1142/S0217979224501315 | |
| 9. | Handenur Esen, Neslihan Ozdemir, Aydin Secer, Mustafa Bayram, Tukur Abdulkadir Sulaiman, Hijaz Ahmad, Abdullahi Yusuf, M. Daher Albalwi, On the soliton solutions to the density-dependent space time fractional reaction–diffusion equation with conformable and M-truncated derivatives, 2023, 55, 0306-8919, 10.1007/s11082-023-05109-9 | |
| 10. | Hira Tariq, Hira Ashraf, Hadi Rezazadeh, Ulviye Demirbilek, Travelling wave solutions of nonlinear conformable Bogoyavlenskii equations via two powerful analytical approaches, 2024, 39, 1005-1031, 502, 10.1007/s11766-024-5030-7 | |
| 11. | Rui Cui, New waveform solutions of Calogero–Degasperis (CD) and potential Kadomtsev–Petviashvili (pKP) equations, 2024, 7, 2520-8160, 1673, 10.1007/s41939-023-00254-w | |
| 12. | Kang-Jia Wang, Ming Li, Variational Principle of the Unstable Nonlinear Schrödinger Equation with Fractal Derivatives, 2025, 14, 2075-1680, 376, 10.3390/axioms14050376 |
Bedr'Eddine Ainseba, Mostafa Bendahmane, Yuan He. Stability of conductivities in an inverse problem in the reaction-diffusion system in electrocardiology[J]. Networks and Heterogeneous Media, 2015, 10(2): 369-385. doi: 10.3934/nhm.2015.10.369
DownLoad:
