1. Introduction

In this paper, we describe how to combine multiple geophysical datasets for the purpose of assisting in better determining physical properties of the Earth structure. The need for combining different datasets comes from the fact that different datasets provide complementary information about the Earth structure. By jointly inverting multiple geophysical datasets, we combine these complementary pieces of information and thus, we get a more accurate description of the Earth structure; see, e.g., (Vozoff and Jupp 1975, Julia et al. 2000, Shen et al. 2003, Colombo and De Stefano 2007, Maceira and Ammon 2009, Shearer 2009, Stein and Wysession 2003).

Specifically, we combine receiver functions, surface wave dispersion measurements, and P-wave travel times. The need to use different datasets comes from the fact that there are two types of seismic waves that travel through the Earth: the body waves and the surface waves. Both types of waves provide different sensitivities and information about the Earth structure, since they are sampling, correspondingly, the interior and surface of the Earth. The information collected from the body waves travels deeper into the Earth and translates into teleseismic P-wave receiver functions. In order to obtain information about the Earth surface, surface waves are analyzed, in our case, by means of surface waves dispersion. Receiver functions resolve discontinuities (impedance contrasts) in seismic velocities, and provide good measurement of crustal thickness, without providing a good average of shear wave velocity. On the other hand, we have surface (Love and Rayleigh) waves whose energy is concentrated near the Earth’s surface, and provide good average of absolute shear wave velocity, without a good shear-wave velocity contrasts in layered structures (Julia et al. 2000, Maceira and Ammon 2009, Shearer 2009, Stein and Wysession 2003, Cho et al. 2007, Obrebski et al. 2010). Therefore these two data sets provide complementary information about the Earth structure. Seismic first-arrival travel times are complementary to the other datasets because the travel time enable us to recover the causative slowness of the Earth structure (Lees and Vandecar 1991).

For each dataset, we usually know the relative variance (uncertainty of data) of different measurement results from this dataset, and thus, we can use the Least Squares method to find the corresponding Earth model. For multiple datasets, we can sometimes still use the Least Squares Method to process all these datasets - provided that we know the variances of different measurements from different datasets. In practice, however, we usually only have an approximate knowledge of these variances. So, instead of producing a single model, several models corresponding to different possible variances are generated. If all these models - corresponding to different possible values of variances - contain a certain geophysical feature, then we can be certain that this feature is also present in the actual Earth model (which corresponds to the actual (unknown) values of the variances).

From the mathematical viewpoint, the task of computing all these models is equivalent to computing the Pareto front of the corresponding Multi-Objective Optimization problem (Kozlovskaya 2000), where different objective functions correspond to different datasets.

In addition to producing all these models, it is also desirable to produce a ”typical” model, so that we only look for features which are present on this typical model. In this paper, we use methods for selecting such a typical model as described in (Sambridge 1999a, Sambridge 1999b, Kozlovskaya 2000).

This paper has the following structure. In Section 2, we describe, in detail, the need for multiobjective optimization. In Section 3, we show how to solve the corresponding optimization problems. In Section 4, we briefly describe the corresponding geophysical datasets. The results of applying multi-objective optimization technique to these datasets are shown and discussed in Section 5. Finally, Section 6 contains conclusions.

2. Need for Multi-Objective Optimization

2.1. Inverse Problems: Brief Reminder

In many real-life situations, we are interested in the values of the quantities x₁, x₂, ..., which are difficult (or even impossible) to measure directly. For example, in geophysics, one of our main objectives is to find the shear velocities x_i at different 3-D points i (i.e., at different depths and at different geographic locations). To find these values, we measure easier-to-measure quantities y₁, y₂, etc., which are related to x = (x₁, ..., x_n) by a known relation y = F(x), and then use the measured quantities y = (y₁, ..., y_m) to find the desired values x.

In particular, in geophysics, to find shear velocities x_i, we can calculate the teleseismic receiver functions y^RF, surface wave dispersion velocities y^SW, travel times y^TT , etc. For each of these types of data, if we know the velocity model x, then we can predict the Earth’s response by using the corresponding (known) operator F: y^RF = F^RF(x), y^SW = F^SW(x), y^TT = F^TT (x), etc.

Measurements are never absolutely accurate, there is always some measurement inaccuracy, there is always some level of noise preventing us from measuring the corresponding quantities exactly. A usual way to estimate parameters in the presence of noise is to use the Least Squares method, i.e., to find the values x that minimize the expression

$\sum\limits_{i = 1}^m {\frac{{{{\left( {{F_i}\left( x \right) - {y_i}} \right)}^2}}}{{\sigma _i^2}}} ,$

(1)

where $\sigma _i$ is the standard deviation of the noise (measurement inaccuracy) of the i-th measurement.

In some cases, all the available data points come from measurements of the same type, obtained by using the same methodology and similar instrumentation. For example, we may only have travel times, or only surface wave dispersion velocities. In such cases, it is reasonable to assume that all these measured values have the same accuracy, i.e., that $\sigma _i$ = const. Under this assumption, minimizing the expression (1) is equivalent to minimizing the sum of the squares

${\left\| {F\left( x \right) - y} \right\|^2}\mathop {{\rm{def}}}\limits_ = \sum\limits_{i = 1}^m {{{\left( {{F_i}\left( x \right) - {y_i}} \right)}^2}} .$

(2)

2.2. Need to Take Constraints into Account

Sometimes, the models x obtained by an appropriate minimization are not physically meaningful. For example, in geophysics, some models x predict higher velocities in the crust and lower velocities in the mantle, contrary to known geophysical models. In other cases, when we expect a smooth dependence on a signal on time, the reconstructed signal x can exhibit abrupt non-physical changes.

To avoid such non-physical solutions, it is desirable to explicitly take into account the corresponding constraints. For example, in most practical problems, there are known physical bounds on the values of the quantities x_i. In particular, in geophysics, for each depth, we can approximate the lower bound and the upper bound on possible values of shear velocity x_i at this depth.

In precise terms, for every i, we know the bounds a_i and b_i such that a_i ≤ x_i ≤ b_i.

Restrictions on smoothness can be described as known bounds $\Delta _{i j}$ on the difference between the values x_i and x_j for nearby points of time or at nearby spatial locations: -$\Delta$ ≤ x_i - x_j ≤ $\Delta _{i j}$.

Under the corresponding constraints, the optimization problem (2) takes the form

$\begin{array}{l} \mathop {min}\limits_x {\left\| {F\left( x \right) - y} \right\|^2}\\ s.t g\left( x \right) \ge 0. \end{array}$

(3)

where g(x) is a vector consisting of the corresponding constraints. For example, to describe bounds a_i and b_i on the values x_i, we use constraints x_i - a_i ≥ 0 and b_i - x_i ≥ 0.

Constraints corresponding to smoothness can also be expressed in the form g(x) ≥ 0, with the corresponding components of the vector g(x) having the form $\Delta _{i j}$ - (x_i - x_j) and (x_i - x_j) - (-$\Delta _{i j}$). Comment. Traditionally, researchers avoid non-physical non-smooth velocity models by adding a regularization term $\lambda {\left\| {Lx} \right\|^2}$ to the minimized function; see, e.g., (Tikhonov and Arsenin 1977). The problem with this term is that it is not clear how to select $\lambda$, and different values of $\lambda$ lead to different solutions; see, e.g., (Hansen 2010, Vogel 2002). Because of this problem, in this paper, instead of using regularization, we explicitly formulate constraints that need to be satisfied. For example, the desired smoothness is described as a bound on the differences x_i - x_j.

2.3. Joint Inversion: Idealized Case

As noted earlier, measurements of different type usually provide complementary information and it is, therefore, beneficial to use measurement results of all the types.

When we use measurements of different types t, t', etc., then while it is reasonable to assume that all the measurements i of the same type t have the same standard deviation ${\sigma _i} = {\sigma ^t}$, standard deviations of measurements of different types are, in general, different: ${\sigma ^t} ≠ {\sigma ^t}$. Let us first consider the idealized case, when we assume that we know the accuracy ${\sigma ^t}$ of measurements of type t.

In this case, we can still use the Least Squares expression (1) to find the desired model x. By grouping together measurements of different type, we can rewrite the expression (1) in the following form:

$\sum\limits_{i = 1}^m {\frac{{{{\left( {{F_i}\left( x \right) - {y_i}} \right)}^2}}}{{\sigma _i^2}}} = \sum\limits_{t = 1}^T {\sum\limits_{i \in t} {\frac{{{{\left( {{F_i}\left( x \right) - {y_i}} \right)}^2}}}{{{{\left( {{\sigma ^t}} \right)}^2}}}} } = \sum\limits_{t = 1}^T {\frac{1}{{{{\left( {{\sigma ^t}} \right)}^2}}}} \cdot \left( {\sum\limits_{i \in t} {{{\left( {{F_i}\left( x \right) - {y_i}} \right)}^2}} } \right)$

(4)

where T is the total number of different types of measurements, and the notation ${i \in t}$ indicates that the i-th measurement is of type t.

We can rewrite this expression as

(5)

where ${c_t}\mathop {{\rm{def}}}\limits_ = \frac{1}{{{\sigma ^t}}}$, y^t is the list (tuple) consisting of all measurements of type t, and F^t(x) is the list consisting of all the corresponding values F_i(x).

To find the desired solution x, we must minimize this expression under the constraint g(x) ≥ 0.

2.4. Reformulation of the Problem

The more measurements of a given type t we have, the larger the contribution of these measurements to the solution. In general, all the terms ${\frac{{{{\left( {{F_i}\left( x \right) - {y_i}} \right)}^2}}}{{\sigma _i^2}}}$ in the sum (4) are approximately of the same type, so we can conclude that the joint contribution of all the measurements of type t is proportional to the number m_t of all measurement results of this type.

To compare the importance of measurements of different types, it is useful to define relative importance as a ratio of the importance m_t of this type to the overall value $\sum\limits_{t'} {{m_{t'}}}$, i.e., as ${\eta _t}\mathop {{\rm{def}}}\limits_ = \frac{{{m_t}}}{{\sum\limits_{t'} {{m_{t'}}} }}$. These influence parameters ${\eta _t}$ are non-negative numbers that add up to 1.

To better understand the minimized expression (5), it makes sense to show the explicit dependence on the influence parameters. This can be done, e.g., by making sure that each term in the new formula is proportional to ${\eta _t}$; this way we will see that the larger the influence parameter, the larger the influence of this term. To do that, we replace each term $c_t^2$ with ${\eta _t} \cdot k_t^2$. From the condition that $c_t^2$ = ${\eta _t} \cdot k_t^2$, we conclude that $k_t^2$ = $\frac{{c_t^2}}{{{\eta _t}}}$. Since c_t = $\frac{1}{{{\sigma ^t}}}$ and ${\eta _t}$ = $\frac{{{m_t}}}{{\sum\limits_{t'} {{m_{t'}}} }}$, we have

${k_t} = \sqrt {\frac{{c_t^2}}{{{\eta _t}}}} = \sqrt {\frac{1}{{{{\left( {{\sigma ^t}} \right)}^2} \cdot {m_t}}}} \cdot \sqrt {\sum\limits_{t'} {{m_{t'}}} } .$

(6)

Thus, each term $c_t^2$ = ${\eta _t} \cdot k_t^2$ has the form $c_t^2$ = $w_t^2 \cdot C$, where ${w_t}\mathop {{\rm{def}}}\limits_ = \sqrt {\frac{{{\eta _t}}}{{{{\left( {{\sigma ^t}} \right)}^2} \cdot {m_t}}}}$ and $C\mathop {{\rm{def}}}\limits_ = \sum\limits_{t'} {{m_{t'}}}$. So, the minimized expression (5) takes the form

$C \cdot \sum\limits_{t = 1}^T {w_t^2 \cdot } {\left\| {{F^t}\left( x \right) - {y^t}} \right\|^2}.$

(7)

The location of the minimum does not change if we divide all the values of a function by the same positive coefficient C. Therefore, minimizing the expression (7) is equivalent to minimizing a simpler expression

$\sum\limits_{t = 1}^T {w_t^2 \cdot } {\left\| {{F^t}\left( x \right) - {y^t}} \right\|^2}.$

(8)

2.5. General Case: A Description

In the previous sections, we considered the ideal case, when we know the exact variance ${\sigma _i^2}$ of each measurement i. In this case, we can use the usual Least Squares approach to solve the joint inversion problem.

In practice, we only have an approximate knowledge of these variances. For example, for each measurement type t, we only know an approximate value ${{{\widetilde \sigma }^t}}$ of the corresponding standard deviation ${{\sigma ^t}}$.

A traditional approach to such situations is to use these approximate values ${{{\widetilde \sigma }^t}}$ and solve the corresponding optimization problem. The problem with this approach is that, if a geophysical features appears in the solution corresponding to these approximate values of variances, there is no guarantee that this feature will still be visible if we use the actual (somewhat different) variances.

It is desirable to separate artifacts that are due to the specific choice of variances from the phenomena that occur no matter what variances we use. For this purpose, we wish to repeatedly solve the joint inversion problem with different possible combinations of variances. If a certain geological feature is visible in all these solutions, then we can be confident that this feature is also present in the actual solution corresponding to the actual (unknown) values of the variances - i.e., that it is the feature of the actual Earth structure.

2.6. General Case: Analysis of the Problem

In the previous sections, we described the need to minimize the expression

$\sum\limits_{t = 1}^T {\frac{1}{{{{\left( {{\sigma ^t}} \right)}^2}}}} \cdot {\left\| {{F^t}\left( x \right) - {y^t}} \right\|^2}$

(9)

under the condition g(x) ≥ 0, where ${{\sigma ^t}}$ are the known standard deviations. We showed that this equivalent to minimizing the expression (8), where ${w_t} = \sqrt {\frac{{{\eta _t}}}{{{{\left( {{\sigma ^t}} \right)}^2} \cdot {m_t}}}}$ and ${\eta _t} = \frac{{{m_t}}}{{\sum\limits_{t'} {{m_{t'}}} }}$.

In situations when we only know an approximate value ${{{\widetilde \sigma }^t}}$, the traditional approach would be to use this approximate value, i.e., to minimize the expression

$\sum\limits_{t = 1}^T {\frac{1}{{{{\left( {{{\widetilde \sigma }^t}} \right)}^2}}}} \cdot {\left\| {{F^t}\left( x \right) - {y^t}} \right\|^2},$

(10)

or, equivalently, to minimize the expression (8), in which

${w_t} = \sqrt {\frac{{{\eta _t}}}{{{{\left( {{{\widetilde \sigma }^t}} \right)}^2} \cdot {m_t}}}} ,$

(11)

with the same values ${\eta _t} = \frac{{{m_t}}}{{\sum\limits_{t'} {{m_{t'}}} }}$ of the influence parameters.

As we have mentioned, a more appropriate approach is to minimize expressions (9) corresponding to all possible combinations of standard deviations ${{\sigma ^t}}$. Let us show that:

· each such constraint minimization problem can be equivalently reformulated into the form (8) with the weights (11) if we select different values of the influence parameters ${{\eta _t}}$ > 0, and that

· for each combination of influence parameters ${{\eta _t}}$ > 0 with $\sum\limits_t {{\eta _t}}$ = 1, there exist values ${{\sigma ^t}}$ > 0 for which the corresponding optimization problem (8) is equivalent to the original optimization problem (9).

Indeed, for each combination of values ${{\sigma ^t}}$, let us take

where the normalization coefficient c is chosen as In this case, ${{\eta _t}}$ > 0 and $\sum\limits_t {{\eta _t}}$ = 1. For the corresponding weights (11), we get

${\eta _t}\mathop {{\rm{def}}}\limits_ = \frac{1}{c} \cdot \frac{{{m_t} \cdot {{\left( {{{\widetilde \sigma }^t}} \right)}^2}}}{{{{\left( {{\sigma ^t}} \right)}^2}}}.$

(12)

Thus, minimizing the expression (8) is equivalent to minimizing the expression

$c \cdot \sum\limits_{t = 1}^T {\frac{1}{{{{\left( {{\sigma ^t}} \right)}^2}}}} \cdot {\left\| {{F^t}\left( x \right) - {y^t}} \right\|^2},$

which, in its turn, is equivalent to minimizing the expression (9).

Vice versa, for each combination of weights ${\eta _t}$ > 0 for which $\sum\limits_t {{\eta _t}}$ = 1, we can take

${\sigma ^t} = \sqrt {\frac{{{m_t}}}{{{\eta _t} \cdot \sum\limits_{t'} {{m_{t'}}} }}} \cdot {\widetilde \sigma ^t}.$

(13)

For these standard deviations ${\sigma ^t}$, the expression (9) takes the form

$\sum\limits_{t=1}^{T}{{{\left( w_{t}^{'} \right)}^{2}}\cdot }\left\| {{F}^{t}}\left( x \right)-{{y}^{t}} \right\|,$

(14)

where we denoted

${{\left( w_{t}^{'} \right)}^{2}}\underset{=}{\mathop{\text{def}}}\,\sum\limits_{{{t}'}}{{{m}_{{{t}'}}}}\cdot \frac{{{\eta }_{t}}}{{{\left( {{\widetilde{\sigma }}^{t}} \right)}^{2}}\cdot {{m}_{t}}}.$

(15)

From the formula (11), we conclude that $w_t^2 = \frac{{{\eta _t}}}{{{{\left( {{{\widetilde \sigma }^t}} \right)}^2} \cdot {m_t}}}$ and thus, that the formula (15) takes the form ${{\left( w_{t}^{'} \right)}^{2}}=C\cdot w_{t}^{2}$, where $C\mathop {{\rm{def}}}\limits_ = \sum\limits_{t'} {{m_{t'}}}$. Thus, the expression (14) takes an equivalent form

$C \cdot \sum\limits_{t = 1}^T {w_t^2 \cdot } \left\| {{F^t}\left( x \right) - {y^t}} \right\| ,$

(16)

and the minimization of this expression is indeed equivalent to minimizing the expression (8).

The equivalence is proven.

Comment. The above analysis holds when we know the approximate values ${{{\widetilde \sigma }^t}}$ of the corresponding accuracies ${{\sigma ^t}}$, but we know no guaranteed bounds on these accuracies. In some practical situations, in addition to the approximate values ${{{\widetilde \sigma }^t}}$, we also know the bounds ${{{\underline \sigma }^t}}$ and ${{{\overline \sigma }^t}}$, for which ${{{\underline \sigma }^t}}$ ≤ ${\sigma ^t}$ ≤ ${{{\overline \sigma }^t}}$. In this case, instead of all possible values ${{\eta _t}}$ of the corresponding influence parameter, we only need to consider possible values - and we can use the above formulas relating ${{\eta _t}}$ with ${\sigma ^t}$ to transform bounds on ${\sigma ^t}$ into the corresponding bounds on ${{\eta _t}}$.

2.7. General Case: Resulting Optimization Problem

So, we arrive at the following equivalent reformulation of our problem: for all possible combination of influence factors ${{\eta _t}}$ > 0 for which $\sum\limits_t {{\eta _t}}$ = 1, we compute the weights

${w_t} = \sqrt {\frac{{{\eta _t}}}{{{{\left( {{{\widetilde \sigma }^t}} \right)}^2} \cdot {m_t}}}} ,$

and then minimize the expression

$\sum\limits_{t = 1}^T {w_t^2 \cdot } {\left\| {{F^t}\left( x \right) - {y^t}} \right\|^2}$

under the corresponding constraints g(x) ≥ 0.

This minimization problem can be reformulated as

$\mathop {min}\limits_x {\left\| {F\left( x \right) - y} \right\|^2},$

(17)

where

$F\left( x \right) = W\left( {\begin{array}{*{20}{c}} {{F^1}\left( x \right)}\\ {{F^2}\left( x \right)}\\ \ldots \\ {{F^t}\left( x \right)}\\ \ldots \\ {{F^T}\left( x \right)} \end{array}} \right) \in {{\rm{R}}^m}, y = W\left( {\begin{array}{*{20}{c}} {{y^1}}\\ {{y^2}}\\ \ldots \\ {{y^t}}\\ \ldots \\ {{y^T}} \end{array}} \right) \in {{\rm{R}}^n}$

and W = diag(w_t) is a diagonal matrix whose elements will be called weights.

In particular, when we reconstruct the values of shear velocities from Receiver Functions (RF), Surface Waves (SW), and Travel Times (TT), the corresponding minimize functional J(x) takes the form

$J = w_{RF}^2{\left\| {{F^{RF}}\left( x \right) - {y^{RF}}} \right\|^2} + w_{SW}^2{\left\| {{F^{SW}}\left( x \right) - {y^{SW}}} \right\|^2} + w_{TT}^2{\left\| {{F^{TT}}\left( x \right) - {y^{TT}}} \right\|^2},$

i.e., equivalently, form (17), with

$F\left( x \right) = W\left( {\begin{array}{*{20}{c}} {{F^{SW}}\left( x \right)}\\ {{F^{RF}}\left( x \right)}\\ {{F^{TT}}\left( x \right)} \end{array}} \right) \in {{\rm{R}}^m}, y = W\left( {\begin{array}{*{20}{c}} {{y^{SW}}}\\ {{y^{RF}}}\\ {{y^{TT}}} \end{array}} \right) \in {{\rm{R}}^n}$

and

$W = diag\left( {{w_i}} \right), {w_i} = \sqrt {\frac{{{\eta _1}}}{{{{\left( {{{\widetilde \sigma }_i}} \right)}^2}p}}} , i = 1, \ldots , p, {w_i} = \sqrt {\frac{{{\eta _2}}}{{{{\left( {{{\widetilde \sigma }_i}} \right)}^2}q}}} , i = p + 1, \ldots , p + q, {w_i} = \sqrt {\frac{{1 - \left( {{\eta _1} + {\eta _2}} \right)}}{{{{\left( {{{\widetilde \sigma }_i}} \right)}^2}r}}} i = p + q + 1, \ldots , p + q + r,$

(18)

${{{\widetilde \sigma }_i}}$ is the approximate standard deviation of each point, and p, q, and r are the number of RF, SW, and TT observations (Sosa et al. 2013).

2.8. Relation to Multi-Objective Optimization

When we have observations of only one type t, then, to find the corresponding model, we minimize the function ${\left\| {{F^t}\left( x \right) - {y^t}} \right\|^2}$. Minimizing this function is equivalent to minimizing the expression

${f_t}\left( x \right)\mathop {{\rm{def}}}\limits_ = \frac{1}{{{{\left( {{{\widetilde \sigma }^t}} \right)}^2} \cdot {m_t}}} \cdot {\left\| {{F^t}\left( x \right) - {y_t}} \right\|^2}.$

In situations when we have observations of different type, and when we only know the approximate values ${{{\widetilde \sigma }^t}}$ of the corresponding accuracies, we need to minimize expressions (8), i.e., equivalently, expressions of the type

$\sum\limits_t {{\eta _t}} \cdot {f_t}\left( x \right).$

(19)

corresponding to all possible combinations ${\eta _t}$ > 0 for which $\sum\limits_t {{\eta _t}}$ = 1.

It is known that, under reasonable conditions, the resulting set of solutions can be described in terms of the corresponding multi-objective optimization problem (MOP), namely, the problem of optimizing

$f\left( x \right)\mathop {{\rm{def}}}\limits_ = \left( {{f_1}\left( x \right), {f_2}\left( x \right), \ldots {f_t}\left( x \right), \ldots {f_T}\left( x \right)} \right).$

For solving multi-objective problems, a natural idea is to generate the Pareto optimal set (also known as Pareto front), i.e., the set of all the values x for which it is not possible to improve all the criteria f_i(x). In precise terms, the Pareto optimal set P(x) is defined as

$P\left( x \right)=\{x\in \Omega :$${x}'\in \Omega \text{ }\left( f\left( {{x}'} \right)<f\left( x \right) \right),$

(20)

where $\Omega$ is the set of all possible solutions that satisfy the corresponding constraints, and f (x') < f (x) means that

$\forall t\left( {{f}_{t}}\left( x' \right)\le {{f}_{t}}\left( x \right) \right)\And \exists t\left( {{f}_{t}}\left( x' \right)<{{f}_{t}}\left( x \right) \right).$

(21)

Under reasonable conditions, elements of the Pareto set can be obtained by finding the minima of all the functions (19) corresponding to all possible weights ${{\eta }_{t}}$ adding to 1, and, vice versa, each such minimum is an element of the Pareto set P(x).

In these terms, we can say that what we want in the general case, when we only know the approximate values of the corresponding accuracies, is to find the Pareto set of the multi-objective problem in which we minimize the criteria

${{f}_{t}}\left( x \right)=\text{const}\cdot {{\left\| {{F}^{t}}\left( x \right)-{{y}_{t}} \right\|}^{2}}$

corresponding to measurements of different types t.

In particular, in our geophysical example, we want to minimize the three criteria ${{f}_{FR}}\left( x \right)=\text{const}\cdot {{\left\| {{F}^{RF}}\left( x \right)-{{y}^{RF}} \right\|}^{2}}$, ${{f}_{SW}}\left( x \right)=\text{const}\cdot {{\left\| {{F}^{SW}}\left( x \right)-{{y}^{SW}} \right\|}^{2}}$, and ${{f}_{TT}}\left( x \right)=\text{const}\cdot {{\left\| {{F}^{TT}}\left( x \right)-{{y}^{TT}} \right\|}^{2}}$.

2.9. How to Generate a “Typical” Solution

When we have data of several types, and we only know approximate values of the corresponding accuracies, our recommendation is to generate solutions corresponding to all possible combinations of actual accuracies. The number of such solutions is huge, and meaningfully analyzing all these solutions is difficult. It is therefore desirable to select, among these solutions, a solution which is, in some sense, typical.

The expectation is that, in general, this “typical” solution will only have features that all other solutions have. Thus, when we look for features common for all possible solutions, a good idea is to first analyze this typical solution, and then to check whether the features that we found on this solution are indeed present in all other solutions as well.

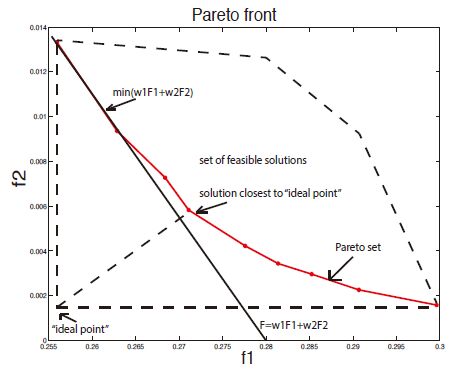
In multi-objective optimization, there are several possible ways of generating such a “typical” solution; see, e.g., (Sambridge 1999a, Sambridge 1999b, Kozlovskaya 2000). For example, once we find all solutions x corresponding to different combinations, then, for each criterion ft, we can find the smallest value $f_{t}^{\min }$ and the largest value $f_{t}^{\max }$. The smallest values form an ideal point ${{f}^{\min }}=\left( f_{1}^{\min }, \ldots , f_{t}^{\min }, \ldots f_{T}^{\min } \right)$. We then select a solution x which is the closest to this ideal point. Specifically, we normalize each differences ${{f}_{t}}\left( x \right)-f_{t}^{\min }\left( x \right)$ to the interval (0, 1) by dividing it by $f_{t}^{\max } - f_{t}^{\min }$, and then we minimize the corresponding normalized distance. In other terms, we select a solution x for which the distance

${{d}^{2}}\left( {{f}^{\min }}, f\left( x \right) \right)=\sum\limits_{t=1}^{T}{{{\left( \frac{{{f}_{t}}\left( x \right)-f_{t}^{\min }\left( x \right)}{f_{t}^{\max }\left( x \right)-f_{t}^{\min }\left( x \right)} \right)}^{2}}}$

(22)

is the smallest possible.

3. Solving the Corresponding Constraint Optimization Problems

In the proposed approach, we need to solve several minimization problems, corresponding to different combinations of the influence parameters ${{\eta }_{t}}$. For each such combination, we need to find the value ${{\left\| F\left( x \right)-y \right\|}^{2}}$ under the constraint g(x) ≥ 0. Let us show how to solve the corresponding constraint optimization problems.

3.1. Linearization

In most practical situations, we know the approximate values ${{{\bar{x}}}_{1}}$ of the corresponding quantities x, i.e., values for which $x\approx {{{\bar{x}}}_{0}}$. Since these values are close to each other, the difference $x - {{{\bar{x}}}_{0}}$ is small and thus, we can expand the functions F(x) and g(x) into Taylor series in this difference and safely ignore terms which are quadratic (or higher order), and only keep the first order Taylor approximation. Once we solve this first-order approximation problem, we get a better approximation ${{{\bar{x}}}_{1}}$. We can use this approximation as the basis of a new linearization and get an even more accurate approximation, etc.

On each of these iterations, we start with an approximate model ${{{\bar{x}}}_{k}}$, and then we use the first order Taylor approximation of the operators F and g around ${{{\bar{x}}}_{k}}$:

$F\left( x \right)\approx F\left( {{{\bar{x}}}_{k}} \right)+F'\left( {{{\bar{x}}}_{k}} \right)\Delta x=F\left( {{{\bar{x}}}_{k}} \right)+F'\left( {{{\bar{x}}}_{k}} \right)\left( x-{{{\bar{x}}}_{k}} \right),$

(23)

$g\left( x \right)\approx g\left( {{{\bar{x}}}_{k}} \right)+\nabla {{g}^{T}}\left( {{{\bar{x}}}_{k}} \right)\left( x-{{{\bar{x}}}_{k}} \right),$

(24)

where $F'\left( {{{\bar{x}}}_{k}} \right)$ is the matrix formed by the partial derivatives of F and $\nabla g$ is the matrix formed by the partial derivatives of different components of g(x).

Substituting the expressions (23) and (24) in the corresponding constraint optimization problem, we get the following linearized constraint optimization problem:

$\begin{align} & \underset{x}{\mathop{min}}\, \frac{1}{2}{{\left\| F'\left( {{{\bar{x}}}_{k}} \right)x+r\left( {{{\bar{x}}}_{k}} \right) \right\|}^{2}} \\ & \text{s}\text{.t}\text{.} g\left( {{{\bar{x}}}_{k}} \right)+\nabla {{g}^{T}}\left( {{{\bar{x}}}_{k}} \right)\left( x-{{{\bar{x}}}_{k}} \right)\ge 0, \\ \end{align}$

(25)

where $r\left( {{{\bar{x}}}_{k}} \right)\underset{=}{\mathop{\text{def}}}\, F\left( {{{\bar{x}}}_{k}} \right)-y-F'\left( {{{\bar{x}}}_{k}} \right){{{\bar{x}}}_{k}}$.

3.2. Primal Dual Interior-Point Method

To solve the linearized problem (25), we will use the Primal Dual Interior-Point method; see, e.g., (Sosa et al. 2013, Nocedal and Wright 2006). To use this method, we first reformulate our problem in a standard form as follows:

$\begin{matrix} \underset{x}{\mathop{min}}\, \frac{1}{2}{{\left\| F'\left( {{{\bar{x}}}_{k}} \right)x+r\left( {{{\bar{x}}}_{k}} \right) \right\|}^{2}} \\ \text{s}\text{.t}\text{.} g\left( {{{\bar{x}}}_{k}} \right)+\nabla {{g}^{T}}\left( {{{\bar{x}}}_{k}} \right)\left( x-{{{\bar{x}}}_{k}} \right)-s=0 \\ s\ge 0 \\ \end{matrix}$

(26)

where components of s 2 R2n are called slack variables.

Then we define the Lagrange function associated to problem (26) as:

$l\left( {{{\bar{x}}}_{k}}, z, s, w \right)=\frac{1}{2}{{\left\| F'\left( {{{\bar{x}}}_{k}} \right)x+r\left( {{{\bar{x}}}_{k}} \right) \right\|}^{2}}-{{\left( g\left( {{{\bar{x}}}_{k}} \right)++\nabla {{g}^{T}}\left( {{{\bar{x}}}_{k}} \right)\left( x-{{{\bar{x}}}_{k}} \right)-s \right)}^{T}}z-{{s}^{T}}w$

(27)

with the Lagrangian multipliers $z, w\in {{\text{R}}^{2n}}$, $z, w\ge 0$. For a given perturbation parameter μ > 0, the perturbed Karush-Kuhn-Tucker (KKT) or necessary conditions are given by:

$\hat{F}\left( {{{\bar{x}}}_{k}}, z, s, w \right)=\left( \begin{matrix} F'{{\left( {{{\bar{x}}}_{k}} \right)}^{T}}\left( F'\left( {{{\bar{x}}}_{k}} \right)x+r\left( {{{\bar{x}}}_{k}} \right) \right)-\nabla {{g}^{T}}\left( {{{\bar{x}}}_{k}} \right)z \\ g\left( {{{\bar{x}}}_{k}} \right)+\nabla {{g}^{T}}\left( {{{\bar{x}}}_{k}} \right)\left( x-{{{\bar{x}}}_{k}} \right)-s \\ z-w \\ SWe-\mu e \\ \end{matrix} \right)=0,$

(28)

where

$\hat{F}:{{\text{R}}^{n+2n+2n}}\to {{\text{R}}^{n+2n+2n}} S=diag\left( {{s}_{1}}, \ldots , {{s}_{2n}} \right), W=diag\left( {{w}_{1}}, \ldots , {{w}_{2n}} \right)$

(29)

and $e=\left( 1, \ldots , 1 \right)\in {{\text{R}}^{2n}}$.

The formula (28) implies, in particular, that z - w = 0, and thus z = w. Hence the perturbed KKT system (28) is rewritten as

$\hat{F}\left( x, z, s, w \right)=\left( \begin{matrix} F'{{\left( {{{\bar{x}}}_{k}} \right)}^{T}}\left( F'\left( {{{\bar{x}}}_{k}} \right)x+r\left( {{{\bar{x}}}_{k}} \right) \right)-\nabla {{g}^{T}}\left( {{{\bar{x}}}_{k}} \right)z \\ g\left( {{{\bar{x}}}_{k}} \right)-s \\ SWe-\mu e \\ \end{matrix} \right)=0;$

(30)

thus the Jacobian associated to (30) is then computed as

$F'\left( \begin{matrix} x \\ z \\ s \\ \end{matrix} \right)=\left[\begin{matrix} F'{{\left( {{{\bar{x}}}_{k}} \right)}^{T}}F'\left( {{{\bar{x}}}_{k}} \right) & -\nabla {{g}^{T}}\left( {{{\bar{x}}}_{k}} \right) & {{0}_{nxn}} \\ \nabla g\left( {{{\bar{x}}}_{k}} \right) & {{0}_{nxm}} & -{{I}_{mxm}} \\ {{0}_{mxn}} & S & Z \\ \end{matrix} \right]\left[\begin{matrix} \Delta x \\ \Delta z \\ \Delta s \\ \end{matrix} \right]=-\left[\begin{matrix} {{\nabla }_{x}}l\left( x, z, s \right) \\ g\left( {{{\bar{x}}}_{k}} \right)-s \\ SZe-\mu e \\ \end{matrix} \right]$

The system (31) can be simplified further by eliminating the third block of equations as follows. From the last block of equation in (31), we have

$S\Delta z+Z\Delta s=-SZe+\mu e,$

therefore

$\begin{matrix} Z\Delta s=-SZe+\mu e-S\Delta z \\ \Delta s=-s+\mu {{Z}^{-1}}e-{{Z}^{-1}}S\Delta z, \\ \end{matrix}$

and then

$\begin{matrix} \nabla {{g}^{T}}\left( {{{\bar{x}}}_{k}} \right)\Delta x-\Delta s=\nabla {{g}^{T}}\left( {{{\bar{x}}}_{k}} \right)\Delta x+s-\mu {{Z}^{-1}}e+{{Z}^{-1}}e+{{Z}^{-1}}S\Delta z=-\nabla {{g}^{T}}\left( {{{\bar{x}}}_{k}} \right)x+s \\ \nabla {{g}^{T}}\left( {{{\bar{x}}}_{k}} \right)\Delta x+{{Z}^{-1}}S\Delta z=\mu {{Z}^{-1}}e-g\left( {{{\bar{x}}}_{k}} \right) \\ \end{matrix}$

which allow us to write the reduced linear system

$\left[\begin{matrix} -F'{{\left( {{{\bar{x}}}_{k}} \right)}^{T}}F'\left( {{{\bar{x}}}_{k}} \right) & \nabla {{g}^{T}}\left( {{{\bar{x}}}_{k}} \right) \\ \nabla g\left( {{{\bar{x}}}_{k}} \right) & {{Z}^{-1}}S \\ \end{matrix} \right]\left[\begin{matrix} \Delta x \\ \Delta z \\ \end{matrix} \right]=\left[\begin{matrix} {{\nabla }_{x}}l\left( x, z, s \right) \\ {{Z}^{-1}}\mu e-g\left( {{{\bar{x}}}_{k}} \right) \\ \end{matrix} \right]$

4. Geophysical Datasets

4.1. Receiver Functions

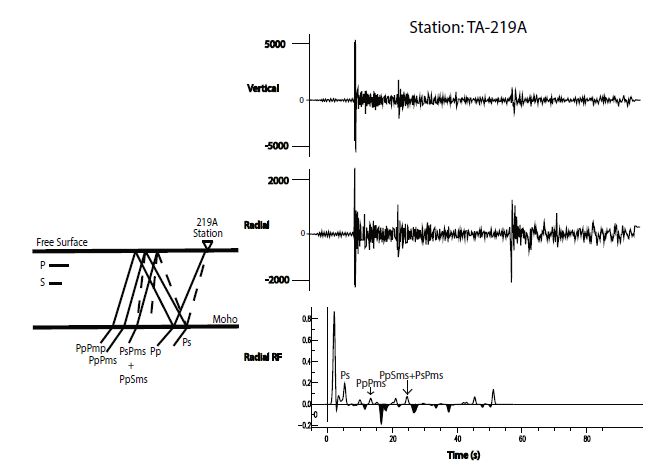
A receiver function is simply a time series representation of the Earth’s response relative to an incoming P-wave propagating near a recording station. A representation of a receiver function is indicated in figure 2, with different incoming P-to-S converted waves and a time series representation of the Earth response underneath a seismic station. Positive or negative spike amplitudes represent positive or negative seismic velocity contrast. A receiver function technique can model the structure of the earth by using seismograms from three component (vertical, north, and east) seismic stations from teleseismic earthquakes. The receiver function technique takes advantage of the fact that part of the energy of seismic P waves is converted into S waves at discontinuities along the ray path (Bashir et al. 2011, Dzierma et al. 2011), and has been utilized in many studies; see, e.g., (Wilson et al. 2005, Wilson and Aster 2005, Bailey et al. 2012, Hansen et al. 2013). For data collection and processing, we use the Standing Order for Data (SOD) (Owens et al. 2004, Bailey et al. 2012) to request three component seismograms for P-wave arrivals and for events with a minimum magnitude 5.5, depth in the range of 1-600 km, and an epicentral distance ranging from 30° to 95°; see, e.g., (Bailey et al. 2012).

Receiver functions were first applied in the late 1970s at solitary stations to obtain local onedimensional structural estimates (Langston 1981). Since then, there was an increase in the number of stations deployed seismic experiments. It is now possible to generate detailed two or three-dimensional images of structures, such as the Moho and upper mantle transition zone discontinuities near 410 km and 670 km depth; see, e.g., (Wilson 2003).

Receiver functions are derived using deconvolution (Liggoria and Ammon 1991), a mathematical method used to filter a signal and isolate the superimposed harmonic waves. Specially, receiver functions are calculated by deconvolving the vertical component of a seismogram from the radial component, resulting in the identification of converted phases where there is an impedance contrast (crustal-mantle boundary) (Shearer, 2009).

4.2. Surface Wave Dispersion

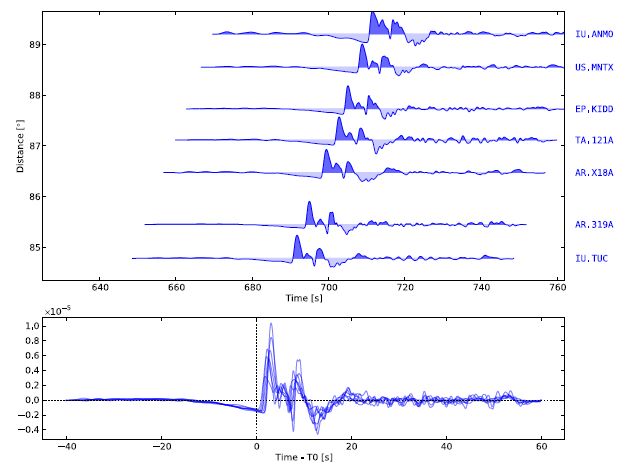
Surface waves in general differ from body waves in many respects: they travel slower, lower frequencies, largest amplitudes, and their velocities are in fact dependent on frequency (Shearer 2009). The surface wave velocities vary with respect to depth being sampled by each period of the surface wave. The sampling by each period of the surface wave is known as dispersion (Shearer 2009). Valuable information can be inferred by measuring surface wave dispersion because it will allow you to be able to better understand the Earth’s crustal and mantle velocity structure (Laske Masters and Reif 2000, Obrebski et al. 2010, Sosa et al. 2013). In particular, Love and Rayleigh wave group dispersion observations generally account for average velocity structure as a function of depth (Julia et al. 2000, Maceira and Ammon 2009). The dispersion curves for surface waves are extracted from station records of three component seismograms for different frequencies and distances, by using reduction algorithms that rely on spectral analysis techniques. The important fact here is that, based on Rayleigh’s principle, surface wave velocities are more sensitive to S wave velocity, although they are also theoretically sensitive to P wave velocity and density. Figure 4 provides an example of teleseismic Rayleigh waveforms for the 12/01/2010 event. The Rayleigh’s principle states that the phase velocity perturbation, denoted by $\frac{\delta c}{c}$, can be viewed as a function of (K_α; K_β; K_ρ), the sensitivity coefficients for P wave velocity, S wave velocity and density, respectively, i.e.,

$\frac{\delta c\left( T \right)}{c\left( T \right)}=\int{\left( {{K}_{\alpha }}\frac{\delta \alpha \left( z \right)}{\alpha \left( z \right)}+{{K}_{\beta }}\frac{\delta \beta \left( z \right)}{\beta \left( z \right)}+{{K}_{\rho }}\frac{\delta \rho \left( z \right)}{\rho \left( z \right)} \right)}$

(31)

where T is the period and z is the depth. By investigating sensitivity function variation in depth, the relative contribution of each property to dispersion can be shown. This subject is beyond the scope of our work, thus we just mention here that such analysis allows geophysicists to show that the relative contribution of P wave velocity, and density to dispersion is smaller than the one for S wave velocity (Julia et al. 2000). That is, surface wave dispersion is much more sensitive with respect to S wave velocity, and therefore we have established the dependence of this data set on shear wave velocity.

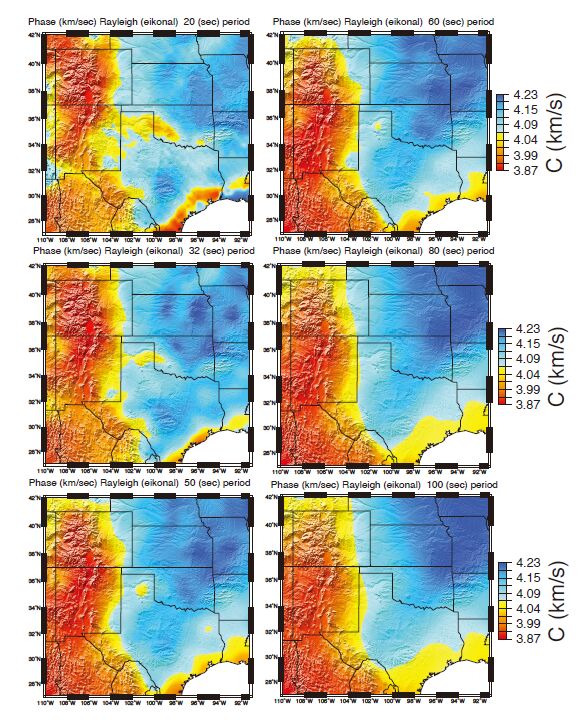
For this research, a Matlab-based software package - that automatically downloads, analyzes, and measures phase as well as amplitude of surface waves to generate surface-wave tomography maps - was used to construct figure 5 describing tomographic images of the Texas region. The Automated Surface-Wave Phase-Velocity Measuring System (ASWMS) was the matlab package developed by (Jin and Gaherty, 2014) that developed this automated cross-correlation based method to generate surfacewave tomography of the entire U.S. The ASWMS tool was used to see what geological signatures that we can resolve using surface wave phase data.

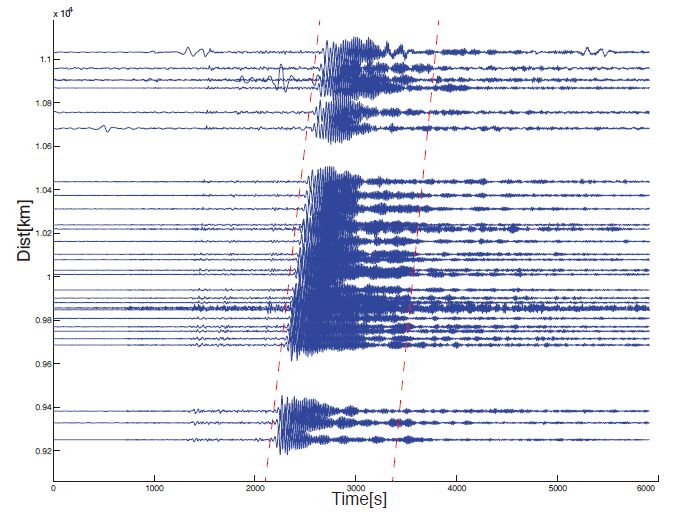
4.3. Delay Travel Times

For this research, we used TauP toolkit ($\tau$(p)) and Antelope (BRTTO) database program to acquire the delayed travel times from the Array Network Facility (ANF) seismic catalog. Figure 6, shows an example of some of the delayed travel time data used for this study that were acquired from the ANF seismic catalog. The TauP toolkit program that we used to acquire the delayed travel times, uses the spherical Earth geometry into the computation. The TauP toolkit uses the relation of Snell’s law, according to which, for each ray k, the ratio $\frac{\sin {{i}_{kj}}}{{{x}_{kj}}}=\frac{\Delta {{T}_{k}}}{{{l}_{kj}}}$ remains constant along the k-th ray, i.e., does not depend on j. This ratio is known as the constant ray parameter, and is usually denoted by pk. We use this law to compute delayed travel times $\Delta {{T}_{k}}$ (i.e., components of the vector F^TT (x)):

$\Delta {{T}_{k}}=\sum\limits_{j=0}^{n}{\frac{{{h}_{j}}}{{{x}_{kj}}\cos \left( {{i}_{kj}} \right)}},$

(32)

where h_j is the thickness of the j-th layer.

By using the Snell’s law as mentioned earlier, the incidence angle ik j can be rewritten as:

${{i}_{kj}}={{\sin }^{-1}}\left( {{p}_{k}}{{x}_{j}} \right)$

(33)

Equation (32) can be rewritten as

$\Delta {{T}_{k}}=\sum\limits_{j=0}^{n}{\frac{{{h}_{j}}}{{{x}_{kj}}\cos \left( {{i}_{kj}} \right)}}=\sum\limits_{j=0}^{n}{{{h}_{j}}{{\left( {{x}_{kj}}\cos \left( {{\sin }^{-1}}\left( {{p}_{k}}{{x}_{kj}} \right) \right) \right)}^{-1}}}$

(34)

Using Snell’s law and rewriting equation (32), we obtained the partial derivatives which are needed to use the primal dual interior point method mentioned earlier:

$\frac{\partial \Delta {{T}_{k}}}{\partial {{x}_{kj}}}=\frac{-{{h}_{j}}}{x_{kj}^{2}\cos {{\left( {{\sin }^{-1}}\left( {{p}_{k}}{{x}_{kj}} \right) \right)}^{2}}}\left( \cos \left( {{\sin }^{-1}}\left( {{p}_{k}}{{x}_{kj}} \right) \right)-\frac{{{\left( {{p}_{k}}{{x}_{kj}} \right)}^{2}}}{\sqrt{1-{{\left( {{p}_{k}}{{x}_{kj}} \right)}^{2}}}} \right)$

(35)

When ray paths between the source and the receiver are short enough, Earth’s curvature is known to be negligible, which provides us with the importance of utilizing equation (35) for our computation of partial derivatives of T.

5. Results and Discussion

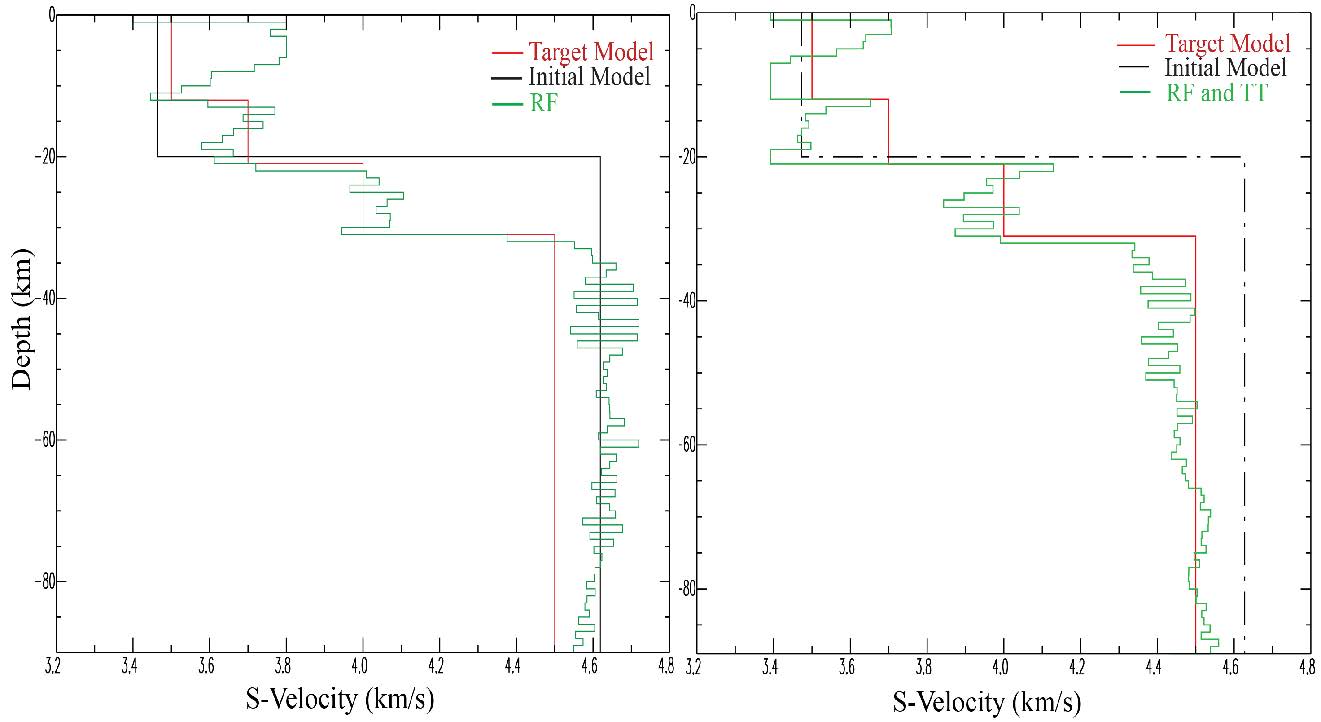
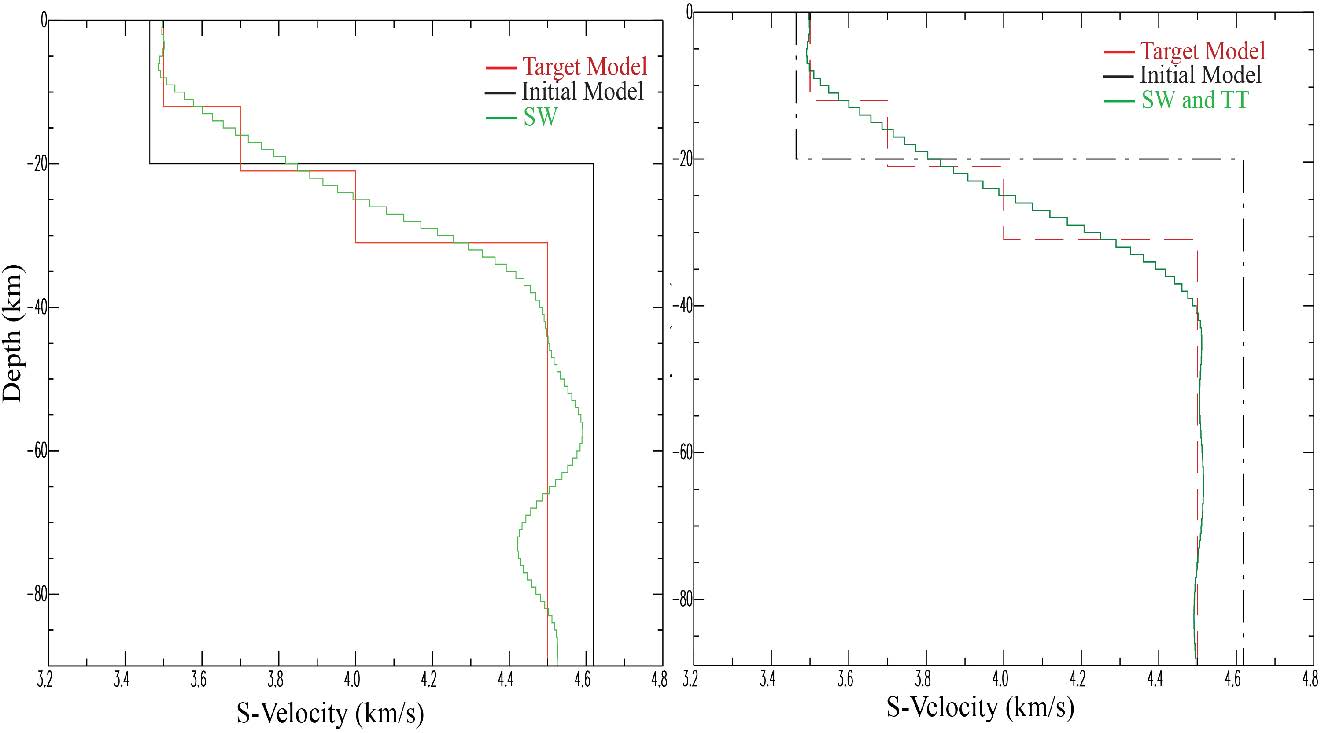
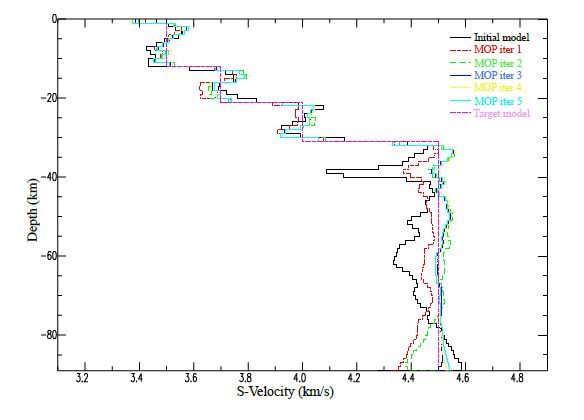
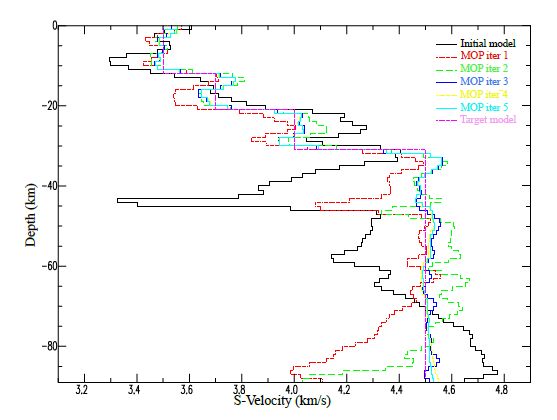
Based on the joint inversion results using multiple geophysical datasets, the compatiability of the datasets provides better estimates of the target model based on numerical experiments with the datasets and the synthetic rift model. In order to illustrate how receiver functions and surface wave dispersion velocities complement each other, we present in figures 6-8 the inversion results for the data sets created from the rift velocity model.

In figure 6, the joint inversion of both RFs and TT data sets gives a better approximation to the target model as expected based on the compatiablity between the two datasets. The single inversion of receiver functions (left top) identifies the velocity interfaces (fig 6), while single inversion of surface waves (fig 7) gives information on the average velocities at different depths. For figure 7, the joint inversion of SWs and TT also provides a better approximation of the target model indicated in red.

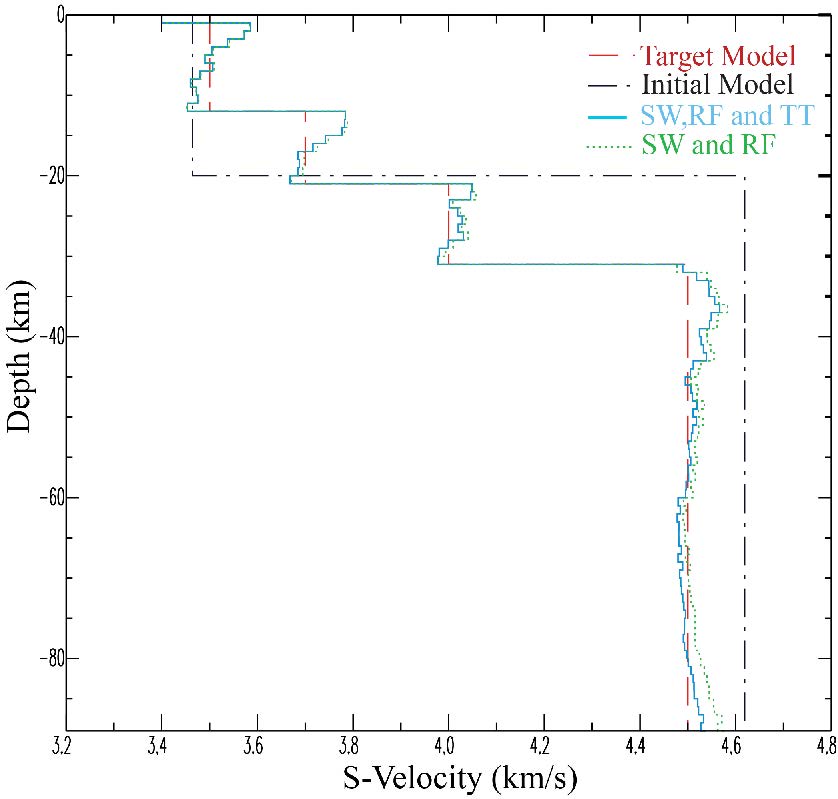
The joint inversion of RFs, SWs, and TT provides more accuracy and compatiability when performing joint inversion of the three geophysical datasets as shown in figure 8.

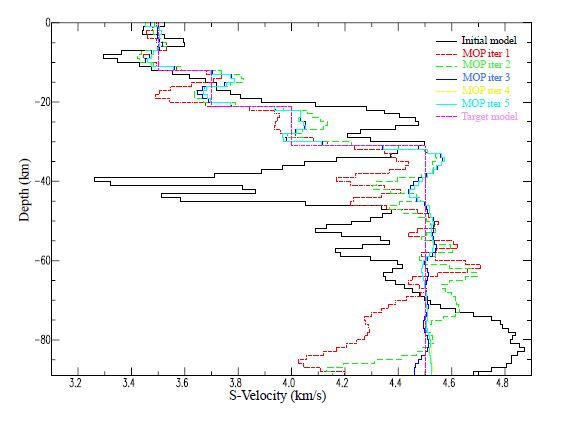
A synthetic rift velocity model that we developed was used as our initial test for the MOP joint inversion scheme. For the MOP joint inversion scheme, a comparison was done with the rift velocity model and the initial velocity test model. The synthetic rift model was the best velocity model used for this joint inversion scheme. Different synthetic Earth velocity models were used but overall, the rift model was the best. Numerous test were performed to test the compatiablity and complementary nature of the multiple geophysical datasets based from the results in figures 9-11. The algorithm used to perform the joint inversion of the multiple geophysical datasets using the multi-objective joint inversion scheme was written in FORTRAN 77 and coupled with a C code that performs the Multi- Objective Optimization method, based on the work of [25].

6. Conclusion

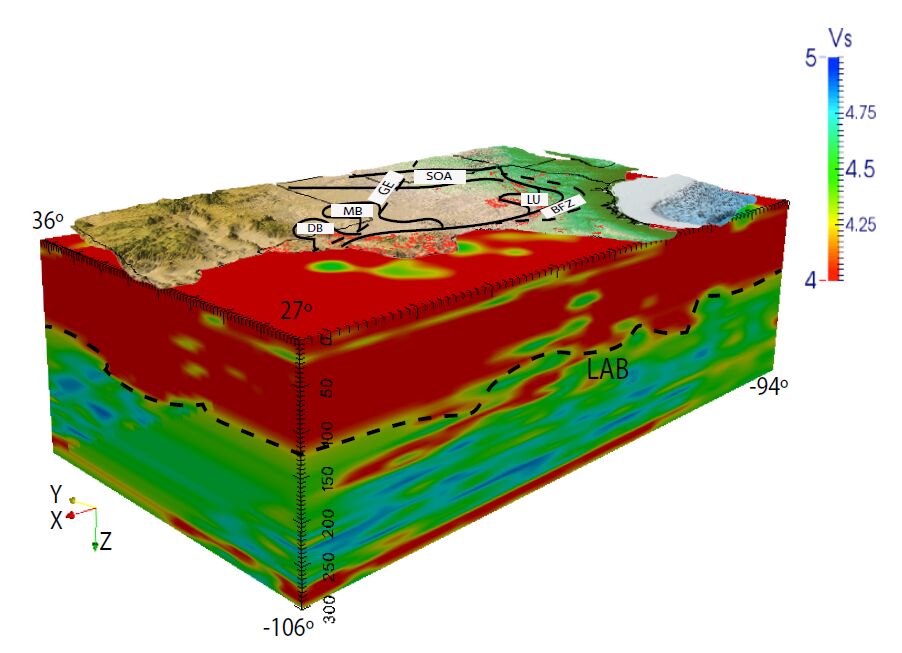
We apply an inversion scheme that expands a joint-inversion constraint least-squares (LSQ) algorithm used to characterize a one-dimensional Earth’s structure. We utilize the Multi-Objective Optimization technique to perform joint inversion of multiple data sets (receiver functions, surface wave dispersion, and travel times) to develop 3-D shear wave models like in figure 12 (e.g., Thompson et al., submitted for publication). By jointly inverting these three geophysical data sets, we improve the model’s accuracy. In the ideal situation when we know the relative accuracy of different datasets, we can formulate the joint inversion problem as a (single) least-square optimization problem. In practice, however, we only know approximate values of these accuracies; so, for inversion, we use the Multi-Objective Optimization Problem (MOP) approach. Different combination of weights were incorporated in the MOP inversion scheme in order to map the Pareto Set (Solution Space) corresponding to receiver functions, surface wave dispersion measurements, and travel times. From the Pareto Set, the MOP technique performs a direct search method that selects the most feasible solution from a set of alternative solutions from the model space (Sambridge 1999a, Sambridge 1999b, Kozlovskaya 2000). For future work, we plan to incorporate gravity into our inversion scheme to obtain a more constrained Earth structure and to better determine physical properties of the Earth structure.

Acknowledgments

We would like to take the time to thank the computational science, mathematical science, and computer science departments from University of Texas at El Paso (UTEP). We would also like to thank Ezer Patlan, and Dr. Anibal Sosa for all of their contributions to this work. This work was sponsored by the NSF CREST under Grant Cybershare HRD-0734825.