On a dependent risk model perturbed by mixed-exponential jump-diffusion processes

1.   Introduction

The increased availability of a large amount of data allows researchers to model and forecast more accurately in many fields (e.g., see Choi and Varian, 2012; Varian, 2014; Varian and Scott, 2014; Einav and Levin, 2014). However, the main issues when dealing with high-dimensional models for large datasets are over-parametrization, over-fitting, and high out-of-sample forecasting errors (Granger, 1998). Various solutions have been proposed, such as regularization (Zou and Hastie, 2005), stochastic search variable selection (George et al., 2008), graphical models (Ahelgebey et al., 2016a, 2016b), and random projections (Koop et al., 2017; Casarin and Veggente, 2021). This paper considers factor models (Stock and Watson, 2002, 2004, 2005, 2012, 2014; Banbura et al., 2010; Casarin et al, 2020; Billio et al., 2022). Relevant information is summarized through a limited number of factors, describing the overall economic conditions and providing accurate forecasts of the variables of interest.

It has been proved, that factor model estimates can be heavily affected by outliers: data points that differ significantly from other observations in the sample. An outlier may be due to variability in the measurement or significant experimental errors; the latter are sometimes excluded from the data set. After the 2009 crisis and the COVID-19 pandemic event, the treatment of outliers attracted the attention of both researchers and the institutes of official statistics, which provided some guidelines on monitoring the effects of outliers when using their data (e.g., see Eurostat, 2020). In this paper we follow Artis et al. (2005), Croux et al. (2003), Bai et al. (2022), Fan et al. (2021) and apply robust estimation methods to factor models to limit the effects of the outliers. We contribute to the robust factor literature by comparing alternative robust factor models in terms of forecasting performances on a set of variables which are central to the economic analysis. Our database includes the 2009 crisis and the beginning of COVID-19 pandemic in March 2020 and consider as a last data January 2021; the pandemic is potentially the most important source of outliers, and its effects on the economic systems have been extensively investigated in some recent studies (Fabeil et al., 2020; Fernandes, 2020; McKibbin and Vines, 2020; McKibbin and Roshen, 2021; Liu, 2021). We shall notice that the amount of sample information is not large enough to estimate forecasting models with structural breaks since adopting them implies that the current model is estimated only using data observed since the most recent break. Similarly, it is not possible to test for a break and compare the two models for the period before and after the pandemic since the spread of contagion and its effects did not yet come to an end. This paper provides an alternative solution and shows that samples from the pandemic period have some information content which can still be used to estimate models without breaks provided a proper inference technique, such as robust inference for outliers, is applied.

The structure of the paper is as follows. Section 2 presents some background on robust inference for outliers. Section 3 introduces standard factors model and the two methodologies used to treat the outliers. Section 4 provides a data description and the empirical results obtained with robust inference methods for factor models. Section 5 concludes the chapter.

2.   Background on robust estimation

The true nature of outliers can be very elusive and dealing with data affected by outliers poses some challenges. There is no unanimous definition for what an outlier is. Outliers could be atypical samples that have an unusually large influence on the estimated model parameters. Outliers could also be perfectly valid samples from the same distribution as the rest of the data that happen to be small-probability instances. Alternatively, outliers could be samples drawn from a different model, and therefore they will likely not be consistent with the model derived from the rest of the data. There is no way to tell which is the case for a particular "outlying" sample point, nevertheless some techniques can be applied to detect outliers. A standard procedure makes use of the linear projection of the dependent variable into the linear space of covariates, the hat matrix of the data. The diagonal of the hat matrix is used to detect outlying observations that may have an impact on the inference. Usually, outliers are excluded from the dataset when estimating the model (data-trimming). See, for example Davidson and McKinnon (2004). In this paper, we compare trimming with two alternative approaches.

The first approach is based on Mahalanobis distances and can applied for detection and robust estimation. We consider robust estimators of multivariate location and scatter computed from the explanatory variables. Many methods for estimating multivariate location and scatter break down in the presence of $T/(n+1)$ outliers, where $T$ is the number of observations and $n$ is the number of variables, as was pointed out by Donoho (1982). For the breakdown value of the multivariate F-estimators of Maronna (1976), see Hampel et al. (1986). In the meantime, several positive breakdown estimators of multivariate location and scatter have been proposed. The Minimum Covariance Determinant (MCD), a highly robust estimator of multivariate location and scatter (Rousseeuw, 1984) which uses only the observations whose covariance matrix has the lowest determinant, was proposed by Rousseeuw and Leroy (1987). Consistency and asymptotic normality of the MCD estimator has been shown by Butler et al. (1993) and Cator and Lopuhaa (2010), whereas has been demonstrated that MVE (Minimum Volume Ellipsoid) has a lower convergence rate (Davies, 1992). The MCD has a bounded influence function (Croux and Haesbroeck, 1999) and it has the highest possible breakdown value (i.e., 50%) when the number of observations used is $⌊\left(T+n+1\right)/2⌋$ (Lopuha and Rousseeuw, 1991). In addition to being highly resistant to outliers, the MCD is affine equivariant, i.e., the estimates behave properly under affine transformations of the data. Although the MCD was already introduced in 1984, its practical use only became feasible since the introduction of the computationally efficient Fast MCD (FMCD) algorithm of Rousseeuw and Van Driessen (1999), and some extensions have been determined (Hubert et al., 2017); in this paper we follow FMCD technique. MCD have been successfully applied in many fields such as finance and econometrics (Gambacciani & Paolella, 2017; Orhan et al., 2001), quality control (Jensen et al., 2007), geophysics (Neykov, et al., 2007), geochemistry (Filzmoser et al., 2005), image analysis (Vogler et al., 2007). MCD has been used for robust factor model estimation by Croux et al. (2003) and Filzmoser et al. (2003).

The second approach considered, is the Iteratively Reweighted Least Squares (IRLS) proposed in (De la Torre and Black, 2004), which relies on the residuals of the linear projection of the dependent variable on a space generated by a set of factors. The outliers are detected as those that have a large residual with respect to the identified subspace. A new subspace is estimated with the outliers downweighted, and this process is then repeated until the estimated model stabilizes. With this algorithm for every multivariate sample a weight is determined iteratively, reducing the weights related to the outliers until the procedure converge. This technique has been used for outliers' reduction, (Bergstrom and Edlund, 2014), outliers afflicted observations (Kargoll et al., 2018) and in forecasting (Mbamalu et al., 1993). Other applications are statistical estimation (Green, 1984), matrix rank minimization (Mohan and Fazel, 2012), and sparse matrix (Daubechies et al., 2009).

3.   Factor models

In the following, we introduce Factor Models (FM), data trimming and three approaches to outlier handling: ⅰ) standard FM (FM Std) where all data are included without any transformation; ⅱ) Fast Minimum Covariance Determinant methodology combined with FM (FM FMCD) and ⅲ) Iterated Reweighted Least Squares combined with Factors Model (FM IRLS).

In the empirical analysis, a Vector Autoregressive (VAR) model is used for predicting the factors, and according to Lütkepohl (2005), series without unit roots should be used when forecasting with VARs. To meet this requirement for the factors, we perform a unit root ADF test on all variables included in the factor analysis. If necessary, variables have been differentiated to obtain a stationary time series; after this step, we normalize the series and extract the factors. Thus, in the following we assume our $T\times n$ data matrix $X$ is covariance stationary with null mean and unitary standard deviation.

3.1.   A standard factor model

3.1.1.   Subheading

In this paper we use factor models, (see, e.g., Stock and Watson, 2002, 2004, 2005, 2012, 2014; Banbura et al., 2010; Banbura et al., 2014; Artis et al., 2005), with reduced number of factors (Bai and Ng, 2002). See Diebold (2003) and Stock and Watson (2009) for review of factor models.

Let ${X}_{t}$, t > 0, be a random process with ${X}_{t} = ({x}_{1t}, \dots, {x}_{nt}){'}$ a $(n\times 1)$ random vector. The time index $t$ represents months or quarters, and we assume the process is covariance stationary with null mean and a standard deviation equal to one. Latent factors extraction relies on the following decomposition:

where ${a}_{i}$ and ${\lambda }_{i},$ $i = 1, \dots, n$, are the $n$-dimensional eigenvectors and the eigenvalues in decreasing order, respectively. Let $A$ be an $(n\times n)$ orthonormal matrix with the normalized eigenvectors in the columns, also called factor loading matrix, then:

where $\mathrm{{{\Lambda}} }$ is a diagonal matrix with elements ${\lambda }_{i},$ $i = 1, \dots, n,$ on the main diagonal. The vector of $n$ factors ${F}_{n, t} = ({f}_{1, t}, \dots, {f}_{n, t}){'}$ is given by the linear transformation:

And ${f}_{k, t}$, $t > 0$ is the $k$-th factor. Let us denote with ${\mathrm{{{\Gamma}} }}_{n}$ the expectation of the external product of the factor, $E\left[{F}_{n, t}{F}_{n, t}^{\mathrm{'}}\right];$ then one obtains the following relationship between ${\mathrm{{{\Gamma}} }}_{n}$ and the eigenvector matrix $\mathrm{{{\Lambda}} }:$

Let ${F}_{k, t} = ({f}_{1, t}, \dots, {f}_{k, t}){'}$ be the collection of the first k factors at time t, with $k < n$, then:

where ${A}_{k}$ is the matrix containing the first k columns of $A$. Since the columns of $A$ are orthogonal, then ${A}_{k}^{\mathrm{'}}{A}_{k} = {I}_{k}.$ The first k factors capture the following proportion of the total variance:

The collection of factors ${F}_{k, t}$ is customarily called standard FM (FM Std).

3.2.   A robust factor model: the fast minimum covariance determinant estimator

In $n$-variate data, n > 2, it is difficult to detect outliers because one can no longer rely on visual inspection, nevertheless a set of summary statistics can be used. One of the statistics used in the literature is the Mahalanobis distance:

where ${x}_{t}$ is the $t$-th row of the data matrix X, $\widehat{\mu }$ is the estimator of the location, and $\widehat{\mathrm{{{\Sigma}} }}$ is the covariance matrix estimator. Using this distance, one obtains the classical tolerance ellipse defined as the set of $n$-dimensional points ${x}_{t}, t = 1, \dots, T$. Detecting outliers by means of the Mahalanobis distance no longer suffices for multiple outliers because of the masking effect, by which multiple outliers do not necessarily have large Mahalanobis distances (Hubert ET AL., 2017). We consider a robust estimator of multivariate location and scatter base on the notion of Minimum Covariance Determinant (MCD) (Rousseeuw, 1984; Rousseeuw and Leroy, 1987; Hubert et al., 2017). In the MCD, only the r observations, $⌊\left(T+n+1\right)/2⌋\le r\le T$, whose classical covariance matrix has the lowest determinant are considered in the computation of the Mahalanobis distance:

where ${\widehat{\mu }}_{MCD}$ and ${\widehat{\mathrm{{{\Sigma}} }}}_{MCD}$ are the MCD estimator of the mean and the covariance matrix respectively defined as follow:

Where $W\left({d}_{t}^{2}\right)$ is an appropriate weight function and ${c}_{1}$ is a consistency factor (e.g., see Lopulhaa and Rousseuw, 1991). Note that the MCD estimator can only be computed when r > n, otherwise the covariance matrix of any r-subset has determinant 0, so we need at least T > 2n. To avoid excessive noise, it is recommended that T > 5n, so that we have at least five observations per dimension.

The MCD estimator is computationally expensive as it requires the evaluation of $\left(\genfrac{}{}{0pt}{}{T}{r}\right)$ subsets of size r and for this reason we use the Fast Minimum Covariance Determinant estimator (FMCD) of Rousseeuw and Van Driessen (1999). A major component of the FMCD algorithm is the concentration step, C-step, which works as follows. Given the initial estimates ${\widehat{\mu }}_{old}$ and ${\widehat{{\mathit{\Sigma}} }}_{old}$:

● Compute the distances ${d}_{old}\left(t\right) = D\left({x}_{t}, {\widehat{\mu }}_{old}, {\widehat{{\mathit{\Sigma}} }}_{old}\right), t = 1, \dots, T.$

● Sort these distances and yield a permutation $\tau$ such that:

● Compute location and scale estimators:

In Theorem 1 of Rousseuw and Van Driessen (1999) it is proved that $det\left({\widehat{\mathrm{{{\Sigma}} }}}_{new}\right)\le det\left({\widehat{\mathrm{{{\Sigma}} }}}_{old}\right)$, with equality only if ${\widehat{\mathrm{{{\Sigma}} }}}_{new} = {\widehat{\mathrm{{{\Sigma}} }}}_{old}$. Thus, if we iterate the C-step, the sequence of determinants obtained in this way converges in a finite number of iterations. The FMCD algorithm supplies a sequence of weights, one or zero (zero for the outliers), that has length $T$, and we repeat this sequence for n column to obtain the matrix ${H}_{MCD}$ with dimension $T\times n$. We multiply the data matrix X by ${H}_{MCD}$:

where $\odot$ denotes the Hadamard's product. We use ${X}_{MCD}$ to extract the factors (Croux et al., 2003; Pison et al., 2003) ${F}_{k, t}$, as described in Section 3.1 and obtain the model FM FMCD. In this paper we set $r = 0.95T$.

3.3.   A robust factor model: the iterated reweighted least squares estimator

The Maximum-Likelihood-Type Estimator (M-Estimator) is another popular robust method for estimating the location and scale of a set of points, and its application leads to the Iterated Reweighted Least Squares (IRLS) (Bergstrom et al., 2014; Daubechies et al., 2009). Define the residual as follows:

where ${A}_{k}$ and ${F}_{k, t}$ have been defined in Section 3.1, and ${||\cdot ||}_{2}$ is the Euclidean norm for vectors. IRLS assumes continuous weights as a function of the residual:

For some given robust loss function $\rho \left(\cdot \right)$ from the set of the real to the positive reals. The objective function then becomes:

Many loss functions have been proposed in the statistics literature (Huber 1981; Barnett and Lewis 1984). When  $\rho \left({\varepsilon }_{t}\right) = {\varepsilon }_{t}^{2}$, all weights are equal to 1, and we obtain the standard least-squares solution, which is not robust. Other robust loss functions are described in Vidal et al. (2016), in this work we use a Geman-McClure loss (Geman and McClure, 1987):

where ${\varepsilon }_{0}^{2}$ is a parameter that we consider equal to the square root of mean of ${\varepsilon }_{t}^{2}$. Following De la Torre and Blank (2004), we use a Geman-McClure loss scaled by ${\varepsilon }_{0}^{2}$ which yields the following procedure. Given an initial parameter ${\varepsilon }_{0}^{2}$ and factor loadings and factors, ${A}_{k}$ and ${F}_{k, t}$, respectively, obtained from the FM Std of Section 3.1, iterate until convergence the following steps:

1. Compute the residuals ${\varepsilon }_{t} = {||{x}_{t}-{A}_{k}{F}_{k, t}||}_{2}$.

2. Compute the weights ${w}_{t} = \frac{{\varepsilon }_{0}^{2}}{{{\varepsilon }_{0}^{2}+\varepsilon }_{t}^{2}}$.

3. Estimate the covariance ${\mathit{\Sigma}} \leftarrow \frac{\sum _{t = 1}^{T}{w}_{t}{x}_{t}{x}_{t}^{'}}{\sum _{t = 1}^{T}{w}_{t}}.$

4. Extract the first $k$ largest eigenvalues of ${\mathit{\Sigma}}$ and collect the corresponding eigenvectors in ${A}_{k}$.

The factor matrix ${F}_{k, t}$ obtained as above is called FM IRLS.

3.4.   A forecasting model

Once factors are extracted a forecasting procedure is needed to predict the variables of interest. We assume the first $k$ latent factors (determined with the three methodologies described above), ${F}_{k, t} = ({f}_{1, t}, \dots, {f}_{k, t})\mathrm{'}$, with $k < n$, follow a VAR model. Using only $k$ factors, the reconstruction of the variables derives from the approximated model:

With the term ${X}_{k, t}$ we mean the approximation of the vector ${X}_{t}$ obtained using the first k factors ${F}_{k, t}$. Considering the dynamic part related to the $k$ factors, our model is thus as follows:

where ${\mathrm{c}}_{k}$ has dimension k x 1 and ${\mathrm{\Phi }}_{k}$ has dimensions k x k. As shown in Billio et al. (2022), under VAR assumption for the factors, the variables of interest ${X}_{k, t}$ follow a VAR model with restrictions. Thus, the conditional forecasts ${X}_{k, t+h}$ at the horizon $h$, $h = \mathrm{ }1, \dots, \mathrm{H}$ are obtained as follows:

where:

To summarize, we first estimate the latent factors and then use a VAR model on factors to forecast both the factors and the variables of interest. After then, the variables will be reconverted to their correct values reversing the procedures of normalization and integrated if they have been previously differentiated.

4.   Empirical applications

4.1.   Data description

We consider a dataset of macroeconomic variables related to the US and the EU economies, provided by Bloomberg. It consists of 42 monthly variables and 2 quarterly variables, sampled from December 2001 to January 2021, and includes some key variables for policy making: core and headline prices, labour market variables, imports, exports, industrial production, consumption, sales, leading indicators of interest rates, and the term structure. See Table 1 for a more detailed description.

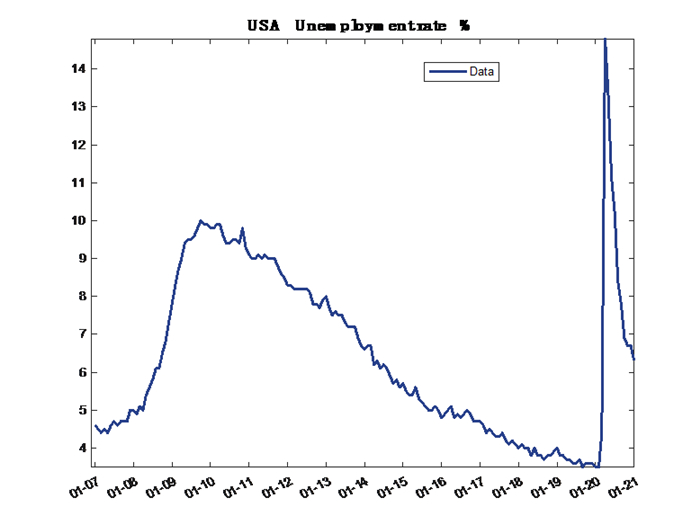
In our dataset, the 2009 financial crisis and the COVID-19 pandemic generated outliers in many time series. For example, a graphical inspection of the US unemployment rate series reveals the dramatic impact of COVID-19 pandemic after March 2021 (Figure 1). In presence of outliers, the researcher can choose to trim the data, that is to reduce or eliminate the outliers and to run inference on a linear model overcoming the inference issues (such as bias) that the outliers can generate. Data trimming requires outliers are detected first. To detect the presence of the outliers, a standard procedure consists in fitting the linear regression model:

By Least Squares and recovering the hat matrix $H$ from the fitted value of Y:

The hat matrix $H$ is a symmetrical and idempotent T x T projection matrix; it has n eigenvalues equal to one and T-n equal to zero. The diagonal elements ${h}_{t, t}$ have the following property:

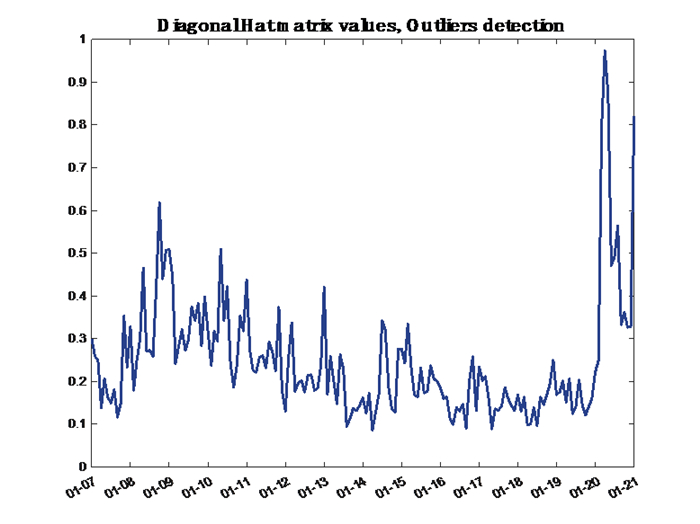
Points where ${h}_{t, t}$ have large values are called leverage points, and it can be proved that the presence of leverage points signals that there are observations that might have a decisive influence on the estimation of the regression parameters. We consider the leverage points as a proxy for the quick survey of presence of the outliers. We can see in Figure 2 the greater values of ${h}_{t, t}$ is detected for the 2009 crisis and COVID-19 pandemic.

4.2.   Factor Analysis

The factors have been extracted from the monthly variables using three FM methodologies (FM Std, FM FMCD, and FM IRLS), and then they supply the forecast using a VAR model as described in Section 3.4. As regards to the quarterly variables we follow a nowcasting procedure. First, we derive the regression coefficients of the quarterly variables on the nowcasted factors and secondly, we use the coefficients and the forecasted factors to forecast the quarterly variables.

We analyze the stability of the factors and the percentage of explained variance. We follow a rolling window estimation approach and analyze the out-of-sample forecast ability of the FM with a twelve-months horizon. There are 61 overlapping windows of 170 observations each. The first window is from December 2001 to January 2016, the second shift is one month from January 2002 to February 2016, and the 61st is from December 2006 to January 2021. See Figure 3 for a graphical illustration of the procedure (see Figure 3).

In our empirical applications, the $k$ factors are used to forecast the variables of interest, which are the Unemployment rate and the Harmonized Index of Consumer Prices (HCPI); with nowcasting procedure we produce the forecast also for GDP. Our choice is to explain a given proportion of variance ${V}_{k} < 1$ in Eq. (6) with a reduced number of factors in order to limit the dimension of forecast model (i.e., the VAR model). For example, in our application we choose to explain at least 80% of the variance, ${V}_{k} = 0.8$, with no more than 9 factors.

Figure 4 reports the values of the leverage point ${h}_{t, t}$ estimated from the panel series in some relevant windows (see plot labels). The value of ${h}_{t, t}$ increases slowly in the observation windows where the 2009 crisis is included (e.g., see plots w1, w19, w31, and w43). When the observations associated to the COVID-19 pandemic period are included in the samples, then ${h}_{t, t}$ reaches much larger values, about $1$ (see w51, w52, w53, and w58). A double peak appeared in the window w61 due to the second wave in the CODIV-19 pandemic.

In conclusion, we consider COVID-19 as the greater cause of outliers that the researchers are facing. For this reason, we choose a percentage of $r = 0.95T$ for the values to be saved in FMCD algorithm.

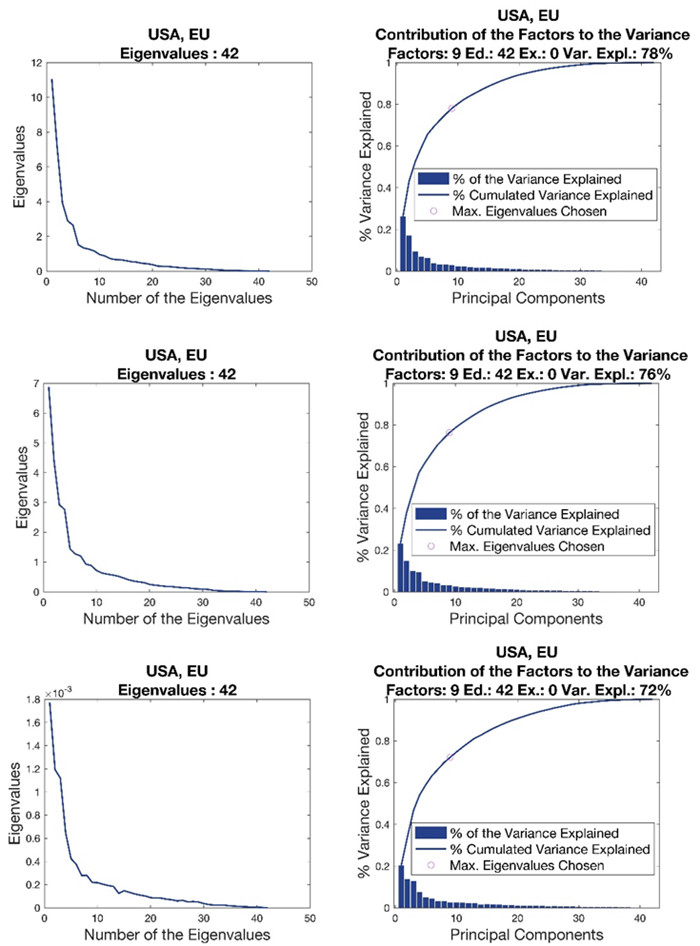
Figure 5 shows the eigenvalues (left column) and the contribution of the first 9 factors (right) to the variance for the three FMs. The graphs refer to the data of the last window in Figure 3. The scale of the eigenvalues differs across models since the weights used in FMCD and IRLS have different size. The decay rate of the spectrum is similar across models, and this indicates small number of factors explain a large proportion of variance. The FM FMCD and FM IRLS models intercept a smaller proportion of variance than in the FM Std case.

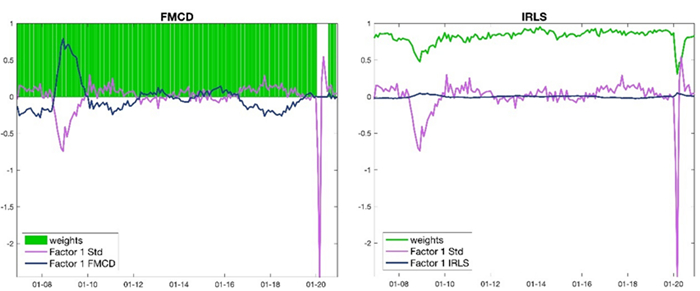
The green lines in Figure 6 shows the weights used in the FMCD (left) and IRLS (right). Setting $r = 0.95T$ yields weight equal to one for all windows expect for the COVID-19 pandemic windows where the weight is equal to zero. For the IRLS the weights are strictly positive for all estimation windows and below one. The two weight sequences have different impact on the extraction of the factors (e.g., see the first factor in the same figure and the three factors in Figure 7).

The FM Std model factors exhibit at least 2 peaks corresponding to the 2009 crisis and COVID-19 pandemics windows. In the robust FM procedures, the weight sequences reduce substantially the effects of the two sources of outliers.

In Table 2, we illustrate the bias issues induced by the presence of outliers, by comparing the correlation between the variables in the dataset (columns) and the first factor of the three models (rows), estimated in the last windows (w61). The first factor in the three models explains the 26%, 23%, and 20% of the variance, respectively. The set of the most correlated variables in the standard FM model differs from the one of the FM FMCD and FM IRLS models, which indicates that the bias in the estimation of the factor can be large in the FM models if the outliers are not treated properly.

FM FMCD and FM IRLS share 9 common variables, and the correlation levels are similar in the two models; the result indicates that the choice of the weights can have an impact on the results, but the economic interpretation of the factors is not affected too much.

4.3.   Forecast comparison

We use the rolling window analysis introduced in the previous section for comparing the three models: FM Std, FM FMCD and FM IRLS. For each window, the models produce 12 forecasts out of sample (see Figure 3). We measure and compare sequentially the ability of the models to forecast the following variables: GDP, Unemployment rate, as well as PCE for both the EU and the US regions.

For every window, we determine the factors and compute the forecast at the horizon of 12 months for the monthly variables and 4 quarters for the quarterly variables. The rolling window of 170 observations is moved forward by one month, and the forecasts are computed again. We repeat this exercise 61 times until the end date of the observation window coincides with January 2021.

For every series, compute the square of the difference between the forecast and the actual values, sum the squared differences, divide them by the total number of forecast points, and take a square root to obtain the Root Mean Square Error (RMSE). Let ${s}_{t}$ be the forecast horizon at time $t$ for monthly data. In our application, it is equal to 12 for all $t$ except when the end of the window is close to January 2021, when the horizon decreases. Moreover, let $TEp = 61$ be the number of forecasts for each one of the ${s}_{t}$ months.

At time t, we have the following error for every forecast (we omit here the identification of the variable):

where $f\left(t+i\right)$ indicates the forecast for the variable $v\left(t+i\right)$. The forecast is made at time $t$ with forecasting horizon $i$. The RMSE is thus defined as follows:

As a first step, we show the RMSE value for the first three factors, that intercept more than 52.5%, 47.8%, 46.7% of the total variance for FM Std, FM FMCD, FM IRLS respectively.

The left column of Figure 8 shows the actual values of the three factors (solid blue lines, in the rows), the 12-step-ahead FM forecasts (dashed lines), and their envelope (solid red lines), which can be considered an approximation of the forecasting error bands. The forecast comparison includes the COVID-19 pandemic period, but cannot be made for the 2009 crisis one, due to the choice of the rolling window size (see Figure 3). Thus, in the following we focus on the forecast ability during the COVID-19 period.

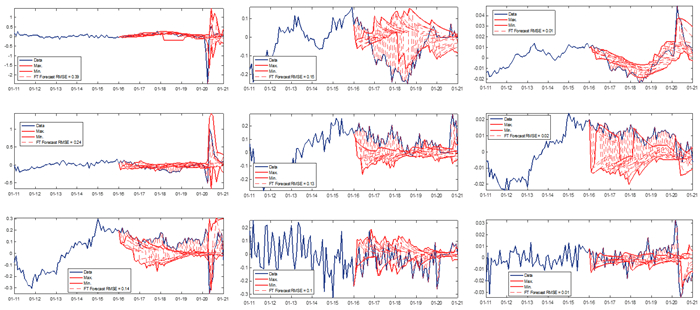
For the first factor, the actual values belong to the envelope region for all periods except for the pandemic crisis periods, which reveal the difficulties in predicting the effects of the pandemic events. A similar behavior can be detected for the second factor. The middle and right columns in Figure 8 show the first three factors for FMCD and IRLS methodologies respectively; their behavior is comparable only by graphical point of view, because they have different scale due to the two applied algorithms. Figure 9 shows the forecasts and the RMSEs for our variables of interest and for the three methodologies: FM Std (left column), FM FMCD (middle) and FM IRLS (right).

By using the envelope (solid red lines) as reference lines, it is possible to compare graphically the forecast performance of the models. Since the actual data belong to the area delimited by the envelope of the FM FMCD and FM IRLS models, we conclude that they usually perform better than FM Std. The lower RMSE level of the FM FMCD and FM IRLS model for both the monthly and quarterly variables allows us to confirm this result (see panel (a) in Table 3).

The effect of outliers on the most impacted variables propagates to the forecast of the other variables through the factors, which can explain the bad performance of the standard FM model. The variables of interest that are the most difficult to predict are the GDPs and the Unemployment rate. Their values have been most affected by the crisis. On the other hand, prices maintain good predictability for both regions because this variable was not heavily penalized by the crisis. The impact of outliers can be reduced in the FM FMCD and FM IRLS models, nevertheless, for the US Unemployment Rate, the effects of COVID-19 on the forecasting performances have been disruptive for all the three methodologies.

In Table 3(b) we can see that RMSE of the 12-month-ahead forecast for USA Unemployment Rate is smaller than one of the forecasts at 5 and 7 months ahead. This is mainly due to the error magnitude of forecast done in April 2020. This forecast exercise includes in its horizon the first sample impacted by the COVID-19 and has a very large forecast error. Since the dataset ends in January 2021, the forecast horizon ${s}_{t}$ in this exercise is 9 months (see Figure 3); which implies that for this forecast it is possible to measure the errors at 1, 5, 7 months but not at 12.

Finally, following the guidelines provided by Eurostat (2020) on modelling outliers due to COVID-19, we monitor sequentially the forecasting errors. The RMSEs for the one-, two-, seven- and twelve-step-ahead forecasts of the three methodologies indicate that the FM FMCD and FM IRLS models have better performances than the FM Std model at all the horizons (see Figures 10, 11 and 12 in Appendix). The numerical results in the panel (b) of Table 3 suggest the FM IRLS model has superior forecasting ability at all horizons.

The bottom line from this section is the following:

● the sample observations during the 2009 crisis and the 2020 COVID-19 pandemic heavily affect factor estimates obtained with the standard procedure;

● consequently, standard factor models can produce significant forecasting errors in the presence of outliers, whereas robust models perform better;

● the variables most impacted by the 2009 crisis and the pandemic (such as GDP and unemployment) exhibit the most significant forecast errors in all estimation procedures;

● the sequential forecasting comparison between MCD and IRLS showed that the latter approach usually leads to superior forecasting performances.

5.   Conclusions

Outliers can have disruptive effects on inference, biasing the estimates and the conclusion of the statistical analysis. Through the lens of factor models we provide evidence of the effects of outliers due to the 2009 crisis and the COVID-19 pandemic on the forecast abilities of the models. We applied two techniques for robust factor estimation based on robust covariance matrix estimators. The robust methodologies that we chose have the advantage of avoiding data deletion or manipulation. We compare the standard factor estimation with the robust estimation approaches for an extended period and on a set of relevant variables. The choice to include the COVID-19 pandemic period in the estimation and forecasting exercises has the scope to highlight the relevance of handling outliers in periods of large shocks to the world's economies. We show that robust estimation can reduce outliers' influence and produce good forecasts.

Conflict of interest

All authors declare no conflicts of interest in this paper.