Microstructural evolution and direct shear strength of cement-stabilized soil under freeze-thaw cycles

1.   Introduction

Partial differential equations (PDEs) on networks have a large number of applications, including fluid flow in pipelines, traffic flow on a network of roads, blood flow in vessels, data networks, irrigation channels and supply chains. A treatment of this wide range of applications can be found in the review articles [6,14] and the references therein. In this paper we will focus on scalar, one-dimensional conservation laws

on a network. Here, $u = u(x, t)$ is the unknown conserved variable and $f$ is a scalar flux function defined either on $\mathbb{R}$ or some subinterval. We aim to make sense of the conservation law on a directed graph and obtain existence, uniqueness, stability and approximability results.

Consider a network represented by a connected and directed graph. We tag the edges of this graph with an index $k$ and impose on each edge a scalar conservation law

for some spatial domain $D^k\subset \mathbb{R}$. (Here and in the remainder, a superscript $k$ will refer to an edge or a vertex.) We may think of edges as pipes or roads and the vertices as intersections, with the convention that the direction of travel is in the positive $x$-direction, as shown in Figure 1.

In this paper we will be interested in uniqueness and stability for nonlinear scalar conservation laws on a network, as well as in constructing a numerical approximation and proving convergence of the numerical scheme. As opposed to many existing results, where the flux function on each edge is the same [10,18], we want to allow for a different flux function $f^k$ on each edge $D^k$ of the network. Assuming that each flux $f^k$ is continuous and independent of the space variable, the problem can be seen as a PDE with a discontinuous flux, with the points of discontinuity sitting on the vertices of the graph. In fact, if our network would be the trivial network with only one ingoing and one outgoing edge then this would be exactly the case of a conservation law on the real line with a flux function with one discontinuity located at the vertex. Because of the connection to the theory for conservation laws with discontinuous fluxes (see e.g. [3]), we will borrow several ideas from this theory. It is well-established that nonlinear hyperbolic conservation laws develop shocks in finite time. Therefore, solutions are always understood in the weak sense. Unfortunately, weak solutions to nonlinear hyperbolic conservation laws turn out to be non-unique, and additional conditions, usually referred to as entropy conditions, are imposed to select a unique solution. If the flux function is continuous then the theory of entropy solutions is covered by Kruzkhov's theory [21]. For conservation laws with discontinuous fluxes the choice of entropy conditions is not obvious, and different physical models might lead to different entropy conditions. Although suitable entropy conditions can yield uniqueness, different entropy conditions are known to yield different solutions; see [30,19,7,3] and references therein. In [30] the author shows convergence of a finite difference scheme scheme under the assumption of a strictly concave flux function with a single maximum. In a later paper [19] a uniqueness result was shown for degenerate parabolic convection-diffusion equations, of which hyperbolic conservation laws are a subcase. In this work, the flux function had to satisfy a so-called "crossing condition". Another convergence result for an Engquist–Osher type scheme was given in [7]. The flux functions $f, \, g$ were assumed to have a single maximum and to satisfy $f(u) = g(u) = 0$ for $u = 0, 1$. The study of different entropy conditions for conservation laws with discontinuous fluxes culminated in the paper by Andreianov, Karlsen and Risebro [3]. The authors relate the question of admissibility of a solution to the properties of a set of constant solutions, a so-called germ. Inspired by the entropy theory of Andreianov, Karlsen and Risebro, we investigate so-called stationary and discrete stationary solutions for our graph problem and thus derive an entropy theory for conservation laws on networks. Although our theory is influenced by the theory in [3], we have strived to make this paper as self-contained as possible.

In [18] the authors show uniqueness and existence to the Riemann problem as well as existence of a weak solution of the Cauchy problem on a network of roads in the case that the flux functions on each edge are identical. In [9,8,1,10] the authors show well-posedness results for vanishing viscosity solutions. In [15] the authors investigate two entropy type conditions. However, in none of the existing literature can one find a general entropy condition which leads to uniqueness and stability of solutions. In the present work we aim to address this deficiency in the existing theory of conservation laws on networks.

The second important question to address is existence of a solution. Our approach will be to construct an approximation of the exact entropy solution by constructing a finite volume scheme. We will prove convergence to an entropy solution, thereby also proving existence of a solution. Convergence to the unique entropy solution of numerical schemes has been shown for conservation laws with strictly concave flux functions. This was done for schemes which are implicit on the nodes in [1,Section 3.2] and [2]. Convergence of a fully explicit scheme for the strictly concave case was shown in [29]. For a general overview over numerical methods for conservation laws on graphs see [6,Section 6].

In this article we focus on monotone fluxes – that is, each flux $f^k$ is either increasing or decreasing. For non-monotone fluxes only some of the techniques in the present paper are applicable; a traffic flow model, in which fluxes are assumed to be strictly concave, will be treated in a forthcoming work [13].

This article is structured as follows: In Section 2 we define our mathematical framework. We show uniqueness of entropy solutions to our problem in Section 3. In Section 4 we define a finite difference scheme appropriate for our problem, and in Section 5 we prove that our numerical scheme converges towards the unique entropy solution. In Section 6 we show that a class of monotone flux functions fits in our general scheme. Numerical experiments for the monotone case are presented in Section 7.

While the theory outlined in Sections 2 through 4 holds for conservation laws with general flux functions, the convergence theory in Sections 5 and 7 focuses on monotone flux functions and upwind numerical fluxes.

2.   Entropy solutions on networks

Consider a network (or directed graph) of vertices and edges; for simplicity we will assume that the network contains a single vertex, along with $N_{ {\mathrm{in}}}\in \mathbb{N}$ edges entering and $N_{ {\mathrm{out}}}\in \mathbb{N}$ edges exiting the vertex (see Figure 1). (The generalization to general networks will follow analogously, due to the finite speed of propagation of the equations considered.) We think of the $N_ {\mathrm{in}}$ edges as being to the left of the vertex and the $N_ {\mathrm{out}}$ edges to its right. The ingoing edges will be labelled $k\in {{\mathscr{I}}_{\mathrm{in}}}: = \{- {N_{\mathrm{in}}}, \dots, -1\}$ and the outgoing edges $k\in {{\mathscr{I}}_{\mathrm{out}}}: = \{1, \dots, {N_{\mathrm{out}}}\}$. We denote $N : = {N_{\mathrm{in}}} + {N_{\mathrm{out}}}$ and we let ${\mathscr{I}}: = {{\mathscr{I}}_{\mathrm{in}}}\cup {{\mathscr{I}}_{\mathrm{out}}}$ denote the set of all edge indices. Placing the vertex at the origin $x = 0$, the incoming edges have coordinates $x\in \mathbb{R}_- = (-\infty, 0)$, while the outgoing edges have coordinates $x\in \mathbb{R}_+ = (0, \infty)$; we will denote the $k$-th edge by

On each edge $D^k$ we now impose the scalar conservation law (1.1), resulting in the $N$ distinct equations

The collection of functions ${\mathbf{u}} = (u^k)_{k\in {\mathscr{I}}}$ can be thought of as a function ${\mathbf{u}}\colon\Omega\to \mathbb{R}$, where

On the Borel $\sigma$-algebra ${\mathscr{B}}(\Omega)\simeq\big\{\prod_{k\in {\mathscr{I}}}A^k\times\{k\}\ :\ A^k\in {\mathscr{B}}(D^k)\big\}$ on $\Omega$ we define the measure $\lambda = {\mathfrak{L}}\times \#$, where ${\mathfrak{L}}$ is the one-dimensional Lebesgue measure and $\#$ is the counting measure; thus, the integral of ${\mathbf{u}} = (u^k)_{k\in {\mathscr{I}}}$ is

The set of $L^\infty$-bounded, real-valued functions on $\Omega$ will be denoted by $L^\infty(\Omega;\lambda)$. We define the total variation of a function ${\mathbf{u}} \in L^\infty(\Omega; \lambda)$ as the sum of the variations of its components:

2.1.   Weak solutions

Definition 2.1 (Weak Solution). We say that a function ${\mathbf{u}}\in L^\infty\big( \mathbb{R}_+;L^\infty(\Omega;\lambda)\big)$ is a weak solution of (2.1) with initial data $\bar {\mathbf{u}}\in L^\infty(\Omega;\lambda)$ if

for all $\varphi^k \in C_c^\infty\big(\overline{D^k}\times[0, \infty)\big)$ satisfying $\varphi^k(0, t)\equiv \varphi^1(0, t)$ for all $k\in {\mathscr{I}}$.

Weak solutions automatically satisfy a Rankine–Hugoniot condition at the intersection:

Proposition 2.2 (Rankine–Hugoniot condition). Let $(u^k)_{k\in {\mathscr{I}}}$ be a weak solution of (2.1) such that $f^k\circ u^k(\cdot, t)$ has a strong trace at $x = 0$ for every $k\in {\mathscr{I}}$ and a.e. $t>0$. Then

Proof. Define

We define $\Phi(x, t) : = \theta_ \varepsilon (x) \psi (t)$ where $\psi \in C_c^\infty ([0, \infty))$. The partial derivatives of $\Phi$ are

By a density argument, $\Phi$ qualifies as an admissible test function. Thus, we can insert $\Phi$ into the weak formulation (2.4) to get

as $\varepsilon \to 0$, which is equivalent to (2.5).

Definition 2.3 (Stationary Solution). A stationary solution of (2.1) is a weak solution of (2.1) which is constant in time and is a strong solution on each edge $D^k$. We see from (2.4) and (2.5) that the stationary solutions are precisely those satisfying $u^k(x, t)\equiv c^k\in \mathbb{R}$ for $x\in D^k, \ t \geqslant0$ and $k\in {\mathscr{I}}$, and where $c^k$ satisfy the Rankine–Hugoniot condition

Thus, we can identify each stationary solution with a vector ${\mathbf{c}} = (c^k)_{k\in {\mathscr{I}}}\in \mathbb{R}^N$.

Remark 2.4. Note that if we only required stationary solutions to be weak solutions on each edge $D^k$ then they could exhibit arbitrarily many jump discontinuities. More precisely, if $f$ is not injective then a "stationary weak solution" could jump arbitrarily often between values $u^k = c^{k, \pm}$, where $f(c^{k, -}) = f(c^{k, +})$.

2.2.   Entropy conditions

Next, we formulate conditions that will single out a unique weak solution.

Definition 2.5 (Kruzkov entropy pairs). The Kruzkov entropy pairs are the pairs of functions $\eta_c(u) = |u-c|$, $q_c^k(u) = {\rm sgn}(u-c)\big(f^k(u)-f^k(c)\big)$ for $c\in \mathbb{R}$.

The Kruzkov entropy pairs lead to a consistency condition on sets of stationary solutions:

Definition 2.6. A subset $\mathscr{G}\subset \mathbb{R}^N$ consisting of stationary solutions of (2.1) is mutually consistent if

for every pair ${\mathbf{c}}, \tilde{ {\mathbf{c}}}\in \mathscr{G}$, where $q_c^k$ are the Kruzkov entropy flux functions. The set $\mathscr{G}$ is maximal if for every ${\mathbf{c}}\in \mathbb{R}^N$, the condition that (2.8) holds for every $\tilde {\mathbf{c}}\in \mathscr{G}$ implies that also ${\mathbf{c}}\in \mathscr{G}$.

The set of stationary solutions $\mathscr{G}$ will determine what class of initial data we can consider:

Definition 2.7. Let $\mathscr{G}\subset \mathbb{R}^N$. We let $L^\infty_{\mathrm{oco}}( \mathscr{G})$ be the set of $L^\infty$-bounded data of $\mathscr{G}$,

Example 2.8. If $N_ {\mathrm{in}} = N_ {\mathrm{out}} = 1$ and $f^k(u) = f(u) = u^2$ then the stationary solutions are all ${\mathbf{c}}\in \mathbb{R}^2$ of the form ${\mathbf{c}} = (c, c)$ or ${\mathbf{c}} = (c, -c)$ for $c\in \mathbb{R}$. Both $\mathscr{G}_1 = \{(c, c):c\in \mathbb{R}\}$ and $\mathscr{G}_2 = \{(c, -c):c \geqslant0\}$ (as well as any subset of these) are mutually consistent, as is $\mathscr{G}_1\cup \mathscr{G}_2$. Note that no point of the form $(-c, c)$ for $c>0$ can be added to any of these sets and remain mutually consistent. Similarly, no set containing both $(-c, c)$ and $(-d, d)$ for distinct $c, d>0$ can be mutually consistent. The set $\mathscr{G}_1$ stands out as the smallest closed set which is such that both components span all of $\mathbb{R}$, i.e. the projection onto either component equals $\mathbb{R}$. It is readily checked that $L^\infty_{\mathrm{oco}}( \mathscr{G}_1) = L^\infty(\Omega;\lambda)$, and that any strict subset of $\mathscr{G}_1$ will yield a strictly smaller set of initial data. It is similarly straightforward to check that $\mathscr{G}_2$ generates a very restrictive set of initial data:

Thus, $\mathscr{G}_1$ is the smallest mutually consistent set of stationary solutions that allows for initial data in all of $L^\infty(\Omega;\lambda)$.

Definition 2.9 (Entropy Solution). Let $\mathscr{G}\subset \mathbb{R}^N$ be a mutually consistent set of stationary solutions of (2.1) and let $\bar{ {\mathbf{u}}}\in L^\infty(\Omega;\lambda)$. We say that a function ${\mathbf{u}}\in L^\infty( \mathbb{R}_+, L^\infty(\Omega;\lambda))$ is an entropy solution of (2.1) with respect to $\mathscr{G}$ with initial data $\bar {\mathbf{u}}$ if each $u^k$ is a Kruzkhov entropy solution on $D^k$ for all $k \in {\mathscr{I}}$ (in the usual sense), and if

for every ${\mathbf{c}}\in \mathscr{G}$ and every $0 \leqslant \varphi \in C_c^\infty\big(\Omega\times[0, \infty)\big)$ satisfying $\varphi^k(0, t)\equiv \varphi^1(0, t)$ for all $k\in {\mathscr{I}}$.

Audusse and Perthame [4] considered an entropy condition similar to (2.10), but in the context of spatially dependent, discontinuous flux functions.

We show first that entropy solutions are invariant in the set $L^\infty_{\mathrm{oco}}$ from Definition 2.7.

Lemma 2.10. Let $\mathscr{G}\subset \mathbb{R}^N$ be a mutually consistent set of stationary solutions of (2.1) and let ${\mathbf{u}}\in L^\infty\big( \mathbb{R}_+, L^\infty(\Omega;\lambda)\big)$ be an entropy solution w.r.t. $\mathscr{G}$ with initial data $\bar {\mathbf{u}}\in L^\infty_{\mathrm{oco}}( \mathscr{G})$. Then ${\mathbf{u}}(t)\in L^\infty_{\mathrm{oco}}( \mathscr{G})$ for a.e. $t>0$.

Proof. Select ${\mathbf{c}}, {\mathbf{d}}\in \mathscr{G}$ such that ${\mathbf{c}} \leqslant \bar{ {\mathbf{u}}} \leqslant {\mathbf{d}}$ (cf. (2.9)). Add inequality (2.10) and equation (2.4) for both $c^k$ and $u^k$ to get

(where $\cdot_+ = \max(\cdot, 0)$ and $H = {\rm sgn}_+$ is the Heaviside function). Replacing $\varphi$ by a sequence of approximations of the identity function on the set $\Omega\times[0, T]$ yields

for a.e. $T>0$, whence ${\mathbf{u}}(T) \geqslant {\mathbf{c}}$. It follows similarly that ${\mathbf{u}}(T) \leqslant {\mathbf{d}}$, and hence, ${\mathbf{u}}(T)\in L^\infty_{\mathrm{oco}}( \mathscr{G})$.

The above lemma enables us to show that entropy solutions have strong traces.

Lemma 2.11. Let $\mathscr{G}\subset \mathbb{R}^N$ be a mutually consistent set of stationary solutions of (2.1) and let ${\mathbf{u}}\in L^\infty( \mathbb{R}_+, L^\infty(\Omega;\lambda))$ be an entropy solution w.r.t. $\mathscr{G}$ with initial data $\bar {\mathbf{u}}\in L^\infty_{\mathrm{oco}}( \mathscr{G})$. Then the functions $q^k\circ u^k$ and $f^k\circ u^k$ admit strong traces on $\{x = 0\}$, for any $k\in {\mathscr{I}}$.

Proof. It follows from Lemma 2.10 that $u^k$ is a Kruzkhov entropy solution on $D^k$, for any $k\in {\mathscr{I}}$. We can therefore apply [25,Theorem 1.4] to obtain the desired conclusion.

Proposition 2.12. Let $\mathscr{G}\subset \mathbb{R}^N$ be a set of stationary solutions of (2.1). Let ${\mathbf{u}}$ be an entropy solution of (2.1) w.r.t. $\mathscr{G}$ such that $q_{c^k}^k\circ u^k(\cdot, t)$ has a strong trace at $x = 0$ for every $k\in {\mathscr{I}}$ and a.e. $t>0$. Then

for every ${\mathbf{c}}\in \mathscr{G}$.

Proof. We take a positive test function $0 \leqslant \psi \in C_c^\infty((0, \infty))$. As in the proof of Proposition 2.2 we define $\Phi(x, t) : = \theta_ \varepsilon (x, t) \psi (t)$ where $\theta_ \varepsilon$ is given by (2.6). Now we insert $\Phi$ as test function into the entropy inequality (2.10) to get

as $\varepsilon\to0$, which shows the desired inequality.

Corollary 2.13. If $\mathscr{G}$ is maximal (cf. Definition 2.6), then the trace of any entropy solution lies in $\mathscr{G}$.

3.   Stability and uniqueness

Theorem 3.1 (Entropy Solutions are $L^1$ stable). Let $\mathscr{G}\subset \mathbb{R}^N$ be a mutually consistent, maximal set of stationary solutions. Let ${\mathbf{u}}, \, {\mathbf{v}}$, be entropy solutions of (2.1) w.r.t. $\mathscr{G}$ with initial data $\bar {\mathbf{u}}, \, \bar {\mathbf{v}} \in L^\infty_{\mathrm{oco}}(\mathscr{G})\cap L^1(\Omega; \lambda)$. Let $f^k$ be Lipschitz continuous for all $k \in {\mathscr{I}}$. Then

for every $t>0$. In particular, there exists at most one entropy solution for given initial data.

Proof. From Lemma 2.10 it follows that ${\mathbf{u}}(t), {\mathbf{v}}(t)\in L^\infty_{\mathrm{oco}}( \mathscr{G})$ for a.e. $t>0$. Let $k\in {{\mathscr{I}}_{\mathrm{in}}}$; the case $k\in {{\mathscr{I}}_{\mathrm{out}}}$ will follow analogously. The first step is a standard doubling of variables argument on each edge $k\in {{\mathscr{I}}_{\mathrm{in}}}$ by selecting $\varphi^k\in C_c^\infty(D^k\times[0, \infty))$ and $\varphi_l\equiv0$ for $l\neq k$. Note that this is the point in the argument where we need the fluxes $f^k, \ k\in {\mathscr{I}}$ to be Lipschitz continuous. The doubling of variables technique on a single edge gives:

Next, for general $\varphi^k\in C_c^\infty\big(\overline{D^k}\times[0, \infty)\big)$, we cut off the functions near $x = 0$ and couple the terms (3.1) on each edge together by utilizing (2.11). For $h>0$ we define

and

The derivative of $\Psi_h$ reads

Define $\varphi^k(x, t) : = \xi^k (x, t) \Psi_h (x)$ for a function $\xi^k \in C_c^\infty \big(\overline{D^k} \times [0, \infty) \big)$. We insert $\varphi$ into equation (3.1) to get

Sending $h \downarrow 0$ we get

Since the traces of $q^k (u^k)$ and $q^k (v^k)$ exist, we get

We therefore obtain

By an analogous argument we get

for $k\in {{\mathscr{I}}_{\mathrm{out}}}$. Fix $s>0$, let $r, \kappa>0$, and let $\alpha_r: \mathbb{R}_-\to \mathbb{R}$ and $\beta_\kappa\colon \mathbb{R}_+\to \mathbb{R}$ be given by

Via a standard regularization argument one can check that $\varphi (x, t) = \alpha_r (x) \beta_\kappa (t)$ is an admissible test function. We compute the partial derivatives of $\varphi$:

and

We insert this into (3.2) to get

Letting $\kappa \to 0$ and $r\to\infty$, we get

An analogous inequality holds for $k\in {{\mathscr{I}}_{\mathrm{out}}}$. We sum over all edges to get

4.   Numerical approximation

In this section we construct a finite volume numerical approximation for (2.1) and prove stability and convergence properties of the method. The numerical method is rather standard for hyperbolic conservation laws, but an important feature of the method is that the vertex is discretized as a separate control volume. Although this control volume vanishes as the mesh parameter ${\Delta x}$ is passed to zero, its presence will ensure that entropy is correctly dissipated at the vertex, even in the limit ${\Delta x}\to0$. As opposed to the method presented in [1], where the problem is an implicit one on the vertex, our method is completely explicit.

4.1.   A finite volume method on networks

Let ${\Delta t}, {\Delta x}>0$ be given discretization parameters. We define the index sets

For $n\in \mathbb{N}_0$ we discretize¹ $t^n = n {\Delta t}$, and for $k\in {\mathscr{I}}$ and $i\in \mathbb{Z}$ we let $x_ {i+{1/2}} = ( {i+{1/2}}) {\Delta x}$, and partition the physical domain into cells

¹In numerical experiments, the timestep ${\Delta t}$ is chosen dynamically at each step $n$ in order to comply with the CFL condition derived in Section 4. We use a uniform timestep for the sake of simplicity only.

We define the mesh size at the vertex by ${\Delta x}_0: = \sum_{k\in {\mathscr{I}}}| {\mathscr{C}}_0^k| = N {\Delta x}/2$, where $|A|$ denotes the Lebesgue measure of $A\subset \mathbb{R}$. We make the finite volume approximation

Fix some $i \in D_ \mathrm{disc}^k$, let $\varphi^k(x, t) = \frac{1}{ {\Delta t} {\Delta x}} \mathbb{1}_{ {\mathscr{C}}_i^k}(x) \mathbb{1}_{[t^n, \, t^{n+1})}(t)$ and $\varphi^l\equiv0$ for $l\neq k$, and (after an approximation procedure) insert these into (2.4). We then obtain the numerical method

where $F_ {i+{1/2}}^{k, n} = F^k\big(u^{k, n}_i, u^{k, n}_{i+1}\big)$ is an approximation of the mean flux through $x_ {i+{1/2}}$ over the time interval $[t^n, t^{n+1})$,

For the special cell $i = 0$ we let $\varphi^k(x, t) = \frac{1}{ {\Delta t} {\Delta x}_0} \mathbb{1}_{ {\mathscr{C}}_0^k}(x) \mathbb{1}_{[t^n, \, t^{n+1})}(t)$ for $k\in {\mathscr{I}}$ to obtain

(This is opposed to the explicit method of Towers [29] where the vertex is modelled as having zero width for any ${\Delta x}>0$.) We will use the notational convention that $u_0^{k, n} \equiv u_0^n$ for all $k\in {\mathscr{I}}$. (We postpone the definition of the initial data $u_i^{k, 0}$ until Section 4.3.)

Given a numerically computed solution $( {\mathbf{u}}_i^n)_{i, n}$, we define the piecewise constant function

We remark that the integral of ${\mathbf{u}}_ {\Delta t}$ w.r.t. the measure $\lambda$ (cf. (2.2)) can be written

for any $t\in[t^n, t^{n+1})$, and the total variation of ${\mathbf{u}}_ {\Delta t}$ (cf. (2.3)) can be written

Note also that a numerical method of the form (4.1) is conservative in the sense that the total mass $\sum_{k\in {\mathscr{I}}} \int_\Omega {\mathbf{u}}_ {\Delta t} \, d\lambda$ is independent of $n$:

As a shorthand for the scheme (4.1) we define the functions

for $k\in {\mathscr{I}}$ and

enabling us to write (4.1) in the update form

As a shorthand for (4.6), we will sometimes use the notation

where ${\mathbf{u}}_i^n$ is the vector containing all numerical values at index $i$ at time $n$.

Definition 4.1 (Monotone scheme). The difference scheme (4.6') is monotone if

where ${\mathbf{u}}^n \leqslant {\mathbf{v}}^n$ means that every component $u_i^{k, n}$ of ${\mathbf{u}}^n$ is no greater than the corresponding component of ${\mathbf{v}}^n$.

We state a straightforward CFL-type condition which ensures monotonicity of the numerical scheme.

Proposition 4.2. Consider a consistent finite volume method (4.1), where $F^k$ is nondecreasing in the first variable and nonincreasing in the second. Then the method is monotone under the CFL condition

Proof. We can calculate the derivatives to the update functions to get

for each $k\in {\mathscr{I}}$, and

on the vertex. We would like these derivatives to be non-negative. The monotonicity of $F^k$ guarantees that the first, second, fourth and fifth expressions are non-negative. Applying monotonicity of $F^k$ to the third and sixth terms, we get

(by (4.7)) and

(using ${\Delta x}_0 = N {\Delta x}/2$)

by (4.7).

Remark 4.3. As opposed to the explicit method that Towers proposes in [29], where the CFL condition gets more restrictive as the number of roads grows, we don't face any issues with the time step with the allowable time step with a high number of roads.

4.2.   Discrete stationary solutions

In the same way that stationary solutions are essential for the well-posedness of entropy solutions (cf. Section 3), they are essential to the stability and convergence of numerical methods on networks. Asserting that a numerical solution is both constant in time and on each edge yields the following definition.

Definition 4.4 (Discrete Stationary Solution). Consider a consistent, conservative numerical method (4.1). A discrete stationary solution for (4.1) is a vector

satisfying the Rankine–Hugoniot condition

as well as the conditions

In the remainder, sets of discrete stationary solutions will be denoted with a superscript, $\mathscr{G}^0$, to signal that they also include a value at the vertex $i = 0$.

Remark 4.5. Note that our definition of a discrete stationary solution is analogous to [1,Definition 2.1]. As opposed to our definition, the authors of [1] only include values on the edges. The value $c_0$, which is called $p$ in [1], is excluded from the vectors of stationary solutions there.

Notation 4.6. We will sometimes index a discrete stationary solution as

for $i\in \mathbb{Z}$ and, by extension,

Using the notation (4.6'), it is readily checked that discrete stationary solutions are precisely those that are constant on each edge and satisfy

Remark 4.7. The conditions (4.9) say that the numerical fluxes at the vertex reduce to the upwind flux on the in edges and the downwind flux on the out edges. This can be interpreted as information only flowing into the vertex, not out of it. This is consistent with the interpretation of the vertex as a stationary shock.

Remark 4.8. Discrete stationary solutions ${\mathbf{c}} = \big(c^{- {N_{\mathrm{in}}}}, \dots, c^{ {N_{\mathrm{out}}}}\big)$ fulfil a discrete version of the Rankine–Hugoniot type condition (2.7),

Lemma 4.9. Consider a consistent, conservative numerical scheme (4.1). Let ${\mathbf{c}} = (c^k)_{k\in {\mathscr{I}}}$ be a stationary solution for (1.1) and let $c^0\in \mathbb{R}$. Then the vector ${\mathbf{c}}_ \mathrm{disc} = (c^{- {N_{\mathrm{in}}}}, \dots, c^{-1}, c^0, c^1, \dots, c^{ {N_{\mathrm{out}}}})\in \mathbb{R}^{N+1}$ is a discrete stationary solution if and only if

where

Proof. We can rewrite conditions (4.9a) and (4.9b) as

for $k\in {{\mathscr{I}}_{\mathrm{in}}}$, and

for $k\in {{\mathscr{I}}_{\mathrm{out}}}$. Hence, if (4.9a), (4.9b) are satisfied then $c^0$ must lie in all of the sets on the right hand side, and hence in their intersection. Conversely, if $c^0$ lies in the intersection, then (4.9a), (4.9b) are satisfied.

4.3.   A stability framework for general consistent, conservative, monotone methods

We set out to prove an $L^\infty$ bound, $L^1$ contractiveness and Lipschitz continuity in time for solutions computed with a general consistent, conservative, monotone finite volume method on a network. Our starting point will be a class of discrete stationary solutions $\mathscr{G}_ \mathrm{disc}^0\subset \mathbb{R}^{N+1}$ for a conservative finite volume method (4.1). We take initial data $\bar u\in L^\infty_{\mathrm{oco}}( \mathscr{G}_ \mathrm{disc}^0)$ (cf. (2.9)), we let ${\mathbf{c}}\in \mathscr{G}_ \mathrm{disc}^0$ be as specified in (2.9), and consider the finite volume method (4.1) initialized by

(The value $c^0$ is chosen for convenience, and any value in $[c^0, d^0]$ will have the desired effect.)

Lemma 4.10. Consider monotone numerical flux functions $F^k$ ($k\in {\mathscr{I}}$). Let ${\mathbf{c}}, {\mathbf{d}}$ be discrete stationary solutions satisfying $c^k \leqslant d^l$ for all $k, l\in {\mathscr{I}}$ (cf. Definition 2.7). Then $c^0, d^0$ can be modified such that ${\mathbf{c}}, {\mathbf{d}}$ remain discrete stationary solutions and such that $c^0 \leqslant d^0$.

Proof. Define

Since all $F^k$ are monotone, each $I^k(c^k)$ is a connected interval which contains $c^k$, and moreover, Lemma 4.9 says that $c^0 \in \bigcap_{k\in {\mathscr{I}}} I^k(c^k)$. This implies that $[\![{c^0}, {c^k}]\!] \subset I^k(c^k)$, where $[\![{a}, {b}]\!] = [\min(a, b), \, \max(a, b)]$. Since $\bigcap_{k\in {\mathscr{I}}}[\![{c^0}, {c^k}]\!]$ is nonempty, the number

exists and satisfies $\tilde{c}^0 \leqslant \max_{k\in {\mathscr{I}}} c^k$. Appealing again to Lemma 4.9, ${\mathbf{c}}$ remains a discrete stationary solution if $c^0$ is replaced by $\tilde{c}^0$. In a similar way we replace $d^0$ by

which satisfies $\tilde{d}^0 \geqslant \min_{k\in {\mathscr{I}}} d^k$. By our hypothesis, it follows that $\tilde c^0 \leqslant \tilde{d}^0$.

Proposition 4.11. Consider a consistent, conservative, monotone finite volume method (4.1), (4.11) with a set of discrete stationary states $\mathscr{G}_ \mathrm{disc}^0$. For any initial data $\bar {\mathbf{u}} \in L^\infty_{\mathrm{oco}}( \mathscr{G}_ \mathrm{disc}^0)$, the numerical solution is uniformly $L^\infty$ bounded.

Proof. Pick discrete stationary states ${\mathbf{c}}, {\mathbf{d}}\in \mathscr{G}_ \mathrm{disc}^0$ as in (2.9). It is clear that the initial data defined in (4.11) satisfy $c^k \leqslant u_i^{k, 0} \leqslant d^k$ for all $i\in D_ \mathrm{disc}^k$ and $k\in {\mathscr{I}}_0$. If the same holds at some time step $n\in \mathbb{N}_0$ then (using the notation (4.6'), (4.10))

for all $i\in D_ \mathrm{disc}^k$ and $k\in {\mathscr{I}}_0$, and similarly, $u_i^{k, n+1} \leqslant d_i^k$.

Definition 4.12 ($L^1$ contractive method). A numerical method (4.6') is $L^1$ contractive if

for all $t \geqslant 0$, where ${\mathbf{u}}_ {\Delta t}$ and ${\mathbf{v}}_ {\Delta t}$ are the projection of the numerical solution (cf. (4.2)) computed with initial data $\bar {\mathbf{u}}, \bar {\mathbf{v}}\in L^\infty_{\mathrm{oco}}( \mathscr{G}_ \mathrm{disc}^0)\cap L^1(\Omega;\lambda)$, respectively. (See (4.3) for the integral of ${\mathbf{u}}_ {\Delta t}$, ${\mathbf{v}}_ {\Delta t}$ w.r.t. $\lambda$.)

We state the well known Crandall–Tartar lemma which we will use in the following proof. Here and below, we use the notation $a\vee b = \max(a, b)$.

Theorem 4.13. (Crandall–Tartar: [11,Proposition 1]). Let $(\Omega, \lambda)$ be a measure space. Let $C \subset L^1 (\Omega; \lambda)$ have the property that $f, g \in C$ implies $f \vee g \in C$. Let $V\colon C \to L^1(\Omega; \lambda)$ satisfy $\int_\Omega V (f)\, d\lambda = \int_\Omega f\, d\lambda$ for $f \in C$. Then the following three properties of $V$ are equivalent:

(a) $f, g \in C$ and $f \leqslant g$ a.e. implies $V(f) \leqslant V(g)$ a.e.,

(b) $\int_\Omega (V(f) - V(g))_+ \leqslant \int_\Omega (f - g)_+$ for $f, g \in C$,

(c) $\int_\Omega \big|V(f) - V(g)\big| \leqslant \int_\Omega |f - g|$ for $f, g \in C$.

We can now prove $L^1$-contractivity of our method.

Theorem 4.14. Every conservative, consistent monotone method (4.1), (4.11) is $L^1$-contractive.

Proof. Let $C = {C_ {\Delta x}}$ be the set of piecewise constant functions,

We define the operator $V: {C_ {\Delta x}}\to {C_ {\Delta x}}$ mapping a numerical solution to the next time step,

By the definition (2.2) of the measure $\lambda$ (cf. also (4.3)), we have $\int_{\Omega} V ({\mathbf{u}}) \, d\lambda = \int_{\Omega} {\mathbf{u}} \, d\lambda$ for all ${\mathbf{u}}\in {C_ {\Delta x}}$. We apply the Crandall–Tartar lemma to conclude $L^1$-contractivity of the numerical solution operator $V$.

From $L^1$-contractivity we get continuity in time as a corollary:

Corollary 4.15. Consider a consistent, conservative and monotone method (4.1). Let ${\mathbf{u}}_ {\Delta t}$ be an approximate solution computed with this method and assume that all numerical fluxes $F^k$ are Lipschitz continuous in both arguments. Then computed solutions are uniformly $L^1$ Lipschitz continuous in time, i.e.,

where the constants $C$ and $\bar{M}$ depend on the flux functions and on the initial data.

Proof. We compute

(using Theorem 4.13(c))

where we collect all constants into the global constant $C$. We can bound $\big|f_ {\mathrm{out}} \big(u_0^0\big) - f_ {\mathrm{in}} \big(u_0^0\big)\big| \leqslant \bar M$ with a constant $\bar M \in \mathbb{R}$ since $f_ {\mathrm{in}}, f_ {\mathrm{out}}$ are continuous and $u_0^0 \in L^\infty$.

5.   Convergence of finite volume schemes

We are now in place to prove convergence in the case where the flux functions $f^k$ are strictly monotone. We do this by using the upwind method where the numerical flux functions are defined by

We shall show that the set of discrete approximations is compact in $L^\infty\big([0, \infty);L^1(\Omega; \lambda)\big)$, and that any limit is an entropy solution. In particular, this convergence result establishes existence of an entropy solution. We show convergence to a weak solution by proving a Lax–Wendroff type theorem:

Theorem 5.1 (Lax–Wendroff theorem). Fix $T > 0$. Assume that each flux function $f^k$ is locally Lipschitz continuous and strictly monotone. Let $\mathscr{G}_ \mathrm{disc}^0$ be a mutually consistent class of discrete stationary solutions for the upwind method and let ${\mathbf{u}}_ {\Delta t}$ be computed from the upwind method with initial data $\bar {\mathbf{u}} \in L^\infty_{\mathrm{oco}}( \mathscr{G}_ \mathrm{disc}^0) \cap L^1(\Omega;\lambda)$. Consider a subsequence $\big({\mathbf{u}}_{ {\Delta t}_{\ell}}\big)_{\ell\in \mathbb{N}}$ such that ${\Delta t}_{\ell} \to 0$ and ${\mathbf{u}}_{ {\Delta t}_{\ell}}\to {\mathbf{u}}$ in $L^\infty([0, T]; L^1(\Omega; \lambda))$ as $k\to\infty$. Then the limit ${\mathbf{u}}$ is the unique entropy solution to (2.1), that is, ${\mathbf{u}}$ satisfies (2.10).

Remark 5.2. The existence of a non-trivial mutually consistent germ $\mathscr{G}_ \mathrm{disc}^0$ for monotone flux functions will be shown in 6.

Proof. We write ${\Delta x}$ and ${\Delta t}$ rather than ${\Delta x}_{\ell}$ and ${\Delta t}_{\ell}$, and we shall show that $u$ satisfies the entropy condition (2.10) for every ${\mathbf{c}}\in \mathscr{G}_ \mathrm{disc}^0$. Choosing stationary solutions ${\mathbf{c}}, {\mathbf{d}}\in \mathscr{G}_ \mathrm{disc}^0$ such that ${\mathbf{c}} \leqslant {\mathbf{u}}_ {\Delta t} \leqslant {\mathbf{d}}$ (cf. Proposition 4.11) in particular shows that $u$ is a weak solution.

Let ${\mathbf{c}}\in \mathscr{G}_ \mathrm{disc}^0$ and consider the Crandall–Majda numerical entropy fluxes

for $i = 0, 1, \dots$ when $k\in {{\mathscr{I}}_{\mathrm{out}}}$, and for $i = \dots, -2, -1$ when $k\in {{\mathscr{I}}_{\mathrm{in}}}$, and

(cf. Notation 4.6 for the definition of $c_i^k$). Recalling the definition (4.5) of the update functions $G^k$, we see that

for $k\in {\mathscr{I}}$ and $i \in D_ \mathrm{disc}^k$. Hence,

Similarly, we find that

We choose $T = M {\Delta t}$ for a natural number $M$, multiply the above $N+1$ inequalities with a test function $\varphi$ and sum up to get

where $\varphi_i^{k, n} = \varphi^k(x_i, t^n)$. After summation by parts we get

After shifting the $i$ index on the second line we get

Taking limits we get for ${\Delta t}, {\Delta x} \to 0$

and for ${\Delta x} \to 0$

Thus, we are left with $A_3$. Since the scheme is the upwind method, we can write

as ${\Delta t}, {\Delta x} \to 0$, due to the a.e. pointwise convergence of ${\mathbf{u}}_{ {\Delta t}}$ to ${\mathbf{u}}$.

Now we have everything in place to proof a compactness theorem.

Theorem 5.3 (Compactness and Convergence to a Weak Solution). Fix $T > 0$. Assume that each flux function $f^k$ is locally Lipschitz continuous and strictly monotone. Let $\mathscr{G}_ \mathrm{disc}^0$ be a set of discrete stationary states for the upwind method. Let ${\mathbf{u}}_ {\Delta t}$ be computed from the upwind method with initial data $\bar {\mathbf{u}} \in L^\infty_{\mathrm{oco}}( \mathscr{G}_ \mathrm{disc}^0) \cap L^1(\Omega;\lambda)$, and assume that ${\rm TV}(\bar {\mathbf{u}})<\infty$. Then the numerical solution $\{ {\mathbf{u}}_ {\Delta t}\}_{ {\Delta t}>0}$ converges in $C([0, T], L_ {\mathrm{loc}}^1(\Omega;\lambda))$ to a weak solution ${\mathbf{u}}$.

Proof. We first show convergence of the sequence of functions ${\mathbf{g}}_ {\Delta t}\colon\Omega\times[0, T]\to \mathbb{R}$,

The sequence ${\mathbf{g}}_ {\Delta t}$ is uniformly $L^\infty$ bounded, by Proposition 4.11, and it is Lipschitz continuous in time:

by Corollary 4.15. We can bound the total variation of ${\mathbf{g}}_ {\Delta t}$ by

Applying Ascoli's compactness theorem together with Helly's theorem, we get the existence of a subsequence ${\Delta t}_\ell\to 0$ such that ${\mathbf{g}}_{ {\Delta t}_\ell} \to {\mathbf{g}}$ in $C([0, T], L^1_ {\mathrm{loc}}(\Omega;\lambda))$ for some function ${\mathbf{g}}$. The strict monotonicity of $f^k$ implies that

and hence, also ${\mathbf{u}}_{ {\Delta t}_\ell}$ converges in $C([0, T], L^1_ {\mathrm{loc}}(\Omega;\lambda))$ to some function ${\mathbf{u}}$. Theorem 5.1 implies that ${\mathbf{u}}$ is the entropy solution; since this solution is unique (Theorem 3.1), the entire sequence $\{ {\mathbf{u}}_ {\Delta t}\}_{ {\Delta t}>0}$ must converge to ${\mathbf{u}}$.

6.   Discrete stationary solutions for monotone flux functions

So far we have shown that if a sufficiently large class of stationary and discrete stationary solutions exists, then our equations on the network are well posed and the finite volume numerical approximations converge to the entropy solution. In this section we show that such classes exist in the case where either all fluxes $f^k$ are strictly increasing or all are strictly decreasing. We also remark on the more general case.

6.1.   Monotone flux functions

We henceforth assume that all fluxes are increasing; one can attain analogous results for decreasing fluxes following the same arguments. In the following we want to investigate the sets of discrete stationary solutions implied by the upwind method.

We define

It is clear that $f_ {\mathrm{in}}, f_ {\mathrm{out}}$ are monotone by the monotonicity of their summand components. In particular, the two functions are invertible.

For the upwind method the conditions (4.9a) and (4.9b) become

This is equivalent to

due to the invertibility of the flux functions $f^k$. It is obvious as well, that for two different discrete stationary solutions ${\mathbf{c}}, {\mathbf{d}}$ satisfying $c^k \leqslant d^k$ for $k \in {\mathscr{I}}$, we also have $c^0 \leqslant d^0$. Henceforth, we denote

and we let

Although it might be too difficult to find a full characterization of the set $L^\infty_{\mathrm{oco}}( \mathscr{G})$ of admissible initial data, we will be able to characterize large subsets of $L^\infty_{\mathrm{oco}}( \mathscr{G})$. Let

where

By the continuity of $f_ {\mathrm{in}}, f_ {\mathrm{out}}$, the sets $I_ {\mathrm{in}}, I_ {\mathrm{out}}$ are closed intervals.

Theorem 6.1. We have $\mathscr{L}\subset L^\infty_{\mathrm{oco}}( \mathscr{G}_ \mathrm{disc})$, where

In particular, if $f_ {\mathrm{in}}, f_ {\mathrm{out}}$ have the same range $R_ {\mathrm{in}}, R_ {\mathrm{out}}$, then $L^\infty_{\mathrm{oco}}( \mathscr{G}_ \mathrm{disc}) = L^\infty(\Omega;\lambda)$.

Proof. Let ${\mathbf{u}}\in\mathscr{L}$. Since ${\mathbf{u}}\in L^\infty(\Omega;\lambda)$, and $I_ {\mathrm{in}}, I_ {\mathrm{out}}$ are closed, we also have

and likewise for $\underline{c}_ {\mathrm{out}}, \overline{c}_ {\mathrm{out}}$. By continuity of $f_ {\mathrm{in}}, f_ {\mathrm{out}}$, there are $\underline{d}_ {\mathrm{in}}\in I_ {\mathrm{in}}$ and $\underline{d}_ {\mathrm{out}}\in I_ {\mathrm{out}}$ satisfying $\underline{d}_ {\mathrm{in}} \leqslant\underline{c}_ {\mathrm{in}}$ and $\underline{d}_ {\mathrm{out}} \leqslant \underline{c}_ {\mathrm{out}}$ so that $f_ {\mathrm{in}}(\underline{d}_ {\mathrm{in}}) = f_ {\mathrm{out}}(\underline{d}_ {\mathrm{out}})$, that is, the vector $\underline{ {\mathbf{d}}}: = \bigl(\underline{d}_ {\mathrm{in}}, \dots, \underline{d}_ {\mathrm{in}}, \underline{d}_ {\mathrm{out}}, \dots, \underline{d}_ {\mathrm{out}}\bigr)$ is a stationary solution. This stationary solution clearly satisfies (6.2), whence ${\mathbf{d}}\in \mathscr{G}_ \mathrm{disc}^0$.

In a similar way one finds a stationary solution $\overline{ {\mathbf{d}}}: = \bigl(\overline{d}_ {\mathrm{in}}, \dots, \overline{d}_ {\mathrm{in}}, \overline{d}_ {\mathrm{out}}, \dots, \overline{d}_ {\mathrm{out}}\bigr) \in \mathscr{G}_ \mathrm{disc}^0$ which bounds ${\mathbf{u}}$ from above. Since now

we conclude that ${\mathbf{u}}\in L^\infty_{\mathrm{oco}}( \mathscr{G}_ \mathrm{disc})$.

Proposition 6.2. Consider a conservation law on a network with strictly increasing fluxes $f^k$. Let $\mathscr{G}_ \mathrm{disc}^0$ denote the set of all discrete stationary solutions for the upwind method. Then the set

is a mutually consistent and maximal set of stationary solutions.

Proof. Every ${\mathbf{c}}\in \mathscr{G}_ \mathrm{disc}$ is a stationary solution due to (4.8).

To prove mutual consistency of $\mathscr{G}_ \mathrm{disc}$ we plug a discrete stationary solution ${\mathbf{d}}\in \mathscr{G}_ \mathrm{disc}^0$ into (5.1) to get for $n \in \mathbb{N}$,

Since we are using the upwind scheme, this reduces to

In the same manner, plugging $d^0$ into (5.2) gives us

Combining these two observations, we get

As ${\mathbf{c}}, {\mathbf{d}}$ were arbitrary, it follows that $\mathscr{G}_ \mathrm{disc}$ is mutually consistent.

If for some vector ${\mathbf{d}}$, the set $\mathscr{G}_ \mathrm{disc} \cup \lbrace {\mathbf{d}} \rbrace$ is mutually consistent, then

We choose $c^k = d^k\ \forall\ k \in {\mathscr{I}}_ {\mathrm{in}}$ and $c^0 = (f_ {\mathrm{out}})^{-1}(\sum_{k\in {\mathscr{I}}_ {\mathrm{in}}} f^k(c^k))$. Since all $f^k$ are monotonically increasing, the entropy flux reduces to $q^k_{c^k}(d^k) = \big|f^k(c^k) - f^k(d^k)\big|$ and thus,

which implies $d^k = c^0$ for $k \in {\mathscr{I}}_ {\mathrm{out}}$, and thus, ${\mathbf{d}}\in \mathscr{G}_ \mathrm{disc}$. In other words, $\mathscr{G}_ \mathrm{disc}$ is maximal.

6.2.   General flux functions

Although the framework presented in this manuscript is only applied to monotone flux functions, we remark here on the generalization of our results to more general choices of $f^k$. The two main ingredients are

● compactness of the sequence of approximations (here achieved via a TV bound on the (upwind) numerical flux);

● the existence of a maximal set of stationary states, and the consistency of the approximations with respect to that set.

A TV bound on the numerical fluxes can be achieved in a more general setting, but that does not easily translate to compactness of the approximation itself. This can be achieved by a detour via the Temple functional [28]. The derivation of a maximal set of stationary states requires a careful design of the numerical method. We address both of these issues in the upcoming paper [13], where we prove convergence of an Engquist–Osher-type finite volume method for more general flux functions.

7.   Numerical examples

We show numerical experiments for some example cases including results for linear and nonlinear as well as convex and concave fluxes. In all experiments we use a CFL number of ${1/2}$ – that is, ${\Delta t}$ is chosen so that there is equality in (4.7). In all experiments we compute the experimental order of convergence (EOC) as $p \approx \dfrac{\log(e^{j+1}/e^{j})}{\log({\Delta x}_{j+1}/ {\Delta x}_j)}$ on a series of successive grids with $2^{j}$ cells, where $e^j$ denotes the $L^1$ error on grid level $j$. The error is computed as the $L^1$ difference to a high-resolution reference solution. All errors and EOC are displayed in Table 1.

Example 7.1 (Burgers' equation with roundabout). In this example we include a roundabout – an edge whose endpoints meet at the same vertex, as shown in Figure 2. This case was not included in the theory but is interesting because it is analogous to a periodic boundary condition. We also include an ingoing edge and two outgoing edges, amounting to a total of two ingoing and three outgoing edges. As initial data we choose constants on the roundabout and the outgoing edges and two different constants on the independent ingoing edge. After a while the shock in the initial data on the independent ingoing edge will reach the edge and create new Riemann problems. We choose the initial data

We take all edges to have length $1$ and choose zero Neumann boundary data on the outer boundaries. On the vertex we set $u_0^0 = 1$. On the ingoing edge with index $-1$ we have a travelling shock wave

which will hit the vertex at $t^* = 1-\frac{1}{\sqrt{2}}$. To compute the solution after $t^*$ we compute the new vertex value $c^0 = \sqrt{5/3}$ and therefore get the Riemann problem

for $k = 1, 2, 3$, which results in a travelling shock wave with speed $s = \frac{1}{\sqrt{5/3} - 1}$. At time $t^{**} : = \sqrt{5/3} - \frac{1}{\sqrt{2}}$ the travelling shock wave which originated on the roundabout edge hits the vertex once again, resulting in a new set of Riemann problems on the outgoing edge. This process will continue in a periodic fashion.

We compute up to time $T = 0.5$. A plot of the exact and approximate solution to this example at two different times is shown in Figure 3. The accuracy and order of convergence of the numerical approximation are shown in Table 1.

Example 7.2. We construct an example where we take the flux function from the traffic flow example in [18], $f(u) = 4u(1-u)$, but allow for different fluxes on different edges, $f^k(u) = \alpha^k f \big(\frac{u}{\alpha^k} \big)$ for $\alpha^k>0$, and compute on a star shaped graph with two ingoing edges and three outgoing edges like in Figure 1. The initial data is chosen so that all fluxes are strictly increasing over the range of $\bar u$; thus, the fluxes $f^k$ are in effect monotonously increasing functions. We choose constant solutions on the two ingoing roads and constant initial data on the outgoing roads which are chosen such that on one road a shock will develop, on one road the solution will stay constant over time and on one road a rarefaction wave will develop.

Solving the conditions (4.8), (4.9) for $c^0$ yields

For the incoming edges to have a monotonically increasing flux we impose $u_{-i} \leqslant \frac{1}{2} \alpha_{-i},$ for $i = 1, 2$ and for outgoing edges $c^0 \leqslant \frac{1}{2} \min \lbrace \alpha_1, \alpha_2, \alpha_3 \rbrace$. We choose $\alpha_{-1} = \alpha_{-2} = 1$, $\alpha_1 = \alpha_2 = 4$ and $\alpha_3 = 2$ with initial data

This gives us $c^0 = \frac{1}{2}(3 - \sqrt{7})$. On the outer boundary we choose zero Neumann boundary conditions. For $u^3$ we will get a shock

with speed $s = \frac{(3-\sqrt{7})(2-\frac{3-\sqrt{7}}{4})-3}{\frac{3-\sqrt{7}}{2}-1},$ and a rarefaction wave for $u^1$ of the form

On edge $2$ we get the constant solution $u^2 \equiv \frac{1}{2}(3 - \sqrt{7})$.

We compute up to time $T = 0.2$. A plot of the exact and approximate solution at two different timepoints is shown in Figure 4. Accuracy and order of convergence of the numerical approximation are shown in Table 1.

In addition to the examples described above we show errors and experimental order of convergence (EOC) for several additional examples in Table 1.

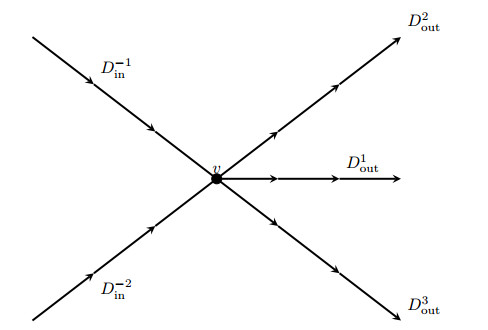
Example 7.3 (EOC: Linear advection). We consider a linear advection equation with two ingoing edges and three outgoing edges as in Figure 1 with initial data

and Dirichlet boundary conditions adapted to the edge values. We initialize the vertex node by $u_0^0 = \frac{2}{3}$. We compute up to time $T = 0.5$.

Example 7.4 (EOC: Burgers' equation with elementary waves). We choose $\bar u^{-1} = \bar u^{-2} \equiv 1$ as initial data on the ingoing roads and $\bar u^1 \equiv 0$, $\bar u^2 \equiv\sqrt{2/3}$ and $\bar u^3 \equiv 2$ on the outgoing edges of a star shaped graph as in Figure 1. The conditions on the numerical flux imply then $3(c^0)^2 = 2 \Leftrightarrow c^0 = \sqrt{3/2}$. Thus, we get the following Riemann problems on the outgoing roads:

with zero Neumann boundary conditions at the outer edges. The solution to these problems are a shock, a constant solution and a rarefaction wave, respectively. We compute up to time $T = 0.3$.

Example 7.5 (EOC: Burgers' equation with travelling shock). We consider a Burgers-type equation with two ingoing edges and three outgoing edges as in Figure 1 with initial data

with Dirichlet boundary conditions of the same value as the associated edge. On the vertex node the initial condition is chosen as $u_0^0 = \sqrt{\frac{2}{3}}$. We compute up to $T = 0.5$.

7.1.   Comments on the experiments

Convergence order estimates for finite volume methods for nonlinear scalar conservation laws are due to Kuznetsov [22] for the continuous flux case and due to Badwaik, Ruf [5] for the case of monotone fluxes with points of discontinuity. In both of those cases the analytically proven convergence rate is at least $\sqrt{ {\Delta x}}$. Our numerical experiments indicate the same lower bound on the convergence rate for our numerical methods on graphs. Considering the fact that $f_ {\mathrm{in}}$ and $f_ {\mathrm{out}}$ from Section 6 are monotone it might be possible to generalize the result of Badwaik and Ruf to networks.

8.   Summary and outlook

In conclusion we have defined a framework for the analysis and numerical approximation of conservation laws on networks. We extended the concepts well known from the conventional case such as weak solution, entropy solution and monotone methods to make sense on a directed graph. We defined a reasonable entropy condition under which we have shown stability and uniqueness of an analytic solution. Existence is shown by convergence of a conservative, consistent, monotone difference scheme. In an upcoming work [13] we want to address convergence of a numerical method where the fluxes $f^k$ are not monotone but concave, as is usually found in traffic flow models. This includes deriving a sufficiently large set of stationary and discrete stationary solutions for this case. Further, we want to extend our model to include boundary conditions and derive a convergence order estimate for numerical approximations. As for future work, a generalization to systems of conservation laws would be highly desirable. One could also try to construct numerical schemes for equations incorporating diffusive fluxes like it was done in [20] on the line. Generalized models would span more complex scenarios such as blood circulation [6] in a network of veins or a river delta by the means of Euler equations and shallow water equations, respectively.

Acknowledgments

We would like to thank the referee for the valuable comments, helping to improve the quality of this work.