Cutaneous allodynia association with migraine and their predictors among primary healthcare visitors

1.   Introduction

Along with the rapid development of biology and biotechnology, the regulation and interaction of mRNAs and the produced proteins in genetic regulatory networks (GRNs) have attracted great research attention, and various related applications have been available to address the burgeoning areas ^[1,2,3]. Furthermore, much effort has been devoted to the biochemical dynamics of GRNs, which can better describe the expression mechanisms of genes from a dynamical system perspective ^[4,5]. The dynamical behaviors of GRNs can considerably provide deeper insights into the processing conditions. Generally speaking, differential equation and Boolean network models are employed and investigated to characterize complex properties of mRNA and protein concentrations in GRNs ^[6,7,8]. In particular, biological evidences have proved the existences of jumping mechanisms of GRNs. This means that the dynamical parameters of GRNs are varying according to different modes rather than kept constant owing to random abrupt changes during gene expressions. This means that the parameters of GRNs should be modified according to certain modes. With this context, mathematical models of Markovian jumping systems with Markov chains have been widely employed to mimic the intrinsic variate of GRNs ^[9,10,11]. As a result, many remarkable results on Markovian jumping GRNs have been reported in the literature, which includes stochastic state estimation ^[12], stability ^[13] and synchronization issues ^[14].

In addition, the accessibility of true jumping mode information of GRNs has also drawn much interest, especially for some actual applications. It is noteworthy that the exact mode information of GRNs in practical applications is always difficult or expensive to acquire, which is mostly because of detection delays or unpredictable disturbances during the transcription and translation processes ^[15,16]. Especially, the mode information characterized by Markov chains for state estimation or control issues is also challenging to main synchronous design. On the other hand, nonsynchronous analysis and synthesis methods are more meaningful and practical for Markovian jumping GRNs with mode-dependent designs. Lately, hidden Markovian jumping systems have been initially investigated by external mode observations and encouraging results of the so-called nonsynchronous designs have been reported accordingly. More precisely, on the basis of conditional probability between true modes and observed modes, the observed models for mode information are effectively utilized without synchronous mode operations ^[17,18,19].

On another active research line, distributed strategies for control systems have been extensively developed due to their increasing requirements for efficiency and robustness in engineering areas. Compared with traditional control techniques, the distributed architecture can process and fuse the information via multiple sensors with each domain data. With respect to its advances, many remarkable analysis and synthesis of distributed control systems can be found in recent works ^[20,21,22]. To name a few, in ^[23], a novel distributed-observer-based distributed control design is developed for affine nonlinear systems and is effectively applied to interconnected cruise control of intelligent vehicles. In ^[24], the distributed observer and controller design issue is discussed for spatially interconnected systems. In ^[25], the distributed state observers and disturbance observers are proposed for cooperative output regulation of LTI system to ensure the reference tracking properly. In ^[26], a distributed Nash equilibrium seeking scheme is designed with nonlinear dynamical system. In ^[27], the leader-following output consensus problem is concerned with distributed nonlinear observers. These notable works have proven that distributed frameworks can effective improve the system performance for complex dynamical systems. However, the problems of network communication burden must be faced among the nodes. It should be emphasized that traditional time-triggered periodic communication schedules have certain drawbacks in computation and network resources. Fortunately, the emerging event-triggered schemes are developed aiming at necessary transmission only when speechified triggering conditions are satisfied ^[28,29,30]. Hence, the event-triggered mechanism could lead to less network consumptions and could be more reliable in line with practical network implementation. Furthermore, in view of distributed control systems, distinguishing advantages can also been made by adopting event-triggered communications ^[31,32,33]. Nevertheless, there are challenging problems for distributed event-triggered control in corresponding algorithm complexity. For the consideration of GRNs with HMJPs, it is reasonable and significant to apply the distributed event-triggered design. Unfortunately, until now, distributed event-triggered state estimation problem of GRNs has not been entirely studied, not to mention the case of HMJPs with NSE. This motivates the authors for current study to shorten such a gap.

To deal with the aforementioned issue, the key idea in this paper is to investigate the distributed event-triggered state estimation problem for GRNs with HMJPs based on the NSE scheme. Compared with most existing literature, the primary novelties of our work are highlighted as follows:

1) The attempt to deal with the distributed NSE design of GRNs with HMJPs is made for the first time, which can better model GRNs dynamics and mode jumping phenomena during the state estimation procedures.

2) The distributed nonsynchronous state estimation framework is also introduced for GRNs with nonsynchronous event-triggered communications, such that more estimation efficiency for concentrations of mRNAs and proteins can be achieved with effective mode information utilization.

3) The sufficient mode-dependent analysis criteria are established by novel Lyapunov-Krasovski functions, and then the desired nonsynchronous mode-dependent estimator gains can be derived with convex optimization.

The remainder of this paper is stated by the following lines. Section 2 introduces some background information regarding GRNs with HMJPs and formulates the state estimation problem. Subsequent session of Section 3 presents the main theoretical developments with details. Section 4 approves the correctness of our developed results through a numerical example. Section 5 concludes the paper and addresses future challenges.

All referred notations are standardly utilized. $\mathscr{R}^{n}$ stands for $n$-Euclidean space. Matrix $\mathbb{P} > 0$ means that $\mathbb{P}$ is symmetric positive definite, and vise versa. $(\mathbb{O}, \mathbb{F}, \mathbb{P})$ corresponds a probability space, where $\mathbb{O}$ denotes sample space, $\mathbb{F}$ represents $\delta$-algebra of subsets within $\mathbb{O}$ and $\mathbb{P}$ stands for probability measurement. $\mathbb{E}$ means the mathematical expectation and $*$ implies a induced term in symmetry matrices, respectively.

2.   Problem statement and preliminaries

Consider the equilibrium points of GRNs model shifted to the origin and the following GRNs model with HMJPs can be described by:

where $x_{m}\left(t\right) = [x_{m1}\left(t\right), x_{m2}\left(t\right), \ldots, x_{mn}\left(t\right) ]^{T}\in \mathscr{R}^{n}$, $x_{p}\left(t\right) = [x_{p1}\left(t\right), x_{p2}\left(t\right), \ldots, x_{pn}\left(t\right) ]^{T}\in \mathscr{R}^{n}$ with $x_{mi}\left(t\right)$ and $x_{pi}\left(t\right),$ $i = 1, 2, \ldots, n$ representing the concentrations of mRNAs and proteins, respectively; $z_{m}\left(t\right) = [z_{m1}\left(t\right), z_{m2}\left(t\right), \ldots, z_{ml}\left(t\right) ]^{T}\in \mathscr{R} ^{l}$, $z_{p}\left(t\right) = [z_{p1}\left(t\right), z_{p2}\left(t\right), \ldots, z_{pl}\left(t\right) ]^{T}\in \mathscr{R}^{l}$ with $z_{mk}\left(t\right)$ and $z_{pk}\left(t\right),$ $k = 1, 2, \ldots, l$ being the concentrations of certain mRNAs and proteins to be estimated through expression level; $g\left(x_{p}\left(t-d_{p}(t)\right) \right) = [g_{1}\left(x_{p1}\left(t-d_{p}(t)\right) \right), g_{2}\left(x_{p2}\left(t-d_{p}(t)\right) \right), \ldots, g_{n}\left(x_{pn} \left(t-d_{p}(t)\right) \right) ]^{T}\in \mathscr{R}^{n}$ stands for the nonlinear feedback regulation function of the protein on transcription, which satisfies the following assumption

i.e.,

$0\leq d_{p}(t)\leq \bar{d}_{p}$ and $0\leq d_{m}(t)\leq \bar{d}_{m}$ are the translation delay and the feedback regulation delay, respectively$;$ $\omega _{1}(t)$ and $\omega _{2}(t)$ refers to the external disturbances that belongs to $\mathcal{L}_{2}[0, \infty)$.

The degradation or dilution rates of mRNAs and proteins can be described by known matrices $A\left(r\left(t\right) \right) = diag\{a_{1}\left(r\left(t\right) \right), a_{2}\left(r\left(t\right) \right), \ldots, a_{n}\left(r\left(t\right) \right) \}$, $C\left(r\left(t\right) \right) = diag\{c_{1}\left(r\left(t\right) \right), c_{2}\left(r\left(t\right) \right), \ldots, c_{n}\left(r\left(t\right) \right) \}$, $D\left(r\left(t\right) \right) = diag\{d_{1}\left(r\left(t\right) \right), d_{2}\left(r\left(t\right) \right), \ldots, d_{n}\left(r\left(t\right) \right) \}$, and the coupling matrix $B\left(r\left(t\right) \right) = (b_{ij}\left(r\left(t\right) \right))\in \mathscr{R}^{n}$ can be defined by the following

Furthermore, $U_{m}\left(r\left(t\right) \right)$, $U_{p}\left(r\left(t\right) \right),$ $E_{m}\left(r\left(t\right) \right)$ and $E_{p}\left(r\left(t\right) \right)$ are also known matrices for a certain mode $r\left(t\right).$

Moreover, the continuous-time discrete-state Markov process $r\left(t\right) \in \mathcal{S} = \{1, \ldots, \mathcal{N}\}$ on $(\mathbb{O}, \mathbb{F}, \mathbb{P})$ is given to model the HMJPs, which can be defined by $\Pi = (\pi _{ij})_{\mathcal{N}\times \mathcal{N}}$, with

and $\pi _{ii} = -\underset{j = 1, \;\;i\neq j}{\overset{\mathcal{N}}{\sum \limits}} \pi _{ij}$.

In this paper, a direct graph $\mathbb{G = }\left\{ \mathbb{V}, \mathbb{E}, \mathbb{A} \right\}$ is given to describe the communication topology of $N$ sensor nodes, where $\mathbb{V = }\left\{ v_{1}, v_{2}, \cdots, v_{N}\right\}$ and $\mathbb{E}\subseteq \mathbb{V}\times \mathbb{V}$ stand for the set of nodes and edges, respectively, $\mathbb{A = }\left[ a_{ij}\right] \in \mathbb{R}^{N\times N}$ represent the adjacency matrix with $a_{ii} = 0$ for any $i$. $\mathbb{A}$ is associated with the edges of $\mathbb{G}$ are positive, i.e., $a_{ij} > 0\Longleftrightarrow \varepsilon _{ij}\in \mathbb{E}$. In addition, the corresponding Laplacian matrix of $\mathbb{G}$ is defined as $\mathbb{L}$.

Moreover, the distributed measurement is achieved by $N$ mode-dependent sensor nodes as follows:

where $y_{m}^{l}(t)$ and $y_{p}^{l}(t)$, $l = 1, 2, \ldots, N,$ represent the measurements of mRNAs and proteins on sensor $l$, respectively; $\omega _{3}(t)$ and $\omega _{4}(t)$ are measurement disturbances; $H_{m}^{l}(r(t)),$ $H_{p}^{l}(r(t)),$ $G_{m}^{l}(r(t))$, $G_{p}^{l}(r(t))$ are known constant matrices.

Then, define the sensor estimation errors $\tilde{y}_{m}^{l}(t)$ and $\tilde{y}_{p}^{l}(t)$ as follows

where $\hat{x}^{l}_{m}(t)$ and $\hat{x}^{l}_{p}(t)$ denote the filter state for sensor $l$.

By considering the event-triggered strategy for data transmission with ZOHs, it is assumed that the sampling period $h_{k}$ with sampling instants $t_{k}$ is assumed to be $h_{k} = t_{k+1}-t_{k}\leq \bar{h},$ $\bar{h} > 0.$ Furthermore, the transmission instant $t_{\delta }^{l}$ for sensor $l$ is determined by the event generation functions as follows:

where $\tilde{y}^{l}(t_{k}) = [(\tilde{y}_{m}^{l}(t))^{T}, (\tilde{y} _{p}^{l}(t))^{T}]^{T}$ and $0 < \kappa < 1$ is a scalar parameter.

Consequently, the following distributed mode-dependent state estimation filter $(\Sigma _{F})$ can be designed for system $(\Sigma _{M})$:

where $t\in \left[ t_{\delta }^{l}, t_{\delta +1}^{l}\right),$ $\delta ^{\ast } = \arg \min_{\mu }\left\{ t-t_{\mu }^{s}|t\geq t_{\mu }^{s}\right\},$ $\hat{z}_{m}^{l}\left(t\right)$ and $\hat{z}_{p}^{l}\left(t\right) \ $ stand for estimation of $z_{m}\left(t\right)$ and $z_{p}\left(t\right),$ respectively; $F_{m}^{l}(\sigma (t)), F_{p}^{l}(\sigma (t))$ and $K_{m}^{l}(\sigma (t)), K_{p}^{l}(\sigma (t))$ represent the nonsynchronous mode-dependent filter gains to be determined later. More precisely, $\sigma (t)\in \mathcal{F} = \{1, \ldots, F\}$ represents another Markov process corresponds to $r\left(t\right)$ with

and $\sum_{\rho = 1}^{F}\lambda _{i\rho } = 1.$

Remark 1. As event-triggered control strategy for networked control systems becomes more important, it is reasonable to investigate the analysis and synthesis issues for GRNs over sensor networks with event-triggered schemes. In comparison with common time-triggered strategies with extensive data transmissions, the event-triggered framework can considerably reduce the communication burden by generated events. Moreover, our developed event-triggered mechanism is related with both measurements of mRNAs and proteins, which is more efficient for potential applications.

Then, it can be deduced by dividing $\left[ t_{\delta }^{l}, t_{\delta +1}^{l}\right)$ into $\cup _{\iota_{k} = t_{\delta }^{l}}^{t_{\delta +1}^{l}-h_{k+1}}\left[ \iota_{k}, \iota_{k+1}\right)$ that

where $\varepsilon _{m}^{l}(\iota _{k}) = \tilde{y}_{m}^{l}\left(\iota _{k}\right) - \tilde{y}_{m}^{l}(t_{\delta }^{l})$ and $\varepsilon _{p}^{l}(\iota _{k}) = \tilde{y}_{p}^{l}\left(\iota _{k}\right) -\tilde{y}_{p}^{l}(t_{\delta }^{l}),$ $t_{\delta }^{l}\leq \iota _{k} < t_{\delta +1}^{l},$ represent the event-triggered measurement errors, respectively.

As a result, by denoting $e_{m}^{l}(t) = x(t)-\hat{x}_{m}^{l}(t),$ $e_{p}^{l}(t) = x(t)-\hat{x}_{p}^{l}(t),$ $\tilde{z}_{m}^{l}(t) = z(t)-\hat{z} _{m}^{l}(t)$ and $\tilde{z}_{p}^{l}(t) = z(t)-\hat{z}_{p}^{l}(t)$, one can deduce that

For simplicity, the resulting closed-loop filter system can be rewritten as follows:

where

Remark 2. It is noticed that the adoption of conditional probability has been proved to be effective to cope with the Markov or semi-Markov jump systems with limited mode information. For the GRNs with hidden Markovian jumping parameters, lack of true operation modes of Markov chains would lead to control performance degradation or even unstable with mode-dependent designs. In this paper, the nonsynchronous mode information corresponds to the distributed sensor mode information, which implies that mode information mismatch between true GRNs model and our developed distributed state estimators is considered during the design. As a consequence, we have developed a novel distributed nonsynchronous filter framework, where the observed Markovian jumping modes are utilized for more practical distributed event-triggered state estimators.

Consequently, by applying the input-delay approach, it can be obtained that

where $\tau (t): = t-\iota _{k}$ with $0\leq \tau (t)\leq \bar{\tau}.$

The aim of our paper is to design the desired nonsynchronous state estimator gains, such that the modified $H_{\infty }$ performance $\gamma$ can be satisfied in the mean-square sense for augmented state estimation error system with zero initial conditions, if it can hold that

In the sequel, the following lemmas are employed for later theoretical derivations.

Lemma 1. ^[34] For any matrix $\mathbb{M} > 0$, scalars $\bar{\xi} > 0$, $\xi (t)$ satisfying $0\leq \xi (t)\leq \bar{\xi}$, vector function $\dot{x} (t):[-\bar{\xi}, 0]\rightarrow \mathbb{R}^{n}$ such that the concerned integrations are well defined in (2.12), then

where

Lemma 2. ^[35] If there exists a parameter $\varepsilon$ and real matrices $\mathbb{X}$, $\mathbb{Y},$ $\mathbb{Z}$, $\mathbb{W}$, and it holds that

then one has

3.   Main results

In this section, sufficient modified $H_{\infty }$ performance conditions are first established for the augmented state estimation error system and the distributed state estimator gains are further designed in terms of convex optimization.

Theorem 1. For given $\bar{d}_{p}$, $\bar{d}_{m}$, $\bar{\tau}$ and mode-dependent filter gains $F_{m}^{l}(\rho), F_{p}^{l}(\rho)$ and $K_{m}^{l}(\rho), K_{p}^{l}(\rho)$, the modified $H_{\infty}$ filtering can be satisfied over distributed sensor networks according to Definition 1, if there exist mode-dependent matrices $P_{m}(i) > 0$, $P_{p}(i) > 0$, and matrices $Q_{m} > 0$, $Q_{p} > 0$, $Q_{\tau} > 0$, $R_{m} > 0$, $R_{p} > 0$, $R_{\tau} > 0$, such that $\Xi _{i} < 0$, for all $i\in \mathcal{N}$, $k = 1, 2, \ldots, N$ and $\rho\in \mathcal{F}$, $k = 1, 2, \ldots, F$, where

and

Proof. Construct the following mode-dependent Lyapunov-Krasovski functions:

where

Then, for all $r(t) = i$ and $\sigma (t) = \rho$, by defining the weak infinitesimal operator $\mathcal{L}$ of $V(i, t)$ as follows

it can be deduced that

Similarly, it can be deduced that

and

where $\psi ^{T}(t) = [e_{m}^{T}(t), e_{m}^{T}(t-\tau (t)), e_{m}^{T}(t-\bar{\tau }), e_{m}^{T}\left(t-\bar{d}_{m}\right), e_{m}^{T}\left(t-d_{m}(t)\right), e_{p}^{T}\left(t-\bar{d}_{p}\right), e_{p}^{T}\left(t-d_{p}(t)\right), e_{p}^{T}(t), e_{p}^{T}(t-\tau (t)), e_{p}^{T}(t-\bar{\tau}), \bar{g} ^{T}\left(e_{p}\left(t-d_{p}(t)\right) \right), \varepsilon _{m}^{T}(t-\tau (t)), \varepsilon _{p}^{T}(t-\tau (t)), \omega _{1}^{T}(t), \omega _{2}^{T}(t), \omega _{3}^{T}(t-\tau (t)), \omega _{4}^{T}(t-\tau (t))]^{T}$ and

In the sequel, by virtue of Lemma 1, one can obtain that

Then, it can be deduced that

where $\eta ^{T}\left(t\right) = [\eta ^{T}_{1}\left(t\right), \eta ^{T} _{2}\left(t\right), \eta ^{T} _{3}\left(t\right), \eta ^{T} _{4}\left(t\right) ]$ with

and $\Lambda = \Lambda _{1}+\Lambda _{2}R_{m}\Lambda _{2}^{T}+\Lambda _{3}R_{p}\Lambda _{3}^{T}+\Lambda _{4}R_{\tau }\Lambda _{4}^{T}+\Lambda _{5}R_{\tau }\Lambda _{5}^{T}$ with

Furthermore, considering the nonlinear properties for the GRNs, it yields that

In addition, by recalling the event-triggering conditions, one has

where $\tilde{y}^{l}(\iota _{k}) = [(\tilde{y}_{m}^{l}(t))^{T}, (\tilde{y} _{p}^{l}(t))^{T}]^{T}$, $\varepsilon ^{l}(\iota _{k}) = [(\varepsilon _{m}^{l}(\iota _{k}))^{T}, (\varepsilon _{p}^{l}(\iota _{k}))^{T}]^{T}$ and it can be further verified that

As a consequence, it can be derived by Schur complement that the modified $H_{\infty}$ performance can be achieved under the mean-square sense when $\Xi(i) < 0$ is satisfied according to Theorem 1, which implies that

and therefore completes the proof.

Remark 3. The above established sufficient convex optimization conditions are derived with aid of linear matrix inequality technique, which can be easily solved by Matlab LMI toolbox or other mathematical softwares. It should be pointed out that the matrix dimension dependents on both system mode information and the sensor networks structure, which means that the more system modes and sensors are involved, the more computational consumption is needed. As a result, the distributed state estimators should be well designed for practical system implements with considerable computational efficiency.

Theorem 2. For given $\bar{d}_{p}$, $\bar{d}_{m}$, $\bar{\tau}$ and the modified $H_{\infty }$ filtering can be satisfied over distributed sensor networks according to Definition 1, if there exist mode-dependent matrices $P_{m}(i) > 0$, $P_{p}(i) > 0$, $X_{m}(i) > 0$, $X_{p}(i) > 0$, $Y_{F, m}\left(\rho \right)$, $Y_{F, p}\left(\rho \right)$, $Y_{K, m}\left(\rho \right)$, $Y_{K, p}\left(\rho \right),$ and matrices $Q_{m} > 0$, $Q_{p} > 0$, $Q_{\tau } > 0$, $R_{m} > 0$, $R_{p} > 0$, $R_{\tau } > 0$, such that $\tilde{\Xi} _{i} < 0$, for all $i\in \mathcal{N}$, $k = 1, 2, \ldots, N$ and $\rho \in \mathcal{F}$, $k = 1, 2, \ldots, F$, where

and

With the aforementioned feasible solutions, the desired mode-dependent filter gains $F_{m}^{l}(\sigma (t)), F_{p}^{l}(\sigma (t))$ and $K_{m}^{l}(\sigma (t)), K_{p}^{l}(\sigma (t))$ can be obtained by the following calculation:

Proof. By pre- and post-multiplying $diag\{I, I, I, I, I, I, I, I, I, I, I, P_{m}\left(i\right), P_{p}\left(i\right), P_{m}\left(i\right), P_{p}\left(i\right) \}$ to $\Xi(i) < 0$, Lemma 2 is employed accordingly.

Eventually, define $Y_{F, m}\left(\rho \right) = X_{m}\left(\rho \right) \bar{F}_{m}(\rho)$, $Y_{F, p}\left(\rho \right) = X_{p}\left(\rho \right) \bar{F}_{p}(\rho)$, $Y_{K, m}\left(\rho \right) = X_{m}\left(\rho \right) \bar{K}_{m}(\rho)$, $Y_{K, p}\left(\rho \right) = X_{p}\left(\rho \right) \bar{K}_{p}(\rho)$, then the remainder of proof will follow directly from Theorem 1.

Remark 4. The proposed modified $H_{\infty}$ performance is more applicable for the distributed sensor networks design. In addition, the performance index $\gamma$ can be further optimized by solving the following convex optimization problem:

4.   Numerical examples

This section is dedicated to validate the applicability of our proposed distributed nonsynchronous designs, while illustrative studies have been performed with simulation results.

Consider the following HMJP GRNs model with a set of biological simulated parameters as

where the transition rate matrix with two modes of hidden Marko chain are assumed by

For the sensor networks, it is assumed that two networked sensors are deployed for mRNAs as well as proteins, such that the communication topology matrix for each network is given by

Moreover, the mode-dependent sensor parameters are set as follows:

In the simulation example, the sampling interval of networked sensors is set by $h = 0.1$s. Furthermore, the probability matrix of observed modes is supposed to be

which indicates that the nonsynchronous mode information is utilized instead of true system modes.

Consequently, with these simulation parameters, the optimized nonsynchronous mode-dependent filter gains are solved by Theorem 2 as follows:

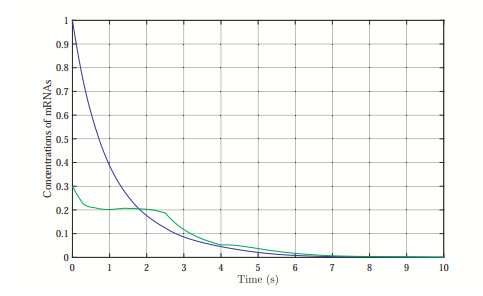
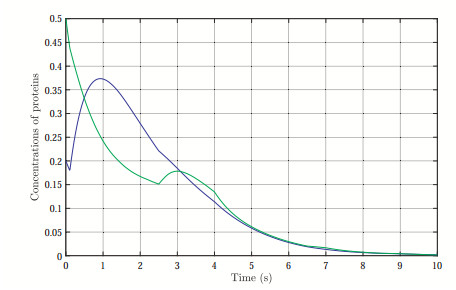
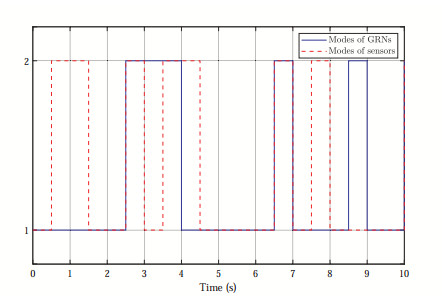
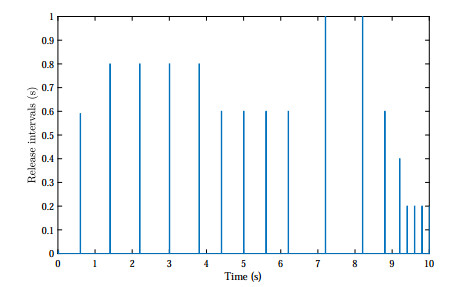
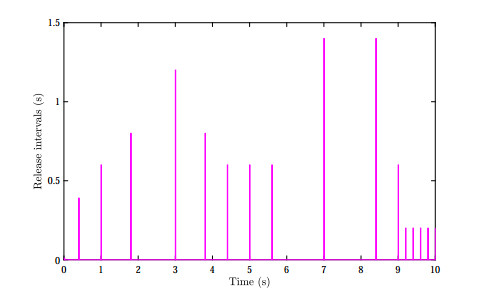
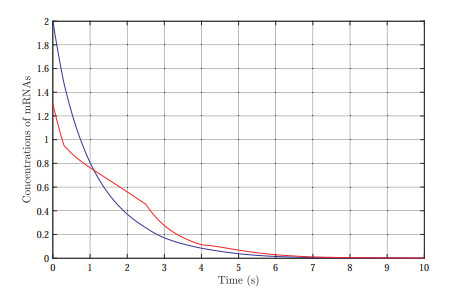
As a result, the concentrations of mRNAs and proteins estimation errors over sensor networks are depicted in Figures 1–4, where the jumping modes of GRNs and sensors are illustrated in Figure 5, respectively. It can be seen that all the sensors can display effective estimations without true GRNs system mode information and thus provides an improved nonsynchronous distributed state estimation approach. Furthermore, the triggering events of the sensors are shown in Figures 6 and 7, respectively. Compared with common time-triggered strategies, one can clearly found that the event-triggered scheme can achieve a considerable improvement of communication efficiency. Therefore, these simulation results well demonstrate our distributed state estimation approach and supports our theoretical findings.

5.   Conclusions

This paper is centered on the state estimation for GRNs with HMJPs over distributed sensor networks. More precisely, a novel event-triggered sensing scheme is developed for more effective estimation. In addition, since the modes of HMJPs might be nonsynchronous with the sensors, the nonsynchronous distributed state estimation is developed with aid of observed information, which is more practical for the implementations. On the basis of model transformation, sufficient mode-dependent conditions for ensuring the modified $H_{\infty}$ performance are established and the desired nonsynchronous state estimation gains are designed by matrix manipulation techniques. In the end, numerical simulations are performed to show the usefulness and advantages of our theoretical results. It is noted that one interesting research issue of our future work is extending the current method to the cases with more complicated mode jumping features.

Acknowledgments

This work is supported by the National Natural Science Foundation of China under Grant 62173326 and the National Key Research and Development Plan of China under Grant 2020AAA0105900, and supported by Beijing Natural Science Foundation under Grant L211023.

Conflict of interest

The authors declare there is no conflict of interest.