An approximate analytical solution for groundwater variation in unconfined aquifers subject to variable boundary water levels and groundwater recharge

1.   Introduction

Let $\Omega$ be a bounded domain in $\mathbb{R}^{d}$ with sufficient smooth boundary $\partial\Omega$. We consider the following initial boundary value problem (IBVP) for the anomalous diffusion model with multi-term time-fractional derivatives

where $\; I = (0, T)\;$ with $\; T > 0\;$ be fixed and $\partial_{0+}^{\alpha_{j}}$ is the Caputo fractional derivative defined by

For a fixed positive integer $s$, the orders $\mathit{\boldsymbol{\alpha}} = (\alpha_1, ..., \alpha_s)$ and the coefficients $\mathit{\boldsymbol{q}} = (q_1, ..., q_s)$ are restricted in the admissible sets

with fixed $0 < \underline{\alpha} < \overline{\alpha} < 1$ and $0 < \underline{q} < \overline{q}$.

$\; -L\;$ is a symmetric uniformly elliptic operator defined on $\; D(-L) = H^2(\Omega)\cap H^1_0(\Omega)\;$ given by

in which the coefficients satisfy

If the number of fractional derivatives $s$, the orders $\mathit{\boldsymbol{\alpha}}$ and its coefficients $\mathit{\boldsymbol{q}}$, elliptic operator $L$ and source functions $p(t), \; f(x)$ are given appropriately, then IBVP Eq (1.1) is a direct problem. Here the spatial source term $f(x)$ is unknown, so the inverse problem in the paper is to determine the spatial source term $f(x)$ based on problem Eq (1.1) and an additional terminal data

Since the measurement is noise-contaminated inevitably, we denote the noisy measurement of $g$ as $g^\delta(x)$ satisfying

It is well known that the time-fractional diffusion equations (TFDEs) have a wide range of applications in physics, chemistry and other aspects ^[1,2,3,4,5]. The most representative is continuous time random walk problem in general non-Markovian processes. However, with the increasing demand on the accuracy of the problem, the single-time fractional diffusion equation gradually failed to meet the needs of the problem, so Schumer et al. ^[6] proposed using the multi-term time-fractional diffusion equation (MTFDE) to increase the accuracy of the model. MTFDE is not only a useful tool for describing the behavior of anomalous diffusion phenomena in highly heterogeneous aquifers and complex viscoelastic materials ^[7], but can also be applied indirectly in the numerical solution of distributed-order fractional differential equations ^[8].

There are many studies on the direct problem for IBVP Eq (1.1) in recent years such as some uniqueness and existence results ^[9], the maximum principle ^[10], and analytic solutions ^[11,12]. In terms of numerical work, there are also some papers on the numerical solutions by finite difference methods ^[13,14,15] and by finite element methods ^{[16,17,18,19]}.

Due to the spectral method needs fewer grid points to obtain highly accurate solution. Therefore, the spectral method is more suitable for discrete MTFDE because of its huge computations. The study of the spectral method can be divided into two categories in MTFDE. On the one hand, the time fractional derivative is discreted by finite difference method and spectral method is applied for the space variable. Guo et al. ^[20] studied the numerical approximation of distributed-order time-space fractional reaction-diffusion equation. Jiang et al. ^[21] considered a Legendre spectral method on graded meshes for handling MTFDE with non-smooth solutions in two-dimensional case. Liu et al. ^[22] applied an alternating direction implicit Legendre spectral method to handle the multi-term time fractional Oldroyd-B fluid type diffusion equation in the two-dimensional case. On the other hand, the spectral method is applied both in space and in time. Zheng et al. ^[23] considered a high order numerical method for handling MTFDE. Zaky ^[24] applied a Legendre spectral tau method to handle MTFDE. However, we are interested not only in obtaining a numerical solution with high precision by using spectral method, but also in determining the spatial source term in an inverse problem of the MTFDE.

As far as we know, the theory as well as numerical methods of inverse source problems for single term (i.e, . $s = 1$) case in Eq (1.1) are relatively abundant. Zhang et al. ^[25] testified a uniqueness result to inverse the spatial source term in one-dimensional case by using one-point Cauchy data and proposed an efficient numerical method. Wei et al. ^[26] studied to identify a spatial source term in a multi-dimensional time-fractional diffusion equation from boundary measured data. The uniqueness for the inverse source problem is proved by the Laplace transformation method. Yan et al. ^[27] studied to identify a spatial source term in a multi-dimensional time-fractional diffusion-wave equation from a part of noisy boundary data. The uniqueness of inverse spatial source term problem is proved by the Titchmarsh convolution theorem and the Duhamel principle. Sun et al. ^[28] devoted to recovering simultaneously the fractional order and the space-dependent source term from partial Cauchy's boundary data in a multi-dimensional time-fractional diffusion equation. Recently, Yeganeh et al. ^[29] came up with an interesting idea. They used a method based on a finite difference scheme in time and a local discontinuous Galerkin method in space to determine a spatial source term in a time-fractional diffusion equation. This has not been seen in previous studies.

For a multi-term case, however, research results on inverse source problem are relatively few at present. Jiang et al. ^[30] built a weak unique continuation property for time-fractional diffusion-advection equations, and they considered an inverse problem on determining identifying the spatial source term by interior measurements. Li et al. ^[31] considered an inverse problem of recovering time-dependent source term from the Cauchy data in a MTFDE, and they applied the conjugate gradient method to identify the approximate source term. Recently, Sun et al. ^[32] investigated an inverse the spatial source term in MTFDE with nohomogeneous boundary condition from partially disturbed boundary data. They proposed the Levenberg-Marquardt regularization method to compute an inverse source problem. In addition, simultaneous inversion of source term and other terms has been studied. For instance, Malik et al. ^[33] studied an inverse problem of identifying a time-dependent source term along with diffusion/temperature concentration from a non-local over-specified condition for a space-time fractional diffusion equation. Sun et al. ^[34] considered a nonlinear inverse problem for simultaneously recovering the potential function and the fractional orders in a MTFDE from the noisy boundary Cauchy data in the one-dimensional case. For other inverse source problems, we can refer to ^[35,36,37]. Nevertheless, to the best knowledge of the authors, no one has used the spectral method to determine a spatial source term in an inverse problem of MTFDE.

In this paper, we will focus on two aspect research on our proposed model Eq (1.1). One is the study on the direct problem. The theoretical analysis and the numerical scheme of the Galerkin spectral method are proposed to solve the IBVP Eq (1.1). On the other hand, we use the Galerkin spectral method to investigate an inverse spatial source term problem in a MTFDE from a noisy final data in a general bounded domain. In the propose method, multi-term Caputo fractional derivatives are discretized by the L1-formula and the Galerkin spectral method is applied for the space variable. At the same time, the comparison between the Galerkin spectral method and the finite difference method is added in this paper. Finally, we not only prove the validity of the Galerkin spectral method in the application of MTFDE, but also verify the superiority of the Galerkin spectral method in forward and inverse problems by comparing the numerical results with the finite difference method.

The remainder of this paper is organized as follows. Some preliminaries are presented in Section 2. The detailed convergence analysis of the presented method is shown in Section 3. Uniqueness and ill-posedness for the inverse problem are showed in Section 4. We present the Galerkin spectral method and the finite difference method algorithm in Section 5. Numerical results for four examples are investigated in Section 6. Finally, we give a conclusion in Section 7.

2.   Preliminary

We firstly introduce some preliminaries as follows in this section.

Definition 2.1. The multinomial Mittag-Leffler function is defined by (see ^[9,38])

where $\theta_0, \; \theta_j\in \mathbb{R}$, and $z_j\in \mathbb{C}$ $(j = 1, \cdots, s)$, and $(k; k_1, \cdots, k_s)$ denotes the multinomial coefficient

where $\; k_j\; (j = 1, \cdots, s)\;$ are non-negative integers.

For the convenience of the later, if the orders $\mathit{\boldsymbol{\alpha}} = (\alpha_1, ..., \alpha_s)$ and its coefficients $\mathit{\boldsymbol{q}} = (q_1, ..., q_s)$ satisfy Eq (1.2) and Eq (1.3), then we adopt the abbreviation

where $\mathit{\boldsymbol{\alpha}}' = (\alpha_1, \alpha_1-\alpha_2, \cdots, \alpha_1-\alpha_s)$ and $\lambda_n$ denotes the $n$-th eigenvalues of elliptic operator $-L$ with the homogeneous Dirichlet boundary condition.

Lemma 2.2. (^[9]) Let $\; 0 < \alpha_s < \alpha_{s-1} < \cdots < \alpha_1 < 1$. Then,

Lemma 2.3. (^[9,39]) Let $\; 0 < \alpha_s < \alpha_{s-1} < \cdots < \alpha_1 < 1$. Then the function $t^{\alpha_1-1}E_{\boldsymbol \alpha^{'}, \alpha_1}^{(n)}(t)$ is positive for $t > 0.$

Lemma 2.4. (^[40]) Let $\; 0 < \alpha_s < \alpha_{s-1} < \cdots < \alpha_1 < 1$. Then

where $M$ ia a positive constant.

Proposition 2.5. Let $\; 0 < \alpha_s < \alpha_{s-1} < \cdots < \alpha_1 < 1$. Then we have $E_{\alpha^{'}, 1+\alpha_1}^{(n)}(t) > 0$.

Proof. By Lemma 2.2 and 2.3, we know that

Hence it is obvious $E_{\boldsymbol \alpha^{'}, 1+\alpha_1}^{(n)}(t) > 0$.

Proposition 2.6. For $\lambda_n > 0$ and $0 < \alpha_s < \alpha_{s-1} < \cdots < \alpha_1 < 1$, we have $0 < 1-\lambda_{n}t^{\alpha_{1}}E_{\boldsymbol \alpha^{'}, 1+\alpha_1}^{(n)}(t) < 1$ for $t > 0$. Moreover, $1-\lambda_{n}t^{\alpha_{1}}E_{\boldsymbol \alpha^{'}, 1+\alpha_1}^{(n)}(t)$ is a strictly decreasing function on $t > 0$.

Proof. By Lemma 2.2 and 2.3, we have

We notice that $1-\lambda_{n}t^{\alpha_{1}}E_{\boldsymbol \alpha^{'}, 1+\alpha_1}^{(n)}(t)$ is a continuous function on $t$. Hence, we have $\lim_{t\rightarrow 0}(1-\lambda_{n}t^{\alpha_{1}}E_{\boldsymbol \alpha^{'}, 1+\alpha_1}^{(n)}(t)) = 1$. By Lemma 2.4 we know $\lim_{t\rightarrow \infty}(1-\lambda_{n}t^{\alpha_{1}}E_{\boldsymbol \alpha^{'}, 1+\alpha_1}^{(n)}(t)) = 0$. The proof is completed.

Lemma 2.7. For $\lambda_n > 0$ and $0 < \alpha_s < \alpha_{s-1} < \cdots < \alpha_1 < 1$, such that

Proof. By Proposition 2.6, we know $0 < E_{\alpha^{'}, 1+\alpha_1}^{(n)}(T) < \frac{1}{\lambda_{n}T^{\alpha_{1}}}$.

Lemma 2.8. Let $k$ be a positive integer, $\Delta t > 0$ and $\; \lim_{k\rightarrow \infty}k\Delta t = T$. We have the following properties from the sequence defined by

where $\alpha_j$ and $q_j$ are defined in equation Eq (1.1). Here we denote $\omega_k^{-1}$ equivalent to $\frac{1}{\omega_k}$.

(1) $\omega_k$ is a decreasing sequence with respect to $k$;

(2) $\omega_1 > \dots > \omega_k > 0$ for each $k$;

(3) $\omega_k^{-1}$ is an increasing sequence with respect to $k$;

(4) $\lim_{k\rightarrow \infty} k^{-\alpha_1}\omega_k^{-1} = \frac{{\Delta t}^{\alpha_1}}{\frac{q_1(1-\alpha_1)}{\Gamma(2-\alpha_1)}+\sum\limits_{j = 2}^{s}q_j\; \frac{T^{\alpha_1-\alpha_j}(1-\alpha_j)}{\Gamma(2-\alpha_j)}}.$

Proof. First, let $\Phi(x) = \omega_x$ be a continuous function with respect to $x$, According to $\frac{d\Phi(x)}{dx} < 0,$ we know $\Phi(x)$ is decreasing function, then we have $\omega_k$ is decreasing the sequence. And we can direct to check that $\omega_1 > \dots > \omega_k > 0$ for each $k$. In addition, we can easy to derive $\omega_k^{-1}$ is increasing function. Further, we have

where

First we have

where we use the Taylor's formula of $(1-1/x)^{1-\alpha_1}$ in the second equation. Similarly, we have

For all these reasons, we arrive at

This proof is complete.

3.   Semi-discretize scheme and full discretize scheme

In this section, we discuss semi-discretize and full discretize schemes of the problem Eq (1.1) in the one-dimensional case. First, let $t_n: = n \Delta t, \; n = 0, 1, \cdots, N, \;$ where $\Delta t: = \frac{T}{N}$ (at leat satisfying $\Delta t < 1$) is the time step. We can denote $u^n\;$ an approximation to $u(x, t_n)$, and in order to convenience we write $\; p(t_n), \; f(x), \; a(x), \; c(x)$ is equal to $\; p^n, \; f, \; a, \; c$, where $f(x), \; p(t_n)$ are the source terms of Eq (1.1), and $a(x), \; c (x)$ come from the definition of the symmetric uniformly elliptic operator $L$. Then we introduce the time-fractional derivative is approximated by the $L1$ formula ^[41].

where $\omega_k = \sum\limits_{j = 1}^{s}q_j\; \frac{{\Delta t}^{-\alpha_j}}{\Gamma(2-\alpha_j)} (k^{1-\alpha_j}-(k-1)^{1-\alpha_j})$ and $r_{\Delta t}^n$ is the truncation error with the estimate

Here $c_1$ is a constant depending on $u, \; a_j$ and $T$.

In this paper, we use $H^1$-norm defined by

where $\omega_1$ is defined in Lemma 2.8.

3.1.   Semi-discretize scheme

In order to establish the complete semi-discrete problem, we define the error term $r^n$ by

Then we have

where $c_2$ is a constant depending on $u, \; a_j$ and $T$.

Using the first term on right hand side of Eq (3.1) as an approximation of $\sum\limits_{j = 1}^{s}q_j\; \partial_{0+}^{\alpha_{j}}u(x, t_{n})$ leads to the following finite difference scheme to Eq (1.1)

Then we have

Multiply both sides by $\nu\in H_0^1(\Omega)$ and integrate over $\; \Omega\;$ and by Green formula. We can find $u^n\in H_0^1(\Omega)$, such that

For convenience and without loss of generality, we consider the case $a_{ij}(x)\equiv1, \; c(x) = 0$. Stability of the scheme Eq (3.5) is given in the following result.

Theorem 3.1. The semi-discretized problem Eq (3.5) is unconditionally stable in sense that for all $\Delta t > 0$, holds

Proof. we prove this theorem using induction. When n = 1, scheme Eq (3.5) has

Taking $\nu = u^1$ and Schwarz inequality, we have

Now for the following inequality to hold

We must prove that $\Arrowvert u^n\Arrowvert_{H^1(\Omega)}\leq \Arrowvert u^0\Arrowvert_{L^2(\Omega)}+\frac{1}{\omega_1}\sum_{k = 1}^{n}p^k\Arrowvert f\Arrowvert_{L^2(\Omega)}$. Taking $\nu = u^n$ in Eq (3.5) and by using Eq (3.7), we have

Hence, we have $\Arrowvert u^n\Arrowvert_{H^1(\Omega)}\leq \Arrowvert u^0\Arrowvert_{L^2(\Omega)}+\frac{1}{\omega_1}\sum_{k = 1}^{n}p^k\Arrowvert f\Arrowvert_{L^2(\Omega)}$.

Now, we give the convergence estimate between the exact solution and the solution of the semi-discretized problem.

Theorem 3.2. Let $u(x, t)$ be the exact solution of Eq (1.1), $\{u^n\}_{n = 0}^{N}$ be the numerical solution of semi-discretized Eq (3.5), and $u(x, t_0) = u^0$. Then there holds the following error estimates

where $c_2$ is a constant depending on $u, \; a_j$ and $T$.

Proof. We will verify that the following estimate

Here, we will prove it by the mathematical induction, let $\hat{e}^n = u(x, t_n)-u^n$. For $j = 1$, we have, by combining Eq (1.1), Eq (3.5), Eq (3.1), the error equation

Taking $\nu = \hat{e}^1$, we have

Hence, Eq (3.9) is proven for the case j = 1. Now, Suppose the inequality Eq (3.9) holds for all $j = 1, 2, \cdots, n-1$. Then we need to prove that it holds also for $j = n$.

Similar to $j = 1$, we have $\nu\in H^1_0(\Omega)$

Taking $\nu = \hat{e}^n$, and using Eq (3.9). We have

Then we obtain

The estimate Eq (3.9) is proved. Notice that $\; \lim_{k\rightarrow \infty}k\Delta t = T$ is clearly true. Then, we have

Then by Eq (3.12) and Lemma 2.8, we deduce that for sufficently large $n$, the assertion of the theorem is valid.

3.2.   Full discretized scheme

First, we set

as the space of polynomials of degree $\leq M$ with respect to $x$. Let $P$ be the orthogonal projection operator from $H_0^1(\Omega)$ into $V^{M}$. Then for all $\psi\in H_0^1(\Omega)$, we have $P\psi \in V^{M}$. Further, we have $\forall \nu_M\in V^{M}$ such that

This the orthogonal projection operator satisfy the inequality ^[42]

where $\psi\in H^m(\Omega)\cap H^1_0(\Omega), \; m\geq 1$.

Now, we consider the Galerkin scheme as follow: find $u_M^n \in V^{M}$, such that for all $\nu_M \in V^{M}$

Theorem 3.3. Let $u(x, t)\in H^1((0, T), H^m(\Omega)\cap H^1_0(\Omega)), \; m > 1$ be the exact solution of Eq (1.1), $\{u^n_M\}_{n = 0}^{N}$ be the numerical solution of full discretization Eq (3.15), and $u_M^0 = \text{P} u^0$. Then there holds the following error estimates

where $c_2$ is a constant depending on $u, \; a_j, \; T$, and $\|u\|_{L^{\infty}(H^m)}: = sup_{t\in(0, T)}\|u(x, t)\|_{H^{m}(\Omega)}$.

Proof. From Eq (1.1), Eq (3.1) satisfy $\; \forall \nu\in H^1_0(\Omega)$,

By projecting $u(x, t_n)$ in $Pu(x, t_n)\in V^{M}$, applying Eq (3.13), we obtain for all $\nu_M\in V^{M}$

Let $\hat{\epsilon}^n_M = Pu(x, t_n)-u_M^n, \; \epsilon^n_M = u(x, t_n)-u_M^n$ by subtracting Eq (3.15) from Eq (3.17), we have

Taking $\nu_M = \hat{\epsilon}^n_M$ in above equation and using the triangular inequality $\|\epsilon^n_M\|_{H^1(\Omega)}\leq \|\hat{\epsilon}^n_M\|_{H^1(\Omega)}+\|u(x, t_n)-Pu(x, t_n)\|_{H^1(\Omega)}$, we obtain

Here, we use the mathematical induction, by Eq (3.19), we can easy to verify when case of n = 1.

Suppose we have proven

And then we need prove $\|\epsilon^n_M\|_{H^1(\Omega)}\leq\omega_1\omega_n^{-1}(c_2 \Delta t^{2-\alpha_1}+cM^{1-m}\|u(x, t_n)\|_{H^m(\Omega)})$ By Eq (3.19), Eq (3.21) we have

Finally, by $\; \lim_{k\rightarrow \infty}k\Delta t = T$ and the last equality have

Then by Eq (3.23) and Lemma 2.8, we deduce that for sufficently large $n$, the assertion of the theorem is valid.

Now we give error estimates for semi-discrete and full discrete problems in the following result.

Theorem 3.4. Let $\{u^n\}_{n = 0}^{N}\in H^m(\Omega) \cap H^{1}_0(\Omega), \; m > 1$ is solution of semi-discrete problem Eq (3.5), $\{u^n_M\}_{n = 0}^{N}$ is the solution of full discrete problem Eq (3.15), and $u_M^0 = \text{P} u^0$. Then we have

Proof. According to the definition of $P$, for solution $u^{n}$ of semi-discrete, we have

Let $\hat{e}^n_M = Pu^n-u_M^n, \; e^n_M = u^n-u_M^n$, by subtracting Eq (3.15) from Eq (3.24), we have

Taking $\nu_M = \hat{e}^n_M$ in above equation and using the triangular inequality $\|e^n_M\|_{H^1(\Omega)}\leq \|\hat{e}^n_M\|_{H^1(\Omega)}+\|u^n-Pu^n\|_{H^1(\Omega)}$, we obtain

Here, we use the mathematical induction similar to Theorem 3.3, and by $\; \lim_{k\rightarrow \infty}k\Delta t = T$. We have follow result

Then by Eq (3.27) and Lemma 2.8, we deduce that for sufficently large $n$, the assertion of the theorem is valid.

4.   Uniqueness and ill-posedness for the inverse problem

In this section, we discuss the uniqueness of solution and the ill-posed analysis of the unknown source identification problem.

Denote the eigenvalues of the operator $-L$ as $\lambda_n$ and the corresponding eigenfunctions as $\varphi_{n}\in H^{2}(\Omega)\cap H^{1}_{0}(\Omega)$, then we have $L\varphi_{n} = -\lambda_n\varphi_{n}$. Without loss of generality, suppose a family of eigenvalues $0 < \lambda_1\leq\lambda_2\leq\cdot\cdot\cdot\leq\lambda_n\leq\cdot\cdot\cdot, \; \lim_{n\rightarrow \infty}\lambda_n = +\infty$, then $\left\{\varphi_{n}\right\}_{n = 1}^{\infty}$ constituting an orthonormal basis in space $L^2(\Omega)$.

Definition 4.1. (^[43]) For any $\gamma > 0$, define

where $(\cdot, \cdot)$ is the inner product in $L^{2}(\Omega)$, and define its norm

Lemma 4.2. (^[34]) For fixed $\mathit{\boldsymbol{\alpha}}\in \mathcal{A}, \; \mathit{\boldsymbol{q}}\in \mathcal{Q}$, let $\; f(x)\in L^d(0, T), \; p(t)\in D((-L)^\gamma)\;$ with some $d\in[1, \infty]$ and $\gamma\in[0, 1]$. Then Eq (1.1) exists a unique solution $u(x, t)$ given by

where $Q_n(t) = \int_0^t p(s)(t-s)^{\alpha_1-1}E^{(n)}_{\mathit{\boldsymbol{\alpha}}', \alpha_1}(t-s)ds$, and $f_n = (f, \varphi_n)$.

From Lemma 4.2, we know there exists a unique weak solution $u\in L^{2}((0, T); H^{2}(\Omega)\cap H^{1}_{0}(\Omega))$ for the direct problem Eq (1.1), if we know a source function $f(x)p(t)\in L^{\infty}(0, T; L^2(\Omega))$. And we know the formal solution for Eq (1.1) can be expressed by

Applying $u(x, T) = g(x)$, we have

where $\; g_n = (g, \varphi_{n}) \; and\; Q_n(T) = \int_{0}^{t}p(s)(T-s)^{\alpha_1-1}E^{(n)}_{\mathit{\boldsymbol{\alpha}}', \alpha_1}(T-s)ds$.

Theorem 4.3. If $\; p(t)\in C[0, T]\;$ satisfying $\; p(t)\geq p_0 > 0\;$ for all $\; t\in[0, T]\;$, then the solution $u(x, t), \; f(x)$ of problem Eq (1.1) is unique.

Proof. By Lemma 2.3, we have $E^{(n)}_{\mathit{\boldsymbol{\alpha}}', \alpha_1}(t) > 0$, for $t > 0$. From Lemma 2.2 and Proposition 2.5, we know

Hence, we know if $g(x) = 0$, we have $f(x) = 0$, and by Eq (4.2) we know $u(x, t) = 0$. The proof is completed.

In the following, we show the inverse source problem Eq (1.1) is ill-posed. Without loss of generality, we take a final data $\; g_k(x) = \frac{\varphi_{k}(x)}{\sqrt{\lambda_k}}\;$ in Eq (1.1) and then know $\|g_k\| = \frac{1}{\sqrt\lambda_k}\rightarrow 0, \; as\; k\rightarrow \infty$. The corresponding source terms are $f_k(x) = \frac{\varphi_{k}(x)}{Q_k(T)\sqrt{\lambda_k}}$, and we have $\|f_k\| = \frac{1}{Q_k(T)\sqrt{\lambda_k}}$. By Lemma 2.7, we have

Hence $\; \|f_k\|\geq\frac{\sqrt{\lambda_k}}{\|q\|_{C[0, T]}}\rightarrow \infty\;$, as $\; k\rightarrow \infty\;$. Then we know the inverse source problem Eq (1.1) is ill-posed.

5.   Numerical algorithm

For the sake of argument, we just talk about the one-dimensional case.

5.1.   The Galerkin spectral method

First, let $L_{M}(x)$ denotes the Legendre polynomial of degree $M$. $\xi_j, \; j = 1, 2, \cdots, M$, are the Legendre-Gauss-Lobatto points, and these points satisfy $(1-x^2)L'_{M}(x) = 0$. we consider the follow equation

We set

Here, $h_i$ is the Lagrangian polynomial defined in $\Omega$ i.e. $h_i\in V^{M}, \; h_i(\xi_j) = \varepsilon_{ij},$ with $\varepsilon_{ij}:$ the Krinecker-delta symbol. Since first equation in Eq (1.1) satisfies Dirichlet boundary condition, therefore, we have $\delta_0^{n} = \delta_{M}^{n} = 0$. Take $\nu_M = h_j(x), \; j = 1, 2, \cdots, M-1,$ we can obtain

Denote

and set

By above equation, we have

where $i, j = 1, 2, \cdots, M-1$, and

Here, we use the Legendre Gauss-type quadratures to approximate Eq (5.4), and by the first equation in Eq (5.3) and Eq (5.2), we can solve the forward problem.

For the inverse problem, by Eq (5.3), we have

For $n = N$, we have

By Eq (5.5), Eq (5.6), we have

And then by solving linear equation Eq (5.7), we can obtain $F$. Further, we recover $f_M$ as an approximation of the source term by using a suitable integration rule.

In order to prove the ill-posedness of equation Eq (5.7), an upper bound of $\|A^{-1}\|_2$ in Eq (5.7) is given below.

Theorem 5.1. Let the orthogonal basis function $\{h_j\}_{j = 1}^{M-1}$ satisfy $h_j(x)\in H^1(\Omega)$. Then the inverse matrix of the coefficient matrix A in Eq (5.7) have

Proof. From the first equation of Eq (5.6), we can get

Combining the second equation of Eq (5.6), we have

Let $k^{'} = N-k\; (also\; denote \; k)$, we have

On the other hand, by Eq (5.5) we have

By substituting Eq (5.12) into Eq (5.11), the equation $AF = G$ is obtained, where

Since $\omega_k$ is non-negative and decreasing with respect to $k$, therefore we have

The definition of $A_k$ tells us that the second part of $A$ is the higher order term of the first part. Therefore, we only need to estimate the matrix

Due to $F\approx\widetilde{A}^{-1}G$, we only have to estimate the upper bound of $\|\widetilde{A}^{-1}\|_2$. According to Eq (5.4), $\hat{K}$ is a diagonal matrix, and

Therefore, we have

where $C$ is dependent on $a, \; c, \; M, \; \mathit{\boldsymbol{\alpha}}, \; q_j$.

Remark 1. It can be seen from Theorem 5.1 that $\|A^{-1}\|_2$ is completely determined by the projection dimension $M-1$ of the spectral method and the maximum and minimum norm of the basis function $h_j(x)$. It can be seen from Eq (5.8) that as the projection dimension increases, the numerator increases with respect to $j$, while the denominator decreases with respect to $j$. Therefore, the projection dimension $M-1$ can be used as regularization parameter. When the appropriate $M$ is selected, the minimum value of $\|A^{-1}\|_2$ can be guaranteed, thus reducing the ill-posedness of the inverse problem.

Remark 2. Here we emphasize that the Galerkin spectral method is a projection method. In the projection method, as long as the appropriate dimension of the projection space is selected, the regularization effect can be effectively generated for the linear ill-posed problem, and it is no longer necessary to adopt other regularization techniques for the problem. This phenomenon is sometimes called self-regularization or regularization by projection. A series of descriptions and proofs of this phenomenon can be found in the literature ^[44].

5.2.   The finite difference method

In order to compare the finite difference method the and Galerkin spectral method in application of the multi-term time-fractional diffusion equation. We derive follow the scheme similar to reference ^[45].

In the finite difference algorithm, we can denote $\; u_i^{n}\approx u(x_i, t_n)$, where $\; x_i = i\Delta x, i = 1, ..., C.\;$ and $\; t_n = n\Delta t, n = 0, 1, ..., N.\;$

The space has the following discrete form:

for $\; i = 1, ..., C-1, n = 1, ..., N\;$ where $\; a_{i+\frac{1}{2}} = a(x_i+\frac{1}{2})\;$ with $\; x_i+\frac{1}{2} = (x_i+x_{i+1})/2$. In problem Eq (1.1), according to initial condition and boundary condition, we can get a numerical solution for forward problem Eq (1.1) from the finite difference scheme

Denote $\; U^{n} = (u_1^{n}, u_2^{n}, ..., u_{C-1}^{n})^T, \; Y = (f(x_1), f(x_2), ..., f(x_{C-1)})^T, \;$ then the scheme Eq (5.18) leads to the following iterative scheme

where $c_n = (\omega_{n}-\omega_{n+1})/\omega_1$ and $B$ is a tridiagonal matrix given by $B_{ii} = \frac{a_{i+\frac{1}{2}}+a_{i-\frac{1}{2}}}{(\Delta x)^2\omega_1}+1-\frac{c(x_i)}{\omega_1}$ for $i = 1, 2, \cdots, C-1$ and $B_{i, i-1} = -\frac{a_{i-\frac{1}{2}}}{(\Delta x)^2\omega_1}$ for $i = 2, 3, \cdots, C-1$ and $B_{i, i+1} = -\frac{a_{i+\frac{1}{2}}}{(\Delta x)^2\omega_1}$ for $i = 1, 3, \cdots, C-2.$

Inverse source problem based on finite difference. Similar to Section 5.1, we can derive a linear equation.

where $D = (g(x_1), g(x_2), ..., g(x_{C-1)})^T, \;$ and $Z$ is a matrix.

6.   Numerical results

In this section, first, we verify the stability and validity of the proposed numerical methods. Without lose of generality, let the maximum time is $T = 1$. The noisy data are generated by adding random perturbations, i.e,

where $\varepsilon$ is relative noise level and $rand(\cdot)$ generate random numbers uniformly distributed on $[0, 1]$. The corresponding noise level is calculated by $\delta = \|g-g^{\delta}\|$. To show the accuracy of numerical solution, we compute the approximate $L^2$-norm error denoted by

and the approximate $L^2$-norm relative error as

where $f^{\delta}$ is term reconstructed and $f$ is the exact solution.

In addition, for the convenience of writing, we will abbreviate the Galerkin spectral method as GSM and the finite difference method as FDM.

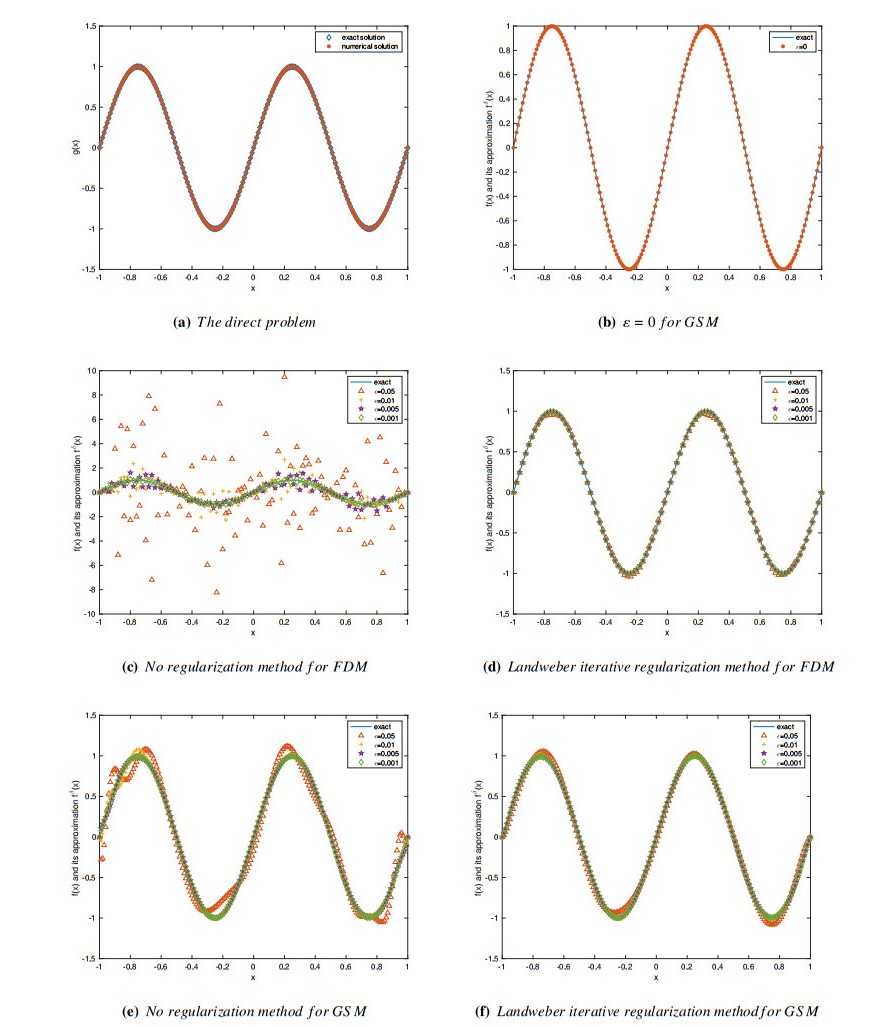
Example 1. In this example, we firstly consider a three-term time fractional diffusion equation with a exact solution. Let $\Omega_T = (-1, 1)\times(0, T)$ and $T = 1, \; q_j\equiv1.$ Take a source function $p(t) = \frac{2}{\Gamma(3-\alpha_1)}t^{2-\alpha_1}+ \frac{2}{\Gamma(3-\alpha_2)}t^{2-\alpha_2}+ \frac{2}{\Gamma(3-\alpha_3)}t^{2-\alpha_3}+4\pi^2t^2,$ and $f(x) = \sin(2\pi x)$. Further more, we have exact analytical solution

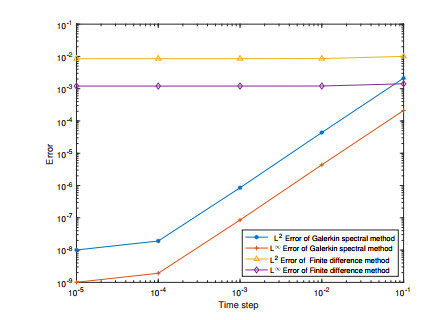
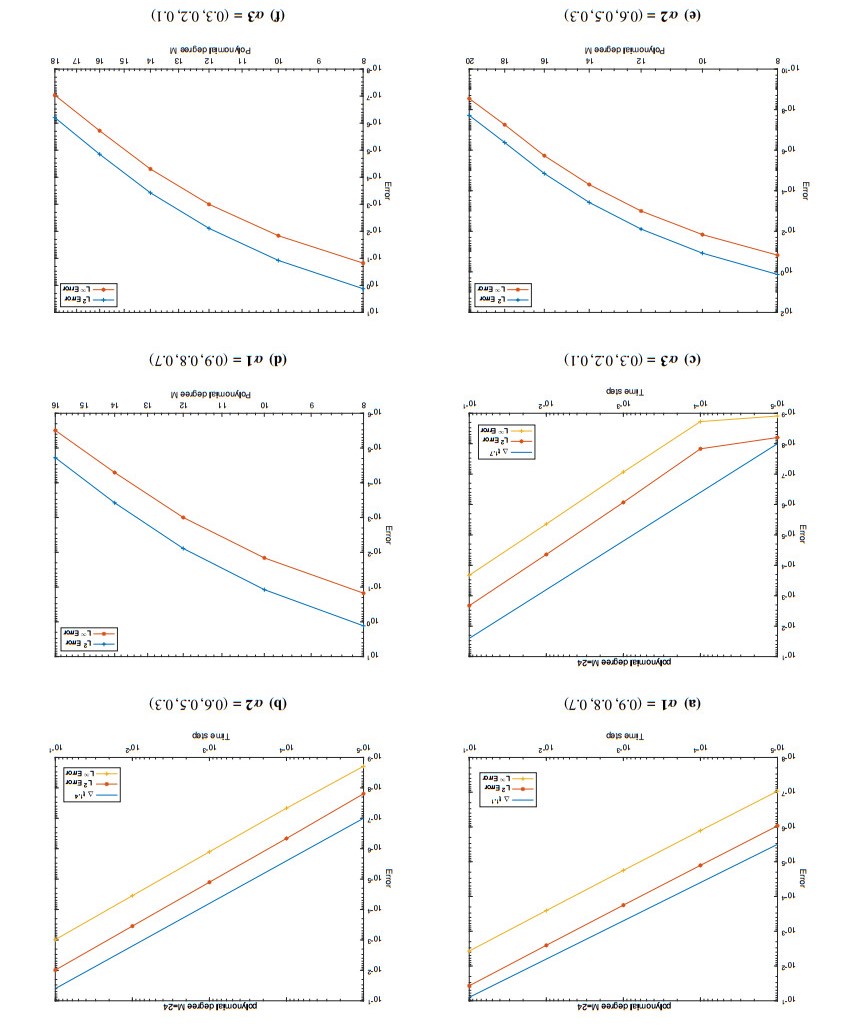
In the first three graphs of Figure 1, namely (a), (b) and (c), we show the errors in $L^2$-norm and $L^\infty$-norm for different time step in case of $\mathit{\boldsymbol{\alpha_1}} = (0.9, 0.8, 0.7), \; \mathit{\boldsymbol{\alpha_2}} = (0.6, 0.5, 0.3)$, and $\mathit{\boldsymbol{\alpha_3}} = (0.3, 0.2, 0.1)$. Here fix the polynomial degree $M = 24$. In the same case, the graphs (d), (e) and (f) from Figure 1 show the the errors in $L^2$-norm and $L^\infty$-norm for different polynomial degree $M$. Here we also take time step $\Delta t = 1e-4$. From Figure 1, we can find that the theoretical convergence accuracy (see Theorem 3.3) is in good agreement with the numerical results.

In Table 1 and Figure 2, we make a comparison with FDM in terms of the forward problem by using the scheme Eq (5.1). Clearly, we observe that the scheme Eq (5.1) has higher accuracy than FDM on the forward problem. As a further step, we choose $\Delta t = 1e-4$ to obtain satisfactory results in time and accuracy.

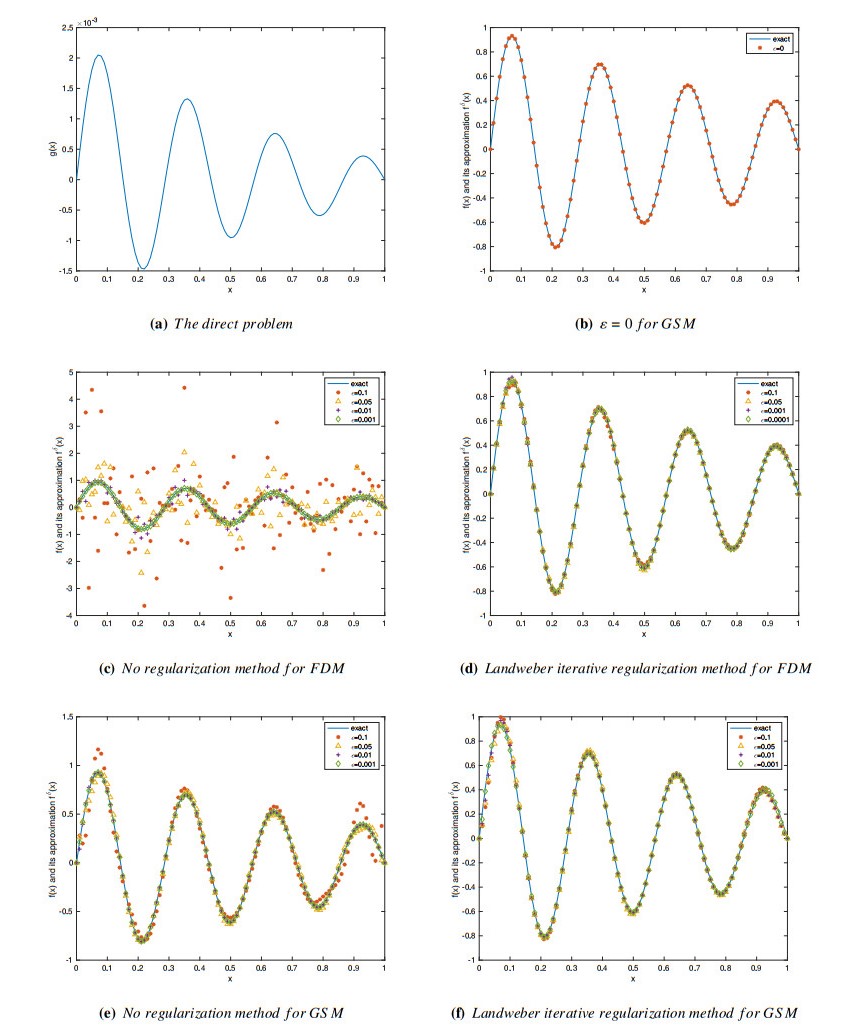
On the inverse source problem aspect. In order to avoid the impact of 'inverse crime'. We take $M = 20, \Delta t = 1e-4$ to solve the direct problem by using the GSM Eq (5.1), and take $M = 20, \Delta t = 1e-3$ to solve the inverse source problem by the scheme Eq (5.7). The related results are shown in (e), (f) of Figure 3 and Table 2. For the inverse source problem based on FDM. We take $C = 100, \Delta t = 5e-3$. Numerical result for ${\alpha_2} = (0.3, 0.2, 0.1)$ with various noise levels $\varepsilon = 5\%, 1\%, 0.5\%, 0.1\%$ are shown in (c), (d) of Figure 3.

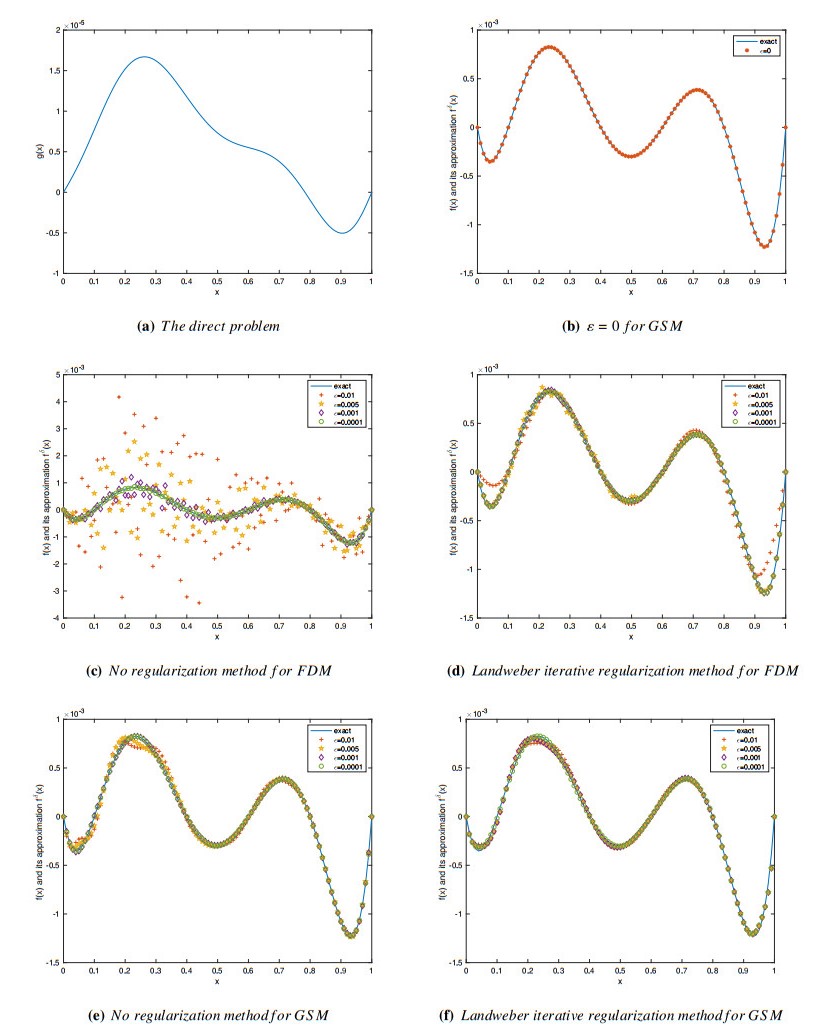
Example 2. In this example, let $\Omega_T = (0, 1)\times(0, T), \; s = 3, \; q_j\equiv1, \; a(x) = 1, \; c(x) = 0$. Take a exact source function $\; p(t) = 1\;$ and $f(x) = x(x-0.4)(x-0.6)(x-0.8)(x-1)$. We first solve the direct problem by using the GSM Eq (5.1) to obtain the additional data $g(x)$. Then we use the scheme Eq (5.7) to solve inverse source problem. Numerical result for $\mathit{\boldsymbol{\alpha_1}} = (0.9, 0.8, 0.7), \; \mathit{\boldsymbol{\alpha_2}} = (0.3, 0.2, 0.1)$, and $\mathit{\boldsymbol{\alpha_3}} = (0.6, 0.5, 0.3),$ with various noise levels $\varepsilon = 1\%, 0.5\%, 0.1\%, 0.01\%$ are presented in (e), (f) of Figure 4 and Table 3. For the inverse source problem based on FDM. We take $C = 100, \Delta t = 5e-3$. Numerical result for ${\alpha_2} = (0.3, 0.2, 0.1)$ with various noise levels $\varepsilon = 1\%, 0.5\%, 0.1\%, 0.01\%$ are shown in (c), (d) of Figure 4.

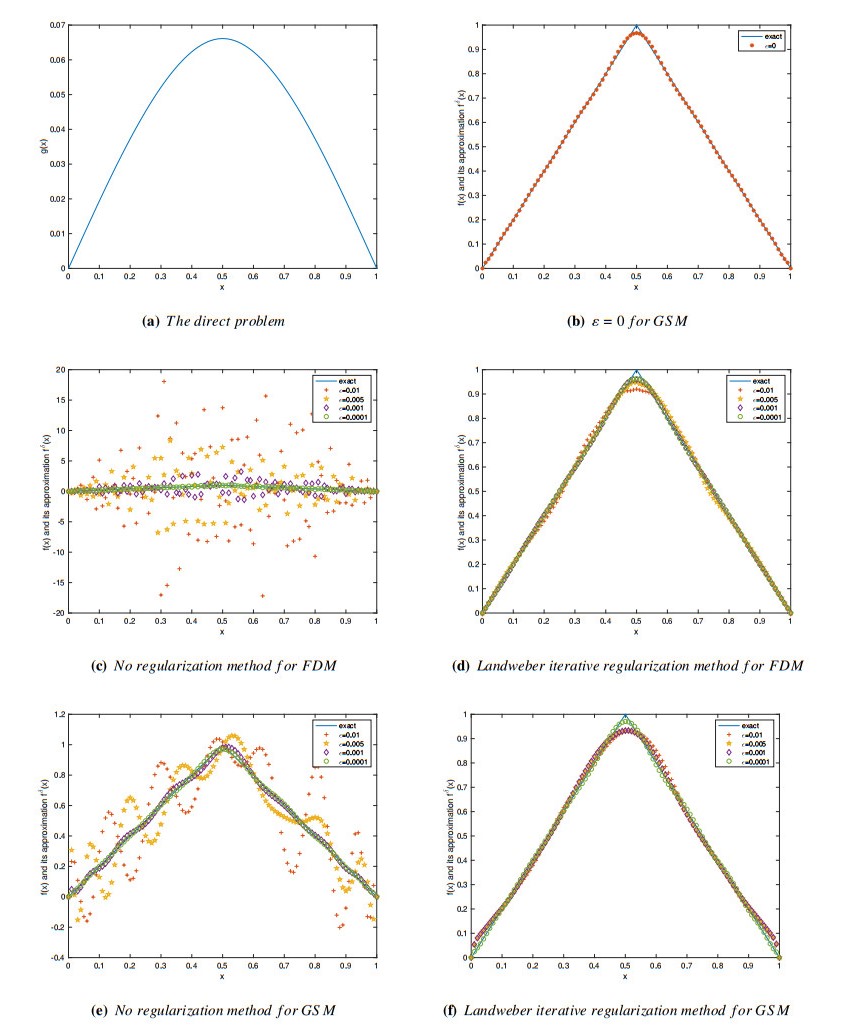
Example 3. In this example, let $\Omega_T = (0, 1)\times(0, T), \; s = 3, \; q_j\equiv1, \; a(x) = 1, \; c(x) = 0$. We consider a continuous piecewise smooth function.

We first solve the direct problem by using the GSM Eq (5.1) to obtain the additional data $g(x)$. Then we use the scheme Eq (5.7) to solve inverse source problem. Numerical result for $\mathit{\boldsymbol{\alpha_1}} = (0.9, 0.8, 0.7), \; \mathit{\boldsymbol{\alpha_2}} = (0.3, 0.2, 0.1)$, and $\mathit{\boldsymbol{\alpha_3}} = (0.6, 0.5, 0.3),$ with various noise levels $\varepsilon = 1\%, 0.5\%, 0.1\%, 0.01\%$ are presented in (e), (f) of Figure 5 and Table 4. For the inverse source problem based on FDM. We take $C = 100, \Delta t = 5e-3$. Numerical result for ${\alpha_2} = (0.3, 0.2, 0.1)$ with various noise levels $\varepsilon = 1\%, 0.5\%, 0.1\%, 0.01\%$ are shown in (c), (d) of Figure 5.

Example 4. Let $\Omega_T = (0, 1)\times(0, T), \; s = 3, \; q_j\equiv1, \; a(x) = x^2+1, \; c(x) = -1$. Take a exact source function $\; p(t) = 1\;$ and $f(x) = e^{-x}\sin(7 \pi x)$. We first solve the direct problem by using the GSM Eq (5.1) to obtain the additional data $g(x)$. Then we use the scheme Eq (5.7) to solve inverse source problem. Numerical result for $\mathit{\boldsymbol{\alpha_1}} = (0.9, 0.8, 0.7), \; \mathit{\boldsymbol{\alpha_2}} = (0.3, 0.2, 0.1)$, and $\mathit{\boldsymbol{\alpha_3}} = (0.6, 0.5, 0.3),$ with various noise levels $\varepsilon = 10\%, 5\%, 1\%, 0.1\%$ are presented in (e), (f) of Figure 6 and Table 5. For the inverse source problem based on FDM. We take $C = 100, \Delta t = 5e-3$. Numerical result for ${\alpha_2} = (0.3, 0.2, 0.1)$ with various noise levels $\varepsilon = 1\%, 0.5\%, 0.1\%, 0.01\%$ are shown in (c), (d) of Figure. 6.

By observing Figures 3–6, we can see that $(a)$ denotes the graph of the numerical solution of the forward problem, namely the input data. $(b)$ is the numerical approximation of the inverse source problem without noisy data. $(c)$ and $(d)$ are results of the inverse source problem based on the FDM with and without regularization method, and $(e)$ and $(f)$ are results of the inverse source problem based on the GSM under the same case.

From Tables 6–9, we show the error levels of two numerical reconstruction method with and without regularization method. We can find that the numerical results of the inverse problem based on FDM with regularization method are obviously better than those without regularization method. However, the numerical results of the inverse problem based on the GSM with and without regularization method do not show a big difference compared with the numerical results of the FDM. There may even be cases where regularization method is not required to get a better result. Hence, we can conclude that scheme Eq (5.7) itself has regularization function compared to the FDM in the inverse source problem. Next, we explain why scheme Eq (5.7) is not sensitive to noise level.

In Table 10, we show $norm$ of matrices $G$, ${A}^{-1}$ and ${A}^{-1}G$ for Example 1. Obviously, $\|{A}^{-1}G\|_{2}$ is small and $\|{A}^{-1}\|_{2}$ has a reasonable size. Therefore numerical solutions are not sensitive with respect to the perturbation in the initial data. But, In Table 11, The numerical format of FDM is sensitive to the perturbation in the initial datal. Therefore, GSM has better anti-interference than FDM. On the other hand, in Tables 12 and 13, We can find that although GSM has better anti-interference than FMD, it can not completely get rid of the regularization method when the unknown source has less regularity and the meased data has a high noise level.

7.   Conclusions

In this paper, we first obtain a high accuracy numerical solution by using the GSM, and give the error estimates between exact solution and semi-discrete solution as well as full-discrete one, and compare with the FDM. It is indicate that our method has a better accuracy. Secondly, the GSM is extended to solve the inverse source problem. Moreover, we find that this method can effectively reduce the ill-posednes of inverse source problem compared with the traditional FDM. Thus the spectral method itself can play a regularization role. It should be mentioned that the estimates given in the paper are also valid in two and three dimensional cases. In the following work, we will continue to try to optimize the GSM numerical scheme so that it can better play the role of regularization method. For example, replacing the original basis functions with smooth periodic functions or equidistant trigonometric functions to avoid Runge phenomenon.

Acknowledgments

This work is supported by the NSF of China (grant no. 12201502), the Youth Science and Technology Fund of Gansu Province (grant no. 20JR10RA099), the Innovation Capacity Improvement Project for Colleges and Universities of Gansu Province (grant no. 2020B-088) and the Innovation star of Gansu Province (grant no. 2022CXZX-324).

Conflict of interest

The authors declare there is no conflict of interest.