Flexible functional data smoothing and optimization using beta spline

1.   Introduction

Survival analysis is a branch of statistics for analyzing time-to-event data. When looking into survival data, one frequently encounters the problem of competing risks in which samples are subject to multiple kinds of failure. The Cox proportional hazards model, introduced by Cox ^[1], is popular in survival analysis for describing the relationship between the distributions of survival times and covariates and is commonly employed to analyze cause-specific survival data. The traditional approach is to separately fit a Cox proportional hazards model to the data for each failure type, after considering the data with other kinds of failure censored. However, this conventional method encounters problems like the estimates are hard to interpret and the confidence bands of estimated hazards are wide, because the method does not cover all failure types ^[2,3].

An alternative approach is to fit competing risks data by using a mixture model that incorporates the distinct types of failure to partition the population into groups, and it assumes an individual will fail from each risk with the probabilities being attributed to the proportions of each group, respectively. Moreover, the mixture approach is helpful for estimating the effects of covariates in each group through parametric proportional hazard regressions such as Cox’s model. McLachlan and Peel ^[4] noted that a mixture model is allowed for both dependent and independent competing risks and it can improve a model’s fit to the data than the traditional approach in which the causes of failure are assumed to be independent. Mixture models are popular in competing risks analysis, because their resultant estimates are easy to interpret ^[2], although complex.

Semi-parametric mixture models are a generalization of parametric mixture models and have become a prominent approach for modelling data with competing risks. Semiparametric approaches to mixture models are preferable for their ability to adjust for the associated variables and allow for assessing the effects of these variables on both the probabilities of eventual causes of failure through a logistic model and the relevant conditional hazard functions by applying the Cox proportional hazards model (cf. ^[2]). Below, we review the existing semiparametric methods of mixture models for competing risks data.

Ng and McLachlan ^[5] proposed an ECM-based semi-parametric mixture method without specifying the baseline hazard function to analyze competing risks data. They noted that when the component-baseline hazard is not monotonic increasing their semi-parametric approach can consistently produce less biased estimates than those done by fully parametric approaches. Moreover, when the component-baseline hazard is monotonic increasing, the two approaches demonstrate comparable efficiency in the estimation of parameters for mildly and moderately censoring. Chang et al. ^[6] studied non-parametric maximum-likelihood estimators through a semiparametric mixture model for competing risks data. Their model is feasible for right censored data and can provide estimates of quantities like a covariate-specific fatality rate or a covariate-specific expected time length. Moreover, Lu and Peng ^[7] set up a semiparametric mixture regression model to analyze competing risks data under the ordinary mechanism of conditional independent censoring. Choi and Huang ^[8] offered a maximum likelihood scheme for semiparametric mixture models to make efficient and reliable estimations for the cumulative hazard function. One advantage with their approach is that the joint estimations for model parameters connect all considered competing risks under the constraint that all the probabilities of failing from respective causes sum to 1 given any covariates. Other research studies for competing risks data are based on semiparametric mixture models, e.g. ^[5,6,7,8].

Although the mixture hazard model is preferable to direct approaches, two important but challenging issues frequently encountered in the applications are the determination of the number of risk types and the identification of the failure type of each individual.

It is understandable that the results of a mixture model analysis highly depend on the number of components. It is also conceivably hard to cover all types of competing risks in a mixture model. Validity indices are a vital technique in model selection. The cluster validity index is a kind of criterion function to determine the optimal number of clusters. Some cluster validity indices presented by ^[9,10,11] are designed to find an optimal cluster number for fuzzy clustering algorithms; some are only related to the membership, while some take into account the distance between the data sets and cluster centers. Wu et al. ^[12] proposed median-type validity indices, which are robust to noises and outliers. Zhou et al. ^[13] introduced a weighted summation type of validity indices for fuzzy clustering, but they are unfeasible for mixture regression models. Conversely, Henson et al. ^[14] evaluated the ability of several statistical criteria such as the Akaike information criterion (AIC) and Bayesian information criterion (BIC) to produce a proper number of components for latent variable mixture modeling. However, AIC and BIC may present the problem of over- and under-estimation on the number of components ^[15], respectively.

As to the identification of failure types, many studies on the problems of competing risks like ^[5,6,7,8] assumed that the failure type of an individual is known if the subject’s failure time is observed, but if an individual is censored and only the censored time is known, then which failure type the subject fails from is unknown. In fact, even if one observes the failure time, then the true cause of failure might not be clear and needs further investigations. Thus, deciding the number of competing risks and recognizing the failure type of each individual are critical in competing risks analysis, but scant work has been done on them.

Besides the above problems, another critical issue existing in mixture Cox hazard models particularly is the estimation of the baseline hazard function. The Cox proportional hazards model consists of two parts: the baseline hazard function and the proportional regression model. Bender et al. ^[16] assumed that the baseline hazard function follows a specific lifetime distribution, but this assumption is obviously restrictive. A single lifetime distribution may not adequately explain all data —for example, the failure rate is not monotonic increasing or decreasing. Alternatively, some scholars adopted nonparametric approaches to estimate the baseline hazard function that are more flexible. Ng and McLachlan ^[5] assumed the baseline hazard function to be piecewise constant by treating each observed survival time as a cut-off point, but the piecewise constant assumption has the disadvantage that the estimated curve is not smooth, while smoothing is required in several applications ^[17]. In fact, our simulation results also show that the derived estimates based on a piecewise constant hazard function are not sufficient in some cases (e.g. model 4 in Figure 4). Understandably, an inadequate estimation of the baseline function affects the selection of the number of model components; and hence leads to insufficient estimates of the model parameters.

In order to solve the above mentioned problems with the Cox mixture hazard modelling for competing risks data, we propose four indices and the kernel estimation for the base line function in this paper. Validity indices are a vital technique in model selection, but they have been less utilized for deciding the number of components of a mixture regression model. By using posterior probabilities and residual functions, we propose four validity indices that are applicable to regression models in this study. Under the EM-based mixture model, the posterior probabilities play an important role in classifying data, which take role of data memberships in fuzzy clustering. Unlike the traditional regression model, the survival model does not meet the assumption that survival time variation is constant for each covariate. Therefore, we incorporate the functions of posterior probabilities and the sum of standard residuals to constitute the new validity indices and verify the effectiveness of the proposed new indices through extensive simulations. Moreover, we extend the kernel method of Guilloux et al. ^[18] to estimate the baseline hazard function smoothly and hence more accurately.

The remainder of this paper is organized as follows. Section 2 introduces the mixture Cox proportional hazards regression model, develops an EM-based algorithm to estimate the model parameters, and also discusses kernel estimations for the baseline hazard function. Section 3 constructs four validity indices for selecting the number of model components in a mixture Cox proportional hazards regression model. Section 4 carries out several simulations and assesses the effectiveness of our validity indices. Section 5 analyzes a practical data set of prostate cancer patients treated with different dosages of the drug diethylstilbestrol. Finally, Section 6 states conclusions and a discussion.

2.   Mixture Cox proportional hazards model with kernel estimation

2.1.   Mixture Cox proportional hazards model

For mixture model analysis, suppose each member of a population can be categorized into g mutually exclusive clusters according to its failure type. Let $D = \left\{ {\; ({t_j}, \mathit{\boldsymbol{X}}_j^T, {\delta _j})\; :j = 1, \cdots, n} \right\}$ , be a sample drawn from this population where T denotes the transpose of a vector, ${t_j}$ is the failure or right censoring time, ${\mathit{\boldsymbol{X}}_j} = {({x_{j1}}, {x_{j2}}, ..., {x_{j\, d}})^T}$ is a d-dimensional vector of covariates, and:

The mixture probability density function (pdf) of t is defined by:

where ${p_i}$ is the mixing probability of failure due to the i^th type of risk and g is the number of model components.

In the i^th component, the hazard function $\; {h_i}(t\left| {{\mathit{\boldsymbol{X}}_j}, {\mathit{\boldsymbol{\beta }}_i}} \right.)\;$ given covariate ${\mathit{\boldsymbol{X}}_j}$ follows a Cox proportional hazards model defined by

where ${\mathit{\boldsymbol{\beta }}_i} = {({\beta _{i1}}, {\beta _{i2}}, ..., {\beta _{id}})^T}$ is the vector of regression coefficients, and ${h_{0i}}(t)$ is the baseline hazard function of the i^th component. We define the i^th component-survival function and pdf by:

and

where ${H_{0i}}(t) = \int_0^t {{h_{0i}}(s)} \; ds$ is the i^th component-cumulative baseline hazard function.

The unknown parameters are the mixing probabilities $\mathit{\boldsymbol{p}} = {({p_{\rm{1}}}, {p_2}, ..., {p_{g - 1}})^T}$ and regression coefficients $\mathit{\boldsymbol{\beta }} = {({\mathit{\boldsymbol{\beta }}_{\rm{1}}}^T, {\mathit{\boldsymbol{\beta }} _2}^T, ..., {\mathit{\boldsymbol{\beta }}_g}^T)^T}$ , where ${\mathit{\boldsymbol{\beta }}_i} = {({\beta _{i1}}, {\beta _{i2}}, ..., {\beta _{id}})^T}$ . Based on (1) and Zhou ^[19], the log-likelihood function under the mixture hazards model with right censored data is given by

where $f({t_j}\left| {{\mathit{\boldsymbol{X}}_j}} \right., \mathit{\boldsymbol{\beta }}) = \sum\limits_{i = 1}^g {{p_i} \cdot {f_i}({t_j}\left| {{\mathit{\boldsymbol{X}}_j}, {\mathit{\boldsymbol{\beta }}_i}} \right.)}$ and $S({t_j}\left| {{\mathit{\boldsymbol{X}}_j}, \mathit{\boldsymbol{\beta }}} \right.) = \sum\limits_{i = 1}^g {{p_i} \cdot {S_i}({t_j}\left| {{\mathit{\boldsymbol{X}}_j}} \right., {\mathit{\boldsymbol{\beta }}_i})}$ .

Assume that the true causes of failure for an individual are unobserved, and hence the data are incomplete. We introduce the latent variable ${z_{ij}}$ as:

The complete-data log-likelihood function is given by:

Subsequently, the parameters are estimated through the expectation and maximization (EM) algorithm.

E-step: On the (k+1)^th iteration of E-step, we calculate the conditional expectation of the complete-data log-likelihood (3) given the current estimates of the parameters, i.e.:

Here, ${\mathit{\boldsymbol{p}}^{(k)}}$ and ${\mathit{\boldsymbol{\beta }}^{(k)}}$ are the estimates of $\mathit{\boldsymbol{p}}$ and $\mathit{\boldsymbol{\beta }}$ , respectively, in the k^th iteration. By Baye’s Theorem, we have:

which is the posterior probability that the j^th individual with survival time $\; {t_j}\;$ fails due to the i^th type of risk.

M-step: The (k+1)^th iteration of M-step provides the updated estimates ${\mathit{\boldsymbol{p}}^{(k + 1)}}$ and ${\mathit{\boldsymbol{\beta }}^{(k + 1)}}$ that maximizes (4) with respect to $\mathit{\boldsymbol{p}}$ and $\mathit{\boldsymbol{\beta }}$ .

Under the constraints $\sum\limits_{i = 1}^g {{p_i}} = 1$ , to maximize ${Q_0} = \sum\limits_{j = 1}^n {\sum\limits_{i = 1}^g {{z_{ij}}^{(k)}\log {p_i}} }$ from (4), we obtain the estimation of mixing probability with

The equation ${Q_i}$ from (4) for $i = 1, ..., g$ can be written as:

Define the score vector $U({\mathit{\boldsymbol{\beta }} _i})$ for $i = 1, ..., g$ as the first derivate of (7) with respect to the vector ${\mathit{\boldsymbol{\beta }}_i}$ given ${H_{0i}}(t)$ fixed at ${H_{0i}}^{{\rm{(}}k + 1{\rm{)}}}(t)$ , and the estimation ${\mathit{\boldsymbol{\beta }}_i}^{{\rm{(}}k{\rm{ + 1)}}}$ satisfies the equation:

2.2.   Kernel estimation for the baseline hazard function

To estimate the baseline hazard function under the mixture hazards model, we propose the kernel estimator. Define ${N_j}(t) = I({t_j} \leqslant t\; \wedge \; {\delta _j} = 1)$ as an event counting process and ${Y_j}(t) = I({t_j} \geqslant t)$ as risk process. The updated kernel estimator of i^th component-baseline hazard function ${h_{0i}}(t)$ on the (k+1)^th iteration is defined by:

where $\; K:\mathbb{R} \to \mathbb{R}\;$ is a kernel function, and ${b^{(k)}}$ is a positive parameter called the bandwidth. There are several types of kernel functions commonly used, appearing in Table 1 and Figure 1. We try these kernel functions in the simulated examples and find no significant differences. In this paper, we choose biweight as the kernel function to estimate the baseline hazard function.

Derived by smoothing the increments of the Breslow estimator, the kernel estimator (9) can be written as:

where $\overline Y = \frac{1}{n}\sum\limits_{j = 1}^n {{Y_j}}$ and ${S_{n\, i}}(u\left| {\mathit{\boldsymbol{X}}, {\mathit{\boldsymbol{Z}}_i}, {\mathit{\boldsymbol{\beta }} _i}} \right.) = \sum\limits_{j = 1}^n {{z_{ij}}\exp ({{\mathit{\boldsymbol{X}}}_j}^T{\mathit{\boldsymbol{\beta }}_i}){Y_j}(u)}$ .

Horova et al. ^[20] and Patil ^[21] introduced the cross-validation method to select the bandwidth of the kernel estimator. We define the cross-validation function for bandwidth b written as CV(b) under our model as:

The selection of bandwidth on the (k+1)^th iteration is given by:

where ${B_n}$ cover the set of acceptable bandwidths.

The algorithm is shown as follows, where we fix n and g and set up initial values for mixing probabilities ${\mathit{\boldsymbol{p}}^{(0)}}$ , which are usually ${{\rm{1}} \mathord{\left/ {\vphantom {{\rm{1}} g}} \right. } g}$ , regression coefficients ${\mathit{\boldsymbol{\beta }} ^{(0)}}$ , baseline hazard rates ${\mathit{\boldsymbol{h}}_0}^{(0)}$ , bandwidth ${b^{{\rm{(0)}}}}$ is 0.5, and a termination value, $\varepsilon \, {\rm{ > }}\, {\rm{0}}$ .

Set the initial counter $\; l = 1$ .

Step 1: Compute ${\mathit{\boldsymbol{Z}}^{(l - {\rm{1}})}}$ with ${\mathit{\boldsymbol{p}}^{(l - 1)}}$ , ${\mathit{\boldsymbol{h}}_0}^{(l - 1)}$ and ${\mathit{\boldsymbol{\beta }} ^{(l - 1)}}$ by (5);

Step 2: Update ${\mathit{\boldsymbol{p}}^{{\rm{(}}l{\rm{)}}}}$ with ${\mathit{\boldsymbol{Z}}^{(l - 1)}}$ by (6);

Step 3: Update $\mathit{\boldsymbol{h}}_0^{(l )}$ with ${\mathit{\boldsymbol{Z}}^{{\rm{(}}l - 1{\rm{)}}}}$ , ${\mathit{\boldsymbol{\beta }} ^{{\rm{(}}l - 1{\rm{)}}}}$ and ${b^{{\rm{(}}l - 1{\rm{)}}}}$ by (10);

Step 4: Update bandwidth ${b^{{\rm{(}}l{\rm{)}}}}$ with ${\mathit{\boldsymbol{Z}}^{(l - 1)}}$ , $\mathit{\boldsymbol{h}}_0^{(l )}$ and ${\mathit{\boldsymbol{\beta }} ^{(l - 1)}}$ by (11);

Step 5: Update ${\mathit{\boldsymbol{\beta }} ^{{\rm{(}}l{\rm{)}}}}$ with ${\mathit{\boldsymbol{Z}}^{(l - 1)}}$ , $\mathit{\boldsymbol{h}}_0^{(l )}$ and ${\mathit{\boldsymbol{\beta }} ^{(l - 1)}}$ by (8);

Step 6: IF $\; {\left\| {\; {\mathit{\boldsymbol{p}}^{(l)}} - \; {\mathit{\boldsymbol{p}}^{(l - 1)}}} \right\|_{\rm{2}}} + {\left\| {\; \mathit{\boldsymbol{h}}_0^{(l )} - \; \mathit{\boldsymbol{h}}_0^{(l - 1)}} \right\|_{\rm{2}}} + {\left\| {\; {\mathit{\boldsymbol{\beta }} ^{(l)}} - \; {\mathit{\boldsymbol{\beta }} ^{(l - 1)}}} \right\|_{\rm{2}}} < \varepsilon$ , THEN stop;

ELSE let $\; l = l{\rm{ + 1}}\;$ and GOTO Step 1.

Note that the superscript (.) represents the number of iterations, $\mathit{\boldsymbol{h}}_0^{(0)} = {({\mathit{\boldsymbol{h}}_{{\rm{01}}}}^{(0)}, {\mathit{\boldsymbol{h}}_{{\rm{0}}2}}^{(0)}, ..., {\mathit{\boldsymbol{h}}_{{\rm{0}}g}}^{(0)})^T}$ is a $g \times n$ matrix, where $\mathit{\boldsymbol{h}}_{{\rm{0}}i}^{(0)} = {(h_{{\rm{0}}i}^{(0)}{\rm{(}}{t_1}{\rm{)}}, h_{{\rm{0}}i}^{(0)}{\rm{(}}{t_2}{\rm{)}}, ..., h_{{\rm{0}}i}^{(0)}{\rm{(}}{t_n}{\rm{)}})^T}$ , and each row is initialized by a constant vector.

3.   Validity indices

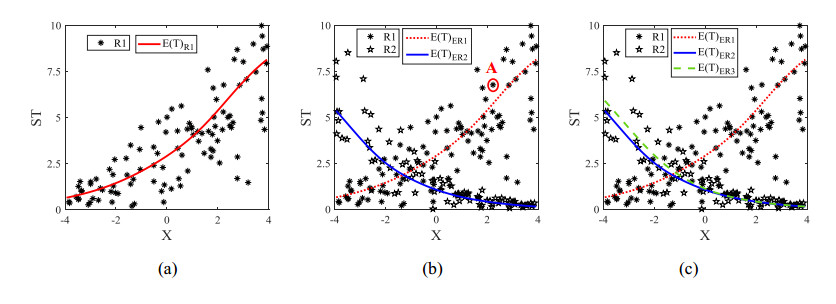
In traditional regression analysis, we select the best model by picking the one that minimizes the sum of squared residuals, but unlike the traditional regression model, the survival model does not meet the assumption that the standard deviation of the survival time is a constant at each covariate. From Figure 2(a), we see that the survival time with higher expectation has higher standard deviation. Therefore, to select the best model we need to adjust the standard deviation to avoid being greatly affected by data that have large standard deviations. Moreover, if the model fits the data well, then each observed survival time will be close to the expectation of the component model, which has the largest posterior probability corresponding to one’s risk type.

Figure 2(b) illustrate that observation A is closer to the mean line (red line) of the component model corresponding to risk type 1, say model 1, than to the mean line (blue line) of model 2. From (5), we see that the posterior probabilities of the observation A corresponding to the first type of risk (red line) will be much larger than that of the second type of risk (blue line). Hence, to build up validity indices for mixture models, we consider the posterior probabilities as the role of weights and define the mixture sum of standard absolute residuals (MsSAE) and mixture sum of standard squared residuals (MsSSE) as follows:

where ${\hat E_i}({t_j}) = \int\limits_0^\infty {\exp {{\left[{- {{\hat H}_{0i}}(t)} \right]}^{\exp \left({{x_j}^T{{\hat \beta }_i}} \right)}}\; dt}$ and $\hat Va{r_i}({t_j}) = {\rm{2}}\int\limits_0^\infty {t \cdot \exp {{\left[{- {{\hat H}_{0i}}(t)} \right]}^{\exp \left({{x_j}^T{{\hat \beta }_i}} \right)}}dt} - {\hat E_i}{({t_j})^{\rm{2}}}$ . The squared distance is considered, because it is easier to catch an abnormal model.

From Figure 2(c) we can see that the expectation (green line) of the survival time according to the third type of risk (ER3) is close to that (blue line) corresponding to the second type of risk (ER2). In order to penalize the overfitting model, which is the model with too many model components, we consider the distance between the expectations of each survival time according to any two types of risk as the penalty. Define the average absolute separation $\overline {ASep}$ , the average squared separation $\overline {SSep}$ , the minimum absolute separation $\min ASep$ and the minimum squared separation $\min SSep$ as:

A good model will possess small mixture standard residuals and large separation of expectations. Hence, based on the above-mentioned functions of residuals and separation of means, we propose four validity indices V₁ ~ V₄ for selecting the number of model components under the mixture hazards regression model.

(V₁). Absolute standard residuals and average separation ${V_{aRaS}}$

We find an optimal number g of types of risk by solving ${\min _{2 \leqslant g \leqslant n - 1}}{V_{aRaS}}$ .

(V₂). Squared standard residuals and average separation ${V_{sRaS}}$

We find an optimal number g of types of risk by solving ${\min _{2 \leqslant g \leqslant n - 1}}{V_{sRaS}}$ .

(V₃). Absolute standard residuals and minimum separation ${V_{aRmS}}$

We find an optimal number g of types of risk by solving ${\min _{2 \leqslant g \leqslant n - 1}}{V_{aRmS}}$ .

(V₄). Squared standard residuals and minimum separation ${V_{sRmS}}$

We find an optimal number g of types of risk by solving ${\min _{2 \leqslant g \leqslant n - 1}}{V_{sRmS}}$ .

4.   Simulation

For the simulated data we consider four different models M₁~M₄. Under the mixture Cox proportional hazards model (2), the i^th component hazard function is:

where d is the number of covariates, k is the degree of models, ${\mathit{\boldsymbol{\beta }} _i} = {({\beta _{i, 1, {\rm{1}}}}, {\beta _{i, 1, k}}, ..., {\beta _{i, d, k}}, {\beta _{i, d, k}})^T}$ is the vector of regression coefficients and ${h_{0i}}(t)$ is the i^th component-baseline hazard function.

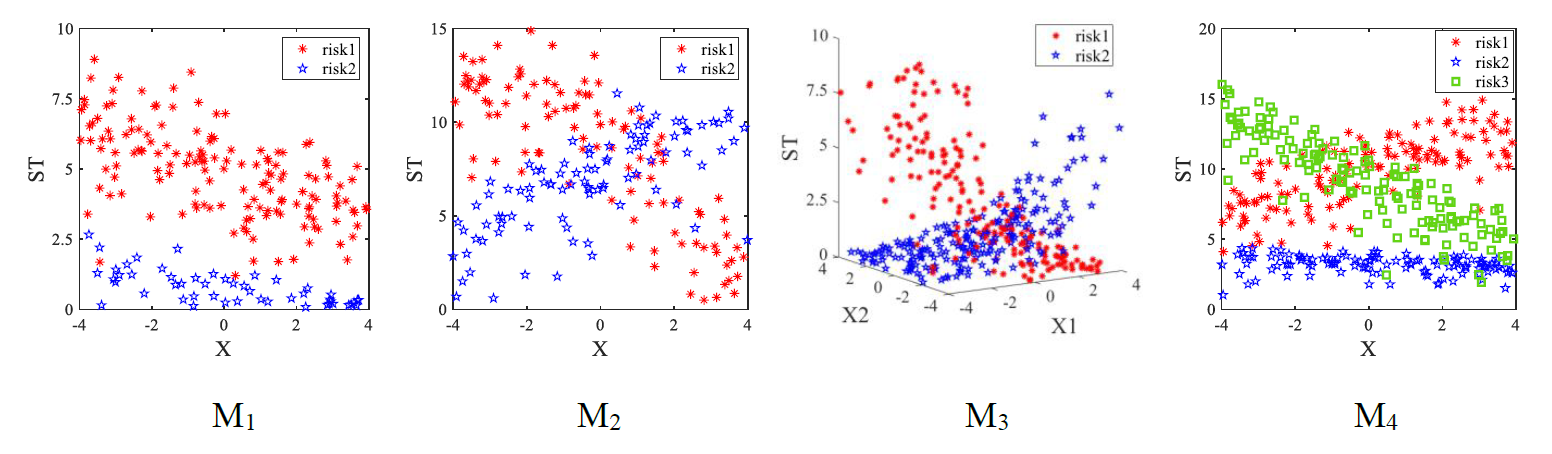
Consider two common distributions for the baseline hazard functions, Weibull and Gompertz; the i^th component Weibull baseline and Gompertz baseline are defined by ${h_{0i}}(t) = {\lambda _i}\, {\rho _i}\, {t^{{\rho _i} - 1}}$ and ${h_{0i}}(t) = {\lambda _i}\exp ({\rho _i}{t_j})$ , respectively, where ${\lambda _i}$ and ${\rho _i}$ are the scale and shape parameters. Let ${\bf{ \pmb{\mathit{ λ}} }} = {{\rm{(}}{\lambda _{\rm{1}}}{\rm{, }}...{\rm{, }}{\lambda _g}{\rm{)}}^T}$ , ${\bf{ \pmb{\mathit{ ρ}} }} = {{\rm{(}}{\rho _{\rm{1}}}{\rm{, }}...{\rm{, }}{\rho _g}{\rm{)}}^T}$ , and $\mathit{\boldsymbol{\beta }} = {({\mathit{\boldsymbol{\beta }} _{\rm{1}}}^T, {\mathit{\boldsymbol{\beta }}_2}^T, ..., {\mathit{\boldsymbol{\beta }} _g}^T)^T}$ . The covariates $X = {({x_1}, {x_2}, ..., {x_n})^T}$ in all cases are generated independently from a uniform distribution $U(- 4, 4)$ . The information for four models is shown in Table 2, and the scatter plots of a sample dataset are presented in Figure 3.

4.1.   Compare two methods of estimating the baseline hazard function

We consider an EM-based semi-parametric mixture hazards model to analyze simulated data, and compare the two methods of estimating the baseline hazard function. For the first method proposed by Ng and McLachlan ^[5], they assume the baseline hazard function is piecewise constant and calculate this function using maximum likelihood estimation (MLE). For the second method introduced in this paper, we use a kernel estimator to estimate the baseline hazard rates and choose biweight as the kernel function.

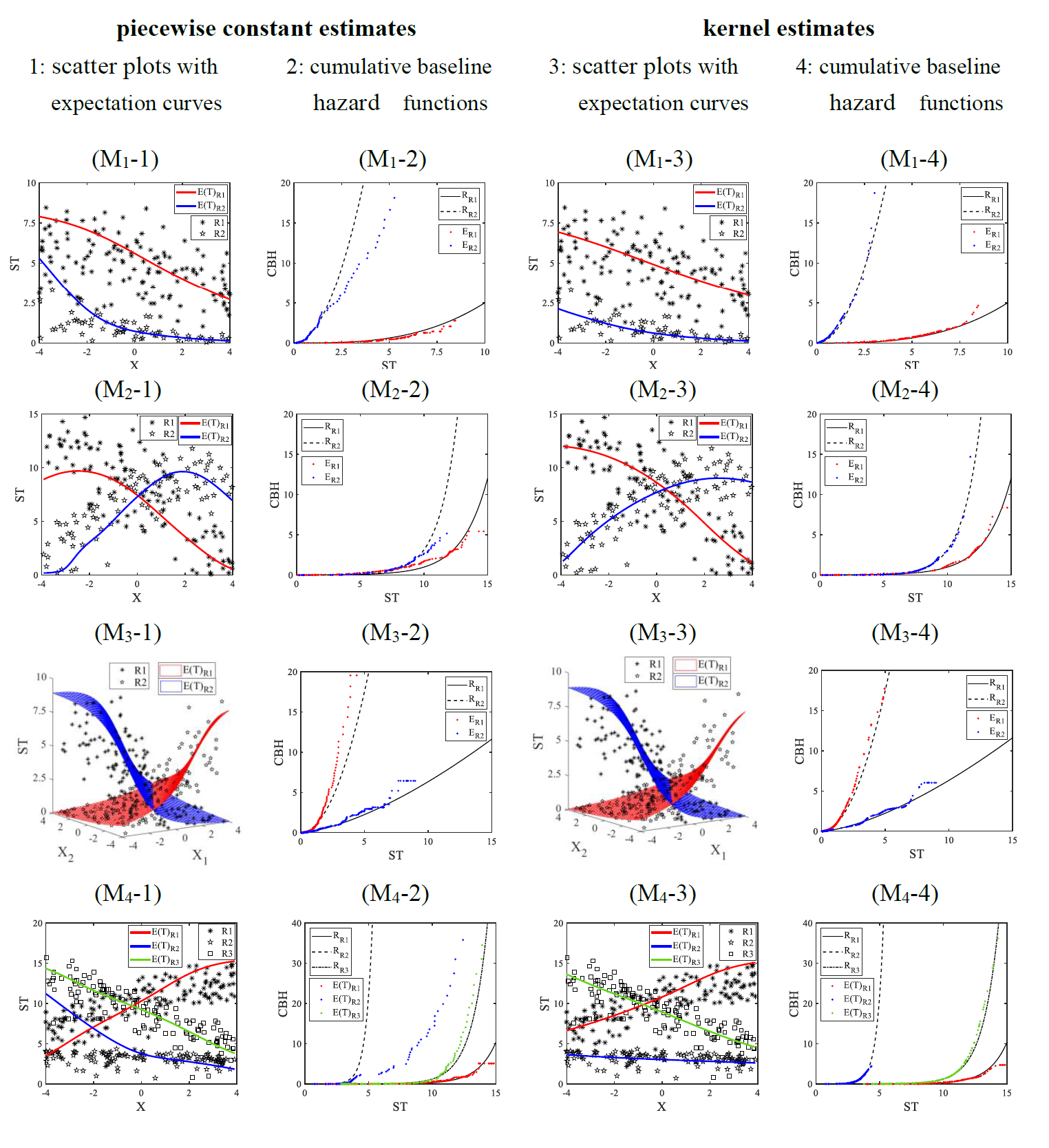
In order to graphically demonstrate the results, we first show the results for a single run of simulation in Table 3 and Figure 4. The correct rate (CR) in Table 3 is the percentage of individuals matched into the true attributable type of risk. According to the results of the estimation, we match the individuals into one type of risk with largest posterior probability. Thus, this correct rate is defined as:

When using a piecewise constant estimator under M₁, from the estimated mixing probabilities, CR in Table 3 and the expectation line in Figure 4(M₁-1), it can be seen that we will misclassify some data into the 2^nd type of risk where their true risk type is the 1^st one. As a result, the estimates of regression coefficients in Table 3 and the cumulative baseline hazard rate in Figure 4(M₁-2) are not close to the true model. Furthermore, under M₄, from the expectation line according to the 1^st and 2^nd types of risk in Figure 4(M₄-1), it can be seen that we will misclassify some data between the 1^st and 2^nd types of risk when using piecewise constant estimator. The estimates of regression coefficients in Table 3 and the cumulative baseline hazard rate in Figure 4(M₄-2) are mismatched with the real model. It is obvious that using the kernel procedure for the baseline hazard estimation will increase CR compared to using the piecewise constant procedure.

We next show the results for 1000 simulations in Table 4. The absolute relative bias (ARB) for parameter θ is defined by:

In Table 4 the mean absolute relative bias ( $\overline {ARB}$ ) of the model with k parameters is defined by $\overline {ARB} = {{\sum\nolimits_{i = 1}^k {ARB({\theta _i})} } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 1}^k {ARB({\theta _i})} } k}} \right. } k}$ . Moreover, $\overline {CR}$ and $\overline {MsSSE}$ are the mean of CR and MsSSE/n for each simulation. Table 4 presents that the $\overline {ARB}$ and $\overline {MsSSE}$ of the kernel estimate are smaller than those of the piecewise constant estimate. Moreover, the $\overline {CR}$ of the kernel estimate is larger than that of the piecewise constant estimate in all cases considered. Thus, the model with the baseline hazard functions estimated by the kernel method fits the data better than that with piecewise constant baseline.

4.2.   Select appropriate number of model components

In section 4.2, we consider an EM-based semi-parametric mixture hazards model to analyze simulated data under models M₁~M₄ by considering several possible number of risk types, that is model components, and use the kernel estimator to estimate the baseline hazard rates with biweight as the kernel function. Next, we use validity indices to select the optimal number of model components. The following six validity indices are used to compare with the validity indices we have come up with ( ${V_{aRaS}}$ , ${V_{sRaS}}$ , ${V_{aRmS}}$ , and ${V_{sRmS}}$ ).

1. Partition coefficient ${V_{PC}}$ proposed by Bezdek ^[22].

2. Normalized partition coefficient ${V_{NPC}}$ proposed by Dave ^[23].

3. Partition entropy ${V_{PE}}$ proposed by Bezdek ^[24].

4. Normalized partition entropy ${V_{NPE}}$ proposed by Dunn ^[25].

5. Akaike information criterion AIC.

6. Bayesian information criterion BIC.

It is well known that memberships play an important role in fuzzy clustering. Similarly, under the EM-based mixture model, the posterior probabilities are closely related to the role of memberships. Therefore, we replace the role of memberships with posterior probabilities in the validity indices ${V_{PC}}$ , ${V_{NPC}}$ , ${V_{PE}}$ , and ${V_{NPE}}$ . Moreover, the formulas for AIC and BIC are computed by

where $\; {l_c}(\mathit{\boldsymbol{\hat p}}, \mathit{\boldsymbol{\hat \beta }})$ is the complete-data log-likelihood (3) given the estimated parameters, and k is the number of parameters for estimation.

All in all we consider ten indices, including ${V_{PC}}$ , ${V_{NPC}}$ , ${V_{PE}}$ , ${V_{NPE}}$ , AIC, BIC, ${V_{aRaS}}$ , ${V_{sRaS}}$ , ${V_{aRmS}}$ , and ${V_{sRmS}}$ , to select the optimal number of model components. Table 5 shows the proportion of choosing the correct number of model components over 1000 simulation runs based on the considered indices respectively. In each simulation run, each model of M₁~M₄ is fitted for components 2, 3, and 4 separately. Note that we assume the number of model components is greater than one for satisfying the requirement of the proposed validity indices. We define the proportion of choosing the correct number of risk types by each index in Table 5 as:

Table 5 shows that the proportion of choosing the correct g by traditional indices ${V_{PC}}$ , ${V_{NPC}}$ , ${V_{PE}}$ , ${V_{NPE}}$ , AIC, and BIC are not consistent under models M₁~M₄, where at least one model is not performing well (denoted by fluorescent yellow color in the table). On the other hand, the proposed indices ( ${V_{aRaS}}$ , ${V_{sRaS}}$ , ${V_{aRmS}}$ , and ${V_{sRmS}}$ ) are consistent and possess high proportions for every model, except that the proportion of ${V_{sRmS}}$ under M₄ is 0.703, which is slightly low, but it is still higher than that of most traditional indices. Hence, the proposed validity indices are superior than others in selecting the correct number of components.

5.   Analysis of prostate cancer data

As a practical illustration of the proposed EM-based semi-parametric mixture hazard model, we consider the survival times of 506 patients with prostate cancer who entered a clinical trial during 1967–1969. These data were randomly allocated to different levels of treatment with the drug diethylstilbestrol (DES) and were considered by Byar and Green ^[26] and published by Andrews and Herzberg ^[27]. Kay ^[28] analyzed a subset of the data by considering eight types of risk, defined by eight categorical variables: drug treatment (RX: 0, 0.0 or 0.2 mg estrogen; 1, 1.0 or 5.0 mg estrogen); age group (AG: 0, < 75 years; 1, 75 to 79 years; 2, > 79 years); weight index (WT: 0, > 99 kg; 1, 80 to 99 kg; 2, < 80 kg); performance rating (PF: 0, normal; 1, limitation of activity); history of cardiovascular disease (HX: 0, no; 1, yes); serum haemoglobin (HG: 0, > 12 g/100 ml; 1, 9 to 12 g/100 ml; 2, < 9 g/100 ml); size of primary lesion (SZ: 0, < 30 cm²; 1, ≥ 30 cm2), and Gleason stage/grade category (SG: 0, ≤ 10; 1, > 10). Cheng et al. ^[26] classified this dataset with three types of risk as: (1) death due to prostate cancer; (2) death due to cardiovascular (CVD) disease; and (3) other causes.

We analyze the same dataset with eight categorical variables (RX, AG, WT, PF, HX, SZ, SG). There are 483 patients with complete information on these covariates, and the proportion of censored observations is 28.8%. We ignore the information about the risk factors and use indices, including ${V_{PC}}$ , ${V_{NPC}}$ , ${V_{PE}}$ , ${V_{NPE}}$ , AIC, BIC, ${V_{aRaS}}$ , ${V_{sRaS}}$ , ${V_{aRmS}}$ , and ${V_{sRmS}}$ to select the optimal number of risk types. From Table 6, the number of risk types selected by ${V_{aRaS}}$ , ${V_{sRaS}}$ , ${V_{aRmS}}$ , and ${V_{sRmS}}$ is three, and that selected by other indices is two. The number of model components selected by the indices we have proposed is the same as that in the previous studies introduced by Cheng et al. ^[3].

From existing medical experience and a previous study, we presume that these model components may agree with some particular types of risk and thus can decide whether there are significant relationships between the covariates and the survival times by using the Wald statistical test. Based on the cause-specific hazard approach, Cheng et al. ^[3] found that treatment with a higher DES dosage (RX = 1) significantly reduces the risk of death due to prostate cancer. Table 7 shows that the DES dosage has a significant effect on time to death due to the 1^st type of risk, and that the estimated regression coefficients of RX is negative. Byar and Green ^[26] found that patients with a big size of primary lesion (SZ = 1) and high-grade tumors (SG = 1) are at greater risk of prostate cancer death. Table 7 lists that SZ and SG have a significant effect on time to death due to the 1^st type of risk, and that the estimated regression coefficients are all positive. Accordingly, we presume the 1^st type of risk relates to prostate cancer. Furthermore, based on the cause-specific hazard approach, Cheng et al. ^[3] found that treatment with a higher DES dosage (RX = 1) significantly increases the risk of death due to CVD. From Table 7, we see that DES dosage has a significant effect on time to death due to the 2^nd and 3^rd types of risk, and that the estimated regression coefficient of RX is positive.

We know that patients with a history of cardiovascular disease (HX = 1) have a higher probability of death due to CVD, compared to those patients without such a history. Table 7 shows that the estimated regression coefficient of HX is positive due to the 2^nd type of risk. Hence, we presume the 2^nd type of risk may relate to CVD. There is no explicit relationship between covariates and survival times adhering to the 3^rd type of risk. Thus, we only presume the 3^rd type of risk may relate to other death causes without specification. According to the significant relationship of covariates and survival times, we assess that the 1^st, 2^nd and 3^rd types of risk for estimation from an EM-based semi-parametric mixture hazard model are classified to prostate cancer, CVD, and other unspecified causes, respectively.

6.   Conclusions and discussion

6.1.   Conclusions

This study introduces four new validity indices, ${V_{aRaS}}$ , ${V_{sRaS}}$ , ${V_{aRmS}}$ , and ${V_{sRmS}}$ , for deciding the number of model components when applying an EM-based Cox proportional hazards mixture model to a dataset of competing risks. We incorporate the posterior probabilities and the sum of standard residuals to constitute the new validity indices. Moreover, our study sets up an extended kernel approach to estimate the baseline functions more smoothly and accurately. Extensive simulations show that the kernel procedure for the baseline hazard estimation is helpful for increasing the correct rate of classifying individual into the true attributable type of risk. Furthermore, simulation results demonstrate that the proposed validity indices are consistent and have a higher percentage of selecting the optimal number of model components than the traditional competitors. Thus, the proposed indices are superior to several traditional indices such as the most commonly used in statistics, AIC and BIC. We also employ the propose method to a prostate cancer data-set to illustrate its practicability.

6.2.   Discussion

It is obvious that if we apply the four new validity indices at the same time, then we have the best chance to select the optimal number of model components. One concern is picking the best one among the proposed validity indices. In fact, the average separation versions ( ${V_{aRaS}}$ , ${V_{sRaS}}$ ) easily neutralizes the effects of small and large distances among the expectations of component models. On the other hand, as long as there is a small distance among the expectations of component models, the minimum separation versions ( ${V_{aRmS}}$ , ${V_{sRmS}}$ ) will catch the information about the overfitting model. Under the analysis of prostate cancer data, we see that ${V_{aRmS}}$ and ${V_{sRmS}}$ behave more sensitively than ${V_{aRaS}}$ and ${V_{sRaS}}$ for detecting the overfitting models (i.e., the distances of indices between overfitting and optimal models are much larger than those between underfitting and optimal models). Furthermore, according to the simulation results, the index ${V_{sRmS}}$ performs slightly poor on a certain model, we thus recommend employing ${V_{aRmS}}$ if just one of the proposed validity indices is to be used.

In the future we may test the effectiveness of the proposed validity indices on statistical models other than the mixture Cox proportional hazards regression models. We could also advance the efficiency of the proposed indices in determining the number of components of mixture models. Another issue is to reduce the computation cost. For instance, the bandwidth of the kernel procedure for baseline hazard function estimates is recalculated on each iteration, which consumes computation time. All these factors need further investigation and will be covered in our future research.

Acknowledgements

The authors thank the anonymous reviewers for their insightful comments and suggestions which have greatly improved this article. This work was partially supported by the Ministry of Science and Technology, Taiwan [Grant numbers MOST 108-2118-M-025-001-and MOST 108-2118-M-003-003-].