Non-null slant ruled surfaces and tangent bundle of pseudo-sphere

1.   Introduction

In mathematics, it is widely acknowledged in surface theory that a surface is considered as ruled if a straight line passes through each point on the surface ^[1,2]. Ruled surfaces are among the most fascinating topics in surface theory since they are fundamental for geometric modeling and commonly utilized in non-lightlike geometry ^[3,4] and in submanifold theory with the view of singularity properties ^{[5,6,7,8,9,10]}. They are also used in many other scientific fields, including mathematical physics and biology. Considering the ruled surface as an inclined tube or asymmetrically inclined channel contributes to a deeper understanding of the profound effect of heat transfer on magnetic peristaltic flows ^[11,12,13]. Moreover, research led to an understanding of experimental tools such as magnetic resonance imaging (MRI) and radiosurgery, the effects of endoscopes, fluid behavior especially in non-Newtonian scenarios, and the behavior of electrocosmotic forces. Slant ruled surfaces, which are special ruled surfaces, were defined in ^[14]. Different from a ruled surface, the Frenet vectors of these surfaces make a constant angle with a fixed direction on a slant ruled surface. In the literature, the theoretical and real-world applications of these surfaces take advantage of the geometric behavior of the slant ruled surface ^{[15,16,17,18,19]}. In ^[15,16,17], the differential geometric properties of these surfaces were supported by significant remarks and theorems. Therefore, these results were used to construct the Frenet frame for these surfaces. In ^[18], it was emphasized that velocity increases with an increase in inclination angle, and the best pumping rate appears in the vertical tube as compared to the horizontal tube. Hence, the results contributed to increasing the velocity of the fluid by using the heat generation parameter. In ^[19], angles of inclination of the magnetic field affected two-phase fluid flow through a horizontal porous channel in the presence of a uniformly inclined magnetic field.

On the other hand, dual numbers were defined by W. K. Clifford as a tool for geometrical research. Moreover, these numbers were applied to screw systems, spatial mechanisms, iterative methods, among others. Then, dual numbers were employed in line geometry and kinematics by E. Study in ^[20,21]. Furthermore, E. Study discovered that there is one-to-one correspondence between oriented lines in Euclidean 3-space and the dual points of the dual unit sphere in dual 3-space. The discovery was adapted to Minkowski 3-space by constructing the relation between oriented lines in Minkowski 3-space and the dual points of the pseudo-spheres in ^[22].

Combining the dual points of the unit dual sphere and the ruled surfaces in $E^{3},$ an isomorphism was constructed among the unit dual sphere, the tangent bundle of the unit 2-sphere, and the non-cyclindirical ruled surface, as shown in ^[23]. In light of this study, each curve on the tangent bundles of unit 2-spheres (or tangent bundles of pseudo-spheres) corresponds to a ruled surface, as discussed in ^[24,25,26]. Furthermore, these concepts have extensive applications on tangent bundles in ^[27,28]. In these studies, the tangent bundles are defined to provide an almost metrical paracontact structure and the conditions for a Lagrangian graph.

Overall, when studying slant ruled surfaces, the relation between non-null slant ruled surfaces and tangent bundles of pseudo-spheres provides us with some feasible approaches to investigate some geometric properties such as developability condition, convenience of physical applications, determining geodesic or non-geodesic cases, or adapting the curve to the new ruled surface. However, no literature exists regarding the non-null slant ruled surface generated by the natural lift curve and the isomorphism between the pseudo-spheres and the subsets of the tangent bundles of pseudo-spheres. Therefore, motivated by the definition of the natural lift curve, which is the endpoint of the unit tangent vector of the main curve in ^[29], a new perspective of the non-null slant ruled surface is given by using E. Study mapping and the correspondence between the subsets of the tangent bundles of pseudo-spheres and the slant ruled surface in $E^{3}_{1}.$ For this aim, the striction curve of the natural lift curve on the subsets of the tangent bundles of pseudo-spheres is related to non-null slant ruled surfaces by exploiting the Frenet frame mentioned in ^[30]. Then, the classification of the slant ruled surface is denoted by non-null $\bar{q}-, \bar{h}-$, and $\bar{a}-$ slant ruled surfaces. Then, some notable theorems and remarks are mentioned for these slant surfaces. The main result of the paper is Theorem 4.7, which gives the classification of the canonical curvature for determining the non-null slant ruled surface.

The rest of this paper is organized as follows. Section 2 shows some basic definitions for Minkowski 3-space, the natural lift curves, and the correspondence among the ruled surfaces and pseudo-spheres. Section 3 describes the differential geometric properties of the ruled surface in $E^{3}_{1}.$ Section 4 shows new results about non-null slant-ruled surfaces. In Section 5, some examples are given to verify the consequences. Section 6 concludes the work and provides future research directions.

2.   Preliminaries

In this section, basic concepts are given about Minkowski 3-space, dual numbers, and the correspondence between the tangent bundles of pseudo-spheres and non-null ruled surfaces.

Assume that $E^{3}_{1}$ is a Minkowski 3-space with Lorentzian metric $\langle, \rangle_{L} = x^{2}_{1}+x^{2}_{2}-x^{2}_{3},$ where $\vec{x} = (x_{1}, x_{2}, x_{3})$ is the vector in Minkowski 3-space. Then, there are three types of vectors in Minkowski space: For $\vec{x} \in E^{3}_{1},$ $\vec{x}$ is called a spacelike, timelike, or lightlike vector if $\langle \vec{x}, \vec{x} \rangle_{L} > 0, \langle \vec{x}, \vec{x} \rangle_{L} < 0$ or $\langle \vec{x}, \vec{x} \rangle_{L} = 0, \vec{x} \neq 0,$ respectively.

In $E^{3}_{1}$, the Lorentzian and the hyperbolic unit spheres are denoted, respectively, by

in ^[1]. $\mathbf{S^{2}_{1}}$ and $\mathbf{H^{2}}$ have tangent bundles that are given by

Assume that $\mathbf{T\tilde{M}}$ and $\mathbf{T\hat{M}}$ are the subsets of $\mathbf{TS^{2}_{1}}$ and $\mathbf{TH^{2}},$ given as follows:

where $\bar{\gamma}$ and $\bar{\vartheta}$ denote the derivatives of $\gamma$ and $\vartheta,$ respectively ^[26]. In $E^{3}_{1},$ the ruled surface is characterized by

where $\beta(u) = \bar{\gamma}(u) \times_{L} \bar{\vartheta}(u)$ and $\gamma(u)$ are the base and the director curves, respectively in ^[25].

The set of dual numbers is represented by

The set

is called $\mathbb{D}-$ Module, which is a module over $\mathbb{D}.$ Moreover, the elements of the set are defined as a dual vector. The dual vector can be written as

Here $\vec{x} = (x_{1}, x_{2}, x_{3})$ and $\vec{x}^{*} = (x^{*}_{1}, x^{*}_{2}, x^{*}_{3})$ are real vectors. For $\vec{X} = \vec{x}+\varepsilon \vec{x}^{*}$ and $\vec{Y} = \vec{y}+\varepsilon \vec{y}^{*},$ the addition and Lorentzian inner product are, respectively,

The norm of $\vec{X}$ is denoted by $|\vec{X}|_{L} = \sqrt{|\langle \vec{X}, \vec{X} \rangle_{L}|}.$ In terms of Lorentzian inner product, a dual Lorentzian vector $\vec{X} = \vec{x}+\varepsilon \vec{x}^{*}$ is called a spacelike, timelike, or lightlike vector if $\vec{x}$ is spacelike, timelike, or lightlike, respectively. The set of all dual Lorentzian vectors is represented by $\mathbb{D}_{1}^{3}.$ For more detailed descriptions, see ^[20,21].

The sets

are called dual hyperbolic and dual Lorentzian unit spheres, respectively ^[1].

Definition 2.1. For the smooth curve $\Gamma,$ $\bar{\Gamma}$ is called the natural lift on the subsets of the tangent bundles (i.e., $\mathbf{T\tilde{M}}$ or $\mathbf{T\hat{M}}$), and it fulfills the equation given in ^[16]:

Proposition 2.2. In ^[16], there are the following isomorphisms:

and

Theorem 2.3. (E. Study mapping) The directed timelike (resp., spacelike) lines in $E_{1}^{3}$ and ordered pairs of vectors on $S^{2}_{1}$ and $H^{2}$ have a one-to-one correspondence ^[22].

In the literature, each curve on the tangent bundle of pseudo-spheres was corresponds to a non-null ruled surface by using E. Study mapping in $E_{1}^{3}$ ^[25]. In light of this correspondence, the relation between the non-null ruled surface generated by the natural lift curve and the subsets of the tangent bundles of pseudo-spheres was constructed in ^[26]:

and

3.   On ruled surfaces in $E_{1}^{3}$

In this section, some geometric properties are given about ruled surfaces in $E_{1}^{3}.$

Assume that

is the parametric representation of $\phi$, where $\vec{k}(u)$ and $\vec{q}(u)$ represent the base curve and the generating lines for $\vec{h}(u, s)$ in ^[30]. The unit normal vector $\vec{m}$ is

Therefore, we have

along a ruling $u = u_{1}.$ Exploiting the orthogonality of $\vec{q},$ $\vec{q}^{'}$ and relation Eq (3.3), the unit vector $\vec{\bar{h}}$ is obtained by

Additionally, the striction curve of the ruled surface is defined by

The orthonormal system $\{\vec{c}; \vec{q}, \vec{h}, \vec{a}\}$ is referred to as the Frenet frame of $\phi$ with respect to the striction curve. Furthermore, the ruling, central normal, and central tangent vectors are denoted as $\vec{q}, \vec{h}$, and $\vec{a}$, respectively.

Definition 3.1. ^[17] Assume that $\phi$ is the ruled surface in $E_{1}^{3}.$ The ruled surface is classified in terms of Frenet vectors as follows:

$(i)$ If $\vec{q}$ and $\vec{a}$ are spacelike vectors, $\vec{h}$ is a timelike vector, and $\phi$ is called a spacelike ruled surface in $E_{1}^{3}.$

$(ii)$ If $\vec{q}$ and $\vec{h}$ are spacelike vectors, $\vec{a}$ is a timelike vector, and $\phi$ is called a timelike ruled surface in $E_{1}^{3}.$

$(iii)$ If $\vec{h}$ and $\vec{a}$ are spacelike vectors, $\vec{q}$ is a timelike vector, and $\phi$ is called a timelike ruled surface in $E_{1}^{3}.$

The character $\phi$ is denoted according to Lorentzian characters of the ruling and central normal vectors as follows ^[17]:

$(i)$ If the central normal vector $\vec{h}$ is spacelike and the ruling $\vec{q}$ is spacelike, the ruled surface $\phi$ is the type of $\phi_{+}.$

$(ii)$ If the central normal vector $\vec{h}$ is spacelike and the ruling $\vec{q}$ is timelike, the ruled surface $\phi$ is the type of $\phi_{-}.$

$(iii)$ If the central normal vector $\vec{h}$ is timelike, the ruled surface $\phi$ is the type of $\phi_{x}.$

We observe that $\phi_{+}$ and $\phi_{-}$ are timelike, and $\phi_{x}$ is a spacelike ruled surface. Hence, the parametrization of $\phi$ is given as follows:

where $\langle \vec{q}(u), \vec{q}(u) = \pm 1 \rangle$ and $\langle \vec{h}(u), \vec{h}(u) = \pm 1 \rangle.$

In the rest of the paper, the orthonormal system $\{\vec{\bar{q}}, \vec{\bar{h}}, \vec{\bar{a}}\}$ is referred to as the Frenet frame of $\bar{\phi}$ concerning the striction curve of the natural lift curve.

4.   Non-null slant ruled surfaces and tangent bundle of pseudo-sphere

In this section, the relation between tangent bundles of pseudo-spheres and non-null slant ruled surfaces is introduced. Then, some substantial theorems and remarks are proved using the relation.

Definition 4.1. A ruled surface $\bar{\phi}(u, s) = \vec{\bar{q}}(u)\times_{L} \vec{\bar{\vartheta}}(u)+s\vec{\bar{q}}(u)$ in $E_{1}^{3}$ is called a non-null $\vec{\bar{q}}-$ (resp., $\vec{\bar{h}}-, \vec{\bar{a}}-$) slant ruled surface if three conditions are met:

First, the base curve is

Second, the equations $|\vec{\bar{q}}(u)|_{L} = 1$ (meaning if $\vec{\bar{q}}(u)$ is spacelike, then $\langle \vec{\bar{q}}(u), \vec{\bar{q}}(u) \rangle_{L} = 1$ and if $\vec{\bar{q}}(u)$ is timelike, then $\langle \vec{\bar{q}}(u), \vec{\bar{q}}(u) \rangle_{L} = -1$) and $\langle \vec{\bar{q}}(u), \vec{\bar{\vartheta}}^{*}(u) \rangle_{L} = 0$ are satisfied.

Last, $\vec{\bar{q}}-(resp., \vec{\bar{h}}-, \vec{\bar{a}}-)$ needs to have a fixed non-zero direction with a constant angle.

Let $\hat{\Gamma}(u) = \vec{\bar{q}}(u)+\varepsilon\vec{\bar{\vartheta}}^{*}(u)$ be a striction curve of the natural lift curve on $S^{2}_{1}$ $(resp., \ H^{2})$ with parameter $u.$ In $E_{1}^{3},$ the timelike (resp., spacelike) slant ruled surface generated by $\hat{\Gamma}(u)$ is denoted by

where the base curve is

As a result, we can give these isomorphisms:

and

Definition 4.2. Let $\hat{\phi}(u, s)$ be a non-null slant ruled surface corresponding to $\hat{\Gamma}(u)$ in $E_{1}^{3},$ represented by the parametrization

where $\bar{\beta}(u)$ is the striction curve of $\hat{\phi}(u, s).$ Let $\{\vec{\bar{q}}, \vec{\bar{h}}, \vec{\bar{a}}\}$ be Frenet vectors of $\hat{\phi}.$ For the canonical curvature $\bar{\kappa} \neq 0,$

if $\theta$ is the angle between the ruling and a fixed non-zero direction $\vec{u}$ in the space. $\hat{\phi}$ refers to a $\vec{\bar{q}}-$ timelike (resp., spacelike) slant ruled surface.

Theorem 4.3. Assume that $\hat{\phi}$ is a $\vec{\bar{q}}-$ slant ruled surface acquired by the striction curve of the natural lift curve with the Frenet vectors $\{\vec{\bar{q}}, \vec{\bar{h}}, \vec{\bar{a}}\}$ satisfying the conical curvature $\bar{\kappa}\neq 0$ in $E^{3}_{1}.$ Then, there are the following conditions:

$(i)$ If $\hat{\phi}$ is $\vec{\bar{q}}-$ spacelike slant ruled surface, then

$(ii)$ If $\hat{\phi}$ is $\vec{\bar{q}}-$ timelike slant ruled surface with spacelike ruling, then

$(iii)$ If $\hat{\phi}$ is $\vec{\bar{q}}-$ timelike slant ruled surface with timelike ruling, then

Proof. By Definition 4.2, we examine three conditions as follows:

$(i)$ Let $\hat{\phi}$ be $\vec{\bar{q}}-$ spacelike slant ruled surface. We know that

From the derivative of Eq (4.7), we obtain

Since $\vec{u}$ is constant and $\vec{\bar{q}}' = \vec{\bar{h}}$, we get

Taking the derivative of Eq (4.8) and using $\vec{\bar{h}}' = \vec{\bar{q}}+\bar{\kappa}\vec{\bar{a}},$ we write

After some calculations, we get the desired result. For the proofs of $(ii)$ and $(iii),$ we use the Frenet formulas for $\vec{\bar{q}}-$ timelike slant ruled surfaces. Therefore, it can be easily seen that the equalities are satisfied by the same steps given above. □

Theorem 4.4. Let $\hat{\phi}$ be $\vec{\bar{q}}-$ slant ruled surface acquired by the striction curve of the natural lift curve with the Frenet vectors $\{\vec{\bar{q}}, \vec{\bar{h}}, \vec{\bar{a}}\}$ satisfying $\kappa \neq 0$ in $E^{3}_{1}.$ Assuming $< \vec{\bar{q}}, \vec{u} > = \lambda,$ $\lambda \in \mathbb{R},$ there are the following conditions:

$(i)$ If $\hat{\phi}$ is a $\vec{\bar{q}}-$ spacelike slant ruled surface, then

$(ii)$ If $\hat{\phi}$ is a $\vec{\bar{q}}-$ timelike slant ruled surface with spacelike ruling, then

$(iii)$ If $\hat{\phi}$ is a $\vec{\bar{q}}-$ timelike slant ruled surface with timelike ruling, then

Proof. Since $\hat{\phi}$ is $\vec{\bar{q}}-$ slant ruled surface, $\vec{\bar{h}}$ is orthogonal to $\vec{u}$ from Eq (4.9). Hence, $\vec{u}$ is written as the linear combination of $\lambda_{1} = \lambda_{1}(u_{1})$ and $\lambda_{2} = \lambda_{2}(u_{1})$ with the arc-length parameter $u_{1}.$ Therefore, we have

$(i)$ Let $\hat{\phi}$ be a $\vec{\bar{q}}-$ spacelike slant ruled surface. Taking the inner product of $\vec{\bar{q}}$ and Eq (4.14), we get

Similarly, taking the inner product of $\vec{\bar{a}}$ and Eq (4.14), we calculate $\lambda_{2} = -\frac{\lambda}{\bar{\kappa}}.$ Substituting $\lambda_{1}$ and $\lambda_{2}$ into Eq (4.14), the proof is completed.

Exploiting the same steps mentioned above, it can be simply seen that $< \vec{\bar{q}}, \vec{u} > _{L} = \lambda_{1} = \lambda$ and $\lambda_{2} = -\frac{\lambda}{\kappa}$ for $(ii).$

$(iii)$ Assume that $\hat{\phi}$ is $\vec{\bar{q}}-$ timelike slant ruled surface with timelike ruling. Taking the inner product of $\vec{\bar{q}}$ and Eq (4.14), we get

Similarly, from the inner product of $\vec{\bar{a}}$ and Eq (4.14), we calculate $\lambda_{2} = -\frac{\lambda}{\bar{\kappa}}.$ Substituting $\lambda_{1}$ and $\lambda_{2}$ into Eq (4.14), we obtain Eq (4.13). □

Remark 4.5. Let $\hat{\phi}$ be a ruled surface with the Frenet vectors $\{\vec{\bar{q}}, \vec{\bar{h}}, \vec{\bar{a}}\}$ satisfying $\bar{\kappa} \neq 0$ in $E^{3}_{1}.$ Then, $\hat{\phi}$ is a non-null $\vec{\bar{q}}-$ slant ruled surface acquired by the striction curve of the natural lift curve if and only if $\bar{\kappa}$ is constant.

Proof. $(i)$ Assume that $\hat{\phi}$ is a non-null $\vec{\bar{q}}-$ slant ruled surface acquired by the natural lift curve. From Theorem 4.4,

Differentiating Eq (4.17), we have

Thus, we find that $\bar{\kappa}$ is constant. Conversely, assume that $\bar{\kappa}$ is constant. If $\vec{u}$ is chosen as $\lambda \vec{\bar{q}}-\frac{\lambda}{\bar{\kappa}}\vec{\bar{a}}$ and the derivative of $\vec{u}$ is considered, we obtain that $\vec{u}$ is constant. Therefore, it is concluded that $\hat{\phi}$ is a non-null $\vec{\bar{q}}-$ slant ruled surface. □

Definition 4.6. Let $\hat{\phi}(u, s)$ be a non-null slant ruled surface corresponding to $\hat{\Gamma}(u)$ in $E_{1}^{3},$ denoted by the parametrization

where $\bar{\beta}(u)$ is the striction curve of $\hat{\phi}(u, s).$ Let $\{\vec{\bar{q}}, \vec{\bar{h}}, \vec{\bar{a}}\}$ be Frenet vectors of $\hat{\phi}.$ For $\bar{\kappa} \neq 0,$

if $\varphi$ is the angle between the central normal vector and a fixed non-zero direction $\vec{u}$ in the space. $\hat{\phi}$ refers to a $\vec{\bar{h}}-$ timelike (resp., spacelike) slant ruled surface.

Theorem 4.7. $\hat{\phi}$ is a $\vec{\bar{h}}-$ slant ruled surface under the assumptions given in Definition 4.6 if and only if there are the following characterizations:

$(i)$ Let $\hat{\phi}$ be a spacelike ruled surface. $\hat{\phi}$ refers to a $\vec{\bar{h}}-$ slant ruled surface if and only if

$(ii)$ Let $\hat{\phi}$ be a timelike ruled surface with spacelike ruling. $\hat{\phi}$ refers to a $\vec{\bar{h}}-$ slant ruled surface if and only if

and

$(iii)$ Let $\hat{\phi}$ be a timelike ruled surface with spacelike ruling. $\hat{\phi}$ refers to a $\vec{\bar{h}}-$ slant ruled surface if and only if

and

Proof. $(i)$ Let $\hat{\phi}$ be a spacelike ruled surface. Assume that $\hat{\phi}$ is a $\vec{\bar{h}}-$ slant ruled surface. Using Definition 4.6, we write

For $b_{1} = b_{1}(s_{1}),$ $b_{2} = b_{2}(s_{1}),$

From the derivative of $\vec{u}$, we write

Since the set $\{\vec{\bar{q}}, \vec{\bar{h}}, \vec{\bar{a}}\}$ is linear independent, we write

from Eq (4.26). Since $\vec{u}$ is constant and $b_{1} = -b_{2}\bar{\kappa}$, we obtain

After some calculations, we get

Conversely, let

and

Taking the derivative of Eq (4.30) and using Eq (4.29), we obtain that $\vec{u}$ is constant. Since $\langle \vec{\bar{h}}, \vec{u}\rangle = -p,$ $\hat{\phi}$ refers to a $\vec{\bar{h}}-$ slant ruled surface. By using the same steps, similar proofs could be done for $(ii)$ and $(iii).$ □

Theorem 4.8. Let $\hat{\phi}$ be the ruled surface acquired by the natural lift curve of the striction curve with the Frenet vectors $\{\vec{\bar{q}}, \vec{\bar{h}}, \vec{\bar{a}}\}$ satisfying $\bar{\kappa} \neq 0$ in $E^{3}_{1}.$ The following assumptions are satisfied for the angle $\theta,$ which is the angle between $\vec{\bar{h}}$ and $\vec{u}$:

$(i)$ Let $\hat{\phi}$ be a spacelike ruled surface and $\vec{u}$ be a spacelike vector. $\hat{\phi}$ refers to a $\vec{\bar{h}}-$ slant ruled surface if and only if

$(ii)$ Let $\hat{\phi}$ be a spacelike ruled surface and $\vec{u}$ be a timelike vector. $\hat{\phi}$ refers to a $\vec{\bar{h}}-$ slant ruled surface if and only if

$(iii)$ Let $\hat{\phi}$ be a timelike ruled surface with spacelike ruling and $\vec{u}$ be a timelike vector. Let the plane spanned by the vectors $\vec{\bar{h}}$ and $\vec{u}$ also be spacelike. $\hat{\phi}$ refers to a $\vec{\bar{h}}-$ slant ruled surface if and only if

$(iv)$ Let $\hat{\phi}$ be a timelike ruled surface with spacelike ruling and $\vec{u}$ be a timelike vector. Let the plane spanned by the vectors $\vec{\bar{h}}$ and $\vec{u}$ also be timelike. $\hat{\phi}$ refers to a $\vec{\bar{h}}-$ slant ruled surface if and only if

$(v)$ Let $\hat{\phi}$ be a timelike ruled surface with spacelike ruling and $\vec{u}$ be a timelike vector. $\hat{\phi}$ refers to a $\vec{\bar{h}}-$ slant ruled surface if and only if

$(vi)$ Let $\hat{\phi}$ be a timelike ruled surface with timelike ruling and $\vec{u}$ be a spacelike vector. Let the plane spanned by the vectors $\vec{\bar{h}}$ and $\vec{u}$ also be spacelike. $\hat{\phi}$ refers to a $\vec{\bar{h}}-$ slant ruled surface if and only if

$(vii)$ Let $\hat{\phi}$ be a timelike ruled surface with timelike ruling and $\vec{u}$ be a spacelike vector. Let the plane spanned by the vectors $\vec{\bar{h}}$ and $\vec{u}$ also be timelike. $\hat{\phi}$ refers to a $\vec{\bar{h}}-$ slant ruled surface if and only if

$(viii)$ Let $\hat{\phi}$ be a timelike ruled surface with timelike ruling and $\vec{u}$ be a timelike vector. $\hat{\phi}$ refers to a $\vec{\bar{h}}-$ slant ruled surface if and only if

Proof. $(i)$ Assume that $\hat{\phi}$ is a spacelike ruled surface and $\vec{u}$ is a spacelike vector. Hence, we write

Taking the derivative of Eq (4.39), we get

If $\langle \vec{\bar{a}}, \vec{u}\rangle = x,$ then

Since $\vec{u}$ is a unit vector, we find

Taking the second derivative of Eq (4.40), we also find

From Eqs (4.42) and (4.43), we have

Integrating Eq (4.44), we calculate

If the parameter change is done as $s_{1} \rightarrow s_{1}-c,$ we find Eq (4.31). Conversely, assume that Eq (4.31) is satisfied and $x = \pm \sinh \theta \sqrt{\coth^{2} \theta-s^{2}_{1}}.$ If

it can be easily seen that $\langle \vec{\bar{h}}, \vec{u}\rangle = - \sinh \theta.$ Thus,

From the derivative of $\vec{u},$ $\vec{u}$ is constant. Hence, $\hat{\phi}$ refers to a $\vec{\bar{h}}-$ slant ruled surface.

$(iv)$ Assume that $\hat{\phi}$ is a timelike ruled surface with spacelike ruling and $\vec{u}$ is a timelike vector. Assume that the plane spanned by $\vec{\bar{h}}$ and $\vec{u}$ is timelike. Then, we know that

Differentiating Eq (4.48), we obtain

If $\langle \vec{\bar{a}}, \vec{u}\rangle = x,$ then

Since $\vec{u}$ is unit vector, we find

Taking the second derivative of Eq (4.49), we also find

From Eqs (4.51) and (4.52), we have

Integrating Eq (4.53), we calculate

If the parameter change is done as $s_{1} \rightarrow s_{1}-c,$ we find Eq (4.34). Conversely, assume that Eq (4.34) is satisfied and $x = \pm \cosh \theta \sqrt{\tanh^{2} \theta+s^{2}_{1}}.$ If

it can be easily seen that $\langle \vec{\bar{h}}, \vec{u}\rangle = - \cosh \theta.$ Thus,

From the derivative of $\vec{u},$ $\vec{u}$ is constant. Hence, $\hat{\phi}$ refers to a $\vec{\bar{h}}-$ slant ruled surface. Proofs of the other assumptions can be done by using similar steps. □

Definition 4.9. Let $\hat{\phi}(u, s)$ be a non-null slant ruled surface corresponding to $\hat{\Gamma}(u)$ in $E_{1}^{3}$ denoted by the parametrization

where $\bar{\beta}(u)$ is the striction curve of $\hat{\phi}(u, s).$ Let $\{\vec{\bar{q}}, \vec{\bar{h}}, \vec{\bar{a}}\}$ be Frenet vectors of $\hat{\phi}.$ For the canonical curvature $\bar{\kappa} \neq 0,$

if $\mu$ is the angle between the central tangent vector and a fixed non-zero direction $\vec{u}$ in the space. $\hat{\phi}$ refers to a $\vec{\bar{a}}-$ timelike (resp., spacelike) slant ruled surface.

From Theorem 4.4 and Remark 4.5, $\hat{\phi}$ is a $\vec{\bar{q}}-$ slant ruled surface if and only if it denotes a $\vec{\bar{a}}-$ slant ruled surface. Thus, all characterizations for $\vec{\bar{q}}-$ slant ruled surfaces are valid for $\vec{\bar{a}}-$ slant ruled surfaces.

5.   Examples

In this section, examples are given as applications and illustration of the main results.

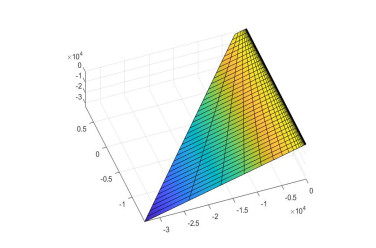
Example 5.1. Let $\hat{\phi}(u, s)$ be the timelike ruled surface with spacelike ruling acquired by the natural lift curve.

where the base curve is

For $\bar{q}(u) = (\frac{1}{\sqrt{3}} \sinh(\sqrt{3}u), \frac{2}{\sqrt{3}}, \frac{1}{\sqrt{3}}\cosh (\sqrt{3}u))$ and $\bar{\vartheta}^{*}(u) = (\frac{1}{\sqrt{3}} \cosh(\sqrt{3}u), 0, \frac{1}{\sqrt{3}}\sinh (\sqrt{3}u)),$ $\langle \vec{\bar{q}}(u), \vec{\bar{\vartheta}}^{*}(u) \rangle_{L} = 0$ and $|\vec{\bar{q}}(u)|_{L} = 1.$ Therefore, $\hat{\Gamma}(u) = (\bar{q}(u), \bar{\vartheta}^{*}(u)) \in \mathbf{T\tilde{M}}.$ Then, the Frenet vectors are computed by

Since $\bar{\kappa} = -2,$ $\hat{\phi}(u, s)$ is $\vec{\bar{q}}-$ timelike slant ruled surface with spacelike ruling.

The following figure is Figure 1.

Example 5.2. Let $\hat{\phi}(u, s)$ be the spacelike ruled surface acquired by the natural lift curve.

where the base curve is

For $\bar{q}(u) = (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\cosh(u\sqrt{2}), \frac{1}{\sqrt{2}}\sinh (u\sqrt{2}))$ and $\bar{\vartheta}^{*}(u) = (0, \frac{1}{\sqrt{2}}\sinh (u\sqrt{2}), \frac{1}{\sqrt{2}}\cosh (u\sqrt{2})),$ $\langle \vec{\bar{q}}(u), \vec{\bar{\vartheta}}^{*}(u) \rangle_{L} = 0$ and $|\vec{\bar{q}}(u)|_{L} = 1.$ Therefore, $\hat{\Gamma}(u) = (\bar{q}(u), \bar{\vartheta}^{*}(u)) \in \mathbf{T\tilde{M}}.$ Then, the Frenet vectors are calculated by

Since $\bar{\kappa} = -1,$ $\hat{\phi}(u, s)$ is $\vec{\bar{q}}-$ slant ruled surface.

The following figure is Figure 2.

6.   Conclusions

Slant ruled surfaces, defined in ^[14], are special ruled surfaces where the Frenet vectors make a constant angle with some fixed directions in the space. In this study, taking the definition of slant-ruled surfaces in literature into consideration, we obtain some considerable consequences, summarized as follows:

(1) We give the new definition for non-null slant ruled surfaces acquired by the striction curve of the natural lift curve in $E^{3}_{1}$. In order to perform the definition, we exploit the E. Study mapping and the relation between the subsets of the tangent bundles of pseudo-spheres and non-null ruled surfaces.

(2) Considering the definition, we examine the $\bar{q}-, \bar{h}-, \bar{a}-$ spacelike and timelike slant ruled surfaces acquired by the striction curves of the natural lift curves in $E^{3}_{1}$.

(3) By using the examinations of these non-slant ruled surfaces, the conditions to be $\bar{q}-, \bar{h}-, \bar{a}-$ spacelike (resp., timelike) are investigated.

(4) With the help of Theorem 4.7, the effect of the canonical curvature of the non-null slant ruled surface is highlighted.

The implications of the findings extend beyond theoretical interest in Minkowski geometry, offering experimental applications for physical and biological problems in solving heat transfer problems, the application of electrocosmotic forces applied to surfaces, the impact of magnetic fields, etc. Future research could further investigate the numerical implementation of axial velocity, pressure gradient, and flow streamlines within this framework in real-world applications. Overall, the paper provides a means to study singularity and submanifold theories for ruled surfaces and opens avenues for further investigation into their applications in various mathematical contexts.

Use of AI tools declaration

The author declares he/she has not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The author would like to thank the referee for valuable comments improving the paper.

Conflict of interest

The author declares that there is no conflict of interest regarding the publication of this paper.