Repdigits base $\eta$ as sum or product of Perrin and Padovan numbers

1.   Introduction

The sequence of Padovan numbers $\{P_n\}_{n\geq0}$ is defined by the following recurrence sequence:

The first few terms are as follows:

The Perrin sequence $\{E_{n}\}_{n\geq0}$ that is derived from the recurrence relation is as follows:

The first few terms are as follows:

The Padovan and Perrin numbers are the sequences $A000931$ and $A001608$ respectively, in the online encyclopedia of integer sequences (OEIS).

A natural number $N$ is called a base $\eta$ repdigit if it is of the form

When $\eta = 10$, the number $N$ is a repdigit. Recently, many mathematicians have investigated the solutions to the Diophantine equations that involve repdigits and linear recurrence sequences. Lomelí and Hernández ^[1] showed that the only repdigits that can be written as sums of two Padovan numbers are $11, 22, 33, 44, 66, 77, 88, 3333$.

Trojovský ^[2] found all repdigits that can be written as sums of Fibonacci and Tribonacci numbers. Bednařík and Trojovská ^[3] studied the repdigits that can be expressed as products of Fibonacci and Tribonacci numbers. Erduvan et al.^[4,5,6] expressed all repdigits in base $b$ as products of two Fibonacci, two Lucas, two Pell, and two Pell-Lucas numbers. In 2022, the same authors ^[7] examined all repdigits in base $b$ that are represented as the difference between two Fibonacci numbers.

Moreover, Bhoi and Ray ^[8] demonstrated that only Perrin numbers that are expressible as the sum of two repdigits are $P_{11}$ and $P_{20}$. Rihane and Togbé ^[9] found all repdigits that can be expressed as products of consecutive Padovan or Perrin numbers. One year later, the same authors ^[10] investigated Padovan and Perrin numbers as a product of two repdigits. Adédji et al. ^[11] found all Padovan and Perrin numbers, which are products of two repdigits in base $b$, and showed that $P_{25}$ and $T_{22}$ are the largest Padovan and Perrin numbers in that form, respectively.

Subsequently, Adédji et al. ^[12] showed that Padovan or Perrin numbers are concatenations of two distinct base $b$ repdigits with $2\leq b\leq 9$. They also found that the largest Padovan and Perrin numbers are concatenations of two distinct base $b$ repdigits, $P_{26}$ and $E_{24}$, respectively. Adédji et al. ^[13] considered the Padovan and Perrin numbers to be expressible as products of two generalized Lucas numbers. Duman et al. ^[14] showed that $2, 3, 4, 5, 7, 9, 12, 16, 28, 37, 49, 86$ and $114$ are the only Padovan numbers that can be expressed as the sum of two repdigits. The findings are as follows

Theorem 1.1. The only solutions of the Diophantine equation

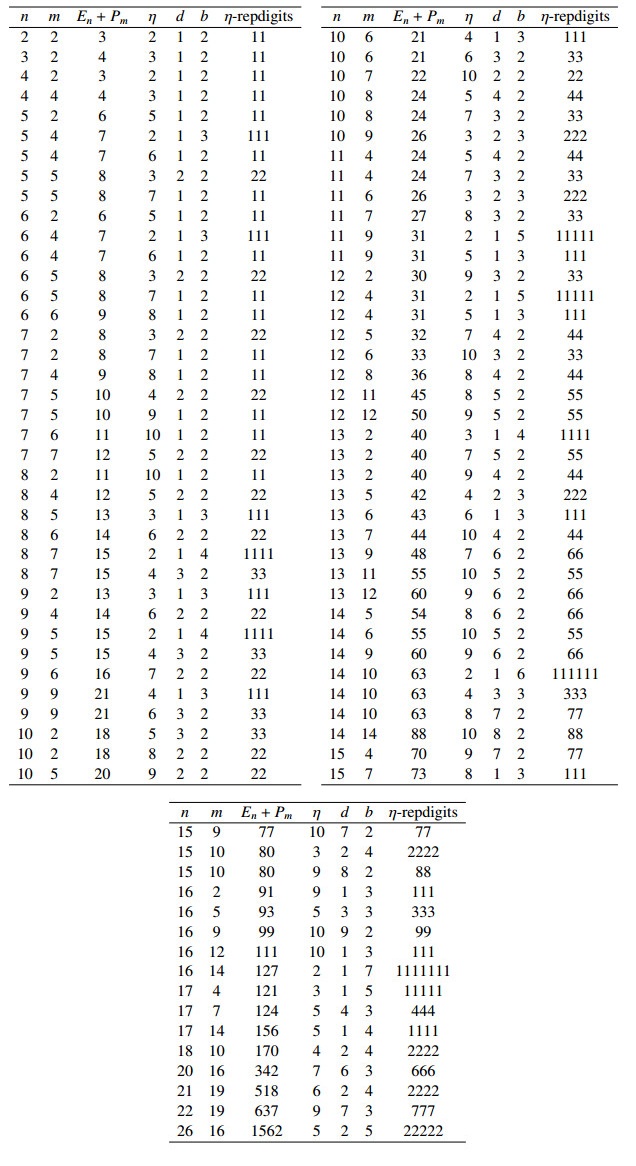
as non-negative integers for $m\leq n$, $1\leq d\leq\eta-1$, $2\leq\eta\leq10$, and $b\geq2$ are given in Table A.1.

Theorem 1.2. The only solutions of the Diophantine equation

as non-negative integers for $m\leq n$, $1\leq d\leq\eta-1$, $2\leq\eta\leq10$, and $b\geq2$ are given in Table A.2.

Remark. We know that $P_{0} = P_{1} = P_{2} = 1$ and $P_{3} = P_{4} = 2$. In both theorems above, we assume that $m\leq n$ and $m\neq0, 1, 3$.

2.   Auxiliary results

2.1.   Padovan and Perrin sequences

This section includes various Padovan and Perrin sequence features that are relevant to our theorems. The characteristic polynomial of the Padovan and Perrin sequences is given by

with roots $\theta_{1}, \theta_{2}$, and $\theta_{3}$, where

and

Let

Binet's formulas for Padovan and Perrin sequences are respectively defined by

and

Numerically, we have

Given that $\theta_{2} = \theta_{1}^{-1 / 2}e^{iR}$ and $\theta_{3} = \theta_{1}^{-1 / 2}e^{-iR}$ for some $R\in(0, 2\pi)$, it follows that

and

Using the method of induction, we can prove that

and

2.2.   Linear forms in logarithms

Definition 2.1. (Absolute logarithmic height) Let $\gamma$ be an algebraic number of degree $d$ with the following minimal polynomial:

where $\gamma^{(i)}$ denotes conjugates of $\gamma$, and $c_{i}$ values are relatively prime to each other with $c_{0} > 0$. Then the logarithmic height of $\gamma$ is given by

If $\gamma = \frac{a}{b}$ is a rational number with $gcd(a, b) = 1$ and $b > 0$, then $h(\gamma) = \log(\max\{|a|, b\})$.

The following are the properties of the logarithmic height function, which will be utilized in the subsequent sections of this paper:

To prove the validity of Theorems 1.1 and 1.2, we use the modified version of the Matveev result ^[15], as stated by Bugeaud et al. [16, Theorem 9.4].

Theorem 2.2. Let $\mathbb{L}$ be the real algebraic number field of degree $D$ over $\mathbb{Q}$. Let $\gamma_{1}, \ldots, \gamma_{t}\in \mathbb{L}$ be positive real algebraic numbers, and let $b_{1}, b_{2}, \ldots, b_{t}$ be nonzero integers such that

is not zero. Then

where

and

2.3.   De Weger reduction method

We need the variation of the Baker-Davenport reduction method developed by de Weger ^[17] to reduce the upper bound. Let $\vartheta_1, \vartheta_2, \beta \in \mathbb{R}$ be given and $x_1, x_2 \in \mathbb{Z}$ be unknowns.

Let

Let $c, \delta$ be positive constants. We set $X = \max \left\{\left|x_1\right|, \left|x_2\right|\right\}$ and let $X_0, Y$ be positive. Assume that

Case 1: If $\beta = 0$ in Eq (2.11), then

Set $\vartheta = -\vartheta_1 / \vartheta_2$. We assume that $x_1$ and $x_2$ are relatively prime. The continued fraction expansion of $\vartheta$ is represented by $\left[a_0, a_1, a_2, \ldots\right]$. The $k$-th convergent of $\vartheta$ is denoted by $p_k / q_k$, where $k = 0, 1, 2, \ldots.$ Without a loss of generality, we may assume that $\left|\vartheta_1\right| < \left|\vartheta_2\right|$ and $x_1 > 0$. We obtain the following lemma.

Lemma 2.3. ([17, Lemma 3.2]) Let

where

If (2.12) and (2.13) hold for $x_1, x_2$ and $\beta = 0$, then

Case 2: If $\beta \neq 0$ in Eq (2.11), then we get

where $\vartheta = -\vartheta_1 / \vartheta_2$ and $\psi = \beta / \vartheta_2$. Let $p / q$ be a convergent of $\vartheta$ with $q > X_0$. The distance between a real number $m$ and the nearest integer is represented by $\|m\| =$ $\min \{|m-n|: n \in \mathbb{Z}\}$. We have the following lemma.

Lemma 2.4. ([17, Lemma 3.3]) Suppose that

Then the solutions of (2.12) and (2.13) satisfy

To prove our theorems, we present the following findings.

Lemma 2.5. ([18, Lemma 7]) If $r\geq 1$, $S\geq(4r^2)^r$, and $\frac{L}{(\log L)^{r}} < S$, then

Lemma 2.6. ([17, Lemma 2.2]) Let $v, x\in \mathbb{R}$ and $0 < v < 1$. If $|x| < v$, then

3.   Main results

3.1.   The proof of Theorem 1.1

In this section, we present the proof of Theorem 1.1. The main process is detailed below.

3.1.1.   Relation between $n$ and $b$

The set of solutions for the Diophantine equation given by Eq (1.1) in the range of $2\leq m \leq n < 350$ and for $m\neq3$ can be obtained by using the Maple program; the solutions are presented in Table A.1. Considering the remaining case, we assume that $n\geq350$ and $m\geq2$, where $m\neq3$. By combining inequalities (2.5) and (2.6) in Eq (1.1), we obtain

and it is clear that $\theta_{1} < 1.33$; then,

We conclude that

3.1.2.   Finding an upper bound for $n$

Putting Eq (2.4) in Eq (1.1), we have

Taking the absolute value for both sides of the above equation, we get

Dividing both sides by $\theta_{1}^{n}$, we deduce that

Let

We claim that $\Lambda_1$ is nonzero. Suppose that $\Lambda_1 = 0$, which implies that

However, this is contradictory since $\theta_{1}^{n}\notin\mathbb{Q}$ for any $n > 0$. Hence $\Lambda_1\neq0$. We apply Theorem $2.2$ to the left hand side of inequality (3.2) in consideration of the parameter $t: = 3$, we set

Since $\mathbb{L}: = \mathbb{Q}(\gamma_{1}, \gamma_{2}, \gamma_{3})$, it follows that $D: = [\mathbb{L}, \mathbb{Q}] = 3$. The heights of $\gamma_{1}, \gamma_{2}, \gamma_{3}$ can be calculated as follows:

and

Thus, we can take $A_{1}: = 0.29$, $A_{2}: = 6.93$ and $A_{3}: = 13.2$. Since $b\leq n+2$, taking $B: = n+2\geq \max\{|-n|, |b|, |1|\}$, by Theorem $2.2$, we get

where $G = (1.4)\left(30^{6}\right)\left(3^{4.5}\right)\left(9\right)\left(1+\log (3)\right)$. By simplifying the computation, we obtain

Rewrite Eq (1.1) as follows

Taking the absolute value of the above equation, we get

for $n\geq350$ and $m\geq2$. Dividing both sides by $\theta_{1}^{n}\left(1+c_{1}\theta_{1}^{m-n}\right)$, we obtain

We apply that, for $n\geq350$ and $m\geq2$, the inequality

holds.

Let

Note that $\Lambda_{2}$ is nonzero. Suppose that $\Lambda_{2} = 0$, which implies that

But, this is a contradiction since $\theta_{1}^{n}(1+c_{1}\theta_{1}^{m-n})\notin\mathbb{Q}$ for any $n\geq m\ge 2$. Hence $\Lambda_{2}\neq0$. By applying Theorem $2.2$ to the left-hand side of inequality $(3.4)$ and considering the parameter $t: = 3$, we have

We have that $D: = [\mathbb{L}, \mathbb{Q}] = 3$, where $\mathbb{L}: = \mathbb{Q}(\gamma_{1}, \gamma_{2}, \gamma_{3})$. By using the definition of logarithmic height, we deduce that

and

So we can take $A_{1}: = 0.29$, $A_{2}: = 6.93$ and $A_{3}: = 18.39+(n-m)\log(\theta_{1})$. Also, by Eq (3.1), we can choose $B: = n+2\geq \max\{|-n|, |b|, |1|\}$. According to Theorem 2.2, we get

where $G = (1.4)\left(30^{6}\right)\left(3^{4.5}\right)(9)\left(1+\log (3)\right)$. Putting inequality (3.3) in the above inequality, by simple calculation, we get

We consider the fact that $1+\log(n+2) < 2\log(n)$ for all $n > 5$. Now we apply Lemma 2.5, taking $S: = 5.57\cdot10^{27}$, $L: = n$, and $r: = 2$. With the help of Maple, we can obtain

3.1.3.   Reducing the upper bound of $n$

In this section, we attempt to reduce the upper bound of $n$ by using Lemmas 2.3 and 2.4.

Let

In inequality (3.2), assume that $n-m\geq2$; then, we get

Choosing $v = 0.86$ in Lemma 2.6, we obtain

It follows that

We consider the following two cases of the above inequality.

Case 1: If $1\leq d < \eta-1$ and $3\leq\eta\leq10$, we see that $\beta\neq0$; then, applying Lemma 2.4, we have

We know that $\vartheta$ is irrational. We take $X_{0}: = 9.2\cdot10^{31}$, which is an upper bound for both $b$ and $n$. Using Maple programming, we obtain Table 1, so we get

Therefore, we obtain that $n-m\leq300$.

Case 2: If $d = \eta-1$ where $2\leq \eta\leq10$, then $\beta = 0$. Now applying Lemma 2.3, we have that $X_{0}: = 9.2\cdot10^{31}$.

and

Upon inspection by using Maple programming, we can find Table 2 for all possibilities of $\eta$, we get

Hence, in both cases, $n-m\leq300$. Substituting this into inequality (3.5), we obtain that $n < 2.9\cdot10^{17}$.

Let

Then, by inequality (3.4), we have

Based on our assumption, $n\geq350$. Given Lemma 2.6, we choose $v = 0.25$. Thus

It follows that

In the above inequality, according to the de Weger reduction method, we obtain that $\beta\neq0$; then, applying Lemma 2.4, we have

where $\vartheta$ denotes an irrational number. For $0\leq(n-m)\leq 300$ and $X_{0}: = 3\cdot10^{17}$, our calculations with the help of Maple programming find Table 3, so we get

Therefore, we can obtain a contradiction based on our assumption that $n\geq350$. Theorem 1.1 is proved.

Corollary 3.1. The largest repdigits in base $\eta$ of the Diophantine equation given by Eq (1.1) are as follows:

3.2.   The proof of Theorem 1.2

In this section, we present the following subsections to prove Theorem 1.2.

3.2.1.   Relation between $n$ and $b$

All solutions to the Diophantine equation given by Eq (1.2) in the range of $2\leq m \leq n < 350$, and for $m\neq3$, with the help of the Maple program, are presented in Table A.2. Considering the remaining possibility, we assume that $n\geq350$ and $m\geq2$ where $m\neq3$. By combining inequalities (2.5) and (2.6) together in Eq (1.2), we obtain

and it is clear that $\theta_{1} < 1.33$; then,

We conclude that

3.2.2.   Finding an upper bound for $n$

Putting Eqs (2.3) and (2.4) in Eq (1.2), we have

Taking the absolute value of both sides, we get

Dividing both sides by $c_{1}\theta_{1}^{n+m}$, we deduce that

It can be seen that

Let

We want to show that $\Lambda_3$ is nonzero. We assume that $\Lambda_3 = 0$, which implies that

However, this is contradictory because $c_{1}\theta_{1}^{n+m}\notin\mathbb{Q}$ is an irrational number. Hence $\Lambda_3\neq0$.

By applying Theorem 2.2 and $t: = 3$ on the left hand side of inequality (3.7). We can take

Since $\mathbb{L}: = \mathbb{Q}(\gamma_{1}, \gamma_{2}, \gamma_{3})$, then $D: = [\mathbb{L}, \mathbb{Q}] = 3$. Furthermore, we can obtain the heights of $\gamma_{1}$, $\gamma_{2}$ and $\gamma_{3}$; thus,

and

Thus, we can take $A_{1}: = 0.29$, $A_{2}: = 6.93$ and $A_{3}: = 16.3$. Also, since $b\leq 2n+1$ and $m\leq n$, we can take $B: = 2n+1\geq \max\{|-(n+m)|, |b|, |1|\}$. By Theorem 2.2, we get

where $G = (1.4)\left(30^{6}\right)\left(3^{4.5}\right)(9)\left(1+\log (3)\right)$. By simplifying the computation, we obtain

Again, rewrite Eq (1.2) as

Taking the absolute values for both sides of the above equation, we get

for $n\geq350$ and $m\geq2$. Dividing both sides by $\theta_{1}^{n}$, we obtain

Let

We claim that $\Lambda_{4}$ is nonzero. Suppose that $\Lambda_{4} = 0$, which implies that

But this is a contradiction since $\theta_{1}^{n}\notin\mathbb{Q}$ for any $n\geq 350$. Hence $\Lambda_{4}\neq0$.

By applying Theorem 2.2 and $t: = 3$ to the left hand side of inequality $(3.9)$, we can take

Since $\mathbb{L}: = \mathbb{Q}(\gamma_{1}, \gamma_{2}, \gamma_{3})$, then $D: = [\mathbb{L}, \mathbb{Q}] = 3$. Moreover, the heights of $\gamma_{1}$, $\gamma_{2}$ and $\gamma_{3}$ were found to be as follows:

and

We can take $A_{1}: = 0.29$, $A_{2}: = 6.93$ and $A_{3}: = 13.2+m\log(\theta_{1})$. Also, by Eq (3.6), can choose $B: = 2n+1\geq \max\{|-n|, |b|, |1|\}$. According to Theorem 2.2, we get

where $G = (1.4)\left(30^{6}\right)\left(3^{4.5}\right)(9)\left(1+\log (3)\right)$. By substituting inequality (3.8) into the above inequality and simplifying the computation, we obtain

We use the fact that $1+\log(2n+1) < 2\log(n)$ for all $n > 6$. Now, we apply Lemma 2.5 by taking $S: = 6.9\cdot10^{27}$, $L: = n$, and $r: = 2$. With the help of Maple, we can obtain

3.2.3.   Reducing the upper bound of $n$

In this section, we apply Lemmas 2.3 and 2.4 to reduce the upper bound of $n$.

Let

In inequality (3.7), assume that $m\geq6$; then, we get

By applying Lemma 2.6 and choosing $v = 0.8$, we obtain

It can be seen that

According to the de Weger reduction method, we see that $\beta\neq0$; then, applying Lemma 2.4, we have

Clearly, $\vartheta$ is an irrational number. We can take $X_{0}: = 2.26\cdot10^{32}$, which is the upper bound for both $b$ and $n$ since $b < 2n+1 < 2.26\cdot10^{32}$. Using Maple programming, we computed Table 4, we get

Therefore, we consider that $m\leq306$. Substituting this into inequality (3.10), we obtain that $n < 2.75\cdot10^{17}$.

Let

It is obvious that

by our assumption that $n\geq350$. Given Lemma 2.6, we can choose $v = 0.25$. Thus

It follows that

For the above inequality, we have the following two cases.

Case 1: If $4\leq m\leq306$ and $1\leq d \leq \eta-1$, then $\beta\neq0$. By applying Lemma 2.4, we have

where $\vartheta$ denotes an irrational number. We can take $X_{0}: = 5.5\cdot10^{17}$, which is the upper bound for both $b$ and $n$ since $b < 2n+1 < 5.5\cdot10^{17}$. We obtained the results in the Table 5 with the help of Maple programming, except for the following cases:

For these exceptional cases, we obtained the following equations

respectively, which are impossible in the region defined above.

Case 2: If $m = 2$ and $d = \eta-1$, then $\beta = 0$. Now, applying Lemma 2.3, we have that $X_{0}: = 5.5\cdot10^{17}$.

and

Upon inspection by Maple programming, we can obtain Table 6 in all possible cases of $\eta$, we get

In both cases, we obtained a contradiction based on the assumption that $n\geq350$. Theorem 1.2 is proved.

Corollary 3.2. The largest repdigits in base $\eta$ of the Diophantine equation given by Eq (1.2) are as follows:

Author contributions

Hunar Sherzad Taher: Writing–original draft, Methodology; Saroj Kumar Dash: Supervision, Data curation, Visualization. We used Maple software programming to calculate the results. All authors have reviewed the results and approved the final version of the manuscript.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in creating this article.

Acknowledgments

The authors wish to express their gratitude to the editor and anonymous referees for their insightful comments and constructive suggestions, which have significantly enhanced the original manuscript. The Vellore Institute of Technology provided financial assistance for this work.

Conflict of interest

The authors declare that there are no competing interests.

Appendix: Tables that include solutions for Theorems 1.1 and 1.2