Potentiality of generative AI tools in higher education: Evaluating ChatGPT's viability as a teaching assistant for introductory programming courses

1.   Introduction

Designing a vaccine candidate is one of most ambitious goals for the treatment or prevention of HIV. One of the preventive strategy is the pre-administsration of antiretroviral therapy (ART) known as pre-exposure prophylaxis (PrEP) and which can reduce the disease transmission, however ART administration was not sufficient for complete blocking of HIV transmission or cure for HIV infection ^[1]. The broadly neutralizing antibodies (bNabs) act very differently from ART: ART suppresses virus replication or production, whereas bNAbs let the host's immune system target the virus or target virus-infected cells. So they can be administered together. Some other advantage for bNAbs are their long half-lives and activation of HIV-specific immune response ^[2,3,4]. A bNab with broad neutralization capacity called eCD4-Ig has successfully prevented Macaque monkeys from multiple SHIV infections ^[5]. We assume there is a correlation between SHIV outcome experiments evaluating HIV dynamics in the presence of eCD4-Ig molecules in humans. However, similar studies evaluating eCD4-Ig molecules in humans and controlling HIV infection are yet to be conducted. Hence, in this study, we propose a mathematical framework to understand HIV dynamics in the presence of the eCD4-Ig molecule and attempt to understand why this has been successful eliminating SHIV virus within the host.

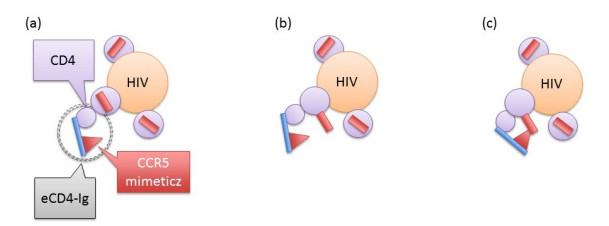
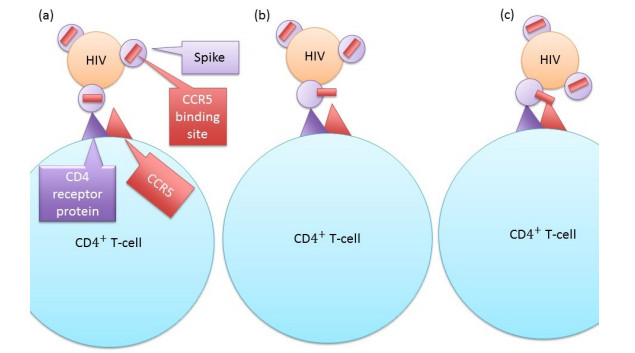
The eCD4-Ig is a new molecule created by Gardner et al ^[5] and has great potential for the prevention and treatment of HIV infection. HIV virus, which is the known cause of AIDS may enter the body either intravenously or via mucosal surfaces. After initial adhesion and invasion, the virus frequently travels to lymph nodes and subsequently infects immune cells carrying the CD4 surface protein. Detailed understanding of the infectious mechanism of HIV virus indicates that the host cell should express co-receptor molecules such as CCR5 or CXCR4, for successful HIV virus infection. Over the last two decades there has been a significant amount of research studying the binding of the HIV envelope to the CD4 molecule and antibodies ^[6,7,8,9]. The studies expanded to understand the conformational change of the spikes of the virus see for example ^{[10,11,12,13]}. The characterization of the mechanism of HIV infection (inspired by ^[10]) is shown in Figure 1. There are main two stages in the HIV infection process. During the first stage, after the HIV enters the body, the "spike" of an HIV virus binds to a CD4 molecule. This binding is necessary because it induces the conformational change of the attached spike to expose the co-receptor binding site. However, this is not enough for the HIV virus to enter the host cell. During the second stage, the exposed co-receptor binding site then binds with the co-receptor. This binding leads to cell entry and the initiation of infection.

The eCD4-Ig is generated combining the CD4-Ig (a fake CD4) and CCR5 mimetic, and mimics the infectious mechanism of the HIV virus ^[5]. See Figure 2 for the eCD4-Ig mechanism. First, the fake CD4 site of eCD4-I binds to a spike on the HIV virus and thus exposes the CCR5 binding site of the spike. Finally, the fake CCR5 site of eCD4-Ig binds to exposed viral CCR5 binding sites to block the activity of the spike. It is important to note that the above mechanism only focuses on a single spike. There are approximately 14 spikes on an HIV viral particle ^[14]. It is believed that all of the spikes need to be covered in order to neutralize the HIV virus ^[15]. The amount of eCD4-Ig requirement per viral particle is thus important in order to either prevent or treat HIV infection. This manuscript will address that concept using our model.

The antibody-dependent cell-mediated cytotoxicity (ADCC) induced by eCD4-Ig should be mentioned ^[16]. The eCD4-Ig not only neutralizes HIV virus, but also kills HIV infected CD4 cells. Given the failure of other HIV neutralizing antibodies, triggering of ADCC along with neutralization capacity may be the explanation for the success of eCD4-Ig. Previous studies evaluating antibody dynamics in HIV patients have considered neutralization effects ^{[17,18,19,20]}. In our study, we included ADCC effects in the antibody dynamics model to better understand the balance between ADCC and the neutralization effect of eCD4-Ig for HIV elimination. We considered two models, one without latently infected cells for the acute infection, and another model of latent infection for the long term dynamics. Even though, eCD4-Ig do not interact with latently infected cells, latently infected cells do turn into actively infected cells which the eCD4-Ig interact with. Since latent infection is important for long-term dynamics, we considered the second model in addition to the first acute infection model. Result of this would help to design the new generation of antibodies or therapeutics.

2.   Model

The efficacy of the eCD4-Ig on preventing HIV infection in primates has been previously demonstrated ^[5]. However, the effect on humans has not yet been reported. We would like to evaluate the effect of eCD4-Ig as a treatment regimen in individuals that are HIV-positive. It has been well documented that during HIV disease progression, the CD4 cell count declines while the HIV viral load increases. From our understanding of the eCD4-Ig molecules, we would expect the rate of the CD4 cell count destruction and thus reduction to slow down. We expect that this effect is caused by eCD4-Ig which will have a major impact on host-HIV dynamics. We model the dynamics of the number of CD4 cells and eCD4-Ig molecules by adding eCD4-Ig (E) compartment, through an ODE model consisting of CD4 cells ($T$), infected CD4 cells ($I$), and HIV virus ($V$). The model is shown below.

where, $T, I, V, E$ stand for count of uninfected CD4 T cells, infected CD4 T cells, HIV virus, and eCD4-Ig respectively. The parameters used in the model (2.1) are demonstrated in Table 1 in the Appendix. One of the characteristics of eCD4-Ig is its capability to trigger greater antibody-dependent cell-mediated cytotoxicity (ADCC) when compared to other antibodies ^[16].Thus, the model has both cytotocity effect and "humoral" immune response which are modeled separately ^{[18,20,21,22]}. That is, model (2.1) combine virus removal through both neutralization $(\kappa_2VE)$ and ADCC $(\kappa_1IE)$ response of eCD4-Ig. The eCD4-Ig covers viral spikes for neutralization, eventually produce inactive virus like protease inhibitor (PI) in ART. Note that both PI and eCD4-Ig yield inactive HIV virus, the process is different. PI create inactive virus, but eCD4-Ig convert "infectious" virus to inactive. The complete inactivation and removal of HIV virus is modeled as $(\kappa_2VE)$ as other antibody models which are different than the PI model ^{[17,18,20,23]}. Because multiple eCD4-Ig molecules bind to virus or infected cells for neutralization and cell killing respectively, $\sigma_1$ and $\sigma_2$ are introduced to adjust these multiple bindings. Since we are considering the gene-therapeutic approach for inoculation, eCD4-Ig production rate $\lambda_2$ is constant. This value increases if more cells are targeted to produce the eCD4-Ig, thus we can increase the amount of eCD4-Ig expresion level.

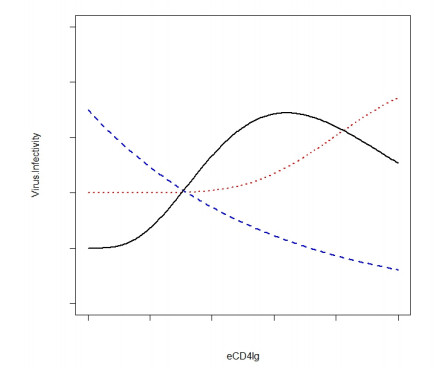
The eCD4-Ig bind to viral spikes that covers the surface of HIV virus. Researchers thus far do not know how the number of spikes an eCD4-Ig molecule can bind to or how many eCD4-Ig molecules are required to neutralize an HIV virus. To address this issue, we have speculated three possible behaviors of the viral infection rate ($\beta$) with a change in eCD4-Ig. This includes an increase over time, a decrease over time, and the third scenario which is an initial increase, followed by a decrease. These scenarios are shown in Figure 3. Several recent studies have shown that the decrease in viral infection rates are seen with an increasing eCD4-Ig, thus we consider the first scenario in the manuscript ^[24,25]. Intuitively, this makes sense since the presence of an increased amount of eCD4-Ig would bind and neutralize more viral spikes which are required for the virus to enter and subsequently infect host cells (figure 4).

The virus neutralization process gradually transforms active virus to in-active virus. Thus, we have adjusted the viral infection rate $\beta$ with the level of eCD4-Ig. The new rate is obtained as $\beta\delta(E)$ where $\delta(E)$ is the proportion of decay in the infection rate due to coverage of viral spikes by eCD4-Ig. Thus, $\delta(E) = 1$ indicates without eCD4-Ig. When we consider the decreasing scenario in the Figure 4, we consider $\delta(E) = \frac{1}{1+\alpha E}$. Alternatively, we can consider the exponential function of eCD4-Ig ($E$), or $\delta = e^{-\alpha E}$. So far, latently infected cells ($L$) or reservoirs have not been considered. Since the existence of the reservoirs would greatly hinder the elimination effort of HIV. The eCD4-Ig only interacts with viral surface protein, thus it interaction with actively infected CD4 T cells and HIV virus only. We do not have to consider the latent reservoirs if the acute infection was cleared before the establishment of the latent reservoir since we are interested in treating initially un-infected subjects. However, latent reservoirs eventually become actively infected cells, participate in the HIV virus and eCD4-Ig dynamics. Thus, incorporating latent reservoirs would refine the model, and may give a more appropriate eCD4-Ig threshold for the HIV virus elimination. The parameter $\theta$ was used to describe the proportion of newly-infected CD4 cells to become latent, so that ($1-\theta$) proportion of newly-infected CD4 cells develop into infected CD4 cells. Latently infected cells have a longer half-life when compared to actively infected cells. Thus, we use a new death rate $\mu_5$ for latently infected cells. This was used to describe the rate of conversion to infected cells from latently infected cells. Considering these arguments, our modified model is shown in the equation below

3.   HIV virus elimination

Elimination of HIV virus from infected individuals is what researchers have been attempting to accomplish for many years. It appears that incorporation of eCD4-Ig seems to be a possible solution in this direction. However, we do not know what characteristic of eCD4-Ig is so distinct, and so different than other antibodies, and thus may offer the high potential of HIV eradication. Additionally, we would also like to know what the minimum amount of eCD4-Ig is required for the elimination of HIV from the host cells.

Because eCD4-Ig is not immunogenic and able to target all HIV strains, we are interested in the "protective ability" of eCD4-Ig ^[5]. From the model (2.1), we can study the elimination property of acute infection. Because we are considering the gene-therapeutic intervention approach for prevention, this would provide information regarding the conditions needed in protecting the patients from HIV infection. However, the latent reservoir may also be established during the course of infection and thus will also be consider in the model (2.2).

To understand the elimination dynamics we evaluated the elimination equilibrium point of the model through Theorem 1. Observe that the equilibrium point for elimination is $\frac{\lambda_1}{\mu_1}$ for uninfected CD4 T cells, $\frac{\lambda_2}{\mu_4}$ for eCD4-Ig level, and 0 for other variables.

Theorem 1. HIV virus elimination condition of eCD4-Ig in gene-therapeutic approach. HIV virus would be eliminated from body in acute infection if following condition satisfies

where, $b = \mu_2+\kappa_1E^*, c = \mu_3+\kappa_2E^*, d = \beta T^* \delta(E^*)\lambda_1$.

Proof. The HIV virus elimination equilibrium point for the model (2.1) is $(T^*, I^*, V^*, E^*) = \left(\frac{\lambda_1}{\mu_1}, 0, 0, \frac{\lambda_2}{\mu_4}\right)$. We would obtain the characteristic equation of

where

For the system to be stable, all the solutions of $f(\lambda)$ need to be negative, and we obtain following inequalities

The above condition hold for when $\delta = e^{-\alpha E}$ and $\delta = \frac{1}{1+\alpha E}$ for some positive real parameter $\alpha$.

In Theorem 1, note that left-hand side (LHS) of the inequality is the basic reproduction rate $R_0$ of the virus. That is, the virus would be eliminated if the average virus produced from an initial virus is less than 1. Also note that decreasing the virus infection rate ($\beta$) and virus production rate ($\rho$) would reduce the LHS of the inequality. These decrease occurs with anti-retroviral therapy (ART).). In addition, we perceive that eCD4-Ig and ART are synergistic and may improve HIV viral elimination. Furthermore, an increase in the infection free eCD4-Ig level ($E^*$) has strong effect on reducing the LHS. That is, eCD4-Ig has the potential for vaccinating the HIV susceptible population. The increase in the concentration can be obtained through either introducing higher amounts of eCD4-Ig during therapy, or designing more stable eCD4-Ig, so that eCD4-Ig molecules do not turn over so rapidly. Another point is that our model state that effect of ADCC and neutralization contribute to elimination condition. The previous study on immune effect did not considered the neutralization effect, resulting non-significant effect of ADCC on viral elimination ^[21].

Corollary 1. Balance of ADCC and virus neutralization effect of eCD4-Ig for HIV virus elimination. In gene-therapeutic approach, the relationship of infected cell removal rates through ADCC are due to eCD4-Ig ($\kappa_1$) and virus neutralization rate of eCD4-Ig ($\kappa_2$) follow an inverse relation as

where, $f(c) = \frac{d}{c}$.

Observe that $f(c)$ is a decreasing function both of $\kappa_2$ and $\delta$. Thus, corollary 1 shows that some of the ADCC effect of eCD4-Ig is required for viral elimination, unless the viral neutralization rate is very high (high $\kappa_2$ and low $\delta$). Since eCD4-Ig induce higher levels of ADCC than other broadly neutralizing antibodies, it is easier to achieve the elimination conditions that supports recently published studies of eCD4-Ig (12).

However, HIV would have long-term complications though latent infection. The similar analysis of model (2.2) yield Theorem 2 below:

Theorem 2. HIV virus elimination condition of eCD4-Ig in gene-therapeutic approach. HIV virus would be eliminated from body if following condition satisfies

where, $a = \mu_5+\gamma$.

Proof. The HIV virus elimination equilibrium point for the model (2.2) is $(T^*, L^*, I^*, V^*, E^*) = \left(\frac{\lambda_1}{\mu_1}, 0, 0, 0, \frac{\lambda_2}{\mu_4}\right)$. We would obtain the characteristic equation of

where,

For the system to be stable, all the solutions of $f(\lambda)$ need to be negative, and we used Routh's stability criterion to obtain following inequalities

The above condition hold for when $\delta = e^{-\alpha E}$ and $\delta = \frac{1}{1+\alpha E}$ for some positive real parameter $\alpha$.

From Theorem 2, we obtain following corollary:

Corollary 2. Balance of ADCC and virus neutralization effect of eCD4-Ig for HIV virus elimination. In gene-therapeutic approach, the relationship of infected cell removal rates through ADCC are due to eCD4-Ig ($\kappa_1$) and virus neutralization rate of eCD4-Ig ($\kappa_2$) follow an inverse relation as

where, $f(x) = \frac{(1-\theta)d}{(a+b+c)-x}$ and $g(c) = \frac{-abc}{x[(a+b+c)-x]}$.

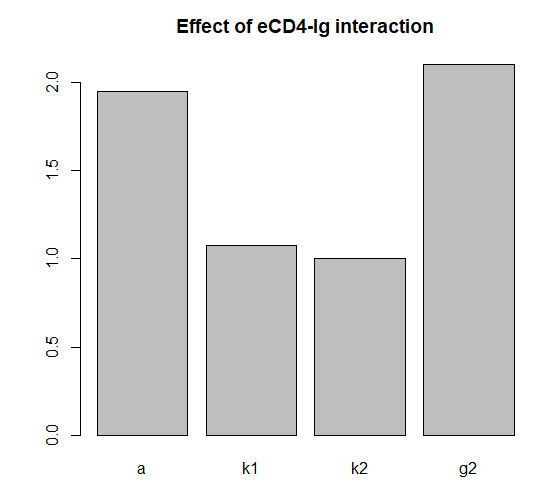
This gives condition of $a, b$, or $c$ (latent removal rate, infected CD4 cell removal rate, and HIV virus removal rate respectively) for HIV removal in gene-therapeutic approaches of eCD4-Ig. This shows the required ADCC activation and viral neutralization property of antibody and the latent activation for HIV virus elimination. However, we do not know the significance of ADCC and neutralization. Figure 5 shows the effect of eCD4-Ig parameters. Because larger the size of eCD4-Ig quantity the HIV virus will cought more frequently, the effect of growth rate of eCD4-Ig have significant role in HIV viral elimination. Similarly, the effect of infectivity reduction parameters is also high due to controlling slower interaction between CD4 T-cells and HIV virus compared to HIV virus and eCD4-Ig. In our model, eCD4-Ig interaction do not plays significant role on elimination as sensitivity of these parameters are high. However, note that the neutralization of viral spikes negatively correlates with infectivity.

Corollary 3. Elimination threshold of eCD4-Ig for HIV virus elimination in gene-therapeutic approach. Unique eCD4-Ig expression threshold for HIV virus elimination exist if

Proof. If we consider $\delta(E) = e^{-\alpha E}$, we would have an unique positive solution of $X$ for following equation

where $a_1, a_2, a_3, a_4 > 0$ if $a_3 < a_4$. From inequality (6), we obtain the second order polynomial and exponential function of $E_0$ inequality as

where,

Observe that $a_1, a_2, a_3, a_4 > 0$. If $a_3\ge a_4$, then HIV virus is naturally eliminated from the host and eCD4-Ig is not required, however we know that this is not the case. Thus, $a_3 < a_4$ would give us the unique minimum eCD4-Ig requirement. The same condition also holds with $\delta = \frac{1}{1+\alpha E}$ for some positive real parameter $\omega$. Here, we would have third order polynomial and exponential function of $E^*$ inequality as

where

Observe that $b_1, b_2, b_3 > 0$, and inflection point is at negative $E^*$ value. Thus, the LHS of the inequality (3.7) is concave up at positive $E^*$ value. If $a_4 > 0$, then HIV virus is naturally eliminated from the host and eCD4-Ig is not required, however we know that this is not the case. Thus $a_4 < 0$, and this would give us the unique minimum eCD4-Ig requirement since LHS of of the inequality (3.7) is strictly increasing function for positive $E^*$.

4.   Control

It is worth note the presence of non-elimination condition as the model indicate we have non-elimination equilibrium point. For details of the non-elimination equilibrium, please see appendix. We are also interested in studying the non-elimination condition useful in the treatment of HIV or in the vaccination of high-risk subjects to prevent infection, effects of combined treatments of ART and eCD4-IG, as well as the effect of antibody diversity development in the course of eCD4-Ig treatments. We simulated the model and qualitative behaviors for each scenario that were studied. We focus on the scenario of gene-therapeutic approach as repeated administration of eCD4-Ig intravenously may not be practical due to economical reason. The gene therapeutic approach allow let the human body to produce and maintain the eCD4-Ig for longer periods of time and have the potential to be used as a preventive vaccination for HIV. Considering practicability, a lack of understanding of the effect of gene-therapeutic approach using adeno-associated virus for HIV infected patients is the limited from studying effect of eCD4-Ig in already infected patients in-vivo. However, we can study the chronic condition numerically for potential usage of virus control through gene therapy. Thus we have also studied the dynamics of chronic condition numerically.

Theorem 1 supports our theory regarding increases in HIV viral elimination potentials of eCD4-Ig, with an increase in the eCD4-Ig level. One way to achieve the eCD4-Ig increase in using these approaches is by designing more stable eCD4-Ig molecules that have longer half-lives in patients.Additionally, we can achieve the higher level of eCD4-Ig molecules by increasing the eCD4-Ig production rate ($\lambda_2$). The increase in production rate depends on the number of cells affected by gene-therapy, thus we may be able to increase the production rate without modifying eCD4-Ig molecule. Because we can increase the eCD4-Ig level to surpass the threshold value, we are also interested in chronic conditions where latent reservoirs are established. Thus, we considered model (2.2) for simulation. For neutralization adjustment function, $\delta(E) = \frac{1}{1+\alpha E}$ was used.

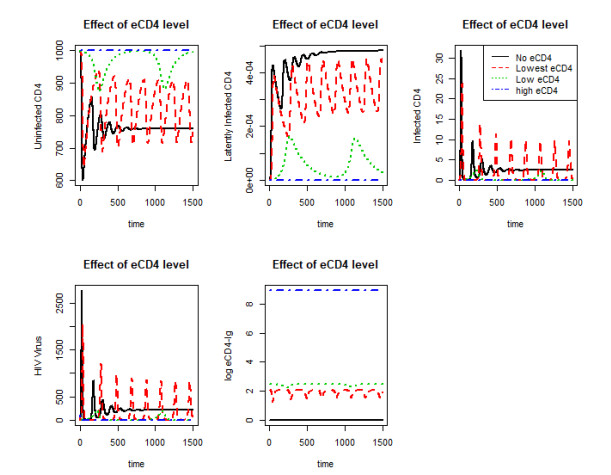
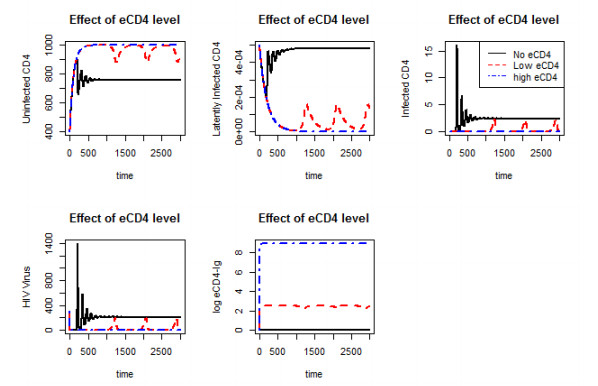
The effect of the level of eCD4-Ig, or the production rate of eCD4-Ig is shown in Figure 6. Black solid line indicates without eCD4-Ig expression case, and other lines indicate cases with varyig degrees of eCD4-Ig expression. Parameters were selected so that only the high eCD4 case in Figure 6 satisfied the elimination condition of Theorem 2. For infectivity reduction rates through eCD4-Ig ($\alpha$), we used $10^{-9}$. This was approximated from $1/IC_{50} = 1/8*10^{-8}$ of eCD4-Ig. Observe that HIV virus establish in the host with lesser eCD4-Ig expression than the Theorem 1 threshold. However, it is important to note that the continuous expression of eCD4-Ig molecules reduce the viral burden and maintain higher levels of CD4 T-cells than do the controls. Moreover, we can observe the presence of latent reservoirs with insufficient eCD4-Ig.

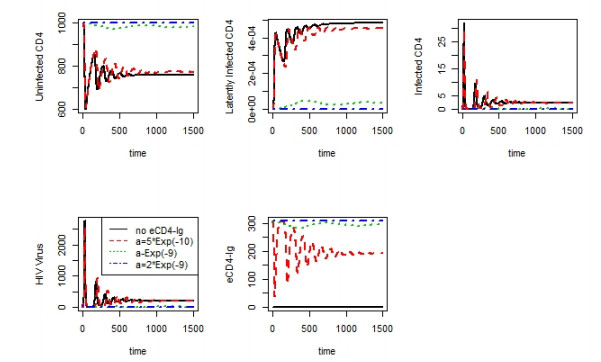
Moreover, we have studied the behavior of $\alpha$ as it has effect on elimination condition. Previous analyses indicate that the amount of eCD4-Ig plays an important role in the HIV virus elimination or reduction from the host and improved uninfected CD4 count. However, ADCC effect or $\alpha$ alone have not been studied. Thus, we have studied the behavior of $\alpha$ with fixed non-eliminating eCD4-Ig level corresponding to $\lambda_2$ = $20.7$/day was used. The result is shown in Figure 7. The, solid black line is for the no eCD4-Ig expression case. The other lines represent varying $\alpha$ for eCD4-Ig expression cases. Here, all eCD4-Ig expressed cases have the same eCD4-Ig expression of 20.7/0.07 = 295.7 molecules/$\mu l$, and demonstrates that the increase in $\alpha$, or improvement in neutralization improves the efficacy of eCD4-Ig as expected from Theorem 2. However, note that this is the partial neutralization of virus and not the complete neutralization of virus. This suggests that even the partial neutralization of HIV virus would increase the efficacy of eCD4-Ig and improve eradication of HIV and its control. Moreover, it is also important to notice is the great change in the dynamics in the simulation. This result does not affect the threshold as eCD4-Ig expression level is so low. In fact it is more than 1000 fold different from the detection threshold of antibody, in this simulation ^[19].

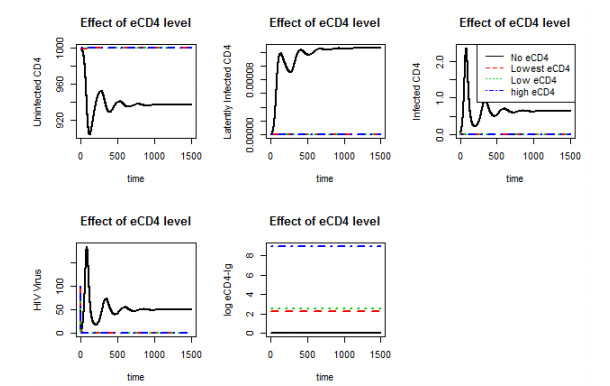
We have also simulated the effect of ART combined with eCD4-Ig. In Figure 8, we have studied effect of very trivial ART with efficacy of 10% in model 2. The varying eCD4-Ig production rate $\lambda2$ used in generating Figure 6 was used. HIV virus was eliminated and CD4 T cell level have increased to normal for all of the scenarios, with the eCD4-Ig expression indicating efficacy of the ART is increased as expected from Theorem 2.

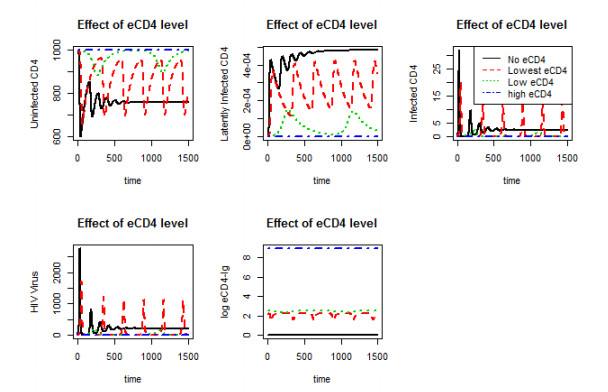
As HIV infection progresses, the HIV virus constantly mutates and generates a broader tropism. The diversity of HIV virus tropism can also apply to antibodies, and eCD4-Ig can activate these spectator antibodies by unlocking the hidden targets (12). Thus, we are interested in the dynamics of HIV virus, CD4 T-cells, and eCD4-Ig with consideration of the effect of spectator antibodies. To see the effect of spectator antibodies on the HIV virus and CD4 T-cells dynamics, we have considered the case with eCD4-Ig level less than Theorem 1 threshold. Also, we have modified the infected cell removal rate by ADCC using eCD4-Ig ($\kappa_1$) as an increasing function over time. The results are shown in Figure 9. The dynamics are similar to Figure 6. however the level of latent reservoirs are smaller when we consider the development of antibodies. Further study on the interaction of eCD4-Ig and other antibodies need to be done to study the effect. We assumed the independence of eCD4-Ig from other antibodies as there is no information on competition between them. This indicates that eCD4-Igs are potentially useful as HIV therapy or to control the infection, as well as the prevention of infection by either vaccination or prophylaxis.

Introduction of eCD4-Ig to the chronic patients was studies. We assumed uninfected 400 CD4 T-cells/$\mu l$ for initial condition. Because latent reservoir counts are not well known, we assumed it from previous simulations without eCD4-Ig. We used the initial latent reservoir size as $5\times 10^{-4}/\mu l$ and HIV virus count as 300$/\mu l$. For eCD4-Ig, we set the initial size as 0, with a different growth rate. The result is shown in Figure 10. Observe that the case with high eCD4-Ig eliminated HIV virus, yet low eCD4-Ig case controls HIV virus size. One interesting observation here is the periodical viral blips for low eCD4-Ig cases, suggesting a combinations of HIV strains with different antibodies that may explain the viral blips, instead of random events.

5.   Conclusion

We have constructed and studied a model of eCD4-Ig, and have described an important condition in Theorem 1 and Theorem 2. This includes the concept of viral eradication in HIV. This Theorem also describes the synergistic effect of ART and eCD4-Ig in the control and elimination of HIV virus from an infected host. From Theorem 2, we have obtained two corollaries: Corollary 2 and Corollary 3. Corollary 2 shows the relation between infected cell removal rate through ADCC due to eCD4-Ig ($\kappa_1$) and virus neutralization rate of eCD4-Ig ($\kappa_2$). The Corollary 1 was obtained for Theorem 1 version of Corollary2, showing the same relationship between removal rate through ADCC due to eCD4-Ig ($\kappa_1$) and the viral neutralization rate of the eCD4-Ig ($\kappa_2$). Whereas Corollary 3 shows the existence of a unique threshold value of eCD4-Ig for the elimination of HIV. This gave concerns for the characteristics of antibodies, and sensitivity analysis shows the neutralization effect plays significant role on elimination condition. We believe this characterization of eCD4-Ig will aid in designing HIV targeting antibodies or in the development of vaccines in the future.

Considering the antibody detection threshold of 0.2ng/ml IgG equivalent to $8\times 10^8$ molecules/ml, concentration of half optimal neutralization of eCD4-Ig ($IC_{50} < 0.05$$\mu$g/ml) is less than $2\times 10^{11}$ molecules/ml ^[5,17,18,19] assuming their molecular mass is similar. eCD4-Ig mass is likely to be higher and thus would reduce the concentration. Also due to ADCC effect, we can use a lower amount of eCD4-Ig for the elimination. In fact, lower eCD4-Ig expression of $8\times 10^8$ has worked with other parameters. For parameters assumed, $\alpha, \kappa_1, \kappa_2$ affect the threshold values. From Theorem 1, we see that $\beta\rho T^* < (1+\alpha E^*)(\mu_2+\kappa_1 E^*)(\mu_3+\kappa_2 E^*)$, and lower $\alpha, \kappa_1, \kappa_2$ would increase the eCD4-Ig threshold values which we may be able to control. The limitation of the study is that we still need exact parameters of eCD4-Ig to obtain numerical threshold values. Further, we also need to understand the effect of the introduction of gene-therapeutic agents through adeno-associated virus in HIV patients.

We have also evaluated the synergetic effect of eCD4-Ig and the diverse antibodies developed by the immune system over time, which are usually not used to target infected CD4 T-cells. Though further investigation regarding the effect of eCD4-Ig on patients are required as antibody diversity evolves over time, the insight on significant interactions between antibody diversity and eCD4-Ig have demonstrated the potential of combination therapy using antibodies and eCD4-Ig for therapy.

Even though the effects are similar, eCD4-Ig and ART are different. A treatment approach considering eCD4-Ig and other antibodies will attempt to remove HIV virus, while the ART approach will try to protect CD4 T cells. ART has been successful in converting HIV to a chronic disease, yet complete cure has not been achieved because the HIV virus is not completely removed ^[26,27]. The eCD4-Ig, which not only neutralizes HIV virus to remove antive HIV virus, but also activates ADCC to remove infected CD4 T cells. Overall, immune systems respond similarly, yet antigenic diversity and latent reservoirs overcome them. Moreover, increased levels of CD8 T cells in patients treated with ART are not desired since they are associated with non-AIDS events ^[27]. The mechanism for the CD8 T cell persistence is yet to be understood. However, we can prevent the disease from progressing into a chronic state or eliminate the HIV virus. This may help in maintaining normal CD8 T cell levels with the removal of chronic infectious agents, and can be achieved through the introduction of eCD4-Ig using gene-therapy as our study shows.

There are two advantages when considering the gene-therapeutic approach. First, production of eCD4-Ig is independent of other biological factors, and production rate is constant. This means constant eCD4-Ig level can be maintained for patrol. Second, the level of eCD4-Ig production rate can be increased as we allow more cells to produce the eCD4-Ig. We can allow above threshold eCD4-Ig to be expressed for years.

Putting the practicality of gene therapy on humans aside, the possible downside the approach is the possible development of immunogenicity of the eCD4-Ig molecule. If the immune system recognize the eCD4-Ig as a foreign compound, eCD4-Ig removal rate would increase with respect to eCD4-Ig concentration and HIV virus may persist. Because constant eCD4-Ig would be produced, subjects may suffer with chronic inflammation condition for years. We did not assumed this scenario into our model as the previous study shows that eCD4-Ig is not immunogenic ^[5].

Our model explains the dynamics of eCD4-Ig and its role in controlling HIV in humans with the latest available experimental results. The dynamics of eCD4-Ig and its interactions with the virus and CD4 and corresponding parameterizations were well preserved in our model. However, there is a scope to include a couple of deeper immunological facts if more experimental results are available in the future. One such thing is to add a sub-modeling component of the number of virus spikes bonding with eCD4-Ig. Currently, the experimental results did not confirm any association between the bonding power of eCD4-Ig with the virus and what would happen to the empty spikes those were not part of the bonding with eCD4-Ig? The second thing so far experimental scientists were unaware of is, whether the distribution of spikes has any role in bonding behavior. Availability of such additional information could lead to improvised model building to ascertain the accurate role of eCD4-Ig in virus elimination and threshold determination.

Through this study, we have tried to model the impact of the eCD4-Ig molecule on HIV virus dynamics by allowing simultaneous bonding HIV with CD4 cells within a host. Up to date knowledge of eCD4-Ig adopted in this paper helped us to speculate the role this molecule could on human HIV control and elimination. It appears that the induction of sufficient eCD4-Ig molecules through gene-therapy method works well in controlling the virus multiplication in the body.

The authors have no conflicts of interest in this paper.

Conflict of interest

The authors have no conflicts of interest in this paper.

Appendix

Parameter Table

Justification for parameter values assumed in parameter table

For the HIV virus neutralization rate ($\kappa_2$), we used rate slower than the virus infection rate. This is because eCD4-Ig tricks the HIV virus by presenting itself as CD4 and CCR5 which are required for infection, it is natural to assume the binding rate of eCD4-Ig to virus should be equal to or better than that of CD4 cell and HIV virus. Since a HIV virus has about 14 surface viral spikes and assuming that all of the 14 spikes are required to be occupied for the neutralization, we have assumed eCD4-Ig binding for neutralization ($\sigma_2$) as 14. For the Infected cell removal rate through eCD4-Ig ($\kappa_1$), we used rate slower than the virus infection rate. This is because of recruitment of effector cells by eCD4-Ig which bind to budding HIV virus or HIV surface proteins expressed in infected cells. We reduced the rate to account for the effector cell to kill the infected cells. Since an infected CD4 cell would produce about 2000 HIV virus per day, we assumed eCD4-Ig binding for ADCC ($\sigma_1$) as 2000.

$IC_{50} <$0.05$\mu$g/ml of eCD4-Ig is less than $2\times 10^{11}$ molecules/ml since 0.2ng/ml IgG equivalent to $8\times 10^8$ molecules/ml ^[5,17,18,19]. The actual concentration need for elimination may be less than this because of ADCC as corollary 1 and 2 states. For this study, we considered a lower eCD4-Ig expression of $8\times 10^8$ unless specified, that is detection threshold for anti-gp41 IgG antibody ^[19]. Because half life of anti-gp41 IgG antibody is 9.7 days and assuming eCD4-Ig half life to be similar, we assigned eCD4-Ig removal rate of 0.07/day ^[36]. The corresponding eCD4-Ig production rate ($\lambda_2$) is $5.6\times 10^{7}\mu l/$day. Note that we can change the growth rate of eCD4-Ig $(\lambda_2)$ for eCD4-Ig removal rate $(\mu_4)$ to match the $E^*$. For the infectivity reduction rate through eCD4-Ig ($\alpha$), we have only assumed its range between 0 and 1.

Non-elimination equilibrium

We have non-elimination equilbrium $(T_0^*, L_0^*, I_0^*, V_0^*, E_0^*)$ at $T_0^* = \frac{\mu_5 +\gamma}{\beta\rho((1-\theta)\mu_5+\gamma)}(\mu_2+\kappa_1E_0^*)(\mu_3+\kappa_2E_0^*)$, $L_0^* = \frac{\theta(\lambda_1-\mu_1T_0^*)}{\mu_5 +\gamma}$, $I_0^* = \left(\frac{(1-\theta)\mu_5+\gamma}{\theta(\mu_5 +\gamma)}\right)L_0^*$, $V_0^* = \frac{\rho}{\mu_3+\kappa_2E_0^*}I_0^*$ where $E_0^*$ is a positive solution of following equation $\theta(\lambda_2-\mu_4E_0^*)(\mu_2+\kappa_1E_0^*)(\mu_3+\kappa_2E_0^*) = E_0^*\left(\frac{\theta\mu_1}{\beta}\left(\delta_1(\mu_3+\kappa_2E_0^*)+\delta_2\rho\right)(\mu_2+\kappa_1E_0^*)(\mu_3+\kappa_2E_0^*)(1+\alpha E_0^*)+\frac{\theta\lambda_1((1-\theta)\mu_5+\gamma)}{\mu_5+\gamma}(\delta_1(\mu_3+\kappa_2E_0^*)+\delta_2)\right).$ Solving intersection of the cubic function with one positive solution at $E_0^* = \lambda_2/\mu_4$ and the quintic function with nonnegative coefficients, there is a positive solution of $E_0^* < \frac{\lambda_2}{\mu_2}$. If half-life of eCD4-Ig increases or $\mu_4$ decreases, then $E_0^*$ increases and equilibrium get closer to elimination equilibrium. The steady-state analysis shows the equilibrium is steady if

where, $H = \mu_5+\gamma, G = \mu_2+\kappa_1E_0^*, D = \frac{\beta V_0^*}{1+\alpha E_0^*}, J = \mu_3+\kappa_2E_0^*, N = \mu_4+\delta_1 I_0^*+\delta_2 V_0^*, M = \delta_2 E_0^*, K = \kappa_2V_0^*, B = \frac{T_0^*}{V_0^*}D, A = \delta_1E_0^*$. The HIV viral level of the non-elimination equilibrium with eCD4-Ig compared with non-elimination equilibrium without eCD4-Ig decreased by factor of $\frac{\mu_2\mu_3}{(\mu_2+\kappa_1E_0^*)(\mu_3+\kappa_2E_0^*)}$, indicating positive effect of eCD4-Ig.