Figure 1.
The flowchart of this research.
In this paper, focusing on individualistic generalist predators and prey living in herds which coexist in a common area, we propose a generalization of a previous model, namely, a two-population system that accounts for the prey response to predator attacks. In particular, we suggest a new prey-predator interaction term with a denominator of the Beddington-DeAngelis form and a function in the numerator that behaves as N for small values of N, and as Nα for large values of N, where N denotes the number of prey. We can take the savanna biome as a reference example, concentrating on large herbivores inhabiting it and some predators that feed on them. Only two conditionally stable equilibrium points have emerged from the model analysis: the predator-only equilibrium and the coexistence one. Transcritical bifurcations from the former to the latter type of equilibrium, as well as saddle-node bifurcations of the coexistence equilibrium have been identified numerically by using MATLAB. In addition, the model was found to exhibit bistability. Bistability is studied by using the MATLAB toolbox bSTAB, paying particular attention to the basin stability values. Comparison of coexistence equilibria with other prey-predator models in the literature essentially shows that, in this case, prey thrive in greater numbers and predators in smaller numbers. The population changes due to parameter variations were found to be significantly less pronounced.
Citation: Francesca Acotto, Ezio Venturino. How do predator interference, prey herding and their possible retaliation affect prey-predator coexistence?[J]. AIMS Mathematics, 2024, 9(7): 17122-17145. doi: 10.3934/math.2024831
| [1] | Xiaodan Zhang, Shuyi Wang, Kemeng Xu, Rui Zhao, Yichong She . Cross-subject EEG-based emotion recognition through dynamic optimization of random forest with sparrow search algorithm. Mathematical Biosciences and Engineering, 2024, 21(3): 4779-4800. doi: 10.3934/mbe.2024210 |
| [2] | Binju Saju, Neethu Tressa, Rajesh Kumar Dhanaraj, Sumegh Tharewal, Jincy Chundamannil Mathew, Danilo Pelusi . Effective multi-class lungdisease classification using the hybridfeature engineering mechanism. Mathematical Biosciences and Engineering, 2023, 20(11): 20245-20273. doi: 10.3934/mbe.2023896 |
| [3] | Basem Assiri, Mohammad Alamgir Hossain . Face emotion recognition based on infrared thermal imagery by applying machine learning and parallelism. Mathematical Biosciences and Engineering, 2023, 20(1): 913-929. doi: 10.3934/mbe.2023042 |
| [4] | Yufeng Qian . Exploration of machine algorithms based on deep learning model and feature extraction. Mathematical Biosciences and Engineering, 2021, 18(6): 7602-7618. doi: 10.3934/mbe.2021376 |
| [5] | Xu Yin, Ming Meng, Qingshan She, Yunyuan Gao, Zhizeng Luo . Optimal channel-based sparse time-frequency blocks common spatial pattern feature extraction method for motor imagery classification. Mathematical Biosciences and Engineering, 2021, 18(4): 4247-4263. doi: 10.3934/mbe.2021213 |
| [6] | Kunpeng Li, Zepeng Wang, Yu Zhou, Sihai Li . Lung adenocarcinoma identification based on hybrid feature selections and attentional convolutional neural networks. Mathematical Biosciences and Engineering, 2024, 21(2): 2991-3015. doi: 10.3934/mbe.2024133 |
| [7] | Dingxin Xu, Xiwen Qin, Xiaogang Dong, Xueteng Cui . Emotion recognition of EEG signals based on variational mode decomposition and weighted cascade forest. Mathematical Biosciences and Engineering, 2023, 20(2): 2566-2587. doi: 10.3934/mbe.2023120 |
| [8] | Yan Yan, Yong Qian, Hongzhong Ma, Changwu Hu . Research on imbalanced data fault diagnosis of on-load tap changers based on IGWO-WELM. Mathematical Biosciences and Engineering, 2023, 20(3): 4877-4895. doi: 10.3934/mbe.2023226 |
| [9] | Jie Bai, Heru Xue, Xinhua Jiang, Yanqing Zhou . Classification and recognition of milk somatic cell images based on PolyLoss and PCAM-Reset50. Mathematical Biosciences and Engineering, 2023, 20(5): 9423-9442. doi: 10.3934/mbe.2023414 |
| [10] | Yuzhuo Shi, Huijie Zhang, Zhisheng Li, Kun Hao, Yonglei Liu, Lu Zhao . Path planning for mobile robots in complex environments based on improved ant colony algorithm. Mathematical Biosciences and Engineering, 2023, 20(9): 15568-15602. doi: 10.3934/mbe.2023695 |
In this paper, focusing on individualistic generalist predators and prey living in herds which coexist in a common area, we propose a generalization of a previous model, namely, a two-population system that accounts for the prey response to predator attacks. In particular, we suggest a new prey-predator interaction term with a denominator of the Beddington-DeAngelis form and a function in the numerator that behaves as N for small values of N, and as Nα for large values of N, where N denotes the number of prey. We can take the savanna biome as a reference example, concentrating on large herbivores inhabiting it and some predators that feed on them. Only two conditionally stable equilibrium points have emerged from the model analysis: the predator-only equilibrium and the coexistence one. Transcritical bifurcations from the former to the latter type of equilibrium, as well as saddle-node bifurcations of the coexistence equilibrium have been identified numerically by using MATLAB. In addition, the model was found to exhibit bistability. Bistability is studied by using the MATLAB toolbox bSTAB, paying particular attention to the basin stability values. Comparison of coexistence equilibria with other prey-predator models in the literature essentially shows that, in this case, prey thrive in greater numbers and predators in smaller numbers. The population changes due to parameter variations were found to be significantly less pronounced.
Retinal tears arise from vitreous traction on the retina or degeneration and atrophy of the retina, and it is frequently observed in individuals who have acute posterior vitreous detachment [1]. The identification of retinal tears, which serve as a risk factor for the occurrence of retinal detachment, poses a significant challenge. In the absence of timely detection and intervention, 30–50% of the cases will progress to retinal detachment [2], a condition that leads to severe blinding. In most cases, retinal tears can be diagnosed by using indirect fundoscopy in conjunction with scleral pressure examination [3]. However, in situations where the patient's refracting media is murky, B-scan ultrasound emerges as a viable option among the limited alternative diagnostic tools available. Moreover, ultrasound is also more accessible and less expensive than other types like OCT and ultra-wide-field imaging. It is widely prevalent and available in many local hospitals and primary community clinics. However, conventional manual methods require the involvement of highly skilled physicians to prevent their potential oversight or misdiagnosis [4]. In this context, only a few of the large hospitals in China have professional sonographers, as is the case in other developing countries and regions. As a result, the development of a model capable of automatically diagnosing retinal tears is critical and urgent [5].
Deep learning represents the most effective approach to automating the development of diagnostic systems. Previous studies have proposed a multitude of models, with predominant focus on the utilization of convolutional neural networks (CNNs) [6,7]. For example, Li et al. [8] screened for notable peripheral retinal lesions (NPRLs) by using numerous models, such as InceptionResNetV2, InceptionV3, ResNet50 and VGG16. Furthermore, with an accuracy of 79.8%, a system based on seResNet50 was developed by Zhang et al. [9] to screen numerous types of NPRLs. However, the inability of the CNN to capture long-distance image features hinders its continued development. In this context, Dosovitskiy et al. [10] proposed the vision transformer (ViT) as a solution to this problem, using the excellent transformer [11] from natural language processing as a point of reference. Subsequently, ViT was observed to outperform CNNs in a multitude of tests after self-attention methods were substituted for convolutional processes. Accordingly, several researchers have made efforts to implement the model in the treatment of ophthalmic disorders, particularly, retinal issues. Jiang et al. [12] employed a ViT to automatically identify normal eyes, age-related macular degeneration, and diabetic macular edema, achieving a classification accuracy of 99.69%. Furthermore, a deep learning model based on a ViT was introduced by Wu et al. [13] to assess diabetic retinopathy, and it realized an accuracy of 91.4% and a kappa score of 0.935. However, studies that report on the automatic diagnosis of retinal tears are few.
The present study involved the collection and construction of a retinal tear dataset comprising 1831 images, with the aim of developing more effective diagnostic algorithms. Despite the widely acknowledged fact that ViT is data-driven and performs exceptionally well with ample training data, our study encountered a hurdle due to the limited availability of data. Although the use of transfer learning has been demonstrated to be able to partially address this challenge, it should be noted that this approach may not be sufficient and could potentially lead to an increase in computational resources. Consequently, a hybrid structure was devised to introduce inductive bias and enhance the model's adaptability to our limited dataset. Furthermore, through experimental analysis, it has been observed that the utilization of deformable convolution [14] affords superior adaptability to the contour of lesions and yields improved performance. Thus, based on the aforementioned rationales, we proposed a novel framework called the deformable convolution and transformer network (DCT-Net) in the current study, which integrates the merits of deformable convolution and the vision transformer. The model was subjected to rigorous testing on two datasets to assess its overall performance and efficacy. Additionally, attention maps were generated in order to validate their interpretability. The current body of research on retinal tear diagnostic systems is limited, and our study has partially addressed this research gap.
To summarize, the main contributions of the present study can be succinctly stated as follows:
● A dataset comprising 1831 B-scan ultrasound images of retinal tears was assembled.
● A novel model that is more appropriate for small datasets of medical images is proposed. To our knowledge, this study represents the first investigation into the utilization of ViT-based architecture for the purpose of identifying retinal tears through the analysis of ultrasound images.
● The efficacy of the model in terms of lesion detection, as well as its commendable performance, are demonstrated through the analysis of two datasets.
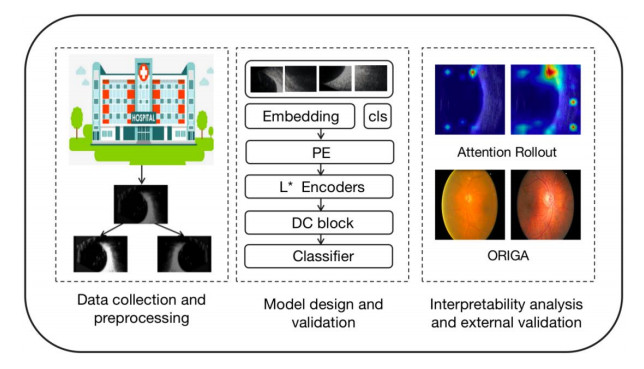
The contents of the current study can be categorized into three primary modules: data collection and preprocessing; model design and validation and interpretability analysis and external validation. The flowchart is illustrated in Figure 1.
The investigation was carried out in adherence to the Protocol for the Declaration of Helsinki, as amended in 2013.
A comprehensive set of 1902 ultrasound B-scan images was collected for this retrospective study. These samples were obtained from the eye hospital of Wenzhou Medical University for the period from October 2017 to April 2022. All positive samples were verified by professional ophthalmologists. However, the images were collected from a variety of devices with varying resolutions and file types. Thus, to accommodate the model's input, each image underwent a resizing process to 224 × 224 pixels, and any blurry pixels were removed. Finally, 1831 samples (910 positive and 927 negative) were utilized for subsequent investigations.
Data augmentation is a data processing technique that is employed to enhance the quantity and diversity of training samples by transforming existing data. There are two distinct categories of data arguments, namely, augment online and augment offline. Typically, the former approach is utilized for larger datasets, wherein operations are executed on the data batch. Conversely, the latter approach is employed for smaller datasets, wherein operations are directly performed on the original data [15]. Accordingly, the offline method was selected as a result of the limited dataset available for our study. Various data augmentation techniques, including rotation, cropping, brightness shift, contrast modification, horizontal flipping, vertical flipping, etc., can be employed for image augmentation [16,17]. However, not all enhancement techniques are universally applicable, because the labels of the image categories could be modified after enhancement. After conducting analysis, we opted to employ horizontal flip, vertical flip and brightness shift techniques in order to enhance the original dataset. Figure 2 illustrates the aforementioned augmentation operations.
The ViT model is based on direct global relationship modeling and has demonstrated significant accomplishments in the extraction of global features through the use of a multi-head self-attention mechanism. However, it has limitations in its ability to effectively accommodate minuscule lesions, and it proves inadequate when confronted with a limited size of training data. In this context, convolution operations, specifically deformable convolutions, exhibit better adaptability to local detail characteristics. This study presents a novel approach that integrates the ViT and deformable convolution to realize the accurate detection of retinal tears with enhanced precision. Figure 3 presents a visual representation of the proposed model. Furthermore, the utilization of transfer learning technology was employed in this particular aspect to enhance network performance and expedite the training process.
The input images (H×W×C) were split into n patches. After these patches were flattened, a linear projection layer was used to convert them to D-dimensional vectors. A class token was also appended, as illustrated in the BERT [18]. Following position embedding, the D-dimensional vectors were subsequently transmitted to the Transformer Encoder. Maintaining the dimensions of the vectors was crucial throughout the entire process.
In the Transformer Encoder, the input vectors undergo an initial step of layer normalization, which expedites the convergence of the network. The procedure is denoted by Eq (1) in terms of the mean and standard deviation of the input, respectively.
| LayerNorm(xi)=xi−μ√σ2+ϵ | (1) |
The resulting output is used to compute the mutual attention by utilizing multi-head attention layers (as demonstrated in Eqs (2)–(4)). Subsequently, the Layer Norm and Multi-Layer Perceptron layer were employed to obtain the final outputs. The inclusion of residual connections in this process effectively mitigated the issue of gradient vanishing. To optimize the utilization of the transfer learning's weight, we employed an equal number of encoders as the conventional ViT model.
| Qi=QWQi,Ki=KWKi,Vi=VWVi | (2) |
| headi=Attention(Qi,Ki,Vi) | (3) |
| Multihead(Q,K,V)=Concact(head1,head2,...,head12) | (4) |
| y(P0)=∑Pn∈Rw(Pn)⋅x(P0+Pn+ΔPn) | (5) |
The diagnosis of retinal tears using ultrasound images is highly dependent on the position and shape of the small lesion areas. However, the standard ViT is insufficient for acquiring such localized data. As a result of conventional convolution employing regular kernels, the receptive field remains constant and is ill-equipped to accommodate variations in edge shape. By appending a learnable offset to the standard convolution kernel, deformable convolution can modify the sampling area's shape, bringing it closer to the object's edge. The sampling procedure for deformable convolution and ordinary convolution is presented in Figure 4. Equation (5) illustrates the calculation process.
Subsequently, a residual deformable convolution block was devised in order to enhance the extraction of intricate features. Similar to the Transformer Encoder, the designed module initially employs a Batch Norm layer to convert inputs into data with a mean of 1 and a variance of 0. Two deformable convolutional layers were used to capture local concrete detail features. To enhance nonlinearity while minimizing computational workload, the convolutional kernel of the first layer was designed to be larger than that of the second layer. Subsequently, an adaptive average pooling layer was incorporated in order to enhance the efficacy of feature extraction and computational processes. Furthermore, the concept of residual connection was incorporated into the model design, drawing inspiration from Resnet [19]. This addition was made in order to mitigate the issue of gradient vanishing [20].
The utilization of pooling layers in a CNN can lead to the merging of position information, potentially resulting in the loss of certain details during the generation of rough heat maps [21,22]. Our model effectively captures global features and is founded upon a self-attention mechanism. Moreover, it has the ability to deliver elaborate visualizations to an adequate degree [23]. However, attention-based networks are incompatible with the traditional Grad-CAM [24] method. This is attributed to the fact that the CNN permits the aggregation of feature map weights from multiple channels, whereas the ViT restricts the addition of distinct patches. Therefore, we adopted the attention rollout method proposed by Samira Abnar [25]. Attention rollout in essence calculates the product of the attention matrix from the low level to the high level of the network. The concrete realization is achieved through the recursive calculation of each layer's tokens, computing information from the input layer to the higher level. Concurrently, the residual connection and the weight must be taken into account. It is represented by Eq (6).
| AttentionRolloutL=(AL+I)AttentionRolloutL−1 | (6) |
where AL is the attention matrix of the L layer and I is the identity matrix.
The adoption of a transfer learning strategy was implemented with the aim of expediting the training process and enhancing the performance of the model. The pre-training process was conducted by using the ImageNet dataset, which comprises a vast collection of more than 1000 categories of nature images. The cross-entropy loss [26,27] was employed as the loss function in our study. This choice was made to address the issue of the sigmoid function's derivative form, which is susceptible to saturation and results in slow gradient updates. Furthermore, the Adam optimizer [28] was also utilized. The approach offers the benefits of rapid convergence and a relatively facile process for configuring hyperparameters.
Furthermore, an early stopping strategy was developed with the intention of mitigating the issue of overfitting. Following each iteration of training, a comprehensive evaluation was conducted on the designated test dataset. The training process was deemed to be complete once the accuracy on the test set ceased to exhibit substantial improvements and stabilized after approximately 10 epochs.
In order to enhance the precision of an evaluation of the performance of the designed model, a set of widely recognized state-of-the-art (SOTA) models, viz. Alexnet [29], Inception v3 [30], Resnet101 [19], VGG16 [31] and ViT, were chosen as the baseline models. The preprocessing steps and training strategies remained consistent across all baselines, with the exception of Inception v3, which required an input size of 299 × 299 pixels.
Table 1 presents a comprehensive overview of the performance metrics for both the baseline models and the model that has been specifically designed for this study. The confusion matrix for multiple models on the test set is depicted in Figure 5. The number in each small square represents the corresponding number of images with the same predicted true label and it is the percentage of the total number of images under the true label. It is worth mentioning that within the category of CNN-based models, Inception v3 exhibited the highest level of performance, achieving an accuracy rate of 96.82%, an F1 score of 0.9605 and an AUC of 0.9828. The ViT model with the pure self-attention mechanism did not perform well; particularly, the performance was even worse than that of the CNN. Nevertheless, our designed model exhibited superior performance across all metrics, surpassing all other models, and only a mere 10 samples were classified incorrectly. To our knowledge, the proposed model exhibited superior performance even as compared to human experts (with a sensitivity of 96%) [32].
| Model | Accuracy | Precision | Recall | F1 Score | AUC |
| Alexnet | 95.11% | 94.64% | 95.68% | 0.9456 | 0.9286 |
| Inception V3 | 96.82% | 96.55% | 96.37% | 0.9605 | 0.9828 |
| Resnet101 | 96.74% | 96.94% | 96.42% | 0.9599 | 0.9772 |
| VGG16 | 96.52% | 96.42% | 96.66% | 0.9595 | 0.9598 |
| Vit | 95.76% | 95.66% | 95.87% | 0.9515 | 0.9444 |
| DCT-Net | 97.78% | 97.34% | 97.13% | 0.9682 | 1.0000 |
DownLoad:
CSV
As an external validation step, we utilized the ORIGA datasets in this section to ensure that the proposed model possesses exceptional generalizability and can adapt to various database types. The dataset comprised a total of 650 images depicting instances of glaucoma. In order to conduct a comparative analysis against other models documented in the literature [33,34,35], we used the original dataset without employing any augmentation techniques. Table 2 shows the results, where NMD denotes that the pre-training was performed by using a non-medical dataset, SOD denotes that the pre-training was performed by using a similar ophthalmic dataset and CT-Net denotes that common convolution replaced the deformable convolution. The ViT did not perform well among them, most likely as a result of the limited dataset. On the other hand, the DCT-Net achieved the highest accuracy at 83.8%, demonstrating the best performance. Additionally, the significance of deformable convolution became apparent when it was compared to CT-Net.
| Model | Accuracy | Sensitivity | Specificity |
| CNN | 70.4% | 70.7% | 74.8% |
| VGG | 70.1% | 69.8% | 71.0% |
| GoogLeNet | 71.8% | 69.8% | 73.5% |
| ResNet | 71.5% | 71.3% | 71.7% |
| Chen [34] | 70.8% | 69.2% | 71.0% |
| Shibata [35] | 73.3% | 73.2% | 76.7% |
| NMD+CNN | 74.5% | 68.7% | 80.7% |
| SOD+CNN | 73.9% | 80.9% | 72.2% |
| NMD+Attention | 74.9% | 71.2% | 77.7% |
| Xu [33] | 76.6% | 75.3% | 77.2% |
| ViT | 71.4% | 74.0% | 67.8% |
| CT-Net | 80.5% | 81.7% | 80.1% |
| DCT-Net | 83.8% | 82.7% | 82.4% |
DownLoad:
CSV
Models that are easily interpretable offer valuable insights into their inner workings, thereby benefiting both patients and clinicians. Figure 6 displays three attention maps that were generated by using our private dataset. We have used the red circle to mark the lesion parts in the original image. In the attention maps, higher intensity of color is indicative of a greater level of attention. The aforementioned images demonstrate a strong correspondence between the regions of heightened attention and the affected areas of the lesion. This indicated that the model possesses a well-defined operational framework and possesses exceptional interpretive qualities.
The hardware configuration utilized in this study is as follows. The central processing unit (CPU) utilized in the system comprised a 7-core Intel(R) Xeon(R) CPU E5-2680 v4 operating at a frequency of 2.40 GHz. Additionally, the system incorporated a single graphics processing unit in the form of an RTX 3070ti with 8 GB of dedicated memory. The training process employed Python version 3.8, PyTorch framework version 1.10.0 for machine learning and CUDA version 11.3.
CNNs have demonstrated remarkable performance on previous image processing tasks and are widely acknowledged as the SOTA approach. For instance, Yu et al. [36,37] employed CNNs for the purpose of detecting concrete cracks, achieving exceptional performance. Ragupathy and Karunakaran [38] proposed a CNN-based model for the detection of meningioma brain tumors. The model demonstrated promising performance metrics. However, due to the constraints imposed by the small convolutional kernel, CNNs may not be able to effectively extract global features. As shown in Table 1, it appears that the performance of the CNN-based model has encountered a bottleneck, making further improvements challenging. When comparing the CNN with the ViT, it can be observed that the ViT utilizes the attention mechanism to calculate the relationship between global pixels, thereby enabling a comprehensive global perspective. Numerous studies have substantiated the impressive efficacy of the ViT model [39]. However, our investigation revealed that the pure ViT did not perform well on small datasets of retinal tears (with the accuracy of 95.76%).
To enhance the efficacy of lesion detection on limited datasets, a novel architecture was initially devised, integrating the merits of convolution and attention mechanisms. As shown in Table 2, the utilization of global feature extraction techniques contributes to the generation of a relatively comprehensive latent space feature representation. Concurrently, as a result of incorporating the inductive bias of convolution, the proposed model demonstrates substantial enhancements on the limited public dataset, achieving an accuracy of 80.5%. Moreover, replacing ordinary convolutions with deformable convolutions has been found to yield more favorable outcomes, as evidenced by an accuracy rate of 83.8%. This phenomenon could potentially be attributed to the enhanced precision resulting from extracting both the location and shape of the lesion areas. From the perspective of external validation and interpretable analysis, the model possesses robustness and sufficient accuracy.
Notwithstanding the enhanced performance achieved in this study, certain constraints remain. First, ophthalmic ultrasound is highly dependent on the equipment, technique and examiner experience. However, the data collected for this study came from a variety of devices. This may compromise the validity of the results. Second, all of the retinal tear images utilized in this study were procured from a single hospital. This may lead to an absence of diversity in the cases. Moreover, only retinal tears were included in our study. Ultrasound imaging can, in fact, be utilized to diagnose additional retinal disorders. Correspondingly, the value of the model can be enhanced through the incorporation of additional disease types. Finally, the incorporation of the residual deformable convolution module and the utilization of a ViT as the feature extractor resulted in an increased number of parameters for our model (Table 3). This results in increased demands on the environment in terms of model deployment.
Utilizing ultrasound to identify retinal tears is an extremely practical method. It is superior to alternative approaches when it comes to handling intricate clinical scenarios, such as ocular media opacity. However, the extraction of useful features via conventional machine learning methods is hampered by low resolution. Fortunately, the progress that has been made in deep learning enables the analysis of these images in an efficient manner. Our current research is, without a doubt, preliminary in nature. Moving forward, we aim to enhance the model's architecture and implement global vision technology that is more streamlined or possesses a reduced number of parameters. This will allow the effortless deployment of lightweight models across diverse environments. Furthermore, our objective is to enhance the quantity and range of samples gathered in order to prevent issues with model generalization that may arise from discrepancies in the training data. Lastly, we will collaborate with clinicians and conduct additional multicenter studies to precisely quantify the extent to which this model can benefit physicians.
| Model | Parameters(1 × 106) |
| Alexnet | 57.01 |
| Inception v3 | 25.12 |
| Resnet101 | 42.5 |
| VGG16 | 134.27 |
| Vision Transformer | 85.80 |
| DCT-Net | 138.36 |
DownLoad:
CSV
A novel model was developed for the diagnosis of ophthalmological conditions in the current study. The model demonstrated superior performance on both our proprietary dataset and the glaucoma dataset that was publicly available. The framework is a comprehensive computing framework that exhibits superior performance and does not necessitate the generation of manually designed features. Overall, this technology provides significant practical value in the field of clinical application, particularly in the realm of automated diagnosis.
The authors declare that they have not used artificial intelligence tools in the creation of this article.
We would like to thank all editors and reviews for their careful review and revision of the paper. This research was supported in part by the National Key R & D Program of China [2018YFA0701700].
The authors declare that there is no conflict of interest.
| [1] | L. B. Hutley, S. A. Setterfield, Savanna, Encyclopedia of Ecology, Academic Press, (2008), 3143–3154. https://doi.org/10.1016/B978-008045405-4.00358-X |
| [2] |
S. L. Lima, Back to the basics of anti-predatory vigilance: the group-size effect, Anim. Behav., 49 (1995), 11–20. https://doi.org/10.1016/0003-3472(95)80149-9 doi: 10.1016/0003-3472(95)80149-9
|
| [3] |
G. Roberts, Why individual vigilance declines as group size increase, Anim. Behav., 51 (1996), 1077–1086. https://doi.org/10.1006/anbe.1996.0109 doi: 10.1006/anbe.1996.0109
|
| [4] | T. M. Caro, Antipredator defenses in birds and mammals, University of Chicago Press, 2005. |
| [5] |
V. Ajraldi, M. Pittavino, E. Venturino, Modeling herd behavior in population systems, Nonlinear Anal. Real World Appl., 12 (2011), 2319–2338. https://doi.org/10.1016/j.nonrwa.2011.02.002 doi: 10.1016/j.nonrwa.2011.02.002
|
| [6] |
I. M. Bulai, E. Venturino, Shape effects on herd behavior in ecological interacting population models, Math. Comput., 141 (2017), 40–55. https://doi.org/10.1016/j.matcom.2017.04.009 doi: 10.1016/j.matcom.2017.04.009
|
| [7] | S. P. Bera, A. Maiti, G. Samanta, Modelling herd behavior of prey: analysis of a prey-predator model, WJMS, 11 (2015), 3–14. |
| [8] |
C. Berardo, I. M. Bulai, E. Venturino, Interactions obtained from basic mechanistic principles: prey herds and predators, Mathematics, 9 (2021), 2555. https://doi.org/10.3390/math9202555 doi: 10.3390/math9202555
|
| [9] |
P. A. Braza, Predator–prey dynamics with square root functional responses, Nonlinear Anal. Real World Appl., 13 (2012), 1837–1843. https://doi.org/10.1016/j.nonrwa.2011.12.014 doi: 10.1016/j.nonrwa.2011.12.014
|
| [10] |
S. Djilali, C. Cattani, L. N. Guin, Delayed predator-prey model with prey social behavior, Eur. Phys. J. Plus, 136 (2021), 940. https://doi.org/10.1140/epjp/s13360-021-01940-9 doi: 10.1140/epjp/s13360-021-01940-9
|
| [11] |
J. Tan, W. Wang, J. Feng, Transient dynamics analysis of a predator-prey system with square root functional responses and random perturbation, Mathematics, 10 (2022), 4087. https://doi.org/10.3390/math10214087 doi: 10.3390/math10214087
|
| [12] |
S. Belvisi, E. Venturino, An ecoepidemic model with diseased predators and prey group defense, Simul. Model. Pract. Theory, 34 (2013), 144–155. https://doi.org/10.1016/j.simpat.2013.02.004 doi: 10.1016/j.simpat.2013.02.004
|
| [13] |
G. Gimmelli, B. W. Kooi, E. Venturino, Ecoepidemic models with prey group defense and feeding saturation, Ecol. Complex., 22 (2015), 50–58. https://doi.org/10.1016/j.ecocom.2015.02.004 doi: 10.1016/j.ecocom.2015.02.004
|
| [14] |
S. Saha, G. P. Samanta, Analysis of a predator-prey model with herd behavior and disease in prey incorporating prey refuge, Int. J. Biomath., 12 (2019), 1950007. https://doi.org/10.1142/S1793524519500074 doi: 10.1142/S1793524519500074
|
| [15] |
F. Acotto, E. Venturino, Modeling the herd prey response to individualistic predators attacks, Math. Meth. Appl. Sci., 46 (2023), 13436–13456. https://doi.org/10.1002/mma.9262 doi: 10.1002/mma.9262
|
| [16] |
S. C. Hayley, J. T. Craig, I. H. K. Graham, Prey morphology and predator sociality drive predator-prey preferences, J. Mammal., 97 (2016), 919–927. https://doi.org/10.1093/jmammal/gyw017 doi: 10.1093/jmammal/gyw017
|
| [17] |
M. Chen, Y. Takeuchi, J. F. Zhang, Dynamic complexity of a modified Leslie-Gower predator-prey system with fear effect, Commun. Nonlinear Sci. Numer. Simul., 119 (2023), 107109. https://doi.org/10.1016/j.cnsns.2023.107109 doi: 10.1016/j.cnsns.2023.107109
|
| [18] |
M. Das, G. P. Samanta, A delayed fractional order food chain model with fear effect and prey refuge, Math. Comput., 178 (2020), 218–245. https://doi.org/10.1016/j.matcom.2020.06.015 doi: 10.1016/j.matcom.2020.06.015
|
| [19] |
S. Garai, N. C. Pati, N. Pal, G. C. Layek, Organized periodic structures and coexistence of triple attractors in a predator-prey model with fear and refuge, Chaos Solit., 165 (2022), 112833. https://doi.org/10.1016/j.chaos.2022.112833 doi: 10.1016/j.chaos.2022.112833
|
| [20] |
S. Kim, K. Antwi-Fordjour, Prey group defense to predator aggregated induced fear, Eur. Phys. J. Plus, 137 (2022), 704. https://doi.org/10.1140/epjp/s13360-022-02926-x doi: 10.1140/epjp/s13360-022-02926-x
|
| [21] |
S. K. Sasmal, Y. Takeuchi, Dynamics of a predator-prey system with fear and group defense, J. Math. Anal. Appl., 481 (2020), 123471. https://doi.org/10.1016/j.jmaa.2019.123471 doi: 10.1016/j.jmaa.2019.123471
|
| [22] |
J. R. Beddington, Mutual interference between parasites or predators and its effect on searching efficiency, J. Anim. Ecol., 44 (1975), 331–340. https://doi.org/10.2307/3866 doi: 10.2307/3866
|
| [23] |
D. L. DeAngelis, R. A. Goldstein, R. V. O'Neill, A model for tropic interaction, Ecology, 56 (1975), 881–892. https://doi.org/10.2307/1936298 doi: 10.2307/1936298
|
| [24] | D. Borgogni, L. Losero, E. Venturino, A more realistic formulation of herd behavior for interacting populations, R.P. Mondaini (eds) Trends in Biomathematics: Modeling Cells, Flows, Epidemics, and the Environment, BIOMAT 2019 (2020), Springer, Cham., Chapter 2, 9–21. https://doi.org/10.1007/978-3-030-46306-9_2 |
| [25] |
E. Venturino, Y. Caridi, V. Dos Anjos, G. D'Ancona, On some methodological issues in mathematical modeling of interacting populations, J. Biol. Syst., 31 (2023), 169–184. https://doi.org/10.1142/S0218339023500080 doi: 10.1142/S0218339023500080
|
| [26] |
M. Stender, N. Hoffmann, bSTAB: an open-source software for computing the basin stability of multi-stable dynamical systems, Nonlinear Dyn., 107 (2022), 1451–1468. https://doi.org/10.1007/s11071-021-06786-5 doi: 10.1007/s11071-021-06786-5
|
| [27] |
P. J. Menck, J. Heitzig, N. Marwan, J. Kurths, How basin stability complements the linear-stability paradigm, Nat. Phys., 9 (2013), 89–92. https://doi.org/10.1038/nphys2516 doi: 10.1038/nphys2516
|
| [28] |
P. J. Menck, J. Heitzig, J. Kurths, H. J. Schellnhuber, How dead ends undermine power grid stability, Nat. Commun., 5 (2014), 3969. https://doi.org/10.1038/ncomms4969 doi: 10.1038/ncomms4969
|
| [29] |
K. A. Johnson, R. S. Goody, The original Michaelis constant: translation of the 1913 Michaelis-Menten paper, Biochem., 50 (2011), 8264–8269. https://doi.org/10.1021/bi201284u doi: 10.1021/bi201284u
|
| [30] |
C. S. Holling, The functional response of predators to prey density and its role in mimicry and population regulation, Mem. Ent. Soc. Can., 97 (1965), 5–60. https://doi.org/10.4039/entm9745fv doi: 10.4039/entm9745fv
|
| [31] | B. Noble, Applied Linear Algebra, Englewood Cliffs: Prentice-Hall, 1969. |
| [32] | R. Woods, Analytic Geometry, New York: Mac Millan, 1939. |
| [33] | L. Perko, Differential Equations and Dynamical Systems, New York: Springer, 2001. https://doi.org/10.1007/978-1-4613-0003-8 |
| [34] |
A. Erbach, F. Lutscher, G. Seo, Bistability and limit cycles in generalist predator-prey dynamics, Ecol. Complex., 14 (2013), 48–55. https://doi.org/10.1016/j.ecocom.2013.02.005 doi: 10.1016/j.ecocom.2013.02.005
|
| [35] |
S. Garai, S. Karmakar, S. Jafari, N. Pal, Coexistence of triple, quadruple attractors and Wada basin boundaries in a predator-prey model with additional food for predators, Commun. Nonlinear Sci. Numer. Simul., 121 (2023), 107208. https://doi.org/10.1016/j.cnsns.2023.107208 doi: 10.1016/j.cnsns.2023.107208
|
| [36] |
R. López-Ruiz, D. Fournier-Prunaret, Indirect Allee effect, bistability and chaotic oscillations in a predator-prey discrete model of logistic type, Chaos Soliton. Fract., 24 (2005), 85–101. https://doi.org/10.1016/j.chaos.2004.07.018 doi: 10.1016/j.chaos.2004.07.018
|
| [37] |
Rajni, B. Ghosh, Multistability, chaos and mean population density in a discrete-time predator-prey system, Chaos Soliton. Fract., 162 (2022), 112497. https://doi.org/10.1016/j.chaos.2022.112497 doi: 10.1016/j.chaos.2022.112497
|
| [38] |
D. Melchionda, E. Pastacaldi, C. Perri, M. Banerjee, E. Venturino, Social behavior-induced multistability in minimal competitive ecosystems, J. Theor. Biol., 439 (2018), 24–38. https://doi.org/10.1016/j.jtbi.2017.11.016 doi: 10.1016/j.jtbi.2017.11.016
|
Figures(13) / Tables(2)
Francesca Acotto, Ezio Venturino. How do predator interference, prey herding and their possible retaliation affect prey-predator coexistence?[J]. AIMS Mathematics, 2024, 9(7): 17122-17145. doi: 10.3934/math.2024831
| Model | Accuracy | Precision | Recall | F1 Score | AUC |
| Alexnet | 95.11% | 94.64% | 95.68% | 0.9456 | 0.9286 |
| Inception V3 | 96.82% | 96.55% | 96.37% | 0.9605 | 0.9828 |
| Resnet101 | 96.74% | 96.94% | 96.42% | 0.9599 | 0.9772 |
| VGG16 | 96.52% | 96.42% | 96.66% | 0.9595 | 0.9598 |
| Vit | 95.76% | 95.66% | 95.87% | 0.9515 | 0.9444 |
| DCT-Net | 97.78% | 97.34% | 97.13% | 0.9682 | 1.0000 |
DownLoad:
CSV
| Model | Accuracy | Sensitivity | Specificity |
| CNN | 70.4% | 70.7% | 74.8% |
| VGG | 70.1% | 69.8% | 71.0% |
| GoogLeNet | 71.8% | 69.8% | 73.5% |
| ResNet | 71.5% | 71.3% | 71.7% |
| Chen [34] | 70.8% | 69.2% | 71.0% |
| Shibata [35] | 73.3% | 73.2% | 76.7% |
| NMD+CNN | 74.5% | 68.7% | 80.7% |
| SOD+CNN | 73.9% | 80.9% | 72.2% |
| NMD+Attention | 74.9% | 71.2% | 77.7% |
| Xu [33] | 76.6% | 75.3% | 77.2% |
| ViT | 71.4% | 74.0% | 67.8% |
| CT-Net | 80.5% | 81.7% | 80.1% |
| DCT-Net | 83.8% | 82.7% | 82.4% |
DownLoad:
CSV
| Model | Parameters(1 × 106) |
| Alexnet | 57.01 |
| Inception v3 | 25.12 |
| Resnet101 | 42.5 |
| VGG16 | 134.27 |
| Vision Transformer | 85.80 |
| DCT-Net | 138.36 |
DownLoad:
CSV
| Model | Accuracy | Precision | Recall | F1 Score | AUC |
| Alexnet | 95.11% | 94.64% | 95.68% | 0.9456 | 0.9286 |
| Inception V3 | 96.82% | 96.55% | 96.37% | 0.9605 | 0.9828 |
| Resnet101 | 96.74% | 96.94% | 96.42% | 0.9599 | 0.9772 |
| VGG16 | 96.52% | 96.42% | 96.66% | 0.9595 | 0.9598 |
| Vit | 95.76% | 95.66% | 95.87% | 0.9515 | 0.9444 |
| DCT-Net | 97.78% | 97.34% | 97.13% | 0.9682 | 1.0000 |
| Model | Accuracy | Sensitivity | Specificity |
| CNN | 70.4% | 70.7% | 74.8% |
| VGG | 70.1% | 69.8% | 71.0% |
| GoogLeNet | 71.8% | 69.8% | 73.5% |
| ResNet | 71.5% | 71.3% | 71.7% |
| Chen [34] | 70.8% | 69.2% | 71.0% |
| Shibata [35] | 73.3% | 73.2% | 76.7% |
| NMD+CNN | 74.5% | 68.7% | 80.7% |
| SOD+CNN | 73.9% | 80.9% | 72.2% |
| NMD+Attention | 74.9% | 71.2% | 77.7% |
| Xu [33] | 76.6% | 75.3% | 77.2% |
| ViT | 71.4% | 74.0% | 67.8% |
| CT-Net | 80.5% | 81.7% | 80.1% |
| DCT-Net | 83.8% | 82.7% | 82.4% |
| Model | Parameters(1 × 106) |
| Alexnet | 57.01 |
| Inception v3 | 25.12 |
| Resnet101 | 42.5 |
| VGG16 | 134.27 |
| Vision Transformer | 85.80 |
| DCT-Net | 138.36 |
