Analysis of a COVID-19 model with media coverage and limited resources

1.   Introduction

The step-length-based techniques and the trust region methods are two types of optimization methods for the least-squares problem (LSP): $\dfrac{1}{2}\|{\bf F}({\bf x})\|^{2}$, where ${\bf F} = \left\{f_{1}, f_{2}, \ldots, f_{{\bf N}} \right\}^{\mathrm{T}}$ is the vector of the non-linear functions, ${\bf M}$ is the number of unknowns ${\bf x}$, (${\bf M}\leq {\bf N}$).

The Newton method and the Gauss-Newton (GN) method are frequently utilized for solving LSPs, belong to the step-length-based category ^[1,2]. The Newton approach calculates the least-squares function's optimum descent direction, resulting in a faster rate of convergence. However, for determining the descent direction, one needs to obtain the precise derivatives of the least-squares function and the time consuming. On the other hand, the GN method approximates the derivatives using a simple approach that is relatively straightforward to evaluate, however the solution may not converge owing to the over-simplification of the derivatives, which may result in an incorrect descent direction. The Levenberg-Marquardt method (LMM) was introduced by Levenberg ^[3] and Marquardt ^[4] for solving the (LSP) using a trust region approach ^[5,6]. In the GN method, the simplified Hessian matrix ${\bf H}_{{\bf GN}}$ is not always invertible, to avoid this problem a modified positive definite Hessian ${\bf H}_{{\bf LM}} = {\bf H}_{{\bf GN}} + \mathcal{S}^k$, is usually used. The LMM takes $\mathcal{S}^k = \beta_k {\bf I}_{{\bf N\times M}}$, where $\beta_k$ represents the Levenberg-Marquardt parameter which is a scalar quantity that changes during optimization and ${\bf I}_{{\bf N\times M}}$ is the identity matrix. The gradient descent method and the GN method are combined in the LM algorithm. When the parameters are far from their ideal value ($\beta_k$ increases) the LM process conducts as a gradient-descent method, while it works as the GN method when the parameters are close to their optimal value ($\beta_k$ decreases) ^[4,7,8,9,10]. Many researchers have expressed interest in Newton-type methods for solving inverse problems because of their rapid convergence for the well-posed problems. The LMM is known to have a quadratic rate of convergence under non singularity conditions ^{[6,11,12,13,14,15]}. Yamashita et al. ^[6], investigated the solution of a nonlinear system of equations ${\bf F}(x) = 0$ under the assumption $\left\|{\bf F}(x) \right\|$, which provides a local error bound, where the convergence rate is still quadratic when $\beta_k = \left\|{\bf F}\left({\bf x}^{k}\right)\right\|^{2}$. Khayat ^[12] has established the quadratic convergence of the LMM for the inverse problem of identifying a Robin coefficient ${\bf R}$ for the Stokes system in the case where ${\bf R}$ is a piecewise constant on some non-accessible part of the boundaryand the velocity of a given reference solution does not vanish on the boundary. In this case, the regularizing parameter is defined by $\beta_k = \left\|{\bf U}\left({\bf R^{k}}\right) - {\bf Z^\eta}\right\|^{2}$, where ${\bf Z^\eta}$ is the noisy observed data.

Elasticity imaging is a relatively new medical technique used to detect several pathologies and especially cancerous tumors. These pathologies are known to affect the elastic properties (elastic modulus, Poisson's ratio and stiffness, $\dots$, etc.) of soft tissues.

Many authors have dealt with the elasticity imaging inverse problem (EIIP). Mei et al. ^[16] have estimated the elastic modulus from surface displacements during multiple observations. Raghavan et al. ^[17] have solved the equilibrium equations using finite difference schemes to recover elastic properties. Doyley et al. ^[18] applied a modified Newton-Raphson method. A variational method based on error functional decomposition was applied by Constantinescu ^[19] for anisotropic elastic body. Oberai et al. ^[20] reconstructed the identification parameter using a first-order adjoint method. Jadamba et al. ^[21] have reconstructed the Lamé parameters using a conjugate gradient trust-region technique. Arnold et al. ^[22] have utilized a numerical clustering procedure to identify the Young's modulus. Abdelhamid et al. ^[23] have investigated the identification problem of reconstructing the modulus of elasticity using the nonlinear conjugate gradient method. Mohammadi et al. ^[24] have used a statistical technique combined with a fixed-point algorithm. In this study we introduce an interesting and rapid converging method (the LMM) for solving the inverse problem of the elasticity imaging inverse problems. This method has the particularity to transform a nonlinear and a non-convex optimization into a convex one. Recently, the LMM is used in a closely related problems in the field. Indeed, Raja et al. ^[25] have combined the LMM with artificial neural networks to study the thermal radiation and Hall effect on boundary layer flow. Shoaib et al. ^[26] have used the same method to study the influence of activation energy on the Third-Grade Nanofluid flow. In the following, a mathematical treatment of the LMM method and an exhaustive numerical study are done. A realistic examples are treated using the proposed procedure.

2.   Mathematical formulation

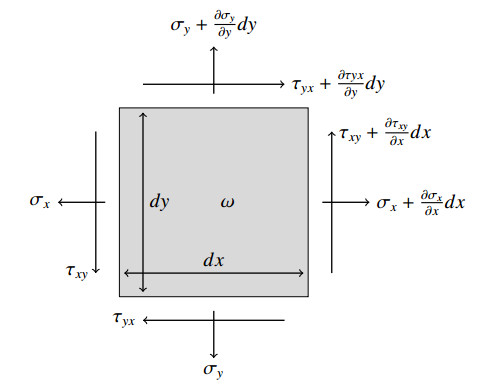
Worldwide, about 19.3 million new cancer cases, where 18.1 million of them excluding nonmelanoma skin cancerand almost 10.0 million cancer deaths occurred in 2020 ^[27]. It has estimated that about 18.1 million new cancer cases recorded and 9.6 million cancer deaths in 2018, across 20 world regions ^[28]. In the literature the soft tissue can be modeled as an incompressible, isotropicand continuous elastic object. The linear elasticity system is introduced to simulate the external and tractional forces on the soft tissue. In this study, the Young's modulus ${\mathcal{E}}$ is defined as a function of the position $(x, y)$ and Poisson's ratio is a given constant $\nu$ ($\nu \approx 0.48$). Reconstructing ${\mathcal{E}}$ of the elasticity imaging inverse problem is important for characterizing the complex mechanical behaviour of the soft tissue. We derive the basic equations for the theory of elasticity. A free body diagram (FBD) is a diagrammatic depiction of a single body or a subsystem of bodies that is separated from its surroundings and depicts all the forces operating on it as shown in Figure 1.

Let $\omega$ be an infinitesimal element ^[29,30], the FBD of $\omega$ is represented in Figure 1 and the stresses components are shown as positive. Summation of the forces in the $x$ and $x + dx$ axes at equilibrium are introduced as follows:

we do the same to the $y$ and $y + dy$ axes:

We denote by $f_x$ and $f_y$ the body forces in $x$- and $y$-axes which are generally assumed to be positive when acted along the positive axes, simplifying Eqs (2.1) and (2.2) we derive the basic equations of the theory of elasticity bellow

The stresses-strains relationship (for an isotropic material) is defined by

where $(\sigma) = (\sigma_{x}, \sigma_{y}, \tau_{x y})^{T}$ denotes the stress and $(\varepsilon) = (\varepsilon_{x}, \varepsilon_{y}, \gamma_{x y})^{T}$ is called small strain tensor:

Where, $\boldsymbol{u} = (u, v)$ represents the displacement field. Here, Eq (2.5) equivalent to

An approximation of the plane stress situation can be used to approximate the body's deformation, for this reason we take the material property matrix $D$ as follow

Where, $\mathcal{E}$ and $\nu$ are the Young's modulus and the Poisson's ratio, $\rho_{1}$ and $\rho_{2}$, are given constants depend on $\nu$.

2.1.   Direct problem

A tumor can be identified by investigating the elastic properties of the soft tissue such as Young's modulus and Poisson ratio from a given measurements. The following forward system of partial differential equations describes the response of an elastic object, when the external body forces and traction are applied to the boundary. Let $\Omega \subset {\mathbb R}^d$, for $d = 2, 3$, be an open bounded and connected domain such that $\partial \Omega = \Gamma_{i} \cup \Gamma_c$. Consider the following elasticity problem with essential (Dirichlet) and natural (Neumann) boundary conditions, governing the displacement $\boldsymbol{u} = (u, v)$ in $x$ and $y$ directions when the body forces $\boldsymbol{f} = (f_x, f_y)$ are applied to $\Omega$:

On the section of the boundary designated by $\Gamma_i$ (left, right and top), the traction vectors $\boldsymbol{q} = (q_x, q_y)$ are specified as Neumann boundary conditions, ${\bf n} = \left(n_{x}, n_{y}\right)$ its unit outward normal, while $\Gamma_c$ (bottom) is taken as constant Dirichlet boundary condition. Young's modulus ${\mathcal{E}}$ is considered as a function of location $\mathcal{E}(x, y)$ and Poisson's ratio is given as a constant (i.e., $\nu = 0.48$). The test function space, represented by ${\bf W}$, is defined by

To determine the weak formulation of the linear elasticity Eq (2.8), we apply the weighted residual method by multiplying Eq (2.8) by a test function and integrate over $\Omega$, such that:

By utilizing the Green's identity, using the integration by parts for the first term of the Eq (2.10) and using the boundary conditions we get:

The variational formulation of Eq (2.8) can be rewritten as follows:

Finally, using Eqs (2.6) and (2.7), the forward problem can be solved to find the displacement field $(u, v)$:

The body deformation represents the solution of the forward problem to find the displacement field on the problem domain. This deformation helps in solving the elasticity imaging inverse problem of identifying the elastic properties from the available measurements on subdomain of the problem.

3.   The Levenberg-Marquardt method

Let $\mathcal{X}$ and $\mathcal{Y}$ two Hilbert spaces, $\boldsymbol{J}: \mathcal{D}(\boldsymbol J) \subset \mathcal{X} \longrightarrow \mathcal{Y}$. Consider the system of nonlinear equations as a continuously differentiable function:

Assume that Eq (3.1) has a solution set $\mathcal{K}^*$ that is not empty. The system (3.1) may not have a solution, i.e., $\boldsymbol{J}(x)$ is not necessarily invertible. To remedy this, we replace Eq (3.1) by the following minimization problem:

The LMM is a Newton type technique for solving nonlinear least squares problems ^[4,8,9,10]. Particularly, LMM is a kind of GN technique for reducing a least squares cost $\dfrac{1}{2}\| \boldsymbol{J}(x) \|^{2}$. In its purest form, the GN technique effectively takes in each iteration:

where the direction of descent $d^k$ is

As in the GN method, the operator $\nabla \boldsymbol{J}\left(x^{k}\right) \nabla \boldsymbol{J}\left(x^{k}\right)^{\prime}$ is not always non-singular. So, the matrix is substituted by the following positive definite matrix:

Here $\mathcal{S}^k$ is the identity matrix $I$ multiplied by $\beta_k$ ($\mathcal{S}^k = \beta_k I$) which is selected as a positive multiple and it is chosen so that the modified matrix is always non-singular. This method has been widely used because of its simplicity. It is used also to have a quadratic convergence rate under some suitable hypothesis.

Remark 1. This is equivalent to the problem of unconstrained minimization:

where $\mathcal{O}^{k}: \mathcal{X} \longrightarrow \mathbb{R}$ is a strictly convex function defined by:

3.1.   Regularization approach of the elasticity imaging inverse problem

First we must define the set of admissible coefficients set for $\mathcal{E}$:

where $\mathcal{E}_{0}$ and $\mathcal{E}_{1}$ are two positive constants.

We are concerned in this section with the inverse problem of identifying $\mathcal{E}$ on $\Omega$ from measurements available on $\Gamma_i$ :

For analyzing inverse problems, the usual output least-squares approach is:

We assume the noise level in the observation data $z^\eta = (z_u, z_v)$ of the true solution $\boldsymbol{u}$ of the system (2.8) is of order $\eta$. Hence

where $\tilde{\mathcal{E}}$ is the exact solution of Eq (3.6). We transform the linear elasticity imaging inverse problem of identifying Young's modulus $\mathcal{E}$ to the following stable minimization with Tikhonov regularization,

where $\Vert \mathcal{E}-\tilde{\mathcal{E}} \Vert^2_{L^2(\Omega)}$ is the Tikhonov regularization term and $\beta$ is the regularization parameter. The LMM iteration is obtained by following the formality as explained above.

3.2.   Sensitivity problem

We assume that the identification parameter $\mathcal{E}(x, y)$ is perturbed by a small amount $\mathcal{E}+\delta\mathcal{E}$, where $\delta\mathcal{E}$ can be any direction in $L^{\infty}(\Omega)$.

and

Let $(u^{1}, v^{1})\equiv(u^{\prime}(\mathcal{E}) \delta\mathcal{E}, v^{\prime}(\mathcal{E}) \delta\mathcal{E}) \in L^{2}(\Omega)\times L^{2}(\Omega)$ the Fréchet derivative at direction $\delta\mathcal{E}$ of the forward solution $\boldsymbol{u}(\mathcal{E}) = (u(\mathcal{E}), v(\mathcal{E}))$ in Eq (2.8). Abdelhamid et al. ^[23] obtained the sensitivity problem of elasticity as follows:

For the sensitivity Eq (3.11), we may describe the relationship between stresses and strains as follows:

The right-hand side of Eq (3.11) can be rewritten similarly:

Now, we'll complete the sensitivity problem's variational formulation:

We get the following result as we use the integration by parts for the second term of (3.14):

After that,

Using Eqs (3.12) and (3.13), the Eq (3.16) can be rewritten in the following manner:

where $D_{\sigma}$ refers to the material property of the applied plane stress condition.

3.3.   Adjoint problem

The Lagrangian multipliers $\mathcal{L}$ are introduced first in this section. Consider the following problem:

The state equations in the $x$ and $y$ directions are represented by $c_x$ and $c_y$, respectively. Consequently, the Neumann boundary conditions on $\Gamma_i$ corresponding to $c_x$ and $c_y$ are defined by $B.C_{cx}$ and $B.C_{cy}$, respectively. The Lagrangian may be shown as:

The Lagrange multiplier is represented with $(\lambda_u, \lambda_v)$. To find the adjoint equation, the differential of $\mathcal{L}$ must be computed:

and

By subtracting Eq (3.21) from Eq (3.20) and two times utilizing integration par part we obtain the adjoint problem:

where $(u, v)$ solves the original forward problem of elasticity (2.8) and $\lambda_0$ is the initial condition. The relationship between stresses $\sigma^*$ and the adjoint solution can be shown as follows:

Using the conditions to the limits in Eq (3.22) and the relation Eq (3.23), we obtain the variational formulation of Eq (3.22):

4.   Numerical procedure

This section explains how to use the LMM to solve the proposed optimization inverse problem. Table 1 introduces the specifications of different algorithms compared with the LMM in terms of the convergence and computation complexity.

According to the study done above, the different steps for computing the Young's modulus $\mathcal{E}(x, y)$ are given by the following algorithm:

The Young's modulus $\mathcal{E}(x, y)$ can be reconstructed using this process. For each iteration with $\mathcal{E}(x, y) = \mathcal{E}(x, y)^k$ the algorithm necessitates the resolution of the forward problem, sensitivity problem and the adjoint problem then calculate the regularization parameter $\beta_k$ and the descent direction $d^k$, next updating the identification parameter $\mathcal{E}$, finally we verify the stopping criteria, the estimated parameter must be accurate enough or satisfies the discrepancy principle.

5.   Numerical results

Let us consider a two dimensional square domain $[0, 1] \times [0, 1]$ with $\Gamma_c = [0, 1]\times\{y = 0\}$ and $\Gamma_i$ is the remaining part of the boundary $\partial\Omega$. In order to identify a smooth $\mathcal{E}(x, y)$, we give numerical examples to prove our study's effectiveness. All calculations are made using Freefem++4.6 ^[31]. CPU: Intel(R) Core(TM) i7-4510U CPU @ 2.00GHz, 2601 MHz, 2 cores, 4 processors, Memory: 8 GB. We generate data $z^{\eta} = (z_u, z_v)\in L^2(\Omega)$ experimentally by:

where $\eta$ is the amount of noise and $\xi$ is a uniformly distributed random variable in $[-1, 1]$, then using the FreeFem function Rand1($\cdot$) we generate this random variable. The exact solution is synthetically generated using the fundamental of elasticity problem:

The body forces $\boldsymbol{f} = (f_x, f_y)$ and the traction $\boldsymbol{q} = (q_x, q_y)$ applied on its boundaries can be derived directly on borders $\Gamma_i$.

5.1.   Reconstruction of the constant Young's modulus

Due to changes in sample composition and test technique, Young's modulus might vary somewhat. The constant values presented here ^{[32,33,34,35]} are approximated and solely intended for relative comparison.

Example 1. We consider a constant Young's modulus for various materials such as Aluminum, Titanium, $\dots$, etc.

Table 2 presents the reconstruction of $\mathcal{E}$ at a number of elements $\mathcal{NE} = 1800$, $\eta = 1\%$ for different materials at constant initial guesses. The obtained results show the rapid convergence and the precision of the introduced procedure.

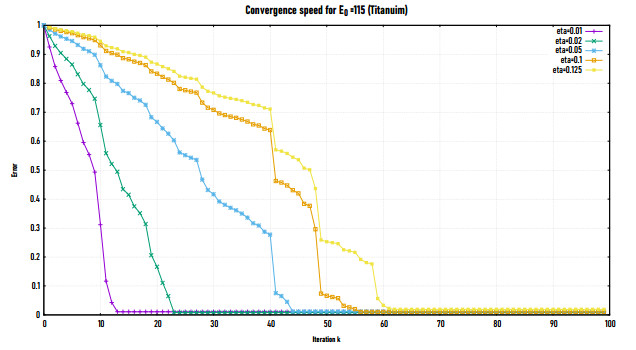
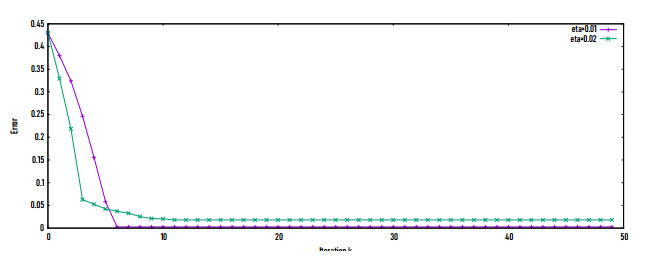
Figure 2 shows the convergence speed of the proposed LMM at different levels of noise $\eta$ in the measurement data for the Titanium material with initial guess $\mathcal{E}_0 = 115$. Figure 3 introduces the convergence speed at $\eta = 1\%$ and $\eta = 2\%$ for the Nylon material with initial guess $\mathcal{E}_0 = 2.5$. It is observed that the best convergence speed is obtained for low level of noise in the data. At large level of noise, the proposed algorithm takes more than 50 iterations to get the optimal solution of the reconstructed parameter. Table 3 presents the decline of the relative error $e_\mathcal{E}$, until the convergence occurs at the 13th iteration.

5.2.   Reconstruction of the variable Young's modulus

Example 2. The exact identification of the Young's modulus is defined by:

In this Example the initial guess is given by $\mathcal{E}^{0} = 3.3$.

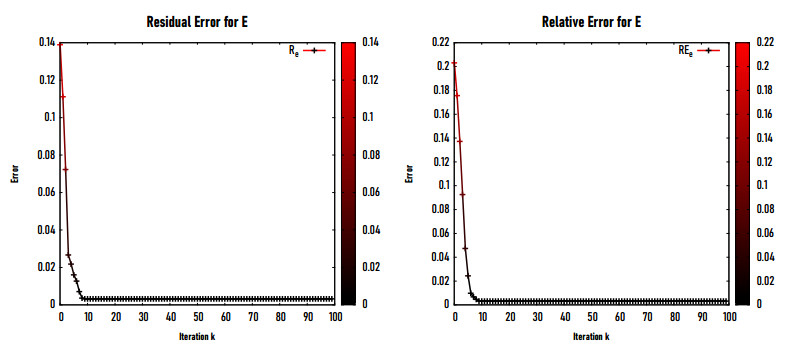
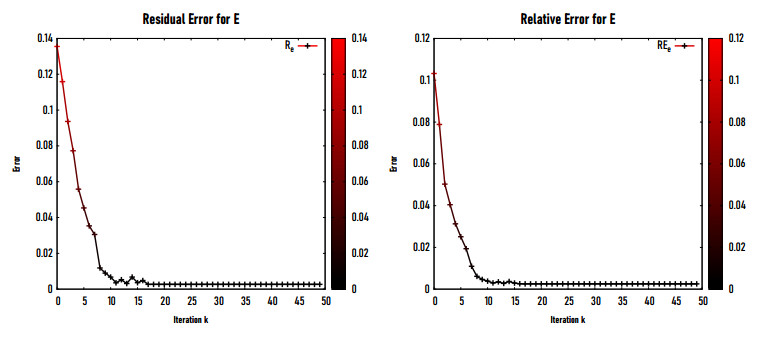
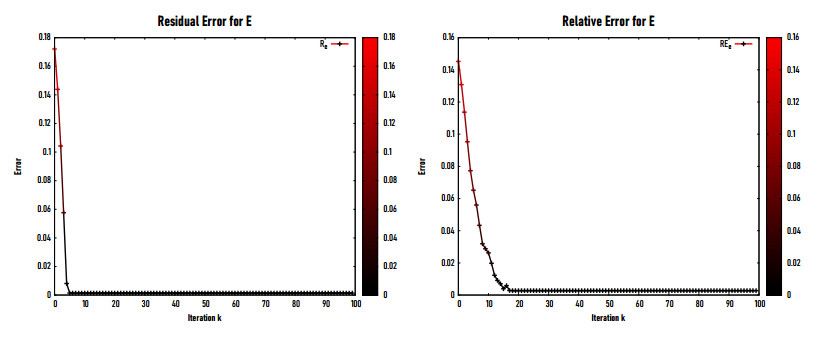
Table 4 presents the variation of the relative error $e_{\mathcal{E}}$ with respect to the noise level in the data. We notice that as the amounts of noise $\eta$ rises, $e_{\mathcal{E}}$ rises as well at chosen $\mathcal{NE} = 1800$. However, this relative error remains interesting upto $\eta = 1.5\%$. We also remark on this table that the solution of the inverse problem fails for $\eta > 2.75\%$. Figure 4 shows the variation of the residual error (left) and the relative error (right) with respect to the number of iterations $k$. We remark that these errors suddenly decrease upto $k = 10$ and then they remain almost constant and independent of $k$.

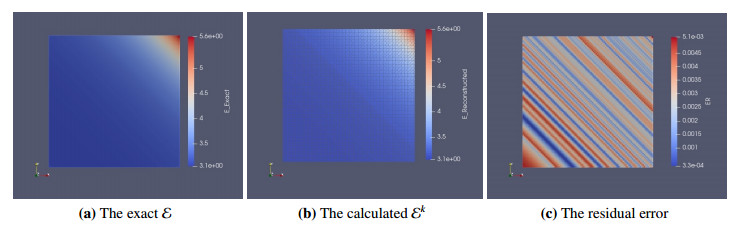
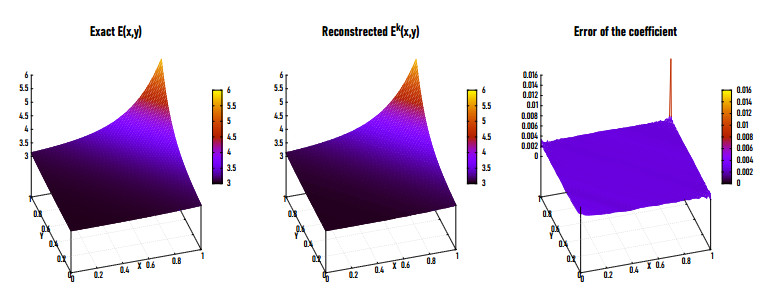
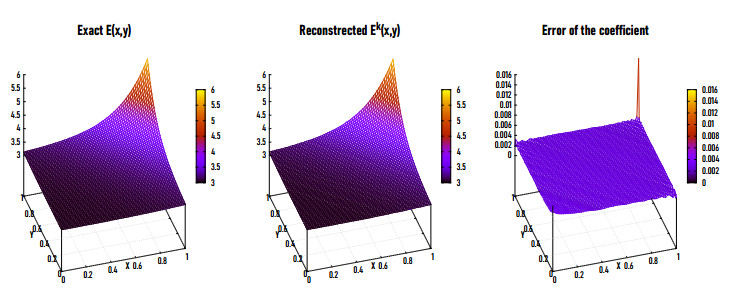
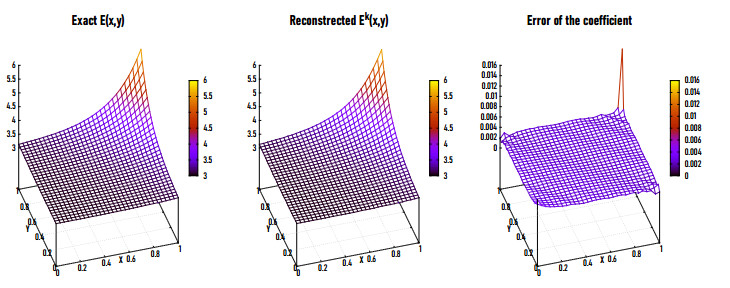
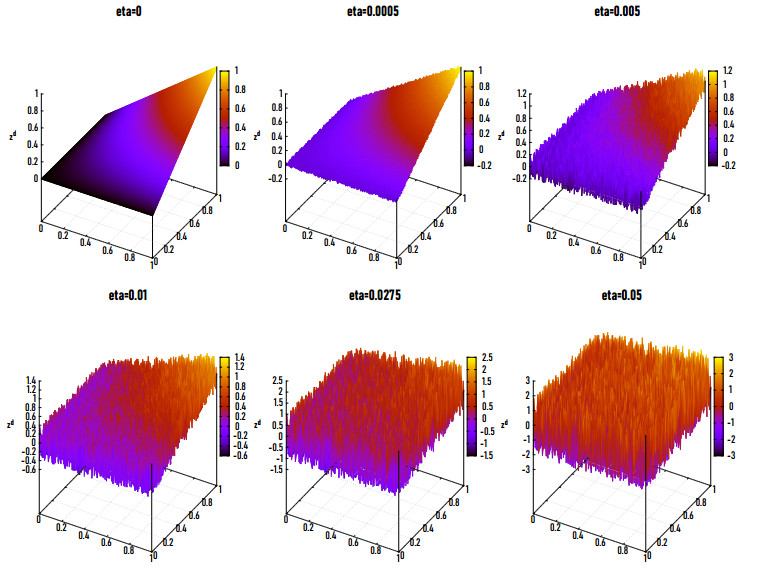
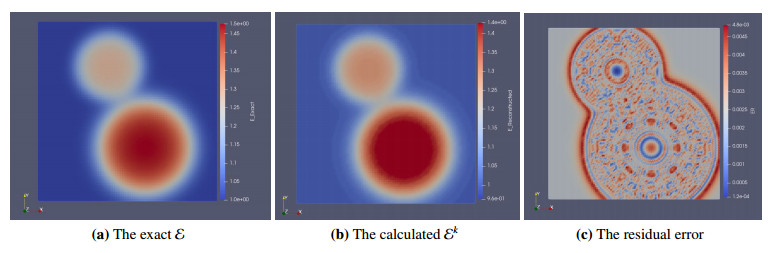
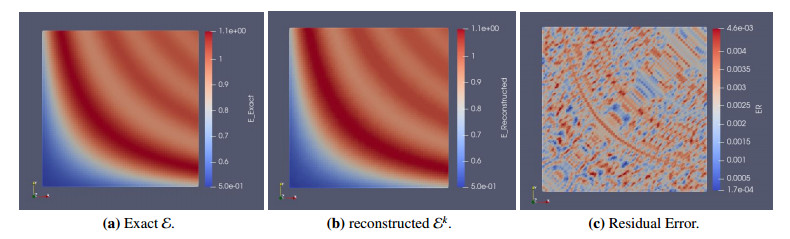
Figures 5(a), (b) and 6 show the exact (left) and reconstructed (middle) $\mathcal{E}^k$ for Example 2 in 2D and 3D at $\eta = 0.5\%$ and $\mathcal{NE} = 20,000$. The obtained results are satisfactory at $k = 9$, where the relative error $e_\mathcal{E} = 0.0032$. Figures 5(c) and 6 (right) show the residual error of the coefficient $\mathcal{E}^k$. It is observed that the relative error grows at a part of the boundary of the problem domain. We have also examined the procedure for different values of $\mathcal{NE}$. Figures 7 and 8 show the exact (left) and reconstructed (middle) $\mathcal{E}^k$and residual error (right) at $\eta = 0.5\%$ for $\mathcal{NE} = 9800$ and $1800$ respectively. Figure 9 represents the variations and sensitivity of the measured data $z^{\eta}$ with respect to the noise level.

Example 3. The exact coefficient is given by:

with initial guess $\mathcal{E}^0 = 1.1.$

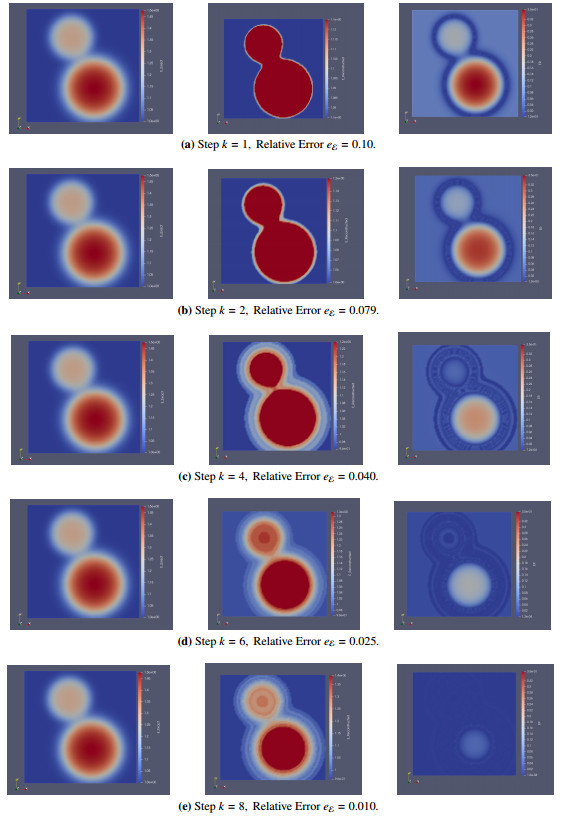
Table 5 shows the numerical convergence for $\mathcal{E}^k$ with respect to the number of iterations $k$. We observe that the relative and the residual errors drop rapidly until the 8th iteration. Then they decline slowly as shown in Figure 10. Figure 11 depicts the exact (left), reconstructed (middle) $\mathcal{E}^k$ and residual error (right) for $\eta = 0.5\%$ at iterations $k = 1, 2, 4, 6\; {\rm{ and }}\; 8$.

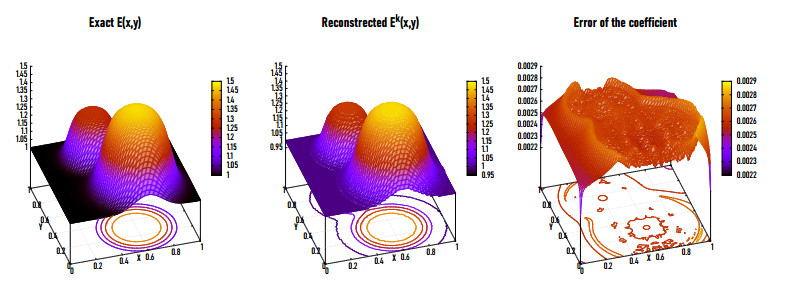
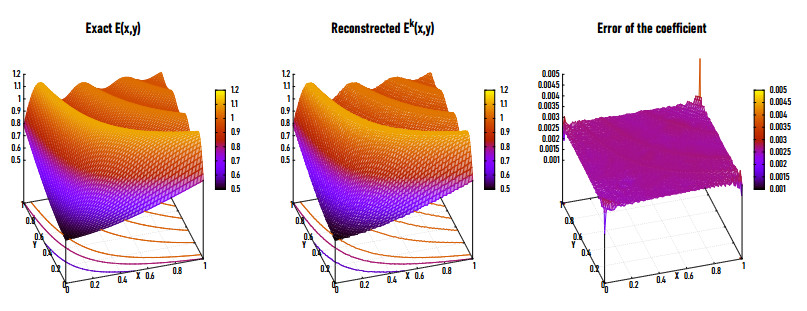
Figures 12(a), (b) and 13 show the exact (left) and reconstructed (middle) $\mathcal{E}^k$ for Example 3 in 2D and 3D at $\eta = 0.5\%$ and $\mathcal{NE} = 20,000$. It is observed that the reconstructed modulus of elasticity $\mathcal{E}^k$ has a very satisfying relative error ($e_\mathcal{E} = 0.0025$) at $k = 18$. Figures 12(c) and 13 (right) show the residual error of $\mathcal{E}^k$ for Example 3 in 2D and 3D. Jadamba et al. ^[36] have implemented both first and second-order adjoint methods and the Newton method with a simple backtracking line search method for solving Example 3. They found that it is possible to achieve a good precision at the 139th iteration (for the first-order adjoint method) as well as at the 49th iteration (for the second-order adjoint method), then decreased very slowly with increasing $k$. These results are in a good accord with the literature. Furthermore, Abdelhamid et al. ^[23] implemented the nonlinear conjugate gradient method for solving this example observing that at the first 25th iteration. The relative and residual errors are decreasing rapidly with increasing $k$, after which they decrease very slow to reach the minimizer at $k = 34$ with relative error $e_\mathcal{E} = 0.0128$. It is found that the LMM gives better results in less number of iterations $k$.

Example 4. The modulus of elasticity coefficient $\mathcal{E}(x, y)$, body force function $\boldsymbol f(x, y)$ and boundary conditions are as follows:

where $\partial\Omega = \Gamma_1\cup\Gamma_2$, $\Gamma_1$ represents the bottom and left sides of the border and $\Gamma_2$ represents the top and the right edges.

Remark 2. The $\operatorname{sinc}$ function also called the "sampling function" defined as following:

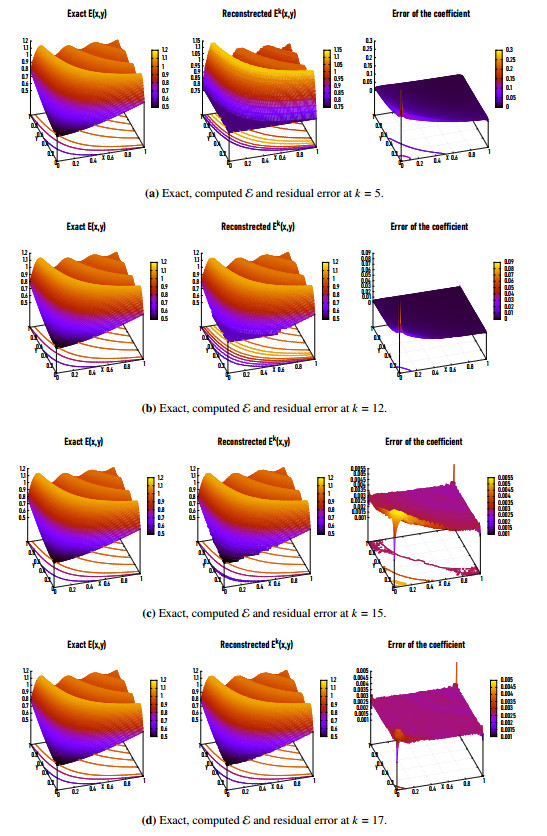
For this example, the suggested method is tested with $\eta = 0.5\%$ and $\mathcal{NE} = 20,000$. Table 6 shows that the relative error $e_\mathcal{E}$ slowly decreases with increasing $k$. We reach to the minimizer and the stopping criteria is satisfied at $k = 19$. Figure 14 shows that the relative error $e_\mathcal{E}$ reduces rapidly as the number of iterations $k$ increases for the first 10 iterations and then slowly approach to the minimizer.

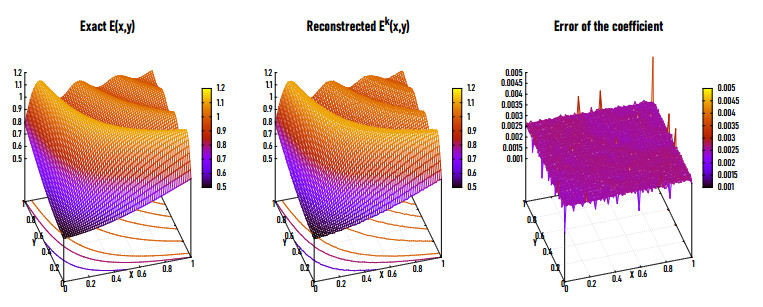
Figures 15(a), (b) and 16 represent the exact (left) and the reconstructed (middle) $\mathcal{E}^k$ for Example 4 in 2D and 3D respectively for $\eta = 0.5\%$ and $\mathcal{NE} = 20,000$. Figure 17 shows the same representation for $\mathcal{NE} = 9800$. The proposed method represents a reasonable results at $k = 19$ for which the relative error is $e_\mathcal{E} = 0.0028$. Figures 15(c) and 16 (right) introduces the residual error of $e_\mathcal{E}$ for Example 4 in 2D and 3D. It is observed that the $e_\mathcal{E}$ grows at the corners of the boundary due to the influence of the gradient computations.

Figure 18 gives a graphical representation of the exact, the reconstructed $\mathcal{E}^k$ and the residual error at $k = 5, 12, 15\; {\rm{ and }}\; 17$, the method converges rapidly to the solution in the first 10th iterations, then gives a good reconstruction $\mathcal{E}^k$ in the $19$th iteration as shown in Figures 15–17 and Table 6. Table 7 introduces a comparison of the relative $e_\mathcal{E}$, residual error $E$ and the number of iterations $k$ using the present work compared to that of Abdelhamid et al. ^[23].

6.   Conclusions

In this paper we develop a theoretical framework for the inverse problem of identifying the modulus of elasticity ${\mathcal{E}}$ at some measurement data on the boundary. The inverse problem is discretized using the finite element approach. The optimization problem of reconstructing the elastic modulus (Young's modulus) of elasticity imaging inverse problem is formulated. The identification parameter is defined on the domain and can be identified from given measurement data at some parts of the boundaries. The LMM method is used to treat this ill-posed inverse problem and the non-convex minimization is changed into a convex one. The mathematical formulation for the forward problem of elasticity is introduced in the 2D plane, where $\Omega \subset R^{d}, d = 2, 3$. The descent direction $d^{k}$ is introduced from the solution of the sensitivity and adjoint equations. The obtained results from the identification problem of the constant and variable identification parameter for various real materials are satisfactory. The obtained results show the accuracy and efficiency of the proposed algorithm. The obtained results of the 2D and 3D view for the reconstruction of the Young's modulus are compared with those obtained from the exact one. At different levels of noise, the proposed algorithm is implemented and show efficient and accurate results upto $\eta = 2.75\%$.

Acknowledgments

The work of Talaat Abdelhamid is supported by Science, Technology & Innovation Funding Authority (STDF) under grant number 39385.

Conflict of interest

The authors declare that there is no conflict of interests regarding the publication of this paper.