1.
Introduction
The COVID-19 pandemic caused by the novel coronavirus (SARS-CoV-2) has received increased attention from both scientists and public health policymakers worldwide compared to previous epidemics such as the Spanish flu and MERS [1]. Indeed, since the first report of SARS-CoV-2 in late 2019, many governments have implemented stringent restrictions (both at the start of the pandemic and repeatedly throughout) to limit the spread of the virus. These include general measures such as the ban of mass gatherings, travel restrictions, lockdowns and curfews, but also individual level measures such as improved personal hygiene, social distancing, and face mask wearing [2,3,4,5,6,7]. A combination of the rapid propagation of SARS-CoV-2, the related symptoms, the resulting deaths, and the responses of public bodies across the world have inspired numerous studies into understanding the biology of the pathogen [8,9,10,11,12], the numerous COVID-19 epidemic outbreaks [13,14,15], and damages to health, social and economic activities among other aspects of human societies [16,17,18,19].
To inform and guide health policies, researchers use two general classes of models to understand the dynamics of epidemic outbreaks: phenomenological (regression) models and mechanistic (compartmental) models [20]. The use of compartmental mathematical models, which currently prevails for SARS-CoV-2 data [21], allows for the explicit structuring of a target population into epidemiological states relevant to the studied pathogen and its effects on exposed and infected patients. One major advantage of these compartmental models is the possibility to structure the target population based on the attitudes of individuals regarding measurements such as personal hygiene, social distancing, face mask-wearing, and vaccination. As a result, these models can be used to simultaneously model the dynamics of a pathogen's spread and the opinions and attitudes related to prophylactic measures [22,23,24,25,26,27,28,29,30,32,33,91]. Unfortunately, many of these models only incorporate vaccine opinions. However, the dynamics of opinion and attitudes regarding other measures and their impact on disease dynamics can substantively differ from the dynamics of vaccine opinions, mainly because these behaviors demand stronger engagement in the required frequency of opinion affirmation [34]. For instance, in the context of the COVID-19 epidemic, individuals needed to regularly wash their hands when the environment was full of potentially contaminated areas, wear face masks when traveling to any shared public space, and maintain the minimum social distance when interacting with others. In the context of insignificant variations of attitudes towards prophylactic measures, the use of approaches that disregard the dynamics of such attitudes when building disease models remains sound. However, significant shifts in attitudes toward prophylactic measures usually follow the outbreak of a disease [35,36,37,38], and a failure to account for the feedback of opinion/attitude dynamics on modeled disease dynamics reduces the reliability of findings and policies based on such models. In addition to these inherent changes in opinions, once a disease outbreaks, the wide accessibility of populations to mass media, in particular social media, can induce quite sharp variations in the distribution of opinions and attitudes because of a rapid spread of evidence, as well as fake pieces of information on the disease, the underlying pathogen, the related symptoms, the advocated barrier measures, and any available vaccines [39,40]. Therefore, integrating opinion dynamics in mathematical models for disease dynamics is a major point to consider when building models to inform public health policies.
Aside from the largely studied dynamics of the spread of SARS-CoV-2, many studies have reported on the adherence of exposed populations to prophylactic measures [41,42,43,44,45,46,47,48,49,50]. The potential or actual effects of the implementation of barrier measures on the dynamics of the spread of SARS-CoV-2 have also been investigated, to some extent [51, 52, 53, 54, 55, 56, 57, 58, 59]. In addition, many works have integrated attitudes toward vaccines in either mechanistic or network models describing COVID-19 dynamics [23,53,60,61,62,63,64,65]. However, so far, few studies have considered information on adherence to barrier measures into the mechanism describing the propagation of the pathogen within a population [52,55,66,67,68,69].
The SIR-Opinion model of Tyson et al. [34] is a simple disease-opinion dynamics model appropriate for joint modeling of COVID-19 dynamics and related prophylactic opinions over a short period. For sound modeling of COVID-19 data along with the levels of adherence to prophylactic measures, we extend the SIR-Opinion model to account for the partial detection of infected individuals. Indeed, only a small amount of SARS-CoV-2-infected individuals are generally identified and reported, mainly because of the prevalence of asymptomatic infectious [70,71,72]. For inference in the resulting SIQR-Opinion model, we consider the hybrid modeling technique introduced by Tovissode et al. [20], where the identified SARS-CoV-2 infected individuals are first modeled using a growth curve, and the result is added into the SIQR model framework to avoid identifiability issues when fitting the model. For illustrative purposes, we use the proposed model to (i) determine the best growth curve to adjust for the number of infected individuals infected and (ii) evaluate the effects of prophylactic attitudes on the dynamics (as measured by the reproduction number) of COVID-19 in West Africa.
2.
Materials and methods
2.1. Model framework
In this study, we developed a two-stage estimation model. The first is an extension of a disease compartmental model. However, instead of estimating the infected individuals, I(t), with this compartmental model, we opted for a growth model.
2.1.1. The Disease Dynamics Models
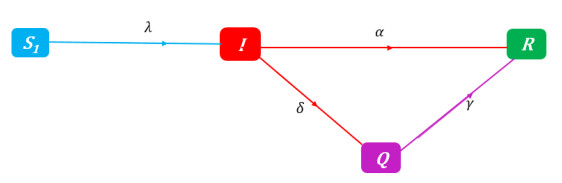
Following Hethcote et al. [73], a susceptible–infectious–quarantined–removed (SIQR) model is used to model the COVID-19 dynamic in West Africa. The four compartments considered in this model are the susceptibles (S), the infectious but undetected individuals (I), the quarantines (Q), and the removed (R). The quarantine state Q stands for the detected active cases of SARS-CoV-2 infected individuals. We assumed neglected births, net migrations, and the natural mortality rates associated with each compartment, given the short period of each considered COVID-19 wave. At a given time t⩾0, the population size is given by:
The SIQR model is described at time t by the following system of differential equations:
with the non-negative initial conditions, S(0) = S0, I(0) = I0, Q(0)=Q0, and R(0) = R0 where (S0,I0,Q0,R0)T∈[0,∞)4.
In System (2.2), α is a rate that measures the removal of non-detected infectives, δ is the rate of detecting new cases of infected people, γ stands for the removal of quarantined people, and the force of infection is λ(t)=βI(t)N(t)−Q(t), where β is the rate of contacts sufficient for SARS-CoV-2 transmission.
2.1.2. The Disease-Opinion Dynamics Models
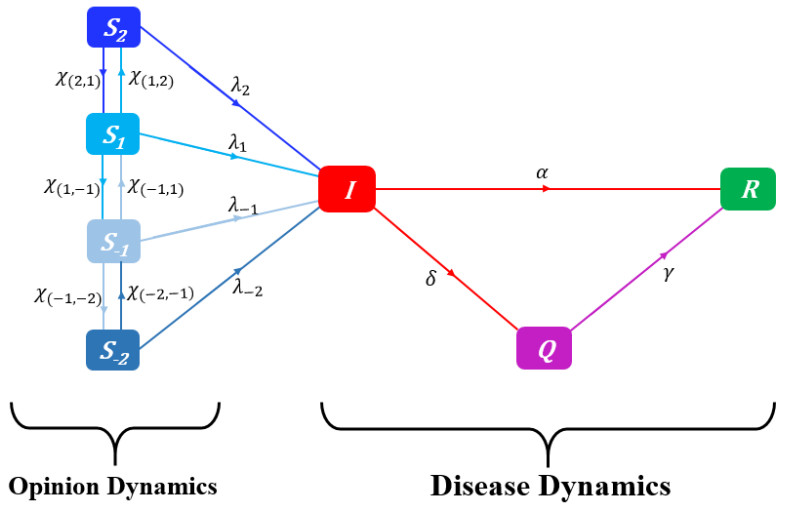
Tyson et al. [34] identified four levels of prophylactic behavior (use of the mask, physical distance, hand hygiene, coughing hygiene, and avoidance of touching the face) represented by the following spectrum of prophylactic attitudes/opinions:
Since the infected do not really have an opinion and the removals are not heard since they have recovered from COVID-19, we considered just the opinion of the susceptible classes. From this spectrum, we have i cases among susceptible individuals, Si symbolizes the susceptible with attitude i for any opinion i∈O: S−2 represents individuals with the highest degree of prophylactic behavior (and thus the least susceptible to disease) and S2 corresponds to individuals with the lowest degree of prophylactic behavior (and thus the most susceptible to disease). Individuals in the middle of the spectrum, S−1 and S1, exhibit moderate levels of prophylactic behavior. At any time t, the identity S(t)=∑i∈OSi(t) represents the susceptible population. The exchange of information about the prevalence of the disease, as well as government control measures, can change an individual's opinion. It is to this end that Tyson et al.[34] insert the "impact" and "amplification" effects into their model, whereby attitudes/opinions are updated in response to either biased assimilation or confirmation bias caused by contact between susceptible individuals. The rates and directions of mutual opinion effects determine the dynamics of opinions in the susceptible population in this framework. They defined the "influence function" as the rate ωi at which a sensitive individual Si influences the rest of the susceptible population. Tyson et al. [34] incorporated linear and saturating impacts wi as functions of the proportion of the infectious population (I). In terms of influence directions, when an Si individual impacts an Sj individual, the affected individual's attitude is updated, and we have one of the two cases: opinion amplification with probability ϕ or no opinion amplification with probability 1−ϕ. Opinion amplification appears to express the tendency to become more confident in one's opinion after interacting with like-minded individuals. It should be noticed that in the sensitive population, changes in opinion are reflected by the rates χ(i,j)(t) of outgoing flows (opinion change i→j), which are defined as follows:
Since the prevalence of the disease drives a shift in the susceptible population, we assume that the influence functions, ωi=ωi(I), vary with the proportion of infected I in the population. To investigate a range of potential epidemic responses, [34] defined four plausible influence functions. As shown in Table 1, the functions considered are linear, saturating, fixed-order saturating, and reverse-order saturating ωi(I) functions. As ωi(I) changes during the epidemic, these functions serve to either increase or decrease the influence of each subpopulation Si. In Table 1, each function ωi(I) starts at the same point, ωi(0)≡0, and "I" comes from equation (2.8). The parameters in Table 1 are described in Table 2. The SIQR model is further detailed in Figure 2. The following system at time t describes the SIQR-Opinion dynamics model:
with the non-negative initial conditions Si(0)=S0i,I(0)=I0, Q(0)=Q0, and R(0)=R0 where (I0,Q0,R0)⊤∈[0,∞)3, and S0i≥0 for i∈O.
In the system (2.4), we assume that a person's attitude affects their susceptibility to infection and the force of infection for Si individuals has the form
where, for i∈O, βi is the rate of contacts sufficient for transmission for a Si susceptible. For simplicity, the infection rate is modeled as a function of attitude using a single parameter a>1 [34]. We assume:
where β0 represents the baseline infection rate, and each increase in prophylactic behavior results in a factor a discounting of the infection rate. In the system (2.4), the dots represent partial derivatives with respect to time (t), and the constant rate parameters of the model are described in Table 2. We allow the removal rate of quarantined people γt from Qt to be time-variable, as previously performed in [20] do, and it takes the logistic form.
This is reasonable when the reported positive cases per unit of time are supplemented by removals. To avoid identifiability problems, we followed the approach described by Tovissode et al. [20] to determine the infected.
2.1.3. Growth model
The growth curve that is fitted to the SARS-CoV-2 infected individuals in West Africa is developed in this section. Following Tovissode et al.[74], the number of infected persons in a target population has the following form:
where
is the number of cases detected at time t (i.e., the number of infected, detected, and isolated cases) and δ∈(0,1] is the detection rate assuming constant during the epidemic. In (2.9), C(t) represents the cumulative SARS-CoV-2 infected individuals and then the growth curve to be fitted. The generalized logistic model (GLM), also known as Richards' model, can improve the fit of SARS-CoV-2 data well since, for real-time outbreak prediction, this empirical function has made major marvellous coincidences with real SARS, Zika, and Ebola epidemic data [75,76,77]. Based on population biology, this model assumes an initial exponential growth phase that saturates as the number of cases increases due to ongoing control efforts and newly acquired human behaviors.
At time t, the dynamics of C can be represented as:
with ut=νω(t−τ), K>0 is the carrying capacity or maximum cumulative case incidence, ν>0 is a growth acceleration parameter, ω>0, the growth rate constant, and τ is a constant of integration determined by the initial conditions of the epidemic (see Tovissode et al. [20] for more information). The expression of the growth curves ˙C(t) and ¨C(t) can be found in Table A1 within the appendix.
2.1.4. Reproduction Number
We calculated the fundamental reproduction number, R0, to determine how the COVID-19 epidemic is impacted by introducing an opinion dynamic. The basic reproduction number is the expected number of secondary cases resulting from a single susceptible individual's infection. To calculate the control reproduction number of the model, we followed the Diekmann et al.[78] next-generation's approach.
At the start of the epidemic, we have S0=N0−1,I0=1,Q0=0,R0=0. The disease-free equilibrium point of the model is given by (S0,0,0,0).
At the infection-free steady state, I=R=0, hence S=N−Q.
Let M be the next generation matrix (NGM) for all new infections and T+Σ be the jacobian of the infection subsystem (2.11). The matrix transmissions T, the transitions matrix Σ, and the NGM M are the following:
The dominant eigenvalue of M is
The number of people in a population who can contract an infection from a single person at any one time is often referred to R. By multiplying the basic reproduction number by the proportion of the host population that is susceptible, one can get the effective reproduction number (R). Thus we have
Thus
2.2. Parameter estimation
The parameters of the system (2.3) are assumed to be known and constant, and they are derived from the literature [34] (Table 2). As for those of equation (2.4), some are assumed to be known and are extracted from [20] and [79]. To obtain the recovery rate γt, the logistic regression parameters in equation (2.15) are adjusted on the new removal Rt. Knowing the new infected case Yt and the active case Qt−1, logistic regression models with probability mass functions (pmf) are used to model the number of new removals (Rt):
where
with θ=(K,ω,ν,τ,σ,κ0,κ)⊤. In equation (2.14), we considered the number of known active cases Q0=0 at t=0.
The maximum likelihood (ML) is used to estimate the parameters K,ω,ν, and τ in (2.10). To do this, each new confirmed infected case Y1,Y2,⋯,Yn is given an appropriate statistical distribution with an expectation of λt=˙Ct and a dispersion parameter σ>0 [74]. The inference under Poisson, negative binomial and log-normal distributions was discussed.
Poisson distribution: Since we are dealing with the counts' incidence, Yt can be assumed to follow the Poisson distribution, and we have Yt∼ Pois (˙Ct) with pmf
The incidence case Yt has an expectation E[Yt]=λt and variance Var[Yt]=λt.
Negative binomial distribution: It can be assumed that Yt follows the negative binomial distribution as new confirmed cases are counts, and we have Yt∼NB(˙Ct,σ) with pmf
The expectation E[Yt]=λt and variance Var[Yt]=λt(1+σλt) are then established for the new detected case Yt.
Log-normal distribution: Since zero incidence cases are common in epidemic data, the logarithmic function is often applied to the shifted cases (Yt+1), and we consider the log-normal distribution assumption, where Yt+1∼LN(Yt+1,σ) with pdf
the mean E[Yt]=λt and the variance Var[Yt]=(λt+1)2(eσ2−1).
Let's consider two components ,ℓY(θ) and ℓG(θ), representing the log-likelihood function for new infected case Yt and new removal Rt, respectively. The conditional maximum likelihood estimates ˆθ of θ can be produced using an optimization technique to maximize the log-likelihood function ℓ [20]:
The maximum likelihood estimates of the components θY=(Ω,ω,ν,τ,σ)⊤ and θG=(κ0,κ)⊤ of the parameter vector θ=(θ⊤Y,θ⊤G′)⊤ can be produced by maximizing ℓY and ℓG, respectively. We consider the common deviance statistic used in generalized linear models to assess the goodness-of-fit of the binomial model associated with Rt and the log-normal models associated with Yt because both the binomial and the log-normal distributions are members of the exponential family [20]. The likelihood ratio statistic is considered while choosing the concise model that best fits the observed data.
2.3. Data source and study period
The sixteen countries of Western Africa (Benin, Burkina Faso, Cape Verde, The Gambia, Ghana, Guinea, Guinea-Bissau, Ivory Coast, Liberia, Mali, Mauritania, Niger, Nigeria, Senegal, Sierra Leone, and Togo) had been considered for this study. Information about these countries are in Table B1. Based on the latest United Nations estimates (worldometers.info), this region has a current population of approximately 5.16% of the world's population and includes nine of the 25 poorest countries in the world. The first case of Covid-19 in West Africa was recorded at the end of February 2020 (oecd). Implementation of prophylactic measures against the spread of COVID-19 in most West African countries began in March (Table B1). We considered the beginning of the pandemic expansion in West Africa (February 28, 2020) as our starting date for our data. The final date considered is February 23, 2021, which represents the last date before vaccine implementation in West Africa (Ghana received 600,000 doses on February 24, 2021, and Ivory Cost received 504,000 doses two days later (unicef portal)).
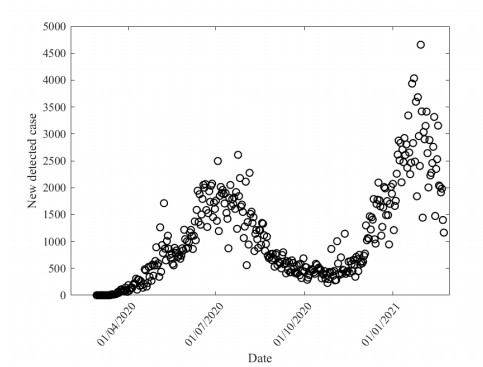
We aggregated the data of newly detected cases, population, recoveries, and death by date. As of February 24, 2021, there were approximately 4.19E+08 humans, among which 397826 were detected cases, 44958145 were recoveries cases, and 5314 were deaths in West Africa (Table B2). The newly detected cases and population data were obtained from the OWID data portal [80]. As for the quarantine recovery data, it was taken [81]. This period corresponds approximately to the first and second waves of the COVID-19 pandemic in West Africa (fig 3).
2.4. Data Analysis
2.4.1. Growth model
We fitted the Bertalanffy-Richards growth curve to Y′t 's new daily infections based on Poisson, negative binomial and log-normal distributions for each wave. The R software's optim function was used to maximize the log-likelihood. Using likelihood ratio tests, we additionally fitted Bertalanffy-Richards. We used the Arkaike Information Criterion (AIC) and the R2 values based on the cumulative detected case to pick the best model. To obtain the recovery rate of quarantined people γt, we used the R procedure glm [82] with the family specification "family = binomial(logit)". We integrate the quadratic interaction in the logistic model. The parameters K,ω,ν,τ,σ in Table 2 are estimated using the R software.
2.4.2. SIQR dynamics model
A recent study on the adherence of the West African population to prophylactic measures [83] revealed that there are individuals who support but do not apply the prophylactic measures and those who support and fully adhere and apply them. This is consistent with the -2, -1 attitude levels defined by [34]. The opinion parameters β0 in Table 2 are estimated using Matlab R2021a. We exclude 1 of the population and set S0=0.01∗N0 because COVID-19 rarely affects children and people living in rural areas in the majority of African countries. We then set S0i=zi∗S0 with zi being the population's susceptible class proportion in 2.3. According to PERC(2022) [83], z1=66, z2=24 (z1+z2=90), z3=5, and z4=5 (equitable distribution of the remaining 10% between z3 and z4) for wave1 and z1=63, z2=25 (z1+z2=88), z3=7, and z4=7 (equitable distribution of the remaining 14% between z3 and z4) for wave 2. We used the Matlab function datasample to estimate the initial conditions of each of the model's state variables. On the first day of the pandemic's expansion, we assume there was only one active person. We then define Q0 to equal 1. The integrated ODE45 function of Matlab was used to obtain the solutions of (2). The parameters K,ω,ν,τ estimated in R are used to find the new detected parameters in (2). The target of the fitting included finding the optimal set of parameter values that minimizes the root mean square differences between the new daily detected COVID-19 cases observed in West Africa and the new daily detected COVID-19 cases predicted from our model. This was done using the nonlinear least squares method in Matlab R2021a, with the function "fminsearchbnd". Since minimization in a multivariate framework uses starting values, we used a cross-validation technique to ensure both the explanative and predictive power of the model. We ran 1000 simulations of starting values considering 90% and 10% for training and test datasets, respectively. Considering 50 simulations, the starting values related to the minimum RMSE (RMSE1) were used to compute the minimum RMSE for the test sets (RMSE2). We found 375.13 and 244.10 for RMSE1 and RMSE2, respectively, for the first wave and 428 and 509 for wave2. Additionally, we determined the estimated parameters' 95% confidence interval.
3.
Results
At this stage, we numerically analyzed the model to assess the effect of prophylactic behavior on the COVID-19 dynamic in West Africa. Therefore, using estimated parameters and the initial circumstances of the model, we calculated the values of the effective reproduction number Rt, and the basic reproduction number R0, and we simulated some scenarios on Rt in order to analyze the impact of opinions on the dynamic of COVID-19.
3.1. Fitted model and estimated parameter values
3.1.1. Growth model
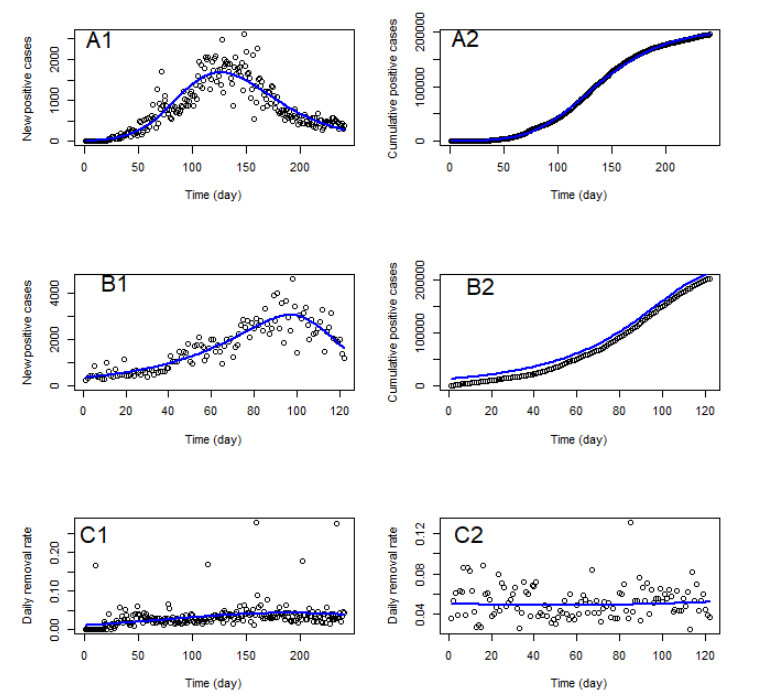
Table 3 indicates that the growth model involving Richard's growth curve under the assumption of the negative binomial distribution has the lowest AIC value for the cumulative COVID-19 case for the first wave and behaved well for the second wave. Therefore, we considered Richard's negative binomial distribution curve for the adjustment. From Figure C1 in the appendix, we observed that our model was well-fitted to the new and cumulative detected cases for West Africa. Figure C1c shows the probabilities of removals from actives (quarantined) and the fitted values based on the logistic regression models for removal probabilities. The logistic model doesn't fit the removals of COVID-19 in West Africa well for both waves. However, we have kept it since the adjustment of active cases is good (Figure C2d-C3d).
Results obtained with Richard's model (Table 4) indicate that the maximum case size is estimated at 206746 people (CI = [205800; 207700]) for wave 1 and 238299 people (CI = [236800; 239800]) for the wave 2. At the outbreak (t = 0), the probabilities of recovery are ^γ0 = 0.009 and ^γ0=0.147 for wave 1 and 2, respectively. In the first wave, an increase in the number of days is associated with an increase in the likelihood of belonging to the COVID-19 removal class (κ1=0.01), and in the second wave, a decrease in the likelihood of being removed from active case COVID-19 (κ1=−0.007).
3.1.2. Compartmental model
a. First wave
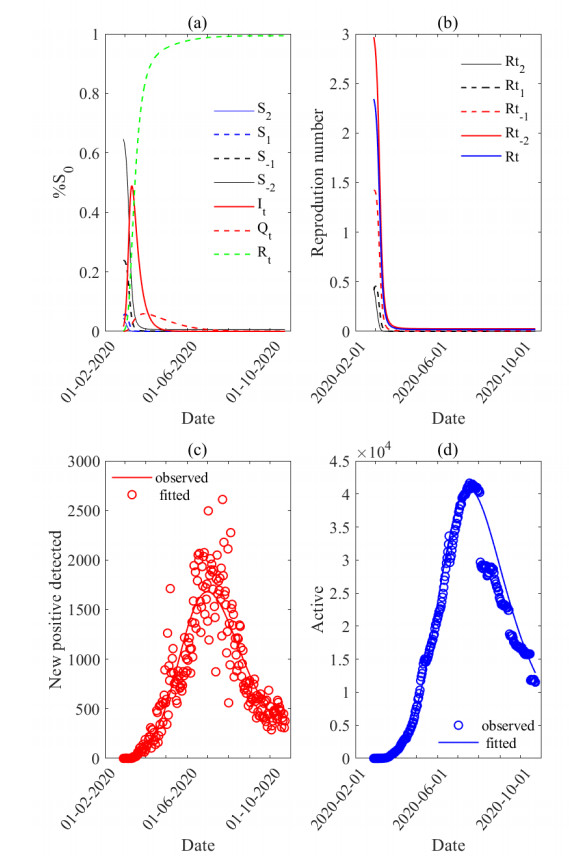
The initial sensitive population estimate is about 100% of the study population size (see Table 5). Each infected transmits the disease to about one individual at the beginning of the disease, indicating a moderate transmission rate, while the reduction factor "a" is weak. Opinion amplification occurs in only 7% of interaction cases (ϕ = 0.07). When there is no control measure, the estimated average number of secondary infections is highly greater than one (R0−2=5.35), and depends more on the reproduction number of prophylactic classes. Regarding the basic reproduction number, it is about 5.35 for the whole model and is more dependent on the reproduction number of the less susceptible population.
Figure C2a shows the evolution trend of each state of the SIQR-opinion model. Given that the susceptibles with prophylactic levels (-1;-2) are a minority in the population, their dynamics are low. When it has the dynamics of the infected, it is symmetric and reaches a peak of about 50% of the population. The effective reproduction number was less than one from April 2020 and depended more on the number of reproductions in the least susceptible classes.
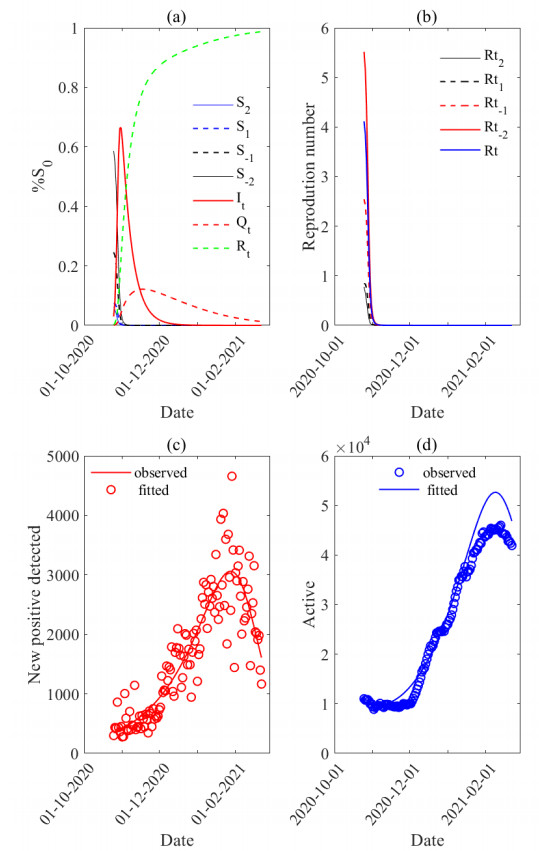
b. Second wave
About 94% of the target population is represented by the initial population estimate (Table 5). Each infected person will transmit the disease to about two other persons at the beginning of the disease while the reduction factor "a" is too weak. When two opinions of the same nature arise, the chance of an amplification, ϕ, is estimated to be 1%. Note that the initial proportion of the most prophylactic individuals decreased from the first to the second wave, and the probability of opinion amplification was very low. R0 values for different susceptible classes indicate that classes (-2 and -1) need less attention to control disease expansion, while classes (1 and 2) require the highest level of prophylactic measures to control the disease (Table 6). The SIQR-opinion model's evolution trend for each state is shown in Figure C3a. A peak of around 60% (higher than those of the first wave) of the population is reached by the asymmetric dynamics of the infected. The time-varying effective reproduction number has fallen since the period's inception (C3b).
4.
Effect of some parameters
4.1. Opinion effect
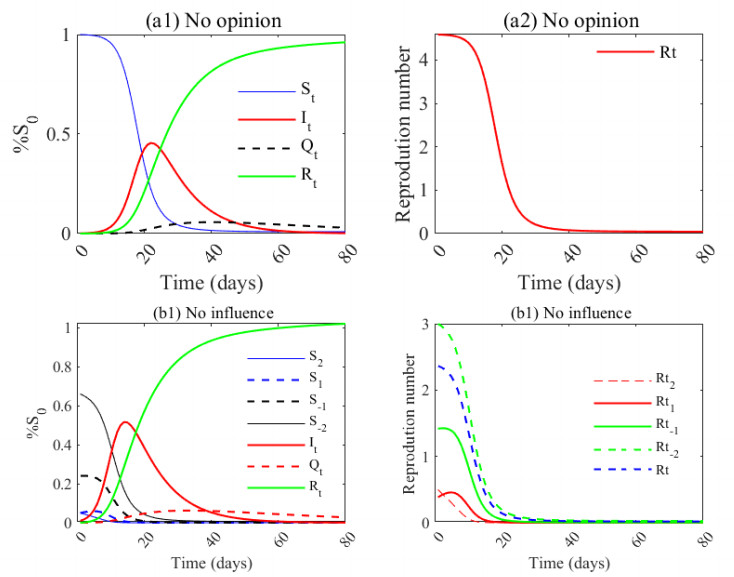
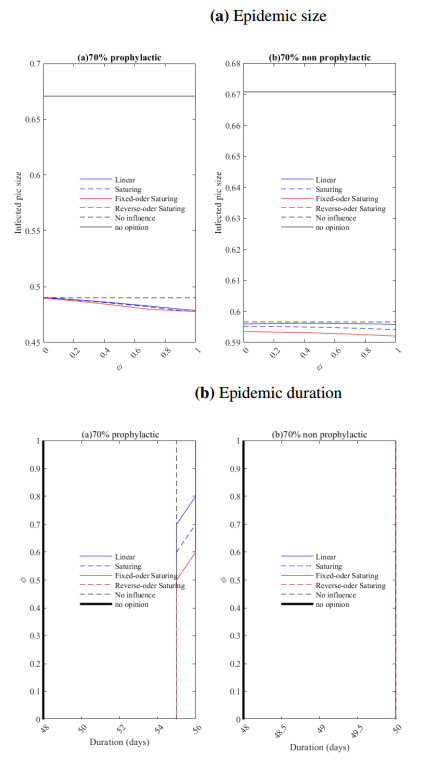
If there is no adherence to prophylactic behaviors, there is no opinion on the prophylactic levels to consider. When there is no opinion, the epidemic lasts longer (Rt decreases from 4.5 to 1 in about 23 days (Figure C3a2)); however, the peak is lower compared to when there is a prophylactic opinion (Imax=0.48 at t=14 days) (Figure C2a-C3a). Thus, the prophylactic opinion, amplifies the size of the epidemic but better controls its spread. The duration of the epidemic is greater when the population's prophylactic opinion intervenes (Figure 8). The progression of the susceptible (S), infected (I), quarantined (Q), and removed (R) in a population where an individual's opinion does not influence another (C3b1) indicates that the peak infection rate is 49% of initial susceptibles at t = 14 days. The influence increases the maximum number of infected but decreases the duration of the pandemic. The reproduction number has decreased from 2.5 to 1 (Figure C3b2).
4.2. Effect of initial proportion of adherence to prophylactic measures
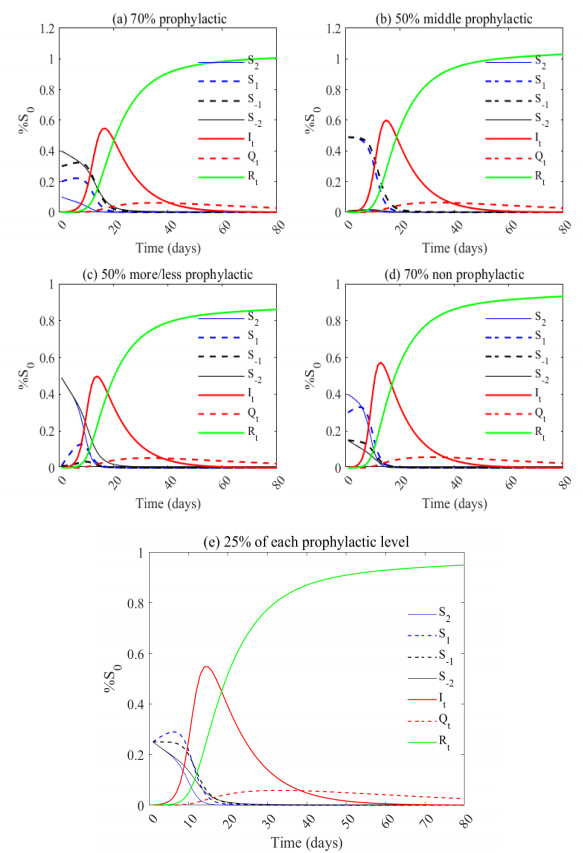
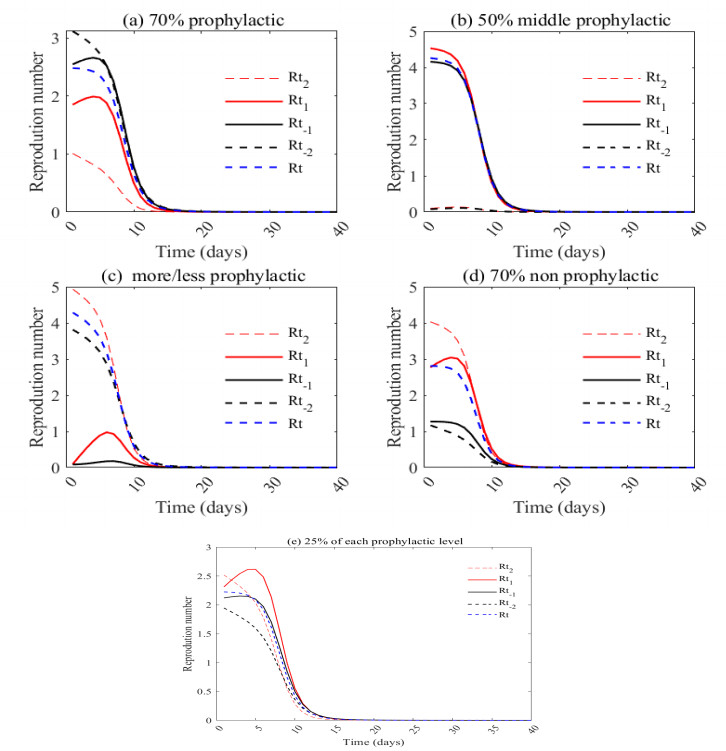
We simulated five cases to show the effect of the initial proportion of adherence to prophylactic measures on the dynamics of the pandemic (Table 6). In the case where we considered that 70% of the initial susceptible population is more prophylactic, the peak of new infections is 55% of initial susceptibles at t=12 days. The initial effective reproduction number is 1.8, but the measures are only effective after 36 days. This indicates that the measures taken to reduce transmission are effective but take some time to have an impact. In the case where 98% medium prophylactic is considered (z2=z3=0.49), the peak of newly infected individuals is 0.60 of initial susceptibles at t=11 days. The initial Rt, which is 3.5, becomes less than one about 34 days after the beginning of the pandemic. This indicates that the disease is spreading rapidly despite the prophylactic measures. When 49% of the initial susceptibles population is on one side of the opinion spectrum, the peak of new infections is 0.48 on day 10, and the reproduction number starts around three before decreasing to 1 after 34 days. This suggests that an individual behavior plays an important role in the spread of disease, with some individuals being more susceptible to infection than others.
The initial proportion affects the maximum number of infected that could be obtained, and the most plausible scenario for a minimal number of infected is to have more prophylactics than non-prophylactics. The number of new cases decreases as the proportion of more prophylactics increases until it reaches a given threshold. However, we notice that as the proportion of the most susceptible increases, the time to reach the peak increases.
4.3. Amplification opinion effect
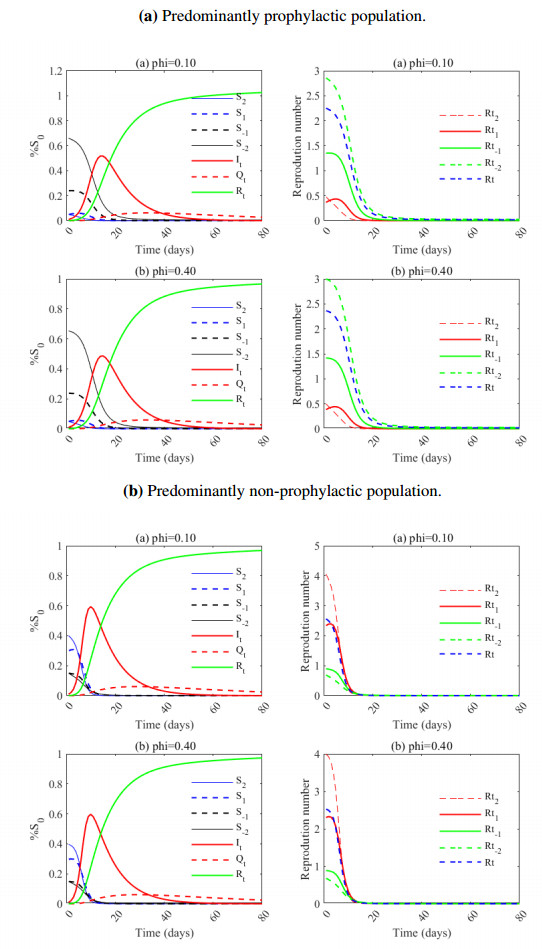
In Figure 7, we compared the distributions of susceptible, infected, and quarantined individuals and their recoveries when ϕ is low (0.10) and when ϕ is high (0.40) in a predominantly prophylactic population. The ϕ increases the size of the predominantly opinion (S2), especially regarding the most positive one; however, it does not affect the number effective reproduction number. Since it increases the size of the less susceptible, the maximum size of the newly infected when ϕ is high is greater than the peak time for the newly infected when ϕ is low. In the second case, we compared the distributions of susceptibles, infected, quarantines, and recoveries when ϕ is low (0.10) and when ϕ is high (0.40), in a non-prophylactic predominantly population (Figure 7). An increase in the probability of opinion amplification leads to an increase in the susceptible S−2 but in a small proportion compared to most prophylactic cases. The majority opinion outweighs the minority.
Since as the size of the less susceptible increases, the epidemic's size decreases, it is natural that an amplification of the more prophylactic side would reduce the size of the infection. The maximum number of infected decreases when ϕ increases (more than in the absence of the influence of one individual on another)(Figure 8). When ϕ increases, the duration of the epidemic increases as the level of prophylaxis is high in the susceptible population (Figure 8).
4.4. Influence function effect
As the initial proportion of the most prophylactic class increases, the influence functions reduce the size of the pandemic compared to the case without the influence function, and the linear function reduces the final size of the pandemic at best (Figure 8a). The saturating function decreases the wave's final size less when the susceptible population is less prophylactic (Figure 8b). Fixed and reversed influence functions increase the duration of the epidemic's wave more quickly in a population with a high prophylaxis level. In a population with a low prophylaxis level, the outcome is the same for all influence functions (Figure 8).
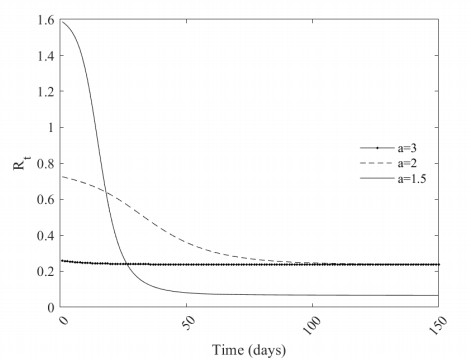
4.5. Effect of reduction parameter
We noticed from Figure 9 that the basic reproduction number is below 1 when the reduction parameter a is two, and the pandemic can be controlled (Rt<1).
5.
Discussion
Opinions and compliance with prophylactic measures have a significant impact on epidemic dynamics [34]. Modeling their effects on the dynamics of an epidemic is crucial for effective decision-making. In this study, we developed a mathematical model to assess the effect of individual behavior towards prophylactic measures on the dynamics of the COVID-19 pandemic in West Africa. For this purpose, we used COVID-19 data from the first case detected in West Africa until the day before the introduction of vaccination. This period corresponds to the first two COVID-19 waves in the region. To avoid identifiability problems when dealing with a large number of parameters [21], we have adjusted the daily infection case data to Richard's growth curve. The unknown parameters were estimated using the maximum likelihood technique. Overall, the Richard model fits the new daily number of confirmed cases well. Despite the lack of fit in the logistic regression, it fits the observed active cases well. The parameters estimated from the Richard and logistic curves are then used to determine the opinion parameters in the SIQR computational model to have more precision due to the lack of fit in phenomenological model estimation [84]. This is a two-step estimation process since the new infections were fitting by minimizing the deviation from the real data while taking the estimated parameters of the growth curve as a basis. Consequently, these estimates of new infections depend on the degree of bias in Richard's model estimates.
To assess the effect of prophylactic behaviors on the disease, we compute the opinion parameter, the basic and effective reproduction numbers. There is a discrepancy between the basic reproduction numbers of the two waves obtained. Our results show the effect of opinions and prophylactic behavior on the dynamics of the disease through the increase in the infection rate from the first to the second wave, which is accompanied by a decrease in the probability of opinion amplification and a decrease in the weight of more prophylactic individuals. These results are consistent with the study of Tyson et al. [34], which showed the importance of opinions in the process of reducing an epidemic. The increase in the infection rate would be the basis of the largest peak observed in the second wave. The decrease in weight and proportion of less susceptible individuals were noticed after the first wave, where West Africans lost confidence in the severity of COVID-19 on the continent and relaxed their prophylactic behavior (Coccia et al. [85]). This relaxation resulted in a larger peak of infection in the second wave.
Our simulations demonstrated that the opinions of susceptible individuals have an impact on the epidemic spread (the R0 and Rt of a population without opinions are higher than those of a population with opinions) [86]. It is worth noting that our simulation was carried out at the beginning of the pandemic when the transmission rate was already high. There are many research works on the spread of SARS-CoV-2, but few have taken into account the opinion of individuals, even though it seems to determine the course of the spread at the beginning of a pandemic. Although the opinion model seems simple, many factors are still difficult to handle (e.g., the correlation between geographical location, gender, age group, and opinion evolution) [87]. Our opinion dynamics model assumes that persuasion is the process by which opinions are changed but that persuasion is also sensitive to information about infection risk. This can also capture the results of knowledge amplification after it circulates on social media. Whatever the relationship between the media and public opinion, it might be more nuanced than we thought.
The results obtained from our simulations suggest that opinion dynamics can have a profound effect on the progression of disease in a population [88,89], and they illustrate the importance of the proportion of opinions at the onset of the epidemic, as well as the relative dynamic speeds of opinions and disease [86]. We simulated several scenarios to highlight the effects of three characteristics of opinion dynamics: influence functions, the initial distribution of opinions along a spectrum, and the degree of opinion amplification. In some simulated scenarios, opinion dynamics significantly reduce the fraction of the population that will be infected and the size of the epidemic's peak. In other scenarios, it is the reverse. We deduce that the intensity of the initial proportion of the less susceptible reduces the propagation dynamics. The most plausible scenario would be to have an equal proportion of all opinions, or more than 50 percent on the more prophylactic sides of the opinion spectrum [68]. Our findings indicate that the initial proportion of susceptible opinions toward disease outbreaks has a major influence on how an epidemic expands, but the effectiveness of those responses doesn't depend solely on them [29]. These simulations also show that the opinion types can interact with each other and the disease dynamics and affect the final size of the epidemic [90]. This result is also consistent with the conclusion of [31] that infectious disease dynamics are often influenced by social and behavioral factors that may interact with each other and with disease dynamics. Different types of influence functions can have varying effects on the spread of pandemics. For example, some types of influence functions will lead to more rapid population responses to the initial increase in infections [92]. In particular, "fixed-order saturating" influence functions may lead to a rapid response. On the other hand, if the initial dominant behavior is not prophylactic, some influence functions, such as linear or reversed order, will lead to the greatest reduction in the final pandemic size [91]. In other words, different influence functions can significantly impact the final outcome of an epidemic. Our results are, therefore, consistent with previous work, highlighting the interaction between opinion and disease dynamics. However, this complexity presents significant challenges for dynamic capture and prediction of epidemics, and our model may under- or overestimate the size of the epidemic peak. As pointed out by Comomdari [93], communication strategies to encourage prophylactic behaviors must take into account social and cultural factors to be effective. Also, adherence to a prophylactic opinion does not imply strict compliance with prophylactic behavior. The proof is that even with 66% adherence at the beginning of the first wave, the transmission was greater than 1. Our work sheds light on how opinion dynamics and influence functions relate to disease dynamics and informs the future development of reliable media and communication functions.
6.
Conclusion
By first fitting curves to observed data (confirmed positive cases, recoveries), this study suggests a hybrid modeling framework combining three approaches: opinions, compartmental, and phenomenological models to assess the effects of prophylactic behaviors on an epidemic dynamic. This model then provides an overall view of the epidemic dynamics by integrating the fitted curves into an opinion dynamics-compartmental model. The proposed method enables estimation of the basic and time-varying reproduction numbers, as well as the peak size of new infections and final epidemic size, and the ability to quickly change the opinion parameter. Application to COVID-19 data from West Africa suggested that its dynamic is heavily influenced by public opinion and behavior. Moreover, contrary to popular belief, the initial proportion of those considering COVID-19 as a severe threat to human health and that of the followers of the prophylactic behavior are decisive in controlling COVID-19 dynamics. The initial proportion of prophylactics in the population, as well as the force of propagation and information sharing, can determine the issue of an epidemic. As a result, it is essential for West African governments to implement control strategies that emphasize public awareness through the media and sensitization.
Acknowledgments
This work is carried out under the Humboldt Research Hub SEMCA, funded by the German Federal Foreign Office with the support of the Alexander von Humboldt Foundation (AvH).
Conflict of interest
The authors declare there is no conflict of interest.
Appendix A.
Richard growth model
Appendix B.
Cumulative, Death, Recovery cases and Population size
Appendix C.
Observed and fitted curve
Appendix C.1. New infected, Cumulative infected and Removal case fitted to growth curve
Appendix C.2. Susceptible, Infected, Quarantined, Removed dynamics and Effective reproduction number









 DownLoad:
DownLoad: