On the stability of Fractal interpolation functions with variable parameters

1.   Introduction

Fractal interpolation provides a framework for interpolating sets of data that may exhibit some self-similarity at different scales. While classical interpolation techniques, such as polynomial interpolation and spline interpolation generate smooth interpolants, fractal interpolation is able to model irregular sets of data. The concept of the fractal interpolation functions (FIFs) was first introduced by Barnsley ^[1,2,3]. Since then, this theory has become a powerful and useful tool in applied science and engineering, especially when dealing with real-world signals such as financial series, time series, climate data and bioelectric recordings.

The iterated function systems (IFSs in short) are useful to construct some fractal sets ^[4,5,6,7,8]). Specifically, IFS employs contractive functions over a complete metric space $(\mathbb X, d)$, where the existence and uniqueness of the fixed point are guaranteed by Banach's theorem. This is done using the Hutchinson operator, which also is a contraction mapping over ${\mathcal H}(\mathbb X)$, where ${\mathcal H}(\mathbb X)$ is the space of all compact subsets of $\mathbb X$ (see, for instance, ^{[4,9,10,11,12,13,14]} for some extension of Hutchinson's framework). Recently, the existence of FIFs through different well-known results given by the fixed point theory have been studied by many researchers ^{[15,16,17,18,19,20]}. Moreover, the wide range of FIFs constructed and studied proved many important properties including calculus, dimensionality, stability, smoothness and disturbance error ^{[17,20,21,22,23,24,25,26]}.

Let $N\ge 2$. In this paper, we consider the generalized affine FIF defined by

where, for each $n$, $\alpha_n$ is a Lipschitz function, $\psi_n$ is a continuous function and $a_n$ and $e_n$ are real numbers. When the functions $\{\alpha_n\}_n$ are constants (they are called vertical scaling factors), this system is extensively studied by many authors ^{[21,22,23,27,28,29,30,31]}. In this case, the set of vertical scaling factors has a decisive influence on the properties and shape of the corresponding FIF. In particular, the smoothness of FIFs can be described through the vertical scaling factor ^[31,32] and, therefore by choosing the appropriate vertical scale factor, they can fit the real rough curve precisely. Moreover, all aforementioned works are dealing with different choices of functions $\psi_n$ and highlighted some choice of these functions. In the section 2 we recall some preliminaries concerning IFS and FIF, and in Section 3, we examine the change of the fractal interpolation curve in response to a minor perturbation on $\alpha_n(x)$. We compute a sufficient condition so that the new (perturbed) IFS satisfies the continuity condition. Additionally, we discuss how these changes influence FIFs by computing the error estimate. In Section 4, we consider the case when $F_n(x, y)$ are defined as follows

where the functions $\alpha_n : I \longrightarrow \mathbb R$ are Lipschitz functions and $b, f$ are continuous functions on $[x_0, x_N]$ such that $b(x_0) = f(x_0)$ and $b(x_N) = f(x_N)$. The FIF interpolates the function $f$ at the nodes of the partition : $x_0 < x_1 < x_2\cdots < x_N$ ^[33,34,35]. We will compute in this case an appropriate upper bound of the maximum range of the perturbed FIF.

2.   Preliminaries

2.1.   Iterated function systems

Let $(\mathbb X, d)$ be a complete metric space. A mapping $g : \mathbb X \longrightarrow \mathbb X$ is called a contraction if there exists $c\in [0, 1)$ such that $d\left(g(x_1), g(x_2)\right)\le c \, d(x_1, x_2)$ for all $x_1, x_2\in \mathbb X$. We define on ${\mathcal H}(\mathbb X)$, the space of compact subsets of $\mathbb X$, the Hausdorff metric $d_H$ as

where $d(K_1, K_2) = \sup_{x\in K_1} \inf_{y\in K_2} d(x, y)$, then $({\mathcal H}(\mathbb X), d_H)$ is complete space ^[5] and compact whenever $\mathbb X$ is compact. Now, we consider $\mathbb I = \{ \mathbb X\, , \ w_n\; \ n\in J\}$ to be an IFS, where $w_n : \mathbb X \longrightarrow \mathbb X$ is a continuous mapping for each $n\in J$. We define also the Hutchinson operator $W : {\mathcal H}(\mathbb X) \longrightarrow {\mathcal H}(\mathbb X)$ as

It is well know that any IFS admits at least one attractor, that is, a set $G\in {\mathcal H}(\mathbb X)$ such that $W(G) = G$ ^[2]. In addition ^[2,5], the Hutchinson operator is a contraction mapping on $({\mathcal H}(\mathbb X), d_H)$ whenever $\mathbb I$ is hyperbolic; that is, for each $n\in J$, $w_n$ is a contraction.

2.2.   FIF

Let $\mathbb N^*$ be the set of positive integers and $I = [x_0, x_N]$ be a real compact interval. We consider the set of data $\Delta = \big\{(x_n, y_n)\in I\times \mathbb R\; \ n\in J_0: = \{0, 1, \ldots, N\}\big\}$, where $N\in \mathbb N^*$, $x_0 < x_1 < \cdots < x_N$, $y_i\in [a, b]$, with $-\infty < a < b < \infty$. Now we consider, for $n\in J$, the set $I_n = [x_{n-1}, x_n]$ and we define the contractive homeomorphism $L_n : I\longrightarrow I_n$ such that

for some $l \in [0, 1)$. We define also $N$ continuous mappings $F_n : K: = I\times [a, b] \longrightarrow \mathbb R$, such that

where $\alpha_n\in (-1, 1), n\in J.$ Now, we define the mapping $W_n: K \longrightarrow I_n\times \mathbb R$, as

Under the conditions (2.1), (2.2) and (2.3), the IFS $\big\{ K, W_n : n\in J\big\}$ has a unique attractor $G$. Furthermore, $G$ is the graph of continuous function $f$ that passes through the points $\big\{(x_n, y_n)\big\}_{n = 1}^N$ ^[2]. On the other hand, we define the complete metric space $({\mathcal G}, \rho)$, where

and

Now, we define the Read-Bajraktarevic operator $T$, defined on $({\mathcal G}, \rho)$ by

then, using (2.3), we obtain $\|T(f)-T(g)\| \le \alpha \| f-g\|_\infty,$ where $\alpha: = \max_n |\alpha_n|$. Hence, $T$ is a contraction mapping and possesses a unique fixed point $f$ on ${\mathcal G}$. From this, the FIF is the unique function satisfying the following functional relation

The most widely studied FIFs are defined by the following system

where the real constants $a_n$ and $e_n$ are determined by condition (2.1), $\psi_n$ are continuous functions such that conditions (2.2) and (2.3) hold and $-1 < \alpha_n < 1$ are free parameters called vertical scaling factors. Recently, many authors managed to construct more general FIFs that do not have to exhibit the strict self similarity (see, for instance, ^[15]). In this work, we consider the IFS with variable parameters ^[32] defined by :

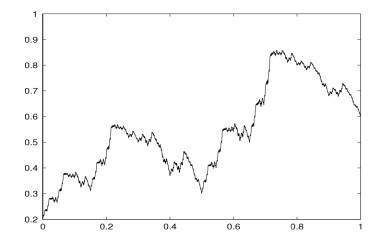
where $\alpha_n : I \longrightarrow \mathbb R$ are Lipschitz functions such that $\| \alpha_n\|_\infty: = \sup\big\{ \alpha_n(x); x\in I \big\} < 1.$ In this case, the FIF will be called generalized affine FIF and denoted by $f_{\Delta, N}^\alpha$ where $\alpha: = (\alpha_1, \alpha_2, \ldots, \alpha_N)$ (or simply by $f$ if there is no ambiguity). Moreover, consider that generalized affine FIF provides a wide variety of systems for different approximations problems. In Figure 1, we plot the FIF with constant parameters : $\alpha_1(x) = 0.4$, $\alpha_2(x) = 0.3$, $\alpha_3(x) = 0.5$ and $\alpha_4(x) = 0.2$. Meanwhile in Figure 2, we plot the FIF with variable parameters : $\alpha_1(x) = 0.4 \sin(5x) + 0.2$, $\alpha_2(x) = 0.3 \cos(10 x)$, $\alpha_3(x) = 0.5 \exp(-2x)+0.3$ and $\alpha_4(x) = 0.2 \exp(x)\sin(x) + 0.1$. As we can see, the self-similarity in Figure 2 is weaker than that of the affine fractal interpolation curve shown in Figure 1 ^[32].

3.   Perturbation on FIFs

In this section we consider the FIFs generated through the following IFS

where $a_n$ and $e_n$ are determined by condition (2.1) and the functions $\psi_n$ are continuous functions such that conditions (2.2) and (2.3) hold. Assume that $\alpha_n : I \longrightarrow \mathbb R$ are Lipschitz functions, with Lipschitz constant $C_n$, such that $\alpha: = \max_n \| \alpha_n\|_\infty < 1$. Now we define, for $x\in I$,

where $n_j\in J$, $k\ge 1,$ $j\in \{1, \ldots, k\}$. Finally, let $\sigma^{j}$ denote the $j$-fold composition of $\sigma$ with itself such that

while $L_{\sigma^k(n_1 n_2\ldots n_k)}(x) = x.$ Using a successive iteration and induction (see ^[36]), we have, for all $n_j\in J$, $j = 1, \ldots, k$,

with the convention $\prod_{j = 1}^0 S_j (x) = 1$ for any family of functions $\{S_j\}_j$. In this section we consider the following perturbation of the IFS defined in (3.1),

where $\beta_n$ and $\lambda_n$ are continuous functions such that $\| \beta_n\|_\infty < 1$. We define also

We will say that the IFS satisfies the continuous condition if, for $1\le n < N$, we have

We assume, for all $1\le n < N$, that

Notice that by using (3.2) and the fact that $|a_{n}| < 1$ for $n\in J$ that

for all $x\in I$. Our main result in this section is the following.

Theorem 1. Let $f$ and $\widetilde f$ be the FIFs generated by the IFSs (3.1) and (3.3), respectively.

1. Under (3.4) the IFS defined by the system (3.3) satisfies the continuous condition.

2. For a given $x\in I,$ let $\{n_j\}, n_j \in J$ be sequence such that $x = \sum_{r = 1}^{\infty}\Big(\prod_{j = 1}^{r-1} a_{n_j}\Big) e_{n_r}$, then

where ${\mathsf L}^r[x] = \sum_{l = 1}^{\infty}\Big(\prod_{j = 1}^{l-1}a_{n_{r+j}}\Big) e_{n_{r+l}}$.

Proof. 1. The continuous condition implies, for each $n = 1, \ldots, N-1$, that $\widetilde F_n(x_N, y_N) = \widetilde F_{n+1}(x_0, y_0)$, then

Thus, we obtain $\delta_{n+1}(x_0) y_0 +\lambda_{n+1}(x_0) = \delta_{n}(x_N) y_N+\lambda_{n}(x_N)$ and then

2. Using (3.2), we have

and

Now remark that $\bigcap_{k = 1}^\infty L_{n_1n_2\ldots n_k} (I)$ consists of a single point in $I$ for any sequence $\{n_k\}$ of integers such that $1\le n_k\le N$. Moreover, for any fixed $x \in I$, there exists a sequence $\{n_k\}$ satisfying

This implies by using (3.2) that

where $x'$ is any point belonging to $I$. Therefore, there exists $x'\in I$ such that

Similarly, we have

then we obtain the desired result.

□

Example 1. We consider the Weierstrass function (see Figure 3) that can be seen as a classical fractal function since it is continuous everywhere, yet differentiable nowhere. Therefore, while its graph is connected, it looks jagged when viewed on arbitrarily small scales. There are many works on fractal dimensions of their graphs, including box dimension, Hausdorff dimension, and other types of dimensions ^[37,38]. Let $l\ge 2$ be an integer, $1/l < \lambda < 1$ and $\phi: \mathbb R\longrightarrow \mathbb R$ is a $\mathbb Z$-periodic real analytic function. We define

In fact, such a function is real analytic, or the Hausdorff dimension of its graph is equal to $2 +\log_l(\lambda)$ ^[39].

In this example, we consider the classical Weierstrass function $f$; that is, when $\phi(x) = \cos(2\pi x)$. Let $I = [0, 1]$, $N = l = 3$ and choose in definition (3.5) the special case $\lambda = 1/2$, then we obtain $f(0) = f(1) = 2$. Now, consider

where $\alpha_n(x) = \frac{1}{2} + (-1)^{1+ \lfloor n/2 \rfloor} \frac{\sin(2\pi x)}{4}$, for $n\in \{1, 2, 3\}$, where $\lfloor n/2 \rfloor$ means the integer part of $x$. In this case, we have that the Weierstrass function $f$ is the FIF defined by $\{W_n\}_{n = 1}^3$ ^[40]. Now, consider the following perturbed system defined by

where $\beta_n(x) = (-1)^{1+ \lfloor n/2 \rfloor} \frac{\sin(2\pi x)}{4}$ for $n\in \{1, 2, 3\}$. In this case, we have $\delta_n(x): = \delta_n = -\frac{1}{2}$. Choose $\lambda_1(x) = x$ and then, by (3.4), we have

Hence, if we take $\lambda_2(x) = \lambda_3(x) = x+1$, the system defined in (3.6) satisfies the continuous condition.

In the following, we consider a special case of Theorem 1. For this, we define the following perturbation of the IFS defined in (2.5):

where $\delta_n$ and $\lambda_n$ are constants such that $| \alpha_n + \delta_n | < 1$. In this situation, we have $\gamma_n = 0$ and we obtain the following result.

Theorem 2. Let $f$ and $\widetilde f$ be the functions generated by the IFSs (2.5) and (3.7), respectively. For a given $x\in I,$ let $\{n_j\}, n_j \in J$ be sequence such that $x = \sum_{r = 1}^{\infty}\Big(\prod_{j = 1}^{r-1} a_{n_j}\Big) e_{n_r}$.

1. Assume for all $1\le n < N$ that

then the IFS defined by the system (3.7) satisfies the continuous condition.

2. For a given $x\in I,$ let $\{n_j\}, n_j \in J$ be sequence such that $x = \sum_{r = 1}^{\infty}\Big(\prod_{j = 1}^{r-1} a_{n_j}\Big) e_{n_r}$, then

where $t: = \max_n |\alpha_n|$ and $s = \max_n |\beta_n-\alpha_n|$.

Proof. The first assertion is a direct application of Theorem 1, and we will only prove the second one. Using Theorem 1, we obtain

Note that (3.8) can be found in [41, Theorem 3]. Moreover, using [32, Lemma 3.2], we have

where $t: = \max_n |\alpha_n|$ and $s = \max_n |\beta_n-\alpha_n|$. □

Remark 1. Consider the IFS defined by (3.7) such that $\alpha: = \alpha_1 = \cdots = \alpha_N$. Choose $\delta = \frac{1-\alpha}{2}$ so that we have $\alpha+\delta < 1$. Therefore, by a direct computation using (2.4), we obtain for all $x\in I$

where $\lambda_\infty: = \max_{n\in J} \lambda_n.$ It follows that

Now, applying Theorem 2, we get

Example 2. In this example, we consider a special case of Theorem 2 by choosing all the parameters $\lambda_n$ as equal for $n \in J$. This is done by choosing $y_0 = y_N = 0$. For this, let us consider the sets of data points:

and we consider the IFS defined by (2.5) where

Now, we consider the following perturbed system

We choose $\lambda_1 = 0$ and we collect the different values of $\delta_n$ in the Table 1. Moreover, different perturbed FIF are plotted in Figure 4. As we may see, we obtain smooth or non-smooth FIF depending on the choice of $\delta_n$. One can describe the self-similar structures of the graph of FIF by computing the box dimension $D$ (also known as the Minkowski–Bouligand dimension or the box-counting dimension), which is a mathematical object used to describe the complexity of certain figures and proved to be an appropriate and effective method for fractal dimension estimate. More precisely,

where $\mathsf N_\epsilon$ is the minimum number of $\epsilon \times \epsilon$ squares needed to cover the graph of $f$.

As an application of Theorem 2, the following result concerning the Weierstrass function is considered in Example 1.

Corollary 1. Let $f$ be the Weierstrass function defined in (3.5) with $\phi(0) = 0$, then there exists an FIF $\widetilde f$ satisfying

Proof. Let $I = [0, 1]$ and the interpolating points $x_0 = 0 < x_1 < \cdots < x_N = 1$ such that $x_n-x_{n-1} = 1/N$ $(N = l)$. We consider the following system defined as

where $\alpha = \lambda$. It is well known that the function $f$ is an FIF ^[40]. Indeed, consider for $n\in J$ the function

It follows that

and, thus,

Now, we consider the following perturbed system

where $\delta = (1-\alpha)/2$ and $\lambda_1 = 0$, and we obtain

Furthermore, using Remark 1, we get

Finally, we get the desired result since $\phi$ is a $\mathbb Z$-periodic function with $\phi(0) = 0$, which implies that $f(0) = f(1)$ and $y_N = y_0$.

□

4.   Upper bound of the maximum range of the perturbed FIF

Let $f\in {\mathcal C}(I)$, the normed space of real valued endowed with the uniform norm continuous function on $I$. We will say that the function $f$ is Hölder continuous with exponent $\beta$ and Hölder constant $c$ if

We denote by ${\mathsf H}^\theta(I)$ the set of all Hölder continuous functions on $I$ with exponent $\theta$. We consider the interpolation points $P = \big\{ (\frac{n}{N}, y_n) \in \mathbb R^2, n\in J \big\}$ and we denote $D = \big\{\frac{n}{N} \in I, n\in J_0 \big\}$. We set

$k$ times composition. In this section, we consider

where the real constants $a_n$ and $e_n$ are determined by condition (2.1), the functions $\alpha_n : I \longrightarrow \mathbb R$ are Lipschitz functions, with Lipschitz constant $C_n$ such that $\alpha: = \max_n \| \alpha_n\|_\infty < 1$ and $b \in {\mathcal C}(I)$ such that $b(x_0) = f(x_0)$ and $b(x_N) = f(x_N)$. The FIF generated by (4.1) will be denoted by $f^\alpha$, which interpolates $f$ at the nodes of the partition. Moreover, using (2.4), the function $f^\alpha$ satisfies

We will denote by $\widetilde f^\alpha$ the FIF generated by the perturbed system; that is

Lemma 1. Assume that $\beta: = \max_n \| \beta_n\|_\infty < 1$. For all $x\in I_n$ and $n\in J$, we have

and

where $\|\lambda\|_\infty = \max_n \|\lambda_n\|_\infty$, $\alpha = \max_n \|\alpha_n\|_\infty$ and $\delta = \max_n \|\delta_n\|_\infty$.

Proof. Using (2.4), we obtain

and

as required. Moreover, from (4.4) and (4.2), $\widetilde f^\alpha(x) = f^\alpha(x)+ \beta_n(L_n^{-1}(x)) \widetilde f^\alpha\big(L_n^{-1}(x)\big) +\lambda_n\big(L_n^{-1}(x)\big)$ and

□

Now, assume that $f\in {\mathsf H}^{\theta_1}(I)$ and $b\in {\mathsf H}^{\theta_2}(I)$ with Hölder constant $H_f$, $H_b$ respectively.

Lemma 2. Let $\widetilde f^\alpha$ be the FIF generated by the system (4.3) and we assume that $\beta = \max_n \|\beta_n\|_\infty < 1$. We denote $\alpha = \max_n \|\alpha_n\|_\infty$, $\delta = \max_n \|\delta_n\|_\infty$ and $A_1 = \frac{\beta \Gamma_1 + H_f+ \alpha H_b+ y_0 \delta}{1-\beta}$, then

Proof. We define, for $k = 1, 2, \ldots,$

First, observe that

For $x \in L^{k}(D)\cap I_n$, we have

and then

We denote by $A = H_f+ \alpha H_b+ y_0 \delta$, which does not depend on $k$. It follows by using (4.5) that

For any $x \in I_n$, there exits a sequence $\{x_j\}_j \in I_n \cap\Big(\bigcup_{k} L^k(D) \Big)$ such that $x_j \longrightarrow x$ and $\lim_{j\to \infty} | \widetilde f^\alpha(x_j) -y_{n-1} | = | \widetilde f^\alpha(x) -y_{n-1} |$, by continuity of the function $\widetilde f^\alpha$. Therefore, we get

□

Given a function $S$ defined on $I$, we define the maximum range $R_S$ of $S$ as

Theorem 3. Let $f^\alpha$ be the $\alpha$-FIF the IFS (4.1) with interpolation points $P$ and $\widetilde f^\alpha$ as the perturbed FIF defined by (4.3). Assume that $\beta = \max_n \|\beta_n\|_\infty < 1$, then

where $A_1 = \frac{\beta \Gamma_1 + H_f+ \alpha H_b+ y_0 \delta}{1-\beta}$, $\alpha = \max_n \|\alpha_n\|_\infty$ and $\delta = \max_n \|\delta_n\|_\infty$.

Proof. From Lemma 2, we have

Now, let $s_1, s_2\in I$, then there exists $n_1 \le n_2 \in J$ such that $s_1\in I_{n_1}$ and $s_2\in I_{n_2}$. It follows that

On the other hand, we may estimate the upper bound of the maximum range $R_{ \widetilde f^\alpha}$ not depending on $N$. Indeed, using Lemma 1 we get

as required. □

Remark 2. Let $f^\alpha$ be the $\alpha$-FIF the IFS (4.1) with interpolation points $P$ such that $\alpha < 1$, then

where $A_2 = \frac{\alpha \Gamma_1 + H_f+ \alpha H_b}{1-\alpha}$.

Example 3. Let $I = [0, 1]$ and $f(x) = x-x^2$. Observe that for any $x, y\in I$, we have

then the function $f$ is Hölder continuous with exponent one and Hölder constant $H_f = 3$. In this example, we consider the following perturbed system

where $\delta = (1-\alpha)/2$, $\lambda_1 = 0$ and $b(x) = f(x)/3$. Since $f(0) = f(1) = 0$, we obtain $\lambda_n = 0$ for all $n\in J$. Therefore, using Lemma 1, we have

and

In particular, if $\alpha = 1/4$, we obtain

Therefore, we have

then $R_{ \widetilde f^\alpha}(I)\le\frac{13}{36}$ for $\alpha = 1/4.$

5.   Conclusions

In this paper, a class of generalized affine FIFs with variable parameters, where ordinate scaling is substituted by real-valued control function, is investigated. More precisely, we considered the FIF generated through the IFS defined by the functions $W_n(x, y) = \big(a_n(x)+e_n, \alpha_n(x) y +\psi_n(x)\big)$, $n = 1, \ldots, N$. We computed the error estimate in response to a small perturbation on $\alpha_n(x)$ and we gave a sufficient condition on the perturbed IFS so that it satisfies the continuity condition.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research at King Faisal University, Saudi Arabia, for financial support under the annual funding track [GRANT 5416].

Conflict of interest

The authors declare no conflicts of interest.