A swarm intelligence-based ensemble learning model for optimizing customer churn prediction in the telecommunications sector

1.   Introduction

Antibiotics are the secondary metabolites of certain microorganisms that can selectively inhibit or kill other microorganisms at low concentrations without bringing serious toxicity to the host. Under the action of antibiotics, a large number of sensitive bacteria are inhibited or killed, but a few sensitive bacteria change their metabolic pathways and become resistant bacteria. Repeated application of the same antibiotics results in a screening of resistant bacteria and antibiotics are ineffective once resistant bacteria become dominant, which aggravates the hazard of bacterial infection to human health ^[1]. Therefore, many scholars have invested their energy in studying bacterial resistance ^{[2,3,4,5,6,7,8,9,10]}. In Reference ^[2], Austin and Anderson formulated a model to describe the transmission dynamics of resistant bacteria between the host and the medical staff. Their study aimed to reveal the necessity of strengthening clinical management of patients infected with bacteria. In Reference ^[3], Blair and Webber expounded the molecular mechanisms of bacterial resistance including intrinsic resistance and acquired resistance. In Reference ^[6], authors assumed that bacterial resistance is acquired by genetic mutation and plasmid transfer and formulated a population dynamic model of sensitive and resistant bacteria to antibiotics. The stability of the coexistence equilibrium and the existence of the limit cycle is discussed. In Reference ^[10], the author formulated the following model to investigate the dynamic changes of bacterial resistance in a single bacterial population that is exposed to a single antibiotic:

where $x(t)$ and $y(t)$ are two distinct populations of the same species of disease-causing bacteria. $x(t)$ denotes the density of sensitive bacteria in the bacterial population and $y(t)$ denotes the density of resistant bacteria in the bacterial population. $\alpha$ is the growth rate of the two kinds of bacteria. In view of limited nutrients in the host, struggle for survival between the two kinds of bacteria will cause them to be sifted out at a rate of $\beta$. $\gamma$ is the antimicrobial ability, which is larger for bactericidal antibiotics compared to bacteriostatic antibiotics. $\eta$ is the antibiotic concentration. $\delta$ is the conversion rate of resistant bacteria losing resistance and converting into sensitive bacteria. All the above parameters are positive constants. By qualitative analysis, Garber gave the conditions under which resistant bacteria will go to extinction.

How to optimize the antibiotic treatment measures is a topic that mathematicians have been interested in for a long time ^{[11,12,13,14,15,16,17,18]}. In Reference ^[11], authors introduced the impulsive state feedback control into the system (1.1) and then got the following system:

The orbital stability of the order-1 periodic solution is presented. It can be seen that the density of resistant bacteria is limited to a lower level in the system with impulsive state feedback control. In Reference ^[14], the authors formulated a model to simulate the contribution of antibiotics and immune system to combat bacterial infection and then propounded an optimal control problem. The optimal control is found by applying Pontryagins Maximum Principle. In reference ^[17], the authors mainly focused on the two subpopulations of the same species. One subpopulation has an intrinsic resistance to drugs and the other one is sensitive to drugs. The authors formulated a nonlinear objective function to achieve the following two goals: (i) minimize the size of the bacterial population, (ii) prevent resistant bacteria from becoming dominant. The results indicate that the optimal control contains a singular interval.

Currently, impulsive state feedback control has been widely applied in various fields such as biology, medicine, etc. ^{[19,20,21,22]}. Meanwhile, the study of the periodic solution has made many new advances ^{[23,24,25,26,27,28,29,30]}. In Reference ^[19], authors established a crop pest management model with impulsive state feedback control. It can be known that observations and records of the pest quantity at different stages of crops can help to control the size of the pest population. In Reference ^[25], authors reviewed the research results of the periodic solution since 2010 and presented the recent research results.

This paper is organized as follows: In Section 2, we formulate a model of conversion between sensitive and resistant bacteria and then introduce impulsive state feedback control to optimize antibiotic treatment measures. In Section 3, the global asymptotic stability of the positive equilibrium is discussed. In Section 4, the orbital stability of the order-1 periodic solution is proved. In Section 5, the numerical simulation is used to confirm our results.

2.   Model description and preliminaries

Motivated by ^[10], the conversion rate of resistant bacteria losing resistance and converting into sensitive bacteria is represented by $\frac{\delta y}{k+y}$. We can obtain $\lim\limits_{y\to+\infty} \frac{\delta y}{k+y} = \delta$, which shows that as the density of resistant bacteria increases, the conversion rate of resistant bacteria losing resistance and converting into sensitive bacteria increases and gradually tends towards $\delta$. We give the following system:

where $x(t)$ and $y(t)$ are two distinct populations of the same species of disease-causing bacteria. $x(t)$ denotes the density of sensitive bacteria in the bacterial population and $y(t)$ denotes the density of resistant bacteria in the bacterial population. $\alpha$ is the growth rate of the two kinds of bacteria. In view of limited nutrients in the host, struggle for survival between the two kinds of bacteria will cause them to be sifted out at a rate of $\beta$. $\gamma$ is the antimicrobial ability, which is larger for bactericidal antibiotics compared to bacteriostatic antibiotics. $\eta$ is the antibiotic concentration. All the above parameters are positive constants.

Severe bacterial infection can endanger life. Clinically, antibiotics are commonly used to inhibit or kill disease-causing bacteria. However, prolonged administration of the same antibiotics can cause bacterial resistance, which, in turn, makes the antibiotic effect worse and even disappear. We can use other antibiotics when one antibiotic loses its effectiveness, but bacteria still become resistant to new antibiotics after long-term use. Thus, replacing antibiotics doesn't fundamentally reduce bacterial resistance. We need to optimize the antibiotic treatment measures to extend or restore the antibiotic effectiveness. Inspired by ^[11,12], we introduce the impulsive state feedback control into the system (2.1) and then get the following system:

where $h$ is the critical threshold value of resistant bacteria at which antibiotics lose best treatment for patients. When the density of resistant bacteria reaches the critical threshold value $h$, $\theta$ multiples of resistant bacteria become sensitive bacteria under the impulsive effect $(0 < \theta < 1)$.

For convenience, we give the following definitions and theorems.

Definition 2.1 ^[25] Consider a two dimensional state dependent impulsive differential equation

Suppose the impulsive set $M$ and phase set $N$ of system (2.3) fall between two parallel lines, the intersection of y-axis with the phase set $N$ line is $F$. Due to the pulse effect, any trajectory starting from $N$ reaches the impulsive set $M$ and then is mapped to $I\in N$. Then the point $I$ is called the successor point of the point $G$ and $g(G) = |FI|-|FG|$ is called the successor function of the point $G$, where $|FI|$, $|FG|$ are the distance between the point $F$ and the point $I$ and between the point $F$ and the point $G$, respectively.

Theorem 2.1 ^[25] The successor function $g$ is continuous.

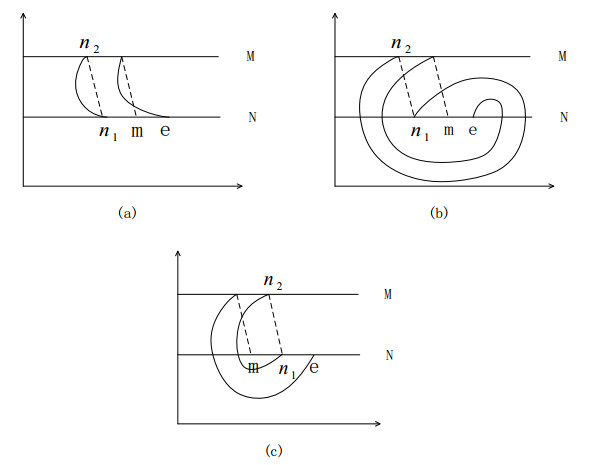
Theorem 2.2 ^[25] Assume $\widehat{n_1n_2}\bigcup\overline{n_1n_2}$ is an order-1 cycle and the point $m$ is the successor point of $e$. According to the position between the points $n_1$, $e$ and $m$, the order-1 periodic solution is classified into three types:

1) Type 1: the order-1 cycle $\widehat{n_1n_2}\bigcup\overline{n_1n_2}$ is convex, and the points $e$ and $m$ are at the same side of $n_1$ as shown in Figure 1(a).

2) Type 2: the order-1 cycle $\widehat{n_1n_2}\bigcup\overline{n_1n_2}$ is not convex, yet the points $e$ and $m$ are at the same side of $n_1$ as shown in Figure 1(b).

3) Type 3: the points $e$ and $m$ are at different sides of $n_1$ as shown in Figure 1(c).

Theorem 2.3 ^[25] If $\Gamma$ is a type 1 order-1 periodic solution with period $T$ and the integral along $\Gamma$ satisfies

$\Gamma$ is orbital stable.

Theorem 2.4 ^[25] If $\Gamma$ is a type 1 order-1 periodic solution and the region that contains $\Gamma$ satisfies

$\Gamma$ is orbital stable.

3.   Qualitative analysis of the system (2.2) without the impulsive effect

Without the impulsive effect, the system (2.2) is reduced to

3.1.   Boundedness

Theorem 3.1. The system (3.1) is uniformly bounded in the first quadrant.

Proof. The positive x-axis is either a single trajectory or a combination of an equilibrium point and two trajectories. However, both cases imply that no trajectory intersects with the positive x-axis.

Obviously, $\left.\frac{dx}{dt}\right|_{x = 0} = \frac{\delta y}{k+y} > 0$ holds for $y > 0$, which shows that when meeting the positive y-axis, the trajectory will pass through it from left to right (see Figure 2).

By investigating the straight line $l\triangleq x+y- \frac{\alpha}{\beta} = 0$, we can obtain

for $x > 0$, which indicates that when meeting the straight line $l = 0$ in the first quadrant, the trajectory will pass through it from upper right to lower left (see Figure 2).

From the above, we can see that the system (3.1) is uniformly bounded in the first quadrant.

The proof is completed. □

3.2.   Existence of equilibria

The equilibria of the system (3.1) are given by

From the second equation of (3.2), we can obtain $y = 0$ or $x = \frac{\alpha}{\beta}-\frac{\delta}{\beta(k+y)}-y$. By substituting $y = 0$ in the first equation of (3.2), we can obtain $x = 0$ or $x = \frac{\alpha-\gamma\eta}{\beta}$, so the equilibrium $E_0(0, 0)$ always exists and the equilibrium $E_1(\frac{\alpha-\gamma\eta}{\beta}, 0)$ exists if $\alpha > \gamma\eta$ holds.

By substituting $x = \frac{\alpha}{\beta}-\frac{\delta}{\beta(k+y)}-y$ in the first equation of (3.2), we can obtain

where

Theorem 3.2. If $\beta k^2 > \alpha k > \delta$ and $\gamma\eta k > \delta$ hold, the system (3.1) has a unique positive equilibrium.

Proof. Suppose $y_1, y_2, y_3$ are three roots of $\Phi(y) = 0$ defined in (3.3) in the complex number field. According to the Vieta theorem, we can obtain

If $\beta k^2 > \alpha k > \delta$ and $\gamma\eta k > \delta$ hold, we can obtain

Thus, $\Phi(y) = 0$ defined in (3.3) has one positive real root and two complex roots with negative real parts. Hence, $\Phi(y) = 0$ defined in (3.3) has a unique positive real root. Consequently, the system (3.1) has a unique positive equilibrium.

The proof is completed. □

3.3.   Stability of equilibria

The Jacobian matrix of the system (3.1) is

Theorem 3.3. If $min\{\gamma\eta, \frac{\delta}{k}\} > \alpha$ holds, the equilibrium $E_0(0, 0)$ is a stable node. If $max\{\gamma\eta, \frac{\delta}{k}\} > \alpha > min\{\gamma\eta, \frac{\delta}{k}\}$ holds, the equilibrium $E_0(0, 0)$ is a saddle point. If $\alpha > max\{\gamma\eta, \frac{\delta}{k}\}$ holds, then the equilibrium $E_0(0, 0)$ is an unstable node.

Proof. The Jacobian matrix at the equilibrium $E_0(0, 0)$ is

The eigenvalues of $J(E_0(0, 0))$ are

If $min\{\gamma\eta, \frac{\delta}{k}\} > \alpha$ holds, we can obtain $\lambda_1 < 0$, $\lambda_2 < 0$. Thus, the equilibrium $E_0(0, 0)$ is a stable node. If $max\{\gamma\eta, \frac{\delta}{k}\} > \alpha > min\{\gamma\eta, \frac{\delta}{k}\}$ holds, we can obtain $\lambda_1 > 0$, $\lambda_2 < 0$ or $\lambda_1 < 0$, $\lambda_2 > 0$. Hence, the equilibrium $E_0(0, 0)$ is a saddle point. If $\alpha > max\{\gamma\eta, \frac{\delta}{k}\}$ holds, we can obtain $\lambda_1 > 0$, $\lambda_2 > 0$. Therefore, the equilibrium $E_0(0, 0)$ is an unstable node.

The proof is completed. □

Theorem 3.4. If $min\{\alpha, \frac{\delta}{k}\} > \gamma\eta$ holds, the equilibrium $E_1(\frac{\alpha-\gamma\eta}{\beta}, 0)$ is a stable node. If $\alpha > \gamma\eta > \frac{\delta}{k}$ holds, the equilibrium $E_1(\frac{\alpha-\gamma\eta}{\beta}, 0)$ is a saddle point.

Proof. The Jacobian matrix at the equilibrium $E_1(\frac{\alpha-\gamma\eta}{\beta}, 0)$ is

The eigenvalues of $J(E_1(\frac{\alpha-\gamma\eta}{\beta}, 0))$ are

If $min\{\alpha, \frac{\delta}{k}\} > \gamma\eta$ holds, we can obtain $\lambda_1 < 0$, $\lambda_2 < 0$. Hence, the equilibrium $E_1(\frac{\alpha-\gamma\eta}{\beta}, 0)$ is a stable node. If $\alpha > \gamma\eta > \frac{\delta}{k}$ holds, we can obtain $\lambda_1 < 0$, $\lambda_2 > 0$. Therefore, the equilibrium $E_1(\frac{\alpha-\gamma\eta}{\beta}, 0)$ is a saddle point.

The proof is completed. □

Theorem 3.5. If $\beta k^2 > \alpha k > \delta$ and $\gamma\eta k > \delta$ hold, the unique positive equilibrium $E^*(x^*, y^*)$ is globally asymptotically stable.

Proof. The Jacobian matrix at the positive equilibrium $E^*(x^*, y^*)$ is

Combined with $x^* = \frac{\alpha}{\beta}-\frac{\delta}{\beta(k+y^*)}-y^*$, we can obtain

If $\beta k^2 > \alpha k > \delta$ and $\gamma\eta k > \delta$ hold, we can obtain

and

Therefore, the unique positive equilibrium $E^*(x^*, y^*)$ is locally asymptotically stable.

Define a Dulac function $D(x, y) = \frac{1}{xy}$ and we can obtain

which implies that there is no limit cycle in the first quadrant. Consequently, the unique positive equilibrium $E^*(x^*, y^*)$ is globally asymptotically stable.

The proof is completed. □

4.   The order-1 periodic solution of the system (2.2)

4.1.   Existence and uniqueness of the order-1 periodic solution

Theorem 4.1. When $h < y^*$, the system (2.2) has a unique order-1 periodic solution.

Proof. From the system (2.2), we can obtain the impulsive set $M = \{(x, y)\in R^2_+|x\geq 0, y = h\}$ and the phase set $N = \{(x, y)\in R^2_+|x\geq \theta h, y = (1-\theta)h\}$. When $h < y^*$, both the impulsive set $M$ and the phase set $N$ are below the positive equilibrium $E^*(x^*, y^*)$.

Now, we will prove the existence of the order-1 periodic solution. Suppose the straight line $y = (1-\theta)h$ intersects with isoclines $\frac{dx}{dt} = 0$ and $\frac{dy}{dt} = 0$ at points $R$ and $S$, respectively (see Figure 3(a)). The trajectory initiating from the point $R(x_R, (1-\theta)h)$ intersects with the impulsive set $M$ at the point $R_M$ and then the point $R_M$ is mapped to $R_N(x_{R_N}, (1-\theta)h)$ due to the impulsive effect. The point $R_N$ is the successor point of the point $R$. The point $R_N$ must be on the right of the point $R$ according to the property of the vector field, and therefore the successor function satisfies

Similarly, the trajectory initiating from the point $S(x_S, (1-\theta)h)$ reaches the impulsive set $M$ at the point $S_M$ and then the point $S_M$ jumps to $S_N(x_{S_N}, (1-\theta)h)$ due to the impulsive effect. The point $S_N$ is the successor point of the point $S$. The point $S_N$ must be on the left of the point $S$ according to the property of the vector field, and hence the successor function satisfies

Following the continuity of the successor function, there must be a point $W$ between $R$ and $S$ that makes $g(W) = 0$ hold. The trajectory initiating from the point $W$ hits the impulsive set $M$ at the point $W_M$ and then the point $W_M$ is mapped back to $W$ itself due to the impulsive effect. In consequence, the system (2.2) has an order-1 periodic solution.

Next, we will prove the uniqueness of the order-1 periodic solution. We arbitrarily choose two points $T$ and $U$ in the phase set $N$ where $x_T < x_U$ (see Figure 3(b)). The trajectory initiating from the point $T$ reaches the impulsive set $M$ at the point $T_M$ and then the point $T_M$ jumps to $T_N$ due to the impulsive effect. The point $T_N$ is the successor point of the point $T$. Similarly, the trajectory initiating from the point $U$ intersects with the impulsive set $M$ at the point $U_M$ and then the point $U_M$ is mapped to $U_N$ due to the impulsive effect. The point $U_N$ is the successor point of the point $U$. Since $x_U-x_T > x_{U_M}-x_{T_M}$ and $x_{U_M}-x_{T_M} = x_{U_N}-x_{T_N}$ hold, we can obtain $x_U-x_T > x_{U_N}-x_{T_N}$. Hence the successor function satisfies

Hence, the successor function $g$ is monotonically decreasing in the phase set $N$. Therefore, there must be only one point $W$ that makes $g(W) = 0$ hold. In consequence, the system (2.2) has a unique order-1 periodic solution.

The proof is completed. □

4.2.   Stability of the order-1 periodic solution

Theorem 4.2. When $h < y^*$, the unique order-1 periodic solution of the system (2.2) is orbital stable.

Proof. From Figure 3(a) and Theorem 2.2, we can conclude that the order-1 periodic solution of the system (2.2) is a type 1 order-1 periodic solution. Define a Dulac function $D(x, y) = \frac{1}{xy}$ and the stability of the order-1 periodic solution of the system (2.2) can be decided by the system:

We can obtain

According to Theorem 2.4, we can know that the unique order-1 periodic solution of the system (2.2) is orbital stable.

The proof is completed. □

4.3.   Numerical simulation and discussion

Let parameters $\alpha = 2$, $\beta = 0.8$, $\gamma = 0.3$, $\eta = 0.9$, $\delta = 1$, $k = 4$ and parameters $\alpha = 2$, $\beta = 0.8$, $\gamma = 0.3$, $\eta = 3$, $\delta = 1$, $k = 4$. Both cases satisfy the conditions of Theorem 3.5, and therefore the unique positive equilibrium $E^*(x^*, y^*)$ is globally asymptotically stable in both cases. The numerical simulation is used to confirm the result (see Figures 4 and 5). We get the positive equilibrium $E^*(x^*, y^*) = (1.898, 0.312)$ for $\eta = 0.9$, which is simulated in Figure 4. With the increase in the antibiotic concentration, we get the positive equilibrium $E^*(x^*, y^*) = (0.434, 1.852)$ for $\eta = 3$, which is simulated in Figure 5. It can be seen that the density of resistant bacteria increases as the antibiotic concentration increases. This means that prolonged administration of the same antibiotics can cause bacterial resistance, which, in turn, makes the antibiotic effect worse and even disappear.

Antibiotics play a vital role in the fight between humans and disease-causing bacteria, so we need to optimize the antibiotic treatment measures to extend or restore the antibiotic effectiveness. In this paper, we formulate a simplified model of conversion between sensitive and resistant bacteria with the impulsive state feedback control. Let parameters $\alpha = 2$, $\beta = 0.8$, $\gamma = 0.3$, $\eta = 3$, $\delta = 1$, $k = 4$, $h = 0.4$, $\theta = 0.9$. This case satisfies the conditions of Theorem 3.5 and Theorem 4.1, and therefore the unique order-1 periodic solution of the system (2.2) is orbital stable in this case. The numerical simulation is used to confirm the result (see Figure 6). It can be seen that there is an oscillation of the density of resistant bacteria in an interval below the critical threshold value when the impulsive state feedback control is adopted. This strongly shows that the impulsive state feedback control can reduce bacterial resistance.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (No.12171193 and 12271346), the project of the Distinguished Professor of colleges and universities of Henan province in 2019 and Project of Foreign expert in Henan (HNGD2023074).

Conflict of interest

The authors declare that they have no conflict of interest in the manuscript.