1.
Introduction
As one of the emerging technologies in the field of neurorehabilitation, the brain-computer interface (BCI) aims to provide a new non-muscular channel for paralyzed people to communicate with outside world [1]. Electroencephalography (EEG) is widely used for BCI systems owing to its convenience, low cost, and high temporal resolution. At present, the commonly used paradigms for BCI system control include steady-state visual evoked potentials (SSVEPs) [2,3], event-related potentials (ERPs) [4,5], and motor imagery (MI) [6,7,8]. Compared with BCIs that requires external active stimulation, MI-based BCI systems are easier to implement [9,10]. Sensory Motor Rhythm (SMR) is characterized as a band power change within a particular EEG frequency band appearing over a sensorimotor area of the brain during MI. Accordingly, BCI systems can be designed to use EEG band power changes associated with MI tasks as control signals [11]. Since EEG is a non-stationary, low amplitude and low signal-to-noise ratio bioelectric signal [12,13], and MI is an unstable, easily disturbed, and no obvious characteristic paradigm [14,15], which poses a huge challenge for correctly identifying MI intentions. Therefore, how to design reasonable algorithms to extract -discriminative features is particularly critical for MI-EEG recognition.
CSP is widely used for feature extraction of MI-related tasks [16,17,18]. However, the performance of CSP on specific subjects is closely related to the selection of time windows and frequency bands, so that some CSP methods for time windows and frequency bands improvements are proposed to increase the robustness and classification performance of the model [19,20,21]. Temporally constrained sparse group spatial pattern (TSGSP) [22] further enhance classification accuracy of MI EEG by the simultaneous optimization of filter bands and time window. Sparse linear discriminant analysis (GSDA) [23] extracted CSP features from the divided time-frequency blocks and used the generalized method to simultaneously select features and classify to improve the classification accuracy. And wrapped time-frequency combined selection in the source domain (WTFS-SD) [19] applied weighted minimum norm estimate and CSP based sub-band feature extraction to decode the MI-tasks.
The main idea of above these algorithms is to extract, fuse and select the CSP features of EEG signals from multiple specific time windows and subbands in a single trail of specific subjects, so as to make up for the defects of high sensitivity to noise and low generalization capacity of CSP, and improve the representation ability of different motor imagery tasks. However, they did not consider the sharp increase of data volume and feature dimension, which will increase the computational complexity of the model, which is not conducive to the development and application of online BCI. In addition, the excessive division of time-frequency blocks will in turn lead to information redundancy, resulting in the reduction of classification accuracy.
To solve the above problem, we propose an optimal channel-based sparse time-frequency block common spatial pattern (OCSB-CSP) feature extraction method to reduce the computational burden and increase the classification accuracy of the model. First, a correlation-based method is implemented to select channels and mark the optimal one. Second, the discriminative ability of each time-frequency block is calculated based on the one-dimensional EEG data of the optimal channel, and the block selection is performed with this index. Then, feature extraction and selection are executed for sparse time-frequency blocks. Finally, support vector machine (SVM) is used for classification.
The rest of this paper is organized as follows. Section 2 explains the proposed method. Section 3 describes the experiment study. Section 4 provides the discussion. Finally, the conclusion is drawn in section 5.
2.
Methods
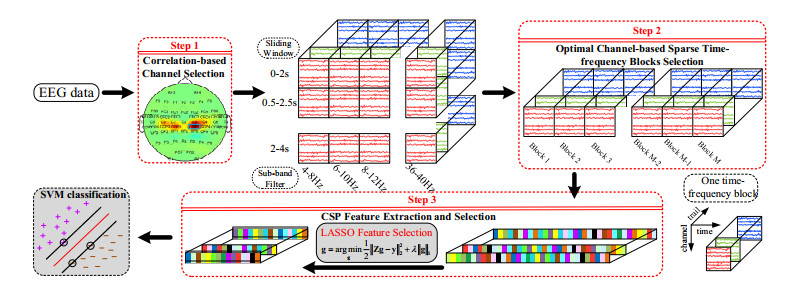
Our proposed framework consists of three main parts, Correlation-based channel selection, Optimal channel-based sparse time-frequency blocks selection, and CSP feature extraction and selection. Firstly, redundant information is removed, and the data dimensionality is initially reduced by step 1, and the optimal channel for subsequent processing is determined. Secondly, we select the time-frequency blocks rapidly and efficiently by step 2. Then the feature extraction and selection of sparse time-frequency blocks are performed by step 3. Finally, the classification is performed with SVM. The overall framework of the proposed method is illustrated in Figure 1.
2.1. Correlation-based channel selection
As the number of electrodes for recording EEG data increases, it is essential to adopt effective channel selection algorithms to reduce the computational complexity and channels redundancy. Different criteria functions are predefined, and different channel selection evaluation algorithms are generated, such as [24,25] proposed a filter method to select the significant channels by using Pearson correlation coefficient and bispectrum analysis; [26] adopted a wrapper method to select the important channels by genetic algorithms (GA) and adjust it according to the classification results of fisher discriminant analysis (FDA); [27] raised a hybrid method of two-stage channel selection. In the first stage, a single channel was formed by averaging the channels were combined according to the neurophysiological information about brain functions acquired from the literature, and in the second stage, selective channels were specified with the common spatial pattern-linear discriminant analysis (CSP-LDA)-based sequential channel removal.
The aim of this paper is to propose a method that can rapidly select time-frequency blocks to reduce the computational burden and improve the classification accuracy. Therefore, we use a filtering method in the first step to efficiently select the channels related to MI, which removes the redundant information between channels and facilitates the improvement of classification accuracy; on the other hand, we mark the optimal channel by this step and use the one-dimensional data based on the optimal channel for the subsequent time-frequency block selection, which significantly reduces the computational complexity of the model compared to using multi-channel data. The combination of these two points shows the reasonableness and necessity of the method. As the specific subjects perform the same MI task, MI-related channels should contain common information, while other channels contain less common information. Based on this principle, we use the Person correlation coefficient, a classic method to quantify the statistical relationship between two or more variables, to measure the similarity between any two channels in reference [28]. In the following, we discuss the necessary steps:
Firstly, in order to reduce the error caused by individual variability or external interference, the raw broadband (1–42 Hz) EEG data is normalized with Z-score, so that the mean of each channel data is equal to 0 and the variance is equal to 1:
where Xc and Sc are the cth channel time series before and after normalizing, and C is the total number of channels.
Secondly, the Person correlation coefficient between the two channels is calculated by the following formula:
where Si and Sj are the time series of the ith and jth channels normalized by formula (1), and N is the number of sampling points in the sequence.
Thirdly, the correlation coefficient matrix R∈RC×C is calculated:
Then the average common information of each channel and all remaining channels is obtained by averaging each row of R, and the channel corresponding to the maximum value among them is regarded as the selection result of this trail. Repeat all trails as described above to obtain cumulative selection results for all channels.
Finally, count the selection results of all trials, the K channels with the most selections are regarded as the final channel selection results, and the channel corresponding to the maximum value is marked as the optimal channel k∗. The selection of channels by the way of this statistical voting does not generate additional hyperparameters that cause an increase in the computational burden.
2.2. Optimal channel-based sparse time-frequency blocks selection
For improving classification accuracy of MI-related EEG, we optimize the filter bands and time windows within CSP simultaneously. Specifically, with regards to bandpass filtering, K channels EEG data determined by section 2.1 is first decomposed into multiple specific frequencies signals at F overlapping filter bands. Each of the specific frequency signals is further segmented into multiple subseries using T overlapping sliding windows. Finally, F×T time-frequency blocks are formed.
The time series of the optimal channel are taken out from each time-frequency block, and the time-domain power feature and frequency-domain power spectral density (PSD) feature are extracted. Then, the two-dimensional features are projected to one-dimension through Fisher ratio, to characterize the MI classification ability of each time-frequency block, and to select the time-frequency blocks based on this. Fisher ratio is a statistic parameter that can be used to measure the discriminant ability of classes by projecting high-dimensional features into one dimension [29], It is defined as:
where F− and F+ are feature vectors from two different classes.
For the time series of the optimal channel in ith trail Xi,k∗ from the each time-frequency block, its power feature is defined as Ti,k∗, PSD feature is defined as Pi,k∗ [30]:
According to the definition of Fisher ratio in formula (4) and the above two features, we define the value of the binary classification capability of each time-frequency block as scoreF by calculating the ratio of the Euclidean distance between classes to the intra-class variances. The specific formula is:
where N1 and N2 are the number of trails in class 1 and class 2, respectively. The scoreF of all F×T time-frequency blocks are obtained by the above formula, and the high-quality M time-frequency blocks are selected by setting reasonable threshold. A reasonable threshold setting will have a significant impact on the subsequent CSP performance. If the threshold is set too large, the number of selected time-frequency blocks will be less, resulting in the loss of a large number of effective information; adversely, if the threshold is set too small, the number of selected time-frequency blocks will be more, resulting in a large number of invalid redundant information. The power features in the time domain and the PSD features in the frequency domain of each time-frequency block are extracted and compressed into a one-dimensional indicator using the Fisher ratio to characterize the binary classification capability of each block. This method also ensures the rationality and efficiency of block selection to a certain extent.
2.3. CSP feature extraction and selection
As we all know, CSP is very sensitive to noise, and the CSP feature extraction and fusion of multiple time-frequency blocks are easy to make the model over-fitting. Therefore, many improved CSP feature extraction and selection methods have been proposed [31,32,33]. We perform CSP feature extraction and selection on the M time-frequency blocks selected by the method in section 2.2 above. For the ith EEG data Xi∈RK×T,i∈Nl,l=1,2 (K is the number of channels after channel selection in section 2.1, T is the number of sampling points from any time-frequency block, and Nl is the number of trails corresponding to class l). The average spatial covariance matrix of class l is:
where T denotes the transpose operator. The purpose of CSP is to find the optimal spatial filter to maximize the variance ratio between the two classes of data:
Where w∈RK is a spatial filter, ‖⋅‖2 is the l2 norm. This maximization solution is equivalent to solving the generalized eigenvalue problem Σ1w=λΣ2w. A set of spatial filters W=[w1,⋯,w2P] is obtained by combining the eigenvectors corresponding to the P largest and P smallest generalized eigenvalues. Finally, the feature vector z(m)=[z(m)1,⋯,z(m)2P] of the mth time-frequency block is extracted by the following formula:
According to the above steps, CSP features are extracted from all selected M time-frequency blocks, and the fusion feature Z∈R2PM is obtained:
LASSO (Least Absolute Shrinkage and Selection Operator), as a filter method for feature selection, uses specific statistical criteria to select features without relying on any classifier, and has been widely used in MI based BCI [34,35]. Lasso aims to minimize the sum of squares of residuals and is constrained that the sum of absolute values of coefficient vectors is less than the given constant. The specific functions are as follows:
where Zi and yi are the fusion features and labels corresponding to the ith trail, and λ is a nonnegative hyperparameter that controls the sparsity of the coefficient vector g. The features in Zi corresponding to those non-zero entries in g are selected to form an optimized feature vector.
After correlation-based channel selection, optimal channel-based sparse time-frequency blocks selection and CSP feature extraction and selection, the final feature vectors are obtained and input into SVM with the radial basis function (RBF) kernel for the classification.
3.
Experiment study
3.1. EEG data description
1) Dataset 1: This dataset is from BCI competition IV dataset 1 [36], which records 59 channels EEG data of 4 healthy subjects (a, b, f, g), and each subject was asked to complete 100 trails of left hand and foot motor imagery. For the first 6 seconds of each trail, a fixed cross will be displayed in the center of the computer screen. The arrow with direction (left: left hand motor imagery; down: foot motor imagery) will be superimposed on the cross in 2–6 seconds as a hint, and the subjects performed the motor imagery tasks according to the cue during this period. Then the screen appears black in 6–8 s.
2) Dataset 2: This dataset is from BCI Competition III dataset Iva [37], which records 118 channels EEG data of 5 healthy subjects (aa, al, av, aw, ay), and each subject was asked to complete 140 trails of right hand and foot motor imagery. For the first 3.5 seconds of each trail, an arrow with direction (right: right hand motor imagery; down: foot motor imagery) is displayed in the center of the computer screen as a prompt, and the subjects performed the motor imagery tasks according to the cue during this period. The subjects were then allowed to relax for 1.75 to 2.25 s.
3.2. Experimental evaluation and result
To investigate the performance of the proposed method on the above two datasets, we performed a uniform preprocessing using the channel selection algorithm described in section 2.1, followed by feature extraction using the FBCSP, B-CSP, B-SCSP and OCSB-CSP methods, respectively (as implemented below), and finally classification using an SVM based on the RBF kernel, where the penalty parameter C was determined by a 5-fold cross-validation is determined. The above experiments were repeated 5 times to evaluate the classification accuracy and computation time.
(1) FBCSP (Filter band CSP): By extracting and fusing CSP features from different filter bands. Specifically, the 4–40 Hz broadband raw data was decomposed into 17 overlapping subbands (4–8 Hz, 6–10 Hz, 8–12 Hz, 10–14 Hz, 12–16 Hz, 14–18 Hz, 16–20 Hz, 18–22 Hz, 20–24 Hz, 22–26 Hz, 24–28 Hz, 26–30 Hz, 28–32 Hz, 30–34 Hz, 32–36 Hz, 34–38 Hz, 36–40 Hz) by the fourth order Butterworth bandpass filter.
(2) B-CSP (Blocks-CSP): By extracting and fusing CSP features from each time-frequency block constructed by simultaneously sliding time windows and dividing frequency bands. Specifically, the data in Dataset 1 was divided into five overlapping time windows (i.e., 0–2 s, 0.5–2.5 s, 1–3 s, 1.5–3.5 s, 2–4 s), and the data in Dataset 2 was divided into four overlapping time windows (i.e., 0–2 s, 0.5–2.5 s, 1–3 s, 1.5–3.5 s). Then used the same method as in (1) to divide the frequency bands for each time window data.
(3) B-SCSP (Blocks-Sparse CSP): Based on (2), features were selected through Lasso. Specifically, 5-fold cross-validation was used to determine the hyperparameters λ in Lasso regression.
(4) OCSB-CSP: The construction method of time-frequency blocks was the same as (2). For specific subjects, optimal channel-based sparse time-frequency blocks CSP method was proposed, and the method described in (3) was used for feature extraction and selection.
After the above four algorithms were used to extract and select the respective CSP features, SVM with RBF kernel function was used for classification, and the penalty factor was determined by 5-fold cross-validation.
Table 1 reports the comparison results of the classification accuracy rates for our proposed algorithm and three other algorithms on Dataset 1. We observe that our proposed method outperforms all these remaining methods. The average improvements achieved by our method were 4.37%, 2.91% and 1.30% in comparison with FBCSP, B-CSP and B-SCSP, respectively. Our proposed method obtained very significant improvement on classification accuracy compared to FBCSP and B-CSP (p<0.01).
Table 2 shows the comparison results on Dataset 2. The average improvements achieved by our proposed method were 3.7%, 1.35% and 1.01% in comparison with FBCSP, B-CSP and B-SCSP, respectively. Our proposed method obtained very significant improvement on classification accuracy compared to FBCSP (p<0.01).
Additionally, we also compared the computational efficiency of each algorithm. Figure 2 shows the computational time evaluated for 5 replicated experiments of the model training and testing phases under the environment of python 3.7.3 on a desktop with 2.80 GHz CPU (i5–8400, 8 GB RAM). It can be seen from Figure 2(a) that our algorithm has relatively more hyperparameters, so it takes most of time for inner loop cross-validation to select the hyperparameters. Although our algorithm requires a longer computational time than other methods, the inner loop cross-validation is not necessary for testing but only for model training. The computational time for testing is shown in Figure 2(b), the proposed OCSB-CSP algorithm not only substantially improves the classification accuracy compared to the conventional FBCSP, but also reduces the computational burden compared to the B-CSP and B-SCSP that employ all time-frequency blocks, which is meaningful for the development and improvement of BCI applications.
In order to demonstrate the superiority of the proposed method, it was also compared with existing winners' methods, including LRFCSP [38], SGRM [39], CCS-RCSP [28], BCS-CSP [40], and OCS-CSP [41]. Table 3 and Table 4 show the average classification accuracy of each method for multiple experiments on Dataset I and II, respectively. As shown in the tables, although the average classification accuracy of our proposed method does not display a significant advantage over existing methods, our method does not lose classification performance after a drastic dimensionality reduction process, but has some enhancement, especially in Dataset 2.
4.
Discussion
4.1. Distribution of selected channels
We used the Pearson correlation coefficient-based channel selection method proposed in section 2.1 to count the channel selection results of all 160 training trails for each subject in the Dataset 1, as shown in Table 5. We can see that the results of channel selection for specific subjects are not the same, that is, different channels are selected, the number of channels selected is different, the number of times each channel is selected is different, and the optimal channels marked are different, so it is necessary to select channels for specific subjects.
To intuitively reflect the distribution results of channel selection and the quality of each channel. We normalize the statistical results of each subject and draw brain topographic maps, as shown in Figure 3. It can be seen that the results of channel selection are indeed related to the specific subjects, but without exception, the channels selected by each subject are located in the motor perception region of the cerebral cortex, and the optimal channel (the warmest channel in the brain topographic map) appears near the CCP3 or CCP4.
4.2. Sparse time-frequency blocks comparison
To improve the performance and efficiency of time-frequency blocks selection, as shown in 3.2, we propose a method that uses one-dimensional data of the optimal channel to calculate the Fisher ratio of each block as the basis for blocks selection. For the four subjects in Dataset 1, we set different thresholds to ensure that 45 blocks are selected for synchronous comparison, as shown in Figure 4. The blue blocks are the selected time-frequency blocks. The darker the color, the larger the Fisher ratio, which means that it has better MI classification ability. It can be found that the time-frequency blocks selected by our proposed algorithm from specific subjects are different, and the positions of significant time-frequency blocks are also different. Since MI tasks are usually unknown and varies between subjects, it is determined that a fixed time-frequency block cannot capture the most distinctive features, resulting in suboptimal accuracy, which further confirms the necessity of selecting time-frequency blocks. Furthermore, we consider that the EEG signal between adjoining sliding windows will not change too much, and the corresponding CSP features will not change too much, so the selection blocks of adjoining sliding windows should also ensure a certain consistency. The results presented in Figure 4 are consistent with the above.
We used 5-fold cross-validation to determine a reasonable threshold for specific subjects. Figure 5 shows the impact of the change in the number of time-frequency blocks on the classification accuracies for all subjects in Dataset 1. It can be seen from this figure that when the number of blocks exceeds a certain number, the classification accuracy of each subject decreases to varying degrees. That is, we need to determine the number corresponding to the highest classification accuracy. Thus, the selection of sparse time-frequency blocks is very significant in improving the performance and operation speed of the model.
4.3. Sparse feature selection
The regularization parameter λ plays an important role in the selection of CSP features based on lasso regression. A too large λ may exclude effective features while a too small one could not eliminate redundancy effectively. In this paper, the appropriate subject-specific λ was determined by 5-fold cross-validation, and the optimal sparse coefficient vector g can be eventually learned from formula (12) to select the significant CSP features extracted from the sparse time-frequency blocks. Figure 6. reflects sparse coefficient vector and the most significant spatial filter learned by OCSB-CSP algorithm for each subject in Dataset 1. We can see that the significant features are sparse and subject-specific, and the brain topographic map of the most significant spatial filter further indicates the effectiveness of the proposed method for capturing the dynamical changing of SMRs.
In summary, we arrived at the following conclusions:
1) The channel selection section, for a single trail on a specific subject, using a filtered approach called Pearson correlation coefficient [17] to quickly eliminate redundant information between channels and diminish the dimensions of the data. In addition, all trails are counted in the form of voting, and the optimal channel with the most votes is marked. The experimental results show that the optimal channel is all from the area around CCP3 and CCP4 where ERD/ERS [42,43] is most obvious.
2) Aiming at the problem that the existing CSP feature extraction methods based on multiple time-frequency blocks have heavy computational burden, we propose an optimal channel-based sparse time-frequency blocks CSP feature extraction method to reduce the computational complexity and improve the classification accuracy of the model. The specific innovations are as follows: the sparsity of time-frequency blocks based on one-dimensional data of the optimal channel, which ensures the accuracy of classification to a certain extent and improves the computational efficiency of the model. The innovative combination of extracting time-domain and frequency-domain features with Fisher ratio to define a reasonable indicator for time-frequency blocks selection, which has achieved better experimental results.
3) The proposed framework involves more hyperparameters, such as the number of time-frequency blocks, penalty parameter of Lasso regression, penalty factor of SVM classifier, etc., and all these hyperparameters need to be determined according to specific subjects, and to some extent lead to an increased computational burden, which cannot be well applied across subjects, and this is not conducive to the development and application of BCI system. Future enhancements to the model are needed to improve the generalization capability of the model.
5.
Conclusions
In this paper, an optimal channel-based sparse time-frequency blocks common Spatial pattern feature extraction method is introduced to enhance the classification accuracy and computational speed of MI tasks by efficiently selecting time-frequency blocks. In this proposed method framework, the channel selection method based on Pearson correlation coefficient was firstly cited to initially reduce the redundant information between channels and to mark the optimal channel for subsequent processing. The selection results show the reasonableness and efficiency of this method. Then the discriminative ability of each time-frequency block measured by defining Fisher ratio index based on the optimal channel of the one-dimensional EEG data was achieved to sparse the time-frequency blocks. The results indicate that the suggested method not only significantly reduces the data dimensionality, but also the selected time-frequency blocks are mostly distributed in the frequency bands relevant to the MI tasks. Finally, Lasso regression was performed to select the extracted multi-blocks CSP features and SVM was used for classification. Significant advantages were obtained when compared with the existing superior methods on both public datasets. The proposed OCSB-CSP algorithm achieves higher classification accuracy while reducing the computational burden of the model, which provides a new idea for the development and improvement of BCI applications.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Nos. 61671197, 61871427 and 61971168), Zhejiang Provincial Natural Science Foundation of China (No. LY18F030009), and the Foundation of Zhejiang Provincial Education Department of China (No. Y202044279). The authors would like to acknowledge the BCI competition IV dataset 1 and BCI Competition III dataset Iva which were used to test the algorithms proposed in this study.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad:











