From trust and dependence commitment to B2B engagement: An empirical analysis of inter-organizational cooperation in FMCG

Fernando Gimeno-Arias; José Manuel Santos-Jaén; María del Carmen Valls Martínez; Manuel Sánchez-Pérez; Fernando Gimeno-Arias; José Manuel Santos-Jaén; María del Carmen Valls Martínez; Manuel Sánchez-Pérez

doi:10.3934/era.2023379

Electronic Research Archive

2023, Volume 31, Issue 12: 7511-7543. doi: 10.3934/era.2023379

Previous Article Next Article

Research article Special Issues

From trust and dependence commitment to B2B engagement: An empirical analysis of inter-organizational cooperation in FMCG

1.
Department of Management, University of Murcia, 30100 Murcia, Spain
2.
Department of Accounting and Finance, University of Murcia, 30100 Murcia, Spain
3.
Economics and Business Department, University of Almeria, 04120 Almeria, Spain
4.
Mediterranean Research Center on Economics and Sustainable Development, 04120 Almeria, Spain

Received: 06 September 2023 Revised: 16 November 2023 Accepted: 22 November 2023 Published: 28 November 2023

This research paper aims to demonstrate that relationships play a pivotal role in fostering inter-organizational cooperation, both at the corporate and individual levels, within the fast-moving consumer goods (FMCG) distribution industry. Despite the extensive body of literature on relationship management, its impact on such a unique and important channel as FMCG remains undetermined. To achieve this objective, we designed a questionnaire for a survey targeting Spanish FMCG distributors, from which we collected 204 responses. We analyzed this data using partial least squares structural equation modeling (PLS-SEM), an emerging methodology in business research that enables us to assess the model's explanatory power and predictive capacity in understanding the relationships between various constructs. Our findings indicate the efficacy of governing inter-organizational relationships to facilitate cooperation. Additionally, we uncover links between corporate and individual relationships that contribute significantly to cooperation. In terms of practical implications for businesses, our results emphasize the importance for managers to prioritize relationships as an integral aspect of efficient channel management. This pertains to relationships within the distribution channel among partners and also individual relationships among business managers. Notably, the existing academic literature has not yet established the effectiveness of relationships in governing channels within the FMCG marketing channel, nor has it established a direct connection between inter-organizational and individual relationships among business managers.

Keywords:

Citation: Fernando Gimeno-Arias, José Manuel Santos-Jaén, María del Carmen Valls Martínez, Manuel Sánchez-Pérez. From trust and dependence commitment to B2B engagement: An empirical analysis of inter-organizational cooperation in FMCG[J]. Electronic Research Archive, 2023, 31(12): 7511-7543. doi: 10.3934/era.2023379

Related Papers:

[1]	Roberto Gianardi, Marina Bisson, Lisa Beccaro, Riccardo De Ritis, Vincenzo Sepe, Laura Colini, Cristiano Tolomei, Luca Cocchi, Claudia Spinetti . High-resolution susceptibility mapping of seismically induced landslides on Ischia island: the 2017 earthquake case study. AIMS Geosciences, 2024, 10(3): 573-597. doi: 10.3934/geosci.2024030
[2]	Maria C. Mariani, Hector Gonzalez-Huizar, Masum Md Al Bhuiyan, Osei K. Tweneboah . Using Dynamic Fourier Analysis to Discriminate Between Seismic Signals from Natural Earthquakes and Mining Explosions. AIMS Geosciences, 2017, 3(3): 438-449. doi: 10.3934/geosci.2017.3.438
[3]	Shieh-Kung Huang, Kuan-Hao Tseng . Peak ground acceleration prediction and seismic intensity estimation based on ensemble framework for earthquake early warning in Taiwan. AIMS Geosciences, 2025, 11(3): 577-599. doi: 10.3934/geosci.2025025
[4]	Alessandro Demichelis, Malvina Ongaro . Public understanding and scientific uncertainty: The communication of risk in the L'Aquila earthquake. AIMS Geosciences, 2024, 10(3): 540-552. doi: 10.3934/geosci.2024028
[5]	Giovanni Messina . Belìce Valley: from earthquake to local development perspectives. AIMS Geosciences, 2019, 5(2): 265-272. doi: 10.3934/geosci.2019.2.265
[6]	Jean-Sébastien L'Heureux, Anders Lindgård, Arnfinn Emdal . The Tiller-Flotten research site: Geotechnical characterization of a very sensitive clay deposit. AIMS Geosciences, 2019, 5(4): 831-867. doi: 10.3934/geosci.2019.4.831
[7]	Teresa Vera San Martín, Leonardo Gutierrez, Mario Palacios, Erick Mas, Adriano Bruno, Shunichi Koshimura . Tsunami damage estimation in Esmeraldas, Ecuador using fragility functions. AIMS Geosciences, 2021, 7(4): 669-694. doi: 10.3934/geosci.2021040
[8]	Nora Tilly, Daniel Kelterbaum . Investigating the Surface and Subsurface in Karstic Regions – Terrestrial Laser Scanning versus Low-Altitude Airborne Imaging and the Combination with Geophysical Prospecting. AIMS Geosciences, 2017, 3(3): 352-374. doi: 10.3934/geosci.2017.3.352
[9]	Takaji Kokusho . State of the practice on energy-based liquefaction evaluation and research significance. AIMS Geosciences, 2024, 10(4): 792-863. doi: 10.3934/geosci.2024039
[10]	Karla E. Campos Díaz, José L. Álvarez Cruz, Miriam L. Lira Rodríguez, Erick R. Bandala . Coupled Inverse Fluidized Bed Bioreactor with Advanced Oxidation Processes for Treatment of Vinasse. AIMS Geosciences, 2017, 3(4): 538-551. doi: 10.3934/geosci.2017.4.538

Abstract

1. Introduction

The cardiovascular system is a complex dynamic system, which contains rich dynamics information to predict the physiological or pathological state. The traditional method for studying cardiovascular hemodynamics is to perform surgery on animals or humans, which is usually limited by ethics and experimental conditions ^[1,2]. As the method and tool in vitro, the numerical model and mock circulatory model can provide technical support for clinical noninvasive diagnosis ^[3]. The numerical modeling is the most widespread research technique due to its proven capability, efficiency and minimized cost in comparison to in-vitro studies in mock flow loop, or in-vivo studies in animals and humans ^[4].

The cardiovascular lumped parameter (CLP) model is a simplified numerical method to study hemodynamics. Researchers have done a lot of work in the CLP modeling in the past ten years. Some lumped parameter models for a single circulation loop were modeled ^[5,6,7]. For example, Figliola et al. ^[5] modeled a lumped parameter model including only right heart and pulmonary circulation. Simaan et al. ^[7] modeled a fifth-order lumped parameter circuit model for left heart and systemic circulation. These simplified Windkessel models can be used to simulate the hemodynamics of a single circulation loop. Some complete CLP models have been developed ^{[8,9,10,11,12,13]}. For example, a CLP model including systemic circulation, pulmonary circulation, and the heart with four chambers was proposed ^[8]. To simulate the hemodynamics of patients with heart failure, Gu et al. ^[9] established the CLP for patients with heart failure, and verified the effectiveness of physiological mechanism by the model. Abdi ^[10] used a lumped method to institute a cardiovascular model with 42 chambers, including arteries, veins, capillaries, and heart chambers. This model was used to evaluate the effect of the abnormal heartbeat on cardiovascular system performance. Although these models are capable of simulating the hemodynamics of the intact cardiovascular system, they are not combined with ventricular assist devices.

Since their first surgical implantation in the 1960s ^[14], ventricular assist devices play an active role in the treatment of heart failure. The new generation of LVADs use axial or centrifugal rotary pumps ^[15]. Compared with the first generation of pulsating pumps, the rotary pumps have the advantages of small size, high reliability, and durability. It is helpful for clinical management to comprehend the coupling relationship between the native heart and the rotary pump. Coupling modeling of the cardiovascular system and ventricular assist device (VAD) is a feasible way to explain the hemodynamic relationship between a native heart and a rotary pump. Shi et al. ^[4,14] proposed a coupled model for the cardiovascular system and VAD to simulate the hemodynamics under left ventricular (LV) failure with VAD support. CARDIOSIM^© is a developed simulator based on the CLP model by Lazzari ^{[15,16,17,18]}. It not only can be used to simulate the physiological and pathological hemodynamics, but also can be combined with various types of ventricular assist devices (pulsating pumps, rotary pumps, etc.). CARDIOSIM^© has also been applied in medical education ^[19]. Lim et al. ^[1] developed a coupled model between the cardiovascular system and implantable rotary blood pump, and it includes the left heart, right heart, systemic circulation, pulmonary circulation, and implantable rotary blood pump. Di et al. ^[20,21,22] established a complete CLP model, which could be connected with pulsating pumps or rotary pumps. In the case of cardiac dysplasia or heart failure, it is helpful to understand the effects of single or two VADs on hemodynamics. However, the autonomic regulation of the cardiovascular system is not considered in the above models.

Baroreflex is a kind of short-term autonomic nerve regulation, which plays a great role in short-term pressure control ^[23]. The work of Ursino ^[24] and Ottesen ^[25] indicates that the baroreflex system can maintain the stability of the hemodynamic environment by regulating neural effectors. Consequently, it is more autonomous and accurate for simulating hemodynamics that a combination of the CLP model and the baroreflex model to form a closed-loop control system. Certainly, baroreflex regulation was also considered in some coupled models for the cardiovascular system and VADs ^{[26,27,28,29,30,31,32]}. In these models, ventricular characteristics or systemic vascular resistance are usually altered to simulate the hemodynamics of the cardiovascular system with impaired heart function. Bozkurt et al. ^[27] reduced left ventricular systolic elastance to 0.5 mmHg/mL from 2.5 mmHg/mL to simulate a dilated cardiomyopathy (DCM) condition in the cardiovascular system model. Cox et al. ^[28] changed left ventricular contractility, initial left ventricular volume and systemic vascular resistance to simulate end-stage DCM. Lim et al. ^[32] decreased the end-systolic elastance value to 40% of normal to implement a heart-failure model. Heart failure is a complex syndrome, it is not only related to the cardiovascular system but also the baroreflex system. These models only consider ventricular characteristics or systemic vascular resistance to simulate heart failure, which is different from clinical observations. However, other hemodynamic parameters in the cardiovascular system, such as systemic vascular compliance and pulmonary vascular resistance, as well as some parameters in the baroreflex system, should also be considered. Otherwise, some changes in hemodynamic parameters during LVAD support and the prediction results of the LVAD operating condition will be affected. The application scope of the above model is limited. Therefore, it is necessary to develop a comprehensive numerical model and consider the mechanism of changes in the cardiovascular system and the baroreflex system to improve the simulation and prediction effect.

In this study, we aim to establish a CLP model coupled with the baroreflex model and the LVAD model to form a comprehensive numerical model, which provides a platform for the hemodynamics simulation and the noninvasive evaluation of LVAD operating condition.

This paper is organized in the following manner: The modeling of the coupling cardiovascular system is introduced in Section 2. Section 3 presents some results including the hemodynamics under different conditions and the hemodynamic variables at different pump speeds. Section 4 discusses the operating condition of HeartMate Ⅲ and its effect on hemodynamics. In addition, the limitations of this study are also described in Section 4. Lastly, conclusions are drawn on the outcomes of this study in Section 5.

2. Materials and method

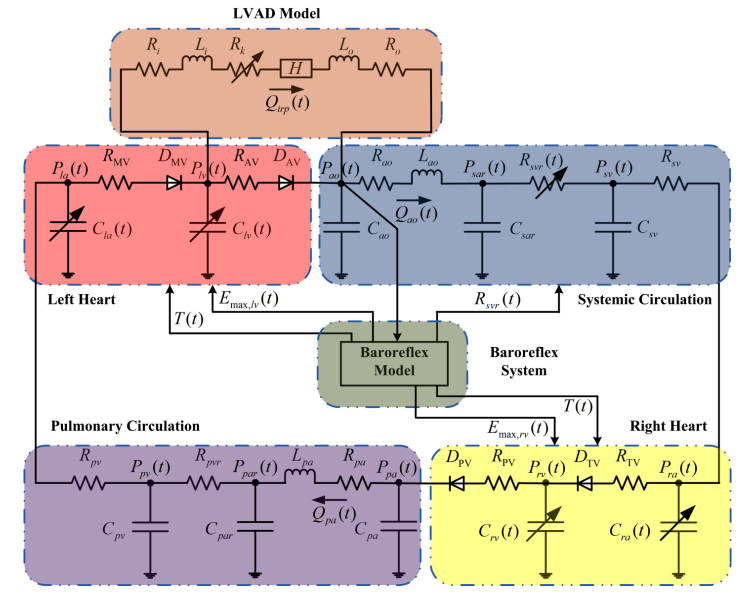
The comprehensive numerical model is illustrated in Figure 1. The numerical model was made up of three parts: a developed CLP model for describing the human cardiovascular circulation system, a baroreflex model for short-term neuroregulation, and an LVAD model for assisting diseased heart. The rotary pump was connected with the diseased heart in parallel. Thus, the pump inlet cannulae was connected to the left ventricular apex and the outlet cannulae was connected to the aorta.

Figure 1. Block diagram of numerical model.

$R$ ,

$L$ and

$C$ denote resistance, inertance and compliance,

$P$ and

$Q$ denote pressure and flow rate,

$D$ denotes ideal diodes,

$H$ is pressure difference between the inlet and outlet of the rotary pump,

$t$ and

$T$ are time variable and heart period,

${E_{\max }}$ denotes ventricular end-systolic elastance, subscripts

${\rm{MV}}$ ,

${\rm{AV}}$ ,

${\rm{TV}}$ and

${\rm{PV}}$ are mitral, aortic, tricuspid and pulmonary valves,

$lv$ ,

$la$ ,

$rv$ and

$ra$ denote left ventricle, left atrium, right ventricle and right atrium,

$ao$ and

$pa$ denote aorta and pulmonary artery,

$sar$ and

$par$ denote systemic artery and pulmonary arteriole,

$svr$ and

$pvr$ denote systemic vascular resistance and pulmonary vascular resistance,

$sv$ and

$pv$ denote systemic and pulmonary veins,

$irp$ is implantable rotary pump.

DownLoad: Full-Size Img PowerPoint

2.1. CLP Model

The lumped parameter method is to concentrate on the human cardiovascular circulation system into several chambers with organ and tissue functions. Each chamber is composed of Windkessel elements representing hemodynamic parameters. This method can not only reduce the number of parameters to improve computational efficiency, but also obtain global hemodynamics. In this paper, the cardiovascular circulation system was divided into four parts: left heart, right heart, systemic circulation, and pulmonary circulation. The heart is a four-chamber pump with time-varying elasticity. The direction of blood flow is controlled by the four valves of the heart. Each chamber of heart was modeled as a Windkessel model.

2.1.1. Ventricles

Suga et al. ^[33] show that the pressure-volume relationship of the ventricle can be expressed by a time-varying ventricle elastance. The ventricle elastance characterizes the elastic of ventricular myocardium and describes the dynamics of ventricular systole and diastole. Numerically, the ventricle elastance is generally defined as the ratio of pressure and volume in the ventricle. In the research field of the cardiovascular model, the ventricle elastance has been recognized and used ^{[1,4,7,11,13,18,21]}.

The time-varying elastances of the left and right ventricles:

${E_{lv}}(t) = \frac{1}{{{C_{lv}}(t)}} = \frac{{{P_{lv}}(t)}}{{{V_{lv}}(t) - {V_{lv, 0}}}}$

(1)

${E_{rv}}(t) = \frac{1}{{{C_{rv}}\;(t)}} = \frac{{{P_{rv}}\;(t)}}{{{V_{rv}}\;(t) - {V_{rv, 0}}}}$

(2)

where ${E_{lv}}(t)$ and ${E_{rv}}(t)$ are the time-varying elastances of left and right ventricles, ${C_{lv}}(t)$ and ${C_{rv}}(t)$ are the time-varying compliances of left and right ventricles, which are the reciprocals of ${E_{lv}}(t)$ and ${E_{rv}}(t)$ , ${P_{lv}}(t)$ and ${P_{rv}}(t)$ are pressures of left and right ventricles, ${V_{lv}}(t)$ and ${V_{rv}}(t)$ are volumes of left and right ventricles, ${V_{lv, 0}}$ and ${V_{rv, 0}}$ are theoretical volumes in the left and right ventricles at zero pressure.

However, when the pressure and volume of the ventricle are not be provided, the time-varying elastance cannot be determined. Accordingly, the calculation formulas commonly used in engineering are as follows ^[7]:

${E_{lv}}(t) = ({E_{\max , lv}} - {E_{\min , lv}}){E_{n, lv}}({t_n}) + {E_{\min , lv}}$

(3)

${E_{rv}}(t) = ({E_{\max , rv}} - {E_{\min , rv}}){E_{n, rv}}({t_n}) + {E_{\min , rv}}$

(4)

where ${E_{n, lv}}({t_n})$ and ${E_{n, rv}}({t_n})$ are the normalized elastic functions. The actions of the left and right ventricles are synchronous, therefore, the same normalized elastic function is used for the left ventricle and right ventricle.

${E_{n,lv}}({t_n}) = {E_{n,rv}}({t_n}) = 1.55 \times [\frac{{{{(\frac{{{t_n}}}{{0.7}})}^{1.9}}}}{{1 + {{(\frac{{{t_n}}}{{0.7}}\;)}^{1.9}}}}\;] \times [\frac{1}{{1 + {{(\frac{{{t_n}}}{{1.17}})}^{21.9}}\;\;}}]$

(5)

${t_n} = \frac{t}{{0.2 + 0.15T}}$

(6)

$T = 60/{\rm{HR}}$

(7)

where $t$ and $T$ are time variable and heart period, ${\rm{HR}}$ is heart rate, ${E_{\max, lv}}$ and ${E_{\min, lv}}$ are left ventricular end-systolic elastance and left ventricular end-diastolic elastance, ${E_{\max, rv}}$ and ${E_{\min, rv}}$ are right ventricular end-systolic elastance and right ventricular end-diastolic elastance.

2.1.2. Atria

The atrium also contracts and relaxes periodically similar to the ventricle, but its contractility is much smaller than that of the ventricle. The main function of the atrium is to store venous blood. Similarly, the time-varying elastance was adopted to describe the pressure-volume relationship of the atrium. The states of the left and right atria are modeled by the time-varying compliances ${C_{la}}(t)$ and ${C_{ra}}(t)$ . ${E_{la}}(t)$ and ${E_{ra}}(t)$ are the time-varying elastances of left and right atria. ${E_{la}}(t)$ and ${E_{ra}}(t)$ can be expressed by Eqs (8) and (9). The meanings of other parameters have resemblance with those for ventricles.

${E_{la}}(t) = \frac{1}{{{C_{la}}(t)}} = \frac{{{P_{la}}(t)}}{{{V_{la}}(t) - {V_{la, 0}}}}$

(8)

${E_{ra}}(t) = \frac{1}{{{C_{ra}}(t)}} = \frac{{{P_{ra}}(t)}}{{{V_{ra}}(t) - {V_{ra, 0}}}}$

(9)

Although the activities of the atrium and ventricle are asynchronous, the formulas for calculating atrial elastances are similar to those for the ventricles. The expressions of ${E_{la}}(t)$ and ${E_{ra}}(t)$ are as follows ^[14]:

${E_{la}}(t) = \frac{{({E_{\max ,la}}\;\; - {E_{\min ,la}}\;\;)}}{2}{e_{la}}(t) + {E_{\min ,la}}$

(10)

${E_{ra}}(t) = \frac{{({E_{\max ,ra}}\;\; - {E_{\min ,ra}}\;\;)}}{2}{e_{ra}}(t) + {E_{\min ,ra}}$

(11)

where ${E_{\max, la}}$ and ${E_{\min, la}}$ are left atrial end-systolic elastance and left atrial end-diastolic elastance, ${E_{\max, ra}}$ and ${E_{\min, ra}}$ are right atrial end-systolic elastance and right atrial end-diastolic elastance, ${e_{la}}(t)$ and ${e_{ra}}(t)$ are the activation functions of the left and right atria.

The synchronous property of left and right atria gives rise to the same activation functions for left and right atria.

${e_{la}}(t) = {e_{ra}}(t) = \left\{ \begin{gathered} 0, \quad \quad \quad \quad \quad \, \, \, \, \;\;\, 0 \leqslant t \lt {T_{asb}} \\ 1 - \cos (\frac{{t - {T_{asb}}}}{{{T_{ase}}{\rm{ - }}{T_{asb}}}}2\pi ), {T_{asb}} \leqslant t \lt {T_{ase}} \\ 0, \quad \quad \quad \quad \quad \, \, \, \, \;\;\, {T_{ase}} \leqslant t \lt T \\ \end{gathered} \right.$

(12)

where ${T_{asb}}$ is the beginning time of atrium contraction and ${T_{asb}} = 0.9T$ , ${T_{ase}}$ is the end time of atrium contraction and ${T_{ase}} = 0.09T + {T_{asb}}$ .

2.1.3. Valves

The heart valves prevent blood from flowing back, it comprises the mitral and tricuspid valves between the atria and ventricles, as well as the aortic and pulmonary valves between the ventricles and arteries. The opening and closing of the valve are similar to the short circuit and open circuit of an ideal diode. Consequently, the circuit model for the valve can be represented by resistor in series ideal diode. Take the aortic valve in for example. The circuit model of the aortic valve is composed of aortic valve resistance ${R_{{\rm{AV}}}}$ and ideal diode ${D_{{\rm{AV}}}}$ , and the opening or closing of the valve is controlled by the difference between the left ventricular pressure ${P_{lv}}$ and the aortic pressure ${P_{ao}}$ . If ${P_{lv}}{\rm{ - }}{P_{ao}} > 0$ , the aortic valve is opened and the flow rate through the valve is ${{({P_{lv}} - {P_{ao}})} / {{R_{{\rm{AV}}}}}}$ , otherwise the aortic valve is closed and the flow rate is 0.

The states of the valve are determined by the transvalvular pressure difference. The function of transvalvular pressure difference $\gamma (\xi)$ is introduced:

$\gamma (\xi ) = \left\{ \begin{gathered} \xi , \quad {\rm{if}} \quad\xi \gt 0 \\ 0, \quad {\rm{if}} \quad \xi \leqslant 0 \\ \end{gathered} \right.$

(13)

The valve flow rate ${Q_V}$ is as follow:

${Q_V} = \frac{1}{{{R_V}}}\gamma (\xi )$

(14)

where $\xi$ is the transvalvular pressure difference, ${Q_V}$ is the flow rate through the valve and the $V$ is the abbreviation of the valve.

2.1.4. Systemic circulation and pulmonary circulation

The systemic circulation is separated into aorta, artery, arteriole, capillary, and vein segments. The aorta was regarded as a vascular chamber with resistance, inertance, and compliance. The artery segment was considered as a vascular chamber with resistance and compliance. The primary role of the arteriole and capillary is to provide resistance to blood flow. Arteriole and capillary were modeled as a vascular chamber with resistance. The vascular resistance is provided by the artery, arteriole, and capillary. All levels of veins were modeled as a vascular chamber. Collecting and storing blood are primary roles played by veins that are possessed of greater compliance. The model for pulmonary circulation is similar to that for systemic circulation.

There is an analogy between fluid network and electric network. An electrical analogy is typically used where pressure is analogous to voltage, flow rate is analogous to electric current, resistance is analogous to resistor, inertance is analogous to inductor, and compliance is analogous to capacitor ^[12,34]. On account of an electrical network is applied to the blood circulation system, this paper used the Kirchhoff's law to expound the coupling relationship between the branches of the blood circulation system. Using the notation given in Figure 1, the equations of the instantaneous pressure and flow rate for systemic circulation are given as follows.

The flow rate balance equations are:

${C_{ao}} \cdot \frac{{d{P_{ao}}(t)}}{{dt}} = \frac{{\gamma ({P_{lv}}(t) - {P_{ao}}(t))}}{{{R_{{\rm{AV}}}}}} - {Q_{ao}}(t) + {Q_{irp}}$

(15)

${C_{sar}} \cdot \frac{{d{P_{sar}}(t)}}{{dt}} = {Q_{ao}}(t) - \frac{{{P_{sar}}(t) - {P_{sv}}(t)}}{{{R_{svr}}(t)}}$

(16)

${C_{sv}} \cdot \frac{{d{P_{sv}}(t)}}{{dt}} = \frac{{{P_{sar}}(t) - {P_{sv}}(t)}}{{{R_{svr}}(t)}} - \frac{{{P_{sv}}(t) - {P_{ra}}(t)}}{{{R_{sv}}}}$

(17)

The pressure balance equation is:

${L_{ao}} \cdot \frac{{d{Q_{ao}}(t)}}{{dt}} = {P_{ao}}(t) - {R_{ao}} \cdot {Q_{ao}}(t) - {P_{sar}}(t)$

(18)

2.2. Baroreflex model

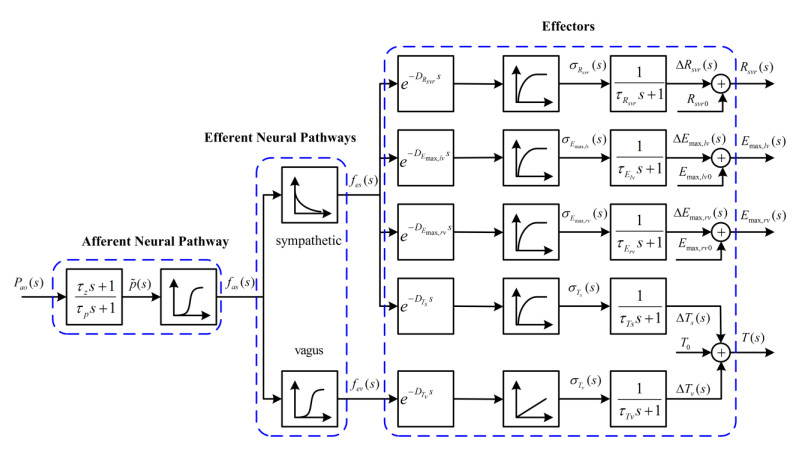
According to Ursino et al. ^[24], the baroreflex model was conducted in the order of afferent neural pathway, efferent neural pathways and effectors. In this study, the baroreflex model was modified to control the corresponding effectors in the cardiovascular system: systemic vascular resistance, left ventricular end-systolic elastance, right ventricular end-systolic elastance, and heart period. The open-loop control system for baroreflex regulation is shown in Figure 2.

Figure 2. Block diagram describing the baroreflex model in complex domain.

DownLoad: Full-Size Img PowerPoint

2.2.1. Afferent neural pathway

Ursino et al. ^[24] described the relationship between arterial pressure and the activity of the afferent nerves by considering two main aspects arising from experiments. First, the relationship between arterial pressure and afferent nerve activity in static conditions exhibits a sigmoidal shape with upper saturation and lower threshold. Second, the arterial baroreceptors are sensitive not only to the arterial pressure but also to its rate of change. These two properties have been reproduced by representing the arterial baroreceptors plus the afferent neural pathway as a first-order linear differential equation, with a static gain and a rate-dependent gain, connected in series with a sigmoidal static function.

${\tau _p} \cdot \frac{{d\tilde p(t)}}{{dt}} + \tilde p(t) = {\tau _z} \cdot \frac{{d{p_{ao}}(t)}}{{dt}} + {p_{ao}}(t)$

(19)

${f_{as}}(t) = \frac{{{f_{\min }}\; + {f_{\max }}\; \cdot {e^{[\tilde p\;(t) - {p_n}\;]/{k_a}}}}}{{1 + {e^{[\tilde p(t) - {p_{n\;}}]/{k_a}}}}}$

(20)

where ${\tau _p}$ and ${\tau _z}$ are the time constants, aortic pressure ${p_{ao}}$ is used as the input pressure to arterial baroreceptors, $\tilde p$ is the output variable of a first-order linear differentiator, ${f_{as}}$ is the frequency of spikes in the afferent fibers, ${f_{\min }}$ and ${f_{\max }}$ are the lower and upper saturation of the frequency discharge, ${p_n}$ is the pressure value at the central point of the sigmoidal functional, ${k_a}$ is a parameter with the dimension of pressure, related to the slope of the static function at the central point, and ${1 /{{k_a}}}$ denotes the baroreceptor sensitivity.

2.2.2. Efferent neural pathways

The efferent pathway includes the efferent sympathetic pathway and efferent vagal pathway. Increasing the frequency of spikes in the afferent fibers results in a decrease in the frequency of the sympathetic fibers and in an increase in vagal activity. These relationships have been reproduced by using a monotonically decreasing monoexponential static curve for the sympathetic efferent activity and a monotonically increasing exponential curve, with upper saturation, for the vagal activity.

${f_{es}}(t) = {f_{es, \infty }} + ({f_{es, 0}} - {f_{es, \infty }}) \cdot {e^{ - {k_{es}} \cdot {f_{as}}(t)}}$

(21)

${f_{ev}}(t) = \frac{{{f_{ev,0}} + {f_{ev,\infty }}\; \cdot \;{e^{[{f_{as}}\;(t) - {f_{as,0}}\;]/{k_{ev}}}}}}{{1 + {e^{[{f_{as}}(t) - {f_{as,0}}\;]/{k_{ev}}}}}}$

(22)

where ${f_{es}}$ is the frequency of spikes in the efferent sympathetic nerves, ${f_{es, \infty }}$ , ${f_{es, 0}}$ and ${k_{es}}$ are constants with ${f_{es, 0}} > {f_{es, \infty }}$ , ${f_{ev}}$ is the frequency of spikes in the efferent vagal fibers, ${f_{ev, \infty }}$ , ${f_{ev, 0}}$ and ${k_{ev}}$ are constant parameters with ${f_{ev, 0}} > {f_{ev, \infty }}$ , and ${f_{as, 0}}$ is the central value in Eq 20.

2.2.3. Effectors

All the effectors in the cardiovascular model change in response to stimulation of sympathetic nerves. The response of a generic effector to sympathetic stimulation includes a pure delay, a monotonic logarithmic static function, and a linear first-order dynamics with a real time constant. The use of logarithmic relationships is justified because the effector static response exhibits a rapid slope at low sympathetic frequencies and then progressively flattens. Of course, the static function is monotonically increasing when the systemic vascular resistance and the end-systolic elastances (left and right ventricles) are considered but monotonically decreasing when heart period is considered. Finally, the first-order dynamics simulates the time required for the effectors to progressively complete its action.

${\sigma _\theta }(t) = \left\{ \begin{gathered} {G_\theta } \cdot \ln [{f_{es}}(t - {D_\theta }) - {f_{es, \min }} + 1], \;if\;{f_{es}} \geqslant {f_{es, \min }} \\ 0, \quad \quad \quad \quad \quad \quad \quad \quad \;\, \, \, \, \, \quad \;\;\, \, if\;{f_{es}} \lt {f_{es, \min }} \\ \end{gathered} \right.$

(23)

$\frac{{d\Delta \theta (t)}}{{dt}} = \frac{1}{{{\tau _\theta }}} \cdot [ - \Delta \theta (t) + {\sigma _\theta }(t)]$

(24)

$\theta (t) = \Delta \theta (t) + {\theta _0}$

(25)

where $\theta$ denotes the generic controlled parameter ( ${R_{svr}}$ , ${E_{\max, lv}}$ , ${E_{\max, rv}}$ , or $T$ ), $\Delta \theta$ is the parameter change caused by sympathetic stimulation, ${\sigma _\theta }$ is the output of the static characteristic, ${\tau _\theta }$ and ${D_\theta }$ are the time constant and pure latency, ${f_{es, \min }}$ is a threshold for sympathetic stimulation, ${G_\theta }$ is a constant gain factor, and ${\theta _0}$ denotes generic controlled parameter in the absence of cardiac innervation.

Heart period is affected not only by the sympathetic but also by the vagal activity. However, the static relationship is assumed to be linear, i.e., heart period increases proportionally to vagal stimulation. The final heart period level is then computed by summing the positive changes induced by the vagal stimulation, the negative changes induced by the sympathetic stimulation, and a constant level representing heart period in the absence of cardiac innervation. Hence, the two mechanisms interact linearly in the heart period control. Of course, this is a crude simplification of the real sympathetic-parasympathetic interaction. However, it provides an acceptable approximation of heart rate changes under a variety of physiological conditions.

${\sigma _{{T_s}}}(t) = \left\{ \begin{gathered} {G_{{T_s}}} \cdot \ln [{f_{es}}(t - {D_{{T_s}}}) - {f_{es, \min }} + 1], \;if\;{f_{es}} \geqslant {f_{es, \min }} \\ 0, \quad \quad \quad \quad \quad \quad \quad \quad \, \;\;\, \, \, \, \;\;\;\;\;\, \, \, if\;{f_{es}} \lt {f_{es, \min }} \\ \end{gathered} \right.$

(26)

$\frac{{d\Delta {T_s}(t)}}{{dt}} = \frac{1}{{{\tau _{{T_s}}}}} \cdot [ - \Delta {T_s}(t) + {\sigma _{{T_s}}}(t)]$

(27)

${\sigma _{{T_v}}}(t) = {G_{{T_v}}} \cdot {f_{ev}}(t - {D_{{T_v}}})$

(28)

$\frac{{d\Delta {T_v}(t)}}{{dt}} = \frac{1}{{{\tau _{{T_v}}}}} \cdot [ - \Delta {T_v}(t) + {\sigma _{{T_v}}}(t)]$

(29)

$T = {T_0} + \Delta {T_s} + \Delta {T_v}$

(30)

where $\Delta {T_s}$ and $\Delta {T_v}$ denote sympathetic and vagal stimulation, ${\sigma _{{T_s}}}$ and ${\sigma _{{T_v}}}$ are the sympathetic and vagal activities, ${\tau _{{T_s}}}$ and ${D_{{T_s}}}$ are the time constant and pure latency for sympathetic, ${\tau _{{T_v}}}$ and ${D_{{T_v}}}$ are the time constant and pure latency for vagus, ${G_{{T_s}}}$ and ${G_{{T_v}}}$ are constant gain factors, and ${T_0}$ denotes heart period in the absence of cardiac innervation.

2.3. LVAD model

A continuous flow LVAD model was connected to the left ventricular and aortic of the CLP model in . It added one state variable to the original model, namely the pressure difference between the pump outlet and pump inlet $H$ as a function of pump flow rate and speed ^[4]:

$H = {\beta _a} \cdot {Q_{irp}}^2(t) + {\beta _b} \cdot {Q_{irp}}(t) \cdot \omega (t) + {\beta _c} \cdot {\omega ^2}(t)$

(31)

where ${Q_{irp}}$ is the pump flow rate (mL/s), $\omega$ is pump speed (revolutions per minute, rpm), and ${\beta _a}$ , ${\beta _b}$ , ${\beta _c}$ are coefficients associated with a rotary pump. In this study, ${\beta _a}$ = −1.8×10⁻³ mmHg·s²·mL⁻², ${\beta _b}$ = −1.2×10⁻⁵ mmHg·s·mL⁻¹·rpm⁻¹ and ${\beta _c}$ = 7.3×10⁻⁶ mmHg·rpm⁻² are derived from a centrifugal pump HeartMate III. Also, corresponding parameters for the resistance and inertance of the outflow cannulae are ${R_i}$ = 0.0677 mmHg·s·mL⁻¹, and ${L_i}$ = 0.0127 mmHg·s²·mL⁻¹. HeartMate III is directly connected to the left ventricular apex and it does not possess inflow cannulae. Therefore, in this study, the parameters for the resistance and inertance of the inflow cannulae are set to 0.

A nonlinear time-varying resistor ${R_k}$ is inserted between the inflow cannulae and the left ventricle to simulate the potential suction event ^[35].

${R_k}(t) = \left\{ \begin{gathered} 0\;, \quad \quad \quad \quad \;\, \, \;\;\;if\;{P_{lv}}(t) \gt \bar P \\ \alpha ({P_{lv}}(t) - \bar P)\;, \quad if\;{P_{lv}}(t) \leqslant \bar P \\ \end{gathered} \right.$

(32)

where $\alpha$ is weight parameter and its value is taken as −3.5 s/mL, $\bar P$ is threshold pressure, and its value is taken as 1 mmHg.

2.4. Simulation protocol

In this study, most parameters under normal conditions in the CLP model and the baroreflex model have values taken from the published literature. The parameters in the CLP model were assigned the values shown in Table A.1 based on the parameter selection in ^[7,14,31]. The parameters in the baroreflex model were set as shown in Table A.2 according to Ref. ^[24]. Table A.1 and Table A.2 were listed in Appendix A.

Compared with normal conditions, heart failure can cause a series of changes, including changes in the cardiovascular system and the baroreflex system. Dilated cardiomyopathy (DCM) is the most common type of nonischemic cardiomyopathy and a major cause of congestive heart failure. The hemodynamic characteristics of patients with DCM usually show some changes, including decreased ventricular end-systolic elastance, increased heart rate, increased systemic vascular resistance, decreased systemic vascular compliance, and increased pulmonary vascular resistance ^[9]. Meanwhile, in the baroreflex system, the baroreflex sensitivity and baroreflex gain for heart failure decreased ^[36,37]. These qualitative and quantitative changes can be mapped into the heart failure model. In the heart failure model, initial changes in left ventricular end-systolic elastance, heart rate, and systemic vascular resistance were simulated by decreasing ${E_{\max, lv0}}$ , ${T_0}$ , and increasing ${R_{svr0}}$ . Besides, increases in ${C_{sar}}$ , ${R_{pvr}}$ , and ${R_{pv}}$ represented increased systemic arterial compliance and pulmonary circulation resistance. A decrease in ${1 / {{k_a}}}$ indicated a decrease in baroreflex sensitivity. The gain constants ( ${G_{{R_{svr}}}}$ , ${G_{{E_{\max, \, lv}}}}$ , ${G_{{E_{\max, \, rv}}}}$ , ${G_{{T_s}}}$ , and ${G_{{T_v}}}$ ) were reduced to simulate the change in the baroreflex gain. The parameters were adjusted to simulate the pathological condition of LV failure, and it was set as shown in Table A.3. Table A.3 was listed in Appendix A.

In this study, a series of hemodynamic responses were conducted under normal condition (no LV failure or LVAD support), LV failure condition (no LVAD support) and LV failure condition with different levels of LVAD support (2200 rpm, 3700 rpm, 4300 rpm). In addition, some variables were compared under different conditions, including pressure, flow rate, volume, heart rate, etc. The area of ventricular pressure-volume (P-V) loop can usually be used to measure ventricular stroke work ^[21]. Consequently, the ventricular P-V loop can provide information about the unloading of the ventricle. The P-V loops under different conditions were also compared in this study.

With different levels of pump support, the LVAD operating condition can be evaluated by changes in pump flow rate and physiological variables. Firstly, the HeartMate III pump speed increased linearly from 0 rpm to 5500 rpm within 60 s. The pump speed range, without pump regurgitation and ventricular suction, could be preliminarily determined by the information of the instantaneous pump flow rate during the linear increase in pump speed. The preliminary speed range was obtained by an instantaneous increase in speed, and it may have errors compared to the stable result with constant speed support. Thus, it is necessary to analyze the hemodynamic variables under constant speed support. Then, the constant pump speeds with 100 rpm interval were selected in the preliminary pump speed range, and the stable values of hemodynamic variables corresponding to constant speeds were calculated.

According to the numerical model described above, a program was developed in MATLAB 2010b (The MathWorks Inc., USA) to perform different simulation experiments. The ode45 solver was used to solve time-varying differential equations. In the system of differential equations, the variable values obtained in the last ode45 calculation was used as the initial value in the next ode45 calculation, and the calculation was repeated until the set time was reached. The time step was set to 0.001 second. All simulation times were set to 60 seconds. The system reaches a stable periodic solution after about 15 seconds. The stable result from the 58th to 60th seconds was chosen in all simulated cases for analysis.

3. Results

3.1. Hemodynamic response under normal condition

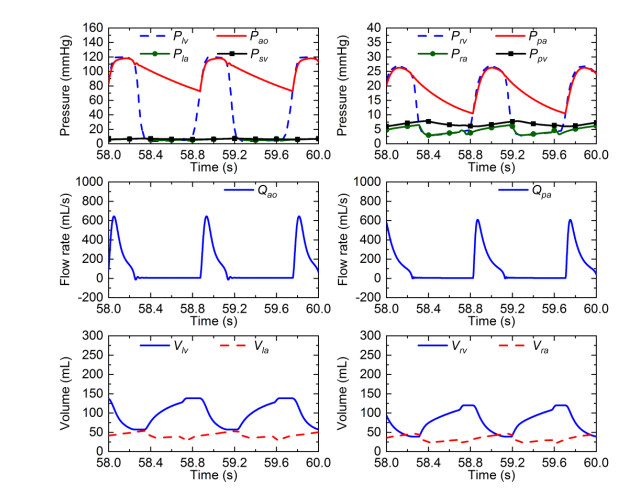
Figure 3 depicts the changes in pressure, flow, and volume under normal condition.

Figure 3. Pressures in left ventricle (

${P_{lv}}$ ), left atrium (

${P_{la}}$ ), aorta (

${P_{ao}}$ ), systemic vein (

${P_{sv}}$ ), right ventricle (

${P_{rv}}$ ), right atrium (

${P_{ra}}$ ), pulmonary artery (

${P_{pa}}$ ), and pulmonary vein (

${P_{pv}}$ ), total flow rates through aorta (

${Q_{ao}}$ ) and pulmonary artery (

${Q_{pa}}$ ), and volumes in left ventricle (

${V_{lv}}$ ), left atrium (

${V_{la}}$ ), right ventricle (

${V_{rv}}$ ) and right atrium (

${V_{ra}}$ ) under normal condition.

DownLoad: Full-Size Img PowerPoint

The heart rate was about 68 bpm (beat per minute, bpm).

The left ventricular systolic pressure was 120 mmHg, the aortic pressure changed between 73 and 118 mmHg, and the systemic venous pressure was about 7 mmHg. The right ventricular pressure changed between 3 and 27 mmHg, pulmonary artery changed between 10 and 27 mmHg, and pulmonary venous pressure was about 7 mmHg. The pressures of the left and right atria fluctuated slightly, ranging from 4 to 7 mmHg and 3 to 7 mmHg, respectively.

The left or right ventricle had a stroke volume of about 81 mL and a cardiac output of about 5.5 L/min.

The peak flow rate of the aorta or pulmonary artery was close to 700 mL/s.

These data and waveforms are all consistent with hemodynamic information in the Textbook of Medical Physiology ^[38,39].

3.2. Hemodynamic response under LV failure condition

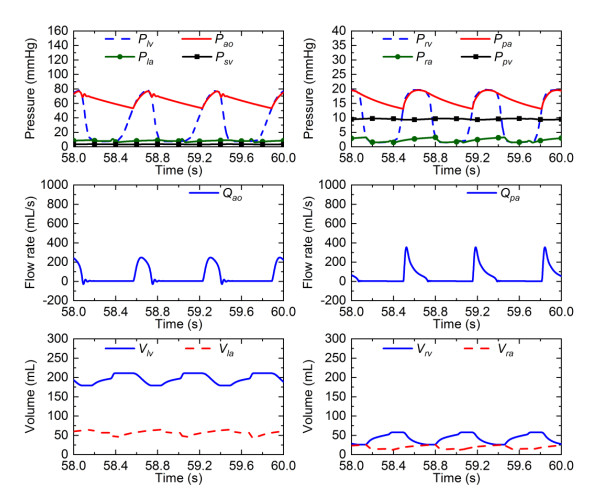
The hemodynamic response under the LV failure condition is given in Figure 4.

Figure 4. Pressures in left ventricle (

${P_{lv}}$ ), left atrium (

${P_{la}}$ ), aorta (

${P_{ao}}$ ), systemic vein (

${P_{sv}}$ ), right ventricle (

${P_{rv}}$ ), right atrium (

${P_{ra}}$ ), pulmonary artery (

${P_{pa}}$ ), and pulmonary vein (

${P_{pv}}$ ), total flow rates through aorta (

${Q_{ao}}$ ) and pulmonary artery (

${Q_{pa}}$ ), and volumes in left ventricle (

${V_{lv}}$ ), left atrium (

${V_{la}}$ ), right ventricle (

${V_{rv}}$ ) and right atrium (

${V_{ra}}$ ) under LV failure condition.

DownLoad: Full-Size Img PowerPoint

The heart rate was adjusted to 91 bpm. LV failure caused an increase in heart rate.

The aortic pressure range was reduced from the normal value of 73–118 mmHg to the current 53−77 mmHg, the value of aortic pulse pressure (the difference between the maximum systolic pressure and minimum diastolic pressure) was reduced from the normal value of 45 mmHg to the current value of 24 mmHg, and the left ventricular systolic pressure was reduced from the normal value of 120 mmHg to the current value of 78 mmHg. The pressures of the left atrium and pulmonary vein were elevated to about 10 mmHg, almost increased 43% from the normal value of about 7 mmHg. When the LV failure develops further and the pressure of the pulmonary vein is elevated to above 18 mmHg, pulmonary edema will manifest itself and serious consequence of pulmonary failure will follow ^[39].

The peak flow rate of the aorta or pulmonary artery was reduced about 60% of the normal healthy values.

It is observed that there are prominent changes to all four-chamber volumes in the heart. The current LV volume varied between 179 and 211 mL, greatly elevated from the normal range of 57−138 mL. The stroke volume decreased from the normal value of 81 mL to the current value of 32 mL. The ejection fraction (the ratio of stroke volume to end-diastolic volume) is usually not less than 50%, but the current ejection fraction of the left ventricle was about 15%. The current value of cardiac output in the left ventricle (LVCO) was 2.9 L/min, which was reduced 47% from the normal value of 5.5 L/min. The left atrial volume was also increased from the normal range of 28−54 mL to the current range of 43−65 mL. Accompanying the dilation in the left heart, there was a great volume reduction in the right ventricle and atrium. The right ventricle volume was reduced from the normal range of 39−120 mL to the current range of 26−58 mL. The right atrial volume was also reduced from the normal range of 22−47 mL to the current range of 12−26 mL.

3.3. Hemodynamic response under LVAD support

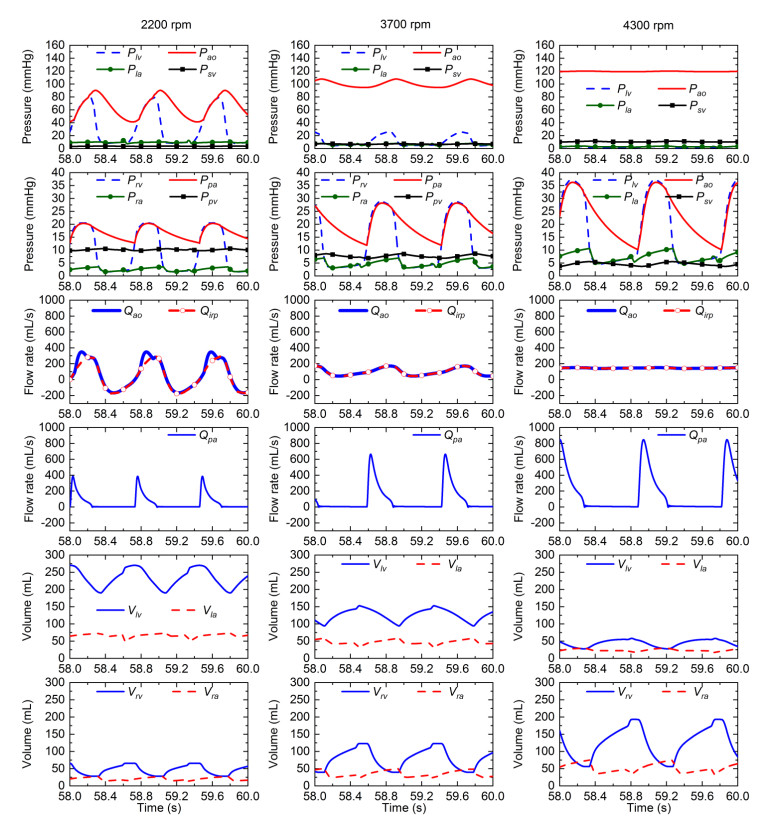
Figure 5 shows the changes in pressure, flow rate, and volume under HeartMate III support at low (2200 rpm), medium (3700 rpm), and high (4300 rpm) speeds.

Figure 5. Pressures in left ventricle (

${P_{lv}}$ ), left atrium (

${P_{la}}$ ), aorta (

${P_{ao}}$ ), systemic vein (

${P_{sv}}$ ), right ventricle (

${P_{rv}}$ ), right atrium (

${P_{ra}}$ ), pulmonary artery (

${P_{pa}}$ ), and pulmonary vein (

${P_{pv}}$ ), total flow rates through aorta (

${Q_{ao}}$ ) and pulmonary artery (

${Q_{pa}}$ ), and volumes in left ventricle (

${V_{lv}}$ ), left atrium (

${V_{la}}$ ), right ventricle (

${V_{rv}}$ ) and right atrium (

${V_{ra}}$ ) under HeartMate III support at 2200 rpm, 3700 rpm or 4300 rpm.

DownLoad: Full-Size Img PowerPoint

Under LV failure condition with pump support at 4300 rpm, left ventricular pressure approached 0 mmHg and the pressure and flow rate in aorta almost lost its pulsation. Further increased in the support level could cause a collapse in the left ventricle.

At 2200 rpm pump operating speed, the flow rates in the rotary pump and aorta had the intermittent regurgitation (the negative flow rate in numerical model represents regurgitation) and the aortic peak flow rate was larger than that of rotary pump over a heart period. It suggested that the total aortic flow rate was provided by both the left ventricle and the rotary pump.

At 3700 rpm or 4300 rpm, the total aortic flow rate and the pump flow rate completely coincided and the aortic pressure was greater than the left ventricular pressure over a heart period. It indicated that the current aortic valve was closed and the total aortic flow rate was completely provided by the rotary pump.

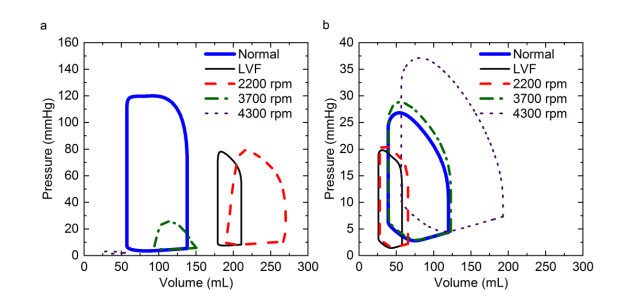
Figure 6 gives the left and right ventricular P-V loops under normal condition, LV failure condition, and different levels of pump support.

Figure 6. The (a) left ventricular P-V loop and (b) right ventricular P-V loop under normal condition (Normal), LV failure condition (LVF) and LVAD support at 2200 rpm, 3700 rpm or 4300 rpm.

DownLoad: Full-Size Img PowerPoint

In contrast to the P-V loop in normal condition, the left ventricular P-V loop shifted to the right due to left ventricular end-diastolic volume dilation in the LV failure condition (Figure 6a). At the same time, the area of the left ventricular P-V loop decreased because of the decreased left ventricular end-systolic pressure and stroke volume. In addition, the right ventricular P-V loop shifted to left and its area decreased in LV failure condition relative to that in normal condition (Figure 6b). Compared with the P-V loop in LV failure condition, the left ventricular P-V loop shifted to the right and its area (stroke work) increased due to increased left ventricular end-diastolic volume and end-systolic pressure at 2200 rpm operating speed. Moreover, at 3700 rpm or 4300 rpm pump operating speed, the left ventricular P-V loop shifted to left and its area decreased, even near to 0 (Figure 6a). With the increase of pump support level, the right ventricular P-V loop continuously shifted to the right and its area (stroke work) was also increasing relative to that in LV failure condition (Figure 6b). And the area of the right ventricular P-V loop at 3700 rpm was relatively closer to that under normal condition.

Ranges of pressures and volumes in left and right heart, arterial and venous pressures, cardiac output, ventricular end-systolic elastances, systemic vascular resistance, and heart rate are shown in Table 1 under different conditions. Under LVAD support, the cardiac output in the left heart was provided by both left ventricle and rotary pump.

Table 1. Simulation values of hemodynamic variables under normal condition, LV failure condition and LVAD support at 2200 rpm, 3700 rpm or 4300 rpm.

	Normal	LVF	2200 rpm	3700 rpm	4300 rpm
${P_{lv}}$ ( ${\rm{mmHg}}$ )	4−120	8−78	8−79	4−26	1−3
${P_{rv}}$ ( ${\rm{mmHg}}$ )	3−27	2−20	2−21	3−29	5−37
${P_{la}}$ ( ${\rm{mmHg}}$ )	4−8	6−11	7−13	5−8	2−4
${P_{ra}}$ ( ${\rm{mmHg}}$ )	3−7	1−3	2−4	3−7	5−11
${P_{ao}}$ ( ${\rm{mmHg}}$ )	73−118	53−77	41−90	95−108	119−120
${P_{pa}}$ ( ${\rm{mmHg}}$ )	10−26	13−20	13−20	12−28	10−36
${\rm{MAP}}$ ( ${\rm{mmHg}}$ )	97	64.2	63.9	100	119.5
${\rm{MPAP}}$ ( ${\rm{mmHg}}$ )	18	17	17	20	23
${P_{sv}}$ ( ${\rm{mmHg}}$ )	7	3	4	7	11
${P_{pv}}$ ( ${\rm{mmHg}}$ )	7	10	10	8	5
${V_{lv}}$ ( ${\rm{mL}}$ )	57−138	179−211	190−270	94−153	28−58
${V_{rv}}$ ( ${\rm{mL}}$ )	39−120	26−58	28−66	40−123	56−193
${V_{la}}$ ( ${\rm{mL}}$ )	28−54	43−65	50−73	32−58	16−30
${V_{ra}}$ ( ${\rm{mL}}$ )	22−47	12−26	13−27	23−50	34-75
${\rm{LVCO}}$ ( ${\rm{L/min}}$ )	5.5	2.9	3.1	6.0	8.7
${\rm{RVCO}}$ ( ${\rm{L/min}}$ )	5.5	2.9	3.1	6.0	8.7
${E_{\max, lv}}$ ( ${\rm{mmHg}}/{\rm{mL}}$ )	2.19	0.44	0.38	0.25	0.14
${E_{\max, \, rv}}$ ( ${\rm{mmHg}}/{\rm{mL}}$ )	0.84	1.19	1.09	0.88	0.71
${R_{svr}}$ ( ${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}}$ )	0.95	1.23	1.12	0.89	0.71
${\rm{HR}}$ ( ${\rm{bpm}}$ )	68	91	83	72	64
* MAP and MPAP denote mean aortic pressure and mean pulmonary artery pressure, LVCO and RVCO denote cardiac output in left ventricle and right ventricle

| Show Table

DownLoad: CSV

Compared with the LV failure condition, the ranges of pressures and volumes in the left or right heart increased at 2200 rpm. But the ranges of pressures and volumes in the left heart decreased and them in the right heart increased, at 3700 rpm or 4300 rpm. Furthermore, both arterial pressure and cardiac output increased with the LVAD support. At 3700 rpm, the mean aortic pressure (MAP) was 100 mmHg and cardiac output in the left ventricle (LVCO) or right ventricle (RVCO) was 6 L/min, which was closer to that in normal condition. With the increase of the LVAD support level, the values of left or right ventricular end-systolic elastance, systemic vascular resistance, and heart rate decreased. At 3700 rpm LVAD operating speed, the heart rate was restored from 91 bpm in LV failure condition to the current 72 bpm.

3.4. Effect of pump speed on hemodynamic variables

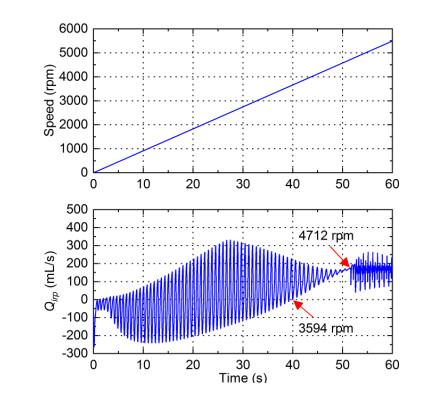
Figure 7 shows the instantaneous pump flow rate during a linear increase in pump speed from 0 rpm to 5500 rpm. The pump flow rate had instantaneous or persistent regurgitation when the pump speed was between 0 and 3594 rpm. And the pump regurgitation disappeared when pump speed was higher than 3594 rpm. However, the amplitude of the pump flow rate signal suddenly increased when the speed reached 4712 rpm. It indicated that the left ventricle had an onset of suction. Therefore, the preliminary pump speed range should be between 3594 rpm and 4712 rpm.

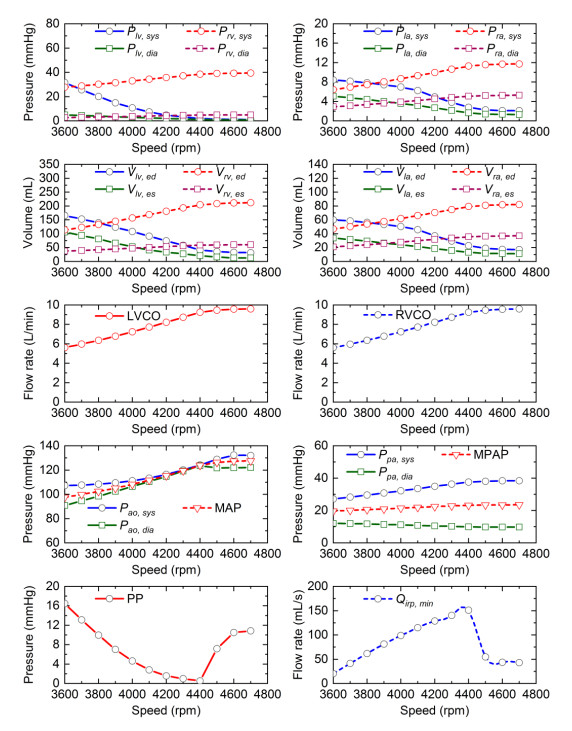
Figure 7. Pump flow rate signal (Q_irp) as a function of linearly increasing pump speed.

DownLoad: Full-Size Img PowerPoint

For convenience of calculation, the constant speeds were varied from 3600 rpm to 4700 rpm with 100 rpm interval, and the corresponding changes in hemodynamic variables are shown in Figure 8.

Figure 8. The hemodynamic variables under LV failure with LVAD support as a function of constant speed varied from 3600 rpm to 4700 rpm with 100 rpm interval.

$P$ and

$V$ denote pressure and volume, LVCO and RVCO denote cardiac output in left ventricle and right ventricle, MAP and MPAP denote mean aortic pressure and mean pulmonary artery pressure, PP denotes aortic pulse pressure,

${Q_{irp, min}}$ denotes minimum pump flow rate over a heart period, subscripts

$lv$ ,

$la$ ,

$rv$ and

$ra$ denote left ventricle, left atrium, right ventricle and right atrium,

$ao$ and

$pa$ denote aorta and pulmonary artery,

$sys$ and

$dia$ denote systolic and diastolic,

$ed$ and

$es$ denote end-diastolic and end-systolic.

DownLoad: Full-Size Img PowerPoint

With the increase of pump speed, the pressures and volumes in the left heart decreased gradually. On the contrary, the pressures and volumes in the right heart gradually increased. Meanwhile, aortic pressure and pulmonary artery pressure were increasing. Moreover, the pulsatility of aortic pressure gradually weakened, and that of pulmonary artery pressure gradually enhanced. The increase of speed also enhanced the cardiac output and the minimum pump flow rate over a heart period. There was no negative value of the minimum pump flow rate within 3600−4700 rpm, which indicated that pump regurgitation disappeared when the speed was higher than 3600 rpm. However, when the pump operating speed is higher than 4400 rpm, the minimum pump flow rate decreased, the aortic pulse pressure increased, the left ventricular pressure approached 0 mmHg, and the left ventricular volume was less than 50 mL, which implied that the left ventricular suction occurred.

4. Discussion

In this study, a CLP model for describing the circulatory loop was developed to simulate hemodynamic responses. The CLP model was coupled with the baroreflex model and LVAD model, which provided a platform for the simulation of hemodynamics and the evaluation of LVAD operating condition.

LVADs have become the standard treatment for advanced heart failure. Nevertheless, pump regurgitation may occur under pump support at low speeds. Inadequate support may cause mean aortic pressure and cardiac output to be lower than the normal level, which is difficult to meet the patients' normal physiological perfusion. Pump support at high speed allows the left ventricle to unload, but it also increases right ventricular load (Figure 6). However, long-term overloading for the right ventricle may cause right heart failure ^[40].

The HeartMate III operating speed should be in the range of 3600−4400 rpm with the selected parameter settings to avoid pump regurgitation and ventricular suction. Generally, an optimal speed range is set for clinical continuous-flow LVADs, and it can be determined by monitoring cardiac index (cardiac output) and left ventricular size based on hemodynamic data ^[40]. In this study, cardiac output in the left ventricle and left ventricular end-diastolic volume are 5.5 L/min and 138 mL in normal conditions, respectively. In Figure 8, the cardiac output of 5.6 L/min at 3600 rpm is near to the normal cardiac output. And at 3800 rpm, the left ventricular end-systolic volume is 139 mL that is closer to the normal value of 138 mL. Hence, the low-end of the optimal speed range can be set to 3600 rpm and the high-end can be set to 3800 rpm.

In the physiological or pathological cardiovascular system, the baroreflex model objectively describes the changes in ventricular end-systolic elastances, systemic vascular resistance, and heart rate. Different levels of LVAD support also affect ventricular end-systolic elastances, systemic vascular resistance, and heart rate. However, heart rate is usually maintained as a constant in cardiovascular models without baroreflex regulation, which may not be in line with the actual situation.

A pulse pressure of greater than 15 mmHg is considered to be pulsatile flow while a pulse pressure of less than 15 mmHg is considered to be nonpulsatile flow ^[41]. In this study, the aortic pulse pressure is less than 15 mmHg for the operating speed between 3600 rpm and 4400 rpm in Figure 8. The continuous flow LVADs usually operate at a constant speed to provide the patient with adequate blood flow. However, long-term LVAD constant support diminishes pulse pressure and vascular pulsatility, which can lead to late complications such as aortic insufficiency, gastrointestinal bleeding, and hemorrhagic strokes ^[31,42]. Recently, the new generation of commercial products, such as HVAD (Medtronic, Inc., Minneapolis, MN, USA) and HeartMate III (Abbott Inc., Abbott Park, IL, USA), come with an artificial pulse. The artificial pulse is formed by intermittent speed change, and its main goal is to reduce the rate of pump thrombosis. Importantly, the cycle of variable speed is asynchronous with the native heart period. Moreover, the aortic pressure waveform becomes non-physiological ^[43]. Therefore, certain issues should be studied and solved, including modulation and optimization of pulsating speed with heart rate synchronization, hemodynamic analysis at pulsating speed support, and design of the physiological controller. These will be the subject of further research.

The limitations of this study are as follows.

From a hemodynamic viewpoint, the numerical model can reflect clinical observations under LV failure and LVAD support conditions. The numerical model cannot replace the importance and significance of in vivo research, and cannot reproduce all the expected clinical responses (such as neurohumoral response, myocardial remodeling). But it can prove the feasibility of some concepts to provide a valuable initial step for further in vivo research.

In this study, the valve model is assumed that valves can be opened and closed immediately, and it ignores the process of valve closure. Thus, the ideal valve model cannot simulate the valve flow rate during valve closure. The non-ideal diode modeling for the heart valves is a feasible way to simulate the dynamic process of valves ^[44,45,46].

The experimental data of HeartMate III are from earlier versions of the product design ^[4]. Since the pump data was first published, the HeartMate III design has gone through several versions. However, the method in this study is still valid.

In this study, the regulation of venous volume in the baroreflex model is ignored. This is because the systemic venous compliance is configured to be constant. But this does not affect the change in systemic venous pressure.

5. Conclusion

In this study, a numerical model had been developed to simulate the hemodynamics and to evaluate the operating condition of continuous-flow left ventricular assist device. The hemodynamic responses under various conditions (normal, left ventricular failure, and different levels of pump support) had been simulated successfully, and the hemodynamic variables under different conditions had been compared. The simulation results had shown that the developed numerical model provides a feasible simulation platform for reproducing hemodynamics. Also, the centrifugal pump HeartMate III had been taken as an example of continuous-flow LVAD, and its operating condition had been evaluated and discussed. The simulation results had shown that in the simulation system, HeartMate III is safe to operate between 3600 rpm and 4400 rpm, and that pump operating speeds are adjusted between 3600 rpm and 3800 rpm to provide optimal physiological perfusion. What makes this paper regret is that some system parameters are quoted or set as constants, it gives rise to some limitations on the final results. Actually, these parameters are variable because of the interpatient and intrapatient variations. The future work will simulate combining the patient data, and obtain the hemodynamic response for variable physiological or pathological parameters.

Acknowledgments

The study is supported by the Key Technology Research and Development Program of Shandong (CN) (No. 2017GSF221009).

Conflict of interest

The authors declare that there is no conflict of interest.

Appendix A

Table A1. Parameters for cardiovascular system in normal condition ^[7,14,31].

Parameters	Physiological Meaning	Value	Unit
${R_{ao}}$	Aortic Resistance	0.0398	${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}}$
${R_{svr}}(t)$	Systemic Vascular Resistance	Time-varying	${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}}$
${R_{sv}}$	Systemic Venous Resistance	0.023	${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}}$
${R_{pa}}$	Pulmonary Artery Resistance	0.005	${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}}$
${R_{pvr}}$	Pulmonary Vascular Resistance	0.12	${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}}$
${R_{pv}}$	Pulmonary Venous Resistance	0.011	${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}}$
${R_{{\rm{MV}}}}$	Mitral Valve Resistance	0.005	${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}}$
${R_{{\rm{AV}}}}$	Aortic Valve Resistance	0.008	${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}}$
${R_{{\rm{TV}}}}$	Tricuspid Valve Resistance	0.001	${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}}$
${R_{{\rm{PV}}}}$	Pulmonary Valve Resistance	0.003	${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}}$
${C_{lv}}(t)$	Left Ventricular Compliance	Time-varying	${\rm{mL}}/{\rm{mmHg}}$
${C_{la}}(t)$	Left Atrial Compliance	Time-varying	${\rm{mL}}/{\rm{mmHg}}$
${C_{rv}}(t)$	Right Ventricular Compliance	Time-varying	${\rm{mL}}/{\rm{mmHg}}$
${C_{ra}}(t)$	Right Atrial Compliance	Time-varying	${\rm{mL}}/{\rm{mmHg}}$
${C_{ao}}$	Aortic Compliance	0.08	${\rm{mL}}/{\rm{mmHg}}$
${C_{sar}}$	Systemic Arterial Compliance	1.33	${\rm{mL}}/{\rm{mmHg}}$
${C_{sv}}$	Systemic Venous Compliance	20.5	${\rm{mL}}/{\rm{mmHg}}$
${C_{pa}}$	Pulmonary Artery Compliance	0.18	${\rm{mL}}/{\rm{mmHg}}$
${C_{par}}$	Pulmonary Arteriolar Compliance	3	${\rm{mL}}/{\rm{mmHg}}$
${C_{pv}}$	Pulmonary Venous Compliance	20.5	${\rm{mL}}/{\rm{mmHg}}$
${L_{ao}}$	Aortic Inertance	0.0005	${\rm{mmHg}} \cdot {{\rm{s}}^2} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}}$
${L_{pa}}$	Pulmonary Artery Inertance	0.0005	${\rm{mmHg}} \cdot {{\rm{s}}^2} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}}$
${V_{lv, 0}}$	Left Ventricular Unstressed Volume	5	${\rm{mL}}$
${V_{la, 0}}$	Left Atrial Unstressed Volume	4	${\rm{mL}}$
${V_{rv, 0}}$	Right Ventricular Unstressed Volume	10	${\rm{mL}}$
${V_{ra, 0}}$	Right Atrial Unstressed Volume	4	${\rm{mL}}$
${E_{\max, lv}}(t)$	Left Ventricular End-systolic Elastance	Time-varying	${\rm{mmHg}}/{\rm{mL}}$
${E_{\min, lv}}$	Left Ventricular End-diastolic Elastance	0.04	${\rm{mmHg}}/{\rm{mL}}$
${E_{\max, rv}}(t)$	Right Ventricular End-systolic Elastance	Time-varying	${\rm{mmHg}}/{\rm{mL}}$
${E_{\min, rv}}$	Right Ventricular End-diastolic Elastance	0.04	${\rm{mmHg}}/{\rm{mL}}$
${E_{\max, la}}$	Left Atrial End-systolic Elastance	0.25	${\rm{mmHg}}/{\rm{mL}}$
${E_{min, la}}$	Left Atrial End-diastolic Elastance	0.15	${\rm{mmHg}}/{\rm{mL}}$
${E_{\max, ra}}$	Right Atrial End-systolic Elastance	0.25	${\rm{mmHg}}/{\rm{mL}}$
${E_{min, ra}}$	Right Atrial End-diastolic Elastance	0.15	${\rm{mmHg}}/{\rm{mL}}$

| Show Table

DownLoad: CSV

Table A2. Parameters for baroreflex system in normal condition ^[24].

Parameters
Afferent neural pathway
${\tau _p}{\rm{ = }}$ 2.076 ${\rm{s}}$		${f_{\min }} =$ 2.52 ${\rm{spikes/s}}$				${p_n} =$ 92 ${\rm{mmHg}}$
${\tau _z} =$ 6.37 ${\rm{s}}$		${f_{\max }} =$ 47.78 ${\rm{spikes/s}}$				${k_a} =$ 11.758 ${\rm{mmHg}}$
Efferent neural pathway
${f_{es, \infty }} =$ 2.1 ${\rm{spikes/s}}$	${f_{ev, \infty }} =$ 6.3 ${\rm{spikes/s}}$			${k_{es}} =$ 0.0675 ${\rm{s}}$				${f_{as, 0}} =$ 25 ${\rm{spikes/s}}$
${f_{es, 0}} =$ 16.11 ${\rm{spikes/s}}$	${f_{ev, 0}} =$ 3.2 ${\rm{spikes/s}}$			${k_{ev}} =$ 7.06 ${\rm{spikes/s}}$
Effector
${G_{{R_{svr}}}} =$ 0.36 ${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}} \cdot {\rm{spike}}{{\rm{s}}^{{\rm{ - }}1}}$			${\tau _{{R_{svr}}}} =$ 6 ${\rm{s}}$		${D_{{R_{svr}}}} =$ 2 ${\rm{s}}$		${f_{es, \min }} =$ 2.66 ${\rm{spikes/s}}$
${G_{{E_{\max, \, lv}}}} =$ 0.475 ${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}} \cdot {\rm{spike}}{{\rm{s}}^{{\rm{ - }}1}}$			${\tau _{{E_{\max, \, lv}}}} =$ 8 ${\rm{s}}$		${D_{{E_{\max, \, lv}}}} =$ 2 ${\rm{s}}$		${R_{svr0}} =$ 0.62 ${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}}$
${G_{{E_{\max, \, rv}}}} =$ 0.282 ${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}} \cdot {\rm{spike}}{{\rm{s}}^{{\rm{ - }}1}}$			${\tau _{{E_{\max, \, rv}}}} =$ 8 ${\rm{s}}$		${D_{{E_{\max, \, rv}}}} =$ 2 ${\rm{s}}$		${E_{\max, lv0}} =$ 1.8 ${\rm{mmHg}}/{\rm{mL}}$
${G_{{T_s}}} =$ -0.13 ${{\rm{s}}^2} \cdot {\rm{spike}}{{\rm{s}}^{{\rm{ - }}1}}$			${\tau _{{T_s}}} =$ 2 ${\rm{s}}$		${D_{{T_s}}} =$ 2 ${\rm{s}}$		${E_{\max, rv0}} =$ 0.6 ${\rm{mmHg}}/{\rm{mL}}$
${G_{{T_v}}} =$ 0.09 ${{\rm{s}}^2} \cdot {\rm{spike}}{{\rm{s}}^{{\rm{ - }}1}}$			${\tau _{{T_v}}} =$ 1.5 ${\rm{s}}$		${D_{{T_v}}} =$ 0.2 ${\rm{s}}$		${T_0} =$ 0.58 ${\rm{s}}$

| Show Table

DownLoad: CSV

Table A3. Partially normal parameters are adjusted to simulate LV failure.

Parameters	Normal	LV failure	Unit
${C_{sar}}$	1.33	1.02	${\rm{mL}}/{\rm{mmHg}}$
${R_{pvr}}$	0.12	0.14	${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}}$
${R_{pv}}$	0.011	0.027	${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}}$
${E_{\max, lv0}}$	1.8	0.05	${\rm{mmHg}}/{\rm{mL}}$
${R_{svr0}}$	0.62	0.71	${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}}$
${T_0}$	0.58	0.52	${\rm{s}}$
${k_a}$	11.758	14	${\rm{mmHg}}$
${G_{{R_{svr}}}}$	0.36	0.3	${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}} \cdot {\rm{spike}}{{\rm{s}}^{{\rm{ - }}1}}$
${G_{{E_{\max, \, lv}}}}$	0.475	0.15	${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}} \cdot {\rm{spike}}{{\rm{s}}^{{\rm{ - }}1}}$
${G_{{E_{\max, \, rv}}}}$	0.282	0.245	${\rm{mmHg}} \cdot {\rm{s}} \cdot {\rm{m}}{{\rm{L}}^{{\rm{ - }}1}} \cdot {\rm{spike}}{{\rm{s}}^{{\rm{ - }}1}}$
${G_{{T_s}}}$	-0.13	-0.07	${{\rm{s}}^2} \cdot {\rm{spike}}{{\rm{s}}^{{\rm{ - }}1}}$
${G_{{T_v}}}$	0.09	0.07	${{\rm{s}}^2} \cdot {\rm{spike}}{{\rm{s}}^{{\rm{ - }}1}}$

| Show Table

DownLoad: CSV

References

[1]	R. S. Achrol, Changes in the theory of interorganizational relations in marketing: Toward a Network Paradigm, J. Acad. Mark. Sci., 25 (1996), 56–71. https://doi.org/10.1177/0092070397251006 doi: 10.1177/0092070397251006
[2]	R. S. Achrol, P. Kotler, Marketing in the network economy, J. Mark., 63 (1999), 146–163. https://doi.org/10.1177/00222429990634s114 doi: 10.1177/00222429990634s114
[3]	E. Anderson, B. Weitz, The use of pledges to build and sustain commitment in distribution channels, J. Mark. Res., 29 (1992), 18–34. https://doi.org/10.1177/002224379202900103 doi: 10.1177/002224379202900103
[4]	A. Kumar, J. B. Heide, K. H. Wathne, Performance implications of mismatched governance regimes across external and internal relationships, J. Mark., 75 (2011), 1–17. https://doi.org/10.1509/jm.75.2.1 doi: 10.1509/jm.75.2.1
[5]	R. M. Morgan, S. D. Hunt, The commitment-trust theory of relationship marketing, J. Mark., 58 (1994), 20–38. https://doi.org/10.1177/002224299405800302 doi: 10.1177/002224299405800302
[6]	R. W. Palmatier, Interfirm relational drivers of customer value, J. Mark., 72 (2008), 76–89. https://doi.org/10.1509/jmkg.72.4.076 doi: 10.1509/jmkg.72.4.076
[7]	G. F. Watson, S. Worm, R. W. Palmatier, S. Ganesan, The evolution of marketing channels: Trends and research directions, J. Retail., 91 (2015), 546–568. https://doi.org/10.1016/j.jretai.2015.04.002 doi: 10.1016/j.jretai.2015.04.002
[8]	J. R. Brown, J. L. Crosno, P. Y. Tong, Is the theory of trust and commitment in marketing relationships incomplete?, Ind. Mark. Manag., 77 (2019), 155–169. https://doi.org/10.1016/j.indmarman.2018.10.005 doi: 10.1016/j.indmarman.2018.10.005
[9]	I. V. Kozlenkova, G. T. M. Hult, D. J. Lund, J. A. Mena, P. Kekec, The role of marketing channels in supply chain management, J. Retail., 91 (2015), 586–609. https://doi.org/10.1016/j.jretai.2015.03.003 doi: 10.1016/j.jretai.2015.03.003
[10]	G. L. Frazier, Organizing and managing channels of distribution, J. Acad. Mark. Sci., 27 (1999), 226–240. https://doi.org/10.1177/0092070399272007 doi: 10.1177/0092070399272007
[11]	F. Gimeno-Arias, J. M. Santos-Jaén, Using PLS-SEM for assessing negative impact and cooperation as antecedents of gray market in FMCG supply chains: An analysis on Spanish wholesale distributors, Int. J. Phys. Distrib. Logist. Manag., 53 (2023), 718–742. https://doi.org/10.1108/IJPDLM-02-2022-0038 doi: 10.1108/IJPDLM-02-2022-0038
[12]	S. S. Andaleeb, An experimental investigation of satisfaction and commitment in marketing channels: The role of trust and dependence, J. Retail., 72 (1996), 77–93. https://doi.org/10.1016/S0022-4359(96)90006-8 doi: 10.1016/S0022-4359(96)90006-8
[13]	N. Sharma, L. C. Young, I. Wilkinson, The nature and role of different types of commitment in inter-firm relationship cooperation, J. Bus. Ind. Mark., 30 (2015), 45–59. https://doi.org/10.1108/JBIM-11-2012-0202 doi: 10.1108/JBIM-11-2012-0202
[14]	T. Suh, J. C. Jung, G. M. Zank, R. J. Arend, Twofold relationship dynamics of supplier's knowledge sharing, J. Bus. Ind. Mark., 34 (2019), 862–874. https://doi.org/10.1108/JBIM-10-2017-0241 doi: 10.1108/JBIM-10-2017-0241
[15]	A. S. Vinhas, R. Gibbs, Exclusive dealing without territory exclusivity in multichannel systems: Managing channel conflict and driving commitment, Mark. Lett., 29 (2018), 291–305. https://doi.org/10.1007/s11002-018-9462-9 doi: 10.1007/s11002-018-9462-9
[16]	L. Wang, C. Zhang, J. Li, D. Huo, X. Fan, The influence of unilateral supplier transaction-specific investments on international buyer opportunism: empirical findings from local suppliers in China, Int. Mark. Rev., 37 (2020), 213–239. https://doi.org/10.1108/IMR-05-2018-0177 doi: 10.1108/IMR-05-2018-0177
[17]	M. Du, J. Zhang, Encouraging customer participation by leveraging interdependence structure and relationship commitments: empirical evidence from chinese industrial firms, Int. J. Bus. Inf., 12 (2017), 433–477.
[18]	F. R. Dwyer, P. H. Schurr, S. Oh, Developing buyer-seller relationships, J. Mark., 51 (1987), 11–27. https://doi.org/10.1177/002224298705100202 doi: 10.1177/002224298705100202
[19]	C. Ferro, C. Padin, G. Svensson, J. Payan, Trust and commitment as mediators between economic and non-economic satisfaction in manufacturer-supplier relationships, J. Bus. Ind. Mark., 31 (2016), 13–23. https://doi.org/10.1108/JBIM-07-2013-0154 doi: 10.1108/JBIM-07-2013-0154
[20]	I. Geyskens, J. B. Steenkamp, L. K. Scheer, N. Kumar, The effects of trust and interdependence on relationship commitment: A trans-Atlantic study, Int. J. Res. Mark., 13 (1996), 303–317. https://doi.org/10.1016/S0167-8116(96)00006-7 doi: 10.1016/S0167-8116(96)00006-7
[21]	D. I. Gilliland, D. C. Bello, Two sides to attitudinal commitment: The effect of calculative and loyalty commitment on enforcement mechanisms in distribution channels, J. Acad. Mark. Sci., 30 (2002), 24–43. https://doi.org/10.1177/03079450094306 doi: 10.1177/03079450094306
[22]	N. Kumar, L. K. Scheer, J. B. Steenkamp, The effects of perceived interdependence on dealer attitudes, J. Mark. Res., 32 (1995), 348–356. https://doi.org/10.1177/002224379503200309 doi: 10.1177/002224379503200309
[23]	M. Mpinganjira, M. Roberts-Lombard, G. Svensson, Validating the relationship between trust, commitment, economic and non-economic satisfaction in South African buyer-supplier relationships, J. Bus. Ind. Mark., 32 (2017), 421–431. https://doi.org/10.1108/JBIM-04-2015-0073 doi: 10.1108/JBIM-04-2015-0073
[24]	N. Ponder, B. B. Holloway, J. D. Hansen, The mediating effects of customers' intimacy perceptions on the trust-commitment relationship, J. Serv. Mark., 30 (2016), 75–87. https://doi.org/10.1108/JSM-04-2014-0117 doi: 10.1108/JSM-04-2014-0117
[25]	W. J. Johnston, A. N. H. Le, J. M. S. Cheng, A meta-analytic review of influence strategies in marketing channel relationships, J. Acad. Mark. Sci., 46 (2018), 674–702. https://doi.org/10.1007/s11747-017-0564-3 doi: 10.1007/s11747-017-0564-3
[26]	W. J. Reinartz, M. Berkmann, From customer to partner engagement: a conceptualization and typology of engagement in B2B, Customer Engagement Mark., (2018), 243–268. https://doi.org/10.1007/978-3-319-61985-9_11 doi: 10.1007/978-3-319-61985-9_11
[27]	V. Kumar, A. Pansari, Competitive advantage through engagement, J. Mark. Res., 53 (2016), 497–514. https://doi.org/10.1509/jmr.15.0044 doi: 10.1509/jmr.15.0044
[28]	S. Sands, C. Campbell, C. Ferraro, K. Plangger, Buffering B2B service failure: The role of customer engagement, Ind. Mark. Manag., 103 (2022), 47–60. https://doi.org/10.1016/j.indmarman.2022.03.007 doi: 10.1016/j.indmarman.2022.03.007
[29]	S. D. Vivek, V. Dalela, M. S. Ahmed, A framework for partner engagement: Episodes in the life of interorganizational partnerships, J. Mark. Theory Pract., 30 (2022), 476–493. https://doi.org/10.1080/10696679.2021.191639898 doi: 10.1080/10696679.2021.1916398
[30]	M. W. Nyadzayo, R. Casidy, P. Thaichon, B2B purchase engagement: Examining the key drivers and outcomes in professional services, Ind. Mark. Manag., 85 (2020), 197–208. https://doi.org/10.1016/j.indmarman.2019.11.007 doi: 10.1016/j.indmarman.2019.11.007
[31]	M. Kleinaltenkamp, I. O. Karpen, C. Plewa, E. Jaakkola, J. Conduit, Collective engagement in organizational settings, Ind. Mark. Manag., 80 (2019), 11–23. https://doi.org/10.1016/j.indmarman.2019.02.009 doi: 10.1016/j.indmarman.2019.02.009
[32]	J. F. Hair, M. Sarstedt, L. Hopkins, V. G. Kuppelwieser, Partial least squares structural equation modeling (PLS-SEM): An emerging tool in business research, Eur. Bus. Rev., 26 (2014), 106–121. https://doi.org/10.1108/EBR-10-2013-0128 doi: 10.1108/EBR-10-2013-0128
[33]	J. M. Santos-Jaén, A. León-Gómez, M. del C. Valls Martínez, F. Gimeno-Arias, The effect of public healthcare expenditure on the reduction in mortality rates caused by unhealthy habits among the population, Healthcare, 10 (2022), 2253. https://doi.org/10.3390/healthcare10112253 doi: 10.3390/healthcare10112253
[34]	M. Martínez Ávila, E. Fierro Moreno, Aplicación de la técnica PLS-SEM en la gestión del conocimiento: un enfoque técnico práctico / application of the PLS-SEM technique in knowledge management: A practical technical approach, RIDE Rev. Iberoam. para la Investig. y el Desarro. Educ., 8 (2018), 130–164. https://doi.org/10.23913/ride.v8i16.336 doi: 10.23913/ride.v8i16.336
[35]	P. B. Lowry, J. Gaskin, Partial least squares (PLS) structural equation modeling (SEM) for building and testing behavioral causal theory: When to choose it and how to use it, IEEE Trans. Prof. Commun., 57 (2014), 123–146. https://doi.org/10.1109/TPC.2014.2312452 doi: 10.1109/TPC.2014.2312452
[36]	R. W. Palmatier, R. P. Dant, D. Grewal, K. R. Evans, Factors influencing the effectiveness of relationship marketing: A meta-analysis, J. Mark., 70 (2006), 136–153. https://doi.org/10.1509/jmkg.70.4.136 doi: 10.1509/jmkg.70.4.136
[37]	A. I. Rokkan, J. B. Heide, K. H. Wathne, Specific investments in marketing relationships: expropriation and bonding effects, J. Mark. Res., 40 (2003), 210–224. https://doi.org/10.1509/jmkr.40.2.210.19223 doi: 10.1509/jmkr.40.2.210.19223
[38]	L. W. Stern, T. Reve, Distribution channels as political economies: A framework for comparative analysis, J. Mark., 44 (1980), 52–64. https://doi.org/10.1177/002224298004400306 doi: 10.1177/002224298004400306
[39]	J. C. Anderson, J. A. Narus, A model of distributor firm and manufacturer firm working partnerships, J. Mark., 54 (1990), 42–58. https://doi.org/10.1177/002224299005400103 doi: 10.1177/002224299005400103
[40]	E. Garbarino, M. S. Johnson, The different roles of satisfaction, trust, and commitment in customer relationships, J. Mark., 63 (1999), 70–87. https://doi.org/10.1177/002224299906300205 doi: 10.1177/002224299906300205
[41]	I. Geyskens, J. B. Steenkamp, N. Kumar, A meta-analysis of satisfaction in marketing channel relationships, J. Mark. Res., 36 (1999), 223–238. https://doi.org/10.1177/002224379903600207 doi: 10.1177/002224379903600207
[42]	I. R. Macneil, Contracts: Adjustment of long-term economic relations under classical, neoclassical, and relational contract law, Nw. UL Rev., 72 (1977), 854.
[43]	D. Narayandas, V. K. Rangan, Building and sustaining buyer–seller relationships in mature industrial markets, J. Mark., 68 (2004), 63–77. https://doi.org/10.1509/jmkg.68.3.63.34772 doi: 10.1509/jmkg.68.3.63.34772
[44]	N. M. Høgevold, G. Svensson, C. Otero-Neira, Validating action and social alignment constituents of collaboration in business relationships, Mark. Intell. Plan., 37 (2019), 721–740. https://doi.org/10.1108/MIP-12-2018-0577 doi: 10.1108/MIP-12-2018-0577
[45]	J. Xue, S. Lu, B. Shi, H. Zheng, Trust, guanxi, and cooperation: A study on partner opportunism in Chinese joint-venture manufacturing, J. Bus. Ind. Mark., 33 (2018), 95–106. https://doi.org/10.1108/JBIM-07-2016-0159 doi: 10.1108/JBIM-07-2016-0159
[46]	Y. Zhou, X. Zhang, G. Zhuang, N. Zhou, Relational norms and collaborative activities: Roles in reducing opportunism in marketing channels, Ind. Mark. Manag., 46 (2015), 147–159. https://doi.org/10.1016/j.indmarman.2015.01.014 doi: 10.1016/j.indmarman.2015.01.014
[47]	J. F. Gaski, N. M. Ray, Alienation in the distribution channel, Int. J. Phys. Distrib. Logist. Manag., 34 (2004), 158–200. https://doi.org/10.1108/09600030410526941 doi: 10.1108/09600030410526941
[48]	J. Crosno, R. Dahlstrom, Y. Liu, P. Y. Tong, Effectiveness of contracts in marketing exchange relationships: A meta-analytic review, Ind. Mark. Manag., 92 (2021), 122–139. https://doi.org/10.1016/j.indmarman.2020.11.007 doi: 10.1016/j.indmarman.2020.11.007
[49]	R. Vázquez-Casielles, V. Iglesias, C. Varela-Neira, Manufacturer–distributor relationships: Role of relationship-specific investment and dependence types, J. Bus. Ind. Mark., 32 (2017), 1245–1260. https://doi.org/10.1108/JBIM-10-2016-0244 doi: 10.1108/JBIM-10-2016-0244
[50]	N. Sharma, An examination of customer relationship value in high vs low technology industries, Acad. Mark. Stud. J., 24 (2020), 1–24.
[51]	J. C. Anderson, J. A. Narus, A model of the distributor's perspective of distributor-manufacturer working relationships, J. Mark., 48 (1984), 62–74. https://doi.org/10.1177/002224298404800407 doi: 10.1177/002224298404800407
[52]	K. H. Wathne, J. B. Heide, Opportunism in interfirm relationships: Forms, outcomes, and solutions, J. Mark., 64 (2000), 36–51. https://doi.org/10.1509/jmkg.64.4.36.18070 doi: 10.1509/jmkg.64.4.36.18070
[53]	J. B. Heide, G. John, The role of dependence balancing in safeguarding transaction-specific assets in conventional channels, J. Mark., 52 (1988), 20-35. https://doi.org/10.1177/002224298805200103 doi: 10.1177/002224298805200103
[54]	S. Ganesan, S. P. Brown, B. J. Mariadoss, H. Ho, Buffering and amplifying effects of relationship commitment in business-to-business relationships, J. Mark. Res., 47 (2010), 361–373. https://doi.org/10.1509/jmkr.47.2.361 doi: 10.1509/jmkr.47.2.361
[55]	J. R. Brown, R. F. Lusch, C. Y. Nicholson, Power and relationship commitment: their impact on marketing channel member performance, J. Retail., 71 (1995), 363–392. https://doi.org/10.1016/0022-4359(95)90019-5 doi: 10.1016/0022-4359(95)90019-5
[56]	A. T. Coughlan, E. Anderson, L. W. Stern, A. El-Ansary, Marketing Channels, Prentice Hall, 2006.
[57]	R. Grewal, G. L. Lilien, S. Bharadwaj, P. Jindal, U. Kayande, R. F. Lusch, et al., Business-to-business buying: Challenges and opportunities, Cust. Needs Solut., 2 (2015), 193–208. https://doi.org/10.1007/s40547-015-0040-5 doi: 10.1007/s40547-015-0040-5
[58]	S. D. Vivek, V. Dalela, S. E. Beatty, Partner engagement: A perspective on B2B engagement, Customer Engagement, Routledge (2015), 53–66.
[59]	R. W. Palmatier, R. P. Dant, D. Grewal, A comparative longitudinal analysis of theoretical perspectives of interorganizational relationship performance, J. Mark., 71 (2007), 172–194. https://doi.org/10.1509/jmkg.71.4.172 doi: 10.1509/jmkg.71.4.172
[60]	A. Pansari, V. Kumar, Customer engagement: the construct, antecedents, and consequences, J. Acad. Mark. Sci., 45 (2017), 294–311. https://doi.org/10.1007/s11747-016-0485-6 doi: 10.1007/s11747-016-0485-6
[61]	S. Vatavwala, B. Kumar, A. Sharma, A. Billore, A. Sadh, Customer disengagement in business-to-business markets: A framework for analysis, Ind. Mark. Manag., 105 (2022), 114–130. https://doi.org/10.1016/j.indmarman.2022.05.018 doi: 10.1016/j.indmarman.2022.05.018
[62]	J. Barnes, Y. Liao, The effect of individual, network, and collaborative competencies on the supply chain management system, Int. J Prod. Econ., 140 (2012), 888–899. https://doi.org/10.1016/j.ijpe.2012.07.010 doi: 10.1016/j.ijpe.2012.07.010
[63]	E. W. Choi, Ö. Özer, Y. Zheng, Network trust and trust behaviors among executives in supply chain interactions, Manag. Sci., 66 (2020), 5823–5849. https://doi.org/10.1287/mnsc.2019.3499 doi: 10.1287/mnsc.2019.3499
[64]	S. Ambulkar, J. V. Blackhurst, D. E. Cantor, Supply chain risk mitigation competency: An individual-level knowledge-based perspective, Int. J Prod. Res., 54 (2016), 1398–1411. https://doi.org/10.1080/00207543.2015.1070972 doi: 10.1080/00207543.2015.1070972
[65]	D. M. Hardesty, W. O. Bearden, The use of expert judges in scale development: Implications for improving face validity of measures of unobservable constructs, J. Bus. Res., 57 (2004), 98–107. https://doi.org/10.1016/S0148-2963(01)00295-8 doi: 10.1016/S0148-2963(01)00295-8
[66]	P. M. Podsakoff, S. B. MacKenzie, J. Y. Lee, N. P. Podsakoff, Common method biases in behavioral research: A critical review of the literature and recommended remedies, J. Appl. Psychol., 88 (2003), 879–903. https://doi.org/10.1037/0021-9010.88.5.879 doi: 10.1037/0021-9010.88.5.879
[67]	J. S. Armstrong, T. S. Overton, Estimating nonresponse bias in mail surveys, J. Mark. Res., 14 (1977), 396–402. https://doi.org/10.1177/002224377701400320 doi: 10.1177/002224377701400320
[68]	S. Cai, M. Jun, Z. Yang, The effects of boundary Spanners' personal relationships on interfirm collaboration and conflict: A study of the role of Guanxi in China, J. Supply Chain Manag., 53 (2017), 19–40. https://doi.org/10.1111/jscm.12132 doi: 10.1111/jscm.12132
[69]	M. Sarstedt, J. F. Hair, C. M. Ringle, K. O. Thiele, S. P. Gudergan, Estimation issues with PLS and CBSEM: Where the bias lies!, J. Bus. Res., 69 (2016), 3998–4010. https://doi.org/10.1016/j.jbusres.2016.06.007 doi: 10.1016/j.jbusres.2016.06.007
[70]	A. Leguina, A primer on partial least squares structural equation modeling (PLS-SEM), Int. J. Res. Method Educ., 38 (2015), 220–221. https://doi.org/10.1080/1743727X.2015.1005806 doi: 10.1080/1743727X.2015.1005806
[71]	J. F. Hair, C. M. Ringle, M. Sarstedt, PLS-SEM: Indeed a silver bullet, J. Mark. Theory Pract., 19 (2011), 139–152. https://doi.org/10.2753/MTP1069-6679190202 doi: 10.2753/MTP1069-6679190202
[72]	A. C. Davison, D. V. Hinkley, Bootstrap Methods And Their Application, Cambridge University Press, UK, 1977.
[73]	B. Efron, R. Tibshirani, Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy, Stat. Sci., 1 (1986), 54–75. https://doi.org/10.1214/ss/1177013815 doi: 10.1214/ss/1177013815
[74]	D. Kushary, Bootstrap methods and their application, Technometrics, 42 (2000), 216–217. https://doi.org/10.1080/00401706.2000.10486018 doi: 10.1080/00401706.2000.10486018
[75]	J. F. Hair Jr, M. Sarstedt, Factors versus composites: Guidelines for choosing the right structural equation modeling method, Proj. Manag. J., 50 (2019), 619–624. https://doi.org/10.1177/8756972819882132 doi: 10.1177/8756972819882132
[76]	D. Ruiz-Palomo, J. Diéguez-Soto, A. Duréndez, J. A. C Santos, Family management and firm performance in family SMEs: The mediating roles of management control systems and technological innovation, Sustainability, 11 (2019), 3805. https://doi.org/10.3390/su11143805 doi: 10.3390/su11143805
[77]	M. Sarstedt, C. M. Ringle, J. H. Cheah, H. Ting, O. I. Moisescu, L. Radomir, Structural model robustness checks in PLS-SEM, Tour. Econ., 26 (2020), 531–554. https://doi.org/10.1177/1354816618823921 doi: 10.1177/1354816618823921
[78]	C. M. Ringle, S. Wende, J. M. Baker, Smart-Pls, SmartPLS 4. Oststeinbek: SmartPLS, (2022). Available from: https://www.smartpls.com.
[79]	S. Streukens, S. Leroi-Werelds, Bootstrapping and PLS-SEM: A step-by-step guide to get more out of your bootstrap results, Eur. Manag. J., 34 (2016), 618–632. https://doi.org/10.1016/j.emj.2016.06.003 doi: 10.1016/j.emj.2016.06.003
[80]	S. Mayr, E. Erdfelder, A. Buchner, F. Faul, A short tutorial of GPower, Tutor. Quant. Methods Psychol., 3 (2007), 51–59. https://doi.org/10.20982/tqmp.03.2.p051 doi: 10.20982/tqmp.03.2.p051
[81]	J. Cohen, Statistical Power Analysis for the Behavioral Sciences, Erbaum Press, Hillsdale, NJ, USA, 2013. https://doi.org/10.20982/tqmp.03.2.p051
[82]	M. Sarstedt, C. M. Ringle, J. F. Hair, Partial least squares structural equation modeling, in Handbook of Market Research, Cham, Springer (2022), 587–632. https://doi.org/10.1007/978-3-319-57413-4_15
[83]	J. Henseler, G. Hubona, P. A. Ray, Using PLS path modeling in new technology research: Updated guidelines, Ind. Manag. Data Syst., 116 (2016), 2–20. https://doi.org/10.1108/IMDS-09-2015-0382 doi: 10.1108/IMDS-09-2015-0382
[84]	J. Henseler, On the convergence of the partial least squares path modeling algorithm, Comput. Stat., 25 (2010), 107–120. https://doi.org/10.1007/s00180-009-0164-x doi: 10.1007/s00180-009-0164-x
[85]	T. K. Dijkstra, J. Henseler, Consistent partial least squares path modeling, MIS Q. Manag. Inf. Syst., 39 (2015), 297–316. https://doi.org/10.25300/MISQ/2015/39.2.02 doi: 10.25300/MISQ/2015/39.2.02
[86]	J. Henseler, C. M. Ringle, M. Sarstedt, A new criterion for assessing discriminant validity in variance-based structural equation modeling, J. Acad. Mark. Sci., 43 (2015), 115–135. https://doi.org/10.1007/s11747-014-0403-8 doi: 10.1007/s11747-014-0403-8
[87]	J. F. Hair, J. J. Risher, M. Sarstedt, C. M. Ringle, When to use and how to report the results of PLS-SEM, Eur. Bus. Rev., 31 (2019), 2–24. https://doi.org/10.1108/EBR-11-2018-0203 doi: 10.1108/EBR-11-2018-0203
[88]	C. Fornell, D. F. Larcker, Evaluating structural equation models with unobservable variables and measurement error, J. Mark. Res., 18 (1981), 39–50. https://doi.org/10.1177/002224378101800104 doi: 10.1177/002224378101800104
[89]	J. Henseler, Some inconvenient truths about PLS path modeling, 9th Int. Conf. PLS Relat. Methods, (2016), 74–76.
[90]	L. T. Hu, P. M. Bentler, Fit indices in covariance structure modeling: Sensitivity to underparameterized model misspecification, Psychol. Methods, 3 (1998), 424–453. https://doi.org/10.1037/1082-989X.3.4.424 doi: 10.1037/1082-989X.3.4.424
[91]	W. W. Chin, How to write up and report pls analyses, in Handbook of Partial Least Squares, Springer, (2010), 655–690. https://doi.org/10.1007/978-3-540-32827-8_29
[92]	G. Shmueli, To explain or to predict?, Stat. Sci., 25 (2010), 289–310. https://doi.org/10.1214/10-STS330 doi: 10.1214/10-STS330
[93]	D. Straub, D. Gefen, Validation guidelines for is positivist research, Commun. Assoc. Inf. Syst., 13 (2004), 380–427. https://doi.org/10.17705/1CAIS.01324 doi: 10.17705/1CAIS.01324
[94]	J. Evermann, M. Tate, Assessing the predictive performance of structural equation model estimators, J. Bus. Res., 69 (2016), 4565–4582. https://doi.org/10.1016/j.jbusres.2016.03.050 doi: 10.1016/j.jbusres.2016.03.050
[95]	G. Shmueli, M. Sarstedt, J. F. Hair, J. Cheah, H. Ting, S. Vaithilingam, et al., Predictive model assessment in PLS-SEM: guidelines for using PLSpredict, Eur. J. Mark., 53 (2019), 2322–2347. https://doi.org/10.1108/EJM-02-2019-0189 doi: 10.1108/EJM-02-2019-0189
[96]	J. F. Hair, M. C. Howard, C. Nitzl, Assessing measurement model quality in PLS-SEM using confirmatory composite analysis, J. Bus. Res., 109 (2020), 101–110. https://doi.org/10.1016/j.jbusres.2019.11.069 doi: 10.1016/j.jbusres.2019.11.069
[97]	A. Calvo-Mora, A. Blanco-Oliver, J. L. Roldán, R. Periáñez-Cristóbal, TQM factors and organisational results in the EFQM excellence model framework: an explanatory and predictive analysis, Ind. Manag. Data Syst., 120 (2020), 2297–2317. https://doi.org/10.1108/IMDS-12-2019-0701 doi: 10.1108/IMDS-12-2019-0701
[98]	C. M. Felipe, J. L. Roldán, A. L. Leal-Rodríguez, Impact of organizational culture values on organizational agility, Sustainability, 9 (2017), 2354. https://doi.org/10.3390/su9122354 doi: 10.3390/su9122354
[99]	A. G. Woodside, Moving beyond multiple regression analysis to algorithms: Calling for adoption of a paradigm shift from symmetric to asymmetric thinking in data analysis and crafting theory, J. Bus. Res., 66 (2013), 463–472. https://doi.org/10.1016/j.jbusres.2012.12.021 doi: 10.1016/j.jbusres.2012.12.021
[100]	A. Martín-Navarro, F. Velicia-Martín, J. A. Medina-Garrido, R. G. Rodrigues, Causal propensity as an antecedent of entrepreneurial intentions, Int. Entrep. Manag. J., 19 (2023), 501–522. https://doi.org/10.1007/s11365-022-00826-1 doi: 10.1007/s11365-022-00826-1

This article has been cited by:

Chih-Hsuan Liu, Ching Hung, Huabei Liu, 2019, Finite Element Studies of an Earthquake-Induced Landslide Using Different Plastic Flow Rules, 9780784482100, 189, 10.1061/9780784482100.020

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

Electronic Research Archive

1.1 1.7

Metrics

Article views(2477) PDF downloads(118) Cited by(2)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(2) / Tables(11)

Electronic Research Archive

From trust and dependence commitment to B2B engagement: An empirical analysis of inter-organizational cooperation in FMCG

Related Papers:

Abstract

1. Introduction

2. Materials and method

2.1. CLP Model

2.1.1. Ventricles

2.1.2. Atria

2.1.3. Valves

2.1.4. Systemic circulation and pulmonary circulation

2.2. Baroreflex model

2.2.1. Afferent neural pathway

2.2.2. Efferent neural pathways

2.2.3. Effectors

2.3. LVAD model

2.4. Simulation protocol

3. Results

3.1. Hemodynamic response under normal condition

3.2. Hemodynamic response under LV failure condition

3.3. Hemodynamic response under LVAD support

3.4. Effect of pump speed on hemodynamic variables

4. Discussion

5. Conclusion

Acknowledgments

Conflict of interest

Appendix A

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

Electronic Research Archive

From trust and dependence commitment to B2B engagement: An empirical analysis of inter-organizational cooperation in FMCG

Related Papers:

Abstract

1. Introduction

2. Materials and method

2.1. CLP Model

2.1.1. Ventricles

2.1.2. Atria

2.1.3. Valves

2.1.4. Systemic circulation and pulmonary circulation

2.2. Baroreflex model

2.2.1. Afferent neural pathway

2.2.2. Efferent neural pathways

2.2.3. Effectors

2.3. LVAD model

2.4. Simulation protocol

3. Results

3.1. Hemodynamic response under normal condition

3.2. Hemodynamic response under LV failure condition

3.3. Hemodynamic response under LVAD support

3.4. Effect of pump speed on hemodynamic variables

4. Discussion

5. Conclusion

Acknowledgments

Conflict of interest

Appendix A

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog