1. Introduction
Rock surfaces are habitats for microbes and primary sources of nutrients. The suitability of rock surfaces for colonization depends on the physical shape of the surfaces and the bioavailability of cations and anions. Processes providing those nutrients are atmospheric deposition and mineral weathering. Geomorphologists apply various methods for rock surface weathering and erosion [1]. The quantification of the weathering state of rocks is often expressed in terms of weathering indices involving various variables such as e.g., strength, porosity, moisture distribution as well as microscopic observations [6].
The non-destructive investigation of rock surfaces and their degradation has been limited to visual techniques. The reactivity of accessible minerals controls the rate of weathering and therefore the rate of initial soil formation and development of soil fertility [7]. This is a prerequisite for the prosperity of life and can influence global climate [8].
To date, the mobilized ions on rock surfaces have been analyzed only indirectly, i.e. via the measurement of the infiltrate [9] or by the weight loss of the rock [10]. The heterogeneity of rock surfaces becomes particularly pronounced on the microscale, the scale of microorganisms. Weathering processes and the microbial colonization develop at particularly vulnerable sites, such as fissures, grain boundaries, as well as kinks and steps within single minerals [11]. The weathering age of rocks has often been determined by lichens, due to their slow growth and longevity [12]. Nevertheless, metabolic processes can hardly be studied, since the cultivation and separation of crustose lichens is fraught with difficulties [13] (and citations therein). The concentration of adenosine triphosphate (ATP) indicates the viability of the lichens [20,21] (and citations therein), but the analysis has been limited to lichens that can easily be separated from the substrate (e.g. [22,23]).
The present work introduces a novel and non-destructive sampling method for the measurement of readily available ions and mobile ATP from rock surfaces that are either bare or covered by lichens. The method (DoR, “Drop on Rock”) is based on the analysis of a drop of pure water spread onto and recollected from the rock surface to be investigated. Dissolved ions and ATP are analyzed by a capillary electrophoresis (CE) instrument and a luminometer, respectively. Both instruments are portable and can deal with sample volumes as low as 25 µL.
We applied the DoR method to freshly broken and pre-weathered granite surfaces, as well as to rock surfaces covered by map lichen (Rhizocarpon geographicum). In particular, we evaluated (i) the macroscopic surface heterogeneity of bare granite surfaces with respect to readily available cations and (ii) the effect of wetting and freezing. In addition, (iii) we analyzed the readily available ions and mobile ATP on lichens. For this purpose, lichen-covered granite surfaces were investigated with respect to their age (size) and to humidity.
2. Materials and Methods
2.1. Granite Samples
All experiments were conducted with granite specimens. Fist-sized samples were collected along the glacier chronosequence of the Damma glacier forefield (Central Alps, Switzerland) from 2012 to 2014. Samples for the lichen experiments were collected in October 2013 and June 2014 using sterile gloves and immediately packed in sterile plastic bags for transportation to the laboratory. From each sampling site, the lichens with the largest diameter were preferred, as they represented the earliest colonization. The investigated granite was composed mainly of plagioclase, quartz, microcline, muscovite, biotite, and epidote. Accessory minerals were chlorite, apatite, and magnetite [24,25]. The granite was formed 300 million years ago, metamorphosed under greenschist conditions and belongs to the Aar massif [26].
To obtain pairs of freshly broken and unweathered rock surfaces, the granite samples for the wetting and freezing experiments were cut to~100 cm3 uniform cuboids or fist-sized chunks using a water-cooled diamond saw. Afterwards, the samples were incised to a depth of 1 cm with the diamond saw, cleaned with pure water, and split with a chisel and a hammer to produce a pair of mirror-imaged specimens. All samples were stored in a clean bench with a high efficiency particulate air filter (HEPA) to avoid contamination. All freshly broken rock surfaces were photographed to document the sampling points.
2.2. Wetting and Freezing-thawing Experiments
The granite samples were placed in plastic boxes filled with pure water up to 1 cm below the freshly broken surface for the duration of six hours. Care was taken not to submerge the surface to be sampled in water to avoid the removal of readily available ions. The assembly was placed in a desiccator (without drying agent) and a vacuum applied causing the pore spaces of the granite sample to fill with water, thus humidifying the granites completely. The water-saturated granite specimen were either stored in the clean bench for drying or frozen at-20°C for 24 h. For thawing, the granite samples were placed back into the clean bench at room temperature for another 24 h. As soon as the granite specimens were visibly dry (color appearance) the next DoR sampling was carried out. The same spots were sampled before and after wetting and freezing.
2.3. Field Exposure Experiments on Mount Pilatus
Freshly broken granite surfaces (6 pairs of mirror-faced samples) were exposed on three field locations within an altitude transect on the northern slope of Mount Pilatus, Central Switzerland. The lowest location (1007 m a.s.l.) was in a fen characterized by low-grown vegetation. The intermediate location (1445 m a.s.l.) was in a forest glade and the topmost location was above the timberline on the roof of the hotel building on top of Mount Pilatus (2075 m a.s.l.) (Figure 1, left). At all sites, humidity and temperature were recorded with a sensor (Hioki LR5001, Nagano, Japan). Additional climate data were provided by the Federal Office of Meteorology and Climatology (IDAWEB 1.1.21© MeteoSwiss). For the study of the influence of atmospheric deposition both halves of the fist-sized granite chunks were mounted side by side. One half of each pair was positioned facing downwards, while the corresponding half was placed facing upwards in open plastic containers (17×25cm) with holes drilled for drainage. Inside the containers the rock samples were suspended with the help of a grid made from cable ties (Figure 1, right). The plastic containers exposed below the timberline were mounted 40 cm above ground to avoid soil contamination. DoR sam ples were taken on site from 2012 to 2014 once each summer.
2.4. The Drop-on-Rock Method
The extraction of readily available ions in a small volume (50 µL) of water from bare rock surfaces requires its confinement in a defined area. We used a ring made of rubber foam (ear plugs) of clinical quality (Ohropax, Germany) with an inner diameter of 8 mm. The rubber foam proved to be chemically inert to the species of interest and allowed easy handling without leaking. While pipetting, the rubber ring was pressed onto the rock surface using a plastic ring as shown in Figure 2 (left). The contact time between the rock and the drop was as short as possible (~1 s) as otherwise the water drop would be absorbed by the pores of the granite samples. The procedure was repeated twice for each sample spot with the same drop of water to guarantee a sufficient mixing. Finally, the remaining solution (~30 µL) was transferred to a 100 µL plastic vial or a sterile 2 mL reaction tube (Greiner Bio One, Germany) for the ion or ATP analysis, respectively.
2.5. DoR Sampling on Lichens and ATP Analysis
Lichen-covered granite samples from 2013 were stored in plastic bags at 5°C, while those from 2014 were placed on the roof of the institute but sheltered to avoid atmospheric deposition. The humidity experiments were conducted with samples from 2013, all other experiments with samples from 2014. Before sampling, all rocks collected in 2014 were conditioned in a self-built humidifier system (plastic box of 16×39×68 cm, containing an automatic humidifier from Le Veil, Spokane, WA, USA) for 0.5 hours with 80% humidity. Note, DoR sampling on lichens was carried out without the ring of rubber foam as the surface of lichens is hydrophobic the drop remained confined. The age of the lichens was derived from their diameter assuming an annual growth rate of 0.5mm [27]. ATP analysis was performed with the BacTiter-Glo Microbial Cell Viability Assay and the GloMax® 20/20 luminometer (Promega, Dübendorf, Switzerland). The ATP for the stock solution was from Thermo Scientific (Waltham, MA, USA). In deviation from the standard procedure given in the manual of the instrument the assay kit was equilibrated at room temperature and 10 mL of the substrate added to the buffer to prepare the reagent. The reagent (30 µL) was then pipetted into sterile reaction tubes (Greiner Bio One, Frickenhausen, Germany) and stored at-20°C for further use. Samples and reagents were warmed up to 25°C for 2 minutes. For the actual measurement, 30µL of the sample was added to the reagent solution and incubated at 25°C for 20 seconds.
2.6. Ion Analysis with Capillary Electrophoresis
The analysis of ions was performed with a portable CE instrument with capacitively coupled contactless conductivity detection (C4D) [27]. The equipment can deal with~25 µL of sample and is suitable for field applications [28]. A detailed measurement protocol and a schematic drawing of the portable capillary electrophoresis instrument are given in Torres et al. [27]. In short, the background electrolyte solution consisted of 11 mmol/L L-histidine, 50 mmol/L acetic acid, and 1.5 mmol/L 18-crown-6. Reagents for the stock solutions were provided by Fluka or Sigma-Aldrich (Buchs, Switzerland; Steinheim, Germany). Pure water for the preparation of the solutions and for the DoR sampling was from Merck (Zug, Switzerland). Vials and pipette tips were cleaned with 0.1 molar acetic acid and pure water, and air dried in a HEPA clean bench. A fused silica capillary (50μm i.d., 360μm o.d., 55 cm length) (BGB Analytic AG, Böckten, Switzerland) was used for the separation of ions under application of a voltage of 15 kV. For the simultaneous analysis of anions and cations, we injected the sample on two different CE instruments (identical set-ups, but different polarities) for 20 seconds hydrodynamically with 15 cm height for anions and 8 cm height for cations. The TraceDec® C4D detector (Innovative Sensor Technologies, Strasshof, Austria) and the eDAQ Chart software (version 5.5.8, Denistone East NSW 2112, Australia) were employed for data acquisition. The statistical significance of the data was evaluated with the Student’s t-test in R (GNU statistical software).
2.7. Scanning Electron Microscopy (SEM)
Scanning electron microscopy (Nova NanoSEM 230 FEI) with a gaseous analytical detector (GAD) was used for the visualization of the surface topography of the granite samples before and after freezing and thawing. To avoid alteration of the rock surfaces, the samples were not coated and a low vacuum mode was chosen (0.7 mbar). The spot size was set to 3.5, and the beam current to 15 kV. The rock surfaces were marked with three dots (~0.25 mm) of colloidal silver paste (Electron Microscopy Sciences, Hatfield, USA) as anchor points of a coordinate system.
3. Results and Discussion
3.1. Reproducibility of the Drop-on-Rock Method
Various eluents were tested to assure that only readily available ions were extracted but not ions released from the crystal lattice by hydrolysis. The differences in ion concentrations removed from the surface with a drop of pure H2O, 1 mmol/L HCl, or 1 mmol/L oxalic acid were statistically not significant. Hence, we conclude that the contact time of a few seconds was short enough to avoid hydrolysis. Repeated sampling of one spot resulted in decreasing concentrations of ions removed from the surface. This behavior suggested that the surface was increasingly exhausted of readily available compounds as a result of stepwise elution. This is one reason for the low reproducibility of the DoR sampling on granite surfaces. Another limitation arises from the fact that the sampled surface area varied at the millimeter scale, since the re-positioning of the confining rubber ring is not accurate enough in comparison with the mineralogical and topographical alterations at the micrometer scale. Therefore, the DoR sampling method was developed for semi-quantitative investigations only. The accuracy of the rubber ring’s re-positioning may be improved by using a special fixing device, which however would require additional technical effort.
The portable CE instrument allowed the ion analysis of tiny sample volumes (~25 µL) within 10 minutes with detection limits in the sub-micromolar range [29]. The quality of the sampling water was critical for low detection limits.
For the analysis of mobile ATP with the luminometer from triplicate measurements we achieved standard deviations of < 10% and < 5% for concentrations of ≤5 nmol/L, and ≤10 nmol/L, respectively. Relative standard coefficients for five point calibration curves were≥99%.
3.2. Ion Availability from Freshly Broken and Water-treated Granite Surfaces
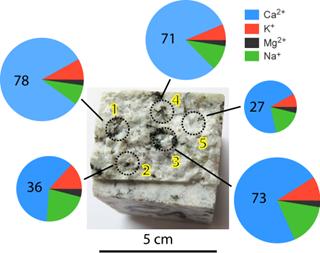
The release of ions from a rock surface is expected to depend on its mineral composition, the orientation of the minerals in relation to the rock’s surface, and its weathering state (e.g. [11]). Therefore, ion availability was tested at selected spots on the rock surface at areas dominated by either quartz or biotite minerals. Measurements were made first on the untreated surface after break-up and repeated after wetting and drying of the rock. The photo in Figure 3 shows one face of a cuboid granite specimen with the investigated DoR sampling spots. Initial measurements on untreated surfaces did not display any significant difference between locations dominated by either quartz or biotite. While quartz is prone to be most resistant with regard to weathering, e.g. biotite (Spots # 1 and 3, Figure 3) and feldspar contain ions that can easily be removed from the crystal lattice by hydrolysis. Results indicated that no dissolution of surface minerals occurred on freshly broken surfaces. However, granite surfaces that had been subjected to six hours of wetting, followed by drying, before sampling showed that all ion concentrations significantly increased. Concentrations were highest on spots dominated by biotite minerals (# 3, 1) and decreased with increasing proportions of quartz (in the sequence of # 4, 2, 5). The results were confirmed with replicate tests on three different granite surfaces (data not shown). In conclusion, wetting caused a correlation between the concentrations of the released ions and the weatherability of the sampled spots.
3.3. Ion Availability from Frozen and Thawed Granite Surfaces
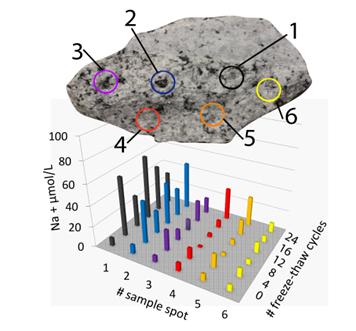
To investigate the impact of physical stress several pairs of mirror-imaged granite specimens were treated by freezing and thawing. Figure 4 shows a surface of a granite specimen with the investigated DoR sampling spots (top) and the sodium concentrations in the DoR samples before and after several freeze-thaw cycles (bottom). Regardless the increasing number of freeze-thaw cycles the concentrations did not show any trend. The scatter of data along the number of freeze-thaw cycles were probably caused by slight deviations of the sampled surface area in the course of the experimental campaign. As seen already in Section 3.2, the DoR samples from spots dominated by feldspar or biotite (# 1, 2, and 3) generally released higher sodium concentrations than other spots.
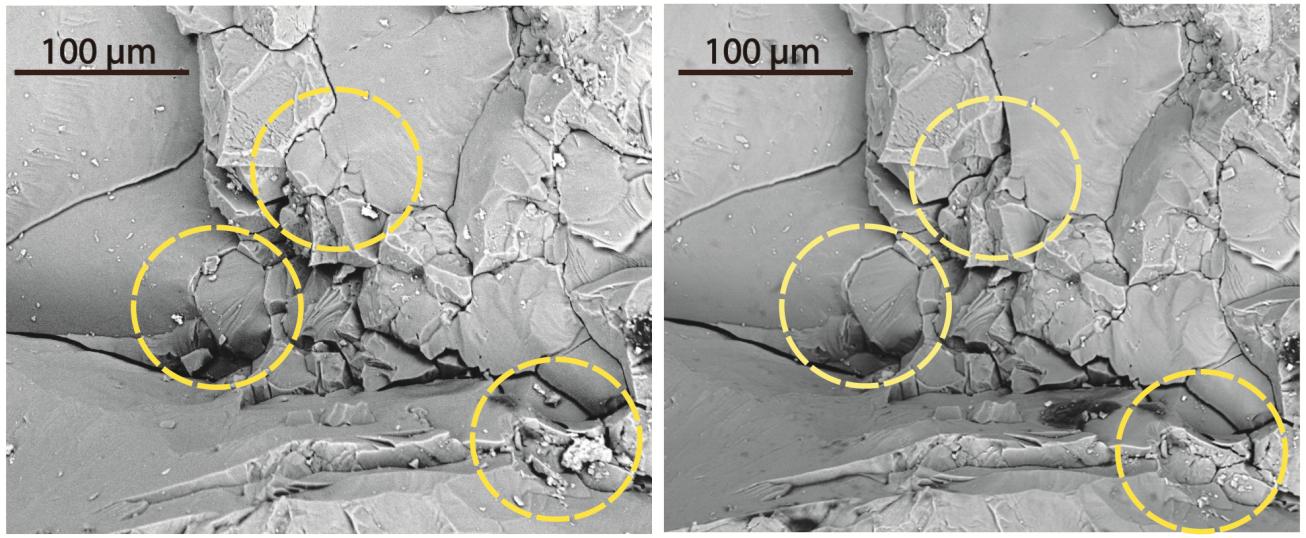
In addition, we compared a pair of mirror-imaged granite specimens, one only wetted, and the other also frozen and thawed. The surfaces of both halves released more ions than before treatment, surprisingly at comparable concentrations. To examine the possibility of additional generation of surface through freezing, the same 300 µm×300 µm surface area before and after freezing and thawing was imaged by SEM (Figure 5). As a consequence of frost action, pronounced surface break-down and rearrangement of particles were observed. However, the expected increase of instantly available cations was not confirmed by the CE measurements. Thus, the mobilization of cations from the granite surface appears to be promoted mainly by wetting rather than by subsequent freezing and thawing.
Again, surface spots dominated by phyllosilicates showed the highest concentrations of instantly available cations after wetting. Frost action did not increase the availability of ions in our experiments. Hence, the creation of new reactive surfaces relevant for the instant availability of cations appears to depend on the scale. Additional alterations on the micrometer scale through freezing and thawing are probably not relevant for increasing the release of ions during the very beginning of exposure. To verify these laboratory results we exposed granite samples to alpine field conditions (next section).
3.4. Ion Availability from Rocks Exposed to an Alpine Environment
We investigated the influence of atmospheric deposition and altitude-dependent climate on the surface-specific availability of nutrients in an alpine environment. Fresh granite surfaces were exposed on the northern slope and on top of Mount Pilatus from 2012 to 2014. On the mountain top, the temperature ranged from-25°C to +55°C. In contrast, the temperature at the lowest exposure site that was surrounded by shrub-sized vegetation, varied only between-5°C and +22°C. Among the approximately 200 DoR samples, no significant differences were found between the different altitudes (data not shown). This applied also to the comparison between granite surfaces that were facing upwards or downwards.
At all three altitudes, the concentrations of phosphate, nitrate and sulfate were mostly below detection limits according to Torres et al. [12]. However, less than 10% of the DoR samples collected on the upwards oriented granite surfaces showed concentrations of phosphate, nitrate and sulfate in the order of 1-40, 0.5-10, and 0.5-5 µmol/L, respectively (data not shown). Annual rates of atmospheric deposition were several orders of magnitude higher [15]. Thus, we conclude that bare granite surfaces did not accumulate atmospheric deposition, and therefore the DoR samples include the recently deposited material only. This can be seen also in the comparison of the three years of exposure, i.e. the highest ion concentrations were observed during the driest summer (2013). In conclusion, the contribution of atmospheric deposition is of limited residence time, if at all. For the given time-span, extrinsic factors such as frost, wind and radiation did not enhance the reactivity of the granite surface. These findings are in agreement with the freeze-thaw experiments (previous chapter). Despite the resistance of granite with respect to extrinsic factors, concentrations of instantly available ions can be significantly increased after the first contact with water, especially on spots with minerals prone to weathering.
3.5. ATP and Cation Availability from Lichen Surfaces
The lichen R. geographicum is one of the first colonizers of freshly exposed rocks. Within the same locality under identical climatic conditions the lichens’diameter is seen to represent their relative age [22]. Although, R.geographicum is widely used for geochronology, the study of crustose lichens is challenging as they grow very slowly and cannot be seperated easily from the substrate [12,30]. Although, ATP represents the vitality of the lichen [31], the analysis of ATP has not been applied yet to crustose lichen.
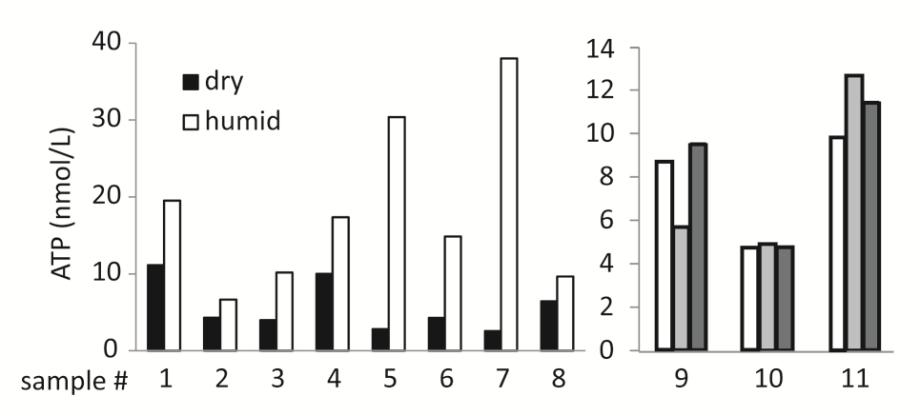
Using the DoR method we analyzed in parallel the concentrations of ions and mobile ATP as a factor of humidity and age (size). As shown in Figure 6 (left panel), initial experiments revealed that the mobile ATP on a lichen surface was highly dependent on ambient humidity. Mobile ATP was significantly higher when lichens were conditioned with moisture in comparison to unconditioned lichens. Thus, the production of ATP was reduced if the relative humidity was not optimal. Lichens are able to constrain their metabolism to protect themselves from desiccation [32,33]. To study the necessary time span of humidification for optimal metabolic rates, we analyzed the ATP concentrations of three individuals as a function of their exposure time (0.5, 2, and 13 hours) to a constant ambient humidity of 80%. The data shown in Figure 6 (right panel) reveal that ATP did not increase further after the first half hour of humidification. An additional parameter important for the metabolic activity of lichens is temperature. However, we worked under ambient conditions, thus we cannot quantify the influence of temperature.
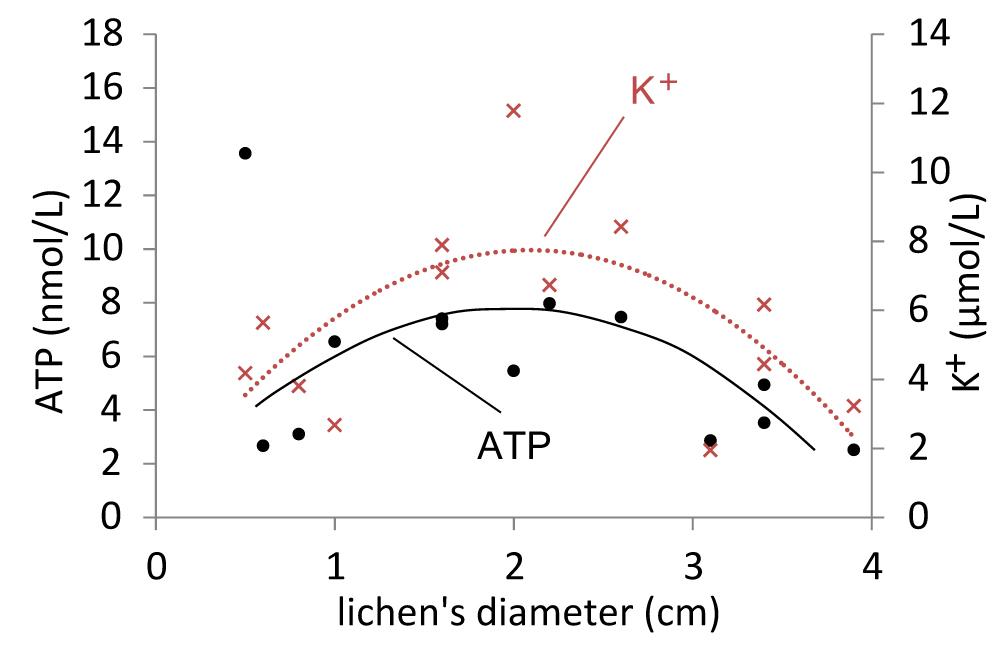
Furthermore, we investigated the relationship of the lichens’size and mobile ATP to estimate the dependence of vitality on age. ATP concentrations measured from R. geographicum individuals of 0.5 to 3.9 cm in diameter (10 to 80 years old) indicate a parabolic trend (Figure 7). Our findings are in accordance with previous observations of Armstrong and Bradwell [12,30]. Their data on radial growth rates of 3 to 50 years old lichens showed also a parabolic trend. Therefore, they concluded that growth accelerates after colonization and decelerates as lichens become older. It is assumed that cell degradation in the senescent phase may slow down growth [31]. This could also explain the decline in ATP concentration in our study. It must be stated, however, that differences in ATP availability from the older part (center) in comparison to the younger part (corona) of R. geographicum were not statistically significant (data not shown).
The analysis of potassium in the same DoR samples revealed a similar parabolic trend as observed from ATP. However, the other prominent cations, i.e. sodium, calcium and magnesium did not show any trend as a function of size. Potassium is an important nutrient for the lichen’s algae and can be mobilized by lichens from biotite [32,33]. To date it is not clear if a limited supply of K+ for the algae cell is corresponding to cell degradation. However, our limited data does not allow a definite conclusion from the ATP and K+ data regarding the weathering capability of R. geographicum. For linking the vitality of the organisms to rates of biological weathering more experimental data are needed. Nevertheless, the DoR method may be a useful tool to study such metabolic interactions.
4. Conclusions
In conclusion, the DoR method proved to be applicable for the investigation of rock and lichen surfaces for their readily available ions and mobile ATP. This opens a new experimental access to surface processes. The sampling procedure is simple, non-destructive and therefore also ideal for on-site studies, especially in remote areas or on samples that cannot be removed, e.g. buildings, monuments or large boulders. The analysis with the portable capillary electrophoresis instrument and the luminometer is reliable, inexpensive, and suitable for fieldwork. A promising future application might be the investigation of microorganisms in interaction with their chemical environment, e.g. by identifying the enrichment of elements on surfaces. As a follow-up to this study, the initial weathering of further rock types will be investigated with the DoR method, e.g. limestone, which is a very common building material and important in global weathering cycles.
Acknowledgments
We are grateful for technical support by Beat Kienholz, Michael Schurter (both Eawag), and Pius Dahinden (Pilatus-Bahnen AG). For the analytical support we thank Brian Sinnet, who helped with the scanning electron microscope and Frederik Hammes, who shared his experiences in the analysis of ATP (both Eawag). Furthermore, we thank Monika Niederhuber and Daniel Trüssel (both ETH Zürich) for the video animation of the SEM pictures. The authors acknowledge support by the Swiss National Science Foundation (Grant no. 200021-137715).
Conflict of Interest
All authors declare no conflict of interest.










 DownLoad:
DownLoad: