1. Introduction
There is no doubt that electrical energy, which dramatically fuels both the development of society and the improvement of people’s living standard, is the lifeline of national economy [2]. Availability of affordable and sustainable electrical energy has been the key to prosperity and continued socioeconomic growth in the nations and the world [2]. The two key characteristics of electrical energy are that it is easy to distribute but hard to store. More precisely, electrical energy can be transmitted to a faraway place through the power transmission lines with only a tiny loss, but unlike other common forms of energy such as chemical or kinetic, electrical energy should be used as it is being generated. If long-term storage is required, electrical energy will typically be converted immediately into another form of energy such as potential, kinetic, or electrochemical.
Electrical energy is currently provided to the end users through an infrastructure, comprised of utility companies, power plants, and transmission lines, which serve millions of electricity customers [3]. Due to the difficulty in storing electrical energy, matching power supply with real-time demand is the usual practice of power generation and distribution networks [4]. This is a challenging problem because the power demand depends on exogenous factors and varies dramatically as a function of time of day and seasonal factors [5]. Meanwhile, the amount of generation, transmission and distribution capacities that utility companies need to provision depends on the peak demand rather than the average, and the huge difference between energy consumption levels at peak usage hours and off-peak hours has resulted in not only cost inefficiencies and potential power delivery failures (brownouts and blackouts), but also environmental pollution due to the over-provisioning of the Power Grid and the resulted energy waste [6]. For example, the US national load factor (i.e., the ratio of average load to peak load) is about 55%, and only 10% of generation plants and 25% of distribution facilities are used only more than 400 hours per year, i.e., 5% of the total time [2].
Dynamic energy pricing provides a potential solution for demand shaping to reduce the peak power demand and smoothen the overall power profile, and has been widely investigated in [2,3,4,5,6,7,8,9,10]. Dynamic changes in energy prices provide an incentive for electricity users to shift their energy consumption from peak hours of energy usage to off-peak hours, and thereby, lower their monthly electric bills. At the same time, by effectively incentivizing users to shift their power demands, utility companies can reduce their capital expenditure without any need of adding new power plants to the Grid to meet the users’ power demands during peak hours. In summary, dynamic energy pricing can potentially benefit both the energy producers and consumers from the economical perspective.
Effective implementation of dynamic energy pricing faces many challenges. The most difficult step is to predict energy users’ reactions to various dynamic energy pricing policies, which calls for accurate behavioral models and practical algorithms. Authors in [6] and [7] provide algorithms for optimal load scheduling and cost minimization incentivized by dynamic energy pricing at the energy consumer side. For the utility companies, reference [8] proposes a real-time energy price determination algorithm under the assumption that each energy consumer will optimize a predefined utility function. However, these papers have focused on either profit maximization for utility companies or cost minimization for energy users. Considering the fact that utility companies tend to make decisions based on the anticipated response from energy users, our work in [11] combined the energy generation model of the utility company and the load scheduling model of residential users, and concurrently optimized the utility company’s power generation cost and the users’ electric bill. However, the optimization framework of [11] is based on a centralized monopolistic electrical grid, where a single utility company supplies all the power demands of electricity consumers in a local area, while the government enforces regulations on electric price in this monopolistic energy market. As a decentralized ”smart grid” becomes the major trend of the future electrical power network architecture [2], each energy user is allowed to have multiple choices among different utility companies. According to this trend, competition between different utility companies will be increasingly widespread, and will be encouraged by the government [12] due to the fact that monopoly results in significant deadweight losses (also known as excess burden or allocative inefficiency) and other types of economic inefficiencies.
To address the issues related to a centralized monopolistic market, in this paper we propose a dynamic pricing optimization framework for multiple utility companies in an oligopolistic energy market. At the beginning of each billing period (i.e., a day), each utility company will announce the time-of-use dependent electricity pricing policy during the billing period. Each energy user is able to perform task scheduling according to the dynamic energy prices, in order to minimize the total daily energy cost. Moreover, each energy consumer can freely select any utility company for energy supply at the beginning of each day, based on the anticipated energy cost on that day. Competition mechanisms among utility companies are introduced in this paper considering that (i) multiple utility companies concurrently make their decisions about dynamic pricing, and (ii) the dynamic pricing policies will affect each consumer’s selection of energy supplier and task scheduling results. Based on this system model, we propose two price determination methods for any utility company to maximize its total profit in the subsequent day, accounting for both the expected revenue obtained from energy consumers and the cost of energy generation. The first method maximizes a lower bound on the total profit that is guaranteed for the utility company. The second method finds the best response for the utility company with respect to the dynamic pricing policies of the other utility companies in the previous day. The first method is relatively conservative, and performs well when other utility companies are also rational and conservative. On the other hand, the second method is more aggressive in profit maximization without a guarantee of certain level of profitability. To exploit the advantages of each method while compensating the weaknesses, we propose an adaptive dynamic pricing policy based on the machine learning technique [18], which finds a desirable tradeoff between the two abovementioned methods. When employing this adaptive policy, the utility company consistently achieves high profit no matter what policies are utilized by the other utility companies.
The remainder of this paper is organized as follows. In the next section, we present the system model of the oligopolistic energy market with multiple utility companies. Section 3 presents the proposed dynamic pricing methods for the utility companies, and Section 4 reports the simulation results. The paper is concluded in Section 5.
2. System model
As stated earlier, our ultimate goal is to maximize the overall profit for a utility company in the oligopolistic market. In classical economics problems between sellers and buyers, sellers need to determine their prices based on the anticipated reaction of the buyers. This is because the sellers and buyers are typically non-cooperative and always make decisions for their own maximum profit [11], while the government would like to maximize the total social welfare. This is also the case for utility companies and energy users.
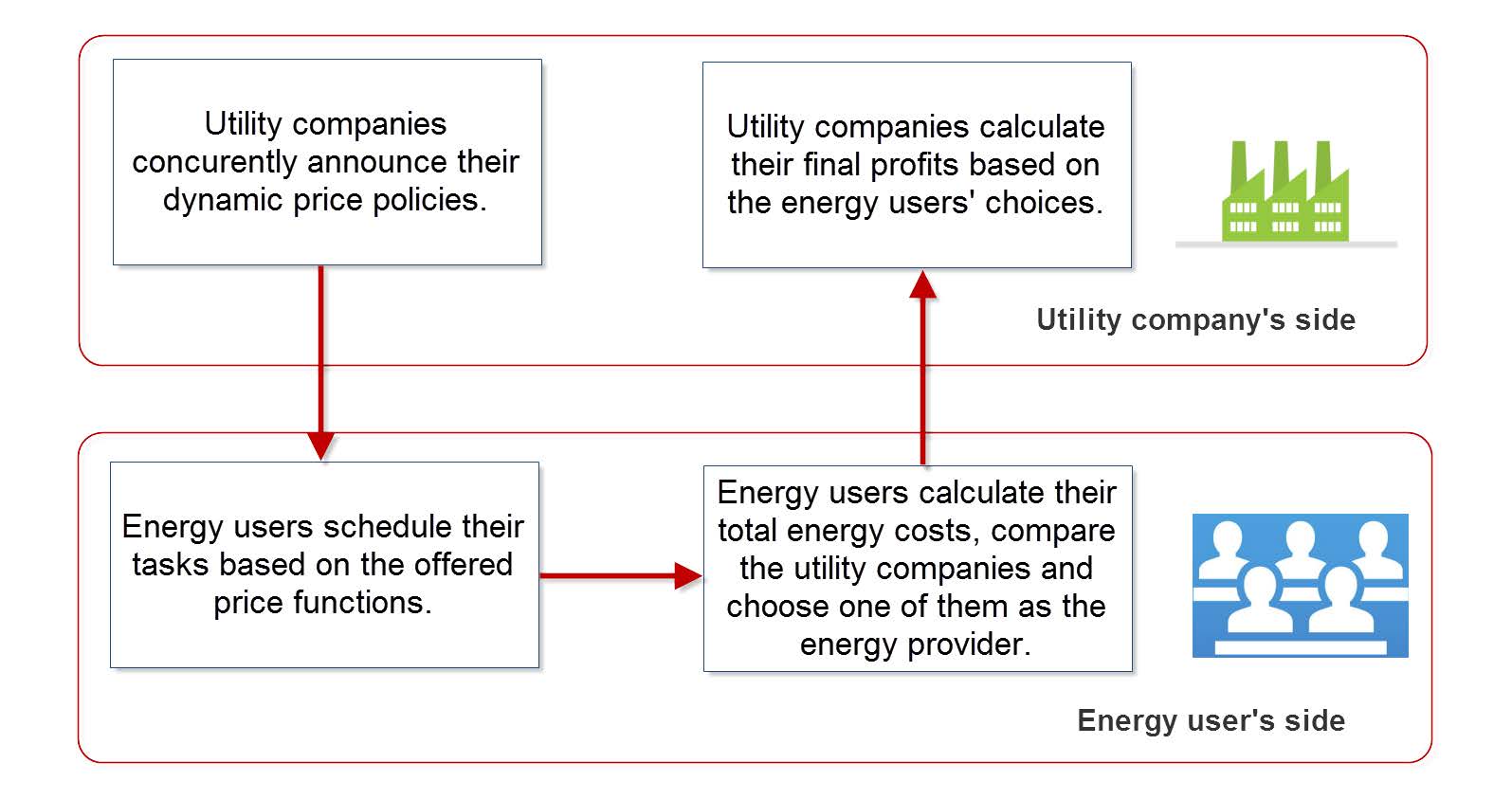
In the proposed system model, utility companies and energy users are assumed to act as noncooperative players, i.e., always trying to maximize their own profits or minimize their own energy costs. Each utility company needs to decide its dynamic energy price during the whole billing period by anticipating the energy users’ responses to various dynamic energy pricing policies. At the beginning of the day* (* We take one full day as the billing period for each utility company in the market.), all the utility companies concurrently announce their dynamic pricing policies over the billing period to energy users, in order to comply with the fair competition rules. Next each energy user (i) schedules its tasks according to the offered energy prices, (ii) calculates the resulting energy cost if it selects a utility company as its energy provider, and (iii) finally chooses one of the utility companies. When all the energy users have made their choices and scheduled their tasks accordingly, utility companies are able to calculate their final profits based on their own energy generation cost functions. This information will be used to set/revise future pricing policies of the utility companies. Figure 1 shows the flow chat of each billing period.
In the following, we first describe the task scheduling problem that each energy user faces and explain the solution method. Since multiple utility companies offer potentially different daily dynamic price functions, we next discuss the users’ responses to these prices (which are based on a modified Bertrand Competition Model) and explain their energy provider selection procedures. Finally, we present the method by which utility companies determine their future pricing policies in this oligopolistic energy market.
2.1. Model and solution of task scheduling for each energy user
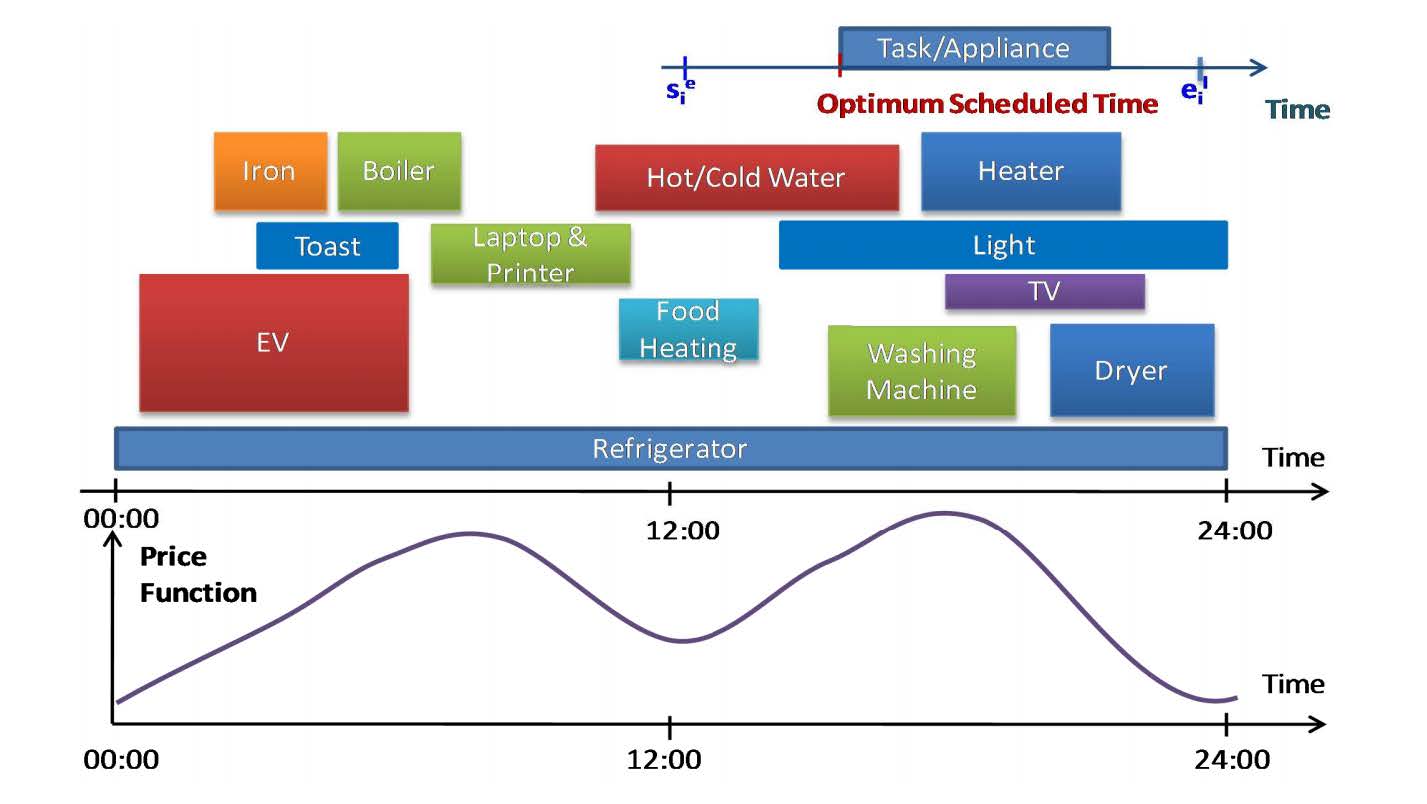
Figure 2 shows an example task scheduling solution based on the given electricity price function. The height of the task box in this figure signifies the amount of power the corresponding household task consumes when running. Under a non-constant price function, energy users tend to assign their tasks to low-price time periods.
In this paper, we adopt a slotted time model, i.e., all system cost parameters and constraints as well as scheduling decisions are provided for discrete time intervals of constant length. The whole billing period is thus divided into a fixed number of equal-sized time slots (in the experiment, a day is divided into 24 time slots, each with duration of one hour). Tasks can be launched only at the beginning of one of these time slots and be completed at the end of a slot.
We define the price function, P[t], as the price of one unit of energy at time slot t where @t\in\{1, 2, \dots, T\}@† († A unified price function is used throughout this paper). In this subsection, we assume that P[t] is fixed and pre-announced by the utility company at the start of the day. Energy users can schedule their tasks for the whole day but their decisions will not affect the energy price function. For the energy user of interest, we assume that there are a number of tasks that should be executed daily, and these tasks are independent of each other. These tasks are identified by index j. The set of task indexes is @\{1, \dots, N\}@ where N is the total number of tasks for the energy user. For each task j, the earliest start time, ES j, the latest end time, LEj, energy consumption per time slot, Cj, and the duration of task, Timej, are specified and provided to the energy user.
To solve the task assigning problem, two additional definitions are needed: start time, S j, which represents the time slot when task j starts and task operation condition, Mj[t], where Mj[t] = 1 if task j is operating at time slot t, i.e., @S_j ≤ t < S_j+Time_j@, and Mj[t] = 0 otherwise.
Using the above definitions, the energy user’s cost minimization problem can be modeled as follows:
Task Scheduling Problem for an Energy User
Find: the optimal S j for @1 ≤ j ≤ N@.
Minimize:
|
@Cost = \sum_t P[t] \cdot \sum_jC_j \cdot M_j[t].@
|
(1) |
Subject to:
|
@S_j \geq ES_j \ \ for\ \ 1 ≤ j ≤ N, @
|
(2) |
|
@S_j + Time_j ≤ LE_j \ \ for\ \ 1 ≤ j ≤ N.@
|
(3) |
A greedy algorithm can be used to achieve the minimal cost for the energy user, as shown in Algorithm
1.
| Algorithm 1 Task Scheduling Algorithm for an Energy User. |
| 1: | for each task j do |
| 2: | for every possible start time @ES_j≤ t≤ LE_j-Time_j+1@ do |
| 3: | Calculate sum[t] = P[t] + P[t + 1] + … + P[t + Timej - 1]. |
| 4: | end for |
| 5: | Find the minimal sum[t] and assign S j = t. |
| 6: | end for |
| 7: | Repeat the above steps until all the tasks are scheduled. |
It can be proved that the proposed greedy algorithm obtains the global optimum solution.
Property 1: Algorithm 1 achieves the minimal energy cost of each energy user.
Proof: In the task scheduling algorithm, every possible start time t of each task j is examined, and thus, an optimal schedule of each task j is achieved. As the tasks are considered to be independent, the minimal total cost of the energy user can be obtained when we apply this algorithm to all the tasks.
2.2. Responses of energy consumers to dynamic prices
Energy users will be the beneficiaries of the competition among utility companies since the competition encourages a larger range of choices of energy provider and results in lower electricity prices. The authors in [13] applied two kinds of competition models, i.e., the Cournot Competition Model and the Bertrand Competition Model, in a conventional electrical energy market. However, both of them may not be applicable in the future smart grid architecture. First of all, demand response is a key element of smart grid technologies, which implies that the usual practice of smart power networks is matching supply to demand instead of the opposite way. For this reason, the Cournot Model, where all the companies compete on the amount of products they produce, is not applicable to the future smart grid. On the other hand, the Bertrand Competition Model, which assumes that consumers always choose the product with the lowest price, also turns out to be oversimplified, because (i) the introduction of daily dynamic prices makes it hard for energy users to determine which utility company actually offers a better price, and (ii) the users may not be absolutely free to switch from one energy supplier to another [12].
In this paper, we use a modification of the Bertrand Competition Model in the energy supplier selection process that yields more realistic results. Let Costc, i denote the total electricity bill of the ith energy user, when it selects the cth utility company as energy supplier and performs optimal task scheduling (as shown in Section 2.1) in the entire billing period. Obviously, each ith energy user could estimate all the Costc, i values based on the dynamic energy prices offered by different utility companies. It is generally agreed by economists (cf. [12]) that each energy user i has a threshold cost value, denoted by threi, which represents the expected amount of money they prepare to pay for electricity bill. The threshold cost may differ for different energy users due to the variation in the energy users’ income level, total electricity consumption, cultural reasons, and other factors. Utility companies can predict each energy user’s threshold cost value by examining its previous reactions as well as other statistics. It has been conjectured in [14] that an energy user i will randomly choose one utility company among those who result in a total electricity cost no higher than the user’s threshold cost, i.e., Costc, i ≤ threi.
There is another situation where none of the utility companies offer a price lower than threshold, i.e., Costc, i > threi for ∀c. Because electrical energy is a necessity for all the energy users (please note that this is different from classical economic theory [12]), each user will choose the utility company that results in the least electricity bill Costc, i in this case.
2.3. Determination of daily energy prices by the utility companies
In the proposed oligopolistic energy market framework, the utility companies are aware of the task profiles and task scheduling/energy supply selection methods of energy users, using the increasingly widespread smart meters and prediction techniques [2]. Hence, each utility company is able to maximize its total profit by effective price determination based on the anticipated reactions of energy users.
At the beginning of day, each utility company c announces its energy price over the day, denoted by Pc[t] (1 ≤ t ≤ T), which is the optimization variable of the utility company. In addition, let cost_ec[t] denote the unit energy cost of each utility company c at time t, which is determined by the type of electricity generation (e.g., steam-power station or solar-energy-power station) as well as weather condition and seasons.
We define a Boolean variable satc, i for each utility company c and energy user i. We have satc, i = 1 if the energy price function offered by utility company c leads to an electricity cost no higher than the threshold cost for that user, i.e., Costc, i ≤ threi. In this case, energy user i is satisfied with utility company c. We have satc, i = 0 otherwise.
Consider the situation where none of the utility companies offer a satisfying price function for a certain energy user i, then the user chooses the utility company that results in the lowest energy cost after performing task scheduling. We set another binary variable winc, i = 1 when utility company c wins the price competition and is chosen by energy user i in this case, and set winc, i = 0 otherwise. Please notice that (i) we have Σc winc, i ≤ 1, which means at most one utility company can win the price competition for a certain energy user and (ii) for an energy user i, winc, i can be 1 only when satc, i = 0 for all c, i.e., the user is satisfied with none of the utility companies.
Based on the above definitions, the profit of each utility company can be separated into two parts: 1) the profit from satisfied users, which is a random variable since the users randomly choose one from all the utility companies that offer satisfying energy prices and, 2) the profit from unsatisfied users. The expected profit maximization problem for a utility company with price restriction can be formed as follows:
Profit Maximization Problem for Each Utility Company c
Find: the optimal price function Pc[t] for 1 ≤ t ≤ T.
Maximize: the expected profit value, given by:
|
@E[profitc]=∑i(11+∑c′≠c⋅satc′,i⋅satc,i+winc,i)⋅[∑t(Pc[t]−cost_ec[t])⋅conc,i[t]]
@
|
(4) |
in which conc, i[t] is the total energy consumption of energy consumer i at time t if it chooses company c and performs optimal task scheduling as discussed in Section 2.1.
Subject to: the price restriction rules:
|
@Pc[t]≥minimalprice for 1≤t≤T,Pc[t]≤maximalprice for 1≤t≤T.
@
|
(5) |
3. Profit maximization methods
The profit maximization problem for a utility company has been discussed in the previous section. In Eq. (4), the values of @\sum_{c'\neq c}sat_{c', i}@ and winc, i can be calculated only when the price strategies of the other utility companies are known in prior, i.e. each utility company’s payoff is determined by not only its own strategy (dynamic energy price), but also the price functions of its competitors. For fair competition, all companies announce their price functions simultaneously at the beginning of a day, implying that the decisions of other utility companies are unknown when one company determines its own price function. Those factors make the profit maximization problem a normal-form game among the non-cooperative utility companies [16].
For a normal-form non-cooperative game, the Nash equilibrium is of primary interest [16]. The Nash equilibrium is the optimal strategy profile for all the players (utility companies) in the sense that no player can benefit by changing its strategy unilaterally while the other players keep their strategies unchanged. However, it is hard to achieve the Nash equilibrium solution in our game formulation because of the following reasons: (i) the payoff of each player (utility company) is integrated with a task scheduling and energy provider selection process of various energy users, and hence is a complex function without explicit expression. As a result, it is difficult to guarantee the existence and uniqueness of Nash equilibrium for the players. (ii) The utility companies achieve best response with respect to the others in the Nash equilibrium only if all the companies are rational players. However, with the introduction of dynamic pricing, different utility companies could employ different price determination policies and it is not easy to tell which method is more ”rational” than the others.
Considering these factors, we present two price determination methods for each utility company. The first method maximizes a lower bound on the total profit that is guaranteed for the utility company and independent of the other utility companies’ strategies. The second method finds the best response of the utility company with respect to the dynamic pricing policies of the other utility companies in the previous billing period. In order to exploit the advantage of each method while compensating the weaknesses, we propose an adaptive dynamic pricing policy based on machine learning [18], which finds a desirable tradeoff between the two methods.
3.1. Lower bound-based profit maximization
In this method, we maximize a lower bound of profit for the company of interest. Notice that in Eq. (4), satc, i, cost_ec[t] and conc, i[t] for all i and 1 ≤ t ≤ T can be determined without knowing the pricing schemes of the other companies. Hence, a lower bound of the utility company’s profit can be estimated if we assume that the energy consumers satisfied with the utility company of interest are also satisfied with all the other companies, i.e., the energy price functions offered by all the utility companies lead to an electricity cost no higher than the threshold costs of those users. In this situation, those satisfied energy users have a probability of 1/K to choose the company of interest, where K is the total number of utility companies. We can maximize the lower bound given as follows:
|
@E[profit_boundc]=1K⋅∑isatc,i⋅[∑t(Pc[t]−cost_ec[t])⋅conc,i[t]]
@
|
(6) |
This lower bound is a conservatively estimated profit for the utility company, and can be guaranteed regardless of the other utility companies’ pricing policies. In this way, each utility company can independently optimize its own objective function (6) and finds the corresponding dynamic pricing policy, regardless of the pricing policies of the other companies. The lower bound-based profit maximization method performs well when the other utility companies are also rational and conservative.
Generally speaking, a simplified profit maximization problem considering fixed (and pre-known) task schedules of energy user is a mixed integer non-linear programming (MINLP) problem which is well known as NP hard. The integer part of the problem comes from the fact that satc;i is 0 or 1 based on the energy prices throughout a day. The complexity of solving this problem is equal to the complexity of selecting the best subset of the energy users and finding the energy price to satisfy their total cost threshold and to maximize the profit of the utility company. By adding the task scheduling model for each energy consumer in the previous section, this problem becomes a multi-level optimization problem and is even harder to find a practical algorithm leading to the best result. Considering these facts, we use simulated annealing (SA), which is a probabilistic technique that comes from annealing in metallurgy for approximating the global optimum of a given function [15], to find a nearly-optimal solution for the target utility company c with an objective function Obj = E[pro fit_boundc]. Details of this method are provided as follows:
In the simulated annealing-based approach, the run-time and the quality of final result can be adjusted by changing some parameters values as well as the running steps [15]. In Algorithm 2, the cooling factor α is a tradeoff between algorithm run-time and the quality of final result. If we decrease this factor, the algorithm run-time will be reduced but the final result will deteriorate. In addition, the final (cooling) temperature Temmin should also be adjusted together with factor a in order to derive the best pricing results.
3.2. Best response-based profit maximization
Although the lower bound-based profit maximization method guarantees a conservative estimated profit for the utility company c, it fails to take into consideration the revenue from those unsatisfied energy users by winning the price competition. However, as stated before, all the utility companies announce their price functions simultaneously at the beginning of each billing period, the decisions of other utility companies are unknown when one company is deciding its own strategy on energy price function. In this method, utility company c predicts its competitors’ price functions based on the information from the previous billing period that is already announced to all the energy users, and optimizes its own price function Pc[t] for 1 ≤ t ≤ T based on these data, i.e., each utility company designs its price function so that it has the best response to the price functions from other companies in the previous billing period. The objective function of utility company c is Eq. (4), where the satc0;i (for c' ≠ c) and winc, i values can be estimated by utility company c since it takes the other companies’ price functions from the previous billing period. Let E[pro f it'c] denote the objective function of the best-response-based profit maximization method. Please note that it is different from E[pro f itc] in Eq. (4) due to the adoption of the other companies’ price functions from the previous billing period. The algorithm of best response-based profit maximization is also based on the simulated annealing approach and is similar to what we have discussed in the previous method. The algorithm details are omitted due to the similarity to Algorithm 2.
| Algorithm 2 Lower bound-based profit maximization algorithm for utility company c. |
| 1: | Initialize Pc[t] for 1 ≤ t ≤ T. |
| 2: | Initialize Objmax to be a large negative number. |
| 3: | Initialize temperature Tem = Temmax. |
| 4: | while (Tem > Temmin) do |
| 5: | Change the price function Pc[t](1 ≤ t ≤ T) by randomly picking one or several successive time slots and changing the price values while satisfying the constraints provided in Eq. (5). |
| 6: | Anticipate the task assignment results for all the energy users under the modified price function. |
| 7: | Calculate conc, i[t](1 ≤ t ≤ T) and satc, i for each i. |
| 8: | Obj←E[pro f it_boundc] in Eq. (6) based on the calculated conc, i[t] and satc, i values. |
| 9: | if Ob j ≥ Ob jmax then |
| 10: | Accept the change of the Pc[t] values. |
| 11: | else |
| 12: | Accept the change with probability e(Obj-Objmax)=Tem. |
| 13: | end if |
| 14: | Ob jmax←Ob j if the change has been accepted. |
| 15: | Decrease the temperature Tem by a factor of α. |
| 16: | end while |
3.3. Learning-based profit maximization
There are some limitations in the best response-based profit maximization method discussed in Section 3.2. The main weakness of the method is that it can only provide a solution that is the best response to the price functions from other companies in the previous billing period, instead of the current billing period. Moreover, compared with the lower bound-based profit maximization method, the best response-based method is more aggressive in profit maximization without a guarantee of certain level of profitability. Our goal is therefore to find an optimal tradeoff between the two methods. More specifically, we set the new objective function for utility company c as Obj = α · E[pro f it_boundc] + (1 - α) · E[pro f it'c], where α ∈ [0,1] is the factor representing the preference of each method.
The most critical task in the new method is the evaluation and selection of the preference factor α. For a utility company, a machine learning algorithm is employed for this purpose [18]. The algorithm is an adaptation of Freund Schapire’s on-line allocation algorithm [19]. The target utility company has L policies to choose from; we number these policies l ∈ {1, 2, ..., L}. Each policy l corresponds to a preference factor αl ∈ [0,1]. The algorithm associates and maintains a weight vector @\mathbf{w}^d=<w_1^d, w_2^d, \dots, w_L^d>@ comprised of weight factors corresponding to different policies, where d ∈ {1, 2, ... } is the index of each billing period. The value of a weight factor @w_L^d@ reflects the estimated performance of a policy l, where a higher value indicates a better performance. In our implementation, the initial weights @w_l^1@ ’s of all the policies are equally set to be 1/L.
At the beginning of each billing period, the utility company simply selects the policy with the highest weight, and subsequently finds the dynamic price based on the corresponding objective function using simulated annealing. If there are multiple policies with the equal weight, the utility company randomly selects one of these policies. Once the billing period (a day) finishes, the utility company evaluates the performance of the selected policy by calculating the actually received profit based on the energy users’ reactions to the announced price function. Dormant (unselected) policies are evaluated on the basis of how energy consumers would have reacted if such policies had been selected. Please note that this is a unique feature of the learning framework in this work since most learning-based policy selection method does not allow for evaluating the unselected policies [20]. In the evaluation phase, a value @loss_l^d@ is used to capture the profit loss of each policy l ∈ {1, 2, ... , L} by comparing with the maximal profit from all the policies:
|
@lossdl=1−profitdlprofitdmax
@
|
(7) |
where @profit_{max}^d=\mathbf{max}_l(profit_l^d)@.
The final step in the evaluation phase involves updating the weight factors for all the policies based on the @loss_l^d@ values they have incurred:
where the learning parameter @\beta@ is set between 0 and 1. Thus, the weight factors corresponding to policies with higher @loss_l^d@ values get reduced more than the policies with lower @loss_l^d@ values. This procedure enhances the chance of selecting the better performing policies in the next billing period. Once the weight factors are updated, the utility company is again ready to select its pricing determination policy for the next billing period. Details of this method are presented as follows:
4. Experimental results
To observe the effectiveness of the proposed profit maximization algorithms, various cases corresponding to the aforesaid pricing models are examined. The proposed algorithms have been implemented in C++ code and tested also for random cases.
4.1. Simulation setup
In our simulations, we consider one day as a billing period and duration of one time slot is set to be one hour. To make the experimental result easier to read, units of energy and cost are all unified with a resolution set to be 1.
We assume that there are 3 utility companies to serve a community of in total 1000 energy users with 10000 aggregated tasks and each company starts with a relatively high initial price of 120‡ (‡ We end up with similar results under low initial price functions). We use the predicted energy users’ profiles to design the price function of each utility company. The duration of each task varies from 1 to 6 time slots, the power consumption of each task varies from 1 to 10 energy units per time slot. The earliest start time and latest end time of each task are also generated randomly.
| Algorithm 3 Machine learning-based profit maximization algorithm for utility company c. |
| 1: | Initialize @w_l^1 = 1/L \; for \; l \in \{1, 2, \dots, L\}@. |
| 2: | for each day @d=\{1, 2, \dots\}@ |
| 3: | At the beginning of day d: |
| 4: | Choose the policy l with the highest weight in @\mathbf{w}^d@ |
| 5: | Find the preference factor @\alpha_l@ with the corresponding l. |
| 6: | Determine the objective function Obj based on @\alpha_l@. |
| 7: | Determine the price function Pc[t] for 1 ≤ t ≤ T using simulated annealing method. |
| 8: | Energy users choose energy provider and schedule their tasks according to the announced price functions. This step is out of the control of the utility company |
| 9: | At the end of day d: |
| 10: | Evaluate the performance of each policy using Eq. (7). |
| 11: | Update the weight vector using Eq. (8). |
| 12: | end for |
To be realistic, the energy generation cost functions of those utility companies are different due to the power-station type as well as the technology. The average energy generation cost for each utility company is set to be between 40 and 50. The first utility company is assumed to be a pure thermal power plant with a constant energy generation cost throughout the day, the second company models a solar power plant where the energy generation cost is lower at daytime, and the third company is a combination of the above two.
For simulated annealing setup, the initial temperature Temmax is set to be 4.0, the cooling factor @\alpha @ is set to be 0.96, and the final temperature Temmin is set to be 1.7. Under each temperature point Tem, we conduct 120 iterations, and the total number of iterations is around 2500.
4.2. Lower bound-based profit maximization results
We first use the lower bound-based profit maximization algorithm to decide the price function for each utility company. Table 1 shows the comparison of initial and final E[pro f it_boundc] calculated using Eq. (4) in the previous section.
Table 1. Comparison of expected profit bound for utility companies between initial price function and optimized price function in lower bound-based profit maximization method.
| Company | Initial expected profit bound | Final expected profit bound | Profit increase factor |
| 1 | 132520 | 622960 | 4.7 |
| 2 | 274284 | 755646 | 2.75 |
| 3 | 193419 | 654224 | 3.38 |
It can be observed from Table 1 that all those 3 utility companies achieved the E[pro f it_boundc] increase by a factor between 2 and 5. This is because they adjusted their price functions to satisfy a certain amount of users while maintaining a gap between the energy price and energy cost. If we take energy prices in June 2014 from Consolidated Edison Company§ (§ http://www.coned.com) as an example (from 0.0116/kWhto0.3032/kWh) and consider U.S. residential energy users each with an average annual electricity consumption as 10,932 kWh¶ (¶ https://www.eia.gov), the average daily revenue increase for each utility company (serving a community of 1000 energy users) can be around $1500.
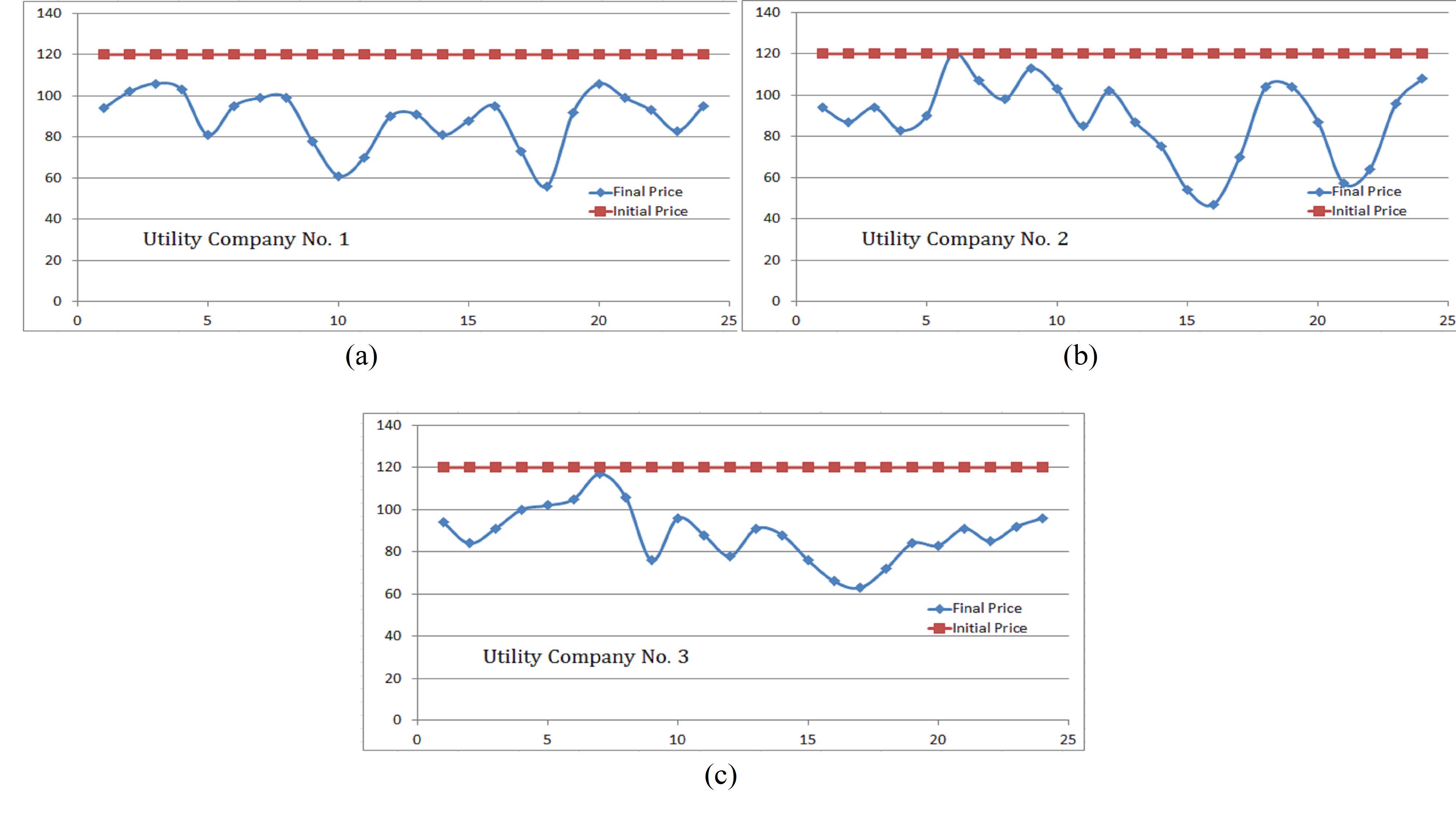
Figure 3 shows the change of price function for each utility company. In Figure 3, the energy price of each utility company significantly decreases after all of them have tried to maximize their expected profit bounds. Remember that there is no price constraint from government. Instead, it is competition in energy market that has brought price down, which has been proven to be more efficient in promoting overall economic well-being than a centrally planned monopoly market [12].
However, all the previous simulations are merely based on profit prediction at the utility company’s side. In order to verify whether the proposed algorithm really guarantees a lower bound on the total profit, another simulation is presented from the energy user’s side. In this simulation, we assume the price functions are given from the previous solution and all energy users give their reactions on which utility company to choose based on the rules discussed in section 2, i.e., randomly choose a utility company which they are satisfied, or choose the utility company which offers a price function resulting in the lowest energy cost if none of the companies offer a satisfied price function. After that the real profit of each utility company is calculated and compared with the lower bound of the expected profit, which is shown in Table 2.
Table 2. Comparison between expected profit bound and real profit for utility companies in lower bound-based profit maximization method under optimized price function.
| Company | Expected profit bound | Real profit | Profit compare ratio |
| 1 | 622960 | 733376 | 1.18 |
| 2 | 755646 | 3275627 | 4.33 |
| 3 | 654224 | 788670 | 1.21 |
It is shown in Table 2 that all the 3 utility companies received a real profit higher than expected. This is because we were using a conservative estimation of final profit during price determination step, and thus a lower bound on the expected total profit is guaranteed for each utility company. Notice that the second utility company turned out to have a real profit much higher than expected, which comes from the winning of price competition of unsatisfied energy users due to its low energy cost. However, the price advantage of the second company didn’t affect other utility companies’ expected profit.
The weakness of the lower bound-based algorithm is also shown in Table 2. For company 2, the real profit is much higher than the expected profit, indicating that there is a large amount of profit from unsatisfied energy users, which failed to be considered in the price determination step.
4.3. Best response-based profit maximization results
In the second set of simulations, the best response-based profit maximization algorithm is used for the utility companies. Each company takes its competitors’ price functions from the previous billing period that is already announced to all the energy users, and decides its strategy on energy price function. The expected profit @\mathbf{E}[profit'_c]@ presented in the previous section is calculated after each company finds its optimal price function. Notice that the expected profit in this algorithm is based on other companies’ price functions in the previous billing period (not the current billing period). When all the utility companies have calculated and announced their current price functions, the real profit of each company is calculated and compared with the expected profit. Table 3 shows the result.
Table 3. Comparison between expected profit and real profit for utility companies in best response-based profit maximization method.
| Company | Expected profit | Real profit | Profit compare ratio |
| 1 | 9335982 | 9599154 | 1.03 |
| 2 | 7233343 | 4291950 | 0.59 |
| 3 | 5021153 | 4089555 | 0.81 |
From the results shown in Table 3, one can see that the real profits turn out to be unpredictable for all the utility companies. Except for the first company, each of the other two utility companies achieves a real profit much less than the expected profit after applying the best response-based profit maximization method. This is because the solution of this method is the best response to the price functions from other companies in the previous billing period, instead of the current billing period. In addition, compared with the results from lower bound-based method, the best response-based method turns out to be more aggressive in profit maximization without a guarantee of certain level of profitability.
4.4. Learning-based profit maximization results
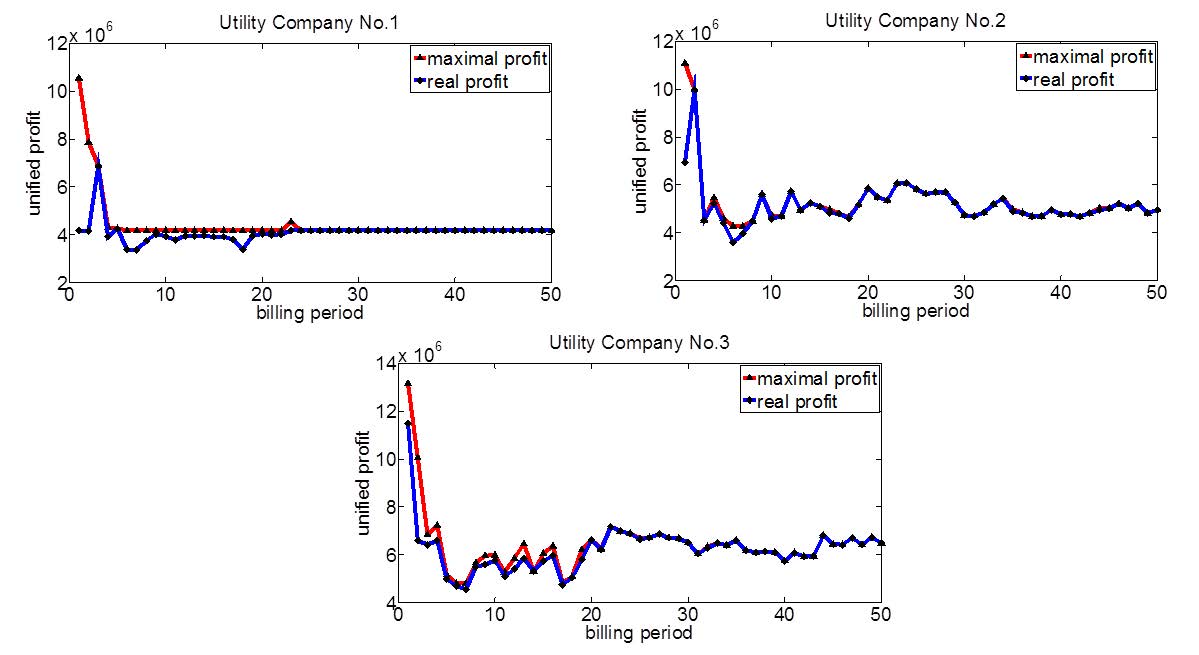
In order to show the effectiveness of our learning-based profit maximization algorithm we consider five profit maximization policies for each utility company based on preference factor @\alpha \in \{0, 0.3, 0.5, 0.7, 1\}@. At the beginning of each billing period, each utility company selects the policy with the highest weight, and subsequently finds the dynamic price based on the corresponding objective function using simulated annealing. At the end of the billing period, both the selected and dormant (unselected) policies are evaluated. The simulation runs for 50 billing periods. For each utility company, the real profit it gets from the selected policy and the maximal possible profit it could get from the optimal policy are compared in each period, as is shown in Figure 4.
It can be observed in Figure 4 that during the first several billing periods, each utility company did not choose the optimal policy, which result in a real profit much less than the maximal achievable profit at the corresponding billing period. However, after the profits from other policies are evaluated and compared, the utility companies are able to learn from the information and finally all the three companies are able to choose the optimal price determination policy. The result shows that our learning-based adaptive policy achieves high profit for the utility company no matter what policies are employed by the other companies.
We also observe that the maximal profit of each utility company has decreased, especially during the first several billing periods. This is because of price competition in the oligopolistic electrical market, which decreases the electricity cost of the energy users.
5. Conclusion
In this paper, we present an oligopolistic energy market model with multiple non-cooperative utility companies including its problem formulation and solutions. The utility companies determine dynamic energy prices concurrently to maximize their anticipated profits, based on a modified Bertrand Competition Model of user behavior. We first propose two price determination methods for any utility company for the purpose of profit maximization. While the first method aims to find a lower bound of the total profit guaranteed for the utility company, the second method is designed to calculate the best response of the utility company with respect to the dynamic energy prices of the other companies in the previous day. We also propose a machine learning-based adaptive dynamic pricing policy to exploit the advantage of both methods. Experimental results show that the adaptive policy results in consistently high profit for the utility company no matter what policies are utilized by the opponent companies.
Acknowledgments
This research is sponsored in part by the Software and Hardware Foundations program of the NSF’s Directorate for Computer & Information.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: