Optimistic expectations and life satisfaction as antecedents of emigration attitudes among Bulgarian Millennials and Zoomers

1.   Introduction

Type 1 diabetes is a chronic condition that is caused by the immune system mistakenly destroying insulin-producing pancreatic Langerhans islets. Treatment requires continuous monitoring and maintenance of insulin levels via external means such as injections or insulin pumps. Islet transplantation from deceased donors provides a new treatment to recover natural insulin production ^[1]. This is not a permanent solution, as a significant percentage of patients do not achieve insulin independence at 5 years ^[1]. Furthermore, such a treatment requires immunosuppressants. As there are only a few suitable donors, it is desirable to increase the durability of the transplanted cells. This could be achieved by protecting the transplanted cells with a physical barrier. Alginate is a promising candidate as it can selectively diffuse or block certain molecules ^[2]. In addition, alginates are relatively inert ^[3,4,5]. This novel treatment shows promising results in mammalian trials ^[6,7,8,9]. Human trials are still in the preliminary phase ^[10,11,12].

King et al. ^[13,14] proposed a model that describes the reaction–diffusion of oxygen through a protective shell encapsulating a core so that hypoxia can be avoided within the donor cells. The encapsulation and core of donor cells are approximately spherical ^[15]. Hence, in ^[13,14], a spherical core and shell with a common center are considered. In that paper the authors derived the governing ODE for stationary solutions and numerically computed these solutions with oxygen concentration above the hypoxia threshold. The existence of these stationary solutions is made rigorous in ^[16] using topological shooting ^[17,18,19]. The latter result considers parameters used in cell encapsulation experiments ^[15,20,21]. Stationary solutions of oxygen concentration in a core without a shell have been extensively studied ^{[22,23,24,25]}.

The oxygen concentration in the core and shell will initially be away from the stationary state. Furthermore, the geometry of the cell is only approximately spherical. Hence, it is important for the validation of the model to determine the stability of stationary solutions for general core-shell geometry, which is the goal of this work. This first requires formulating the corresponding PDE and showing its well-posedness, which was not considered in ^[13,14]. The resulting PDE is of parabolic type. On the boundary of the outside shell, we assume the oxygen concentration to be constant. As the shell and the core have different diffusion coefficients, there is a discontinuity of this coefficient at the interface separating them. This discontinuity makes the corresponding stationary problem a diffraction problem ^[26]. We make the natural assumption that the concentration and the flux of oxygen are continuous at the interface. Oxygen is consumed only by the donor cells in the core but not by the protective shell. This leads to a nonlinear reaction–diffusion PDE in the core, where the non-linearity corresponds to Michaelis–Menten consumption and consequently is bounded and monotone. In the shell, however, the problem reduces to linear diffusion.

Our main results for our newly formulated PDE model are

- Well-posedness of the strong form,

- Uniqueness and asymptotic stability of stationary solutions.

The results are necessary theoretical steps in the validation of the biological model. Furthermore, we will see that all the results hold for more general kinetics described by Hill's equation. We note that similar results have been obtained in the one-dimensional setting for the internal transition layer, which arises by scaling the discontinuous diffusion coefficient by a small parameter ^[27].

The sum of the reaction term and the spatial differential term is a nonlinear monotone operator. Hence, for the well-posedness result we can apply classical monotone operator theory. We apply the well-known theorems of Komura and Browder–Minty ^[28]. We emphasize that the monotonicity of the nonlinear operator defining our evolution problem results from the underlying structure of the problem as a gradient flow with respect to a convex functional. This structure also enables us to show the uniqueness and asymptotic stability of the stationary solution.

In Section 2, we present the governing equations. The well-posedness result is proved in Section 3. The stability results are presented in Section 4. In Section 5, we formulate the PDE donor cell model, transform it to the setting considered in Section 2, and apply the theorems from Sections 3 and 4. Finally, in Section 6, we conclude with remarks and an outlook on further questions.

2.   Core-shell parabolic PDE

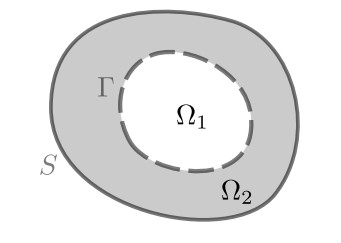
We start with a description of the geometry of the core and its protective shell. The domain is denoted by $\Omega \subset \mathbb{R}^N$ with $\overline{\Omega}$ compact and $N \geq 2$. For the application $N = 3$, but the results hold for $N \geq 2$. Let $\Gamma$ be an $(N-1)$-dim surface that divides $\Omega$ into two open domains $\Omega_1, \Omega_2$ such that $\partial\Omega_1 = \Gamma$ is a closed connected hypersurface and $\Omega_2$ has 2 boundary components, $S: = \partial \Omega$ and $\Gamma$, see Figure 1. We take $S, \Gamma$ of class $C^2$. We refer to $\Omega_1$ as the core, $\Omega_2$ as the shell, and $\Omega$ as the core-shell.

We consider the following PDE:

In Eq (2.1), $b: \Omega \rightarrow \mathbb{R}$ is given by

with $b_1, b_2 > 0$, the map $f: L^2(\Omega)\rightarrow L^2(\Omega)$ given by

with $\varphi_i: \mathbb R \rightarrow \mathbb R$, $i = 1, 2$.

The following assumptions are the requirements for well-posedness of the strong form as well as uniqueness and asymptotic stability of stationary solutions:

Assumption 2.1. Let $\varphi_i$ satisfy

- $0 \leq \varphi_i \leq 1$;

- $\varphi_i$ is decreasing;

- $\varphi_i(z) z \leq c$ for all $z \in \mathbb R$ with $c > 0$;

- $\varphi_i$ is Lipschitz with constant $L > 0$.

In Eqs (2.3) and (2.4), the square brackets $[\cdot]_\Gamma$ are denoting the jump of the quantity in the brackets across $\Gamma$, i.e., the trace from $\Omega_2$ minus the trace of $\Omega_1$. In Eq (2.4), $\nu$ is the normal directed towards $\Omega_2$.

3.   Well-posedness results

Define $V: = H^{1}_0(\Omega), H: = L^2(\Omega)$. The inner product on $V$ is defined by $(u, v)_V = (u, v)_H + (\nabla u, \nabla v)_H$. Denote by $\langle \cdot, \cdot \rangle$ the pairing between $V^{*}$ and $V$. So we have the evolution triplet

where $H^\ast$ and $V^\ast$ denote the dual space of $H$ and $V$, respectively. Moreover, we write $V\subset\subset H$ to emphasize the compactness of the embedding of $V$ in $H$.

Define the nonlinear operator $A : D(A) \rightarrow H$ given by

with

We consider the equation

as an equality in $L^2(0, T; H)$. We denote by $C_w(0, T; H)$ the space of weakly continuous functions from $[0, T]$ to $H$.

Theorem 3.1. For $u(0) = u_0 \in D(A)$, Eq (3.2) has a unique solution $u \in C^0(0, T; H)$ for any $T > 0$ with

Furthermore, $u_0 \mapsto u(t) \in C^0(D(A), D(A))$.

Proof. We will apply Theorem 31.A from ^[28]. Recall that $A$ is called monotone if $({A}(u)-{A}(v), u-v)_H \geq 0$ for all $u, v \in D(A)$. Let $R$ denote the range of an operator and let $I$ denote the identity operator. The assumptions to check are:

$(\text{H}1):$ $A$ is monotone,

$(\text{H}2):$ $R(I+A) = H$.

Proof (H1): Since $\varphi$ is decreasing - we obtain

for $u, v \in D(A)$.

Proof (H2). We consider $\tilde{A}: V \rightarrow V^\ast$ given by

Recall that $\tilde{A}$ is called hemicontinuous if the real function $t \mapsto \langle \tilde{A}(u+tv), w \rangle$ is continuous on $[0, 1]$ for all $u, v, w \in V$ and that $\tilde{A}$ is called coercive if

We apply Theorem 26.A ^[28] to $\tilde{A}$, which gives that for fixed $g \in H$, there exists a $u \in V$ such that $\tilde{A} u = g$. The assumptions to check are:

- $\tilde{A}$ monotone: Take $u, v \in V$, then similarly to Eq (3.3), we have that

- $\tilde{A}$ coercive: Recall from Assumptions 2.1 that $\varphi(z)z \leq c_0$ for all $z \in \mathbb R$. Hence, we have that

and therefore, we have Eq (3.4).

- $\tilde{A}$ hemicontinuous: for $t, s \in [0, 1]$ $u, v, w \in V$, the Lipschitz continuity of $\varphi_i$ by Assumption 2.1, we have

This implies the continuity of $t \mapsto \langle \tilde{A}(u + tv), w \rangle$.

Hence, for fixed $g \in H$, there exists a $u \in V$ such that $\tilde{A} u = g$, i.e.,

It remains to show that $u \in D(A)$, which can be done by adapting standard arguments on the regularity of weak solutions to elliptic boundary value problems to our two-phase setting ^[29]. More precisely, since $-u+f(u)+a\in H$ and $b$ is constant in $\Omega_i$, we can show, as in ^[30] Theorem 6.3.1, that Eq (3.5) implies $u|_{\Omega_i}\in H^2_{\rm loc}(\Omega_i)$ and

To obtain $H^2$-regularity up to the boundary, we modify the proof of ^[30] Theorem 6.3.4. (with partly changed notation) in the following way: We fix $x^0\in \Gamma$ and "flatten" $\Gamma$ locally in a neighborhood $U_{x^0}$ of $x^0$ by an appropriate $C^2$-diffeomorphism $\Phi: U_{x^0}\longrightarrow B(0, 1)$ so that we have

For the transformed problem, the jump of $b$ occurs along the plane $y_N = 0$. Therefore, the estimates for the difference quotients of the transformed solution in the first $N-1$ coordinate directions can be carried out in both half balls as in the proof of the cited theorem. Thus, we analogousy obtain $u|_{\Omega_i}\in H^2(\Omega_i)$. Hence, applying integration by parts in the subdomains,

so by Eq (3.5), the boundary integral vanishes for all $w\in V$, which implies Eq (2.4), and $u\in D(A)$ is proved.

Finally, applying Corollary 31.1 from ^[28] gives that $u_0 \mapsto u(t) \in C^0(D(A), D(A))$.

4.   Stability results

We define the functional $E: V \rightarrow \mathbb R$ given by

where

Lemma 4.1. $E$ is Fréchet differentiable with derivative at $u$ given by

Proof. The first term in Eq (4.1) is a quadratic term in $V$. $F_i$ has a bounded, integrable weak second derivative. Hence, for $z, \zeta \in \mathbb R$ we have

Thus, for $u, h \in V$

and $u_i \mapsto \int_{\Omega_i}F_i(u)dx$ is Fréchet differentiable with derivative given by

Lemma 4.2. $E'$ is strongly monotone, i.e., for all $u, v \in V$, there exists $\gamma > 0$ such that

Proof. Take $u, v \in V$, then using $\varphi_i$ decreasing and Poincaré's inequality we obtain

From Lemma 4.1, it follows that we can write Eq (3.2) as a gradient flow:

in the sense that

Recall that $u^\ast \in V$ is called a critical point if $E'(u^\ast)v = 0$. Hence, stationary solutions are critical points of $E$.

Theorem 4.3. There is precisely one stationary solution to Eq (3.2).

Proof. If $E$ is a continuous, strictly convex, coercive functional then $E$ has a unique critical point which is also a global minimum by Theorems 1.5.6 and 1.5.7 in ^[31]. $E$ is continuous. Strict convexity of $E$ follows from Lemma 4.2. So we only need to show coercivity. Observe that if $s > 0$, then $F_i(s) \leq s$, and if $s \leq 0$, then $F_i(s) \leq 0$. Hence, $F_i(s) \leq |s|$ for all $s \in \mathbb R$. Therefore, using Poincaré's inequality, we have that

Hence, $E$ is coercive. The result follows from Lemma 4.1.

Denote the unique stationary solution by $u^\ast \in V$.

Theorem 4.4 (Global asymptotic stability in $H$). Let $u$ be a solution of Eq (3.2), then $t \mapsto {\rm e}^{\gamma t} \|u(t)- u^\ast \|_H$ is bounded for $t \geq 0$.

Proof. Observe that $E'(u^\ast) = 0$. From $u \in L^2(0, T; V)$, $\frac{du}{dt} \in L^2(0, T; V^\ast)$ we have that

by Theorem 7.2 in ^[32]. Now let $u$ be the solution of Eq (3.2). Then by Eq (4.3) and Lemma 4.2 we have that

Hence, we obtain that $\|u(t)- u^\ast \|_H^2 \leq e^{2 \gamma t} \|u(0)- u^\ast \|_H^2$.

Asymptotic stability in the $V$-norm does not follow from Theorem 4.4, but we can obtain a weak $V$-stability result:

Corollary 4.5. $u(t) \rightharpoonup u^\ast$ in $V$ as $t \rightarrow \infty$.

Proof. We first show that

We can bound $\| u \|_V$ in terms of $E(u)$ and $\| u \|_H$:

Now Eq (4.4) follows because $E(u)$ is decreasing and $\|u\|_H$ is bounded by Theorem 4.4.

Now suppose the opposite of Corollary 4.5. Then, there exists $\varepsilon > 0$ and $\phi \in V^\ast$ and a sequence $(t_n), t_n \rightarrow \infty$ such that

for all $n$. Write $u_n : = u(t_n)$. Since $V$ is reflexive and $(u_n)$ is bounded according to Eq (4.4), we obtain from Alaoglu's compactness theorem that there is a subsequence again denoted by $(u_n)$ that converges weakly in $V$. As $V \subset \subset H$, the subsequence $(u_n)$ converges strongly in $H$; therefore, the limit is $u^\ast$ which is in contradiction with Eq (4.5).

5.   Application to diabetes donor model

We will formulate a PDE for the model considered in ^[13]. We assume that the transplanted cells are injected in an oxygen-stable environment ^[1]. Hence, we consider on $S$ a Dirichlet boundary condition. At $\Gamma$ we require the concentration and flux to be continuous. Finally, on $\Omega_1$ there is a non-linear term corresponding to Michaelis–Menten consumption ^[13]. It is assumed that on $\Omega_2$ there is no oxygen consumption. We also assume that Michaelis–Menten consumption is zero when the oxygen concentration is zero. This condition ensures that the non-linear term is bounded and monotone. The equations for the non-dimensional oxygen concentration, $v = v(x, t)$, are then given by

where $g: L^2(\Omega) \rightarrow L^2(\Omega)$ is defined by

with $\phi: \mathbb R \rightarrow \mathbb R$ given by

with $\hat{c} > 0$. Let $u = -v+c_0$ and we obtain Eqs (2.1)–(2.5). Setting $c_1 : = c_0 + \hat{c}$ we have that

where $0 < c_0 < c_1$, see Figure 2.

It is straightforward to see that $\varphi_1$ satisfies the properties in Assumptions 2.1. More specifically, the Lipschitz constant is $1/(c_1-c_0)$, and $z\varphi_1(z)\leq c_0$ for all $z\in \mathbb R$. Consequently, we can apply Theorems 3.1, 4.3, and 4.4 to obtain well-posedness and global asymptotic stability of the unique stationary solution.

For the most general form of kinetics, Hill's equation, the theorems can also be applied. In the transformed variables we then obtain that

with $n, \hat{c} > 0$ which satisfies Assumption 2.1. Note that for $n = 1$, Eq (5.2) becomes Michaelis–Menten Eq (5.1).

6.   Conclusions

In this work, we have shown the well-posedness of a nonlinear reaction–diffusion equation for general core-shell geometry. Furthermore, the corresponding stationary solutions are unique and asymptotically stable in a suitable topology. These results extend the model by ^[13], which only considers stationary solutions for spherical core-shell geometry.

The well-posedness theorem, Theorem 3.1, allows us to define a semi-dynamical system: $(D(A), \{S(t)\}_{t\geq 0})$. This can be used to prove the existence of a global attractor following techniques in ^[32]. We expect that Theorem 10.13 from ^[32] can be applied and consequently that the global attractor is equal to the unique stationary solution. We note that the techniques from ^[32,33] can be used to prove well-posedness by only relying on an $L^2$ bound on $f$ and not on the monotonicity of $f$ ^[34].

In view of general results on parabolic PDE systems, we expect our evolution problem to be well-posed in Hölder spaces as well, if $\Gamma$ is smooth enough. However, the proof would be rather technical, and the improvement might not be essential from the point of view of the application. Consequently, it was not considered in this work.

In an experimental set-up, $f$ might be unknown. Suppose that the following are known: $b$, $\Omega_1, \Omega_2$, and spatially dependent data for $u$ when $u$ has become stationary. The nonlinear $f$ can be approximated using the Sparse Identification of Nonlinear Dynamics (SINDy) framework, which in short, is a regression-type fitting process, typically LASSO, over a set of library functions ^[35]. There are specialized SINDy frameworks for PDEs ^[36]. Observe that the data concerns stationary $u$ in time so we can ignore the time derivative, which reduces the complexity of the fitting process. We note that the problem can be further reduced if we can control $\Omega_1$ and $\Omega_2$ in the experimental set-up. We would then select a spherical geometry such that $\Omega_1$ and $\Omega_2$ have a common center. Assuming that the obtained data for $u$ also has spherical geometry, the problem reduces to applying the SINDy-framework to a first-order ODE, which is a vanilla-type SINDy.

It is tempting to make the connection between this work and bulk-surface PDEs ^{[37,38,39,40]}. In our setting bulk-surface geometry means that the outer shell is a surface. If we would consider our governing equations and then take the limit to zero for the thickness of the shell it appears to be necessary to assume that Neumann boundary conditions are imposed on the shell, to arrive at the Bulk-Surface PDE ^[41].

Besides oxygen transport, glucose transport is also needed to sustain encapsulated donor cells. In ^[42], a coupled glucose–oxygen transport model is proposed based on biological assumptions from ^[21,43]. As in ^[13], stationary solutions are considered, and a numerical study is performed to find solutions that have concentrations which are above the donor cell survival threshold. The well-posedness and stability of the corresponding PDE is a topic we would like to explore in future work.

Author contributions

Thomas de Jong: Conceptualization, Writing original draft. Georg Prokert: Review, Methodology. Alef Sterk: Review, Methodology.

Use of AI tools declaration

The authors declare they have not used artificial intelligence (AI) tools in the creation of this article.

Acknowledgements

During this research Thomas de Jong was also affiliated with Xiamen University and University of Groningen. This research was supported by JST CREST grant number JPMJCR2014.

Conflicts of interest

The authors declare that there are no conflicts of interest.