1.
Introduction
A particular feature of the fractional calculus that can be grasped by comprehending tautochrone problem is that scientists and engineers can create novel models containing fractional differential equations. Another outstanding feature that makes fractional operators important is that it can be applied eligibly in various disciplines such as physics, economics, biology, engineering, chemistry, mechanics and so on. In such models as epidemic, logistic, polymers and proteins, human tissue, biophysical, transmission of ultrasound waves, integer-order calculus seems to lagging behind the requirement of those applications when compared with the fractional versions of such models. Under the rigorous mathematical justification, it is possible to investigate many complex processes by means of the non-local fractional derivatives and integrals which enable us to observe past history owing to having memory effect represented by time-fractional derivative. One of the scopes of the fractional calculus is to provide flexibility in modelling under favour of real, complex or variable order. Interestingly enough, fractional operators can also be utilized in mathematical psychology in which the behavior of humankind is modeled by using the fact that they have past experience and memories. So, it is clear that to benefit from non-integer order derivatives and integrals is beneficial for modelling memory-dependent processes due to non-locality represented by space-fractional derivative. A great amount of phenomena in nature are created to provide more accurate and more flexible results thanks to non-integer derivatives. Some of the most common fractional operators capturing many advantageous instruments for modeling in numerous fields are that Riemann-Liouville (RL) developed firstly in literature and Caputo fractional derivatives which are the convolution of first-order derivative and power law. The former constitutes some troubles when applying to the real world problems whereas the latter has the privilege of being compatible with the initial conditions in applications. One can look for [1] for more information about RL and Caputo fractional derivatives.
We shall remark that some fractional operators are composed by the idea of fractional derivative and integral of a function with respect to another function presented by Kilbas in [1]. The left and right fractional integrals of the function f with respect to the g on (a,b) are as below:
and
where Re(α)>0, g(t) is an increasing and positive monotone function on (a,b] and have a continuous derivative g′(t) on (a,b). Also, the left and right fractional derivatives of f with respect to g are presented by
where Re(α)>0, n=[Re(α)]+1 and g′(t)≠0. Note that by choosing the convenient g(t), one can get Riemann-Liouville, Hadamard, Katugampola fractional operators. So, an open problem is that it is possible to create novel fractional operators by choosing other productive and suitable function g(t), which allow us to utilize more variety of non-local fractional operators. Moreover, for these generalized fractional derivatives and integrals, Jarad and Abdeljawad in [2,3] have introduced the generalized LT which is the strong and useful method for many fractional differential equations. On the other hand, there also some non-local frational operators with non-singular kernel, for instance, Caputo-Fabrizio (CF) defined by the convolution of exponential function and first-order derivative and Atangana-Baleanu (AB) fractional derivative obtained by the convolution of Mittag-Leffler function and first-order derivative. By making use of aforementioned fractional operators, many authors have addressed fractional models in various areas. For example, Bonyah and Atangana in [4] have submitted the 3D IS-LM macroeconomic system model in economics in which past fluctuations or changes in market can be observed much better by non-local fractional operators with memory than classical counterparts. Also, the fractional Black-Scholes model has been presented by Yavuz and Ozdemir in [5]. In [6], Atangana and Araz have submitted modified Chuan models by means of three different kind of non-local fractional derivatives including Caputo, CF and AB. The fractional chickenpox disease model among school children by using real data for 25 weeks and the modeling of deforestation on wildlife species in terms of Caputo fractional operator have been investigated by Qureshi and Yusuf in [7,8]. Yavuz and Bonyah in [9] have examined the fractional schistosomiasis disease models which target to prevent the spread of infection by virtue of the CF and AB fractional derivatives. A fractional epidemic model having time-delay has discussed by Rihan et all in [10]. All of these fractional models mentioned above are only a few of the studies using an advantage of fractional operators. In these studies and in many other studies, the authors aim to find the most appropriate fractional derivative that they can utilize, to understand which fractional derivative works better for their objective under favour of real data and to determine which fractional derivative tends to approach the integer-order derivative more rapidly. Therefore, having several fractional operator definitions is of great importance in order to apply them to different type of models and to state much more accurate results. For more application on fractional operators, we refer the readers to [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29].
Generally, in order to obtain fractional solutions of some models similar to the above-mentioned models, the authors replace the integer order derivative by a fractional derivative. However, when it comes to applying to physical models, this approach is not exactly correct due to the need to maintain the dimension fractional equation. For example, in [30], the authors have introduced the fractional falling body problem by preserving the dimension. They have done this as follows:
where σ has the dimension of seconds. Also, in [31,32], the falling body problem by means fractional operators with exponential kernel has been investigated. In this study, we also examine the falling body problem relied on the Newton's second law which expresses the acceleration of a particle is depended on the mass of the particle and the net force action on the particle.
Let us consider an object of mass m falling through the air from a height h with velocity v0 in a gravitational field. By utilizing the Newton's second law, we get
where k is positive constant rate, g represents the gravitational constant. The solution of the equation (1.5) is
and by integrating for z(0)=h, we have
Considering all the information presented above, we organize the article as follows: In section 2, some basic definitions and theorems about non-local fractional calculus are given. In section 3, the fractional falling body problem is investigated by means of ABC, generalized fractional derivative and generalized ABC including Mittag-Leffler function with three parameters. Also, we carry out simulation analysis by plotting some graphs in section 4. In section 5, some outstanding consequences are clarified.
2.
Some fundamental tools on fractional calculus
Before coming to the main results, we provide some significant definitions, theorems and properties of fractional calculus in order to establish a mathematically sound theory that will serve the purpose of the current article.
Definition 2.1. [1] The Mittag-Leffler (ML) function including one parameter α is defined as follows
whereas the ML function with two parameters α,β is
As seen clearly, Eα,β(t) corresponds to the ML function (2.1) when β=1.
Definition 2.2. [33] The generalized ML function is defined by
where (ρ)k=ρ(ρ+1)...(ρ+k−1) is the Pochhammer symbol introduced by Prabhakar. Note that (1)k=k!, and so E1α,β(t)=Eα,β(t).
Definition 2.3. [33] The ML function for a special function is given by
and
It should be noticed that Eα,1(λ,t)=Eα(λ,t). Also, the modified ML function with three parameters can be written as
Definition 2.4. [1] The left and right Caputo fractional derivative are defined as below
and
where α∈C, Re(α)>0, n=[Re(α)]+1.
Definition 2.5. [34] The left and right Caputo-Fabrizio fractional derivative in the Caputo sense (CFC) are given by
and
where 0<α<1, M(α) is a normalization function and λ=−α1−α.
Definition 2.6. [35] The left and right ABC fractional derivative are
and the right one
where 0<α<1, B(α) is a normalization function and λ=−α1−α.
Definition 2.7. [33] The left and right ABC fractional derivative containing generalized ML function Eγα,μ(λtα) such that γ∈R, Re(μ)>0, 0<α<1 and λ=−α1−α are defined by
and also
Definition 2.8. [36] The generalized left and right fractional integrals are defined by
and
respectively.
Definition 2.9. [37] The generalized left and right fractional derivatives in the Caputo sense are given respectively by
and
Definition 2.10. [33] Let υ,ω:[0,∞)→R, then the convolution of υ and ω is
Proposition 2.11. [33] Assume that υ,ω:[0,∞)→R, then the following property is valid
Theorem 2.1. [38] The LT of Caputo fractional derivative is presented by
where F(s)=L{f(t)}.
Theorem 2.2. [34] The LT of CFC fractional derivative is given as
Theorem 2.3. [39] The LT of the ABC is as below
Theorem 2.4. [3] Let f∈ACnγ[0,a], a>0, α>0 and γk=(t1−ρddt)kf(t), k=0,1,...,n has exponential order ectρρ, then we have
where s>0.
Theorem 2.5. [33] The LT of the generalized ABC can be presented by
Lemma 2.12. The LT of some special functions are as below
● L{Eα(−atα)}=sαs(sα+a).
● L{1−Eα(−atα)}=as(sα+a).
● L{tα−1Eα,α(−atα)}=1sα+a.
Lemma 2.13. [40] Let α,μ,γ,λ,s∈C, Re(μ)>0, Re(s)>0, |λs−α|<1, then the Laplace transform of Eγα,μ(λtα) is as follows
3.
Main results
The purpose of this section is to introduce the solutions for fractional falling body problem by means of some non-local fractional derivative operators such as ABC, Katugampola and generalized ABC. We put a condition for ABC type falling body problem in order to achieve right result. Also, dimensionality of the physical parameter in the model is kept by using different auxiliary parameters for each fractional operator.
3.1. The fractional falling body problem in the frame of ABC
The ABC type fractional falling body problem relied on Newton's second law is presented as follows
where the initial velocity v(0)=v0, g represents the gravitational constant, the mass of body is indicated by m and k is the positive constant rate.
If we apply LT to the Eq (3.1), then we have
and applying the inverse LT to the both side of the (3.6) and using the condition v(0)=v0, we obtain the velocity as follows
Because α=σk, 0<σ≤1k, the velocity v(t) can be written in the form below
where Eα(.) is the ML function. Note that we put the condition v0=−gk in order to satisfy initial condition v(0)=v0. By benefiting from the velocity (3.7), vertical distance z(t) can be get in the following way
By applying the LT to the Eq (3.9), we have
by utilizing the inverse LT for the Eq (3.12) and taking the z(0)=h, we obtain the vertical distance z(t) as below
where v0=gσ1−αB(α). Due to the fact that α=σk, 0<σ≤1k, the vertical distance z(t) can be written as follows
3.2. The fractional falling body problem in the frame of generalized fractional derivative
The fractional falling body problem relied on Newton's second law by means of generalized fractional derivative introduced by Katugampola is given by
where the initial velocity v(0)=v0, g is the gravitational constant, the mass of body is represented by m and k is the positive constant rate.
Applying the LT to the both side of the Eq (3.15), we have
If the inverse LT is utilized for (3.18), one can obtain the following velocity
by inserting the α=σk, 0<σ≤1k, we get
From the velocity (3.19), we obtain the vertical distance z(t) in terms of generalized fractional derivative after some essential calculations below
applying the LT to the both side of (3.21), one can have
after applying the inverse LT to the (3.23) and for z(0)=h, we get
substituting the α=σk, 0<σ≤1k to the Eq (3.24), we obtain as follows
3.3. The fractional falling body problem in the frame of generalized ABC
The fractional falling body problem relied on Newton's second law in terms of generalized ABC including ML function with three parameters is as follows
where the initial velocity v(0)=v0, g represents the gravitational constant, the mass of body is indicated by m and k is the positive constant rate.
If we apply the LT to the (3.26), we have
In order to obtain inverse LT of the (3.29), this equation should be expanded as below
by applying inverse LT to the expression (3.30), one can get the following velocity
plugging the α=σk, 0<σ≤1k to the (3.31), we reach
We can obtain the vertical distance z(t) in terms of generalized ABC by benefiting from the velocity (3.31) after the following calculations
utilizing the inverse LT for the Eq (3.34) and when z(0)=h, one can have
after inserting the α=σk, 0<σ≤1k to the (3.35), we get
4.
Comparative analysis and discussions
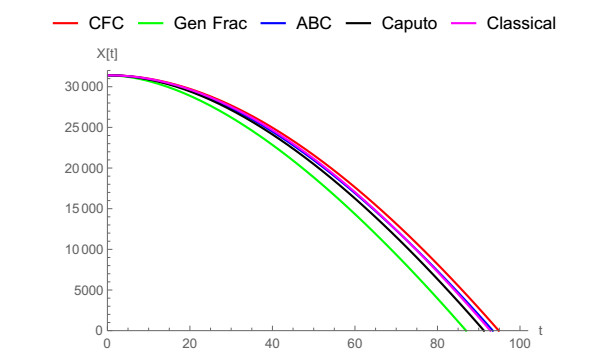
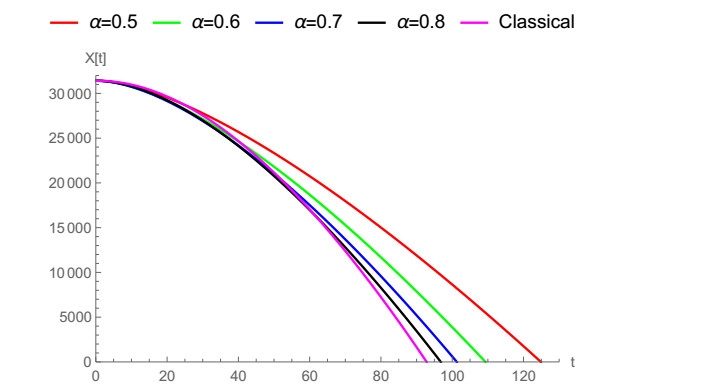
This section is dedicated to demonstrate a comparison between such non-local fractional operators and traditional derivative. We compare these fractional operators with traditional derivative to observe which fractional derivative approaches the classical derivative faster. By this way, the behavior of each non-integer order derivative is shown by plotting. Additionaly, the main objective is to elaborate and expatiate the main findings of our results via graphical illustrations. To this aim, we set some suitable values of α and ρ to see the actual characteristic of behavior of our model. The comparison we made is between ABC, generalized ABC, generalized fractional derivative, Caputo, CFC and their corresponding classical version. So it can be seen that the presented graphs availed the main difference between the mentioned non-local fractional operators and classical version with the help of different parameter values.
In order to comprehend the exact advantage of non-local fractional derivative operators for some governing models, one should utilize the real data. So, without using real data we can only observe the behavior of the solution curves and see the accuracy of our results. As can be seen in [30,31,32], the Caputo and CF type fractional falling body problem are handled by some authors. By benefiting from them, we discuss the relation between these fractional operators and our results obtained by ABC, generalized ABC and generalized fractional derivative.
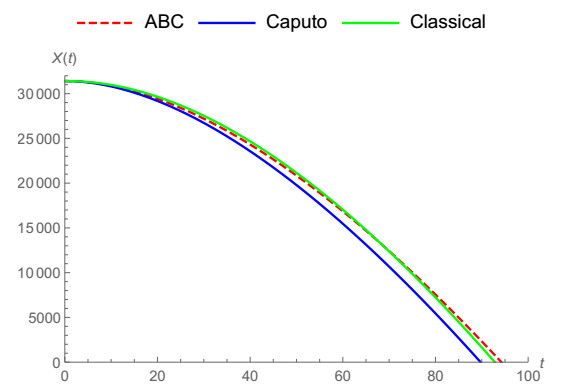
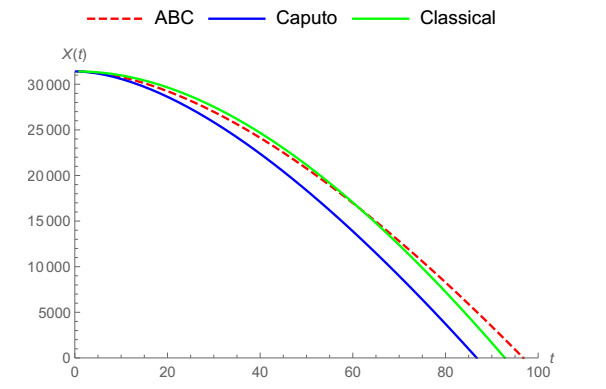
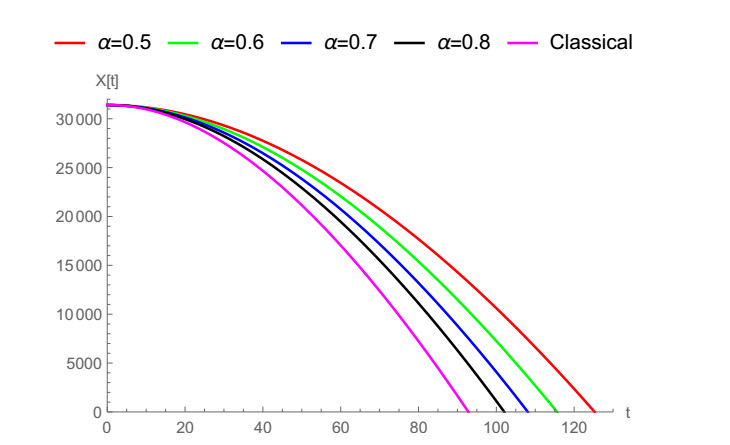
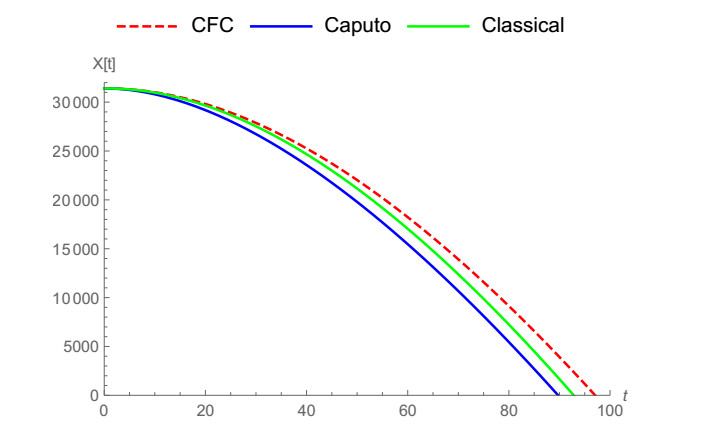
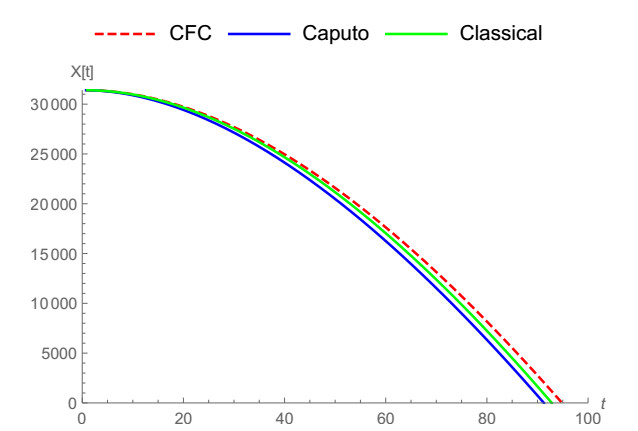
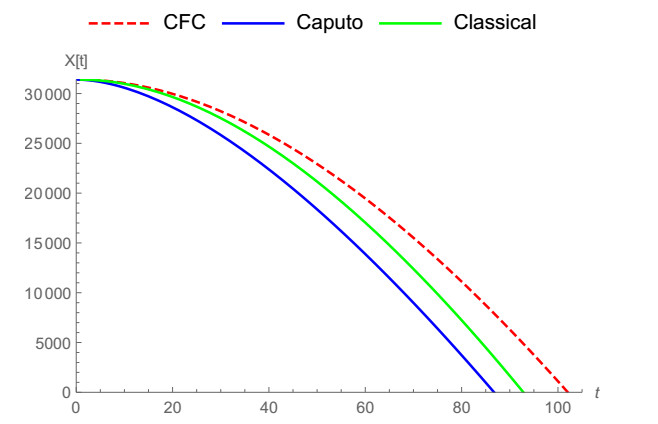
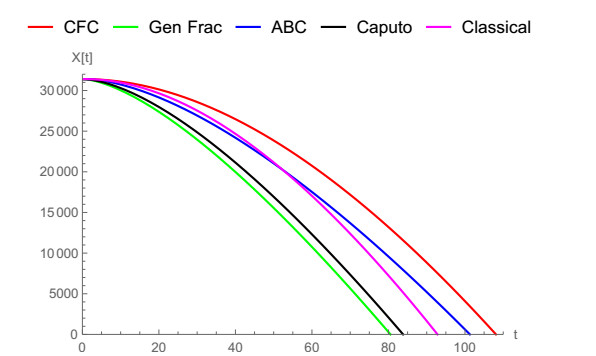
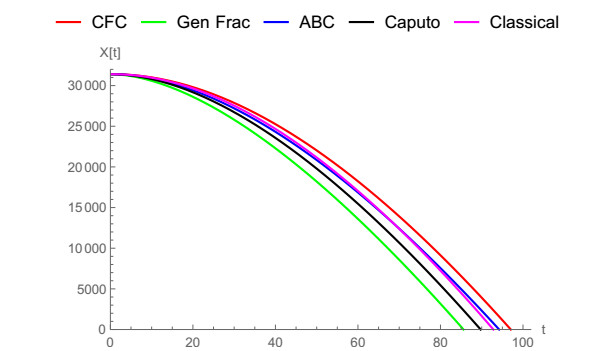
In Figure 1, the vertical notion of a falling body is demonstrated by means of ABC fractional derivative when α=0.5,0.6,0.7,0.8,1. Caputo and ABC fractional operators are compared with classical derivative for α=0.9 in Figure 2 and for α=0.8 in Figure 3. It can be noticed clearly that ABC tends to approach the integer-order case faster. In Figure 4, we show the vertical motion of a falling body in terms of CF fractional operator when α=0.5,0.6,0.7,0.8,1. Also, CFC, Caputo and classical derivative are compared with each other when α=0.9,0.95,0.8 in Figures 5–7 while CFC, generalized fractional derivative, ABC and Caputo are compared with integer-order derivative for ρ=0.9 and α=0.7, ρ=0.9 and α=0.9, ρ=0.9 and α=0.95. In Figures 8–10 CFC, generalized fractional derivative, ABC and Caputo operators are compared when ρ=0.9, α=0.7,0.9,0.95. Similarly, ABC fractional derivative operator tends approach the classical derivative faster then other counterparts.
5.
Conclusions
In recent years, fractional derivative operators have been utilized frequently in the solution of many physical models. On the other hand, various physical problems investigated using real data show that problems solved by means of fractional operators exhibit closer behavior to real data. So, we have analyzed an outstanding physical model called falling body problem in terms of some beneficial non-local fractional operators such as ABC, generalized ABC and generalized fractional derivative. Also, we have noticed that in order to solve a constant coefficient linear differential equation with initial condition, we have to put a convenient condition to satisfy the initial condition. Thereby, when solving the ABC type fractional falling body problem, we put a condition for velocity and vertical distance of falling body.
In order to keep the dimensionality of the physical parameter, an auxiliary parameter σ has been used in different forms like σ1−α, σ1−αρ and σ1−αμ for each fractional operator. Moreover, for generalized ABC type fractional falling body problem containing the Mittag-Leffler function with three parameters, power series has been used to apply inverse Laplace transform for getting velocity and vertical distance. Ultimately, all results obtained in this study have been strengthened by graphs.
It is worth pointing out that in all graphs, the case of α=1 and ρ=1 corresponds to the traditional solutions and by comparing the classical solutions with the fractional solutions, each with different parameters, we can see clearly that our solutions behaves similar to the traditional one and as α and ρ values approach 1, the solution curves tends to approach classical solutions. This shows that our fractional solutions are accurate. So, the characteristic behavior of solution curves has been observed by comparing the solutions obtained above-stated operators.
Conflict of interest
The authors declare no conflict of interest in this paper.









 DownLoad:
DownLoad: