Nonlocal scalar conservation laws with discontinuous flux

1.   Introduction

The aim of this paper is to study nonlocal conservation laws characterized by a flux discontinuous in space. In particular, the nonlocality consists in the fact that the velocity function depends on a convolution term that averages the solution in space. It is worth pointing out that the discontinuity appears in the flux through a multiplicative way. We will focus on the following equation,

where the function $\mathfrak{v} = \mathfrak{v}(x)$ is defined as follows:

The idea comes from the work in ^[27] in which traveling waves are studied for a nonlocal scalar space discontinuous traffic model that describes the beaviour of drivers on two consecutive roads with different speed limits. Indeed, in recent years nonlocal conservation laws have been provided to describe several phenomena, for example: flux granular flows ^[2], sedimentation ^[6], supply chains ^[19], conveyor belts ^[18], structured populations dynamics ^[26] and traffic flows ^{[7,9,10,16,28]}. For these reasons, we believe the matter of discontinuous nonlocal conservation laws mathematically challenging and interesting while applicable to different real-life scenarios. Here, we prove the wellposedness of a nonlocal space discontinuous problem and our approach is based on a viscous regularizing approximation of the problem and standard compactness estimates. To our knowledge, these are the first results regarding discontinuous nonlocal problem using the vanishing viscosity technique. In particular, we have been inspired by the adaptation of the classical vanishing viscosity argument for scalar conservation laws ^[23] to erosion models ^[15], scalar equations with discontinous fluxes ^[8,24,25] and triangular systems ^[14]. This technique is based on the approximation of the solution of the starting problem through a sequence of smooth solutions of the corresponding viscous parabolic problem. The convergence to a solution of the starting problem is obtained proving compactness estimates on the sequence of smooth solutions. The existence of the approximate smooth solutions is proved through a fixed point theorem. In ^[9,10,27] conservation laws with nonlocal flux have been applied to the traffic flow setting. In particular, in ^[9,10] the authors study conservation laws with continuous flux functions and the well-posedness is obtained approximating the problem through an adapted numerical scheme and proving standard compactness estimates on the sequence of approximate solutions. In ^[27], travelling waves for a space-discontinuous traffic model describing two roads with rough conditions are studied. In the present work we do not need to apply an appropriate numerical discretisation of our problem due to the vanishing viscosity technique. We would like to count other more recent, noteworthy and interesting results about discontinuous nonlocal problems in ^[21] obtained with the fixed-point theorem technique. Our aim is to study a nonlocal equation in which the space-discontinuity occurs in the multiplicative term. It is not straightforward to deal with more general flux functions in the nonlocal setting satisfying the 'crossing condition' as in the paper ^[20]. Indeed, considering two different nonlocal flux functions for $x < 0$ and $x > 0$ would imply that the crossing point is not fixed but it changes position in time and this makes harder the analytical study. The paper is organized as follows. In Section 2, we describe the main results in this paper. In Section 3, we prove the existence of weak solutions of our problem, approximating it through a viscous problem and giving ${{\bf{L}}^\infty}$ and BV bounds. Finally, in Section 4, we show the uniqueness of entropy solutions, deriving an $\bf{L^1}$ contraction property using a doubling of variables argument.

2.   Main results

We consider the following scalar conservation equation with discontinuous nonlocal flux coupled with an initial datum

where

and the velocity function $\mathfrak{v} = \mathfrak{v}(x)$ is defined as follows

In this context $\rho$ represents the unknown function, $w_\eta$ is a non-increasing kernel function whose length of the support is $\eta.$ The equation in (2.1) is the space discontinuous version of the one in ^[7], where a nonlocal traffic model is presented.

On $w_\eta, \, \mathfrak{v}, \, \rho_0$ we shall assume that

Assumption (2.3) implies that, if $\rho$ is continuous,

Remark 2.1. The assumption Eq (2.3) does not allow the usual choices of kernels in traffic literature, such as: the constant and the linear decreasing kernels. Our kernels are like restrictions to $[0, \eta]$ of cut-off functions that are equal to 1 in $[-\eta/2, \eta/2]$ and vanish outside $[-\eta, \eta]$ or, for example,

observing that ${\lim_{x\to \eta^-}}w'_\eta(x) = 0.$

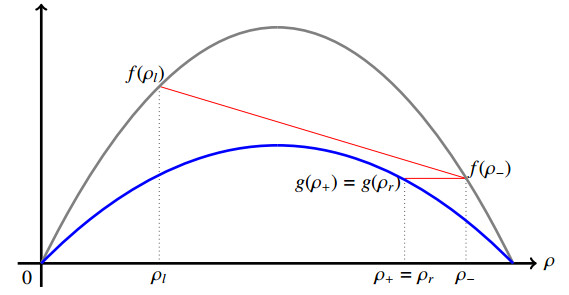
Remark 2.2. It is interesting to notice that if Eq (2.2) does not hold, namely $v_l > v_r,$ we cannot say even in the local case that

Let us consider this very easy example in the classical local case

where

The entropy weak solution to the above Cauchy problem is

A complete description of conservation laws with discontinuous flux can be found in ^[17,22].

We use the following definitions of solution.

Definition 2.1. We say that a function $\rho:[0, \infty)\times \mathbb{R}\to \mathbb{R}$ is a weak solution of Eq (2.1) if

for almost every $t > 0$ and for every test function $\varphi\in {{\bf{C_c^{1}}}}(\mathbb{R}^2)$

Definition 2.2. A function $\rho\in(L^1\cap L^\infty)(\mathbb{R}^+\times \mathbb{R}; [0, \rho_{\max}])$ is an entropy weak solution of Eq (2.1), if

(1) for all $\kappa\in \mathbb{R},$ and any test function $\varphi\in{\bf{C_c^{1}}}(\mathbb{R}^2; \mathbb{R}^+)$ which vanishes for $x\leq0,$

(2) for all $\kappa\in \mathbb{R},$ and any test function $\varphi\in{\bf{C_c^{1}}}(\mathbb{R}^2; \mathbb{R}^+)$ which vanishes for $x\geq0,$

(3) for all $\kappa\in \mathbb{R},$ and any test function $\varphi\in{\bf{C_c^{1}}}(\mathbb{R}^2; \mathbb{R}^+)$

(4) the traces are such that the jump

is the smallest possible that satisfies the Rankine-Hugoniot condition

where we denoted with

Remark 2.3. We would like to underline that the existence of strong right and left traces, respectively $\rho_r$ and $\rho_l$, is ensured by the genuine non-linearity of our flux function, as it is proved in ^[1,4].

The main result of this paper is the following.

Theorem 2.1. Assume Eq (2.2), Eq (2.3), and Eq (2.4). Then, the initial value problem in Eq (2.1) possesses an unique entropy solution $u$ in the sense of Definition 2.2. Moreover, if $u$ and $v$ are two entropy solutions of Eq (2.1) in the sense of Definition 2.2, the following inequality holds

for some suitable constant $K > 0.$

3.   Existence

Our existence argument is based on passing to the limit in a vanishing viscosity approximation of Eq (2.1). We have been inspired by the viscous approximation in [11,Theorem 3.1], the sign of the term in absolute value $|1-w_\eta* \rho_\varepsilon|$ follows from Lemma 3.1 below.

Fix a small number $\varepsilon > 0$ and let $\rho_\varepsilon = \rho_\varepsilon(t, x)$ be the unique classical solution of the following problem

where $\rho_{0, \varepsilon}$ and $\mathfrak{v_\varepsilon}$ are $C^\infty(\mathbb{R})$ approximations of $\rho_0$ and $\mathfrak{v}$ such that

for every $\varepsilon > 0$ and some positive constant $C_0$ independent on $\varepsilon$. The well-posedness of Eq (3.1) can be obtained following the same arguments of ^[11,12,13].

Let us prove some a priori estimates on $\rho_\varepsilon$ denoting with $C_0$ the constants which depend only on the initial data, and $C(T)$ the constants which depend also on $T$.

Lemma 3.1 ($L^\infty$ estimate). Let $\rho_\varepsilon$ be a solution of (3.1). We have that

for every $\varepsilon > 0$.

Proof. Thanks to Eq (3.2), $0$ is a subsolution of Eq (3.1), due to the Maximum Principle for parabolic equations we have that

We have to prove

Assume by contradiction that Eq (3.4) does not hold.

Let us define the function $r(t, x) = e^{-\lambda t} \rho_\varepsilon(t, x).$ We can choose $\lambda > 0$ so small that

Thanks to Eq (3.1), $r$ solves the equation

Since

we can write

Let $(\bar t, \bar x)$ be such that

Since, thanks to Eq (3.5),

we must have

Therefore we can evaluate Eq (3.6) in $(\bar t, \bar x)$ and gain

Since, this cannot be, Eq (3.4) is proved.

Using Eq (2.3) and Lemma 3.1, we know that

and then we can rewrite Eq (3.1) as follows

Lemma 3.2 ($L^1$ estimate). Let $\rho_\varepsilon$ be a solution of Eq (3.1). We have that

for every $t\ge0$ and $\varepsilon > 0$.

Proof. We have

Therefore,

and Eq (3.10) follows from Eq (3.2).

Using Eqs (2.3), (2.5), (3.8), and Lemma 3.1

Therefore, Eq (3.10), Eq (3.11), and Eq (3.12) follow from Eq (3.2).

Lemma 3.3 ($BV$ estimate in $x$). Let $\rho_\varepsilon$ be a solution of Eq (3.1). We have that

for every $t\ge0$ and $\varepsilon, \, \delta > 0$ where $C_\delta$ is a constant depending on $\delta$ but not on $\varepsilon$.

Proof. Let us consider the function

such that

It is not restrictive to assume $\varepsilon < \delta$. In such a way we have that the supports of $\chi$ and $\mathfrak{v_\varepsilon}'$ are disjoint. Finally, we observe that

Differentiating the equation in (3.9) w.r.t. the space variable

Using [5,Lemma 2] and Lemmas 3.1, and 3.2

where $\delta_{\{ \partial_x \rho_\varepsilon = 0\}}$ is the Dirac delta concentrated on the set $\{ \partial_x \rho_\varepsilon = 0\}$ and $c$ is a constant that depends on $\delta$ and does not depend on $\varepsilon.$ Thanks to the Gronwall Lemma we get

and using (3.2) we get the claim.

Lemma 3.4 (Compactness). There exists a function $\rho:[0, \infty)\times \mathbb{R}\to \mathbb{R}$ and a subsequence $\{\varepsilon_k\}_k\subset (0, \infty), \, {\varepsilon_k}\to0,$ such that

Proof. Thanks to Lemma 3.3 the sequence $\{ \rho_\varepsilon \chi_{I_\delta}\}_{\varepsilon, \delta > 0}$ of approximate solutions to Eq (2.1) constructed by vanishing viscosity has uniformly bounded variation on each interval of the type $I_\delta = (-\infty, -\delta)\cup(\delta, +\infty), \, \delta > 0.$ Moreover, thanks to Lemma 3.1 the $L^\infty-$norm of the sequence $\{ \rho_\varepsilon \chi_{I_\delta}\}_{\varepsilon, \delta > 0}$ is bounded by 1. Thus, applying Helly's Theorem and by a diagonal procedure, we can extract a subsequence $\{\rho_{\varepsilon_k}\chi_{I_{\delta_{k}}}\}_{k\in \mathbb{N}}$ that converges to a function $\rho:[0, \infty)\times \mathbb{R}\to \mathbb{R}$ that satisfies the following conditions: $\rho\in BV((0, \infty)\times((-\infty, -\delta)\cup(\delta, \infty)))$ and $0\leq\rho\leq1,$

Thus, we obtain the compactness of the sequence $\{\rho_{\varepsilon_k}\}_{k\in \mathbb{N}}$ a.e. in $(0, \infty)\times \mathbb{R}$ and for this reason we get the claim. It is worth remarking that being $\delta$ as small as we want we get the convergence on the whole space $\mathbb{R}.$

4.   Uniqueness and Stability

We are now ready to complete the proof of Theorem 2.1.

Proof of Theorem 2.1. The existence of entropy solutions follows using the same arguments of ^[3] and Lemma 3.4. In particular, the nature of entropy solution of our limit function is related to the equivalence between [3,Definition 3] and [3,Definition 4] based on the germs theory, being our solution obtained through the vanishing viscosity technique. Moreover, one can observe that the points 1 and 2 of Definition 2.2 are directly satisfied multiplying equation (3.9) times the ${\rm{sgn}}(\rho-k),$ integrating with respect to time and space, and passing to the limit as $\varepsilon\to 0$. The sketch of this proof is the following: we start from an $L^1$ contraction property proved using the doubling of variables technique. After that we choose appropriate test functions in order to deal with the discontinuity in $0.$ We apply some limit procedures on the test functions and the classical Rankine-Hugoniot condition. At the end the Gronwall's inequality gives us the statement.

Let us prove the inequality Eq (2.11). In Lemma 4.1 we prove the following inequality through the doubling of variables technique. For any two entropy solutions $u$ and $v$ we derive the $L^1$ contraction property:

for any $0\leq \phi \in {\bf{C}}_{\bf{c}}^{\infty}\left(\mathbb{R}^+\times \mathbb{R}\setminus{\{0\}}\right).$ We remove the assumption in Eq (4.1) that $\phi$ vanishes near $0,$ by introducing the following Lipschitz function for $h > 0$

Now we can define $\Psi_h(x) = 1-\mu_h(x),$ noticing that $\Psi_h \to 1$ in $L^1$ as $h\to 0.$ Moreover, $\Psi_h$ vanishes in a neighborhood of $0.$ For any $0\leq \Phi \in {{\bf{C}}_{\bf{c}}^{\infty}}(\mathbb{R}^+\times \mathbb{R}),$ we can check that $\phi = \Phi\Psi_h$ is an admissible test function for Eq (4.1). Using $\phi$ in Eq (4.1) and integrating by parts we get

Sending $h\to 0$ we end up with

We can write

where we indicate the limits from the right and left at $x = 0.$ The aim is to prove that the limit ${\lim_{h \to 0}} \, J(h)\leq 0,$ then it is sufficient to prove

In particular, denoting the right and left traces of $u$ and $v$ with $u_\pm$ and $v_\pm,$ we can write

A simple application of the Rankine-Hugoniot condition yields $S = 0,$ being $u_+ = \frac{v_l}{v_r}u_-$ and $v_+ = \frac{v_l}{v_r}v_-.$

In this way we know that (4.1) holds for any $0\leq\phi\in {{\bf{C}}_{\bf{c}}^{\infty}} (\mathbb{R}^+\times \mathbb{R}).$ For $r > 1,$ let $\gamma_r: \mathbb{R} \to \mathbb{R}$ be a $C^\infty$ function which takes values in $[0, 1]$ and satisfies

Fix $s_0$ and $s$ such that $0 < s_0 < s.$ For any $\tau > 0$ and $k > 0$ with $0 < s_0+\tau < s+k,$ let $\beta_{\tau, k}:[0, +\infty]\to \mathbb{R}$ be a Lipschitz function that is linear on $[s_0, s_0+\tau[\cup[s, s+k]$ and satisfies

We can take the admissible test function via a standard regularization argument $\phi = \gamma_r(x)\beta_{\tau, k}(t).$ Using this test function in Eq (4.1) we obtain

Sending $s_0\to 0,$ we get

Observe that the second and the third terms on the right-hand side of the inequality tends to zero as $\tau\to 0$ following the same argument in [20,Lemma B.1], because our initial condition is satisfied in the "weak" sense of the definition of our entropy condition. Sending $\tau\to 0$ and $r\to\infty,$ we have

Sending $k\to0$ and an application of Gronwall's inequality gives us the statement.

Lemma 4.1 (A Kružkov-type integral inequality). For any two entropy solutions $u = u(t, x)$ and $v = v(t, x)$ the integral inequality of Eq (4.1) holds for any $0\leq \phi\in {{\bf{C}}_{\bf{c}}^{\infty}}(\mathbb{R}^+\times \mathbb{R}\setminus\{0\}).$

Proof. The proof follows ^[20]. Let $0\leq\phi\in {{\bf{C}}_{\bf{c}}^{\infty}}\left((\mathbb{R}^+\times \mathbb{R}\setminus\{0\})^2\right), \: \phi = \phi(t, x, s, y), \: u = u(t, x)$ and $v = v(s, y).$ From the definition of entropy solution for $u = u(t, x)$ with $\kappa = v(s, y)$ we get

Integrating over $(s, y)\in \mathbb{R}^+\times \mathbb{R},$ we find

Similarly, for the entropy solution $v = v(s, y)$ with $\alpha(y) = u(t, x)$

Note that we can write, for each $(t, x)\in \mathbb{R}^+\times \mathbb{R}\setminus\{0\},$

so that

Similarly, writing, for each $(y, s)\in \mathbb{R}^+\times \mathbb{R}\setminus\{0\}$

so that

Let us introduce the notations

Adding Eq (4.2) and Eq (4.3) we obtain

We introduce a non-negative function $\delta\in {{\bf{C}}_{\bf{c}}^{\infty}}(\mathbb{R}),$ satisfying $\delta(\sigma) = \delta(-\sigma), \, \delta(\sigma) = 0$ for $\left|{\sigma}\right|\geq 1,$ and $\int_{ \mathbb{R}} \delta(\sigma) d \sigma = 1.$ For $u > 0$ and $z\in \mathbb{R},$ let $\delta_{p}(z) = \frac{1}{p}\delta(\frac{z}{p}).$ We take our test function $\phi = \phi(t, x, s, y)$ to be of the form

where $0\leq \phi\in {{\bf{C}}_{\bf{c}}^{\infty}}\left(\mathbb{R}^+\times \mathbb{R}\setminus\{0\}\right)$ satisfies

for small $h > 0.$ By making sure that

one can check that $\Phi$ belongs to ${{\bf{C}}_{\bf{c}}^{\infty}}\left(\left(\mathbb{R}^+\times \mathbb{R}\setminus\{0\}\right)^2\right).$ We have

Using $\Phi$ as test function in Eq (4.4)

where

where $F(x, u, c): = {\rm{sgn}}{(u-c)}\left(f(t, x, u)-f(t, x, c)\right).$

We now use the change of variables

which maps $(\mathbb{R}^+\times \mathbb{R})^2$ in $\Omega\subset \mathbb{R}^4$ and $(\mathbb{R}^+\times \mathbb{R}\setminus\{0\})^2$ in $\Omega_0\subset \mathbb{R}^4,$ where

resepectively. With this changes of variables,

Now we can write

where

Employing Lebesgue's differentiation theorem, to obtain the following limits

Let us consider the term $I_3.$ Note that $I_3(\tilde t, \tilde x, \tau, z) = 0$, if $\tilde x\in[-h, h],$ since then $\phi(\tilde t, \tilde x) = 0$ for any $\tilde t,$ or if $\left|{z}\right|\geq p.$ On the other hand, if $\tilde x \not\in [-h, h],$ then $\tilde x\pm z < 0$ or $\tilde x\pm z > 0,$ at least when $\left|{z}\right| < p$ and $p < h.$ Defining $U(t, x) = 1-w_\eta\ast u$ and $V(t, x) = 1-w_\eta\ast v,$ and sending $p\to0:$

In fact,

The term $I_4$ converges to zero as $p\to0.$ Finally, the term $I_5$

5.   Conclusions and open problems

In this paper we proved the well-posedness of a Cauchy problem characterized by a nonlocal conservation law with space-discontinuous flux using the vanishing viscosity technique. This kind of equations can be applied to describe different real phenomena, such as: traffic flow, sedimentation, conveyor belts and others. It is worth noticing that the discontinuity appears in a multiplicative way. For this reason, one can think to consider more general nonlocal flux functions satisfying proper 'crossing conditions' in a future work and to study nonlocal-to-local limit in this space-discontinuous setting.

Acknowledgements

The authors are members of the Gruppo Nazionale per l'Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA) of the Istituto Nazionale di Alta Matematica (INdAM). GMC has been partially supported by the Research Project of National Relevance "Multiscale Innovative Materials and Structures" granted by the Italian Ministry of Education, University and Research (MIUR Prin 2017, project code 2017J4EAYB and the Italian Ministry of Education, University and Research under the Programme Department of Excellence Legge 232/2016 (Grant No. CUP - D94I18000260001).

Conflict of interest

The authors declare there is no conflict of interest.