Decomposing and reconstructing dynamic risks in the crude oil market based on the VMD and Lempel–Ziv algorithms

1.   Introduction

Crude oil markets have been evolving into more risky environments with increasing uncertainty in recent years ^[1,2,3,4]. With the development of the financialization of crude oil markets, they have come to be characterized by dual attributes: commodity and financial ^[5,6,7]. Global capital flows and investor speculation increase the uncertainty of risk evolution in these markets ^{[8,9,10,11,12,13]}. According to the USA's Energy Information Administration report, the number of trading contracts in the crude oil future market in January 2008 numbered 49,120. A decade later, the largest number of transactions in one month was recorded as 482,780 in January 2018. Then, more recently, in November 2020, the contract volume for the crude oil market was reported to be 330,100. Such changes in trading volume make crude oil returns a "roller coaster" ride. In this sense, the risk evolution of the crude oil market can be characterized as dynamic.

We can decompose the crude oil risk into components associated with different sources of risk ^[14]. As the most actively traded commodity and the most important energy input for economic activity, crude oil has a host of influencing factors with varied and complicated natures ^[6,15,16]. These cause high crude oil price volatility, creating significant risks for market participants ^[17,18]. On the one hand, for example, the USDX shows that there is a phased nature to crude oil price movement ^[19,20,21]. Since 2003, the USDX has been negatively correlated with crude oil price fluctuation, showing a marked downward trend when crude oil prices increased from 2003 to 2011. Additionally, the heterogeneity of information, as based on investors' varying abilities to obtain data, has created shocks due to the speculative nature of many investors' activities as a result. The likelihood of such a shock has become a basic element that, in turn, affects the crude oil risk ^{[15,22,23,24]}.

Meanwhile, crude oil market fundamentals, such as the supply, the demand and their balance, also exert a power to create risks ^[25,26]. Since 2003, crude oil demands in developing countries, mainly from the BRIC countries of China, India, Brazil and Russia, have grown rapidly. Among them, China has become the main crude oil consumer, rising from 7.21% of global consumption in 2003 to 13.88% in 2018. What is more, the development of alternative energy in recent years has added greater uncertainty to crude oil demand ^[27,28,29]. Furthermore, as a constant factor, the effect of demand on crude oil risk is usually related to the prevailing economic conditions ^[30]. Moreover, as a non-renewable resource, crude oil's volatility could be impacted by the oil storage capacity, resource endowment, production costs, production capacities and OPEC announcements ^[31,32].

In addition, the crude oil risk is frequently influenced by diverse sources of risk, such as financial risk and market fundamental risk ^[32,33,34]. For the former, a low amplitude, random changes around zero and a clustering effect are associated with financial assets ^[35,36], a picture that can be defined by the main sources of financial risks, such as the trading volume, investor attention and speculative investing ^{[37,38,39,40,41]}. Commonly, these factors exert an effect on crude oil price movement in the short term, rather than producing long-term effects. In contrast, the aggregate economic risk, which is caused by crude oil supply and demand, has a high amplitude ^[35,42] and the potential to cause dramatic changes in crude oil prices, or even change the price mechanism ^[43,44]. In practice, the crude oil risk components are developed from the interaction of these factors.

In this study, we employed a comprehensive approach to identify oil commodity and oil financial risks. We propose using the variational mode decomposition (VMD) algorithm, which combines the strengths of econometrics with artificial intelligence models. To proceed, we first measure the crude oil risk via the conditional autoregressive value at risk (CAViaR) model, developed by Engle and Manganelli ^[45]. We decomposed the crude oil risk into different components using the VMD algorithm, as put forward by Dragomiretskiy and Zosso ^[46]. Finally, we identified the oil commodity and oil financial risks by combining forecasts for all modes by using the Lempel-Ziv (LZ) algorithm. Specifically, the oil commodity or oil financial risk is related to the commodities or financial attributes of oil, as caused by crude oil demand or monetary policies, respectively ^[5,6]. By combining the two, with their different frequencies and amplitudes, we characterize the seemingly random changes that have affected the crude oil market.

The contributions of this paper are as follows. First, this paper focuses on the crude oil risk, setting it apart from the existing literature, which has mainly investigated the evolution of crude oil prices or their movement process ^[9,34,40], while the crude oil risk has received little attention. Second, compared to existing studies that used decomposition methods for crude oil price prediction, we have creatively extended the methodological options for the decomposition of the crude oil risk ^[33,47]. In contrast to previous studies that mostly used empirical mode decomposition (EMD) or ensemble EMD (EEMD) to decompose price series ^[48,49], we have employed the VMD algorithm to decompose the crude oil risk. Third, this methodology uses the LZ algorithm to distinguish submodes of the crude oil risk (commodity or financial). As oil's dual attributes are increasingly noted, such risk components may provide important identifying information. Accordingly, we decompose and reconstruct the crude oil risk using the VMD and LZ algorithms, respectively. As the outcome of that research, our empirical results outline the characteristics of oil commodity and oil financial risks.

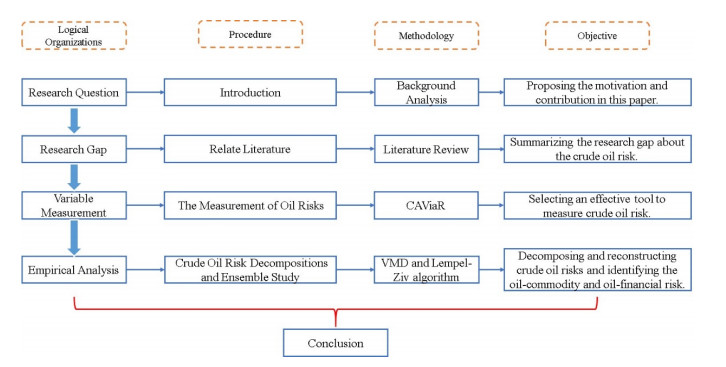
A flowchart of the structure of this study is shown in Figure 1. Section 2 reviews the previous studies on crude oil risk measurement, uses of series decomposition and research gaps. Section 3 then reports the results of our crude oil risk measurements. Section 4 describes the decomposition and reconstruction of the crude oil risk. Section 5 concludes the paper and outlines further research opportunities.

2.   Related literature

There is a field of literature on risk measures such as value at risk (VaR), extreme theory and CAViaR ^[45,50,51]. Among them, the VaR is the most widely used, and it is based on the heteroscedasticity of asset price returns. For example, Cabedo and Moya ^[52] analyzed three VaR calculation methods and concluded that the Historical Simulation with ARMA Forecasts (HSAF) methodology provides an accurate flexible VaR quantification. Since then, researchers have employed a VaR generalized autoRegressive conditional heteroskedasticity (GARCH)-type model to forecast static and dynamic financial risks ^{[53,54,55,56]}. Additionally, Zhao et al. ^[57] investigated the long memory, asymmetry and fat tails of energy commodity returns and further discussed the dynamic behaviors of their risks. Yang and Hamori ^[58] proposed a wavelet-based semiparametric model to perform a VaR forecast and the expected shortfall. Valenti et al. ^[59], meanwhile, predicted the crude oil risk by using a regression model and identified a specific shock component related to oil speculators; they also found that a shift in the global demand for crude oil exerted a significant shock on the expected returns of a long futures investment.

Other methodologies to measure the asset price risk are based on clustering features and the asymmetric impacts of different trends of return on the risks. Engle and Manganelli ^[45] proposed the CAViaR model based on quantile regression theory. The model, which has become an important tool of quantile modeling, describes the dynamic change characteristics of VaR, as well as provides accurate descriptions of the risk autoregression and the impacts of a shock factor on the market return ^{[60,61,62,63,64]}. Dong et al. ^[65] used four types of CAViaR models to measure crude oil market risks and found that the asymmetric CAViaR model can best predict crude oil market risks, indicating that positive and negative returns in the crude oil market have a strong asymmetric impact on risks. In addition, Wen et al. ^[66] employed the multivariable multi-quantile CAViaR model and the pseudo quantile impulse response functions to investigate the spillover effect between crude oil and foreign rate exchange markets.

At the same time, decomposition-ensemble approaches combining parametric and nonparametric models' advantages have emerged in VaR research. On the one hand, financial asset prices are decomposed by using EMD, and the original price is further predicted by summarizing the submode series using different models. For instance, Zhu ^[67] forecasted carbon prices by employing a multiscale ensemble forecasting model integrating EMD, a genetic algorithm and an artificial neural network (ANN), and they indicated that the decomposition-ensemble method improved the simple ANN's forecast ability for carbon prices. A similar conclusion was reached by Zhu et al. ^[68], who employed EMD and least squares support vector regression to predict EU futures prices. Li and Lu ^[69], meanwhile, confirmed EMD's and GARCH's good performance for Chinese carbon price forecasting. Additionally, Zhu et al. ^[70] improved the VaR estimation accuracy by using an EMD model to identify extreme events in carbon markets.

In recent developments in decomposition methods, researchers have adopted several data-adaptive forms. Sun et al. ^[71], for instance, presented the advantages of the VMD-spiking neural network model for predicting carbon prices. He et al. ^[49], meanwhile, demonstrated the high reliability and accuracy of VaR forecasting when employing the VMD-quantile regression neural network. In another study, Zou et al. ^[72] forecasted the crude oil risk movement by proposing a VMD-convolutional neural network, based on which they provided a high forecasting accuracy for typical risk measures, such as the value at risk. Elsewhere, Hao and Tian ^[73] predicted carbon prices in different carbon markets based on a kernel extreme-learning machine (KELM) model. Using the KELM method, they found that the best prediction could be obtained when using improved complementary EEMD with adaptive noise. Lu et al. ^[74], meanwhile, employed the complete EEMD with adaptive noise and a support vector machine to forecast eight Chinese carbon markets' prices.

The LZ algorithm, which reflects the complexity of a finite series, may be used as a tool for feature extraction. Huang et al. ^[35] employed this to identify high- and low-frequency components of carbon prices automatically. Their empirical results showed that the low-frequency component can be regarded as the carbon price's long-term trend after removing irregular noise, while the high-frequency modes have low variance contribution rates, showing that they offer a weaker interpretation of carbon prices and contain some random information. Cristescu et al. ^[75] chose the chaos game exchange-rate series based on LZ complexity. To produce optimal forecasts, Li et al. ^[76] used the LZ algorithm to identify the complexity of different components of crude oil prices. Additionally, some researchers have focused on multiscale LZ complexity. For example, Yan et al. ^[77] employed generalized composite multiscale LZ complexity and calculated the extracted gear fault features. Gao et al. ^[78], meanwhile, calculated the LZ complexity of two composite stock indices and analyzed the efficient market hypothesis in the USA and Chinese financial markets.

We determined certain research gaps based on the existing studies. On the one hand, most explored the characteristics of crude oil prices or fluctuation processes. However, with the development of crude oil's dual attributes, it has been attracting international investors, who have increased the market's complexity. This raises concerns about how well we can predict crude oil risk components. On the other hand, the existing applications of decomposition-ensemble frameworks are not yet comprehensive. Specifically, few studies have sought to identify the crude oil risk component combined with crude oil dual attributes. To fill those research gaps, this paper employs VMD and combines it with LZ to identify the oil commodity and oil financial risks.

3.   Measurement of the crude oil risk

This section first briefly introduces the selection of measurement methods. Then, we estimate the CAViaR model and choose the best forecasting model based on the dynamic quantile (DQ) test. Finally, we describe the effect of events on crude oil risk evolution.

3.1.   CAViaR

This methodology employs the CAViaR model to measure the crude oil risk. Previous researchers have tended to measure financial asset risks in two ways: factor mapping and extreme value models. For the former, financial asset risks are measured by the heteroscedasticity of their returns. In this sense, the existing literature has employed VaR GARCH-type models to predict static and dynamic risks, such as risks to the stock market, crude oil markets and virtual financial markets ^[50,53,54]. For the latter, financial asset risks are forecasted by accounting for extreme events and return clustering effects. However, these approaches are often based on invariable distribution assumptions of crude oil returns or risks. In reality, the crude oil volatility clusters over time, which means that the distribution of the crude oil return is time-varying. In addition, the accuracy and fitting effectiveness are two further aspects to consider in risk measurements. The measurement of crude oil risk, which is highly associated with the standard deviation of the distribution, is no exception. For these reasons, we chose to employ the CAViaR model proposed by Engle and Manganelli ^[45].

The basic form of CAViaR is as follows:

where $p = q+r+1$ represents the $\beta$ dimension, $l\left(\bullet \right)$ is a function of the crude oil lagged return, as calculated by ${R}_{t} = ln\left({price}_{t}\right)-ln\left({price}_{t-1}\right),$ and ${price}_{t}$ represents the crude oil price at time $t$. The lagged term ${Risk}_{t-i}\left(\beta \right)$ represents the lagged variable used to guarantee the smoothness in crude oil volatility. Moreover, the role of $l\left({R}_{t-j}\right)$ is to link ${Risk}_{t}\left(\beta \right)$ to crude oil returns that belong to ${\Omega }_{t-1}$.

Furthermore, following Engle and Manganelli's ^[45] process, we have also developed four type-specific CAViaR models, as described in Eqs (2)–(5).

Symmetric absolute value:

Asymmetric slope:

where ${\left({R}_{t-1}\right)}^{+ = max\left({R}_{t-1}, 0\right)}$ or ${\left({R}_{t-1}\right)}^{- = min\left({R}_{t-1}, 0\right)}$, depicting positive or negative daily returns on the crude oil markets, respectively.

Indirect GARCH (1, 1):

Adaptive model:

where $G$ is a finite positive integer.

What is more, the tests that Engle and Manganelli ^[45] proposed are used to evaluate the crude oil risk predictions. This methodology employs the hit and DQ tests, which are based on the properties of VaR and DQ testing, to test the model fitting effect. Specifically, the hit test describes the difference between crude oil returns and risks. The DQ test reports the goodness-of-fit of the CAViaR models. The HIT test can be defined as follows:

where $I\left(\cdot \right)$ is an indicative function. ${Hit}_{t}\left(\beta \right)$ is assumed to encompass the value $\left(1-\alpha \right)$ when crude oil returns are smaller than the quantile, and $-\alpha$ when returns are greater than the quantile, with $E\left[{Hit}_{t}\left(\beta \right)\right] = 0$ and $E\left[{Hit}_{t}\left(\beta \right)\right]\left|{I}_{t-1}\right. = 0$. For this particular purpose, ${Hit}_{t}\left(\beta \right)$ must be uncorrelated with its own lagged values. If ${Hit}_{t}\left(\beta \right)$ satisfies these assumptions, then we can verify that there will be no hits and we will be able to retrieve the correct proportion of exceptions.

In addition, to test the adequacy of the models, we used in-sample (${DQ}_{IS}$) and out-of-sample (${DQ}_{OS}$) DQ tests, as shown in Eqs (7) and (8), respectively.

where

where $X\left(\widehat{\beta }\right)$ and $\widehat{\beta }$ are related and their relationship is used to measure the information on crude oil returns (i.e., $Hit\left(\widehat{\beta }\right) = {\left[{Hit}_{1}\left(\widehat{\beta }\right), {Hit}_{2}\left(\widehat{\beta }\right), \dots, {Hit}_{T}\left(\widehat{\beta }\right), \right]}^{\text{'}}$). In the same way, $X\left(\widehat{{\beta }_{{T}_{R}}}\right)$ and $\widehat{{\beta }_{{T}_{R}}}$ stand for the out-of-sample information on crude oil returns.

${DQ}_{IS}$ and ${DQ}_{OS}$ play quite different roles. ${DQ}_{IS}$ is a specification test for any of the CAViaR processes, and it contributes to model selection. ${DQ}_{OS}$, instead, can be useful for regulatory purposes, such as checking whether the VaR forecast satisfies the minimum requirements of a good quantile, such as unbiasedness, the inclusion of independent hits and independence of the quantile estimates.

3.2.   Forecasting the crude oil risk

This subsection reports the forecasting results for the crude oil risk. We used data from December 27, 2001 to July 26, 2022, according to the data availability. We employed the first observation (4516, 85% of full sample) to estimate the model and the last return (798, 15%) for out-of-sample testing. In addition, for the adaptive model, we set G = 120. For our empirical analysis, we used data from the Wind database to forecast the 1 and 5% daily crude oil risk. All of the results are shown in Table 1, and the forecasting results are plotted in Figure 2.

An asymmetric slope does a good job of describing the evolution of the crude oil risk under study. The first striking result is that the coefficient of the autoregressive term ${\beta }_{2}$ is always highly significant. The interesting results also indicate that volatility clustering is relevant in the tail of the distribution. In addition, turning our attention to the asymmetric slope (refer to Column (b)), a second interesting point is the coefficient of positive ${\beta }_{3}$ or negative returns ${\beta }_{4}$. The result for the 1% VaR shows that the effect of a positive return on crude oil risk is insignificant, while a negative return has a significant positive effect on the risk. The same picture can be found with the results for 5% VaR. Similar to the existing literature, these results reveal that a crude oil negative return exerts a positive effect on the crude oil risk. This is not surprising since a crude oil negative return is highly related to oil's financial attributes and investors' expectations. Another interesting outcome is the precision of the specifications measured by the hit or DQ test. With the hit in-sample, it is clear to see that its value in the asymmetric slope (refer to Column (b)) is close to the confidence level. Specifically, the results for the 5% VaR, as depicted by the asymmetric slope, show that the hit in-sample was 5.0044, which is much closer to 5.00 than those for the other models. This result also reveals the usefulness of the asymmetric slope.

The crude oil risk has clustering and phased characteristics. On the one hand, as shown in Figure 2, there are three clusters of crude oil risk evolution. This is not surprising when we consider the effect of the external environment (discussed in Section 3.3). On the other hand, it is interesting to note that the crude oil risk displays different evolutionary trends pre- and post-2014. Before 2014, there were downward trends in the crude oil market, except for 2008. After 2014, the crude oil risk evolved and reached a higher level. These results could be explained by the increasing popularity of crude oil markets, which have attracted the attention of investors. It is well known that the greater the complexity of information in crude oil markets, the larger the changes to the crude oil risk. The effectiveness of the crude oil markets reflects their timeliness of price and risk responses when uncertainty factors increase. In practice, oil's financial attributes attract many institutional investors and speculative groups to enter the crude oil markets, which increases the complexity of market participants. Accordingly, compared with the risk evolution before 2014, the complexity of market participants has been greater after 2014 because of oil's financial attributes. Institutional investors and speculative groups can withdraw from the market quickly before returns fall or price trends change. Such trading strategies can reduce the capital level and thereby affect the stability of crude oil markets.

3.3.   Further discussion

According to the analysis in Section 3.2, the asymmetric slope results can be used as a tool to predict the crude oil risk. In such a way, here, we describe the effects of major events on the crude oil risk. This relationship is shown in Figure 3.

There are significant differences between the impacts of different event types on the crude oil risk. Major events can be divided into three types: oil supply, oil demand and emergency. Since we can anticipate the features of oil supply events, they exert predictable effects. For example, the crude oil risk evolutions under the OPEC "increase" and "maintain" decisions support cyclical change, while there is a downward trend under the OPEC "cut" decision. This is due to asymmetric investor attention to different event types. When an increase or maintenance of oil production is announced, crude oil production can promote the instability of crude oil markets, and the crude oil risk can be related to those market conditions. OPEC's announcement may be regarded as a sign to those participating in the crude oil markets, resulting in uncertainty.

Next, we charted oil demand events in the markets. Taking USA dollar devaluations, Brexit and trade disputes as examples, these have each proven to cause a delayed cyclical shock to the crude oil risk. Due to the varying abilities of market participants to obtain market information, as well as the resulting symmetry of information, some investors have a certain lag when setting investment strategies. Yet, their changes in trading strategy will ultimately affect the stability of crude oil markets, thus increasing the market risk.

Of the three types of major events, an emergency exerts the greatest effect on crude oil risk evolution. As shown in Figure 3, an emergency, such as the dot-com bubble bursting, the global financial crisis, COVID-19 or the Russo-Ukrainian war, triggers significant responses in terms of the crude oil risk. In 2008, the financial crisis caused by the subprime mortgage crisis ultimately affected the global economy. The more recent global outbreak of the COVID-19 pandemic, meanwhile, highlights the key role of health systems in affecting financial stability, economic development and people's lives. Compared with the financial crisis, the pandemic had a greater impact on crude oil markets. The Russo-Ukrainian war has also significantly shocked crude oil markets given the importance of Russia and Ukraine for oil production and supply. Yet, as the war goes on, countries and regions around the world are bolstering their economies and adjusting people's consumption to minimize their dependency on crude oil from Russia. We can surmise that, due to the great impact of the emergency and the possibilities of it sustaining, worsening and recurring, market participants' expectations were changed and the crude oil risk increased.

4.   Crude oil risk decomposition and ensemble study

This section reports our decompositions and reconstructions of the crude oil risk. First, we briefly describe the VMD and LZ algorithms, which were employed to decompose and reconstruct the crude oil risk, respectively. Then, we report the decomposition results, and finally, we reconstruct the crude oil risk and identify oil financial and oil commodity risks.

4.1.   Decompositions and ensemble algorithm

We first employed the VMD algorithm to decompose the crude oil risk. The VMD algorithm, which was proposed by Dragomiretskiy and Zosso ^[46], is an improvement on EMD. Traditional decomposition has strict limitations on the crude oil risk. For example, a Fourier transformation is suitable for periodic volatility of the crude oil risk. Wavelet analysis can effectively capture transient effects in the crude oil risk under the assumptions of non-stationarity and linearity. In contrast, with good flexibility and adaptability, EMD can capture complex characteristics of the crude oil risk without a priori information. Yet, despite the merits, EMD also has limitations, such as end effects and mode mixing of the crude oil risk, which restrain the decomposition performance ^[35]. In this study, crude oil risk decompositions based on VMD were proposed to overcome those limitations.

VMD can be regarded as a tool to decompose the crude oil risk ${Risk}_{t}$ into $K$ submodes, with each mode having a limited bandwidth with central frequency ${\omega }_{k}$. The calculation steps for each crude oil risk mode are as follows:

1) For each crude oil risk mode (${Risk}_{t, k}$), perform the Hilbert transformation and construct an analytical crude oil risk to obtain a unilateral spectrum.

2) Via exponential mixing tuned to each frequency of the crude oil risk, the frequency spectrum of ${Risk}_{t, k}$ is tuned to the baseband.

3) The bandwidth of the crude oil risk mode is estimated from the H1 Gaussian smoothness of the frequency.

VMD can be written as follows:

subject to

where ${Risk}_{t}$ is the crude oil risk, represented by the signal to be decomposed. ${\{Risk}_{t, k}\} = \{{Risk}_{t, 1}, {Risk}_{t, 2}, \dots, {Risk}_{t, K}\}$ and ${\{\omega }_{k}\} = \{{\omega }_{1}, {\omega }_{2}, \dots, {\omega }_{K}\}$ represent the set of all crude oil risk modes and their frequency, respectively. $\delta$ is the Dirac distribution, $K$ is the number of modes and * is convolution, $j = \sqrt{-1}$.

By introducing a penalty term and Lagrange multiplier, the constraint problem of (9) can be transformed into Eq (10), which is easier to solve.

where $\alpha$ is a balancing parameter of crude oil risk.

Equation (10) is easily solved as Eqs (11) and (12).

where $\widehat{Risk}\left(\omega \right)$, $\widehat{{Risk}_{i}}\left(\omega \right)$, $\widehat{\lambda }\left(\omega \right)$ and ${\widehat{Risk}}_{k}^{n+1}\left(\omega \right)$ represent the Fourier transformations of ${Risk}_{t}$, ${Risk}_{t, k}$, $\lambda \left(t\right)$ and ${Risk}_{t, k}^{n+1}$, respectively, and $n$ is the number of iterations.

Then, we reconstructed the crude oil risk and identified the frequency components based on the LZ algorithm ^[79]. The crude oil risk was decomposed into $K$ modes with different amplitudes and frequencies, arranged from high to low frequency. The modes of crude oil risk were set as independent of each other.

Interestingly, after decomposition, the crude oil risk can be divided into two categories according to frequency: high and low components. These are associated with crude oil's dual attributes. The high-frequency component depicts a low amplitude and characterizes the random change in the crude oil risk, thus potentially relating to the oil financial risk in the short-term market. Moreover, wild fluctuations in the crude oil markets are often followed by wild ones, and minor fluctuations are followed by minor ones, revealing that there is volatility clustering, which is a surprising oil financial attribute.

In terms of low-frequency components, instead, they have a high amplitude and capture crude oil risk changes caused by the imbalance between supply and demand in the crude oil markets. At the same time, major events cause the value of low-frequency components to rise and fall rapidly. Despite the low frequency of fluctuations, this component may cause dramatic changes in the crude oil risk or even change its evolution mechanism, offering us an insight into an interesting oil commodity attribute.

So, different crude oil risk frequency components have different features, which can make crude oil risk reconstructions challenging. If the crude oil risk for each component is reconstructed well, then the accuracy of crude oil risk predictions can be improved. To that end, after identifying risk-frequency components, we applied the LZ complexity algorithm after VMD decomposition to predict the crude oil risk associated with each attribute. The LZ algorithm measures the emerging rate of crude oil risk. The higher the LZ value that it calculates, the faster the new crude oil risk emerges. Since high-frequency oil risk components demonstrate mostly short-term oscillations, their changing patterns will repeat in a short period, while the opposite is true for the long-term crude oil risk. Accordingly, the LZ value of high-frequency risk components (short period) should be much smaller than that of low-frequency risk components (long period). Based on that, we applied the LZ value to separate the high- and low-frequency risks in the crude oil markets. The identification process is as follows:

Step 1: Binarize the crude oil risk into a 0-1 character string.

The LZ complexity algorithm measures the complexity of the crude oil risk frequency components. To do so, the crude oil risk must be transformed into characters first. We calculated 1 as a crude oil risk larger than the median, and 0 indicates the crude oil risk is less than the median.

Step 2: Calculate the LZ value ${c}_{k}$ of the mode $k$, $k = \mathrm{1, 2}, \dots, K$.

Scan the 0-1 crude oil risk series from left to right, with the LZ complexity increasing by 1 whenever a new sub-string appears. In this way, the output $c\left(T\right)$, which is the LZ value of each crude oil risk mode, is determined. Then, we can normalize the LZ value as follows:

where $T$ is the time span of each mode.

Step 3: Set the critical value ${\lambda }_{0}\left(\ge 0.8\right)$ and find the minimum value $m$ that satisfies Eq (14).

Step 4: Identify the modes from 1 to $m$ as the high-frequency risk components, and the modes from $m+1$ to $k$ as the low-frequency risk components.

4.2.   Decompositions of the crude oil risk

This subsection presents the crude oil risk decompositions. The crude oil risk is measured by the asymmetric slope, according to Section 3.2. Our decomposition results for the crude oil risk are plotted in Figure 4; a boxplot of each crude oil risk mode is shown in Figure 5.

The high-frequency risk modes are characterized by randomness, and the low-frequency risk modes exert strong periodic fluctuations. As shown in Figure 4, Modes 1–3 exhibit randomness and clustering. Mode 4 yields a periodic evolution, while Mode 5 reflects the overall trend of the crude oil risk. Another interesting result is that the average values for Modes 1–4 are around zero, which means that there is a positive or negative overall crude oil risk. Moreover, these results highlight crude oil's dual attributes. As a major energy input for economic development, oil commodity attributes fully reflect the effect of production activities. Specifically, oil commodity attributes are responsible for how crude oil prices gradually reflect the characteristics of production costs and supply-demand balance conversion, which are affected by the crude oil consumption, oil production capacity and energy strategic reserves. Additionally, crude oil markets have been involved in the financial market, with investors opting to invest in crude oil as a hedge asset.

Compared with the crude oil risk (original), Modes 1–5 show simple structures and stable fluctuations. Clearly, the high-frequency oil risk has a low amplitude, while the low-frequency risk has a high amplitude. These interesting results could be caused by a variety of factors. The high-frequency crude oil risk could be highly related to investor attention, trading strategies, speculative investment and the spillover effect. Conversely, changes in the low-frequency crude oil risk could be caused by imbalance between oil supply and demand. What is more, a major event causes the high-frequency risks to cluster and the low-frequency crude oil risks to rise or fall rapidly.

The heterogeneity of these crude oil risk components is captured in Figure 5, in which we can note that the distribution of Modes 1–3 is symmetrical, representing random change around the means of crude oil risk components. Yet, for the crude oil risk components of Modes 4 and 5, there are asymmetric evolutions of crude oil risk. These boxplots also reflect the different amplitudes between high- and low-frequency crude oil risk components.

4.3.   Prediction of oil commodity and oil financial risk

This subsection reports the reconstructions of the crude oil risk based on the LZ complexity algorithm. According to (13) and (14), we plotted the complexity in Figure 6 to identify the high- and low-frequency risks in the crude oil markets. Furthermore, we discuss their evolutions (Figure 7), their correlations with crude oil prices and returns (Figures 8 and 9) and the percentage of oil financial risk (Figure 10).

How the dual attributes of crude oil risk combine is highly related to the evolution frequency. As shown in Figure 6, the crude oil risk component does not reach the ${\lambda }_{0}$ until Mode 3, where $\eta$ is 88.02%. Therefore, Modes 1–3 are identified as high-frequency, and Modes 4 and 5 are low-frequency. Combining the results with Figure 5, we can clearly note that the random fluctuations of the high-frequency components are evident, and that the oil's low-frequency components, namely, Modes 4 and 5, numerically represent a large proportion of the crude oil risk. In addition, as shown in Figure 5, Mode 5 has low complexity, which is consistent with the conclusions of Tang et al. ^[36] and Huang et al. ^[35]. Accordingly, the low-frequency risk could be regarded as the crude oil risk's long-term trend. In this vein, this methodology identifies the high-frequency crude oil risk components as representing the oil financial attribute risk, and the low-frequency crude oil risk components can be regarded as representing the oil commodity attribute risk. Furthermore, we discuss some characteristics of oil commodity and oil financial attribute risks, as shown in Figure 6.

There are significant differences between oil commodity and oil financial risk evolutions. As shown in Figure 7, the first striking result is that the oil commodity risk shows the same trend as the original crude oil risk series. This confirms the phenomenon of the crude oil commodity attribute. In addition, compared with the oil commodity risk, the oil financial risk better explains the random fluctuations and clustering effects. The analysis above indicates that the crude oil risk exhibits various characteristics of the oil commodity and oil financial risks, signifying "multiple drivers" coupling. As one of the main forms of a commodity market, crude oil markets' risk could be impacted by market fundamentals, such as an imbalance between supply and demand. Meanwhile, crude oil markets are undergoing financialization. Environmental factors external to the crude oil markets (e.g., investor attention, speculative investment, capital flows, financial crises and political changes) cause primary shocks to them. Yet, these random disturbances change rapidly, meaning that they have little effect on the long-term trend of the crude oil risk. To explore this, we further describe the relationships between the oil commodity risk and oil spot price (Figure 8) and the oil financial risk and oil returns (Figure 9).

The oil commodity risk is highly related to downward trends in prices. According to Figure 8, the oil commodity risk exerts an asymmetric trend during upward and downward oil spot price periods. Specifically, during upward oil spot price periods, such as 2002–2007, 2009–2013, 2016–2018 and 2021–, it is clear to see that the oil commodity risk shows a much lower fluctuation than normal. Conversely, when the oil spot price decreases (e.g., 2008, 2014, 2015, 2020), the oil commodity risk changes rapidly. These results highlight shocks to the downward trends in the oil spot price due to market fundamentals that, in turn, affect the oil commodity risk. In reality, changes in the oil spot price can exert effects on the expected returns of enterprises or crude oil markets. These effects may further impact the oil supply or demand, which will ultimately affect the crude oil price mechanism and increase the oil commodity risk. Therefore, the analysis above concludes that a downward trend in the oil spot price can be regarded as an effective tool to forecast the oil commodity risk.

The oil financial risk exerts the same clustering effect as oil returns. In Figure 9, we can clearly see that the oil financial risk has a periodic amplitude and largely matches the oil returns. Specifically, the evolutions of oil financial risk are random changes around the average value, which is 0. Comparing the before and after 2014 data revealed that there are significant differences in the amplitudes of the oil financial risk. An emergency can cause the amplitudes to rise rapidly since its uncertainty shocks investors' expectations, or, perhaps, these interesting results are caused by investor expectations in the crude oil markets. For instance, changes in the crude oil returns may cause a market panic, with market participants' expectations declining. At this time, "copycat trading" will begin in the crude oil markets, leading to changes in the market capital levels. In such ways as those just described, we conclude that there are clear relationships between the oil financial risk and oil returns.

It is quite important to decompose the crude oil risk into oil commodity and oil financial components. According to the VMD algorithm, negative oil financial risks can reduce the overall degree of crude oil risk. In Figure 10, we further describe the percentage of oil financial risk, which is calculated as $\frac{Oil-Financialrisk}{Crudeoilrisk}*100{\%}$. As shown in Figure 9, negative percentages exist and show an increasing trend. For example, due to shocks of the global financial crisis, COVID-19 and the Russo-Ukrainian war, the percentage values of the oil financial risk measured in at -21.49, -48.61 and -38.52%, respectively. These interesting results could be caused by differences in market recovery efforts. For example, in 2008, the financial crisis caused by the subprime mortgage crisis in the USA ultimately affected the global economy. The global outbreak of the COVID‐19 pandemic in 2020 then highlights the key role of the health system in all aspects of financial stability, economic development and people's lives. Compared to the financial crisis, the global pandemic outbreak had a greater impact on the international crude oil market, and as such, securing its recovery required greater effort. Accordingly, COVID-19 constituted the largest shock to the crude oil markets of the three events considered.

These results reflect the significant roles of dynamic oil commodity attributes and oil financial attributes. Similar to existing literature, the percentage of oil financial risk proves the existence of crude oil financialization. With the development of forward markets and future markets, which were established due to oil financial attributes, crude oil usually acts as a hedge asset since it is negatively related to financial asset returns. This phenomenon attracts speculative investors with high information abilities. They can shock the stability of crude oil markets and increase crude oil components' complexity, in turn, increasing the crude oil risk. However, since the positive and negative risks may balance, the overall crude oil risk, which is a summary of the oil commodity and oil financial risks, can appeal to investors. Above all, it is necessary to divide the crude oil risk into oil commodity and oil financial components so that the accuracy of risk forecasting can be improved.

5.   Conclusions

Crude oil markets have been evolving into riskier market environments with dual attributes. The present article has offered a decomposition-ensemble framework to identify the oil commodity and oil financial risks. First, we employed the CAViaR model to estimate and forecast the crude oil risk. Then, we decomposed and reconstructed the crude oil risk based on the VMD and LZ complexity algorithms. Finally, we provided evidence of the main evolutionary features. The following main findings were obtained.

The heterogeneity between different crude oil risk modes was captured. According to the crude oil risk decompositions, high-frequency crude oil risks have random changes and low-frequency risks show periodic fluctuation. The former has a low amplitude, while the latter shows a high amplitude.

The evolution of oil commodity and oil financial risks was found to have an asymmetric feature. On the one hand, the evolutions of the oil financial risk are random changes around the mean value, which is 0, while the mean value of the oil commodity risk is 0.04. On the other hand, the oil commodity risk is highly related to oil downward prices, while the oil financial risk exerts the same clustering effect as oil returns.

Based on the above conclusions, these results have certain policy implications. In today's digital economy, enterprises and policymakers should strengthen their technological capabilities to identify and forecast the crude oil risk components. Investors can, in the same way, improve their information acquisition and judgment when it comes to upward and downward crude oil prices and returns. Enhancing these capabilities is beneficial to monitoring the risk resources in the crude oil markets and the expected returns. Certain digital technology, such as artificial intelligence, blockchain, the cloud and big data, may be applied to build an information collection and analysis mechanism. Establishing a warning mechanism for major events is of key importance; attention should be paid to shocks that may arise as a result of major events that are brewing in order to protect the legitimate rights and interests of investors and prevent spillover effects between financial markets.

This study is not without limitations. On the one hand, future research may go further to identify the impact factors, such as oil supply, oil demand, investor attention and speculation. These factors support investors to set investment strategies with the aim of maximizing their profits. On the other hand, researchers may go further to conduct network structure analyses of oil commodity and oil financial risks, particularly financial asset risks given the development of crude oil financialization ^[39,80,81]. Finally, we propose that further studies may extend the asymmetric reaction charted in this paper by adding economic/financial cycles.

Acknowledgments

This work was supported by the National Office for Philosophy and Social Sciences (No. 21CTJ014).

Conflicts of interest

The authors declare no conflicts of interest.