A higher order Galerkin time discretization scheme for the novel mathematical model of COVID-19

1.   Introduction

Over the last few decades, the number of organizations and individuals working on the web has increased remarkably. Because of the widespread availability of data and information in every field, which is accessible to everyone, serious issues such as unauthorized access to confidential information have cropped up. As a result of this massive quantity of work and traffic, the risks of valuable data theft have significantly increased, and preventing these situations is a challenging task. Various researchers in their respective fields have worked to secure data by employing various cryptographic, watermarking, and stenographic schemes. Cryptography is a technique that restricts access to original information to the sender and recipient only ^[1]. It contains algorithms to block potential unauthorized access. Cryptographic algorithms are mathematical tools that helps in protection of data. The cryptography has two main types, symmetric and asymmetric cryptography. A symmetric cryptography ^[2] involves the procedures requires sole key to encrypt and decrypt the related content, while the algorithm in asymmetric cryptography contains two different keys for the process of encryption and decryption ^[3]. The symmetric cipher is further classified into two types: stream cipher and block cipher. The stream cipher modifies the original information bit-by-bit or byte-by-byte while the block cipher does so in blocks involving several bits or bytes simultaneously ^[4]. Data Encryption Standard (DES), GOST, Advanced Encryption Standard (AES), BLOWFISH, etc., are the well-known block ciphers. The substitution box (S-box) is a pertinent non-linear ingredient in block cipher that plays a very decisive role in encrypting the plaintext ^[5]. An $n\times n$ S-box is a Boolean function $f:{\mathbb{Z}}_{2}^{n}⟶{\mathbb{Z}}_{2}^{n}$ which maps an input of $n$ bits to an $n$ bits output. It generates perplexity and responsible for the complex relationship between actual and encrypted contents ^[6]. Therefore, it is not an overstatement to state that the security level of a block cipher can be determined by analyzing the performance of S-box.

Considering the importance of the S-box in the security of cryptosystems, designing complex mathematical techniques to construct robust S-boxes has become a goal of cryptographers. The scientists working in this field are primarily interested in improving the performance of block ciphers. For this purpose, thousands of studies have been conducted and published in leading journals in recent years. A novel approach of S-box creation is introduced in ^[7]. The authors developed their proposed S-box using a chaotic system and fitness function. Javeed et al. ^[8] developed an effective framework for generating strong S-boxes relying on chaotic maps and symmetric groups. The authors designed an initial S-box with the help of chaotic dynamical system. Then the final proposed S-box is obtained by applying a permutation of ${S}_{256}$. In ^[9] a specific type of graphs based the concepts of group theory were employed to develop a new S-box. Multiple performance evaluation metrics validate the resilience of the suggested S-box.

In ^[10] Si et al. proposes a method to create a secure S-Box for symmetric cryptography using a 2D enhanced quadratic map, and an algorithm is designed to eliminate vulnerabilities. Experimental results confirm the method's effectiveness. Lambic ^[11] used usual multiplication and circular shift to generate an innovative discrete-space chaotic map which further employed in the construction of S-box having good security properties. Anees and Ahmed ^[12] designed a potent S-box by investigating the behavior of van der pol oscillator. Firstly, the author used a numerical technique to obtain the iterative solution of chaotic map. Then the ceiling function is employed to those solution to achieve the task. Liu et al. ^[13] proposes a strong S-Box construction method using a non-degenerate 3D improved quadratic map. The proposed algorithm satisfies six criteria and eliminates fixed points, reverse fixed points, and short cycles. Results show effectiveness in encrypting color images and verified security. A systematic scheme to evolve a S-box with high non-linearity value is given in ^[14]. The chaotic map iteration yields a $16\times 16$ matrix on which the genetic technique is applied to obtain the suggested S-box. We recommend to read ^{[15,16,17,18,19,20]} for further information on S-box generation methodologies. In ^[21], a secure image encryption method was introduced. It used a new framework to create chaotic signals with finite computer precision, and includes circular diffusion and local/global scrambling. In ^[22] the authors introduced a new encryption algorithm for color images using DNA dynamic encoding, self-adapting permutation, and a new 4D hyperchaotic system. Zhou et al. ^[23] proposes a secure color image cryptosystem using deep learning to train hyper-chaotic signals, which are then applied to increase the system's security. Liu et al. ^[24] developed a secure color image encryption algorithm using a conservative chaotic system without attractors. They employed techniques such as plane element rearrangement, dynamic selection row-column cross scrambling, and cross-plane diffusion to enhance the encryption's security and mixing. The study ^[25] proposed a 2D hyperchaotic map to generate S-boxes and combine them to create a secure image encryption algorithm that passed NIST and TestU01 tests and resists common attacks. In ^[26], a new n-dimensional conservative chaos was designed to address security issues with encryption algorithms based on dissipative chaos. A new image encryption system using true random numbers and chaotic systems has been proposed in ^[27]. The method is found to be more secure and resistant to classical attacks compared to existing models.

The study presents a novel method for constructing robust S-boxes for use in block ciphers. The following factors were considered during the creation of the S-box:

i. The generated S-box must be cryptographically robust and comply with the mandatory information security standards.

ii. The S-box must exhibit a sufficient level of confusion and complexity, while the method used to construct it remains simple and computationally efficient.

iii. The S-box should demonstrate good performance when evaluated using modern cryptographic performance assessment parameters.

iv. The S-box must meet the requirements for suitability in multimedia image encryption, as determined through a thorough evaluation of its cryptographic properties and performance under relevant metrics.

The following paragraph summarizes the main contributions and proposed scheme of this article.

By utilizing the action of the modular group on a Galois field of order 1024, $GF\left({2}^{10}\right) = \left\{{0, \kappa }^{1}, {\kappa }^{2}, {\kappa }^{4}, \dots , {\kappa }^{1023}\right\}$ a coset graph is constructed. The vertices of the coset graph are utilized in a specific manner to generate a random sequence of the elements in ${GF\left({2}^{10}\right)}^{*} = \left\{{\kappa }^{1}, {\kappa }^{5}, {\kappa }^{9}, \dots , {\kappa }^{1021}\right\}$, which is presented in a $16\times 16$ matrix. Then, a bijective mapping from the group ${GF\left({2}^{10}\right)}^{*}$ to $GF\left({2}^{8}\right)$ yields an initial S-box that exhibits reasonable security. A new notion named "matrix transformer" which transforms a matrix into another matrix has been introduced. By applying a specific matrix transformer to the initial S-box, we obtain a proposed S-box with almost optimal features. Furthermore, a series of well-established analyses are carried out to establish the potential effectiveness of the proposed S-boxes for image encryption in the context of multimedia encryption.

The arrangement of the remaining content of this paper is as follows: The purpose of Section 2 is to discuss the newly developed matrix transformer and modular group-based coset graphs over finite fields. Using the concepts described in Section 2 as a foundation, we propose our S-box design scheme in Section 3. Assessing the algebraic robustness of the constructed S-box is the focus of Section 4. This section also includes a comparison with some recently developed S-boxes. Sections 5–7 are devoted to examining the suitability of constructed S-box for image protection. We reveal the concluding remark in Section 8.

2.   Preliminaries

In this section, we will discuss some fundamental concepts that are required to comprehend the proposed S-box construction scheme.

2.1.   Coset diagrams for modular group

The modular group $\mathcal{M}$ is an infinite non-cyclic group of linear transformations. It is generated by $x$ and $y$ such that $\left(s\right)x = \frac{-1}{s}$ and $\left(s\right)y = \frac{s-1}{s}$. The finite presentation of $\mathcal{M}$ is $⟨x, y:{x}^{2} = {y}^{3} = 1⟩$. Let $p$ be a prime number and $n\in \mathbb{N}$. Then $GF\left({p}^{n}\right)$ denote a Galois field of order ${p}^{n}$, it is well known that $\mathcal{M}$ cannot act directly on $GF\left({p}^{n}\right)$ as $\left(0\right)x = \frac{-1}{0}\notin GF\left({p}^{n}\right)$, so the action of $\mathcal{M}$ is possible if $\mathcal{\infty }$ is adjoined with $GF\left({p}^{n}\right)$, that is $\mathcal{M}$ acts on $GF\left({p}^{n}\right)\cup \left\{\infty \right\}$. The graphical interpretation of the action of $\mathcal{M}$ is described with the help of coset graphs ^{[28,29,30,31]}. As $\left(s\right){y}^{3} = s$, so $y$ has cycles of length three which are represented by triangles whose vertices are elements of $GF\left({p}^{n}\right)\cup \left\{\infty \right\}$ are permuted counter-clockwise by $y$. Moreover, since $\left(s\right){x}^{2} = s$, therefore an undirected line connecting a pair of vertices of the triangles is drawn to represent $x$. The heavy dots are used to denote fixed points of $x$ and $y$, if they exist. For the better understanding of readers, here we describe the action of $\mathcal{M}$ on $GF\left(23\right)\cup \left\{\infty \right\}$ and draw the corresponding coset graph. We apply $\left(s\right)x = \frac{-1}{s}$ and $\left(s\right)y = \frac{s-1}{s}$ on each element of $GF\left(23\right)\cup \left\{\infty \right\}$ and obtain permutation representations of $x$ and $y$. For example, $\left(1\right)x = \frac{-1}{1}\equiv 22$ and $\left(22\right)x = \frac{-1}{22}\equiv 1$ mean a cycle $\left({\rm{1, 22}}\right)$ of $x$. Moreover, $\left(2\right)y = \frac{1}{2}\equiv 12$, $\left(12\right)y = \frac{11}{12}\equiv 22$ and $\left(22\right)y = \frac{21}{22}\equiv 2$ give rise to a cycle $\left({\rm{2, 12, 22}}\right)$ of $y$. In a similar way, all other cycles of $x$ and $y$ can be computed and we have the following permutation representations of $x$ and $y$.

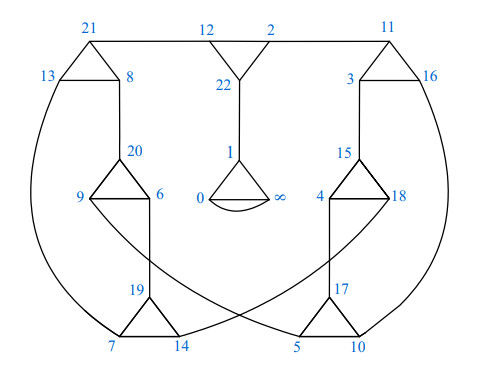
The permutation representation of $y$ consists of 8 cycles. Consequently, the resulting coset graph has eight triangles. The graphical version of the cycle $\left({\rm{1, 0}}, \infty \right)$ in $y$ is a triangle with the vertices ${\rm{1, 0}}$ and $\infty$ permuted counter-clockwise by $y$. In a similar way, we can draw and label all triangles. The permutation representation of $x$ contains 12 transpositions which correspond to12 undirected lines joining all 24 vertices of 8 triangles. For instance, $\left(1, 22\right)$ means the vertices 1 and 22 are connected through an undirected line. Similarly, the remaining vertices can be joined with each other through $x$ and the following coset graph is emerged (See Figure 1).

In the next subsection, we have introduced a new notion namely matrix transformer to generate a strong S-box from an initial S-box.

2.2.   Matrix transformer

Suppose $M$ is a square matrix of order $n$. Let us define the position of the elements of $M$ as follows;

k^th element $=$ m^th element of ${⌈\frac{k}{n}⌉}^{th}$ row

where $m = \left\{\begin{array}{l}n \ \ \ \ \ \ \ \ if \ n \ divides \ m\\ k \ \ mod \ \left(n\right) \ \ \ \ \ otherwise\end{array}\right.$, and $⌈\frac{k}{n}⌉$ means ceiling of $⌈\frac{k}{n}⌉$.

For example, in a $3\times 3$ matrix, we have 1^st element means 1^st element of 1^st row, 2^nd element means 2^nd element of 1^st row, 3^rd element means 3^rd element of 1^st row, 4^th element means 1^st element of 2^nd row and so on.

Definition 2.1. A square matrix $A$ of order $n$ with entries from $\left\{{\rm{1, 2}}, 3, \dots , {n}^{2}\right\}$ is called matrix transformer of square matrix $M$ of order $n$ if the action of $A$ on $M$ evolves a new matrix ${M}^{\text{'}}$ of order $n$ in the following way; $t\in \left\{{\rm{1, 2}}, 3, \dots , {n}^{2}\right\}$ is the i^th element of the matrix transformer $A⟺$ t^th element of ${M}^{\text{'}}$ is equal to i^th element of $M.$

Example 2.1. Consider $M = \left(\begin{array}{ccc}f& d& g\\ c& a& i\\ e& h& b\end{array}\right)$ and $A = \left(\begin{array}{ccc}3& 9& 7\\ 8& 6& 2\\ 4& 1& 5\end{array}\right)$. Then the action of of $A$ on $M$ generates ${M}^{\text{'}} = \left(\begin{array}{ccc}h& i& f\\ e& b& a\\ g& c& d\end{array}\right)$.

3.   S-box generation

In this section, we propose our S-box construction method based on the concepts describe in the previous section.

3.1.   Coset graphs used in the proposed scheme

The proposed S-box generation scheme involves coset graph of the modular group $\mathcal{M}$ on $GF\left({2}^{10}\right)\cup \left\{\infty \right\}$. So, in the 1^st phase, we have to construct the Galois field $GF({2}^{10}$). It is well-known that a primitive irreducible polynomial of degree $10$ over ${\mathbb{Z}}_{2}$ is required to compute all the elements of $GF({2}^{10}$) ^[32]. For that purpose, we choose $p\left(\kappa \right) = {\kappa }^{10}+{\kappa }^{7}+1$ and obtain $GF\left({2}^{10}\right) = \left\{0, {\kappa }^{1}, {\kappa }^{2}, {\kappa }^{3}, \dots , {\kappa }^{1023} = 1\right\}$. In Table 1, we present some of the elements of $GF({2}^{10}$) along with their binary and decimal form.

To draw the coset graph of $\mathcal{M}$ on $GF\left({2}^{10}\right)\cup \mathit{\infty }$, we firstly apply the generators $\left(s\right)x = \frac{-1}{s}$ and $\left(s\right)y = \frac{s-1}{s}$ of $\mathcal{M}$ on all elements of $GF\left({2}^{10}\right)\cup \mathit{\infty }{\rm{t}}{\rm{o}}{\rm{ }}{\rm{g}}{\rm{e}}{\rm{t}}$ permutation representations of $x$ and $y$. For instance, $\left({\kappa }^{1}\right)x = \frac{-1}{{\kappa }^{1}} = \frac{1}{{\kappa }^{1}} = \frac{{\kappa }^{1023}}{{\kappa }^{1}} = {\kappa }^{1022}$ and $\left({\kappa }^{1022}\right)x = \frac{-1}{{\kappa }^{1022}} = \frac{1}{{\kappa }^{1022}} = \frac{{\kappa }^{1023}}{{\kappa }^{1022}} = {\kappa }^{1}$ yield a cycle $\left({\kappa }^{1}, {\kappa }^{126}\right)$ of $x$. Moreover, $\left({\kappa }^{1}\right)y = \frac{{\kappa }^{1}-1}{{\kappa }^{1}} = \frac{{\kappa }^{947}}{{\kappa }^{1}} = {\kappa }^{946}$, $\left({\kappa }^{946}\right)y = \frac{{\kappa }^{946}-1}{{\kappa }^{946}} = \frac{{\kappa }^{1022}}{{\kappa }^{946}} = {\kappa }^{76}$ and $\left({\kappa }^{76}\right)y = \frac{{\kappa }^{76}-1}{{\kappa }^{76}} = \frac{{\kappa }^{77}}{{\kappa }^{76}} = {\kappa }^{1}$, generate a $\left({\kappa }^{1}, {\kappa }^{946}, {\kappa }^{76}\right){\rm{o}}{\rm{f}} \ y$.

Similarly, the remaining cycles of $x$ and $y$ can be found and some of them are presented below;

Both permutations of $x$ and $y$ produced a disconnected coset graph which contains 172 number of patches. It is important to note that out of these 172 patches, 170 are of the same type, denoted by ${\eta }_{1}, {\eta }_{2}, {\eta }_{3}, \dots , {\eta }_{170}$. The other two patches are denoted by ${\eta }_{171}$ and ${\eta }_{172}$. We denote this coset graph by $D$ and $D = {\eta }_{1}\cup {\eta }_{2}\cup {\eta }_{3}\cup \dots \cup {\eta }_{170}\cup {\eta }_{171}\cup {\eta }_{172}$ The Figures 2–4 represent ${\eta }_{1}, {\eta }_{171}$ and ${\eta }_{172}$ respectively.

3.2.   The proposed scheme

Step I: We first construct a square matrix of order 16 using vertices of coset graph in a specific way.

Consider a patch ${\eta }_{1}$ containing ${\kappa }^{1}$ as vertex from the coset graph $D$. The application of $xyx{y}^{-1}x$ on ${\kappa }^{1}$ carries us to ${\kappa }^{77}$ by following the route ${\kappa }^{1}\stackrel{x}{\to }{\kappa }^{1022}\stackrel{y}{\to }{\kappa }^{947}\stackrel{x}{\to }{\kappa }^{76}\stackrel{{y}^{-1}}{\to }{\kappa }^{946}\stackrel{x}{\to }{\kappa }^{77}$ (see Figure 2). So, in this way, we generate a sequence ${\kappa }^{1}, {\kappa }^{1022}, {\kappa }^{947}, {\kappa }^{76}, {\kappa }^{946}, {\kappa }^{77}$ of vertices. Consider a sub-sequence $\left\{{\kappa }^{i}:i\equiv 1 \ mod \ \left(4\right)\right\} = {\kappa }^{1}, {\kappa }^{77}\}$ of this sequence and place ${\kappa }^{1}$ and ${\kappa }^{77}$ at 1^st and 2^nd position of the first row respectively. Thereafter, we find the vertex from $D-\left\{{{\rm{ \mathsf{ η} }}}_{1}\right\}$ having the smallest power of $\kappa$, that is, ${\kappa }^{2}$. Let us denote the copy from $D-\left\{{{\rm{ \mathsf{ η} }}}_{1}\right\}$ containing ${\kappa }^{2}$ by ${{\rm{ \mathsf{ η} }}}_{2}$. Note that if ${\kappa }^{2}$ would been exhausted in ${{\rm{ \mathsf{ η} }}}_{1}$ , then ${{\rm{ \mathsf{ η} }}}_{2}$ is a copy from $D-\left\{{\Gamma }_{1}\right\}$ containing ${\kappa }^{3}$ . Generate a sequence of the vertices of the type ${\kappa }^{i}:i\equiv 1 \ mod \ \left(4\right)$, present in ${{\rm{ \mathsf{ η} }}}_{2},$ in a similar way as done in the case of ${{\rm{ \mathsf{ η} }}}_{1}$. Write this sequence at the 1^st row after ${\kappa }^{77}$ by maintaining the order of sequence. After that, we chose a copy from $d-\left\{{{\rm{ \mathsf{ η} }}}_{1}, {{\rm{ \mathsf{ η} }}}_{2}\right\}$ possessing a vertex ${\kappa }^{m}$, where $m$ is the least positive integer. In a similar way, continue to select the copies ${\eta }_{i}$ and write vertices of the type ${\kappa }^{i}$ such that $i\equiv 1 \ mod \ \left(4\right)$ in the matrix until all copies ${{\rm{ \mathsf{ η} }}}_{i}$ are used. So, a square matrix of 256 distinct entries from ${GF\left({2}^{10}\right)}^{*} = \left\{{\kappa }^{1}, {\kappa }^{5}, {\kappa }^{9}, \dots , {\kappa }^{1021}\right\}$ is generated (see Table 2).

We can generate 3 more tables simply by replacing the type of vertices in step I, from ${\kappa }^{i}:i\equiv 1 \ mod \ \left(4\right)$ to ${\kappa }^{i}:i\equiv 0 \ mod \ \left(4\right)$, ${\kappa }^{i}:i\equiv 2 \ mod \ \left(4\right)$ and ${\kappa }^{i}:i\equiv 3 \ mod \ \left(4\right)$ .

Step II: The outcome of Step I yields a $16\times 16$ matrix of distinct element from ${GF\left({2}^{10}\right)}^{*} = \left\{{\kappa }^{1}, {\kappa }^{5}, {\kappa }^{9}, \dots , {\kappa }^{1021}\right\}$. To bring all the element in the range of 0 to 255, we define a mapping $f:{GF\left({2}^{10}\right)}^{*}⟶GF\left({2}^{8}\right)$ by $f\left({\kappa }^{n}\right) = {\beta }^{\frac{n-1}{4}}$. Note the Galois $GF\left({2}^{8}\right)$ is generated by primitive irreducible polynomial ${\beta }^{8}+{\beta }^{6}+{\beta }^{5}+{\beta }^{3}+1$. Table 3 shows some of the elements of $GF({2}^{8}$) and their binary and decimal form.

In this manner, we have designed our initial S-box (See Table 4). We have examined its cryptographic strength via some well-known performance evaluation criteria and found that it provides adequate security for transmitting sensitive information. To increase its security even further, let us proceed to step III.

Step III: Since an S-box is a square matrix of order $16$. Therefore, the newly defined notion "matrix transformer" (see Section 2.2) can be used on initial S-box to enhance the security level. For this purpose, we tried several matrix transformers on our initial S-box by using MATLAB program and found that the matrix transformer displayed in Table 5 is the most suitable. The application of this matrix transformer on our initial S-box gives rise an S-box (See Table 6) with very high NL value 111. We call it our proposed S-box. An algorithm illustrating the process of using matrix transformers on the initial S-box is presented in Figure 5, while a flowchart can be found in Figure 6 to facilitate comprehension.

4.   Performance evaluation

This section contains performance evaluation of the suggested S-box through different state of the art metrics such as the nonlinearity test, differential uniformity, bit independence criterion, strict avalanche criterion and linear approximation probability. We see that the outcome scores of our S-box obtained via these analyses are nearly equals to the ideal ones, demonstrating the effectiveness and capability of the proposed scheme. The analyses applied on our S-box are detailed below.

4.1.   Nonlinearity (NL)

Nonlinearity is a key factor to determine the robustness of a substitution box. If an S-box maps input to output linearly, its resistance is very low ^[33]. A powerful S-box nonlinearly maps input to output. Any S-box with a higher nonlinearity value guarantees more security against cryptanalytic attacks. In the case of Boolean function of the form $\theta :{F}_{2}^{n}⟶{F}_{2}$, The nonlinearity is calculated as

Note that, ${S}_{\theta }\left(h\right) = \sum _{g\in GF{\left(2\right)}^{n}}{\left(-1\right)}^{\theta \left(g\right) \oplus g.h}$ represents the Walsh spectrum of $\theta \left(g\right)$. Table 7 indicates the nonlinearity values of all Boolean functions of the proposed S-box. The average Non-linearity of our S-box is 110.75.

4.2.   Strict Avalanche Criteria (SAC)

SAC is another effective tool to judge the security of an S-box. It was proposed by Webster and Tavares ^[34]. To meet this requirement, the input bit of any cryptosystem must change along with a 50% change in the output bits. The SAC performance of the S-box is determined by the dependency matrix. The perfect SAC score for the best cryptographic confusion is 0.5. Table 8 shows the dependency matrix of SAC values obtain by proposed S-box. The mean SAC value of proposed S-box is 0.5051, which differs slightly from the optimal value. Therefore, the suggested S-box fulfills the SAC criterion.

4.3.   Bit independence criterion (BIC)

This test ^[34] is satisfied if the output bits operate independently, i.e., do not depend on each other. More specifically, no statistical dependencies or patterns should be present in the bits of the output vectors. It is intended to boost output bit autonomy for greater security. An S-box is said to be meet the BIC criterion if it satisfies SAC and possess nonlinearity score for all Boolean mappings. The Tables 9 and 10 depict the dependency matrices for BIC-nonlinearity and BIC-SAC respectively. The results show that the proposed S-box conforms to the required BIC standards.

4.4.   Linear Probability

Modern block ciphers are designed to create as much complexity among the bits as possible to protect the privacy of the information and to offer protection against various decryption techniques employed by the cryptanalysts. It is accomplished by S-box. The lower the value of LP, the better the capability of S-box to withstand linear attacks. The LP value of an S-box can be calculated by using the following equation ^[35];

where $K = \left\{{\rm{0, 1}}, . . . , {2}^{n}\right\}$ and ${\rm{\Gamma }}{\rm{w}}$ and ${\rm{\Gamma }}{w}^{\text{'}}$ are the input mask and output mask respectively $.$ The designed S-box has an LP score of 0.0781.

4.5.   Differential uniformity (DU)

The resistance of S-box to differential cryptanalysis is investigated by DU ^[35]. To determine DU, a input differential $\Delta {\sigma }_{i}$ is uniquely linked to an output differential $\Delta {\rho }_{i}$, for all $i$. For a given S-box, its value can be calculated by using the following equation:

It is necessary to develop an S-box with smaller DU values in order to withstand differential cryptanalysis attacks. The maximum DU score of the proposed S-box is 6 (See Table 11), indicating its ability to counter differential attacks.

According to the performance study and comparative analysis, our S-box has better cryptographic properties than many recently designed S-boxes based on optimization, chaos and algebraic techniques. The comparison present in Table 12 demonstrates the suggested technique of designing S-boxes outperforms many of the available approaches. Here are our findings:

1. The S-box must have a high nonlinear value to resist linear attacks. According to Table 12, the average nonlinearity of our S-box is almost equal to AES, outperforming all other S-boxes show in Table 12. Therefore, there is considerable confusion, which makes the proposed method resistant to all the existing linear cryptanalysis.

2. The prime goal of every S-box designer is to achieve a SAC score close to the optimal value (0.50). From Table 12 demonstrates that the suggested S-box satisfies the requirements of strict avalanche criterion.

3. The reading of BIC-NL and BIC-SAC obtained from the prosed S-box are very encouraging are better than those of most of the S-boxes in Table 12

4. A potent S-box has a smaller DU value. As seen in Table 12, the DU score of the suggested S-box is less than the S-boxes developed in ^{[37,38,39,40,41,42,43,44]}.

5. A smaller LP score makes an S-box more resistant to linear cryptanalysis. The LP score of our S-box is 0.0781, which is slightly higher than AES but lower than the LP values of all S-boxes in Table 12.

5.   Majority logic criterion

The evaluating the suitability of an S-box to be employed in an encryption process using the majority logic criteria (MLC) is a useful approach ^[45]. Randomness in the encoded picture is assessed using these five analyses energy, entropy, homogeneity, contrast and correlation.

Homogeneity and energy are utilized to identify the features of the encoded picture. The correlation test assesses the resemblance level between the host and encrypted picture. The lower correlation value implies more distortion caused by encryption. Through contrast, the decrease of brightness of the plaintext image is assessed. The greater the contrast value, the more efficient the encryption procedure. The process of encryption distorts the plaintext, and statistical parameters characterize the resiliency of S-box. The S-box that is formed is utilized to encrypt digital photos. To conduct MLC four 256 × 256 JPEG photos of Cameraman, Pepper, Lena and Baboon are selected. Two steps of substitution using our S-box are performed in the encrypting process. Encryption is accomplished through two steps of S-box substitution. During the 1^st phase, the substitution is performed in a forward direction (from the start pixel to the end pixel) and subsequently in an opposite way. All simulations were conducted using the MATLAB programming. The original and encrypted photos are shown in Figure 7. The distorted pictures differ significantly from their corresponding undistorted versions. The level of visual distortion is quite large, since the graphics lack a pattern that promotes security breaches from the host picture. Table 13 shows the findings of all MLC testing performed. Table 14 presents the calculated correlation coefficients for pictures.

The results suggest that the created substitution box is suitable for encryption purposes and are good enough to be used in the systems designed to ensure the reliability and security of sensitive data.

6.   Measurement of encrypted image quality

The experimental assessments of the proposed image encryption technique are discussed in this section. The $256\times 256$ pixel grayscale photos of Cameraman, Pepper and Baboon are picked for the experiment. Table 15 contains a variety of image quality measurements that have been suggested for use with two rounds of encryption using S-boxes. These methods have been thoroughly discussed. The findings indicate that the recommended S-box is robust enough to survive various attacks.

6.1.   Mean Square Error (MSE)

During encryption MSE analysis assesses the unpredictability of the encrypted picture ^[46]. This technique computes the squared difference between the original and distorted picture. It can be computed as follows:

where U and V represent the dimensions of original $O\left({y}_{1}, {y}_{2}\right)$ and distorted $E\left({y}_{1}, {y}_{2}\right)$ pictures respectively. For effective encryption methods, the MSE rating must be as high as conceivable ^[46].

6.2.   The Peak Signal-to-Noise Ratio (PSNR)

The PSNR test ^[38] is an ideal criterion for assessing the quality of picture encryption techniques. It estimates how well the original picture matches the ciphertext. PSNR value is calculated using the following formula;

where $V$ is the amount of variance that was at its highest in the original picture data. It is necessary to have a higher value of PSNR in order to get a superior encoded picture ^[47].

6.3.   Average & Maximum Difference (AD & MD)

To determine the average and maximum dissimilarities between the unencrypted $O$ and encrypted $E$ pictures, researchers used the AD and MD test ^[47]. AD and MD values are determined using the following formulas;

6.4.   Mutual Information (MI)

MI measures how much information can be retrieved about the original picture from a distorted version of it. Let us denote the joint probability function of $O$ and $E$ by $\rho \left({y}_{1}, {y}_{2}\right)$, then the value of MI can be determined by using the formula below;

The MI value must always be kept to a minimum in a decent encryption system ^[48].

6.5.   Universal Quality Index (UQI)

As stated in reference ^[49], the UQI method partitions the evaluation of image distortion into three components: luminance, structural comparisons and contrast. The UQI metric for a pair of images $O$ and $E$ can be expressed as follows;

where ${\rho }_{o}$, ${\rho }_{E}$ represent the mean values of the original and distorted images, respectively, and ${\varphi }_{o}$, ${\varphi }_{E}$ represent the standard deviation of the original and distorted images, respectively.

6.6.   Structural Similarity (SSIM)

SSIM is an enhanced version of the UQI designed to assess the similarity between two images. In particular, SSIM evaluates the fidelity of one of the images by assuming that the other image is free from errors. The computation of the SSIM score involves analyzing a pair of windows $\left(R, S\right)$ of the image using the following formula:

where ${\varphi }_{R}$ and ${\varphi }_{S}$ are the variances of R and S and ­ ${\nu }_{R}$ and ${\nu }_{S}$ are the average scores of R and S respectively. The range of the SSIM score lies between -1 to 1, where a score of 1 indicates that the images are identical. A score close to 0 indicates a strong encryption scheme ^[48].

6.7.   Normalized Cross Correlation (NCC)

As stated in citation ^[49], the correlation function provides a means of measuring the proximity of two digital images. The NCC method is a well-established technique for assessing the similarity between two images. Its calculation is based on the following formula:

6.8.   Normalized Absolute Error (NAE)

NAE ^[49] can be used to assess the efficiency of an image encryption process by comparing the pixel values of the original image with those of the encrypted (ciphered) image. To calculate the NAE between the plain and ciphered image, the formula is:

6.9.   Root Mean Square Error (RMSE)

The assessment of an image encryption algorithm's effectiveness can be facilitated by utilizing RMSE as a performance metric. The calculation of RMSE involves determining the square root of the average of all the squared errors ^[49]. Its frequent use and flexibility make it a versatile and valuable error metric for numerical forecasting. The mathematical expression for RMSE is indicated below;

6.10.   Structural Content (SC)

SC is a correlation-based measure that quantifies the similarity between two images. The following mathematical equation is used to compute its score;

7.   Differential analysis of image protection

A robust cryptosystem is extremely sensitive to modifications in one bit of the plaintext. Through UACI, NPCR and BACI testing, the sensitivity of the system is assessed.

UACI indicates the unified mean intensity change between original and encrypted image while NPCR calculates the number of pixels change rate of the encrypted image if a single pixel is altered in the original image. In BACI analysis, the image difference $\Delta = abs\left({E}_{1}-{E}_{2}\right)$ is partitioned into blocks of pixels and arranged in a 2 × 2 matrix. This involves dividing the image into smaller, non-overlapping regions, or "blocks", to facilitate the comparison of pixel values before and after the intervention.

The following formulae are used to compute the values of UACI, NPCR and BACI:

where ${E}_{1}\left(j, k\right)$ and ${E}_{2}\left(j, k\right)$ denote the grayscale values of pixels obtained $\left(j, k\right)$ th position and $D\left(j, k\right) = \left\{\begin{array}{l}0 \ \ \ \ \ \ \ \ \ if \ {E}_{1}\left(j, k\right) \ \text{and} \ {E}_{2}\left(j, k\right) \ are \ equal\\ \ \ 1 \ \ \ \ \ \ \ otherwise\end{array}\right.$ and ${Z}_{i} = \frac{1}{6}\left(\left|{a}_{1}-{a}_{2}\right|+\left|{a}_{1}-{a}_{3}\right|+\left|{a}_{1}-{a}_{4}\right|+\left|{a}_{2}-{a}_{3}\right|+\left|{a}_{2}-{a}_{4}\right|+\left|{a}_{3}-{a}_{4}\right|\right)$ and ${\Delta }_{i} = \left[\begin{array}{cc}{a}_{1}& {a}_{2}\\ {a}_{3}& {a}_{4}\end{array}\right]$.

Table 16 depicts the findings of the differential analysis for NPCR, UACI, and BACI, confirming the excellent performance of encryption effect provided by the designed S-box.

8.   Conclusions

Summing up, the present work has discussed and examined the development of modular group coset graphs over a finite field of order 1024 and a matrix transformer for application in S-box construction. An initial S-box is formed through coset graphs and after that the application of a matrix transformer on it enhances its working efficiency significantly, resulting in a robust S-box. Comparison of proposed method with other state-of-the-art S-box construction algorithms shows that the proposed mechanism outperforms other algorithms in terms of mean nonlinear score, LP, SAC, BIC and DU scores. In addition, the performance of the designed S-box when applied to encrypt certain plaintext graphics has been determined to be extraordinary using a variety of assessment tools.

As our experience with applying matrix transformer to coset graph S-box to improve its resilience has been promising, we plan to research novel ways for designing S-boxes combining matrix transformers and chaotic systems. Moreover, we intend to evaluate the application of S-box to cloud encryption.

Acknowledgments

This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (Grant No. 3011).

Conflict of interest

The authors declare there is no conflict of interest.