A new local non-integer derivative and its application to optimal control problems

1.   Introduction

In recent decades, several definitions for fractional derivatives (FDs) have been introduced ^{[1,9,10,13,15]}. In most of them, the FDs are given in the integral form. The (left) Riemann-Liouville and (left) Caputo FDs of order $0 < \beta\le1$, are the most popular FDs and they are defined as follows, respectively:

where $\eta(.)$ is a given function, and $\Gamma(.)$ is the gamma function. It is trivial that the Riemann-Lioville and Caputo FDs are linear operators. Also, it is easy to show that if $\beta \to 1^{-}$, then they are the classical derivatives. However, these properties are not sufficient for defining FDs. Note that these FDs do not satisfy the following known formulas:

where $_{\zeta_0}D_{\zeta}^{\beta}$ can be Riemann-Liouville or Caputo FD. Note that Riemann-Liouville and Caputo FDs are non-local operators. Also, if $\eta(.)$ is a constant function, then the Riemann-Lioville fractional derivative does not satisfy $_{\zeta_0}D_t ^\beta \eta(\zeta) = 0$ for all $0 < \beta\le1$.

Recently, Khalil et al. ^[9] have defined a new local derivative which is called conformable derivative. So far, several researchers have used it and generalized its properties (see ^[1,10]). They have investigated that the conformable derivative for order $\beta = 1$ is the classical differential operator. They have also proved that conformable derivatives satisfy the well-known properties of usual derivative such as relations (1.3) and (1.4). But, these types of non-integer derivatives have a basic difficulty. For any function $\eta(.)$ with bounded first order derivative on interval $(\zeta_0, \zeta_1)$, we have $\lim_ {\zeta\to {\zeta_0^{+}}}{_{\zeta}^{kh}D_\zeta^\beta \eta(\zeta)} = 0$ where ${_{\zeta_0}^{kh}D_\zeta^\beta}$ shows the Khalil conformable derivative. This relation for Riemann-Liouville and Caputo FDs is also satisfied. Hence, a simple differential equation based on the Riemann-Liouville, Caputo or Khalil fractional derivatives, such as ${_0 D_\zeta^\beta \eta(\zeta)} = \eta(\zeta)$ defined on interval $[0, 1]$ with initial condition $\eta(0) = \lambda \neq 0$, has no solution on the space of functions with bounded first order derivative.

By motivation from above, specially from ^[1,9], we define a new local non-integer order derivative and name it adaptive derivative. This type of non-integer derivative satisfies the properties (1.3) and (1.4) and has not difficulties of the other non-integer order derivatives. We prove several properties for adaptive derivative. Moreover, we extend the concept of adaptive derivative to optimal control problems and apply one of the most powerful numerical methods, namely Legendre spectral collocation (LSC) method for solving the adaptive optimal control problems. Spectral and pseudo-spectral methods have been utilized for different continuous-time problems, recently. For instance, in ^[6], an spectral method is given to solve smooth non-fractional optimal control problems. Works ^[7,12,14] applied spectral methods to solve some fractional optimal control problems. Also, in ^{[2,3,8,16,18]}, these methods are utilized to solve some special fractional partial differential equations. Note that spectral and pseudo-spectral methods have a good accuracy and high speed convergence compared with other methods such as finite difference, finite element methods and wavelet methods and this can be seen in results given in above-mentioned works.

We organize the sections of our work as follows. In Section 2, the adaptive fractional derivative and integral are defined and their important attributes are introduced and proved. In Section 3, we introduced the optimal control problems under adaptive fractional differential equations. In Section 4, we present a LSC method to solve these problems. In Sections 5 and 6, three numerical test problem are approximately solved and the conclusions of work are presented.

2.   The adaptive derivative

We will introduce the adaptive derivative and presented some of its results and properties.

Definition 2.1. Let $\eta:[\zeta_0, \zeta_1]\longrightarrow \mathbb{R}$ be a given function. The adaptive derivative of function $f(\cdot)$ of order $0 < \beta\leqslant1$ at point $\zeta\in (\zeta_0, \zeta_1)$ is defined as follow:

Moreover, $^AD^\beta \eta(\zeta_0)$ and $^AD^\beta \eta(\zeta_1)$ are defined as

and

Theorem 2.1. Let $\eta:[\zeta_0, \zeta_1]\longrightarrow \mathbb{R}$ be a given function, $0 < \beta\leqslant1$ and $\zeta\in (\zeta_0, \zeta_1)$. The existence of classical derivative of function $\eta(\cdot)$ at point $\zeta$, i.e. $\eta^\prime (\zeta)$, is a necessary and sufficient condition for the existence of adaptive derivative of $\eta(\cdot)$ at point $\zeta$, i.e. $^AD^\beta \eta(\zeta)$ for $0 < \beta\leqslant1$. Moreover, we have

Proof. By taking $h = \varepsilon e^{(1-\beta)(\zeta-\zeta_0)}$, we get

The limits in left hand side and right hand side of the above equation are the adaptive derivative and classical derivative of function $\eta(\cdot)$, respectively. Hence, existence of the classical derivative is equivalent with the existence of adaptive derivative.

By relation (2.5), the adaptive derivative of order $\beta = 1$ coincides with classical derivative. Also, by assumptions of Theorem 2.1 and relations (2.2) and (2.3), we have

where

Note that, by Definition 2.1 and relation (2.4), the adaptive derivative inherits the properties of classical derivatives. Some of them are provided below.

Theorem 2.2. Every adaptive differentiable function is continuous.

Proof. By Theorem 2.1, every adaptive differentiable function is a classical differentiable function, and by mathematical analysis, every classical differentiable function is continuous.

Theorem 2.3. Suppose $\eta:[\zeta_0, \zeta_1]\rightarrow \mathbb{R}$ and $\psi:[\zeta_0, \zeta_1]\rightarrow \mathbb{R}$ are two adaptive differentiable functions of order $0 < \beta\leqslant1$ and $\eta\in(\zeta_0, \zeta_1)$. Then

(1) $^AD^\beta (c) = 0$, for all $c\in\mathbb{R}$;

(2) $^AD^\beta (c_1\eta+c_2\psi)(\zeta) = c_1 \ ^AD^\beta \eta(\zeta)+c_2\ ^AD^\beta \psi(\zeta)$, for all $c_1, c_2\in\mathbb{R}$;

(3) $^AD^\beta (\eta\psi)(\zeta) = \psi(\zeta)\ ^AD^\beta \eta(\zeta)+\eta(\zeta)\ ^AD^\beta \psi(\zeta)$;

(4) $^AD^\beta (\frac{\eta}{\psi})(\zeta) = \frac{\psi(\zeta)\ ^AD^\beta \eta(\zeta)-\eta(\zeta)\ ^AD^\beta \psi(\zeta)}{\psi^2(\zeta)}$ if $\psi(\zeta)\neq 0$;

(5) $^AD^\beta (\eta o\psi)(\zeta) = \; \big(\; ^AD^\beta \psi(\zeta)\big) \eta'(\psi(\zeta))$.

Proof. Parts (1)–(4) follow directly from Definition 2.1 and relation (2.4). We choose to prove only the items (3) and (5). We have

Also, we have

Theorem 2.4. (Rolle's theorem) Let $\eta:[\zeta_0, \zeta_1]\subseteq\mathbb{R}\rightarrow \mathbb{R}$ be an adaptive differentiable function of order $0 < \beta\leqslant1$ such that $\eta(\zeta_0) = \eta(\zeta_1)$. There is an $c\in (\zeta_0, \zeta_1)$ such that $^AD^\beta \eta(c) = 0$.

Proof. By Theorem 2.1, $\eta(\cdot)$ is a classical differentiable function. So by classical Rolle's theorem, there is $c\in (\zeta_0, \zeta_1)$ such that $\eta^\prime (c) = 0$. Hence, by relation (2.4), we get

The mean-value theorem for adaptive derivative of order $\beta = 1$ is equivalent with the classical mean-value theorem, since for every differentiable function $\eta:I\subseteq\mathbb{R}\rightarrow \mathbb{R}$, by relation (2.4) we have $^AD^1 \eta(\zeta) = \eta^\prime (\zeta)$, for all $\zeta\in I$. Hence, in the following lines we give the mean-value theorem for adaptive derivatives of order $0 < \beta < 1$.

Theorem 2.5. (Mean-value theorem) Let $\eta:[\zeta_0, \zeta_1]\rightarrow \mathbb{R}$ be an adaptive differentiable function of order $0 < \beta < 1$. There is an $c\in (\zeta_0, \zeta_1)$ such that

Proof. Define function

It is trivial that $\psi(\cdot)$ is an adaptive differentiable function and $\psi(\zeta_0) = \psi(\zeta_1) = 0$. Hence, by Rolle's theorem, there is $c\in (\zeta_0, \zeta_1)$ such that $^AD^\beta \psi(c) = 0$. Now, via Theorem 2.4 and the relation $^AD^\beta (e^{(\beta-1)(\zeta-\zeta_0)}) = \beta-1$, for all $\zeta$, we can reach relation (2.7).

Remark 2.1. Note that by using relation (2.7) and applying the Hopital's rule, we can get the classical mean-value theorem as follow:

Definition 2.2. Assume that $\eta:[\zeta_0, \zeta_1]\longrightarrow \mathbb{R}$ is a continuous function. The adaptive integral of order $0 < \beta\leqslant1$, for $\eta(\cdot)$, is defined by

Theorem 2.6. Assume that $\eta:[\zeta_0, \zeta_1]\longrightarrow \mathbb{R}$ is a continuous function. Then $^AD^\beta\left(^AI^\beta \eta(\zeta)\right) = \eta(\zeta)$, for all $\zeta\in (\zeta_0, \zeta_1)$. Moreover, if function $\eta:[\zeta_0, \zeta_1]\longrightarrow \mathbb{R}$ has a continuous derivative, then

Proof. Since $\eta(\cdot)$ is continuous, then $I^\beta \eta(\cdot)$ that is defined by (2.9) is differentiable. Hence, $^AD^\beta\left(I^\beta \eta(\cdot)\right)$ exists and by relation (2.4), we have

Also, if function $\eta:[\zeta_0, \zeta_1]\longrightarrow \mathbb{R}$ has a continuous classical derivative, $^AD^\beta \eta(\cdot)$ is adaptive integrable and we have

Now, we generalize the definition of adaptive derivative for any $\beta \in (n-1, n]$ where $n\in \mathbb{N}$. Assume that $\eta^{(0)}(\cdot) = \eta(\cdot)$.

Definition 2.3. Let $\eta:[\zeta_0, \zeta_1]\longrightarrow \mathbb{R}$ be a classical differentiable function of order $n\in \mathbb{N}$. The adaptive fractional derivative of $\eta(\cdot)$ of order $n-1 < \beta\leqslant n$ at point $\zeta_0 < \zeta < \zeta_1$ is defined as follow:

Moreover, $^A D^\beta \eta(\zeta_0)$ and $^AD^\beta \eta(\zeta_1)$ are defined as

and

Theorem 2.7. Let $\eta:[\zeta_1, \zeta_0]\longrightarrow \mathbb{R}$ be a classical differentiable function of order $n\in \mathbb{N}$, $n-1 < \beta\leqslant n$ and $\zeta\in (\zeta_0, \zeta_1)$. Then $^AD^\beta \eta(\zeta) = e^{(n-\beta)(\zeta-\zeta_0)} \eta^{(n)}(\zeta)$.

Proof. This is a consequence of Definition 3 and it can be given similar to the proof of Theorem 2.1.

In the next section, we extend the concept of adaptive derivative to optimal control problems.

3.   Adaptive optimal control problem

Here, we introduce the adaptive optimal control (AOC) problem as follow:

where $0 < \beta\le1$, $^AD^{\beta}$ is the adaptive derivative, $\bar y_0 \in \mathbb{R}^n$, $z:\mathbb{R}\times \mathbb{R}^n \times \mathbb{R}^m \to \mathbb{R}$ and $e:\mathbb{R}\times \mathbb{R}^n \times \mathbb{R}^m \to \mathbb{R}^n$ are known differentiable functions. Also, $y(\cdot)$ and $v(\cdot)$ are the state and control variables, respectively. In next section, we propose the LSC approach to solve (3.1) and (3.2). However, before that we transform the time interval of the AOC problem (3.1) and (3.2) into $[-1, 1]$ using transformation

Theorem 3.1. Assume that $0 < \beta\le 1$, function $y(.)$ is defined on $[\zeta_0, \zeta_1]$ and $Y(s) = y(\lambda(s))$, $s\in[-1, 1]$, where $\lambda(.)$ is defined by (3.3). Then for any $s \in [-1, 1]$,

Proof. Assume that $s\in[-1, 1]$ is given and put $\zeta = \lambda(s)$. We have

By (3.3) and (3.4), we can rewrite the AOC problem (3.1) and (3.2) as follow:

where $\lambda(.)$ satisfies (3.3) and

4.   LSC method for AOC problem

We here illustrate and implement the LSC method to solve the AFOC problem (3.5) and (3.6). We show that, by utilizing this method, we can get an approximate optimal solution by solving the associated nonlinear programming (NLP) problem. We need the Legendre polynomials which are defined on $[-1, 1]$ by the following recurrence relation:

To discrete the AFOC problem, the Legendre-Gauss-Lobatto (LGL) nodes are used which are the zeros of $(1-s^2)R_N^\prime(s)$. We show them by ${\{s_k\}}_{k = 0}^{N}$ where $s_0 = -1 < s_1 < \dots < s_{N-1} < s_N = 1$. We also need the Lagrange interpolating polynomials:

where

Now, we approximate ${Y}(\cdot)$ and ${V}(\cdot)$ by the LSC method. We have

where

Also,

Moreover,

To obtain the derivatives ${Y}^{\prime}_N(\cdot)$ and $^AD^\beta {Y_N}(\cdot)$ at the LGL nodes $\{s_k\}_{k = 0}^N$ and get

where

and

By applying the Theorem 3.29 in ^[17], the performance index can be approximated as follow:

where $s_j, j = 0, 1, ..., N$, are the LGL nodes and $p_j, j = 0, 1, ..., N$, are the corresponding weights.

We apply (4.3), (4.6) and (4.8) to approximate the AOC problem (3.1) and (3.2) and get

where $\psi_k = \lambda(s_k)-\tau_k-1-\zeta_0$ and $\lambda(.)$ satisfies (3.3). Having solved this NLP problem with variables $(y_k, v_k), k = 0, 1, 2, ..., N$, we reach the estimated solutions (4.2) for the AOC problem (3.1) and (3.2).

Remark 4.1. The convergence analysis of obtained approximate solutions to the exact optimal solutions (in the suggested spectral method), can be discussed by a similar process given in the works ^[6,7,12,14] with a slight differences and hence we do not repeat it.

5.   Numerical examples

Here, we provide three numerical test problem. The simulations are performed by applying MATLAB R2017b software and FMINCON command. We also compute the absolute errors of the obtained numerical results using

where $y^\star(.)$ and $v^\star(.)$ are the exact state and control solutions and $y(.)$ and $v(.)$ are the approximate state and control solutions of the AOC problem, respectively.

Example 5.1. Consider the following AFOC problem:

where $0 < \beta\leqslant1$. The exact solutions are $y^*(\zeta) = sin(\pi \beta \zeta)$ and $v^*(\zeta) = \pi e^{(1-\beta)\zeta} cos(\pi \beta \zeta)$ with $J^* = 0$.

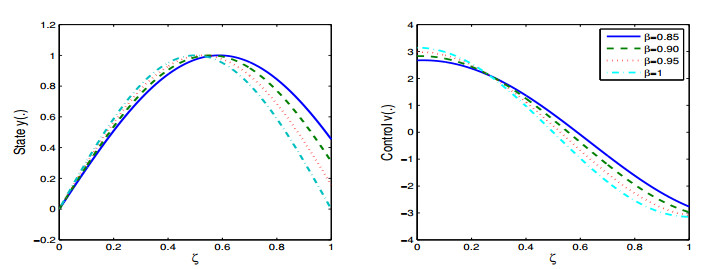
We solve the related NLP problem (4.9) and (4.10) for the values of $\beta = 0.85, \; 0.90, \; 0.95, \; 1$ and $N = 8$. Figure 1 shows the obtained approximate optimal solutions. Also, the logarithm of absolute errors are illustrated in Figure 2. Moreover, in Table 1, we demonstrate the obtained values of performance index for some values of $\alpha$. It can be observed that the gained approximate optimal solutions have acceptable accuracy and the presented method is efficient and applicable to solve this problem.

Example 5.2. Consider the following AOC problem:

where $0 < \beta\leqslant1$. The exact solutions for $\beta = 1$ are $y^*(\zeta) = e^\zeta$ and $v^*(\zeta) = \ln(1+\zeta)$. For other values of $\beta$, the analytic form of exact optimal solutions are not known.

By solving the related NLP problem (4.9) and (4.10) for $N = 6$, we achieve the approximate solutions which are illustrated in Figure 3. The error of approximate solution for $\beta = 1$ is shown in Figure 4. Also, the values of $J_N$ for different values of $\beta$ are summarized in Table 2. We see, as $\beta$ increases, the approximate solutions approach the exact solution corresponding to $\beta = 1$.

Example 5.3. Consider the following AFOC problem:

where $0 < \beta\le1$. The analytical form of optimal solutions is not available.

We solve this problem by presented approach for values $\beta = 0.4, \; 0.6, \; 0.8, \; 1$ with $N = 8$. The obtained approximate solutions are illustrated in Figure 5. It can be seen that when $\beta$ tends to 1, the trajectories go to the approximate optimal trajectory corresponding to $\beta = 1$. In Table 3, the approximate optimal values of $J$ are shown. We see this values by increasing $N$ tends to a fixed value and results are stable.

6.   Conclusions

In this study, we defined the adaptive derivative. We showed that this type of local non-integer derivatives, for positive integer orders, adapts with the classical derivative and we extended the classical main theorems and relations of mathematical analysis according to this new derivative. Also, we applied the LSC method to solve the adaptive optimal control problem. The achieved results approved that the presented scheme in the sense of adaptive derivatives is highly accurate. For some theoretical discussions, we can investigate the associated integral methods, that may be useful for analytical methods for this type of derivative, in our future work similar to ^[5]. Also, physical interpretations can be analyzed similar to ^[19]. Similar to the investigations that are associated to the derivative of Khalil ^[9], we can discuss about some applications of this new type of non-integere derivative in space-time fractional nonlinear (1+1)-dimensional Schrodinger-type models ^[4] and fractional delay differential equations ^[11] in our future research projects. Also, we can extend this new non-integer derivative and presented work to optimal control problems governed by non-integer delay ordinary and partial differential equations.

Acknowledgments

The first author (Xingfa Yang) was supported by the OutstandingYouth Program of Hunan Provincial Department of Education (No. 21B0772) and the Hunan Provincial Natural Science Foundation Committee Youth Project (No. 2020JJ5619). The second author (Yin Yang) was supported by the National Natural Science Foundation of China Project (No. 12071402) and the Project of Scientific Research Fund of the Hunan Provincial Science and Technology Department (No. 2020JJ2027).

Conflict of interest

The authors declare no conflicts of interest.