A survey comparative analysis of cartesian and complexity science frameworks adoption in financial risk management of Zimbabwean banks

Gilbert Tepetepe; Easton Simenti-Phiri; Danny Morton; Gilbert Tepetepe; Easton Simenti-Phiri; Danny Morton

doi:10.3934/QFE.2022016

Quantitative Finance and Economics

2022, Volume 6, Issue 2: 359-384. doi: 10.3934/QFE.2022016

Previous Article Next Article

Research article

A survey comparative analysis of cartesian and complexity science frameworks adoption in financial risk management of Zimbabwean banks

1.
School of Business Management, University of Bolton University, Deane Road, Bolton, BL3 5AB, United Kingdom
2.
School of Engineering, University of Bolton, Deane Road, Bolton, BL3 5AB, United Kingdom

Received: 06 May 2022 Revised: 11 June 2022 Accepted: 17 June 2022 Published: 21 June 2022
JEL Codes: G15, G23, F36

Traditionally, financial risk management is examined with cartesian and interpretivist frameworks. However, the emergence of complexity science provides a different perspective. Using a structured questionnaire completed by 120 Risk Managers, this paper pioneers a comparative analysis of cartesian and complexity science theoretical frameworks adoption in sixteen Zimbabwean banks, in unique settings of a developing country. Data are analysed with descriptive statistics. The paper finds that overally banks in Zimbabwe are adopting cartesian and complexity science theories regardless of bank size, in the same direction and trajectory. However, adoption of cartesian modeling is more comprehensive and deeper than complexity science. Furthermore, due to information asymmetries, there is diverging modeling priorities between the regulator and supervisor. The regulator places strategic thrust on Knightian risks modeling whereas banks prioritise ontological, ambiguous and Knightian uncertainty measurement. Finally, it is found that complexity science and cartesianism intersect on market discipline. From these findings, it is concluded that complexity science provides an additional dimension to quantitative risk management, hence an integration of these two perspectives is beneficial. This paper makes three contributions to knowledge. First, it adds valuable insights to theoretical perspectives on Quantitative Risk Management. Second, it provides empirical evidence on adoption of two theories from developing country perspective. Third, it offers recommendations to improve Quantitative Risk Management policy formulation and practice.

Keywords:

Citation: Gilbert Tepetepe, Easton Simenti-Phiri, Danny Morton. A survey comparative analysis of cartesian and complexity science frameworks adoption in financial risk management of Zimbabwean banks[J]. Quantitative Finance and Economics, 2022, 6(2): 359-384. doi: 10.3934/QFE.2022016

Related Papers:

[1]	Toyohiko Aiki, Kota Kumazaki . Uniqueness of solutions to a mathematical model describing moisture transport in concrete materials. Networks and Heterogeneous Media, 2014, 9(4): 683-707. doi: 10.3934/nhm.2014.9.683
[2]	Thomas Geert de Jong, Georg Prokert, Alef Edou Sterk . Reaction–diffusion transport into core-shell geometry: Well-posedness and stability of stationary solutions. Networks and Heterogeneous Media, 2025, 20(1): 1-14. doi: 10.3934/nhm.2025001
[3]	Magali Tournus, Aurélie Edwards, Nicolas Seguin, Benoît Perthame . Analysis of a simplified model of the urine concentration mechanism. Networks and Heterogeneous Media, 2012, 7(4): 989-1018. doi: 10.3934/nhm.2012.7.989
[4]	Naoki Sato, Toyohiko Aiki, Yusuke Murase, Ken Shirakawa . A one dimensional free boundary problem for adsorption phenomena. Networks and Heterogeneous Media, 2014, 9(4): 655-668. doi: 10.3934/nhm.2014.9.655
[5]	Leonid Berlyand, Mykhailo Potomkin, Volodymyr Rybalko . Sharp interface limit in a phase field model of cell motility. Networks and Heterogeneous Media, 2017, 12(4): 551-590. doi: 10.3934/nhm.2017023
[6]	Mingming Fan, Jianwen Sun . Positive solutions for the periodic-parabolic problem with large diffusion. Networks and Heterogeneous Media, 2024, 19(3): 1116-1132. doi: 10.3934/nhm.2024049
[7]	Ken-Ichi Nakamura, Toshiko Ogiwara . Periodically growing solutions in a class of strongly monotone semiflows. Networks and Heterogeneous Media, 2012, 7(4): 881-891. doi: 10.3934/nhm.2012.7.881
[8]	Brahim Amaziane, Leonid Pankratov, Andrey Piatnitski . An improved homogenization result for immiscible compressible two-phase flow in porous media. Networks and Heterogeneous Media, 2017, 12(1): 147-171. doi: 10.3934/nhm.2017006
[9]	Bendong Lou . Self-similar solutions in a sector for a quasilinear parabolic equation. Networks and Heterogeneous Media, 2012, 7(4): 857-879. doi: 10.3934/nhm.2012.7.857
[10]	F. R. Guarguaglini, R. Natalini . Nonlinear transmission problems for quasilinear diffusion systems. Networks and Heterogeneous Media, 2007, 2(2): 359-381. doi: 10.3934/nhm.2007.2.359

Abstract

1. Introduction

Recently, the electrical circuit equations as Resistor-Capacitor (RC) and Resistor-Inductor (RL) have attracted many mathematicians ^[3,15]. The analytical solutions of the electrical circuit equations described by a singular and a no-singular fractional derivative operators have been proposed. In ^[6], Aguilar et al. have introduced the electrical circuit equations considering the Caputo fractional derivative. They have proposed the analytical solutions of the electrical RC and RL equations described by the Caputo fractional derivative. In ^[6], the authors have proposed the graphical representations to illustrate the main results. The Caputo fractional derivative is a fractional derivative with a regular kernel. Recently, the fractional derivative operators with no-singular kernels were introduced in the literature. The Caputo-Fabrizio fractional derivative and the Atangana-Baleanu fractional derivative. In ^[5], Aguilar et al. have introduced electrical equations considering the fractional derivative operators with two parameters. They have proposed the solutions of the electrical RL and RC circuit equations described by the fractional derivative operators with two parameters $\alpha, \beta\in(0, 1]$ . In ^[5], the authors have introduced electrical circuit equations using the Atangana-Baleanu fractional derivative. They have proposed the analytical solutions using the Laplace transform. They have presented the numerical scheme of the Atangana-Baleanu fractional derivative of getting the analytical solutions of the electrical RC and RL circuit equations. In ^[4], Aguilar et al. have presented the electrical circuit equations using the Caputo-Fabrizio fractional derivative. They have proposed the graphical representations of the analytical solutions. In ^[8], Aguilar et al. have investigated of getting the analytical solution of the RLC circuit equation described by the Caputo fractional derivative. In ^[7], Aguilar et al. have analyzed and proved the jerk dynamics can be obtained with the electrical circuit equations. There exist many other works related to the analytical solutions, seen in ^[11,20]. The stability problem interests many mathematicians. The stability problem studies the behaviors of the analytical solutions of the fractional differential equations. The analytical solution of the electrical circuit described by the singular and the no-singular fractional derivative operators is an open problem in fractional calculus and continues to receive many investigations. The analytical solutions of the electrical circuits exist. We can get them. The problem is how to analyze the behaviors of these solutions using stability notions. In ^[14], the authors have analyzed the stability of the electrical RLC circuit equation. The electrical RL and RC circuit equations contain source terms. The source terms have some properties. The source term of the electrical circuit equations can be constant ^[10]. The source term can be sinusoidal ^[5]. They exist some source terms which converge in the times ^[10]. In stability problems, there exists a novel notion of studying the behaviors the fractional differential equations with these characteristics. This notion is called the fractional input stability recently introduced in the literature by Sene in ^[18,19]. In this paper, the function containing the source term will be considered as the exogenous input. The contribution of our paper is to recall the analytical solutions of the electrical RL and RC circuit equations described by the Riemann-Liouville and the Caputo fractional derivative using the Laplace transform. Secondly, we will analyze the behaviors of the obtained analytical solutions of the electrical RL and RC circuit equations using the fractional input stability. In other words, we investigate the fractional input stability of the electrical RL and RC circuit equations described by the Riemann-Liouville and the Caputo fractional derivative. The fractional input stability resumes three properties. Firstly, when the considered exogenous input converges, then the analytical solution of the considered electrical circuit converges as well. In other words, a converging input generates a converging state. That is the CICS property of the fractional input stability. Secondly, when the exogenous input is bounded, then the analytical solution of the considered electrical circuit is bounded as well. In other words, a bounded input generates a bounded state. That is the BIBS property of the fractional input stability. And at last, when the the exogenous input is null, then the trivial solution of the unforced electrical circuit is globally asymptotically stable. A fractional differential equation is said to be fractional input stable when the norm of the analytical solution at all times is bounded by a function proportional to the initial state and converging to zero in times plus a positive function depending to the norm of the exogenous input.

In stability problems in fractional calculus, the asymptotic stability is provided in many manuscripts. Using the fractional input stability, we can study the uniform global asymptotic stability of the fractional differential equations. Presently, the stability conditions for the asymptotic stability were provided in the literature. This paper offers an alternative to study the (uniform) global asymptotic stability of the fractional differential equations. It is the main contribution of this paper. The application of the fractional input stability of the fractional differential equations is the second contribution of this paper.

The paper is described as the following form. In Section 2, we recall preliminary definitions of the fractional derivative operator and recall the definitions of the stability notions. In Section 3, we investigate the analytical solutions of the electrical RL, RC and LC circuit equations described by the Riemann-Liouville fractional derivative and the Caputo fractional derivative. We analyze the fractional input stability of the obtained analytical solutions. In Section 4, we give the graphical representations of the fractional input stability of the electrical RC and RL circuit equations described by the Caputo fractional derivative operator. In Section 5, we give the conclusions and the remarks.

Notation: $\mathcal{PD}$ denotes the set of all continuous functions $\chi:\mathbb R_{\geq 0}\to\mathbb R_{\geq 0}$ satisfying $\chi(0) = 0$ and $\chi(s)>0$ for all $s>0$ . A class $\mathcal{K}$ function is an increasing $\mathcal{PD}$ function. The class $\mathcal{K}_{\infty}$ denotes the set of all unbounded $\mathcal{K}$ function. A continuous function $\beta : \mathbb{R}_{\geq 0}\times \mathbb{R}_{\geq 0}\rightarrow \mathbb{R}_{\geq 0}$ is said to be class $\mathcal{KL}$ if $\beta(., t)\in \mathcal{K}$ for any $t\geq0$ and $\beta(s, .)$ is non increasing and tends to zero as its arguments tends to infinity. Let $x\in\mathbb R^n$ , $\left\|x\right\|$ stands for its Euclidean norm: $\left\|x\right\|: = \sqrt{x_1^2+\ldots+x_n^2}$ .

2. Preliminary definitions

In this section, we recall the definitions of the fractional derivative operators and the definition of the fractional input stability introduced in the literature ^[18,19] of fractional calculus. We recall the definition of the Caputo fractional derivative.

Definition 1. ^[9,16,17] Consider a function $f:[0, +\infty[\longrightarrow\mathbb{R}$ , the Caputo fractional derivative of the function $f$ of order $\alpha$ is formulated as the following form

$\begin{equation} D^{c}_{\alpha}f(t) = \frac{1}{\Gamma(1-\alpha)}\int^{t}_{0}\frac{f'(s)}{(t-s)^{\alpha}}ds \end{equation}$

(2.1)

for all $t>0,$ we consider $\alpha\in\left(0, 1\right)$ and $\Gamma(.)$ is the gamma function.

The Riemann-Liouville fractional derivative is recalled in the following definition.

Definition 2. ^[9,13] Consider a function $f:[0, +\infty[\longrightarrow\mathbb{R}$ , the Riemann-Liouville fractional derivative of the function $f$ of order $\alpha$ is formulated as the following form

$\begin{equation} D^{RL}_{\alpha}f(t) = \frac{1}{\Gamma(1-\alpha)}\frac{d}{dt}\int^{t}_{0}\frac{f(s)}{(t-s)^{\alpha}}ds \end{equation}$

(2.2)

for all $t>0,$ we consider $\alpha\in\left(0, 1\right)$ and $\Gamma(.)$ is the gamma function.

The Riemann-Liouville fractional integral is recalled in the following definition.

Definition 3. ^[12,18,19] Consider a function $f:[0, +\infty[\longrightarrow\mathbb{R}$ , the Riemann-Liouville fractional integral of the function $f$ of order $\alpha$ is represented as the following form

$\begin{equation} I^{RL}_{\alpha}f(t) = \frac{1}{\Gamma(1-\alpha)}\int^{t}_{0}(t-s)^{\alpha-1}f(s)ds \end{equation}$

(2.3)

for all $t>0,$ we consider $\alpha\in\left(0, 1\right)$ and $\Gamma(.)$ is the gamma function.

Definition 4. ^[1,2] The Mittag–Leffler function with two parameters is expressed as the following form

$\begin{equation}\label{conformableexp} E_{\alpha, \beta}\left(z\right) = \sum\limits^{\infty}_{k = 0}\frac{z^{k}}{\Gamma(\alpha k+\beta)} \end{equation}$

(2.4)

where $\alpha>0,$ $\beta\in\mathbb{R}$ and $z\in \mathbb{C}$ .

We consecrate this section of recalling some stability notions introduced in ^[18,19]. In general, the fractional differential equation under consideration is defined by

$\begin{equation}\label{eq2.5} D^{c}_{\alpha}x = f(t, x, u)\end{equation}$

(2.5)

where $x\in \mathbb{R}^{n}$ , a continuous and locally Lipschitz function $f:\mathbb{R}^{+}\times \mathbb{R}^{n}\times \mathbb{R}^{m}\longrightarrow\mathbb{R}^{n}$ and $u\in \mathbb{R}^{m}$ represents the exogenous input. Note that the solution of the fractional differential equation (2.5) exists under the assumption "the function $f$ is continuous and locally Lipschitz". The existence of the solution is fundamental in the stability problems. It is not necessary to study the stability of the fractional differential equation when we are not sure its the solution exists.

Definition 5. ^[18,19] The fractional differential equation (2.5) is fractional input stable if for any exogenous input $u\in\mathbb{R}^{m}$ , there exists a function $\beta \in \mathcal{KL}$ , a function $\gamma \in \mathcal{K}_{\infty}$ such that for any initial state $x_{0}$ the solution of (2.5) satisfies

$\begin{equation}\label{eq2.6} \left\|x(t, x_{0}, u)\right\| \leq \beta (\left\|x_{0}\right\| , t)+\gamma(\left\|u\right\|_{\infty}).\end{equation}$

(2.6)

The function $\gamma$ is a class $\mathcal{K}_{\infty}$ function and the function $\beta$ is a class $\mathcal{KL}$ . Thus, from equation (2.6), when the exogenous input $u$ of the fractional differential equation (2.5) is bounded it follows its solution is bounded as well, that is the BIBS property. See the proof in the next section or in the original paper ^[18]. We can also notice, when the exogenous input of the fractional differential equation (2.5) converges, when $t$ tends to infinity, then its solution converges as well, that is CICS property, see in ^[18] for more details. At last, we observe from equation (2.6) when the exogenous input into the fractional differential equation (2.5) is null; we recover the definition of the global asymptotic stability described in the following definition.

Definition 6. ^[16] The trivial solution of the unforced fractional differential equation defined by $D^{c}_{\alpha}x = f(t, x, 0)$ is said to be (uniform) globally asymptotically stable if there exist a function $\beta \in \mathcal{KL}$ , such that for any initial condition $x_{0}$ the solution of $D^{c}_{\alpha}x = f(t, x, 0)$ satisfies

$\begin{equation}\label{eq2.7} \left\|x(t, x_{0}, 0)\right\| \leq \beta (\left\|x_{0}\right\| , t).\end{equation}$

(2.7)

The last remark is the main contribution of the fractional input stability of the fractional differential equations. We finish this section by recalling the following lemma. It will be used to introduce comparison functions.

Lemma 1. ^[21] Let $\alpha\in(0, 2)$ , $\beta$ is a real number, a matrix $A\in \mathbb{C}^{n\times n}$ , $\mu$ is such that $\frac{\pi\alpha}{2}<\mu< \min\left\{\pi, \pi\alpha\right\}$ and $C>0$ is a real, then it holds that

$\begin{equation}\label{eq2.8} \left\|E_{\alpha, \beta}\left(A\right)\right\|\leq\frac{C}{1+\left\|A\right\|}\end{equation}$

(2.8)

where $\mu\leq \arg\left(\lambda(A)\right)\leq\pi$ , $\lambda(A)$ represents the eigenvalues of the matrix $A.$

3. Fractional input stability of the electrical circuits equations described by certain fractional derivative operators

In this section, we address the fractional input stability of the electrical circuit equations described by the Riemann-Liouville and the Caputo fractional derivative operators. The electrical circuit equations under consideration are the electrical RL circuit equation, the electrical LC circuit equation, and the electrical RC circuit equation. We analyze the bounded input bounded state (BIBS), the converging input converging state (CICS) and the (uniform) global asymptotic stability of the unforced fractional electrical circuit equations, properties derived to the fractional input stability of the electrical circuit equations. It is important to note, in the rest of the paper, the second term of all the fractional electrical circuit equations is considered as a single function which represents the exogenous input.

3.1. Fractional input stability of the electrical RL circuit equation described by the Riemann-Liouville fractional derivative

In this section, we address the fractional input stability of the electrical RL circuit described by the Riemann-Liouville fractional derivative. We consider the electrical RL circuit represented by the following fractional differential equation

$\begin{equation}\label{eq3.1} D^{\alpha}_{RL}I(t)+\frac{\sigma^{1-\alpha}R}{L}I(t) = u(t)\end{equation}$

(3.1)

with the initial boundary condition defined by $\left(I^{1-\alpha}I\right)(a) = I_{0}$ . $I$ represents the current across the inductor. The parameter $\sigma$ is associated with the temporal components in the system, see more details in ^[5,6]. $R$ represents the resistance, and $L$ represents the inductance. In the second member, $u(t)$ is considered as the exogenous input. It contains the source term $E(t)$ (eventually depend on time), the function $1/L$ and the temporal coefficient $\sigma^{1-\alpha}$ . Summarizing $u(t) = \frac{\sigma^{1-\alpha}E(t)}{L}$ .

Theorem 1. The electrical RL circuit defined by equation (3.1) described by the Riemann-Liouville fractional derivative is fractional input stable.

Proof: We first determine the analytical solution of the fractional differential equation defined by equation (3.1). Applying the Laplace transform to both sides of equation (3.1), we obtain the following relationships

$\begin{eqnarray}\label{eq3.2} s^{\alpha}\mathcal{L}(I(t))-\left(I^{1-\alpha}I\right)(0)+\frac{\sigma^{1-\alpha}R}{L}\mathcal{L}(I(t))& = &\mathcal{L}(u(t))\nonumber\\ s^{\alpha}\mathcal{L}(I(t))-I_{0}+\frac{\sigma^{1-\alpha}R}{L}\mathcal{L}(I(t))& = &\mathcal{L}(u(t))\nonumber\\ \mathcal{L}(I(t))\left\{s^{\alpha}+\frac{\sigma^{1-\alpha}R}{L}\right\}& = &I_{0}+\mathcal{L}(u(t))\nonumber\\ \mathcal{L}(I(t))& = &\frac{I_{0}}{s^{\alpha}+\frac{\sigma^{1-\alpha}R}{L}}+\frac{\mathcal{L}(u(t))}{s^{\alpha}+\frac{\sigma^{1-\alpha}R}{L}}\nonumber\\ \mathcal{L}(I(t)) = I_{0}\mathcal{L}\left(t^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}R}{L}t^{\alpha}\right)\right)&+&\mathcal{L}\left(t^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}R}{L}t^{\alpha}\right)\right)\mathcal{L}\left(u(t)\right)\nonumber\\ \mathcal{L}(I(t)) = I_{0}\mathcal{L}\left(t^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}R}{L}t^{\alpha}\right)\right)&+&\mathcal{L}\left(t^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}R}{L}t^{\alpha}\right)\ast u(t)\right)\end{eqnarray}$

(3.2)

where $\mathcal{L}$ represents the usual Laplace transform and " $\ast$ " represents the usual convolution product. Applying the inverse of Laplace transform to both sides of equation (3.2), we obtain the following analytical solution

$\begin{equation}\label{eq3.3} I(t) = I_{0}t^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}R}{L}t^{\alpha}\right)+\int^{t}_{0}\left(t-s\right)^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}R}{L}\left(t-s\right)^{\alpha}\right)u(s)ds.\end{equation}$

(3.3)

From which it follows by applying the euclidean norm

$\begin{equation}\label{eq3.4} \left\|I(t)\right\|\leq\left\|I_{0}t^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}R}{L}t^{\alpha}\right)\right\|+\left\|u\right\|\int^{t}_{0}\left\|\left(t-s\right)^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}R}{L}\left(t-s\right)^{\alpha}\right)\right\|ds.\end{equation}$

(3.4)

We know the term $-\frac{\sigma^{1-\alpha}R}{L}\leq 0$ , then there exists a positive constant $M$ such that we have the following inequality ^[17]

$\begin{equation}\label{eq3.5} \int^{t}_{0}\left\|\left(t-s\right)^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}R}{L}\left(t-s\right)^{\alpha}\right)\right\|ds\leq M.\end{equation}$

(3.5)

Using Lemma 1 and inequality (3.5), we obtain the following inequality

$\begin{equation}\label{eq3.6} \left\|I(t)\right\|\leq\frac{I_{0}C_{1}}{\left\|t^{1-\alpha}\right\|+\frac{\sigma^{1-\alpha}R}{L}\left\|t\right\|}+\left\|u\right\|M.\end{equation}$

(3.6)

Let the function $\beta\left(I_{0}, t\right) = \frac{I_{0}C_{1}}{\left\|t^{1-\alpha}\right\|+\frac{\sigma^{1-\alpha}R}{L}\left\|t\right\|}$ . We observe the function $\beta\left(., t\right)$ is a class $\mathcal{K}$ function. Furthermore, $\beta\left(s, .\right)$ decays with the time and converges to zero when $t$ tends to infinity, thus $\beta\left(s, .\right)$ is a class $\mathcal{L}$ function. In conclusion the function $\beta$ is a class $\mathcal{KL}$ function. Let the function $\gamma\left(\left\|u\right\|\right) = \left\|u\right\|M$ , it is straightforward to see $\gamma$ is a class $\mathcal{K}_{ \infty}$ function. Finally, equation (3.6) is represented as follows

$\begin{equation}\label{eq3.7} \left\|I(t)\right\|\leq\beta\left(I_{0}, t\right)+\gamma\left(\left\|u\right\|\right).\end{equation}$

(3.7)

It follows from equation (3.7) the electrical RL circuit described by the Riemann-Liouville fractional derivative is fractional input stable.

Let the exogenous input $\left\|u\right\| = 0$ then $\gamma\left(0\right) = 0$ (because $\gamma$ is a class $\mathcal{K}_{ \infty}$ function), thus equation (3.7) becomes

$\begin{equation} \left\|I(t)\right\|\leq\beta\left(I_{0}, t\right). \end{equation}$

(3.8)

Then the equilibrium point $I = 0$ of the electrical RL circuit defined by

$\begin{equation}\label{eq3.9} D^{\alpha}_{RL}I(t)+\frac{\sigma^{1-\alpha}R}{L}I(t) = 0\end{equation}$

(3.9)

is (uniformly) globally asymptotically stable. Then, the fractional input stability of the electrical RL circuit equation (3.1) implies the global asymptotic stability of the unforced electrical RL circuit equation (3.9). Proving the global asymptotic stability of the equilibrium point $I = 0$ of the unforced electrical RL circuit equation (3.9) using the fractional input stability is essential. The classical tools give the asymptotic stability of the equilibrium point $I = 0$ . Its don't give the global asymptotic stability. Thus, the fractional input stability is a good compromise in the stability problems. We observe when the exogenous input of equation (3.1) converges; then from equation (3.7), we notice the analytical solution of the electrical RL circuit equation (3.1) converges as well. That is the CICS property. Furthermore, from equation when the exogenous input equation (3.1) is bounded, then the analytical solution of the electrical RL circuit equation (3.1) is bounded as well. We give the proof. Let the exogenous input $\left\|u\right\|\leq\eta$ then from the fact $\gamma$ is a class $\mathcal{K}_{ \infty}$ , there exists $\epsilon$ such that $\gamma\left(\left\|u\right\|\right)\leq\epsilon$ . Then equation (3.7) becomes

$\begin{equation} \left\|I(t)\right\|\leq\beta\left(I_{0}, t\right)+\epsilon\leq\beta\left(I_{0}, 0\right)+\epsilon. \end{equation}$

(3.10)

Thus the analytical solution is bounded as well.

3.2. Fractional input stability of the electrical RL circuit described by the Caputo fractional derivative

In this section, we replace the Riemann-Liouville fractional derivative by the Caputo fractional derivative. We address the fractional input stability of the electrical RL circuit described by the Caputo fractional derivative. The following fractional differential equation defines the electrical RL circuit equation described by the Caputo fractional derivative

$\begin{equation}\label{eq3.11} D^{\alpha}_{c}I(t)+\frac{\sigma^{1-\alpha}R}{L}I(t) = u(t)\end{equation}$

(3.11)

with the initial boundary condition defined by $I(0) = I_{0}$ . The term $u(t)$ represents the exogenous input as defined in the previous section.

Theorem 2. The electrical RL circuit defined by equation (3.11) described by the Caputo fractional derivative is fractional input stable.

Proof: We apply the Laplace transform to both sides of equation (3.11), we obtain the following relationships

$\begin{eqnarray}\label{eq3.12} s^{\alpha}\mathcal{L}(I(t))-s^{\alpha-1}I(0)+\frac{\sigma^{1-\alpha}R}{L}\mathcal{L}(I(t))& = &\mathcal{L}(u(t))\nonumber\\ s^{\alpha}\mathcal{L}(I(t))-s^{\alpha-1}I_{0}+\frac{\sigma^{1-\alpha}R}{L}\mathcal{L}(I(t))& = &\mathcal{L}(u(t))\nonumber\\ \mathcal{L}(I(t))\left\{s^{\alpha}+\frac{\sigma^{1-\alpha}R}{L}\right\}& = &s^{\alpha-1}I_{0}+\mathcal{L}(u(t))\nonumber\\ \mathcal{L}(I(t))& = &\frac{s^{\alpha-1}I_{0}}{s^{\alpha}+\frac{\sigma^{1-\alpha}R}{L}}+\frac{\mathcal{L}(u(t))}{s^{\alpha}+\frac{\sigma^{1-\alpha}R}{L}}\nonumber\\ \mathcal{L}(I(t)) = I_{0}\mathcal{L}\left(E_{\alpha}\left(-\frac{\sigma^{1-\alpha}R}{L}t^{\alpha}\right)\right)&+&\mathcal{L}\left(t^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}R}{L}t^{\alpha}\right)\right)\mathcal{L}\left(u(t)\right)\nonumber\\ \mathcal{L}(I(t)) = I_{0}\mathcal{L}\left(E_{\alpha}\left(-\frac{\sigma^{1-\alpha}R}{L}t^{\alpha}\right)\right)&+&\mathcal{L}\left(t^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}R}{L}t^{\alpha}\right)\ast u(t)\right)\end{eqnarray}$

(3.12)

where $\mathcal{L}$ represents the usual Laplace transform and " $\ast$ " represents the usual convolution product. We apply the inverse of Laplace transform to both sides of equation ((3.12). We obtain the following analytical solution

$\begin{equation}\label{eq3.13} I(t) = I_{0}E_{\alpha}\left(-\frac{\sigma^{1-\alpha}R}{L}t^{\alpha}\right)+\int^{t}_{0}\left(t-s\right)^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}R}{L}\left(t-s\right)^{\alpha}\right)u(s)ds.\end{equation}$

(3.13)

We apply the usual euclidean norm to equation ((3.13). It follows the following inequality

$\begin{equation} \left\|I(t)\right\|\leq\left\|I_{0}E_{\alpha}\left(-\frac{\sigma^{1-\alpha}R}{L}t^{\alpha}\right)\right\|+\left\|u\right\|\int^{t}_{0}\left\|\left(t-s\right)^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}R}{L}\left(t-s\right)^{\alpha}\right)\right\|ds \end{equation}$

(3.14)

The characteristic term $-\frac{\sigma^{1-\alpha}R}{L}\leq 0$ , then there exists a positive constant $M$ such that the following inequality is held

$\begin{equation}\label{eq3.15} \int^{t}_{0}\left\|\left(t-s\right)^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}R}{L}\left(t-s\right)^{\alpha}\right)\right\|ds\leq M\end{equation}$

(3.15)

Using Lemma 1 and the inequality defined by equation (3.15), we obtain the following inequality

$\begin{equation}\label{eq3.16} \left\|I(t)\right\|\leq\frac{I_{0}C_{1}}{1+\frac{\sigma^{1-\alpha}R}{L}\left\|t^{\alpha}\right\|}+\left\|u\right\|M\end{equation}$

(3.16)

Let the function $\beta\left(I_{0}, t\right) = \frac{I_{0}C_{1}}{1+\frac{\sigma^{1-\alpha}R}{L}\left\|t^{\alpha}\right\|}$ . We observe the function $\beta\left(., t\right)$ is a class $\mathcal{K}$ function. Furthermore, $\beta\left(s, .\right)$ decays in time and converges to zero when $t$ tends to infinity, thus the function $\beta\left(s, .\right)$ is a class $\mathcal{L}$ function. In conclusion the function $\beta$ is a class $\mathcal{KL}$ function. Let the function $\gamma\left(\left\|u\right\|\right) = \left\|u\right\|M$ . The function $\gamma$ is a class $\mathcal{K}_{ \infty}$ function. Finally, equation (3.16) is represented as the following form

$\begin{equation}\label{eq3.17} \left\|I(t)\right\|\leq\beta\left(I_{0}, t\right)+\gamma\left(\left\|u\right\|\right)\end{equation}$

(3.17)

It follows from equation (3.17) the electrical RL circuit equation described by the Caputo fractional derivative is fractional input stable.

Let the exogenous input $u = 0$ . From the fact $\gamma$ is a class $\mathcal{K}_{ \infty}$ function, we have $\gamma\left(0\right) = 0$ . Equation (3.17) is represented as the following form

$\begin{equation}\label{eq3.18} \left\|I(t)\right\|\leq\beta\left(I_{0}, t\right)\end{equation}$

(3.18)

From equation (3.18), the equilibrium point $I = 0$ of the electrical RL circuit equation described by the Caputo fractional derivative defined by

$\begin{equation}\label{eq3.19} D^{\alpha}_{c}I(t)+\frac{\sigma^{1-\alpha}R}{L}I(t) = 0\end{equation}$

(3.19)

is globally asymptotically stable. Then, the fractional input stability of equation (3.11) implies the global asymptotic stability of the unforced electrical RL circuit equation (3.19). We observe when the exogenous input of equation (3.11) converges, then from equation (3.17), we notice the analytical solution of the electrical RL circuit equation (3.11) converges as well. From equation (3.17), the analytical solution of the electrical RL circuit equation (3.11) described by the Caputo fractional derivative is bounded as well when the exogenous input is bounded.

3.3. Fractional input stability of the electrical LC circuit described by the Riemann-Liouville fractional derivative

In this section, we study the fractional input stability of the electrical LC circuit described by the Riemann-Liouville fractional derivative. The electrical LC circuit equation under consideration is defined by the following fractional differential equation

$\begin{equation}\label{eq3.20} D^{2\alpha}_{RL}I(t)+\frac{\sigma^{1-\alpha}}{\sqrt{LC}}I(t) = u(t)\end{equation}$

(3.20)

with the initial boundary condition defined by $\left(I^{1-2\alpha}I\right)(0) = I_{0}$ and $\alpha\leq1/2$ (in this paper). $I$ represents the current across the inductor. The parameter $\sigma$ is associated with the temporal components in the system, see more details in ^[6]. In the second member, $u(t)$ represents the exogenous input. It is expressed using the source term $E(t)$ (eventually depend on time), the function $C/\sqrt{LC}$ and the temporal coefficient $\sigma^{1-\alpha}$ . Summarizing, we have $u(t) = \frac{\sigma^{1-\alpha}CE(t)}{\sqrt{LC}}$ . We make the following theorem.

Theorem 3. The electrical LC circuit equation defined by equation (3.20) described by the Riemann-Liouville fractional derivative is fractional input stable.

Proof: Let $\beta = 2\alpha$ . We apply the Laplace transform to both sides of equation (3.20), we obtain the following relationships

$\begin{eqnarray}\label{eq3.21} s^{\beta}\mathcal{L}(I(t))-\left(I^{1-\beta}I\right)(0)+\frac{\sigma^{1-\alpha}}{\sqrt{LC}}\mathcal{L}(I(t))& = &\mathcal{L}(u(t))\nonumber\\ s^{\beta}\mathcal{L}(I(t))-I_{0}+\frac{\sigma^{1-\alpha}}{\sqrt{LC}}\mathcal{L}(I(t))& = &\mathcal{L}(u(t))\nonumber\\ \mathcal{L}(I(t))\left\{s^{\beta}+\frac{\sigma^{1-\alpha}}{\sqrt{LC}}\right\}& = &I_{0}+\mathcal{L}(u(t))\nonumber\\ \mathcal{L}(I(t))& = &\frac{I_{0}}{s^{\beta}+\frac{\sigma^{1-\alpha}}{\sqrt{LC}}}+\frac{\mathcal{L}(u(t))}{s^{\beta}+\frac{\sigma^{1-\alpha}}{\sqrt{LC}}}\nonumber\\ \mathcal{L}(I(t)) = I_{0}\mathcal{L}\left(t^{\beta-1}E_{\beta, \beta}\left(-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}t^{\beta}\right)\right)&+&\mathcal{L}\left(t^{\beta-1}E_{\beta, \beta}\left(-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}t^{\beta}\right)\right)\mathcal{L}\left(u(t)\right)\nonumber\\ \mathcal{L}(I(t)) = I_{0}\mathcal{L}\left(t^{\beta-1}E_{\beta, \beta}\left(-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}t^{\beta}\right)\right)&+&\mathcal{L}\left(t^{\beta-1}E_{\beta, \beta}\left(-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}t^{\beta}\right)\ast u(t)\right)\end{eqnarray}$

(3.21)

$\begin{equation}\label{eq3.22} I(t) = I_{0}t^{\beta-1}E_{\beta, \beta}\left(-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}t^{\beta}\right)+\int^{t}_{0}\left(t-s\right)^{\beta-1}E_{\beta, \beta}\left(-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}\left(t-s\right)^{\beta}\right)u(s)ds\end{equation}$

(3.22)

We apply the euclidean norm to both sides of equation (3.22). We get the following relationship

$\begin{equation}\label{eq3.23} \left\|I(t)\right\|\leq\left\|I_{0}t^{\beta-1}E_{\beta, \beta}\left(-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}t^{\beta}\right)\right\|+\left\|u\right\|\int^{t}_{0}\left\|\left(t-s\right)^{\beta-1}E_{\beta, \beta}\left(-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}\left(t-s\right)^{\beta}\right)\right\|ds\end{equation}$

(3.23)

From the assumption $-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}\leq 0$ , there exists a positive constant $M$ such that we have the following inequality.

$\begin{equation}\label{eq3.24} \int^{t}_{0}\left\|\left(t-s\right)^{\beta-1}E_{\beta, \beta}\left(-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}\left(t-s\right)^{\beta}\right)\right\|ds\leq M\end{equation}$

(3.24)

We use Lemma 1 and inequality (3.23), we obtain the following inequality

$\begin{equation}\label{eq3.25} \left\|I(t)\right\|\leq\frac{I_{0}C_{1}}{\left\|t^{1-\beta}\right\|+\frac{\sigma^{1-\alpha}}{\sqrt{LC}}\left\|t\right\|}+\left\|u\right\|M.\end{equation}$

(3.25)

Let the function $\mu\left(I_{0}, t\right) = \frac{I_{0}C_{1}}{\left\|t^{1-\beta}\right\|+\frac{\sigma^{1-\alpha}}{\sqrt{LC}}\left\|t\right\|}$ . We observe the function $\mu$ is a class $\mathcal{KL}$ function. Let the function $\gamma\left(\left\|u\right\|\right) = \left\|u\right\|M$ , it is straightforward to verify the function $\gamma$ is a class $\mathcal{K}_{ \infty}$ function. Finally, equation (3.25) is represented as follows

$\begin{equation}\label{eq3.26} \left\|I(t)\right\|\leq\mu\left(I_{0}, t\right)+\gamma\left(\left\|u\right\|\right)\end{equation}$

(3.26)

It follows from equation (3.26) the electrical LC circuit described by the Riemann-Liouville fractional derivative is fractional input stable.

Let the exogenous input $\left\|u\right\| = 0$ . From the fact $\gamma\left(0\right) = 0$ , equation (3.26) becomes

$\begin{equation}\label{eq3.27} \left\|I(t)\right\|\leq\mu\left(I_{0}, t\right).\end{equation}$

(3.27)

Thus the equilibrium point $I = 0$ of the electrical LC circuit defined by

$\begin{equation}\label{eq3.28} D^{2\alpha}_{RL}I(t)+\frac{\sigma^{1-\alpha}}{\sqrt{LC}}I(t) = 0\end{equation}$

(3.28)

is globally asymptotically stable. As in the previous sections, the fractional input stability of equation (3.20) implies the global asymptotic stability of the unforced electrical LC circuit equation (3.28). We observe when the exogenous input of equation (3.20) converges, it follows from equation (3.26), the analytical solution of the electrical LC circuit equation (3.20) converges as well. It follows from equation (3.26), the analytical solution of the electrical LC circuit equation (3.20) is bounded as well when its exogenous input of equation is bounded.

3.4. Fractional input stability of the electrical LC circuit described by the Caputo fractional derivative

We consider the Caputo fractional derivative in this section. We investigate the fractional input stability of the electrical LC circuit equation defined by the following fractional differential equation

$\begin{equation}\label{eq3.29} D^{2\alpha}_{c}I(t)+\frac{\sigma^{1-\alpha}}{\sqrt{LC}}I(t) = u(t)\end{equation}$

(3.29)

with the initial boundary condition defined by $I(0) = I_{0}$ and $\alpha\leq1/2$ . The exogenous input is $u(t)$ .

Theorem 4. The electrical LC circuit equation defined by equation (3.29) described by the Caputo fractional derivative is fractional input stable.

Proof: Let $\beta = 2\alpha$ . We determine the analytical solution of the fractional differential equation defined by (3.29). We apply the Laplace transform to both sides of equation (3.29). We obtain the following relationships

$\begin{eqnarray}\label{eq3.30} s^{\beta}\mathcal{L}(I(t))-s^{\beta-1}I(0)+\frac{\sigma^{1-\alpha}}{\sqrt{LC}}\mathcal{L}(I(t))& = &\mathcal{L}(u(t))\nonumber\\ s^{\beta}\mathcal{L}(I(t))-s^{\beta-1}I_{0}+\frac{\sigma^{1-\alpha}}{\sqrt{LC}}\mathcal{L}(I(t))& = &\mathcal{L}(u(t))\nonumber\\ \mathcal{L}(I(t))\left\{s^{\beta}+\frac{\sigma^{1-\alpha}}{\sqrt{LC}}\right\}& = &s^{\beta-1}I_{0}+\mathcal{L}(u(t))\nonumber\\ \mathcal{L}(I(t))& = &\frac{s^{\beta-1}I_{0}}{s^{\beta}+\frac{\sigma^{1-\alpha}}{\sqrt{LC}}}+\frac{\mathcal{L}(u(t))}{s^{\beta}+\frac{\sigma^{1-\alpha}}{\sqrt{LC}}}\nonumber\\ \mathcal{L}(I(t)) = I_{0}\mathcal{L}\left(E_{\beta}\left(-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}t^{\beta}\right)\right)&+&\mathcal{L}\left(t^{\beta-1}E_{\beta, \beta}\left(-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}t^{\beta}\right)\right)\mathcal{L}\left(u(t)\right)\nonumber\\ \mathcal{L}(I(t)) = I_{0}\mathcal{L}\left(E_{\beta}\left(-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}t^{\beta}\right)\right)&+&\mathcal{L}\left(t^{\beta-1}E_{\beta, \beta}\left(-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}t^{\beta}\right)\ast u(t)\right)\end{eqnarray}$

(3.30)

where $\mathcal{L}$ represents the usual Laplace transformation and " $\ast$ " represents the usual convolution product. We apply the inverse of Laplace transform to both sides of equation (3.30). We obtain the following analytical solution

$\begin{equation}\label{eq3.31} I(t) = I_{0}E_{\beta}\left(-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}t^{\beta}\right)+\int^{t}_{0}\left(t-s\right)^{\beta-1}E_{\beta, \beta}\left(-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}\left(t-s\right)^{\beta}\right)u(s)ds\end{equation}$

(3.31)

We apply the euclidean norm to both sides of equation (3.31). We obtain the following inequality

$\begin{equation}\label{eq3.32} \left\|I(t)\right\|\leq\left\|I_{0}E_{\beta}\left(-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}t^{\beta}\right)\right\|+\left\|u\right\|\int^{t}_{0}\left\|\left(t-s\right)^{\beta-1}E_{\beta, \beta}\left(-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}\left(t-s\right)^{\beta}\right)\right\|ds\end{equation}$

(3.32)

From the assumption $-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}\leq 0$ , there exists a positive constant $M$ such that the following inequality is held

$\begin{equation}\label{eq3.33} \int^{t}_{0}\left\|\left(t-s\right)^{\beta-1}E_{\beta, \beta}\left(-\frac{\sigma^{1-\alpha}}{\sqrt{LC}}\left(t-s\right)^{\beta}\right)\right\|ds\leq M\end{equation}$

(3.33)

We use Lemma 1 and equation (3.33), we obtain the following inequality

$\begin{equation}\label{eq3.34} \left\|I(t)\right\|\leq\frac{I_{0}C_{1}}{1+\frac{\sigma^{1-\alpha}}{\sqrt{LC}}\left\|t^{\beta}\right\|}+\left\|u\right\|M\end{equation}$

(3.34)

Let the function $\mu\left(I_{0}, t\right) = \frac{I_{0}C_{1}}{1+\frac{\sigma^{1-\alpha}}{\sqrt{LC}}\left\|t^{\beta}\right\|}$ . We observe the function $\mu\left(., t\right)$ is a class $\mathcal{K}$ function. Furthermore, $\mu\left(s, .\right)$ decays in time and converges to zero when $t$ tends to infinity. Thus $\mu\left(s, .\right)$ is a class $\mathcal{L}$ function. In conclusion the function $\mu$ is a class $\mathcal{KL}$ function. Let the function $\gamma\left(\left\|u\right\|\right) = \left\|u\right\|M$ , it is straightforward to see $\gamma$ is a class $\mathcal{K}_{ \infty}$ function. Finally equation (3.34) is represented as follows

$\begin{equation}\label{eq3.35} \left\|I(t)\right\|\leq\mu\left(I_{0}, t\right)+\gamma\left(\left\|u\right\|\right)\end{equation}$

(3.35)

It follows from equation (3.35) the electrical LC circuit equation (3.29) described by the Caputo fractional derivative is fractional input stable.

Let's analyze the BIBS, the CICS properties and the global asymptotic stability of the unforced electrical LC circuit equation. Let the exogenous input $\left\|u\right\| = 0$ . From the fact $\gamma$ is a class $\mathcal{K}_{ \infty}$ function, we have $\gamma\left(0\right) = 0$ . Then the equation (3.35) becomes

$\begin{equation} \left\|I(t)\right\|\leq\mu\left(I_{0}, t\right) \end{equation}$

(3.36)

That is the trivial solution of the electrical LC circuit equation described by the Caputo fractional derivative defined by

$\begin{equation} D^{2\alpha}_{c}I(t)+\frac{\sigma^{1-\alpha}}{\sqrt{LC}}I(t) = 0 \end{equation}$

(3.37)

is globally asymptotically stable. That is to say the fractional input stability implies the global asymptotic stability of the unforced electrical RL circuit described by the Caputo fractional derivative. From equation (3.35), when the exogenous input of equation (3.29) converges then the analytical solution of the electrical LC circuit equation (3.29) converges as well. We notice from equation (3.35), when the exogenous input of equation (3.29) is bounded, then the analytical solution of the electrical LC circuit equation (3.29) described by the Caputo fractional derivative is bounded as well.

3.5. Fractional input stability of the electrical RC circuit equation described by the Riemann-Liouville fractional derivative

In this section, we investigate the fractional input stability of the electrical RC circuit equation described by the Riemann-Liouville fractional derivative. Let the electrical RC circuit equation defined by the following fractional differential equation

$\begin{equation}\label{eq3.38} D^{\alpha}_{RL}V(t)+\frac{\sigma^{1-\alpha}}{RC}V(t) = u(t)\end{equation}$

(3.38)

with the initial boundary condition defined by $\left(I^{1-\alpha}V\right)(0) = V_{0}$ . $C$ represents the capacitance and $R$ represents the resistance. $V$ represents the voltage across the capacitor. The parameter $\sigma$ is associated to the temporal components in the system, see more details in ^[5]. The second member, $u(t)$ is considered as the exogenous input. It contains the source term $E(t)$ (eventually depend on time), the function $1/RC$ and the temporal coefficient $\sigma^{1-\alpha}$ . Summarizing $u(t) = \frac{\sigma^{1-\alpha}E(t)}{RC}$ . We make the following theorem.

Theorem 5. The electrical RC circuit defined by equation (3.38) described by the Riemann-Liouville fractional derivative is fractional input stable.

Proof: Applying the Laplace transform to both sides of equation (3.38), we get the following relationships

$\begin{eqnarray}\label{eq3.39} s^{\alpha}\mathcal{L}(V(t))-\left(I^{1-\alpha}V\right)(0)+\frac{\sigma^{1-\alpha}}{RC}\mathcal{L}(V(t))& = &\mathcal{L}(u(t))\nonumber\\ s^{\alpha}\mathcal{L}(V(t))-V_{0}+\frac{\sigma^{1-\alpha}}{RC}\mathcal{L}(V(t))& = &\mathcal{L}(u(t))\nonumber\\ \mathcal{L}(V(t))\left\{s^{\alpha}+\frac{\sigma^{1-\alpha}}{RC}\right\}& = &V_{0}+\mathcal{L}(u(t))\nonumber\\ \mathcal{L}(V(t))& = &\frac{V_{0}}{s^{\alpha}+\frac{\sigma^{1-\alpha}}{RC}}+\frac{\mathcal{L}(u(t))}{s^{\alpha}+\frac{\sigma^{1-\alpha}}{RC}}\nonumber\\ \mathcal{L}(V(t)) = I_{0}\mathcal{L}\left(t^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}}{RC}t^{\alpha}\right)\right)&+&\mathcal{L}\left(t^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}}{RC}t^{\alpha}\right)\right)\mathcal{L}\left(u(t)\right)\nonumber\\ \mathcal{L}(V(t)) = I_{0}\mathcal{L}\left(t^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}}{RC}t^{\alpha}\right)\right)&+&\mathcal{L}\left(t^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}}{RC}t^{\alpha}\right)\ast u(t)\right)\end{eqnarray}$

(3.39)

$\begin{equation}\label{eq3.40} V(t) = V_{0}t^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}}{RC}t^{\alpha}\right)+\int^{t}_{0}\left(t-s\right)^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}}{RC}\left(t-s\right)^{\alpha}\right)u(s)ds\end{equation}$

(3.40)

Applying the euclidean norm on equation (3.40), we have

$\begin{equation}\label{eq3.41} \left\|V(t)\right\|\leq\left\|V_{0}t^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}}{RC}t^{\alpha}\right)\right\|+\left\|u\right\|\int^{t}_{0}\left\|\left(t-s\right)^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}}{RC}\left(t-s\right)^{\alpha}\right)\right\|ds\end{equation}$

(3.41)

From the assumption $-\frac{\sigma^{1-\alpha}}{RC}\leq 0$ , there exists a positive constant $M$ such that we have the following inequality

$\begin{equation}\label{eq3.42} \int^{t}_{0}\left\|\left(t-s\right)^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}}{RC}\left(t-s\right)^{\alpha}\right)\right\|ds\leq M\end{equation}$

(3.42)

We use Lemma 1 and the inequality (3.42), we obtain the following inequality

$\begin{equation}\label{eq3.43} \left\|V(t)\right\|\leq\frac{V_{0}C_{1}}{\left\|t^{1-\alpha}\right\|+\frac{\sigma^{1-\alpha}}{RC}\left\|t\right\|}+\left\|u\right\|M\end{equation}$

(3.43)

Let the function $\beta\left(V_{0}, t\right) = \frac{V_{0}C_{1}}{\left\|t^{1-\alpha}\right\|+\frac{\sigma^{1-\alpha}}{RC}\left\|t\right\|}$ . We observe the function $\beta$ is a class $\mathcal{KL}$ function. Let the function $\gamma\left(\left\|u\right\|\right) = \left\|u\right\|M$ . It is straightforward to see $\gamma$ is a class $\mathcal{K}_{ \infty}$ function. Finally, equation (3.43) is represented as the following form

$\begin{equation}\label{eq3.44} \left\|V(t)\right\|\leq\beta\left(V_{0}, t\right)+\gamma\left(\left\|u\right\|\right)\end{equation}$

(3.44)

It follows from equation (3.44) the electrical RC circuit equation described by the Riemann-Liouville fractional derivative is fractional input stable.

Let the exogenous input $\left\|u\right\| = 0$ , then we have $\gamma\left(0\right) = 0$ . Thus the equation (3.44) becomes

$\begin{equation}\label{eq3.45} \left\|V(t)\right\|\leq\beta\left(I_{0}, t\right)\end{equation}$

(3.45)

Then the equilibrium point $V = 0$ of the electrical RC circuit equation defined by

$\begin{equation}\label{eq3.46} D^{\alpha}_{RL}V(t)+\frac{\sigma^{1-\alpha}}{RC}V(t) = 0\end{equation}$

(3.46)

is (uniformly) globally asymptotically stable. Thus the fractional input stability implies the global asymptotic stability of the unforced electrical RC circuit described by the Riemann-Liouville fractional derivative. We observe from (3.44) when the exogenous input of equation (3.38) converges, we notice the analytical solution of the electrical RC circuit equation (3.38) converges as well. From (3.44), when the exogenous input term of equation (3.38) is bounded, then the analytical solution of the electrical RC circuit equation (3.38) is bounded as well.

3.6. Fractional input stability of the electrical RC circuit equation described by the Caputo fractional derivative

In this section, we investigate the fractional input stability of the electrical RC circuit equation described by the Caputo fractional derivative defined by the following fractional differential equation

$\begin{equation}\label{eq3.47} D^{\alpha}_{c}V(t)+\frac{\sigma^{1-\alpha}}{RC}V(t) = u(t)\end{equation}$

(3.47)

with the initial boundary condition defined by $V(0) = V_{0}$ . The term $u(t)$ represents the exogenous input as defined in the previous section.

Theorem 6. The electrical RC circuit defined by equation (3.47) described by the Caputo fractional derivative is fractional input stable.

Proof: Applying the Laplace transform to both sides of equation (3.47), we obtain the following relationships

$\begin{eqnarray}\label{eq3.48} s^{\alpha}\mathcal{L}(V(t))-s^{\alpha-1}V(0)+\frac{\sigma^{1-\alpha}}{RC}\mathcal{L}(V(t))& = &\mathcal{L}(u(t))\nonumber\\ s^{\alpha}\mathcal{L}(V(t))-s^{\alpha-1}V_{0}+\frac{\sigma^{1-\alpha}}{RC}\mathcal{L}(V(t))& = &\mathcal{L}(u(t))\nonumber\\ \mathcal{L}(V(t))\left\{s^{\alpha}+\frac{\sigma^{1-\alpha}}{RC}\right\}& = &s^{\alpha-1}V_{0}+\mathcal{L}(u(t))\nonumber\\ \mathcal{L}(V(t))& = &\frac{s^{\alpha-1}V_{0}}{s^{\alpha}+\frac{\sigma^{1-\alpha}}{RC}}+\frac{\mathcal{L}(u(t))}{s^{\alpha}+\frac{\sigma^{1-\alpha}}{RC}}\nonumber\\ \mathcal{L}(V(t)) = V_{0}\mathcal{L}\left(E_{\alpha}\left(-\frac{\sigma^{1-\alpha}}{RC}t^{\alpha}\right)\right)&+&\mathcal{L}\left(t^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}}{RC}t^{\alpha}\right)\right)\mathcal{L}\left(u(t)\right)\nonumber\\ \mathcal{L}(V(t)) = V_{0}\mathcal{L}\left(E_{\alpha}\left(-\frac{\sigma^{1-\alpha}}{RC}t^{\alpha}\right)\right)&+&\mathcal{L}\left(t^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}}{RC}t^{\alpha}\right)\ast u(t)\right)\end{eqnarray}$

(3.48)

$\begin{equation}\label{eq3.49} V(t) = V_{0}E_{\alpha}\left(-\frac{\sigma^{1-\alpha}}{RC}t^{\alpha}\right)+\int^{t}_{0}\left(t-s\right)^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}}{RC}\left(t-s\right)^{\alpha}\right)u(s)ds\end{equation}$

(3.49)

From which we have the following inequality

$\begin{equation}\label{eq3.50} \left\|V(t)\right\|\leq\left\|V_{0}E_{\alpha}\left(-\frac{\sigma^{1-\alpha}}{RC}t^{\alpha}\right)\right\|+\left\|u\right\|\int^{t}_{0}\left\|\left(t-s\right)^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}}{RC}\left(t-s\right)^{\alpha}\right)\right\|ds\end{equation}$

(3.50)

From the assumption $-\frac{\sigma^{1-\alpha}}{RC}\leq 0$ , there exists a positive constant $M$ such that the following inequality is held

$\begin{equation}\label{eq3.51} \int^{t}_{0}\left\|\left(t-s\right)^{\alpha-1}E_{\alpha, \alpha}\left(-\frac{\sigma^{1-\alpha}}{RC}\left(t-s\right)^{\alpha}\right)\right\|ds\leq M\end{equation}$

(3.51)

We use Lemma 1 and equation (3.51), we obtain the following relationships

$\begin{equation}\label{eq3.52} \left\|V(t)\right\|\leq\frac{V_{0}C_{1}}{1+\frac{\sigma^{1-\alpha}}{RC}\left\|t^{\alpha}\right\|}+\left\|u\right\|M\end{equation}$

(3.52)

Let the function $\beta\left(V_{0}, t\right) = \frac{V_{0}C_{1}}{1+\frac{\sigma^{1-\alpha}}{RC}\left\|t^{\alpha}\right\|}$ . We observe the function $\beta$ is a class $\mathcal{KL}$ function. Let the function $\gamma\left(\left\|u\right\|\right) = \left\|u\right\|M$ . It is straightforward to see $\gamma$ is a class $\mathcal{K}_{ \infty}$ function. Finally, equation (3.52) is represented as follows

$\begin{equation}\label{eq3.53} \left\|V(t)\right\|\leq\beta\left(V_{0}, t\right)+\gamma\left(\left\|u\right\|\right)\end{equation}$

(3.53)

From equation (3.53) the electrical RC circuit equation (3.47) described by the Caputo fractional derivative is fractional input stable.

Let the exogenous input $\left\|u\right\| = 0$ . From the fact $\gamma$ is a class $\mathcal{K}_{ \infty}$ function, we have $\gamma\left(0\right) = 0$ . Then equation (3.53) becomes

$\begin{equation} \left\|V(t)\right\|\leq\beta\left(V_{0}, t\right) \end{equation}$

(3.54)

We conclude the equilibrium point $V = 0$ of the electrical RC circuit equation described by the Caputo fractional derivative defined by

$\begin{equation} D^{\alpha}_{c}V(t)+\frac{\sigma^{1-\alpha}}{RC}V(t) = 0 \end{equation}$

(3.55)

is globally asymptotically stable. We observe when the input term of equation (3.47) converges; then from equation (3.53), we notice the analytical solution of the electrical RC circuit equation (3.47) described by the Caputo fractional derivative converges as well. We notice when the exogenous input of equation (3.47) is bounded, then the analytical solution of the electrical RC circuit equation (3.47) described by the Caputo fractional derivative is bounded as well.

4. Numerical simulations

In this section, we analyze the CICS and the global asymptotic stability properties obtained with the fractional input stability. Let's the electrical RL circuit equation described by the Caputo fractional derivative defined by

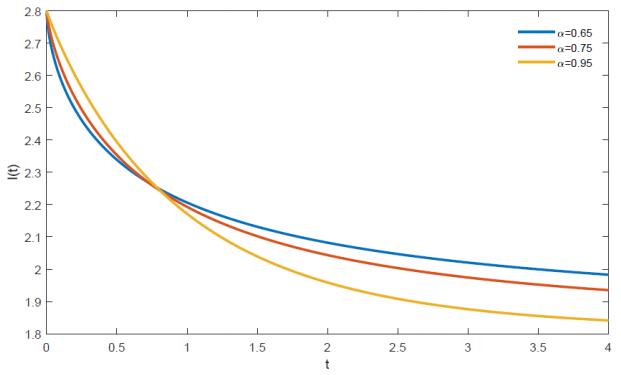
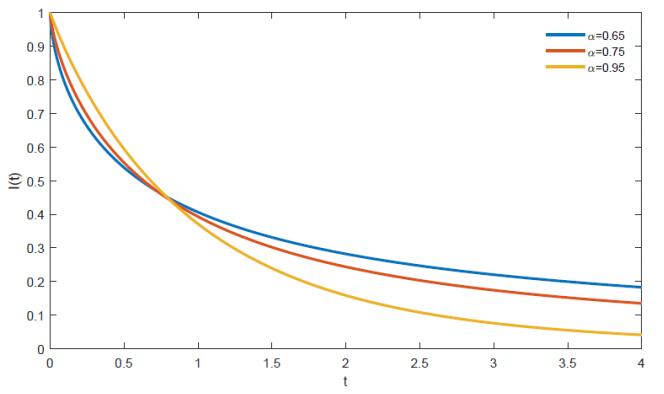
$\begin{equation}\label{eq4.1} D^{\alpha}_{c}I(t)+\frac{\sigma^{1-\alpha}R}{L}I(t) = u(t)\end{equation}$

(4.1)

with numerical values: the resistance $R = 10{}\Omega$ and induction $L = 10H.$ Let's the exogenous input $u(t) = 0$ . The current across the inductor is depicted in Figure 1. We observe all the analytical solutions $I$ decay everywhere except at the equilibrium point itself, thus the equilibrium point $I = 0$ of the electrical RL circuit equation (4.1) is (uniformly) globally asymptotically stable.

Figure 1.

$I = 0$ the electrical RL circuit equation (4.1) is globally asymptotically stable.

DownLoad: Full-Size Img PowerPoint

In Figure 2, we observe the behavior of the current in the inductor when the electrical RL circuit equation is fractional input stable.

Figure 2. Fractional input stability of the electrical RL circuit equation.

DownLoad: Full-Size Img PowerPoint

Let's the electrical RC circuit equation described by the Caputo fractional derivative with numerical values defined by

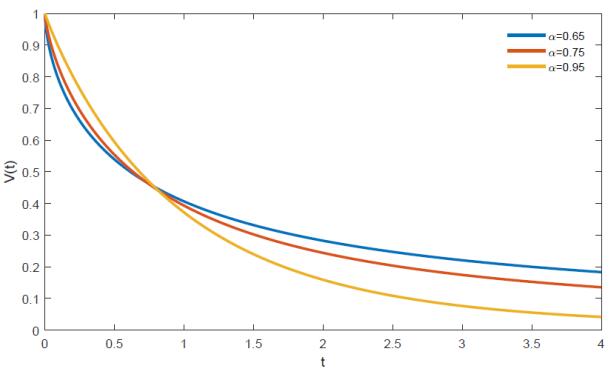
$\begin{equation}\label{eq4.2} D^{\alpha}_{c}V(t)+\frac{\sigma^{1-\alpha}}{RC}V(t) = u(t)\end{equation}$

(4.2)

with the resistance $R = 10k\Omega$ and the capacitance $C = 1000\mu F$ . Let's the exogenous input $u(t) = 0$ , we can, observe all the analytical solutions $V$ decay everywhere except at the equilibrium point itself, thus the equilibrium point $V = 0$ of the electrical RL circuit equation (4.2) is globally asymptotically stable, see figure 3.

Figure 3.

$V = 0$ of the electrical RC circuit equation is globally asymptotically stable.

DownLoad: Full-Size Img PowerPoint

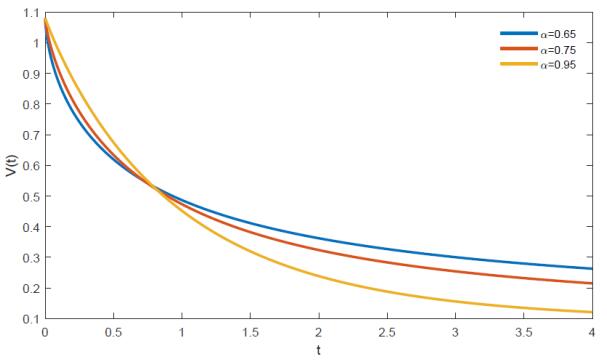
In Figure 4, we observe the behavior of the analytical solution of the electrical RC circuit equation when it is fractional input stability.

Figure 4. Fractional input stability of the electrical RC circuit.

DownLoad: Full-Size Img PowerPoint

5. Conclusion

In this paper, we have discussed the fractional input stability of the electrical circuit equation described by the Riemann-Liouville and the Caputo fractional derivative operators. This paper is the application of the fractional input stability in the electrical circuit equations. And we have noticed the fractional input stability is an excellent compromise to study the behavior of the analytical solution of the electrical RL, RC and LC circuit equations.

Conflict of interest

The author declare that there is no conflict of interest.

References

[1]	Aikman D, Galesic M, Gigerenzer G, et al. (2014) Taking uncertainty seriously: simplicity versus complexity in financial regulation. Ind Corp Change 30: 317–345. https://doi.org/10.1093/icc/dtaa024 doi: 10.1093/icc/dtaa024
[2]	Allan N, Cantle N, Godfrey P (2013) A review of the use of complex systems applied to risk appetite and emerging risks in ERM practice: Recommendations for practical tools to help risk professionals tackle the problem of risk appetite and emerging risks. Brit Actuar J 18: 163–234. https://doi.org/10.1017/S135732171200030X doi: 10.1017/S135732171200030X
[3]	Allen F, Gale D (2000) Financial Contagion. J Polit Econ 108: 1–33. https://doi.org/10.1086/262109 doi: 10.1086/262109
[4]	Althaus CE (2005) A disciplinary perspective on the epistemological status of risk. Risk Anal 25: 567–588. https://doi.org/10.1111/j.1539-6924.2005.00625.x doi: 10.1111/j.1539-6924.2005.00625.x
[5]	Anagnostou I, Sourabh S, Kandhai D (2018) Incorporating Contagion in Portfolio Credit Risk Models using Network Theory. Complexity 2018. https://doi.org/10.1155/2018/6076173 doi: 10.1155/2018/6076173
[6]	Anderson N, Noss J (2013) The Fractal Market Hypothesis and its implications for the stability of financial markets. Available from: https://www.bankofengland.co.uk/-/media/boe/files/financial-stability-paper/2013/the-fractal-market-hypothesis-and-its-implications-for-the-stability-of-financial-markets.pdf?la=en&hash=D096065EA97BE61902BDE5CC022D1E6EA38AAC49.
[7]	Anderson PW (1972) More is different. Science 177: 393–396. https://doi.org/10.1126/science.177.4047.393 doi: 10.1126/science.177.4047.393
[8]	Arthur WB (2021) Foundations of Complexity. Nat Rev Phys 3: 136–145. https://doi.org/10.1038/s42254-020-00273-3 doi: 10.1038/s42254-020-00273-3
[9]	Arthur WB (2013) Complexity Economics: A Different Framework for Economic Thought. Complexity Economics, Oxford University Press. https://doi.org/10.2469/dig.v43.n4.70
[10]	Arthur WB (1999) Complexity and the economy. Science 284: 107–09. https://doi.org/10.1126/science.284.5411.107 doi: 10.1126/science.284.5411.107
[11]	Aven T (2017) A Conceptual Foundation for Assessing and Managing Risk, Surprises and Black Swans. In: Motet, G., Bieder, C., The Illusion of Risk Control, Springer Briefs in Applied Sciences and Technology. Springer, Cham. https://doi.org/10.1007/978-3-319-32939-0_3
[12]	Aven T (2013) On how to deal with deep uncertainties in risk assessment and management context. Risk Anal 33: 2082–2091. https://doi.org/10.1111/risa.12067 doi: 10.1111/risa.12067
[13]	Aven T, Flage R (2015) Emerging risk – Conceptual definition and a relation to black swan type of events. Reliab Eng Syst Safe 144: 61–67. https://doi.org/10.1016/j.ress.2015.07.008 doi: 10.1016/j.ress.2015.07.008
[14]	Aven T, Krohn BS (2014) A new perspective on how to understand, assess and manage risk and the unforeseen. Reliab Eng Syst Safe 121: 1–10. https://doi.org/10.1016/j.ress.2013.07.005 doi: 10.1016/j.ress.2013.07.005
[15]	Babbie ER (2011) The Practice of Social Science Research. South African Ed. Cape Town. Oxford University Press.
[16]	Baranger M (2010) Chaos, Complexity, and Entropy. A Physics Talk for Non-Physicists. Report in New England Complex Systems Institute, Cambridge.
[17]	Barberis N (2017) Behavioural Finance: Asset Prices and Investor Behaviour. Available from: https://www.aeaweb.org/content/file?id=2978.
[18]	Basel Committee on Banking Supervision (2017) Basel Ⅲ: Finalising Post-Crisis Reforms. Available from: https://www.bis.org/bcbs/publ/d424.htm.
[19]	Basel Committee on Banking Supervision (2013) Fundamental Review of the Trading Book: A Revised Market Risk Framework. Available from: https://www.bis.org/publ/bcbs265.pdf.
[20]	Basel Committee on Banking Supervision (2006) Basel Ⅱ International Convergence of Capital Measurement and Capital Standards: A Revised Framework-Comprehensive Version. Available from: https://www.bis.org/publ/bcbs128.pdf.
[21]	Basel Committee on Banking Supervision (1996) Amendment to the Capital Accord to Incorporate Market Risks. Available from: https://www.bis.org/publ/bcbs24.pdf.
[22]	Basel Committee on Banking Supervision (BCBS) (1988) International Convergence of Capital Measurement and Capital Standards. Available from: https://www.bis.org/publ/bcbs107.pdf.
[23]	Battiston S, Caldarelli G, May R, et al. (2016a) The Price of Complexity in Financial Networks. P Natl A Sci 113: 10031–10036. https://doi.org/10.1073/pnas.1521573113. doi: 10.1073/pnas.1521573113
[24]	Battiston S, Farmer JD, Flache A, et al. (2016b) Complexity theory and financial regulation: Economic policy needs interdisciplinary network analysis and behavioural modelling. Science 351: 818–819. https://doi.org/10.1126/science.aad0299 doi: 10.1126/science.aad0299
[25]	Bayes T, Price R (1763) An Essay towards Solving a Problem in the Doctrine of Chances. Philos T R Soc London 53: 370–418. https://doi.org/10.1098/rstl.1763.0053 doi: 10.1098/rstl.1763.0053
[26]	Beck U (1992) Risk society: towards a new modernity. Sage London.
[27]	Beissner P, Riedel F (2016) Knight-Walras Equilibria. Centre for Mathematical Economics Working Paper 558.
[28]	Bharathy GK, McShane MK (2014) Applying a Systems Model to Enterprise Risk Management. Eng Manag J 26: 38–46. https://doi.org/10.1080/10429247.2014.11432027 doi: 10.1080/10429247.2014.11432027
[29]	Black F, Scholes M (1973) The Pricing of Options and Corporate Liabilities. J Polit Econ 29: 449–470.
[30]	Blume L, Durlauf (2006) The Economy as an Evolving Complex System Ⅲ: current perspectives and future directios. https://doi.org/10.1093/acprof:oso/9780195162592.001.0001
[31]	Bolton P, Despres M, Pereira da Silva L, et al. (2020) The green swan: central banking and financial stability in the age of climate change. Available from: https://www.bis.org/publ/othp31.pdf.
[32]	Bonabeau E (2002) Agent-Based Modeling: Methods and Techniques for Simulating Human Systems. Natl Acad Sci 99: 7280–7287. https://doi.org/10.1073/pnas.082080899 doi: 10.1073/pnas.082080899
[33]	Brace I (2008) Questionnaire Design: How to Plan, Structure, and Write Survey Material for Effective Market Research, 2 Eds., London: Kogan Page. https://doi.org/10.5860/choice.42-3520
[34]	Bronk R (2011) Uncertainty, modeling monocultures and the financial crisis. Bus Econ 42: 5–18.
[35]	Bruno B, Faggini M, Parziale A (2016) Complexity Modeling in Economics: the state of the Art. Econ Thought 5: 29–43.
[36]	Burzoni M, Riedel F, Soner MH (2021) Viability and arbitrage under Knightian uncertainty. Econometrica 89: 1207–1234. https://doi.org/10.3982/ECTA16535 doi: 10.3982/ECTA16535
[37]	Chan-Lau JA (2017) An Agent Based Model of the Banking System. IMF Working Paper. https://doi.org/10.5089/9781484300688.001
[38]	Chaudhuri A, Ghosh SK (2016) Quantitative Modeling of Operational Risk in Finance and Banking Using Possibility Theory, Springer International Publishing Switzerland. https://doi.org/10.1007/978-3-319-26039-6
[39]	Collis J, Hussey R (2009) Business Research: a practical guide for undergraduate and postgraduate students, 3^rd ed., New York: Palgrave Macmillan.
[40]	Corrigan J, Luraschi P, Cantle N (2013) Operational Risk Modeling Framework. Milliman Research Report. Available from: https://web.actuaries.ie/sites/default/files/erm-resources/operational_risk_modelling_framework.pdf.
[41]	De Bondt W, Thaler R (1985) Does the stock market overact? J Financ 40: 793–808. https://doi.org/10.2307/2327804 doi: 10.2307/2327804
[42]	Diebold FX, Doherty NA, Herring RJ (2010) The Known, Unknown, and the Unknowable. Princeton, NJ: Princeton University Press.
[43]	Dorigo M (2007) Editorial. Swarm Intell 1: 1–2. https://doi.org/10.1007/s11721-007-0003-z doi: 10.1007/s11721-007-0003-z
[44]	Dorigo M, Maniezzo V, Colorni A (1996) Ant system: optimisation by a colony cooperating agents. IEEE T Syst Man Cy B 26: 29–41. https://doi.org/10.1109/3477.484436 doi: 10.1109/3477.484436
[45]	Dowd K (1996) The case for financial Laissez-faire. Econ J 106: 679–687. https://doi.org/10.2307/2235576 doi: 10.2307/2235576
[46]	Dowd K, Hutchinson M (2014) How should financial markets be regulated? Cato J 34: 353–388.
[47]	Dowd K, Hutchinson M, Ashby S, et al. (2011) Capital Inadequacies the Dismal Failure of the Basel Regime of Bank Capital Regulation. Banking & Insurance Journal.
[48]	Easterby-Smith M, Thorpe R, Jackson PR (2015) Management and Business Research, 5 Eds., London: Sage.
[49]	Ellinas C, Allan N, Combe C (2018) Evaluating the role of risk networks on risk identification, classification, and emergence. J Network Theory Financ 3: 1–24. https://doi.org/10.21314/JNTF.2017.032 doi: 10.21314/JNTF.2017.032
[50]	Ellsberg D (1961) Risk, ambiguity, and the savage axioms. Q J Econ 75: 643–669. https://doi.org/10.2307/1884324 doi: 10.2307/1884324
[51]	Evans JR, Allan N, Cantle N (2017) A New Insight into the World Economic Forum Global Risks. Econ Pap 36. https://doi.org/10.1111/1759-3441.12172 doi: 10.1111/1759-3441.12172
[52]	Fadina T, Schmidt T (2019) Default Ambiguity. Risks 7: 64. https://doi.org/10.3390/risks7020064 doi: 10.3390/risks7020064
[53]	Fama EF (1970) Efficient Capital Markets: A review of Theory and Empirical Work. J Financ 25: 383–417. https://doi.org/10.2307/2325486 doi: 10.2307/2325486
[54]	Farmer JD (2012) Economics needs to treat the economy as a complex system. Institute for New Economic Thinking at Oxford Martin School. Working Paper.
[55]	Farmer D (2002) Market force, ecology, and evolution. Ind Corp Change 11: 895–953. https://doi.org/10.1093/icc/11.5.895 doi: 10.1093/icc/11.5.895
[56]	Farmer D, Lo A (1999) Fronties of finance: Evolution and efficient markets. Pro Nat Acad Sci 96: 9991–9992. https://doi.org/10.1073/pnas.96.18.99 doi: 10.1073/pnas.96.18.99
[57]	Farmer JD, Gallegati C, Hommes C, et al. (2012) A complex systems approach to constructing better models for financial markets and the economy. Eur Phys J-Spec Top 214: 295–324. https://link.springer.com/article/10.1140/epjst/e2012-01696-9
[58]	Farmer JD, Foley D (2009) The economy needs agent-based modeling. Nature 460: 685–686. https://www.nature.com/articles/460685a
[59]	Fellegi IP (2010) Survey Methods and Practices, Available from: https://unstats.un.org/wiki/download/attachments/101354131/12-587-x2003001-eng.pdf?api=v2.
[60]	Field A (2009) Discovering Statistics Using SPSS, 3 eds., London: Sage.
[61]	Fink A (2009) How to Conduct Surveys, 4 eds., Thousand Oaks, CA: Sage.
[62]	Fink A (1995) How to Measure Survey Reliability and Validity, Thousand Oaks, CA: Sage.
[63]	Forrester JW (1969) Urban Dynamics. Cambridge Mass M.I.T Press.
[64]	Ganegoda A, Evans J (2014) A framework to manage the measurable, immeasurable and the unidentifiable financial risk. Aust J Manage 39: 5–34. https://doi.org/10.1177/0312896212461033 doi: 10.1177/0312896212461033
[65]	Gao Q, Fan H, Shen J (2018) The Stability of Banking System Based on Network Structure: An Overview. J Math Financ 8: 517–526. 10.4236/jmf.2018.83032 doi: 10.4236/jmf.2018.83032
[66]	Gebizlioglu OL, Dhaene J (2009) Risk Measures and Solvency-Special Issue. J Comput Appl Math 233: 1–2. https://doi.org/10.1016/j.cam.2009.07.030 doi: 10.1016/j.cam.2009.07.030
[67]	Gigerenzer G (2007) Gut feelings: The Intelligence of the unconscious. New York: Viking Press.
[68]	Gigerenzer G, Hertwig R, Pachur T (Eds) (2011) Heuristics: The foundations of adaptive behaviour, New York: Oxford University Press.
[69]	Glasserman P, Young HP (2015) How likely is contagion in financial networks? J Bank Financ 50: 383–399. https://doi.org/10.1016/j.jbankfin.2014.02.006 doi: 10.1016/j.jbankfin.2014.02.006
[70]	Gros S (2011) Complex systems and risk management. IEEE Eng Manag Rev 39: 61–72.
[71]	Hair J, Black W, Babin B, et al (2014) Multivariate Data Analysis, 7 eds., Pearson Prentice Hall, Auflage.
[72]	Haldane AG (2017) Rethinking Financial Stability. Available from: https://www.bis.org/review/r171013f.pdf.
[73]	Haldane AG (2016) The dappled world. Available from: https://www.bankofengland.co.uk/-/media/boe/files/speech/2016/the-dappled-world.pdf.
[74]	Haldane AG (2012) The Dog and the Frisbee. Available from: https://www.bis.org/review/r120905a.pdf.
[75]	Haldane AG (2009) Rethinking the financial network. Available from: https://www.bis.org/review/r090505e.pdf.
[76]	Haldane AG, May RM (2011) Systemic risk in banking ecosystems. Available from: https://www.nature.com/articles/nature09659.
[77]	Hayek FA (1964) The theory of complex phenomena. The critical approach to science and philosophy, 332–349. https://doi.org/10.4324/9781351313087-22
[78]	Helbing D (2013) Globally network risks and how to respond. Nature 497: 51–59. https://doi.org/10.1038/nature12047 doi: 10.1038/nature12047
[79]	Holland JH (2002) Complex adaptive systems and spontaneous emergence. In Curzio, A.Q., Fortis, M., Complexity and Industrial Clusters: Dynamics and Models in Theory and Practice, New York: Physica-Verlag, 25–34. https://doi.org/10.1007/978-3-642-50007-7_3
[80]	Hommes C (2011) The heterogeneous expectations hypothesis: Some evidence from the lab. J Econ Dyn Control 35: 1–24. https://doi.org/10.1016/j.jedc.2010.10.003 doi: 10.1016/j.jedc.2010.10.003
[81]	Hommes C (2001) Financial markets as nonlinear adaptive evolutionary systems. Quant Financ 1: 149–167. https://doi.org/10.1080/713665542 doi: 10.1080/713665542
[82]	Hull J (2018) Risk Management and Financial Institutions, 5 eds., John Wiley.
[83]	Ingram D, Thompson M (2011) Changing seasons of risk attitudes. Actuary 8: 20–24.
[84]	Joshi D (2014) Fractals, liquidity, and a trading model. European Investment Strategy, BCA Research.
[85]	Karp A, van Vuuren G (2019) Investment's implications of the Fractal Market Hypothesis. Ann Financ Econ 14: 1–27. https://doi.org/10.1142/S2010495219500015 doi: 10.1142/S2010495219500015
[86]	Katsikopoulos KV (2011) Psychological Heuristics for Making Inferences: Definition, Performance, and the Emerging Theory and Practice. Decis Anal 8: 10–29. https://doi.org/10.1287/deca.1100.0191 doi: 10.1287/deca.1100.0191
[87]	Keynes JM (1921) A Treatise on Probability, London: Macmillan.
[88]	Kimberlin CL, Winterstein AG (2008) Validity and Reliability of Measurement Instruments in Research. Am J Health Syst Pharma 65: 2276–2284. https://doi.org/10.2146/ajhp070364. doi: 10.2146/ajhp070364
[89]	Kirman A (2006) Heterogeneity in economics. J Econ Interact Co-ordination 1: 89–117. https://doi.org/10.1007/s11403-006-0005-8 doi: 10.1007/s11403-006-0005-8
[90]	Kirman A (2017) The Economy as a Complex System. In: Aruka, Y., Kirman, A., Economic Foundations for Social Complexity Science. Evolutionary Economics and Social Complexity Science, Singapore. https://doi.org/10.1007/978-981-10-5705-2_1
[91]	Klioutchnikova I, Sigovaa M, Beizerova N (2017) Chaos Theory in Finance. Procedia Comput Sci 119: 368–375. https://doi.org/10.1016/j.procs.2017.11.196 doi: 10.1016/j.procs.2017.11.196
[92]	Knight FH (1921) Risk, Uncertainty and Profit, Boston and New York: Houghton Mifflin Company.
[93]	Krejcie RV, Morgan DW (1970) Determining the sample size for research activities. Educ Psychol Meas 30: 607–610.
[94]	Kremer E (2012) Modeling and Simulation of Electrical Energy Systems though a Complex Systems Approach using Agent Based Models, Kit Scientific Publishing.
[95]	Kurtz CF, Snowden DJ (2003) The new dynamics of strategy: Sense-making in a complex and complicated world. IBM Syst J 42: 462–483. https://doi.org/10.1147/sj.423.0462 doi: 10.1147/sj.423.0462
[96]	Li Y (2017) A non-linear analysis of operational risk and operational risk management in banking industry, PhD Thesis, School of Accounting, Economics and Finance, University of Wollongong. Australia.
[97]	Li Y, Allan N, Evans J (2018) An analysis of the feasibility of an extreme operational risk pool for banks. Ann Actuar Sci 13: 295–307. https://doi.org/10.1017/S1748499518000222 doi: 10.1017/S1748499518000222
[98]	Li Y, Allan N, Evans J (2017) An analysis of operational risk events in US and European banks 2008–2014. Ann Actuar Sci 11: 315–342. https://doi.org/10.1017/S1748499517000021 doi: 10.1017/S1748499517000021
[99]	Li Y, Allan N, Evans J (2017) A nonlinear analysis of operational risk events in Australian banks. J Oper Risk 12: 1–22. https://doi.org/10.21314/JOP.2017.185 doi: 10.21314/JOP.2017.185
[100]	Li Y, Evans J (2019) Analysis of financial events under an assumption of complexity. Ann Actuar Sci 13: 360–377. https://doi.org/10.1017/S1748499518000337 doi: 10.1017/S1748499518000337
[101]	Li Y, Shi L, Allan N, et al. (2019) An Analysis of power law distributions and tipping points during the global financial crisis. Ann Actuar Sci 13: 80–91. https://doi.org/10.1017/S1748499518000088 doi: 10.1017/S1748499518000088
[102]	Liu G, Song G (2012) EMH and FMH: Origin, evolution, and tendency. 2012 Fifth International Workshop on Chaos-fractals Theories and Applications. https://doi.org/10.1109/IWCFTA.2012.71
[103]	Lo A (2004) The adaptive markets hypothesis: Market efficiency from an evolutionary perspective. J Portfolio Manage 30: 15–29. https://doi.org/10.3905/jpm.2004.442611 doi: 10.3905/jpm.2004.442611
[104]	Lo A (2012) Adaptive markets and the new world order. Financ Anal J 68: 18–29. https://doi.org/10.2469/faj.v68.n2.6 doi: 10.2469/faj.v68.n2.6
[105]	Macal CM, North MJ, Samuelson MJ (2013) Agent-Based Simulation. In: Gass, S.I., Fu M.C., Encyclopaedia of Operations Research and Management Science, Springer, Boston MA.
[106]	Mandelbrot B (1963) The Variation of Certain Speculative Prices. J Bus 36: 394–419. http://www.jstor.org/stable/2350970
[107]	Mandelbrot B, Hudson RL (2004) The (Mis) behaviour of Markets: A Fractal View of Risk, Ruin, and Reward, Basic Books: Cambridge.
[108]	Mandelbrot B, Taleb N (2007) Mild vs. wild randomness: Focusing on risks that matter. In: Diebold, F.X., Doherty, N.A., Herring, R.J., The Known, the Unknown, and the Unknowable in Financial Risk Management: Measurement and Theory Advancing Practice, Princeton, NJ: Princeton University Press, 47–58.
[109]	Markowitz HM (1952) Portfolio Selection. J Financ 7: 77–91. https://doi.org/10.1111/j.1540-6261.1952.tb01525.x doi: 10.1111/j.1540-6261.1952.tb01525.x
[110]	Martens D, Van Gestel T, De Backer M, et al. (2010) Credit rating prediction using Ant Colony Optimisation. J Oper Res Soc 61: 561–573.
[111]	Mazri C (2017) (Re)Defining Emerging Risk. Risk Anal 37: 2053–2065. https://doi.org/10.1111/risa.12759 doi: 10.1111/risa.12759
[112]	McNeil AJ, Frey R, Embrechts P (2015) Quantitative Risk Management (2^nd ed): Concepts, Techniques and Tools, Princeton University Press. Princeton.
[113]	Merton RC (1974) On the pricing of corporate debt: the risk structure of interest rate. J Financ 29: 637–654. https://doi.org/10.1111/j.1540-6261.1974.tb03058.x doi: 10.1111/j.1540-6261.1974.tb03058.x
[114]	Mikes A (2005) Enterprise Risk Management in Action. Available from: https://etheses.lse.ac.uk/2924/.
[115]	Mitchell M (2006) Complex systems: Network thinking. Artif Intell 170: 1194–1212. https://doi.org/10.1016/j.artint.2006.10.002 doi: 10.1016/j.artint.2006.10.002
[116]	Mitchell M (2009) Complexity: A Guided Tour. Oxford University Press.
[117]	Mitleton-Kelly E (2003) Complex systems and evolutionary perspectives on organisations: the application of complexity theory to organisations. Oxford: Pergamon.
[118]	Mohajan H (2017) Two Criteria for Good Measurements in Research: Validity and Reliability. Annals of Spiru Haret University 17: 58–82.
[119]	Mohajan HK (2018) Qualitative Research Methodology in Social Sciences and Related Subjects. J Econ Dev Environ Peopl 7: 23–48.
[120]	Morin E (2014) Complex Thinking for a Complex World-About Reductionism, Disjunction and Systemism. Systema 2: 14–22.
[121]	Morin E (1992) From the concept of system to the paradigm of complexity. J Soc Evol Sys 15: 371–385. https://doi.org/10.1016/1061-7361(92)90024-8 doi: 10.1016/1061-7361(92)90024-8
[122]	Motet G, Bieder C (2017) The Illusion of Risk Control, Springer Briefs in Applied Sciences and Technology. Springer, Cham.
[123]	Mousavi S, Gigerenzer G (2014) Risk, Uncertainty and Heuristics. J Bus Res 67: 1671–1678. https://doi.org/10.1016/j.jbusres.2014.02.013 doi: 10.1016/j.jbusres.2014.02.013
[124]	Muth JF (1961) Rational Expectations and the Theory of Price Movements. Econometrica 29: 315–35.
[125]	Newman MJ (2011) Complex systems: A survey. Am J Phy 79: 800–810. https://doi.org/10.1119/1.3590372 doi: 10.1119/1.3590372
[126]	Pagel M, Atkinson Q, Meade A (2007) Frequency of word-use predicts rates of lexical evolution throughout Indo-European history. Nature 449: 717–720.
[127]	Pallant J (2010) SPSS Survival Manual: A Step-by-Step Guide to Data Analysis using SPSS for Windows, Maidenhead: Open University Press.
[128]	Peters E (1991) Fractal Market Analysis: Applying Chaos Theory to Investment and Economics. London: Wiley Finance. John Wiley Science.
[129]	Peters E (1994) Fractal Market Analysis: Applying Chaos Theory to Investment and Economics. New York: John Wiley & Sons.
[130]	Pichler A (2017) A quantitative comparison of risk measures. Ann Oper Res 254: 1–2. https://doi.org/10.1007/s10479-017-2397-3 doi: 10.1007/s10479-017-2397-3
[131]	Plosser M, Santos J (2018) The Cost of Bank Regulatory Capital. Mimeo, Federal Reserve Bank of New York. Staff Report Number 853.
[132]	Ponto J 2015) Understanding and Evaluatin Survey Research. J Adv Pract Oncol 6: 66–171. https://doi.org/10.6004/jadpro.2015.6.2.9 doi: 10.6004/jadpro.2015.6.2.9
[133]	Quinlan C (2011) Business Research Methods. South Westen Cengage Learning.
[134]	Ramsey FP (1926) Truth and Probability. In Ramsey 1931, The Foundations of Mathematics and Other Logical Essays, Chapter Ⅶ, 156–198, edited by R.B. Braithwaite, London: Kegan, Paul, Trench, Trubner and Co., New York: Harcourt, Brace and Company.
[135]	Righi BM, Muller FM, da Silveira VG, et al. (2019) The effect of organisational studies on financial risk measures estimation. Rev Bus Manage 21: 103–117. https://doi.org/10.7819/rbgn.v0i0.3953 doi: 10.7819/rbgn.v0i0.3953
[136]	Ross SA (1976) The arbitrage theory of capital asset pricing. J Econ Theory 13: 341–360. https://doi.org/10.1016/0022-0531(76)90046-6 doi: 10.1016/0022-0531(76)90046-6
[137]	Saunders M, Lewis P, Thornhill A (2019) Research Methods for Business Students, New York Pearson Publishers.
[138]	Saunders M, Lewis P, Thornhill A (2012) Research Methods, Pearson Publishers.
[139]	Savage LJ (1954) The Foundations of Statistics. New York: John Wiley and Sons.
[140]	Sekaran U (2003) Research Methods for Business (4^th ed.), Hoboken, NJ: John Wiley &Sons. Shane, S. and Cable.
[141]	Senge P (1990) The Fifth Discipline- The Art and Practice of the Learning Organisation. New York, Currency Doubleday.
[142]	Shackle GLS (1949) Expectations in Economics. Cambridge: Cambridge University Press.
[143]	Shackle GLS (1949) Probability and uncertainty. Metroeconomica 1: 161–173. https://doi.org/10.1111/j.1467-999X.1949.tb00040.x doi: 10.1111/j.1467-999X.1949.tb00040.x
[144]	Sharpe WF (1964) Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk. J Financ 19: 425–442. https://doi.org/10.1111/j.1540-6261.1964.tb02865.x doi: 10.1111/j.1540-6261.1964.tb02865.x
[145]	Shefrin H (2010) Behaviouralising Finance. Found Trends Financ 4: 1–184. http://dx.doi.org/10.1561/0500000030 doi: 10.1561/0500000030
[146]	Shefrin H, Statman M (1985) The disposition to sell winners to early and ride loses too long: Theory and evidence. J Financ 40: 777–790. https://doi.org/10.2307/2327802 doi: 10.2307/2327802
[147]	Snowden D, Boone M (2007) A leader's framework for decision making. Harvard Bus Rev 85: 68–76.
[148]	Soramaki K, Cook S (2018) Network Theory and Financial Risk, Riskbooks.
[149]	Sornette D (2003) Why Stock Markets Crash: Critical Events in Complex Financial Systems, Princeton University Press.
[150]	Sornette D, Ouillon G (2012) Dragon-kings: mechanisms, statistical methods, and empirical evidence. Eur Phys J Spec Topics 205: 1–26. https://doi.org/10.1140/epjst/e2012-01559-5 doi: 10.1140/epjst/e2012-01559-5
[151]	Sweeting P (2011) Financial Enterprise Risk Management. Cambridge University Press.
[152]	Tepetepe G, Simenti-Phiri E, Morton D (2021) Survey on Complexity Science Adoption in Emerging Risks Management of Zimbabwean Banks. J Global Bus Technol 17: 41–60
[153]	Thaler RH (2015) Misbehaving: The Making of Behavioural Economics. New York: W. W. Norton and Company.
[154]	Thompson M (2018) How banks and other financial institutions. Brit Actuar J 23: 1–16.
[155]	Tukey JW (1977) Exploratory Data Analysis, MA: Addison-Wesley.
[156]	Turner RJ, Baker MR (2019) Complexity Theory: An Overview with Potential Applications for the Social Sciences. Sys Rev 7: 1–22. https://doi.org/10.3390/systems7010004 doi: 10.3390/systems7010004
[157]	Virigineni M, Rao MB (2017) Contemporary Developments in Behavioural Finance. Int J Econ Financ Issues 7: 448–459.
[158]	Yamane T (1967) Statistics: An Introductory Analysis (2^nd ed), New York: Harper and Row.
[159]	Zadeh LA (1965) Fuzzy sets. Inf Control 8: 335–338. http://dx.doi.org/10.1016/S0019-9958(65)90241-X doi: 10.1016/S0019-9958(65)90241-X
[160]	Zadeh LA (1978) Fuzzy sets as basis for a theory of possibility. Fuzzy Set Syst 1: 3–28. https://doi.org/10.1016/0165-0114(78)90029-5 doi: 10.1016/0165-0114(78)90029-5
[161]	Zikmund W (2003) Business Research Methods, 7^th Ed, Mason, OH. and Great Britain, Thomson/South-Western.
[162]	Zimbabwe (2011) Technical Guidance on the Implementation of the Revised Adequacy Framework in Zimbabwe. Reserve Bank of Zimbabwe.
[163]	Zimmerman B (1999) Complexity science: A route through hard times and uncertainty. Health Forum J 42: 42–46.

This article has been cited by:

1.	Bin Chen, Sergey A. Timoshin, Optimal control of a population dynamics model with hysteresis, 2022, 42, 0252-9602, 283, 10.1007/s10473-022-0116-x
2.	Kota Kumazaki, Toyohiko Aiki, Naoki Sato, Yusuke Murase, Multiscale model for moisture transport with adsorption phenomenon in concrete materials, 2018, 97, 0003-6811, 41, 10.1080/00036811.2017.1325473
3.	Toyohiko Aiki, Sergey A. Timoshin, Existence and uniqueness for a concrete carbonation process with hysteresis, 2017, 449, 0022247X, 1502, 10.1016/j.jmaa.2016.12.086
4.	Sergey A. Timoshin, Bang–Bang Control of a Prey–Predator Model with a Stable Food Stock and Hysteresis, 2023, 88, 0095-4616, 10.1007/s00245-023-09984-2

Reader Comments

Your name:*

Email:*
© 2022 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

Quantitative Finance and Economics

2.5 2.0

Metrics

Article views(3340) PDF downloads(114) Cited by(1)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(2) / Tables(4)

Quantitative Finance and Economics

A survey comparative analysis of cartesian and complexity science frameworks adoption in financial risk management of Zimbabwean banks

Related Papers:

Abstract

1. Introduction

2. Preliminary definitions

3. Fractional input stability of the electrical circuits equations described by certain fractional derivative operators

3.1. Fractional input stability of the electrical RL circuit equation described by the Riemann-Liouville fractional derivative

3.2. Fractional input stability of the electrical RL circuit described by the Caputo fractional derivative

3.3. Fractional input stability of the electrical LC circuit described by the Riemann-Liouville fractional derivative

3.4. Fractional input stability of the electrical LC circuit described by the Caputo fractional derivative

3.5. Fractional input stability of the electrical RC circuit equation described by the Riemann-Liouville fractional derivative

3.6. Fractional input stability of the electrical RC circuit equation described by the Caputo fractional derivative

4. Numerical simulations

5. Conclusion

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

Quantitative Finance and Economics

A survey comparative analysis of cartesian and complexity science frameworks adoption in financial risk management of Zimbabwean banks

Related Papers:

Abstract

1. Introduction

2. Preliminary definitions

3. Fractional input stability of the electrical circuits equations described by certain fractional derivative operators

3.1. Fractional input stability of the electrical RL circuit equation described by the Riemann-Liouville fractional derivative

3.2. Fractional input stability of the electrical RL circuit described by the Caputo fractional derivative

3.3. Fractional input stability of the electrical LC circuit described by the Riemann-Liouville fractional derivative

3.4. Fractional input stability of the electrical LC circuit described by the Caputo fractional derivative

3.5. Fractional input stability of the electrical RC circuit equation described by the Riemann-Liouville fractional derivative

3.6. Fractional input stability of the electrical RC circuit equation described by the Caputo fractional derivative

4. Numerical simulations

5. Conclusion

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog