On the complete aggregation of the Wigner-Lohe model for identical potentials

1.   Introduction

Infectious diseases are massive threat for humans and also economy of the state. Proper understanding of a disease dynamics plays an important role in curtailing of the infection in a community. Implementation of a suitable strategy against the disease transmission is another challenge. Mathematical modeling approach is one of the key tools in order to handle these challenges. A number of disease models have been developed in existing literature which enables us to explore and control the spread of infectious diseases in a better way ^[1,2,3].

Most of these models are based on integer-order differential equations (IDEs). However, in the last few years, it is noticed that fractional-order differential equations (FDEs) can be used to model universal phenomena with greater degree of accuracy and its applications can be found in virous fields for example engineering, economics, control theory, finance and in epidemiology ^[4,5]. Fractional calculus is the generalization of classical integer-order calculus. The increasing interest of using FDEs in modeling of real world complex problems is due to its various properties which are not found in IDEs. In contrast of IDEs which local in nature, the FDEs are non-local and posses the memory effects which make it more superior because in many situations the future state of the model depends not only upon the current state but also on the previous history. These features enables FDEs to model the phenomena having not only the non-Gaussian but also for non-Markovian behavior. Further, the classical IDEs are unable to provide the information in between two different integer values. Various type of fractional-order operators were introduced in existing literature to over come such limitations of integer-order derivative ^[6,7,8]. The applications of these fractional operators can be found in various fields ^[9,10,11]. In epidemiology, the previous experiences and history of the past states of an epidemic have a great impact to explored its dynamics in a better way. Additionally, due to the non-Markovian behavior of any real epidemic process, models with FDEs are more realistic and therefore, play an essential role in the understanding the spread and possible control of diseases. Some recent and interesting work regarding fractional analysis to the real life problem have been studied in ^{[12,13,14,15]}. In these work, the authors studied mathematical model with delay in fractional derivatives and presented the results for stability and bifurcation.

In Mathematical models, the transmission of a disease i.e., the progression at which susceptible become infected is known as incidence rate function. This function plays a key role in epidemiological models and ensure that the model provides an acceptable qualitative analysis of the disease under consideration. A verity of incidence rate function have been implemented in the literature ^[16,17,18]. Most commonly, in disease models the bilinear incidence rate of the type $bSI$ has been adopted, where b indicates the per unit contact rate. In 1927 Kermack and McKendrick ^[19] introduced a simple epidemic model using bilinear incidence rate and the assumptions that there are no births or deaths from the infection and each person of the population is initially susceptible to the disease. In ^[20] the authors introduced the saturated incidence after the cholera epidemic in Bari. Latter on, Korobeinikov and Maini^[20] studied the global analysis of the SIR and SIRS models with nonlinear incidence rate. Recently, a fractional order SIR epidemic model with nonlinear incidence rate has been developed in ^[21].

Keeping the above discussion in view and applicability of fractional order derivatives, in the preset investigation, we develop a fractional SIR epidemic model with generalized incidence rate function of the form $f (I)S$. The fractional derivative is considered in the Caputo and Atangana-Baleanu sense. We simulate the proposed SIR model for different values of relevant parameters and $\alpha\in(0, 1]$. Further, we provide a detail stability analysis of both disease free and endemic equilibriums of the model. The reaming sections of the manuscript are organized as: The basic definitions and relevant results are provided in section 2. Model description in Caputo case and its basic properties are presented in section 3. The stability result of the Caputo model is discussed in section in 4 and its numerical simulations and brief discussion are given in section 5. Model formulation of the ABC case and its existence and uniqueness are presented in section 6. In section 7 the iterative scheme is developed for ABC model and simulation results are presented. finally, concluding remarks are given in section 8.

2.   Preliminaries

Here some background material for the Caputo and Atangana-Baleanu fractional derivatives are presented ^[7,22,23].

Definition 2.1. Consider $h\in C^n$ be a function then the fractional Caputo derivative of order $\alpha$ is defined as:

where $\alpha\in(n-1, n)$ and $n\in \mathbb{N}$. Clearly, ${}^CD^\alpha_{t}(h(t))$ tends to $h'(t)$ as $\alpha\rightarrow 1$.

Definition 2.2. The corresponding fractional integral is described as:

In the above integral $\Gamma$ represents the Gamma function.

Definition 2.3. A fixed point $x = x^*$ is said to be the equilibrium point (or solution) of the Caputo fractional system defined by:

if and only if $\mathcal{F}(t, x^*) = 0$.

To present the stability analysis of non linear fractional system in the caputo sense via Lyapunov method we first recall the following necessary results from ^[24,25].

Theorem 2.4. Suppose $x^*$ be an equilibrium point for the system (2.1) and $\Upsilon\in \mathbb{R}^n$ be a domain containing $x^*$. Let $L:[0, \infty)\times\Upsilon$ tend to $\mathbb{R}$ be a continuously differentiable function such that

and

$\forall$ $0 < \alpha < 1$ and $x\in\Upsilon$. Where $M_1(x)$, $M_2(x)$ and $M_3(x)$ are continuously positive definite functions on $\Upsilon$, then $x^*$ is uniformly asymptotically stable equilibrium point for the system (2.1).

Definition 2.5. Let $\mathcal{F}\in H^1(b_1, b_2)$, $b_2 > b_1$, $\alpha \in (0, 1],$ then Atangana-Beleanu-Caputo (ABC) derivatives is defined as ^[7]:

The term $B(\alpha)$ represents a normalization function such that $B(0) = B(1) = 1$.

The corresponding AB integral is given as:

3.   Mathematical model and discussion

To formulate the model, the total population is represented with $N(t) = S(t)+I(t)+R(t)$, where $S(t)$ represents susceptible, $I(t)$ represents number of infected and $R(t)$ represents the number of recovered individuals. The complete model that describes a system of fractional differential equation is presented as follows

The initial condition is given by

In the model (3.1), $\Lambda$ is used for the recruitment rate, $d$ denotes the natural mortality rate in all classes and $\delta$ is disease induced death rate. Parameter $\mu_1$ shows the rate at which the infected individuals move to the susceptible class and $\mu_2$ is the transfer rate from the infected class to the recovered class. The parameter $\theta$ is the susceptibility of recovered individuals.

To start the analysis of the system (3.1), it is necessary to present the existence, uniqueness, and non-negativity of the system solution.

To make our study more effective we have assumed that $f(I)$ is to be non-negative and continuously differentiable in the interior of $\mathbb{R}_+$ and further, the same hypotheses is taken in account as in ^[26] that is, $f(I)$ is a real locally Lipschitz function on $\mathbb{R}_+ = [0, \infty)$ satisfying

(ⅰ) $f(0) = 0$ and $f(I) > 0$ for $I > 0$;

(ⅱ) $f(I)/I$ is continuous and monotonously non-increasing for $I > 0$ and $\lim_{I\rightarrow 0^+}\frac{f(I)}{I}$ exists.

It is easy to analyze from condition (ⅱ) that

Then $\int_{0+}^1 1/f(u)du = 1$ and hence assumption (ⅲ) in ^[26] is redundant. The incidence rate $f(I)$ is dependent on the concentration of infection. Furthermore, it most famous generalized forms satisfying the above hypothesis are given in the Table 1.

3.1.   Existence and positivity of the solution

This section investigates the positivity of the solution of the fractional SIR model system (3.1). Let we consider

To proceed further first we recall the generalized mean values theorem ^[34].

Lemma 3.1. Consider that $h(y) \in \mathbb{C}[a_1, a_2]$ and ${}^CD_t^\alpha h(y) \in (a_1, a_2]$, then

with $a_1\leq\Im\leq t,$ $\forall$ $t\in (a_1, a_2]$.

Corollary 3.2. Consider that $h(y) \in \mathbb{C}[a_1, a_2]$ and ${}^CD_t^\alpha h(y) \in (a_1, a_2]$, where $\alpha \in (0, 1]$, then if

The following main result is presented:

Theorem 3.3. A unique solution $y(t)$ of the system (3.1) will exists and remains in $\mathbb{R}^3_+$. Furthermore, the solution is positive.

Proof. The existence of the Caputo fractional SIR model can be shown with the help of theorem (3.1) in ^[35], while the uniqueness of the solution can be easily obtained by making use of the remark 3.2, ^[35], $\forall$ $t > 0$. In order to explore the solution non-negativity, it is necessary to show that on each hyperplane bounding the positive orthant, the vector field point $\mathbb{R}^3_+$. Form the system (3.1) we obtained

Therefore, by using the above theorem, we conclude that the solution will stay in $\mathbb{R}^3_+$

and hence biologically feasible region is constructed as:

3.2.   Equilibria and reproduction number

To obtain the equilibria of the fractional SIR model we solve the system (3.1) at the steady state we have

then the following is established:

Theorem 3.4. The proposed model (3.1) have at most two equilibria obtained as below:

1. The disease free equilibrium (DFE) expressed by ${\mathcal{E}^0} = \Big(S^0, I^0, R^0\Big) = \Big(\frac{\Lambda}{d}, 0, 0\Big)$,

2. and the endemic equilibrium (EE) expressed by ${\mathcal{E}_1} = \Big(S^{**}, I^{**}, R^{**}\Big),$

such that,

where $I^{**}$ is a positive solution of the function $H$,

By condition (ⅱ) $H$ is a strictly increasing function on $\mathbb{R}_+$. Furthermore,

$\lim_{I\rightarrow0^+} H(I) = \frac{d(d+\mu_1+\mu_2+\delta)}{\beta }-\Lambda$ and $H(\frac{\Lambda}{d}) > 0$. Therefore, $H$ has a positive zero (and only one in this case) iff $\frac{d(d+\mu_1+\mu_2+\delta)}{\beta}-\Lambda < 0$ or equivalently

The expression for the most biologically important threshold parameter known as the basic reproduction number ${\cal{R}}_0$ obtained by the next generation approach which is given as below:

where $\frac{\partial f(0)}{\partial I}$ denote partial dervative of incidence functios with respect to $I$ at disease free state.

4.   Stability of DFE

In this section we proceed to confirm the stability results in both local and global case. The corrosoponding Jacobian of (3.1) around the DFE is given as

Theorem 4.1. For any $p_1, p_2\in \mathbb{Z},$ such that $gcd(p_1, p_2) = 1$. Let $\alpha = (\frac{p_1}{p_2})$ and consider $M = p_2$, then the DFE of the system (3.1) is locally asymptotically stable $(LAS)$ if $|arg(\Pi)| > \frac{\pi}{2M}$, for all roots $\Pi$ of the characteristic equation (4.2) of the matrix $J_{\mathcal{E}^0}$.

Proof. Evaluating the determinant (4.2), we derived the below equation in term of $\Pi$.

where the coefficients are given below:

The arguments of the roots of the equation $\Pi^{p_1}+d = 0,$ are as follow:

In similar patren, if ${\cal{R}}_{0} < 1,$ then the nessarry condition fulfil for all the roots of polynomial (4.3) i.e., $|arg(\Pi)| > \frac{\pi}{2M}$. Thus the DFE is $LAS$ for ${\cal{R}}_{0} < 1$.

Theorem 4.2. For $\alpha\in (0, 1)$ and $\mathcal{R}_0 <1$ then the DFE, of the fractional $SIR$ model (3.1) is globally asymptotically stable (GAS) and unstable for $\mathcal{R}_0 > 1$.

Proof. To confirm the $GAS$ around the DFE, we formulate the suitable Lyapunov function as:

Calculative the time fractional derivative of the above function $\mathcal{L}(t)$ we obtain

Utilizing system (3.1) we get

Clearly once $\mathcal{R}_0 < 1$ then ${}^CD_t^\alpha \mathcal{L}(t)$ is $-ve$, and hence, by result (2.4), we ensure that the DFE, $\mathcal{E}^0$ is $GAS$ in $\Phi$.

4.1.   Global stability of endemic case

Here, we investigate the global stability of the endemic equilibrium of the fractional SIR model (3.1). At the steady state of the model (3.1) we obtained

Theorem 4.3. If $\mathcal{R}_0 > 1$ and with condition (4.10) satisfy, then the endemic equilibrium of the system (3.1) is globally asymptotically stable.

Proof. We define the following Lyapunov function

The differentiation of $\mathcal{V}(t)$ with the solution of (3.1) is

By direct calculations, we have

After some arrangement we have

It follows from the property arithmetic mean and we have

and if

then it ensures that the model given by (3.1) at the EE case is $GAS$ when ${\cal{R}}_0 > 1$ and with the condition (4.10) satisfied.

5.   Numerical results for the Caputo model

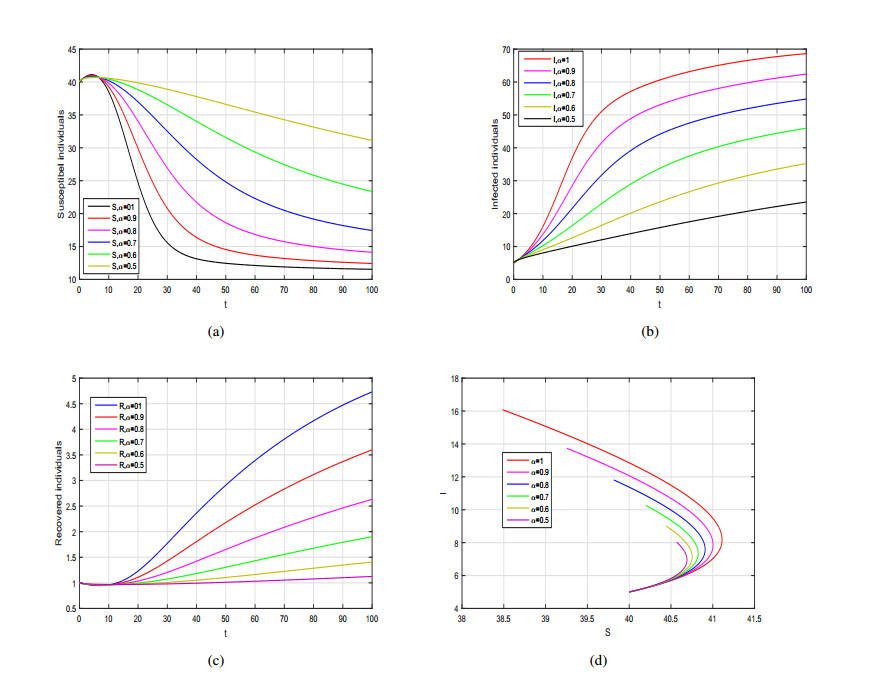
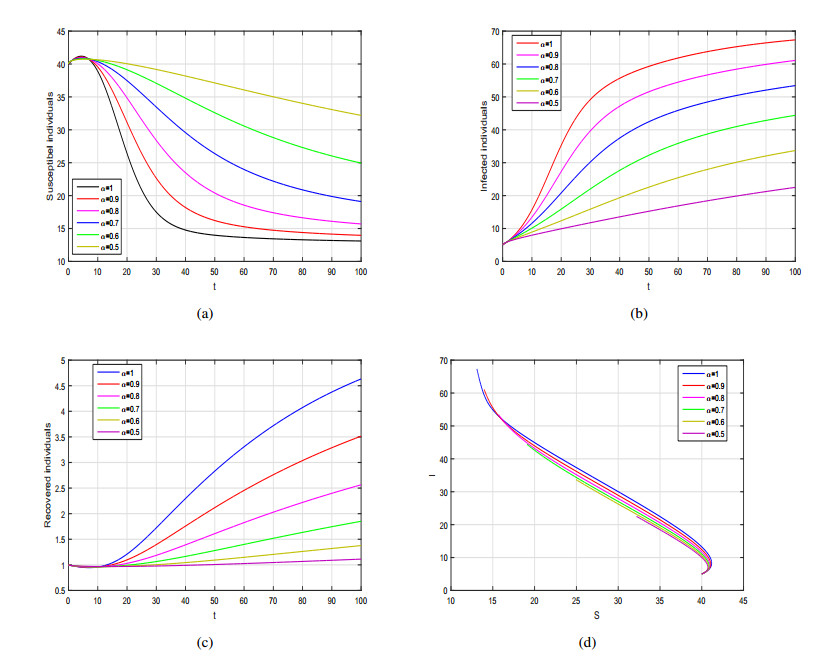
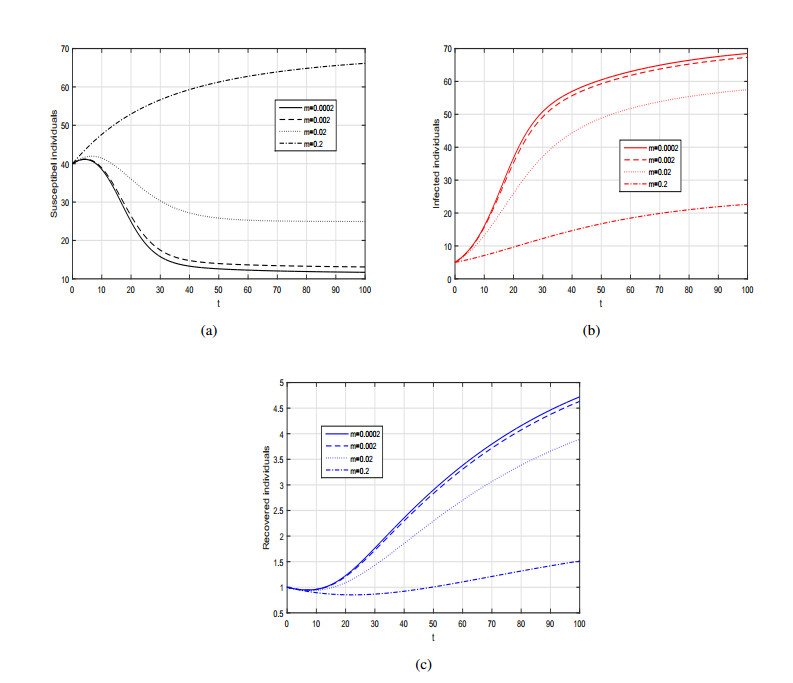
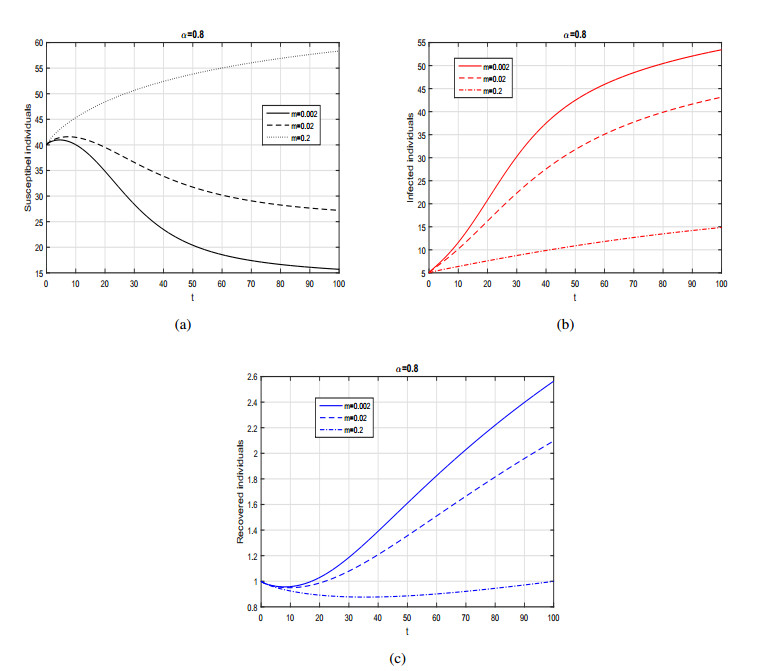
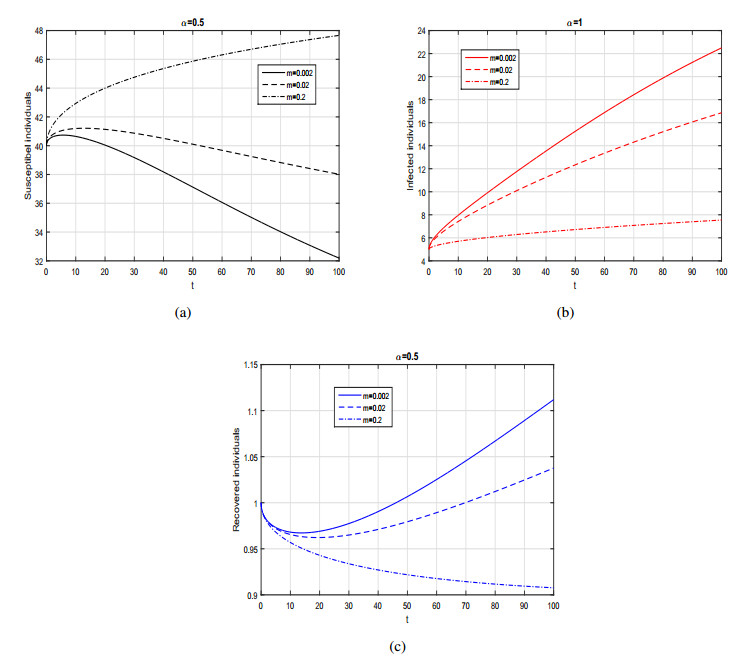
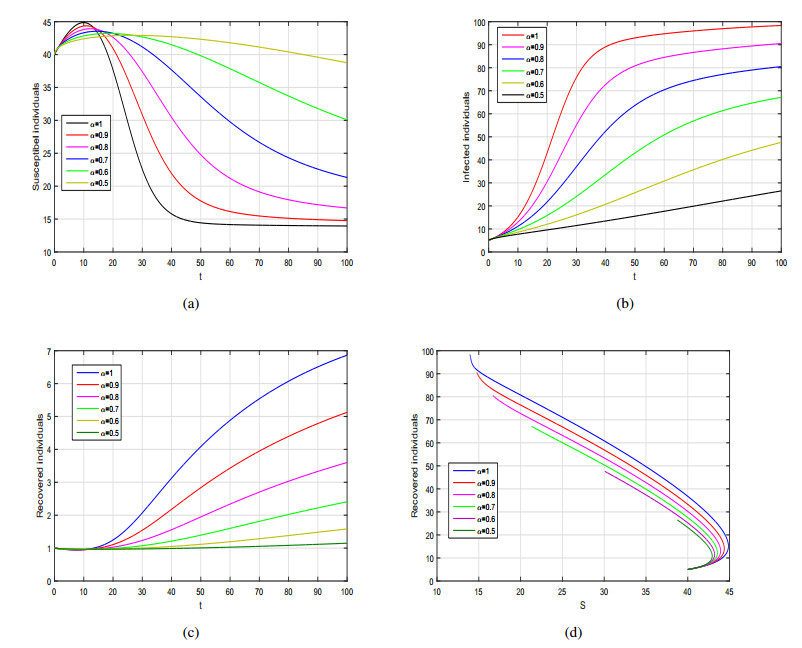
In the current section, we investigate the numerical results of the Caputo SIRS model given by system (3.1) with general incidence rate. The model in each case is solved numerically using predictor corrector of molten type technique. In order to perform the numerical experiment and analyze the importance of incidence function on disease dynamics we assign different incidence rate to the generalized incidence function $f$ and simulate the model with various fractional values of $\alpha$. The parameter values considered in the numerical solution for the fractional SIRS model are depicted in each Figure caption. Initially, we consider the incidence rate $f$ in the form as a bilinear incidence rate i.e., $f(S, I) = \beta S I$ and obtain the graphical results in sub-plots (a-c) of Figure 1, while in sub-plot (d), we depicted the phase portrait analysis of the model variables. We can observed that the by decreasing the fractional order $\alpha$ the population in suspectable class is increasing whereas the population of infected and recovered classes is decreasing sharply. The graphical dynamics of the model (3.1) for various values of $\alpha$ with non-linear incidence function is shown in sub-plots (a-c) of Figure 2. The corresponding phase portrait analysis in this case is depicted in sub-plot (d) of Figure 2. The influence of parameter $m$ (the half saturation constant) for different values of $\alpha = 1, 0.8, 0.5$, is shown in Figures 3, 4 and 5 respectively. We can see that population in the infected class is decreasing sharply with the increasing values of $m$. The influence of $m$ is more significant biologically for fractional order of ABC operator rather than integer case. Finally, the dynamics of the Caputo model (3.1) with Beddington-DeAngelis incidence function with various fractional order $\alpha$ of the derivative are depicted in Figure 6. The corresponding phase portrait analysis in this case is presented in sub-plot (d) of Figure 6. These graphical interpretations explore the importance of the fractional derivative to the proposed model where one can see the behavior of the model for any non-integer case.

6.   Model formulation in Atangana-Baleanu framework

In this part of the paper we reconstruct the proposed model using the generalized fractional operator known as Atangana-Baleanu-Caputo (ABC) derivative in order to explore the dynamics of the model in more better way. The model in ABC sense is given by the following system

with some appropriate nonnegative inial conditions. Before to analyze the dynamics of fractional model (6.1), first we study the existence and uniqueness od the model in the following theorem.

6.1.   Existence and uniqueness of the solution

We apply the fixed point theory in order to explore the existence and uniqueness of the solution of fractional model (6.1). To do this we firstly re-write the system (6.1) in the following form:

The vector $u(t) = (S, I, R)$ and $G$ in the system (6.2) represent the state variables and a continuous vector function respectively defined as follows:

with the initial condition by $u_0(t) = (S(0), I(0), R(0))$. Furthermore, the $G$ satisfies the Lipschitz condition given as:

To confirm the existence and uniqueness for the solution of system (6.1) with fractional order, we proceed as in the following theorem.

Theorem 6.1. The exists a unique solution of the SIR epidemic model (6.1) if the below condition holds:

Proof. On applying the ABC fractional integral to both sides of the model (6.2), we get the non-linear Volterra integral equation:

Consider $J = (0, \mathcal{T})$, and $\Xi:\mathcal{C}(J, \mathbb{R}^3)\rightarrow \mathcal{C}(J, \mathbb{R}^3)$ stated as

Eq (6.5) becomes:

The supremum norm on $u$ denoted by $\|.\|_J$ and is defined as:

Clearly, $\mathcal{C}(J, \mathbb{R}^3)$ with the norm $\|.\|_J$ construct a Banach space. Further, the following inequality fulfil

with $w(t)\in \mathcal{C}(J, \mathbb{R}^3)$, $\mathcal{H}(t, \zeta)\in \mathcal{C}(J^2, \mathbb{R})$ such that

Applying result in (6.7), we have

Furthermore, taking in account equations (6.3), (6.9) and triangular inequality, we have:

Finally, we derived the following expression

where,

The operator $\Xi$ is known as a contraction if it follows the condition in equation (6.4). Hence, the solution of the model (6.2) will also has a unique solution.

7.   Numerical scheme of the ABC model

Here firstly, we obtain the iterative scheme for the system (6.1). The approach developed in ^[36] is applied in order to approximate the ABC integral. To proceed further, using the fundamental theorem on the system (6.2), we obtained

At $t = t_{m+1}$, $m = 0, 1, 2, ...,$ we have

Utilizing the interpolation polynomial approach, the function $G (\zeta, u(\zeta))$ can be approximated over $[t_j, t_ {j + 1}]$:

Equation (7.2) becomes:

On further simplifications we finally arrived the approximate solution as below:

Hence, for the presented fractional system, we have the following recursive formulae:

7.1.   Simulation

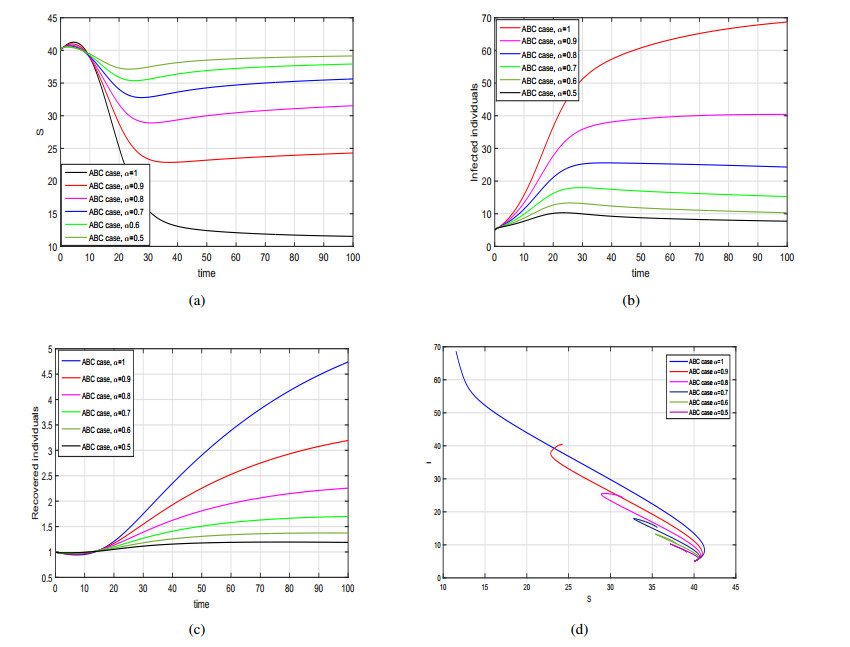
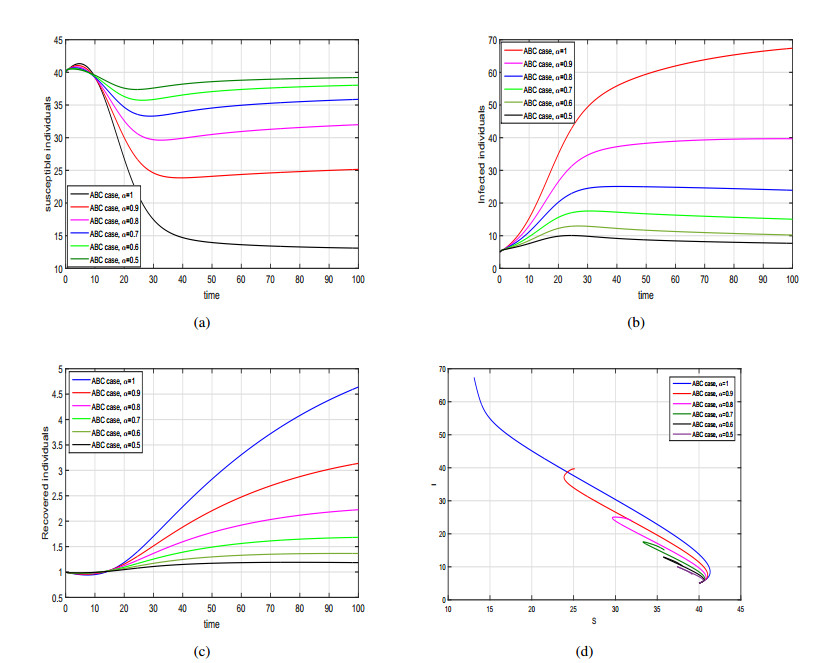
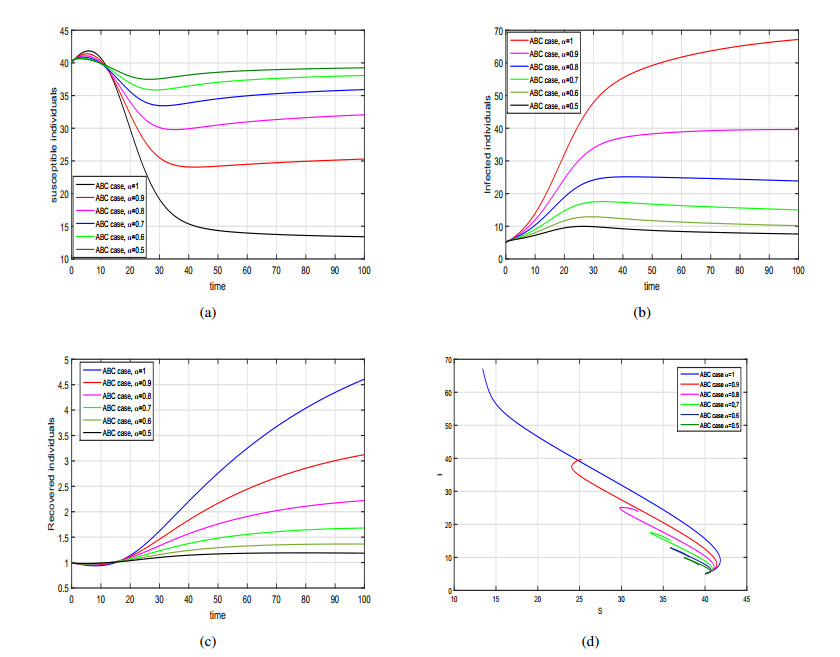
Based on numerical scheme derived in (7.6), we present the graphical results of the proposed ABC fractional model (6.1) in Figures 7–9. To analyze the influence of fractional order and incidence function on the disease dynamics and control we simulate the ABC SIRS model (6.1) with different incidence rates as in Caputo case. In Figure 7, we have shown the dynamics of the model by taking bilinear incidence rate in account. The graphical behavior of the model with nonlinear saturated incidence rate and for different values of $\alpha\in(0, 1]$ is analyzed in Figure 8. Finally, the graphical results of fractional SIRS model by incorporating Beddington-DeAngelis type incidence function for various values of $\alpha$ are depicted in Figure 9.

From the graphical analysis, we observed that the population in infected class decrease significantly by decreasing the fractional order and the disease endemic state move to disease free state in each case. Further, from the graphical results of ABC model reveal that this operator is more helpful to explore the model dynamics and provide biologically more feasible results in compression with Caputo case.

8.   Conclusion

In this paper, we analyzed the dynamics of a fractional SIR model with nonlinear generalized incidence rate. Initially, we formulated a general SIR model by apply the Caputo derivative. The local and global stability for the fractional SIR model are obtained and discussed in detailed. It is shown that the model at the disease free case is locally asymptotically stable when the basic reproduction number less than 1. Further, we obtain that the fractional SIR model at the disease free case is globally asymptotically stable for the case of basic reproduction number less than 1. We used fractional Lyapunov function for the proof of the global stability of the disease free case and also we proved by defining the fractional Lyapunov function for the proof of the global stability of the endemic equilibrium when the basic reproduction number greater than 1. Numerical results with various values of the fractional order parameter are obtained and discussed in detailed by choosing some different type of incidence functions. Since the Caputo fractional operator has singular kernel and can not explore the crossover behavior of some biological phenomena. Therefore, we further reformulated the proposed model using ABC derivative having nonsingular and nonlocal kernel. The existence and uniqueness of the ABC model is proved via Picard-Landelof approach. An efficient numerical scheme is used to carried out the iterative solution of the model and perform various simulation results r to analyzed the role of different incidence function in disease dynamic and control. These results indicates that the fractional order model in ABC case is more beneficial and important than that of the ordinary integer order model.

Conflict of interest

All authors declare no conflict of interest in this paper.