Abbreviations: CCS: carbon capture and storage; CO2: carbon dioxide; EJ: exajoule (1018 joule); EROI: energy return on investment; EU: European Union; EV: electric vehicle; FF: fossil fuel; GHG: greenhouse gas; Gt: gigatonne (109 tonne); GW: gigawatt (109 watt); HFCV: hydrogen fuel cell vehicle; HVAC: heating, ventilation and air conditioning; IAEA: International Atomic Energy Agency; ICEV: internal combustion engine vehicle; IEA: International Energy Agency; IPCC: Intergovernmental Panel on Climate Change; Mt: megatonne (106 tonne); MW: megawatt (106 watt); NG: natural gas; OECD: Organization for Economic Cooperation and Development; OPEC: Organization of the Petroleum Exporting Countries; p-km: passenger-kilometre; RE: renewable energy; SUV: sports utility vehicle; TWh: terawatt-hour (1012 watt-hour); v-k: vehicle-km; V2G: vehicle-to-grid
1.
Introduction
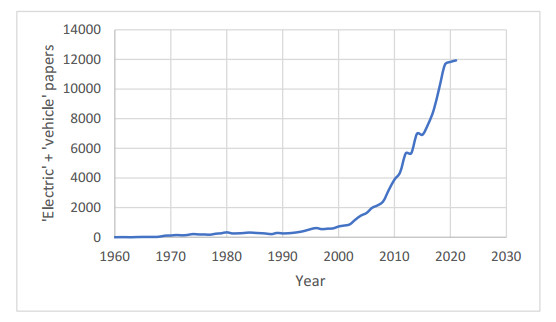
Electric vehicles (EVs) have a history stretching back more than a century. After being eclipsed by internal combustion engine vehicles (ICEVs) early in the 20th century, they experienced brief revivals with electric milk floats in the UK in the 1930s and 1940s, and in the US (particularly California) in the 1990s [1]. Now, however, many transport researchers see EVs as here to stay. Figure 1 shows papers in the Scopus database with the words 'electric' + 'vehicles' in the title, abstract, or keywords. Annual articles increased after year 2000, with a sharp rise over the past decade or so. Scopus articles with the word 'vehicles' in the title, abstract, or keywords also rose rapidly after 2000, but the ratio of the two rose even faster, from about 7% in 2000 to 18.2% in 2021. The global EV fleet has exhibited a similar rise, from 50,000 in 2010 to 11.3 million in 2021 [2].
The reasons for the present popularity of EVs among consumers are easy to understand. Governments in many countries, including all the world's major economies, have enacted policies to encourage the purchase of electric vehicles (EVs). Inducements include rebates on EV purchases, and waiving of fuel taxes, road tolls and even parking fees [2]. Table 1 shows that the leading nations for EVs as a percentage of all new car sales are from OECD countries, mainly European, although China leads in total EV sales. The two leading countries have very high shares of non-fossil fuel (FF) electricity, but others with high non-FF shares, such as Canada and Korea, have much lower EV sales.
A recent report [3] forecast that, globally, EVs of all types, including buses and heavy commercial vehicles, will reach 229 million as early as 2027. The International Energy Agency (IEA) 2021 forecasts are smaller, with the total global EV fleet numbering between 139 and 227 million by year 2030, and cars accounting for nearly 90% of this total [2]. Another forecast for 2030 sees EVs accounting for 30% of the global car fleet [4]. Even the Organization of the Petroleum Exporting Countries [5] forecast that EVs will form around 35% of the global car fleet by year 2045.
Leading car manufacturers have likewise invested heavily in an EV future. Globally, by 2021, around 370 light duty EV models were available on the market [2]. EV sales in 2021 were about 5.5 million, and car manufacturers have a target of 40 million by year 2030 [7]. Some like Tesla, were new entries into the car market. According to the IEA [2], the majority of these models were sports utility vehicles (SUVs).
This emphasis on EVs has been further helped by the decision of many governments to phase out the sale of internal combustion engine vehicles (ICEVs) in a decade or two [8,9,10]. Presently, the other main competitors to EVs are natural gas fuelled vehicles and liquid biofuels. Despite both presently having a larger share of the transport fuel market than electricity (which, incidentally, also powers electric rail systems) [11], they will disappear as transport fuels if ICEVs are scrapped. For liquid biofuels, a decline in global energy share may have already started [6].
Hydrogen fuel cell vehicles (HFCVs) are also electric drive, and so, like EVs, have zero air pollution exhaust emissions and do not use oil. HFCVs have been considered as serious competitors to EVs, but by mid-2021 the global HFCV fleet numbered only around 40,000 vehicles [12], less than 0.5% of the EV fleet. The key reason for the success of EVs has been the provision of abundant recharging stations. By 2020 the world had 1.3 million public charging stations, considering both slow and fast public chargers. Their number had risen seven-fold in the space of only five years [2]. Not only did hydrogen refuelling stations globally total only around 530 in 2020, but the ratio of HFCVs to refuelling stations is steadily rising, presenting a further obstacle to HFCV uptake [12].
This review has the following structure. Section 2 discusses the criteria used to select articles for discussion. The key benefits claimed for EVs, improved energy efficiency, energy security and climate change mitigation, are discussed in Sections 3 and 4. Other undoubted benefits, if modest, are engine exhaust air pollution and engine noise reductions. However, EVs do not avoid the other serious challenges facing all road passenger travel. These are all assessed in Section 5. Section 6 puts the assessment of EVs in a wider context, examining the feedback effects likely from EV purchase and use, and the alternatives to private vehicular transport. Section 7 offers a brief conclusion.
The main findings from this review are that the present energy and GHG savings from EVs are contested with different studies reporting conflicting conclusions. Further, given the short time remaining for effective action on climate change, EVs are unlikely to appreciably reduce transport's contribution, because it will take decades for renewable energy (RE) to be the dominant energy source. Also, EVs, in common with other passenger transport vehicles, produce a variety of serious environmental harms. Instead, vehicular transport itself will need to be greatly reduced for climate stabilisation and environmental sustainability in general.
2.
Methods used for this review
Figure 1 has shown that papers published annually on EVs now run at around 12,000 annually, and a large proportion of these are relevant to one or more aspects of EV energy use, greenhouse gas (GHG) emissions, or other environmental effects. Clearly, a choice has to be made. Accordingly, more recent papers were favoured, particularly those published after the outbreak of the current pandemic in early 2020. Some of the topics covered are non-controversial, such as the oil savings from a switch to EVs (globally, only 2.8% of electricity is generated from oil, although decades ago it was a major input fuel [6]). Where the published literature indicated differences of opinion, representative papers from both sides of the controversy were consulted and discussed, as is the case for the global potential for RE, and the energy and climate change benefits of EVs. Also, many papers on EVs are focused on one particular country, or only on one or another aspect of EVs such as their impact on GHGs or air pollution. This review recognizes that climate change from energy consumption is a global problem, requiring globally-based solutions.
The review also briefly considers the comparative effects of EVs and conventionally-fuelled vehicles on a variety of other environmental criteria. The justification for their inclusion is, as explained in Section 4, that at least some of these, such as exhaust air pollution emissions, can be expressed in energy terms, by calculating the energy costs of their removal. This approach is often used for the energy costs of climate change mitigation, for instance by carbon capture and sequestration (CCS). It thus enables a fairer comparison of RE sources with FF sources, and EVs with ICEVs.
Finally, global statistical data on energy supply and its composition were sourced from BP [6] and the IEA [11]. Data and projections also relied heavily on IEA publications for EVs [2] and HFCVs [12]. For the latest science on climate change, the latest report of the Intergovernmental Panel on Climate Change (IPCC) [13] was used.
3.
Electric vehicles: Comparative energy use
Energy efficiency is one of the key reasons for official support for EVs [14]. Of all the comparisons that can be made between EVs and ICEVs, the energy savings advantages (or otherwise) of EVs, even when calculated on a vehicle-km (v-k) basis for a given ICEV and the equivalent EV model, are contested. This section first critically reviews the published literature on comparative energy efficiency, while the next section covers the related subject of comparative GHG emissions, although it is not always easy to separate the two issues, as most publications deal with both.
Several recent publications are available for comparison of relative energy consumption of EVs and ICEVs. For Alberta in Canada, Doluweera et al. [15] reported higher energy efficiency for EVs, but the energy costs for EVs are not converted to primary energy terms, and only cover operating energy. As shown in the next section on comparative GHG emissions, embodied energy costs must also be considered. This 'well-to-wheels' was used by Michaelides [16], who concluded: 'When the electricity is generated from both conventional and renewable sources, the overall efficiency of EVs is comparable to those of conventional IC-powered vehicles'. Zhang and Fujimori [17] even concluded that: 'The results showed that transport electrification without the replacement of fossil-fuel power plants leads to the unfortunate result of increasing emissions instead of achieving a low-carbon transition'.
An important variable to consider for both energy and GHG comparisons is climate. As Yuksel et al. [18] have reported, based on their study of regional differences in EV energy use in the US: 'However, temperature has an important effect on vehicle efficiency due to heating, ventilation, and air conditioning (HVAC) use and temperature related battery efficiency effects'. For ICEVs with their low thermal efficiency, sufficient waste heat is available for heating the interior of the vehicle. EV batteries have much higher conversion efficiency, so that in regions with cold winters, an additional source of heating energy is needed, such as propane or by use of a heating, ventilation and air conditioning (HVAC) system. The authors further reported on research that use of HVAC can increase EV energy use by 24% in cold climates, and lower driving range. Based on earlier research by Archsmith et al. [19], they concluded that 'temperature can have as large an effect on electric vehicle charging emissions as regional grid mix'. For Japan, Liu et al. [20] found that for EVs: 'The most economic energy efficiency was achieved in the range of 21.8–25.2 ℃.'
The fuel efficiency of EVs can be further improved. Shaffer et al. [9] have advocated making EVs lighter as a means of improving both their energy efficiency and safety. They pointed out that the present heavy batteries mean that EVs weigh more than their ICEV equivalents, offsetting any efficiency gains from electric drive. Developing lighter battery packs are thus a top priority. Lovins [21] has stressed the importance of also reducing tractive load, which will reduce the size of the battery pack. However, improving energy efficiency is not restricted to EVs; ICEVs also still have significant room for energy improvement [10].
So far, the analysis has been based on the current energy situation. However, several difficulties will become increasingly serious as RE increases its share of electricity production. One problem with comparing relative energy use is that ICEVs are powered by heat engines, whereas EVs are powered by electricity provided from a battery. If the electricity for EVs was solely provided from FF or nuclear power stations there is no problem: simply compare the primary energy used per kilometer of travel (MJ/v-k). The difficulty arises when EVs are at least partly powered from primary electricity sources, mainly hydro, PV solar and wind power [22]. The two key references for energy statistics account for primary electricity in different ways. The IEA [11] convert such electricity on a 1:1 basis. In contrast, BP [6] convert these non-thermal electricity forms by dividing the electricity produced by 0.38, the average efficiency of thermal power stations. The consequence is that the calculation of EV energy efficiency by these two methods will produce increasingly divergent answers as the share of RE in electricity production rises. At present, the differences are not significant, and in any case, do not affect GHG comparisons.
A further difficulty arises as RE becomes the dominant energy source, not only for electricity production but for all energy. First, intermittent RE, mainly wind and solar, will necessarily be the main energy sources in a nearly 100% RE future [23,24]. Because of their intermittent nature, energy storage will be needed. This storage could take the form of large battery systems, compressed air stored underground, pumped water storage (if available), or compressed hydrogen stored in underground caverns [25]. With energy storage, the following conversion steps are now involved in providing electricity to EV motors:
Each conversion step involves energy losses and use of conversion devices, with their embodied energy.
With no need for energy storage, the energy conversion chain would be simply:
In other words, the need to store (some of) the intermittent RE electricity, as for example, compressed air in underground caverns, and later reconvert to mains electricity would not be needed. The need for energy storage will be even higher when all energy, not just electricity, is from RE, as increasing energy conversion will be needed to cater for non-electric energy uses. Interestingly, if compressed hydrogen was used as storage, it could be directly used in HFCVs, avoiding the need for conversion to mains electricity and then to battery chemical energy. This might seem to suggest that in a nearly 100% RE future, HFCVs should be favoured over EVs from an energy efficiency viewpoint. However, HFCVs would also need vehicle interior heating in cold climates. Further, as discussed later, vehicle-to-grid (V2G) technology could potentially raise EV energy efficiency. This option is not possible for HFCVs. As already discussed, EVs won favour because of the ubiquity of mains electricity, and thus recharging points.
The published literature is deeply divided on such important questions as the energy return on investment (EROI) for RE sources, their future costs, their global potential, and the date when a largely RE future is possible [26]. Included among optimistic researchers are Jacobson [27], Davis et al. [28], Fthenakis et al. [29], those expressing a more pessimistic view about general RE potential include Seibert and Rees [30], Moriarty and Honnery [22,31,32,33], and Nieto et al. [34], while de Blas et al. [35] express their doubts specifically about 'The limits of transport decarbonization under the current growth paradigm'. The differences of opinion are unlikely to be resolved any time soon. However, despite the urgency to more away from FFs and three decades of IPCC reports, RE in 2019 still only accounted for 14.1% of global energy (including non-commercial fuel wood), not much above the 12.1% in 1973 [11].
The above analyses assume the various non-FF sources of electricity all presently exhibit zero carbon emissions. But climate forcing from RE sources can even overlap with that from NG-based electricity [36,37]. One reason is that material inputs for RE per TWh output are often far larger than for FF power plants [38]. The IEA [39] further reported that: 'A typical electric car requires six times the mineral inputs of a conventional car […]'. There are large environmental costs of mining these material inputs, but these often occur in countries remote from the high EV ownership countries given in Table 1. Lawton [40] titled his article on this 'Net zero's dirty secret'. For ecological sustainability, the energy costs of restoring the environment to its original state should be included in the analysis [31].
If these ecosystem maintenance energy costs were included in assessing the net green energy output from RE sources, the EROI for RE sources would fall, because the input energy costs of providing net green energy would rise. As EROI values for RE fall, dynamic energy considerations become important. As shown in [26,41,42], to rapidly raise RE share of global energy, output energy from RE plants will be increasingly needed as energy inputs to construct new RE plants, leaving less energy to power the economy. The monetary costs of RE sources will also rise, impacting on transport energy costs and thus travel volumes. Furthermore, generally lower EROI values for RE could mean that the global technical energy potential for RE sources is much less than usually thought, given that EROI values must be greater than unity, perhaps appreciably greater [32].
The above discussion has suggested that the energy savings of EVs are, at present, marginal at best, at least in cold climates needed vehicle heating. Unfortunately, this condition applies to most of the world's EVs (see Table 1). However, some papers focusing on comparative GHGs, discussed in the next section, suggest otherwise. Whether EVs are presently more or less energy efficient than equivalent conventional vehicles depends on climate and annual km travelled. In future, if most energy is supplied by RE, the situation is far less clear, depending as it does on the primary energy calculation method and the degree to which energy storage from intermittent is needed.
4.
Electric vehicles: Comparative climate change mitigation
The main message from recent publications on climate change is that it is happening now, as evidenced by the recent spate of unprecedented floods, wildfires and heatwaves around the globe [13,43,44]. Lenton et al. [43] have warned of climate tipping points, while Ripple et al. [44] have argued that climate change is now best seen as an emergency. Time is running out for effective action.
EVs are also widely thought to have an important role to play in combatting climate change from transport [45,46]. As Fatih Birol, the head of the IEA, stated: 'While they can't do the job alone, electric vehicles have an indispensable role to play in reaching net-zero emissions worldwide' [2]. EVs can only play an important role in mitigating climate change (CC) if electricity is predominantly from non-carbon sources. For the world overall, non-FF sources accounted for 38.7% of electricity generation in 2020, but was usually higher in Europe.
However, the higher value in Europe is partly the result of nuclear power use [6], which is being phased out in a number of European Union (EU) countries. It may be that global nuclear output will decline in the coming decades from its 2020 level of 10.1% of global electricity production. One reason is that the global reactor fleet is aging, so that much new reactor construction will be needed to merely replace closed reactors [47]. This value is already well below its peak share of 17.5% in 1996% [6]. Even the International Atomic Energy Agency (IAEA) in their 2020 report stated that: 'In the low case, nuclear electrical generating capacity is projected to gradually decline by about 10% until 2040 and then rebound, resulting in only a 7% reduction by 2050' [48]. Any downturn in nuclear output will hinder the growth in the share of non-carbon sources in electricity.
EVs use only a minor share of global electricity: the IEA [2] forecast that their projected total EV fleet numbers will only raise their share from its present one percent to two percent in 2030. Nevertheless, Zhao et al. [49] have reported potential undesirable effects on Chinese electric grids as EV numbers rise.
A number of analyses have been done comparing CO2 emissions from EVs with those from equivalent conventional vehicles. The results will, of course, vary from grid to grid, depending on the energy mix used for electricity generation, so no general definitive answer can be given. Nevertheless, for Europe, Dillman et al. [50] 'found a subset of countries across the EEA where there is a potential that EVs could lead to greater life-cycle GHG emissions than a comparable diesel counterpart'. Lifetime distance is also important, since, according to Hawkins et al. [51]: 'In contrast with ICEVs, almost half of an EV's life cycle GWP is associated with its production'. They estimated 87–95 gm CO2-eq/km for EV production compared with only 43 gm CO2-eq/km for ICEVs. For European grids, they found, for example, a 10–24% decrease in global warming potential compared with ICEVs, assuming vehicular lifetime travel of 150,000 km. Ager-Wick Ellingsen et al. [52] also showed that the greenhouse gas (GHG) emission advantage for EVs over ICEVs was reduced because of their greater production energy costs. Hence GHG emissions can overlap for both vehicle types, especially at lower lifetime vehicle km. On the other hand, Xu et al. [53] found that for Europe, controlled unidirectional charging and V2G technology could by themselves reduce vehicle GHG emissions (and presumably also energy use) by between 4% and 11% in year 2050.
Energy and climate change comparisons from outside OECD countries sometimes present a different picture. The potential importance of both climate and electricity mix is evidenced by a Brazilian study. Teixeira and Sodré [54] modelled the savings in both energy use and GHGs from replacing ICEVs by EVs, and found that CO2 emissions from EVs can be as much as 10–26 times lower than that of ICEVs. Even allowing for the fact that the share of non-FF in the Brazilian electricity mix was over twice the world average (86% compared with 39% in 2020 [6]) their findings suggest very substantial savings from such a switch.
Qiao et al. [55] examined full life cycle GHG emissions in year 2015 in China. For an EV and a similarly matched ICEV, they found that total emissions over a 150,000 km lifetime travel distance were about 41.0 tonne CO2 equivalent, 18% lower than those of an ICEV. This is significant, since China's share of non-FF in its electricity mix, although increasing, was less than the global average in 2020 (about 34% compared with 39% [6]).
It is evident that in countries like Norway and Sweden, with nearly all their electricity generated from low-carbon sources (Table 1), that the GHG savings from EVs will be very significant. But, as already mentioned, a global approach is needed for climate change mitigation. What if Norway's exports to neighbouring countries is reduced because of increased electricity use for the growing EV fleet? Importing countries will then have less RE electricity available, and ceteris paribus, RE electricity share in these countries will fall.
5.
EVs and transport: General environmental challenges
As a number of researchers have made clear [eg., 56, 57], climate change is not the only environmentally-related crisis Earth's inhabitants must resolve soon. Environmental problems relevant to all vehicular transport, including EVs, are covered in Section 5.1. They are included in this review, not only to give a fuller picture of EVs compared with conventional vehicles, but because it is at least theoretically possible to calculate the energy costs of, for example, eliminating tail pipe emissions from ICEVs, to enable fairer comparison. Air pollution, especially in cities, is an additional important driver for government policies favouring EVs, and is covered in detail in Section 5.2.
5.1. General environmental problems facing private vehicles
Private car transport, regardless of propulsion type, needs vast areas for roads, car parks, driveways and service stations. Akbari et al. [58] have shown in the case of metropolitan Sacramento, California, covering around 800 km2, 'the total paved surfaces (roads, parking areas, side-walks) are about 310 km2, or some 39%. Heavy traffic also causes community disruption. One important cause of the Urban Heat Island (UHI) effect is paved surfaces replacing natural vegetation; paved surfaces suppress the cooling effect of evapotranspiration from such vegetation [59]. The road and parking space needs of EVs are evidently the same as those for more conventionally-powered vehicles.
In wilderness areas, intrusion of roads presents a different problem. Laurance and Arrea [60] have stressed that by 2050, an extra 25 million km of roads are planned. Even today, there are few wilderness areas not near roads—even the Amazon had 100,000 km of roads by 2013 [61]. These roads not only cause millions of animal and bird fatalities each year, but also present barriers to wildlife movement, and edge effects for both flora and fauna species [62]. Night-time light pollution can also affect wildlife; Marshall [63] titled his paper: 'Light is leaking into vital habitats', and this light can change animal lifecycles. Münzel1 et al. [64] have documented its adverse effects on human health, and Nadybal et al. [65] have shown that these ill-effects disproportionately affect lower-income communities in the US.
A variety of other specific environmental challenges face all types of private transport. According to World Health Organization (WHO) statistics, in recent years some 1.3 million persons were killed in road traffic collisions, with tens of millions injured at varying degrees of severity [66]. The majority of these fatalities occur in low- or middle-income countries, and disproportionately involve pedestrians and cyclists. In high-income countries, the risk of such accidents may deter such modes, especially cycling.
Traffic noise is by far the leading source of noise pollution in Europe, with adverse effects on the cardiovascular system, mental health, and sleep disorders [67]. Such adverse health effects will occur if traffic noise levels exceed roughly 50 decibels [68]. Even prolonged exposure at lower levels causes severe annoyance to residents living near busy roads. Traffic noise will also adversely affect urban wildlife.
EVs will of course eliminate engine noise, but road/tyre and air friction noise are the same as for ICEVs. For both vehicle types, the effects rise with speed. Also, noise from both vehicle horns and radios will be the same. The lower overall noise level for EVs, will help reduce noise pollution's adverse effects mentioned in the previous paragraph, but according to Senecal and Leach [10], it may decrease the safety of non-motorised road users, such as pedestrians. Paradoxically, the overall relative quietness of EVs will especially be a problem in mixed EV/ICEV traffic as is presently the case today, and will be for decades to come. Under high ambient noise levels, Karaaslan et al. [69] found a 30% higher traffic safety risk for pedestrians from EVs.
Another environmental challenge for road travel in colder climates arises from the use of salt for de-icing roads [70], which not only damages adjacent vegetation, but also road infrastructure such as bridges. The runoff also pollutes streams. A further damaging effect of road runoff has been found in the North West US, where coho salmon deaths in urban rivers have been traced to a chemical used in tyre manufacturing to prevent ozone damage [71]. Khare et al. [72] have also found that asphalt pavements themselves are the source of 'secondary organic aerosol precursors.'
Wear from car tyres is not the only chemical pollution problem that all vehicles produce. Most arise in the disposal of cars (and their batteries) at the end of their life, as in 2017 all transport globally consumed nearly 11 Gt of materials [73]. Plastic is an important constituent of vehicles, including tyres, and plastic contamination is already a global problem [74]. Morse [75] has stressed the environment risks posed by the many millions of used Li battery packs resulting from rising EV use. Skeete et al. [76] have stressed the technical and economic difficulties in recycling high-voltage lithium-ion batteries.
5.2. Vehicle air pollution
As already discussed, a number of countries and many of the world's leading metropolises, have pledged to phase out ICEV sales. To what extent would overall air pollution be cut, especially in cities? Vehicle tailpipe emissions would fall to zero—a clear benefit, particularly for countries with high tailpipe emission levels. However, Guttikunda et al. [77] found that for four Indian cities, transport only contributed between 14% and 26% of all PM2.5 emissions in those cities. Nevertheless, for China, Guo et al. [78] found some correlation between particulate pollution level and EV sales. Further, Ma [79] has reported on the equity implications: urban particulate emissions are persistently higher in minority neighbourhoods.
Tailpipe emissions are only part of the total emissions load from road vehicle operation; others include particulate emissions from tyre wear and brake linings, and re-suspension of road dust caused by moving vehicles. Together, they can account for up to 90% of all vehicle-related particulates [80]. Those from EVs may be greater than for the equivalent ICEVs, because tyre and brake lining wear are proportional to vehicle mass, which is greater for EVs because of the battery pack [81]. According to Timmers and Achten [82]: 'As a result, total PM10 emissions from EVs were found to be equal to those of modern ICEVs. PM2.5 emissions were only 1–3% lower for EVs compared to modern ICEVs'. Liu et al. [19] found slightly higher PM10 and PM2.5 emission levels for EVs if regenerative braking was not used. Tyre wear rises for both higher speeds and for acceleration/deceleration [83].
Also, Hawkins et al. [51] used a life cycle analysis to show that the indirect environmental effects of EV manufacture could be significant. For example, freshwater and terrestrial ecotoxicity, human toxicity, and mineral resource depletion impacts were more than three times greater for EVs than for equivalent ICEVs. However, photochemical oxidation formation was greater for ICEVs. Bicer and Dincer [84] found similar results.
6.
Discussion
So far, it has been assumed in the discussion on energy use and emissions that EV ownership leaves annual driving distance unchanged. However, all transport is subject to various spill-over effects, such as ‘energy rebound’ and ‘moral licensing’. Energy rebound can occur when an improvement in vehicle energy efficiency (or provision of subsidies) lower fuel costs and accordingly increases travel km, a result found by Klöckner et al. [85] for EVs in Norway. A more recent paper by Hasan and Simsekoglu [86] also found evidence of induced travel by EV owners in Norway, which they attribute to lower operating costs.
Moral licensing, according to Dütschke et al. [87] ‘assumes that past morally positive behaviour increases the probability that people will subsequently show potentially less moral behaviour’, but the opposite effect has also been observed. Huwe and Essner [88] found that for a German sample, EV ownership is associated with a 23% reduction in travel, although they caution against generalising the results. On the other hand, the popularity of SUV models among EV purchasers suggests that moral licensing may already be at work. Such SUVs will need more materials for their manufacture and larger batteries, which will lead to higher demands for materials, and the attendant recycling problems. Overall, EV purchasers may presently be more environmentally conscious than ICEV purchasers, but this effect may disappear as EV ownership becomes more mainstream. Only time will tell.
EVs are increasingly popular with the motoring public, industry, and governments of OECD countries because they offer the prospect of a technical solution to the many problems facing private car travel. Technical solutions are preferred by governments and the vehicle industry because they deflect attention from the problems of excess mobility, and are an excellent fit to the requirements of growth-oriented market economies. Also, unlike some other proposed technological panaceas, such as bioenergy with CCS, or fusion energy, millions of EVs are actually on the world’s roads.
However, we need to examine the global, not just national, consequences of EVs on travel (see e.g., Henderson [89] and Sovacool et al. [90]). Rapid adoption of EVs by OECD countries—and China—will signal to the rest of the world the perception that private car travel can continue as the dominant form of surface passenger travel, and that, because of minor air pollution and GHG benefits, can pass as ‘green transport’.
It is also necessary to allow for future uncertainty, as exemplified by the changes produced by the unexpected covid-19 pandemic. Zhang and Zhang [91] looked at potential travel energy reductions in an urban Chinese context possible in a post-pandemic world, including measures such as working from home. The concluded that: ‘The arrival of the post-COVID world may contribute to an 11% reduction in CO2 emissions by 2060, while the maximum reduction potential could be as high as 44%’.
Wanitschke and Hoffmann [92] examined three options for road transport in a German context: EVs, ICEVs and hydrogen fuel cell vehicles. They found that all three options ‘face irreducible, conceptual, and ignorance-affected uncertainty’, and concluded that: ‘It seems thus strategically useful to keep all technological options open to stay adaptive to unforeseeable developments’. Senecal and Leach [10] arrived at a similar conclusion by a different set of arguments. They pointed out that ICEVs still have significant untapped efficiency potential, and further that the choice of vehicle type will depend on the region. Interestingly, they considered hybrid vehicles to be the best option.
So far, discussion in this review has focused on comparing EVs with ICEVs, but these two types of transport far from exhaust the possible options. One important alternative is to greatly lower vehicular travel levels, especially in high-mobility countries. In 1900, global vehicular travel per capita was only an estimated 100–150 passenger-km (p-k) annually. By 2018, this value (which includes all surface modes plus air travel) had risen to over 6300 p-k, of which nearly 60% was by private passenger vehicles [36]. Growth in global p-k per capita was even about seven times faster than growth in real global product per capita. John Adams [93] used the term ‘hypermobility’ to describe this huge growth in motorised travel. At present, car ownership—and vehicular travel in general—are much skewed globally: car ownership at the national level varies by around 100-fold [62], roughly mirroring income inequality. Any catch-up by presently low car-ownership countries will soon lead to the marginal environmental benefits of EVs being swamped.
Given the environmental problems besetting all road transport, and the extraordinary growth in personal mobility discussed above, we need to focus more on what purpose hypermobility actually serves, and far less on largely ineffectual attempts to green its image. As argued in an earlier paper [62], what is needed is a significant reduction in vehicle km—regardless of propulsion source—particularly in the high travel countries of the OECD, a point also stressed by Milovanoff et al. [94].
Policies needed include a reversal of present transport modes priority, giving priority to non-motorised modes (walking and cycling), with public transport favoured for remaining vehicular transport. Possible measures to encourage such a shift include closing inner city areas to traffic, parking restrictions, and reductions in road vehicular speed limits. Such measures would increase the convenience of alternative modes compared to private car travel, and should lead to lower levels of vehicular travel overall, which will reduce the entire suite of transport’s environmental problems discussed earlier in this paper.
7.
Conclusions
The key findings from this review are as follows. At present, primary energy and GHG emission reductions from EVs are contested, with estimates dependent on assumptions regarding electricity energy mix, battery type, vehicle mass, and lifetime km. It is important that future research more tightly constrain the comparative energy costs for EVs and ICEVs, by standardising comparisons. Also, RE will likely take decades to be the dominant energy source, meaning it cannot help in reducing GHG emissions in the short term. Nevertheless, it is true that a global shift to EVs will eliminate vehicle exhaust emissions, and greatly reduce oil imports, thus enhancing energy security. As Delannoy et al. [85] have argued, continuing oil consumption at present levels will soon lead to rising oil prices as EROI levels fall.
On the other hand, another important finding is that all road vehicles, electric or not, cause serious environmental damage in other areas. Further, for traffic casualties and air pollution resulting from vehicles (not just exhaust emissions), the costs fall disproportionately on lower-income communities. What is needed is deep reductions in vehicular travel, regardless of propulsion type. Promotion of EVs is at best a distraction from the many environmental challenges facing transport.
Acknowledgments
The author declares no financial support was provided for this research.
Conflict of interest
The author declares no conflict of interest.









 DownLoad:
DownLoad:





